Towards the Automatic Creation of Optimized Classifier Ensembles
Julius Voggesberger
1 a
, Peter Reimann
1,2 b
and Bernhard Mitschang
1 c
1
Institute for Parallel and Distributed Systems, University of Stuttgart, Universit
¨
atsstr. 38, Stuttgart, Germany
2
Graduate School of Excellence advanced Manufacturing Engineering,
University of Stuttgart, Nobelstr. 12, Stuttgart, Germany
Keywords:
Classifier Ensembles, Classifier Diversity, Decision Fusion, AutoML, Machine Learning.
Abstract:
Classifier ensemble algorithms allow for the creation of combined machine learning models that are more
accurate and generalizable than individual classifiers. However, creating such an ensemble is complex, as
several requirements must be fulfilled. An expert has to select multiple classifiers that are both accurate and
diverse. In addition, a decision fusion algorithm must be selected to combine the predictions of these classifiers
into a consensus decision. Satisfying these requirements is challenging even for experts, as it requires a lot
of time and knowledge. In this position paper, we propose to automate the creation of classifier ensembles.
While there already exist several frameworks that automatically create multiple classifiers, none of them meet
all requirements to build optimized ensembles based on these individual classifiers. Hence, we introduce and
compare three basic approaches that tackle this challenge. Based on the comparison results, we propose one of
the approaches that best meets the requirements to lay the foundation for future work.
1 INTRODUCTION
Classification algorithms make it possible to automate
decision making and to cast predictions by extracting
insights from data. However, often a single classifica-
tion model is not sufficient for the task at hand. The
reasons can be manifold: Small data sets that may lead
to overfitting, data sets with high dimensionality, or
the underlying task is too complex for a single classi-
fier, which results in inaccurate predictions (Dietterich,
2000; Polikar, 2006; Hirsch et al., 2019; Wilhelm et al.,
2020; Hirsch et al., 2023).
For such tasks, a classifier ensemble can be used
to achieve more accurate results. Ensembles have the
advantage of being less sensitive to noise and gen-
eralizing better to new, unseen data (Polikar, 2006;
Dietterich, 2000). Ensemble algorithms train multiple
classifiers and combine their predictions with decision
fusion algorithms to reach a consensus decision. The
goal is to achieve more accurate predictions in com-
parison to a single classifier (Polikar, 2006; Kuncheva,
2004; Dietterich, 2000). To this end, the classifiers
should be diverse in their predictions, i. e., they should
make both errors and correct predictions for different
a
https://orcid.org/0000-0003-4808-1922
b
https://orcid.org/0000-0002-6355-4591
c
https://orcid.org/0000-0003-0809-9159
data instances (Hansen and Salamon, 1990; Dietterich,
2000; Brown et al., 2005).
However, creating an ensemble for a given clas-
sification task is not straightforward. First, a set of
classifier algorithms has to be selected and their hyper-
parameters have to be optimized. Thereby, the training
and optimization has to result in a set of not only accu-
rate, but also diverse classifiers (Hansen and Salamon,
1990; Dietterich, 2000). Second, another challenge
is to select a decision fusion algorithm and its hyper-
parameters to ensure that the ensemble prediction is
more accurate than the predictions of its single clas-
sifiers. Both the optimization of the classifiers and
the decision fusion algorithm are complex and require
expert knowledge and time (Wilhelm et al., 2023).
A possible solution to these challenges, i. e., to re-
duce the amount of knowledge and time needed for
the ensemble creation, is the use of Automated Ma-
chine Learning (AutoML) (Z
¨
oller and Huber, 2021;
He et al., 2021). AutoML frameworks are used to au-
tomatically create optimized machine learning models,
requiring minimal user interaction so that even novice
users can utilize machine learning. However, currently
no existing AutoML framework solves all challenges
for creating an ensemble. Current frameworks opti-
mize classifiers w. r. t. their accuracy, but not their
diversity. Furthermore, pre-selected decision fusion
Voggesberger, J., Reimann, P. and Mitschang, B.
Towards the Automatic Creation of Optimized Classifier Ensembles.
DOI: 10.5220/0011988800003467
In Proceedings of the 25th International Conference on Enterprise Information Systems (ICEIS 2023) - Volume 1, pages 615-622
ISBN: 978-989-758-648-4; ISSN: 2184-4992
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
615

algorithms are often used and optimizing the decision
fusion algorithm is rarely considered.
In this position paper, we address the above-
mentioned challenges by introducing three approaches
to automatically create an optimized classifier ensem-
ble. The approaches create a set of classifiers that is
optimized in terms of classifier diversity and classifica-
tion performance, while the decision fusion algorithm
is optimized w. r. t. classification performance to fur-
ther increase the ensemble accuracy. We discuss and
compare these approaches regarding specific require-
ments, e. g., regarding the complexity of the configura-
tion space from which an optimal classifier ensemble
has to be selected. We use the comparison results to
identify the approach that best meets the requirements.
The rest of the paper is structured as follows: Sec-
tion 2 introduces the problem statement and the re-
quirements for an automatic creation of classifier en-
sembles. Related work of the paper is discussed in Sec-
tion 3. The three proposed approaches to the ensemble
creation problem and their comparison are discussed
in Section 4. Lastly, Section 5 concludes the paper and
discusses directions for future work.
2 PROBLEM STATEMENT
In this section, the problem of creating an optimized
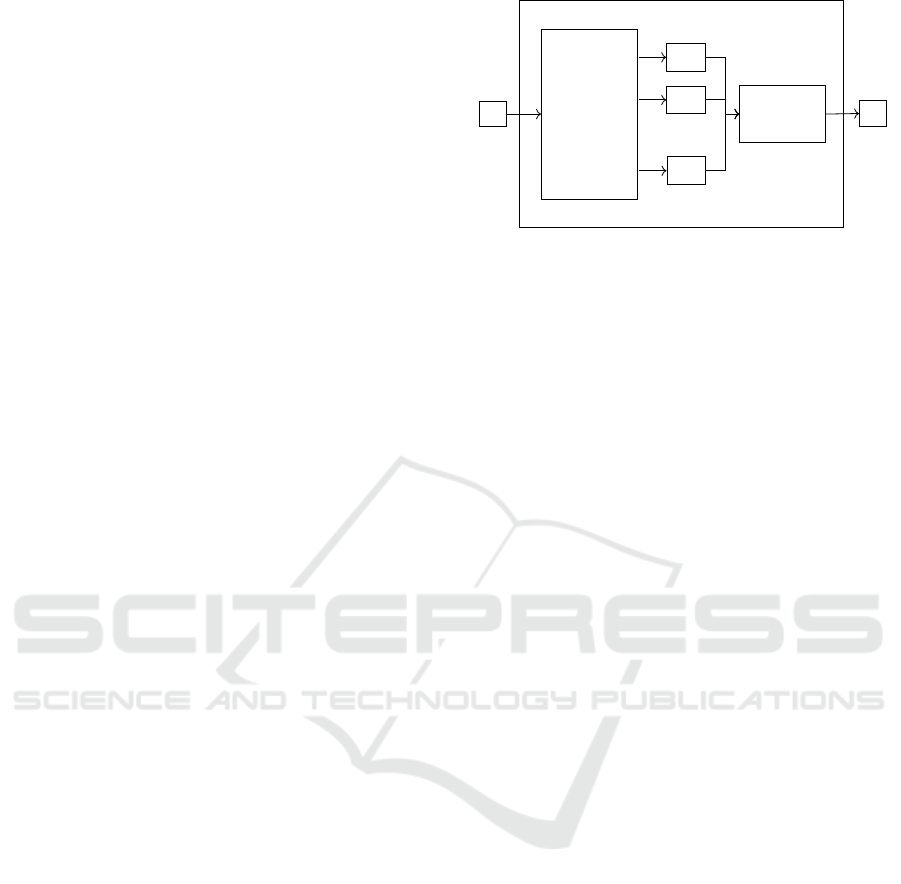
classifier ensemble is described. As shown in Figure 1,
a classifier ensemble consists of a set of classifica-
tion models (i. e., classifiers) and a decision fusion
algorithm which combines the predictions of the clas-
sifiers into a consensus prediction. In the following,
we discuss requirements for the ensemble creation so
that the resulting ensemble is able to make accurate
predictions:
R1: Classification Performance The first require-
ment in the creation of an ensemble is the classification
performance. If the individual classifiers have a clas-
sification performance better than random, a higher
performance can be achieved for the ensemble (Hansen
and Salamon, 1990).
R2: Classifier Diversity The second requirement
is the classifier diversity. In the context of ensem-
bles, high classifier diversity means that individual
classifiers make both errors and correct predictions
for different data instances (Polikar, 2006; Kuncheva,
2004). Several classifiers that have high diversity thus
complement each other w. r. t. their correct predictions,
so that a decision fusion algorithm may reduce the
overall error. As a consequence, having high diver-
sity leads to a higher classification performance of the
ensemble. In addition, it increases the generalization
x
i
Ensemble
Set of
Classifiers
y
i,1
y
i,2
.
.
.
y
i,k
Decision
Fusion
y
i
Figure 1: Representation of an ensemble. The input x
i
is a
data instance, y
i, j
are the predictions of the individual classi-
fiers and the output y
i
is the combined ensemble prediction.
capability of the ensemble, as the risk of overfitting
is reduced by compensating for individual errors (Po-
likar, 2006). Two kinds of methods exist to generate
diversity: Implicit and explicit methods (Brown et al.,
2005). Implicit methods induce diversity by manipu-
lating the training processes of the classifiers, e. g., by
using different feature subsets for each classifier. Ex-
plicit methods instead optimize the classifier diversity
directly, e. g., by utilizing diversity measures.
R3: Decision Fusion Optimization The decision
fusion algorithm has to be selected in such a way that
the resulting classification performance and general-
ization is high (Polikar, 2006). This results in a second
optimization problem that has to be solved in addi-
tion to the optimization of the individual classifiers.
Multiple decision fusion algorithms exist that employ
different combination strategies in order to derive a
consensus decision from the diverse predictions of the
individual classifiers. They can be divided into three
groups: utility-based, evidence-based and trainable
algorithms (Wilhelm et al., 2021). Utility-based algo-
rithms heuristically combine the classifier predictions
without using any prior information, e. g., via a major-
ity voting scheme. Evidence-based algorithms make
use of prior information about the classifiers, i. e., its
evidence, to combine their predictions. Usually, the
classifier performance is used as evidence, e. g., the
accuracy on a validation data set. Trainable algorithms
train a decision fusion algorithm by using predictions
of the classifiers as training data. Furthermore, stacked
generalization (Wolpert, 1992) can be seen as a kind
of trainable decision fusion algorithm.
R4: Automatic Optimization The last require-
ment is that the ensemble has to be created automat-
ically, i. e., with minimal user interaction. As such,
the above requirements have to be fulfilled automat-
ically, e. g., by using an AutoML approach to create
and optimize the ensemble.
ICEIS 2023 - 25th International Conference on Enterprise Information Systems
616

3 RELATED WORK
In this section, we discuss literature related to the au-
tomatic creation of classifier ensembles. We first re-
view literature that deals with ensembles, decision
fusion and diversity, followed by an analysis of exist-
ing AutoML frameworks. Table 1 gives an overview
of the key findings.
3.1 Ensemble Algorithms
The most prominent ensemble algorithms are boost-
ing (Schapire, 1990) and bagging (Breiman, 1996), in
particular their representations AdaBoost (Freund and
Schapire, 1997) and Random Forest (Breiman, 2001).
Random Forests consist of a diverse set of decision
trees. Here, diversity is induced by using bootstrap
samples for training. i. e., the individual decision trees
are trained with different subsets of the training data.
Thus, the classification performance of each tree is
optimized w.r.t. its data subset. The predictions of the
decision trees are aggregated using majority voting or
averaging.
AdaBoost, as a prominent example for boosting
algorithms, trains a diverse set of classifiers itera-
tively. In each iteration, the training data instances
are reweighted according to the errors of the classi-
fier trained in the previous iteration in order to reduce
the classification error. The decision fusion is accom-
plished by using a weighted averaging scheme over
the individual classifiers.
Both algorithms use fixed decision fusion algo-
rithms and thus do not consider finding an optimal one.
Thus, automatic optimization is neither performed for
the decision fusion algorithms nor for the individual
classifiers. Furthermore, bagging does not explicitly
optimize diversity and instead assumes that randomly
changing the training data via bootstrapping is suffi-
cient to induce implicit diversity. On the other hand,
AdaBoost does explicitly optimize its classifier diver-
sity by reweighting the training data. This however
entails that the classifiers have to be trained sequen-
tially and that the resulting ensemble tends to overfit
on noisy data (Dietterich, 2000).
Some of the more recent literature focuses on
the creation of ensembles through the use of multi-
objective optimization. Examples are multi-objective
ensemble generation (MEG) (Moussa et al., 2022) or
ensembles for imbalanced data (Wegier et al., 2022).
The latter method uses multi-objective optimization
to optimize the weights of the majority voting fusion
w. r. t. precision and recall. However, the set of classi-
fiers is not optimized, no further decision fusion meth-
ods are considered, and diversity is only implicitly in-
duced. MEG, on the other hand, uses multi-objective
optimization to explicitly optimize the ensemble w. r. t.
both diversity and classification performance (Moussa
et al., 2022). However, the pool of available classifiers
and decision fusion methods is highly limited to only
four classification algorithms with 15 hyperparameter
variations and to four decision fusion methods.
A framework that allows for optimizing decision
fusion algorithms is PUSION (Wilhelm et al., 2023).
While PUSION enables the automatic selection of the
best performing decision fusion algorithm, it does
not optimize their hyperparameters. Furthermore,
PUSION assumes that a sufficiently diverse set of clas-
sifiers already exists.
3.2 AutoML
Automated Machine Learning (AutoML) denotes the
automated creation of a machine learning model for
given data within a given budget (Feurer et al., 2015).
The goal of an AutoML framework is to solve the prob-
lem of searching for an algorithm and its hyperparam-
eters that minimize a loss function L . This problem
is formalized as the ”Combined Algorithm Selection
and Hyperparameter optimization” (CASH) problem
(Thornton et al., 2013):
λ
∗
∈ argmin
λ
j
∈Λ
L (λ
j
, D
train
, D
valid
). (1)
Here, Λ is a configuration space consisting of ma-
chine learning algorithms and their hyperparameters.
Each point λ
j
in this space is a configuration, i. e., an
algorithm and its assigned hyperparameters. Then,
λ
∗
∈ Λ is the optimal algorithm and its optimal hyper-
parameters w. r. t. the loss function.
Several existing AutoML frameworks tackle the
CASH problem, but only a few of them create en-
sembles, e. g., Auto-sklearn (Feurer et al., 2015),
H2O (LeDell and Poirier, 2020), ESMBO (Lacoste
et al., 2014), Bayesian Optimization for Ensembles
(L
´
evesque et al., 2016) and AutoGluon-Tabular (Er-
ickson et al., 2020). However, they do not consider
optimizing diversity explicitly, but instead assume that
using different algorithms and hyperparameters leads
to sufficiently diverse ensembles. Furthermore, most
of them use preselected decision fusion algorithms and
therefore do not consider optimizing them. H2O is the
only AutoML framework that optimizes the decision
fusion algorithm, but it restricts the set of possible de-
cision fusion algorithms to stacked generalization (Vil-
lanueva Zacarias et al., 2021).
Towards the Automatic Creation of Optimized Classifier Ensembles
617

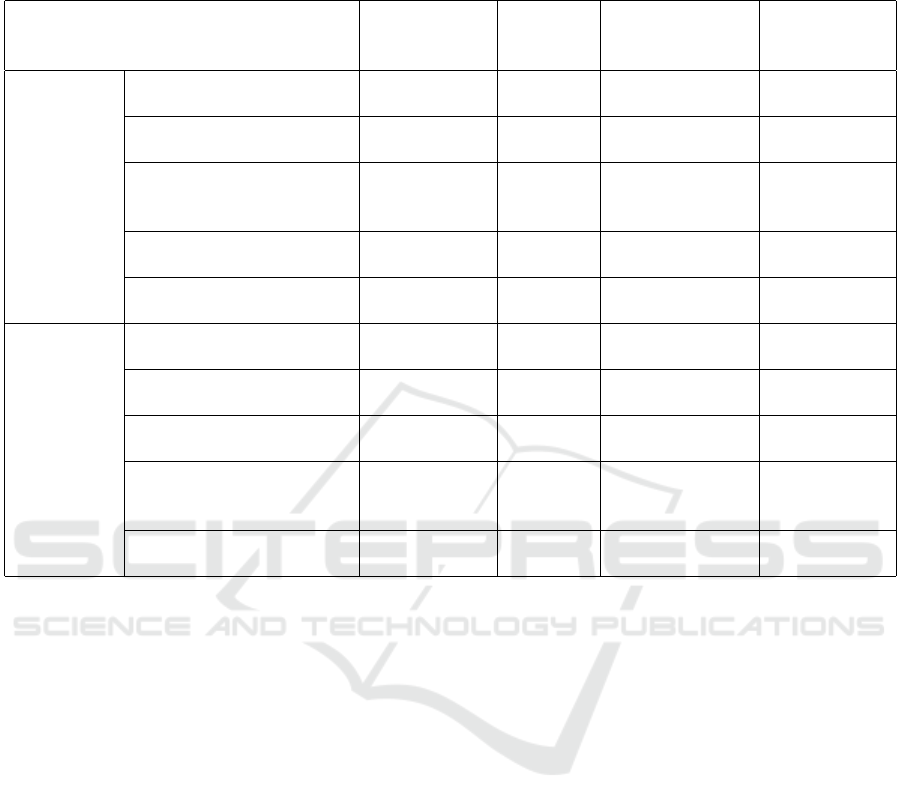
Table 1: Comparison of related work by requirements for automatically creating an ensemble. If a method fulfills a requirement,
a tick 3 is written, a tick in braces ( 3 ) means that the method partially fulfills the requirement, and a cross 7 denotes that a
requirement is not met.
Methods
R1:
Classification
Performance
R2:
Classifier
Diversity
R3:
Decision Fusion
Optimization
R4:
Automatic
Optimization
Ensemble
Algorithms
Bagging
(Breiman, 1996)
3 (3) 7 7
Boosting
(Schapire, 1990)
3 (3) 7 7
Ensemble for
Imbalanced Data
(Wegier et al., 2022)
3 (3) (3) 7
MEG
(Moussa et al., 2022)
3 (3) (3) (3)
PUSION
(Wilhelm et al., 2023)
7 7 (3) (3)
Automated
Machine
Learning
Auto-Sklearn
(Feurer et al., 2015)
3 (3) 7 3
H2O
(LeDell and Poirier, 2020)
3 (3) (3) 3
ESMBO
(Lacoste et al., 2014)
3 (3) 7 3
Bayesian Optimization
for Ensembles
(L
´
evesque et al., 2016)
3 (3) 7 3
AutoGluon-Tabular
(Erickson et al., 2020)
3 (3) 7 3
4 OPTIMIZATION PROBLEM
The discussion in the previous section shows that none
of the existing frameworks allows the automatic cre-
ation of ensembles that optimize both their diversity
and decision fusion. Therefore, we investigate basic
approaches to address these problems. We propose
three approaches that extend AutoML to not only op-
timize several classifiers w. r. t. classification perfor-
mance, but also regarding classifier diversity. These
approaches are capable of automatically optimizing
decision fusion algorithms and their hyperparameters.
In the following, we introduce and compare the
three approaches according to the requirements de-
fined in Section 2. The requirements R1 and R3 are
not discussed in detail, as they are solved by all ap-
proaches in a similar way. To compare the approaches
in terms of their ability to create diverse classifiers,
the requirement R2 is split into two parts: Creating
diversity implicitly and explicitly. Finally, the require-
ment R4 for automatic optimization of the ensemble
is compared according to the configuration space com-
plexity of an approach. The higher the complexity of
a configuration space, the more resources, e. g., time
and memory, are needed to find an optimal ensemble
configuration. A summary of the comparison is given
in Table 2.
4.1 Combined Configuration Space
In this approach, the ensemble is viewed as one unit
which allows to formulate the problem defined in Sec-
tion 2 as a single optimization problem (see Figure 2a)
with one configuration space. This entails that the
components of the ensemble, i. e., the individual clas-
sifiers and the decision fusion algorithm, are optimized
together. Thus, the configuration space of the optimiza-
tion problem consists of both the classification algo-
rithms for all individual classifiers and the decision
fusion algorithms.
To fulfill the requirements specified in Section 2,
the loss function for the AutoML problem must be
modeled to include both a metric for classification per-
formance and an explicit metric for classifier diversity.
Another method to increase classifier diversity with-
out using explicit diversity metrics is to use implicit
ICEIS 2023 - 25th International Conference on Enterprise Information Systems
618

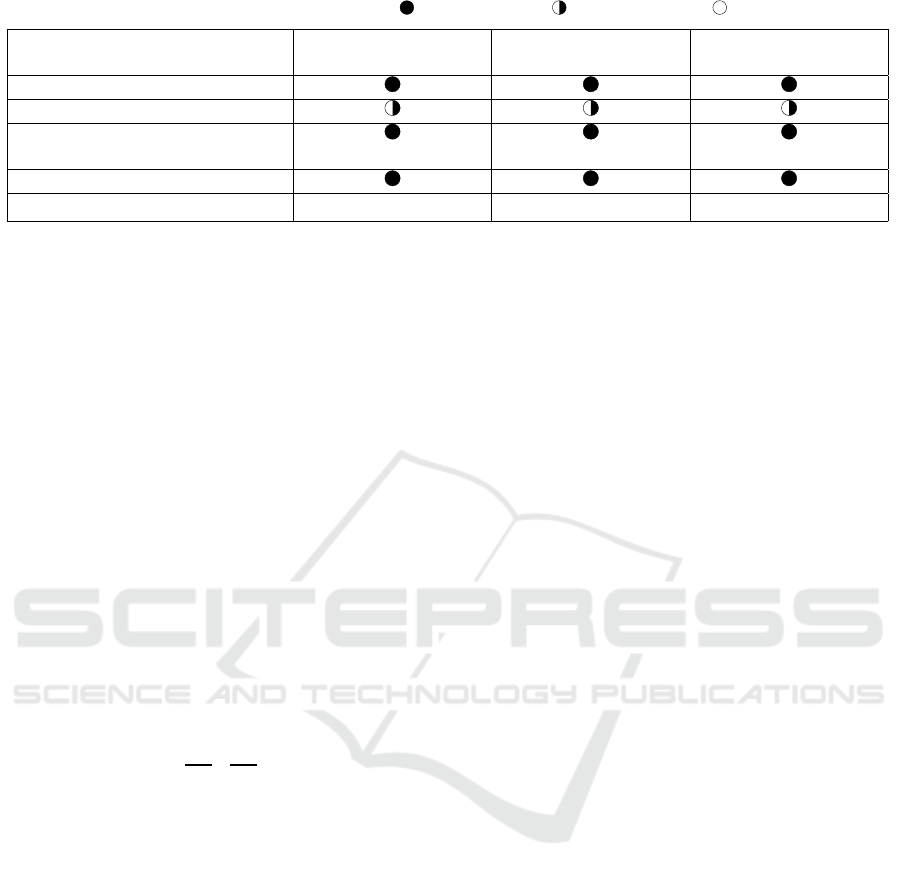
Table 2: Comparison of the presented solutions. = fully supported, = partly supported, = not supported.
Combined
Configuration Space
Separated
Configuration Space
Simplified
Configuration Space
Classification Performance
Implicit Diversity
Explicit Diversity
(via Loss Function) (via Loss Function) (via Model Selection)
Decision Fusion Optimization
Configuration Space Complexity O(

|Λ|
k

· |Γ|) O(

|Λ|
k

+ |Γ|) O(|Λ| + |Γ|)
diversity methods. This can be done by extending
the configuration space with data transformation algo-
rithms for each classifier, such as bootstrapping or a
random subspace method (Tin Kam Ho, 1998), with
the drawback of increasing its complexity. Note that
this extension is also possible for the following ap-
proaches.
Since the creation of an ensemble is viewed as a
single optimization problem, each point in the configu-
ration space must represent an ensemble configuration.
Hence, each ensemble configuration has to consist of k
classifiers and one decision fusion algorithm – where
k is the ensemble size. The optimization problem is
then to search for one ensemble configuration that
minimizes the loss function. It is necessary that all k
classifier configurations are selected simultaneously,
since the decision fusion algorithm can only be trained
using a set of classifiers. As such, the configuration
space CS must consist of the cross product of k classi-
fier configuration spaces Λ and of one decision fusion
configuration space Γ:
CS = Λ × · · · × Λ
| {z }
k times
×Γ. (2)
As the order of the classifiers in the ensemble is
not relevant, there are

|Λ|
k

possible classifier combi-
nations for an ensemble of size k , with |Λ| being the
size of a single classifier configuration space. With the
addition of the decision fusion algorithm, this results
in a final complexity in O(

|Λ|
k

· |Γ|) . Using this kind
of configuration space, we can select the ensemble that
exhibits the best overall performance.
To illustrate the complexity, we assume a simple
scenario with a configuration space consisting of three
classification algorithms (e. g., decision tree, kNN,
Random Forest) and two decision fusion algorithms
(e. g., majority voting, decision template).Assuming
that there are ten possible hyperparameter assignments
for each classification algorithm and five for each de-
cision fusion algorithm, we get |Λ| = 3 · 10 = 30 and
|Γ| = 2 · 5 = 10 possible configurations. If we now
want to create an ensemble of size k = 5 , the size of the
combined configuration space is

|Λ|
k

· |Γ| =

30
5

· 10 ,
which are around 1.5 million possible configurations.
4.2 Separated Configuration Space
In the second approach, the optimization of the de-
cision fusion algorithm is considered as a separate
problem, i. e., independent from the classifier set op-
timization (see Figure 2b). Thus, the configuration
space has a lower complexity, while it is still possible
to evaluate multiple ensemble configurations. To this
end, the classifier set has to be optimized first, fol-
lowed by the decision fusion in a separate step. Here,
each classifier set configuration consists of k individ-
ual classifier configurations. These are then evaluated
w. r. t. classifier performance and diversity. In the
subsequent optimization, multiple ensemble configura-
tions, i. e., combinations of classifier set and decision
fusion configurations, are evaluated. This can be done
by iterating over the previously evaluated classifier
set configurations and performing the decision fusion
optimization for each of these configurations.
The creation of classifier diversity is the same as
in the first approach, since one configuration in the
configuration space is still a set of k classifiers. Conse-
quently, they are optimized w. r. t. classification perfor-
mance and explicit diversity so that the same diversity
creation methods apply.
On the other hand, the complexity of this approach
decreases compared to the first approach, since the
decision fusion optimization is viewed as a separate
optimization problem. This results in two configu-
ration spaces: One for the classifier set and one for
the decision fusion. The configuration space for the
classifier set optimization is the same as for the first
approach, but without Γ , i. e., the complexity is in
O(

|Λ|
k

) . For the decision fusion optimization, the con-
figuration space then consists only of the algorithms
in Γ , i. e., its complexity is in O(|Γ| ). The overall com-
plexity is then the sum of the complexities of both
individual configuration spaces.
Adapting the example of Section 4.1 for this ap-
proach, we get

|Λ|
k

=

30
5

= 142 506 as the number of
possible configurations for the classifier set optimiza-
tion and ten possible configurations for optimizing the
decision fusion algorithm. Thus, the resulting configu-
Towards the Automatic Creation of Optimized Classifier Ensembles
619

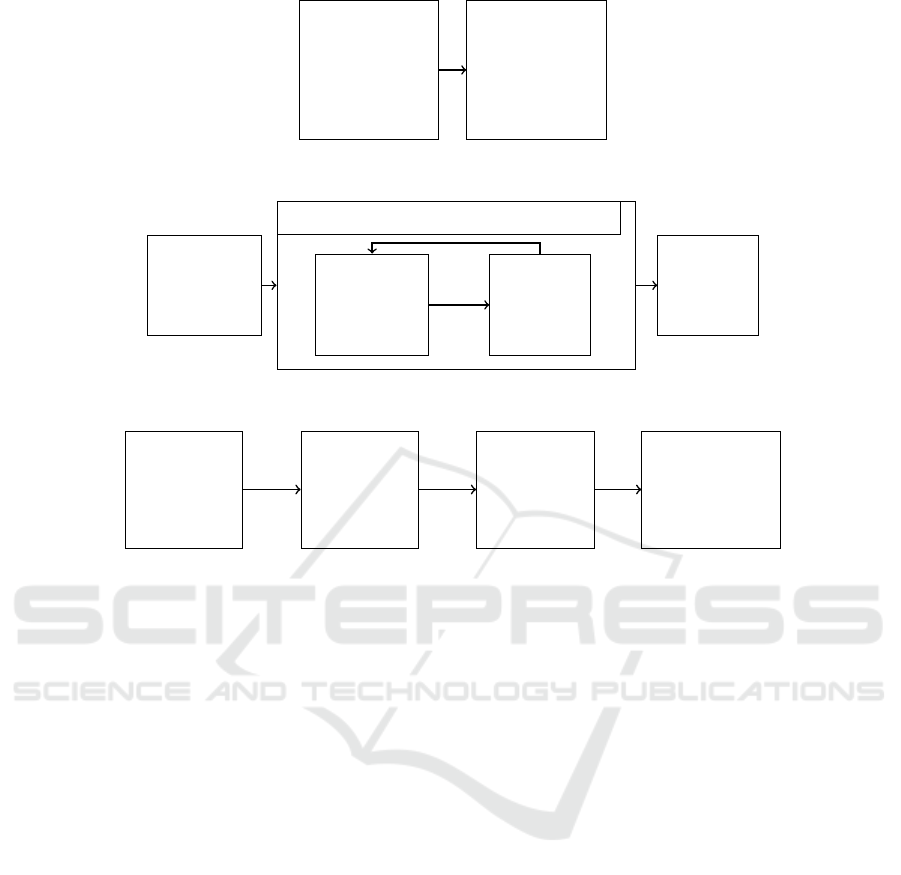
3
Classifier set
and
decision fusion
optimization
Get best
ensemble
w. r. t. loss
(a) Representation of the approach ”combined configuration space”.
Iterate over classifier set configurations î
3
Classifier set
optimization
3
Decision
fusion
optimization
Select best
decision
fusion
w. r. t. loss
Get best
ensemble
w. r. t. loss
(b) Representation of the approach ”separated configuration space”.
3
Classifier
optimization
Select set
of classifiers
w. r. t.
diversity
3
Decision
fusion
optimization
Get best
decision fusion
w. r. t. loss
(c) Representation of the approach ”simplified configuration space”.
Figure 2: Representations of the three basic approaches to optimize classifier ensembles. 3= Optimization Problem.
ration space is about ten times smaller than that of the
previous approach.
4.3 Simplified Configuration Space
Instead of directly retrieving a configuration consisting
of k classifiers, we can first address the optimization
problem for CS = Λ and then select a subset of size k
from all evaluated configurations (see Figure 2c).
However, in this approach it is no longer possible
to integrate a diversity metric into the loss function, as
these metrics have to be computed by comparing mul-
tiple classifiers. Alternatively, the diversity can be ex-
plicitly optimized using the above-mentioned classifier
selection step. This can be done by using an ”overpro-
duce and select” approach, i. e., creating a large set of
classifiers (overproduce) and then selecting a diverse
and accurate subset of these (select) (Kuncheva, 2004).
The classifier optimization of the current approach can
be seen as the overproduce step, as multiple configura-
tions of classification algorithms are evaluated when
optimizing a classifier. Out of all evaluated configu-
rations, a subset of k classifiers can then be selected
using their classification performance and diversity.
The separation of classifier optimization and clas-
sifier set selection leads to a far lower complexity of
the configuration space compared to the previously in-
troduced approaches. Since only single classifiers are
optimized in the first step, the configuration space of
this step is Λ , i. e., its complexity is in O(|Λ|) and thus
only grows linearly with the size of the classifier con-
figuration space. The configuration space complexity
for the decision fusion optimization is again in O(|Γ|) .
So, the overall complexity is in O(|Λ| + |Γ|) . Contin-
uing the example from Section 4.1, the configuration
space for classifiers contains 30 possible configura-
tions, while the one for decision fusion contains 20,
i. e., we have in total 50 possible configurations that
can be evaluated. Compared to the second approach,
the size of the configuration space is smaller by ap-
proximately a factor of 3 000 or of 30 000 compared
to the first approach.
4.4 Final Discussion
As shown in Table 2, all three approaches fulfill most
of the requirements defined in Section 2 in a similar
way. For example, creating classifiers with high classi-
fication performance is solved by all approaches via
a loss function for decreasing prediction errors. Simi-
larly, inducing implicit diversity is partly possible for
all approaches, since they all create a set of classifiers
ICEIS 2023 - 25th International Conference on Enterprise Information Systems
620

consisting of different algorithms and hyperparameters.
Furthermore, the classifier configuration spaces of all
approaches can easily be extended to include implicit
diversity methods such as bootstrapping. However,
this would result in a higher complexity of the config-
uration space Λ . Explicit diversity can also be created
by all approaches, but they differ in the way to realize
this. The approaches described in Section 4.1 and 4.2
can incorporate a diversity measure into the loss func-
tion. The third approach instead uses an overproduce
and select approach, i. e., it creates multiple classifiers
and then utilizes explicit diversity measures to select
the k most diverse classifiers among them. Finally, all
three approaches fulfill the requirement to optimize
the decision fusion algorithm to the same extent.
The requirement in which the three approaches dif-
fer most is the complexity of the configuration space,
which depends strongly on how the ensemble is opti-
mized. In the first approach introduced in Section 4.1,
the entire ensemble, including the classifier set and
the decision fusion algorithm, is optimized simultane-
ously. Consequently, the complexity of the associated
configuration space, which lies in O(

|Λ|
k

·|Γ|) , is high.
Due to the exploding complexity with increasing k , the
optimization is therefore not feasible in practice.
The second approach introduced in Section 4.2
has a slightly smaller configuration space with a com-
plexity in O(

|Λ|
k

+ |Γ|) , as it carries out the classifier
set optimization and the decision fusion optimization
in two separate steps. However, the first step of op-
timizing the classifier set still shows the same high
complexity as in the first approach. It thus accounts
for the largest part of the overall complexity.
Finally, the third approach proposed in Section 4.3
exhibits the lowest complexity of the configuration
space. This is possible by reducing the optimization
problem of creating an optimized set of k classifiers
to the problem of creating single classifiers that are
optimized independently of each other. Consequently,
the complexity of the configuration space is only in
O(|Λ|+|Γ|) and is thus independent of k . By applying
this approach, the creation of an automatically opti-
mized ensemble becomes feasible in an efficient way.
The complexity of the configuration space has the
highest impact on the ensemble creation, as having a
high complexity results in an inefficient optimization.
Here, the third approach presents the greatest advan-
tage, as its complexity is considerably lower than the
complexity of the other two approaches. Therefore,
we suggest that the approach presented in Section 4.3
should be explored in more detail in future work.
5 CONCLUSION AND OUTLOOK
Classifier ensembles allow for generating accurate clas-
sification models with high generalizability. However,
the creation of such an ensemble is complex: An ac-
curate and diverse set of classifiers has to be created
and a decision fusion algorithm has to be selected and
optimized. To simplify the creation of an ensemble,
we propose to automate it. To this end, we first iden-
tified the requirements for such a solution. We then
introduced three basic approaches for the automatic
creation and optimization of classifier ensembles and
discussed the extent to which these approaches satisfy
the requirements. One of the approaches surpassed the
other two, as its configuration space is of considerably
lower complexity than the complexities of the other
two approaches.
In future work, we intend to implement the third
approach as an extended AutoML framework. For
this purpose, several questions remain to be addressed,
such as which metrics have to be used to measure clas-
sification performance and classifier diversity, as well
as which optimization method is able to solve the op-
timization problem in the most efficient and effective
way. The extended AutoML framework should then be
evaluated on several real-world datasets, e. g., based on
the predictive performance of the resulting optimized
classifier ensembles.
In addition, the optimization w. r. t. diversity is of
particular interest for future research. While diversity
is known to be an important requirement for ensembles,
it is still unclear how it influences the classification
performance. Moreover, the automatic selection of
decision fusion algorithms already showed promise
when using the PUSION framework (Wilhelm et al.,
2023). However, the combination with AutoML and
the optimization of the hyperparameters of decision
fusion algorithms are still unexplored.
While we presented three basic approaches, vari-
ants of these are possible. In particular, the third ap-
proach may be studied more closely. Finally, com-
pletely new approaches to solve the presented chal-
lenge of automatic ensemble creation may be explored
in future work.
ACKNOWLEDGEMENTS
Parts of this work were financially supported by the
Ministry of Science, Research and the Arts of the
State of Baden Wurttemberg within the sustainability
support of the projects of the Exzellence Iinitiative II.
Towards the Automatic Creation of Optimized Classifier Ensembles
621

REFERENCES
Breiman, L. (1996). Bagging predictors. Machine Learning,
24(2):123–140.
Breiman, L. (2001). Random Forests. Machine Learning,
45(1):5–32.
Brown, G., Wyatt, J., Harris, R., and Yao, X. (2005). Diver-
sity Creation Methods: A Survey and Categorisation.
Information Fusion, 6(1):5–20.
Dietterich, T. G. (2000). Ensemble Methods in Machine
Learning. In Goos, G., Hartmanis, J., and van Leeuwen,
J., editors, Multiple Classifier Systems, volume 1857,
pages 1–15. Springer-Verlag, Berlin, Heidelberg.
Erickson, N., Mueller, J., Shirkov, A., Zhang, H., Larroy,
P., Li, M., and Smola, A. (2020). AutoGluon-Tabular:
Robust and Accurate AutoML for Structured Data.
Feurer, M., Klein, A., Eggensperger, K., Springenberg, J.,
Blum, M., and Hutter, F. (2015). Efficient and Robust
Automated Machine Learning. In Cortes, C., Lawrence,
N., Lee, D., Sugiyama, M., and Garnett, R., editors,
Advances in Neural Information Processing Systems,
volume 28. Curran Associates, Inc.
Freund, Y. and Schapire, R. E. (1997). A Decision-Theoretic
Generalization of On-Line Learning and an Applica-
tion to Boosting. Journal of Computer and System
Sciences, 55(1):119–139.
Hansen, L. and Salamon, P. (Oct./1990). Neural Network
Ensembles. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 12(10):993–1001.
He, X., Zhao, K., and Chu, X. (2021). AutoML: A Survey of
the State-of-the-Art. Knowledge-Based Systems, 212.
Hirsch, V., Reimann, P., and Mitschang, B. (2019). Data-
Driven Fault Diagnosis in End-of-Line Testing of Com-
plex Products. In Proc. of the 6
th
IEEE International
Conference on Data Science and Advanced Analytics
(DSAA), Washington, D.C., USA. IEEE.
Hirsch, V., Reimann, P., Treder-Tschechlov, D., Schwarz, H.,
and Mitschang, B. (2023). Exploiting Domain Knowl-
edge to Address Class Imbalance and a Heterogeneous
Feature Space in Multi-Class Classification. The VLDB
Journal.
Kuncheva, L. I. (2004). Combining Pattern Classifiers:
Methods and Algorithms. J. Wiley, Hoboken, NJ.
Lacoste, A., Larochelle, H., Marchand, M., and Laviolette, F.
(2014). Sequential Model-Based Ensemble Optimiza-
tion. In Proc. of the 13
th
Conference on Uncertainty in
Artificial Intelligence, UAI’14, page 440–448, Arling-
ton, Virginia, USA. AUAI Press.
LeDell, E. and Poirier, S. (2020). H2O AutoML: Scalable
Automatic Machine Learning. In Proc. of the AutoML
Workshop at ICML.
L
´
evesque, J.-C., Gagn
´
e, C., and Sabourin, R. (2016).
Bayesian Hyperparameter Optimization for Ensemble
Learning. In Ihler, A. and Janzing, D., editors, Proc.
of the 32
nd
Conference on Uncertainty in Artificial
Intelligence, New York City, NY, USA. AUAI Press.
Moussa, R., Guizzo, G., and Sarro, F. (2022). MEG: Multi-
objective Ensemble Generation for Software Defect
Prediction. In ACM / IEEE International Symposium
on Empirical Software Engineering and Measurement
(ESEM), pages 159–170, Helsinki Finland. ACM.
Polikar, R. (2006). Ensemble Based Systems in Decision
Making. IEEE Circuits and Systems Magazine, 6(3):21–
45.
Schapire, R. E. (1990). The Strength of Weak Learnability.
Machine Learning, 5(2):197–227.
Thornton, C., Hutter, F., Hoos, H. H., and Leyton-Brown, K.
(2013). Auto-WEKA: Combined Selection and Hyper-
parameter Optimization of Classification Algorithms.
In Proc. of the 19
th
ACM SIGKDD International Con-
ference on Knowledge Discovery and Data Mining,
pages 847–855, Chicago, IL, USA. ACM.
Tin Kam Ho (Aug./1998). The Random Subspace Method
for Constructing Decision Forests. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
20(8):832–844.
Villanueva Zacarias, A. G., Weber, C., Reimann, P., and
Mitschang, B. (2021). AssistML: A Concept to Rec-
ommend ML Solutions for Predictive Use Cases. In
Proc. of the 8
th
International Conference on Data Sci-
ence and Advanced Analytics (DSAA), pages 148–155.
IEEE.
Wegier, W., Koziarski, M., and Wozniak, M. (2022). Multi-
criteria Classifier Ensemble Learning for Imbalanced
Data. IEEE Access, 10:16807–16818.
Wilhelm, Y., Reimann, P., Gauchel, W., Klein, S., and
Mitschang, B. (2023). PUSION- A Generic and Auto-
mated Framework for Decision Fusion. In Proc. of the
39
th
International Conference on Data Engineering
(ICDE), Anaheim, CA, USA. IEEE.
Wilhelm, Y., Reimann, P., Gauchel, W., and Mitschang,
B. (2021). Overview on Hybrid Approaches to Fault
Detection and Diagnosis: Combining Data-driven,
Physics-based and Knowledge-based Models. Pro-
cedia CIRP, 99:278–283.
Wilhelm, Y., Schreier, U., Reimann, P., Mitschang, B., and
Ziekow, H. (2020). Data Science Approaches to Qual-
ity Control in Manufacturing: A Review of Problems,
Challenges and Architecture. In Proc. of the 14
th
Sym-
posium on Service-Oriented Computing (SummerSOC),
Communications in Computer and Information Science
(CCIS), pages 45–65. Springer-Verlag.
Wolpert, D. H. (1992). Stacked Generalization. Neural
Networks, 5(2):241–259.
Z
¨
oller, M.-A. and Huber, M. F. (2021). Benchmark and
Survey of Automated Machine Learning Frameworks.
Journal of Artificial Intelligence Research, 70:409–
472.
ICEIS 2023 - 25th International Conference on Enterprise Information Systems
622