
Beyond the Third Dimension: How Multidimensional Projections and
Machine Learning Can Help Each Other
Alexandru Telea
a
Department of Information and Computing Science, Utrecht University, Netherlands
Keywords:
Multidimensional Projections, Visual Quality Metrics, Explainable AI.
Abstract:
Dimensionality reduction (DR) methods, also called projections, are one of the techniques of choice for visu-
ally exploring large high-dimensional datasets. In parallel, machine learning (ML) and in particular deep learn-
ing applications are one of the most prominent generators of large, high-dimensional, and complex datasets
which need visual exploration. As such, it is not surprising that DR methods have been often used to open the
black box of ML methods. In this paper, we explore the synergy between developing better DR methods and
using them to understand and engineer better ML models. Specific topics covered address selecting suitable
DR methods from the wide arena of such available techniques; using ML to create better, faster, and simpler
to use direct and inverse projections; extending the projection metaphor to create dense representations of
classifiers; and using projections not only to explain, but also to improve, ML models. We end by proposing
several high-impact directions for future work that exploit the outlined ML-DR synergy.
1 INTRODUCTION
Machine learning (ML) techniques support tasks such
as classification and regression and have become fun-
damental instruments in daily practice in a myriad of
fields. Developments in the past decade have made
such techniques increasingly accurate, computation-
ally scalable, but most importantly, able to address
efficiently and effectively an increasing range of prob-
lems such as image analysis (e.g., classification, seg-
mentation, and restoration), sentiment identification,
natural language processing, to mention just a few.
The advent of deep learning (DL) techniques coupled
with recent advances in GPU and parallel computing
has massively simplified the ease of creating trained
ML models to solve these problems at industrial scale.
Dimensionality reduction (DR), also called pro-
jection, is a popular technique for visualizing high-
dimensional datasets by low-dimensional scatterplots.
Globally put, a good projection scatterplot captures
well the so-called data structure present in the orig-
inal high-dimensional data in terms of point clus-
ters, outliers, and correlations (Nonato and Aupetit,
2018; Espadoto et al., 2019a; Lespinats and Aupetit,
2011). As such, high-quality projections allow users
to reason about the data structure by exploring the vi-
sual structure of the low-dimensional scatterplots they
produce. Tens of different DR techniques (Espadoto
a
https://orcid.org/0000-0003-0750-0502
et al., 2019a) have been designed to address the sev-
eral requirements one has for this class of methods,
such as computational scalability, ease of use, stabil-
ity vs noise or small data changes, projecting addi-
tional points along those existing in an original dataset
(out-of-sample ability), and visual quality that pre-
serves the high-dimensional data structure.
ML and DR techniques, while having emerged
from different fields, share a key similarity: They
both deal with high-dimensional data – a challeng-
ing endeavor. In ML, such data are the so-called
features used during training and inference by mod-
els. In DR, such data represent the samples, or obser-
vations, whose data structure we aim to understand
by means of low-dimensional scatterplots. The two
fields also share other important commonalities: ML
strongly needs methods to open up the ‘black box’
formed by architecting, training, and using the mod-
els it creates, and many such models are visual, like
the DR scatterplots. Conversely, the task of creating
high-quality projections from high-dimensional data,
with guaranteed stability, out-of-sample ability, gen-
eralizability, and computational scalability shares all
typical requirements met by ML engineering.
In this paper (and related talk), we aim to pro-
vide an overview of the research at the crossroads
of ML and DR with a particular emphasis on high-
lighting commonalities between the two fields and re-
cent ways in which they can benefit from each oth-
Telea, A.
Beyond the Third Dimension: How Multidimensional Projections and Machine Learning Can Help Each Other.
DOI: 10.5220/0011926400003417
In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 5: VISAPP, pages
5-16
ISBN: 978-989-758-634-7; ISSN: 2184-4321
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
5

ers’ advances. We start by a short overview of ML
and DR that outlines common aspects of these two
fields (Sec. 2). We next outline how DR methods are
used to assist ML engineering tasks (Sec. 3). Next, we
discuss how the converse fertilization occurs, namely
ML methods being used to create better DR tech-
niques (Sec. 4). Section 5 merges the insights of
the previous two sections and outlines high-potential
future research directions in which the DR and ML
fields can benefit from each other. Finally, Section 6
concludes the paper.
2 BACKGROUND
Providing a full introduction of both ML and DR is
out of scope of thos paper. This section aims to pro-
vide a brief outline of the key concepts in the two
fields which are needed to follow the further discus-
sion and, importantly, highlight commonalities of ML
with DR that next lead to cross-fertilization.
2.1 Machine Learning
We start by listing some notations. Let D = {x
i
}
be a dataset of N-dimensional samples or points x
i
,
1 ≤ i ≤ N. A point x
i
= (x
1
i
, . . . , x
n
i
) consist of n
components x
j
i
, also called feature or attribute values.
Without generality loss, we assume next for simplic-
ity that each of these is a real-value, i.e., x
i
∈ R
n
. The
sets X
j
= (x
j
1
, . . . , x
j
N
), 1 ≤ i ≤ N are called the fea-
tures, or dimensions, of the entire dataset D. Sim-
ply put, D can be seen as a table having N rows (one
per sample) and n columns (one per dimension). An
annotated dataset D
a
associates an additional value
y
i
∈ A to each sample x
i
of a given dataset D.
Machine learning aims to create so-called mod-
els f : R
n
→ A which, when applied to a so-called
test set D
T
⊂ D
a
, deliver the expected annotations,
i.e., d( f (x
i
), y
i
) ≃ 0, for ideally all x
i
∈ D
T
. Here,
d : A × A → R
+
is a distance function used to com-
pare the so-called ground-truth annotations y
i
with the
model’s predictions f (x
i
), e.g., an L
p
norm. Models
f are built by using a so-called training set D
t
⊂ D
a
,
D
t
∩D
T
= ∅, to adjust f ’s parameters so as to achieve
the above-mentioned goal. Two main types of models
exist in ML. Classifiers use an annotation set having
categorical values (also called labels), in which case
one strives for d = 0. Regressors use an annotation
set having real values (in one or more dimensions), in
which case one strives for d ≃ 0.
Many methods exist to measure the performance
of ML models. The most widespread such methods
measure several so-called quality metrics on the train-
ing set (training performance) and, separately, on the
unseen test set (testing performance). Common met-
rics include accuracy, precision, recall, F-score, and
Cohen’s kappa score. More advanced methods take
into account hyperparameters that allow optimizing
between precision and recall, e.g. the Receiver Oper-
ator Characteristic (ROC) curve and area underneath.
Recent surveys of such metrics and related bench-
marks are given in (Botchkarev, 2019; Jiang et al.,
2020; Thiyagalingam et al., 2022).
2.2 Dimensionality Reduction
Consider a high-dimensional dataset D defined as for
the ML context (Sec. 2.1). A dimensionality reduc-
tion technique, or projection P, is a function that maps
D to P(D) = {y
i
}, where y
i
∈ R
q
is the projection of
x
i
. Typically q ≪ n, yielding 2D projections (q = 2)
and 3D projections (q = 3) that are used to visual-
ize D by depicting the respective scatterplots. Pro-
jections aim to preserve the so-called structure of the
dataset D. Intuitively put, this means that patterns in
D such as clusters of densely packed points, outliers,
and gaps between such point formations, should be
visible in P(D).
How well a projection preserves data structure is
measured by several quality metrics. A quality metric
is a function M(D, P(D)) → R
+
that tells how well
the scatterplot P(D) captures aspects of the dataset D.
Such metrics can be roughly divided into those that
measure distance preservation between R
n
and R
2
,
such as normalized stress and the Shepard diagram
correlation; and metrics that look at how well (small)
neighborhoods of points are preserved between D and
P(D), such as trustworthiness, continuity, or, more
specific ones, e.g. Kullback-Leibler divergence. Ex-
tensive surveys of projection quality metrics are given
in (Nonato and Aupetit, 2018; Espadoto et al., 2019a).
2.3 Common Sspects of ML and DR
Tens, if not hundreds, of algorithms and techniques
have been proposed for both ML and DR. As our goal
is to highlight ways in which ML can help DR (and
conversely), we next do not discuss such specific al-
gorithms in detail. Rather, we focus our analysis on
common aspects of the two fields. To this end, it is
already important to note that both ML models f and
DR projection methods P can be seen as specialized
cases of inference. More specifically, P can be seen
as a particular type of regressor from R
n
to R
2
. Given
this, we next use the notation X to jointly denote an
ML model or DR algorithm, when distinguishing be-
VISIGRAPP 2023 - 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications
6

tween the two is not important.
Without claiming full coverage, we identify the
following key aspects that both ML and DR tech-
niques X strive to achieve:
Genericity. X should be readily applicable to any
dataset D – that is, of any dimensionality, attribute
types, and provenance application domain.
Accuracy. X should deliver highly accurate results
(inferences for ML; projection scatterplots for DR) as
gauged by specific quality metrics in the two fields.
Scalability. X should scale well computationally with
the number of samples N and dimensions n – ideally,
X should be linear in both N and n. In practice, X
should be readily able to handle datasets with millions
of samples and hundreds of dimensions on commod-
ity hardware at interactive rates. This further on en-
ables the use of X in visual analytics scenarios where
the iterative and interactive exploration of complex
hypotheses via data visualization is essential.
Out of Sample (OOS). An operator X is said to be
OOS if it can extrapolate its behavior beyond the data
from which it was constructed. In ML, this usually
means that the model f extrapolates from a training
set D
t
to an unseen test set D
T
and beyond. By anal-
ogy, a projection P is OOS if, when extending some
dataset D with additional samples D
′
, the projection
P(D ∪ D
′
) ideally keeps the points originally in D
at the locations they had in P(D), i.e., P(D ∪ D
′
) =
P(D) ∪ P(D
′
). This is essential in scenarios where
one has a growing dataset to be projected. Existing
points should not change their existing projection lo-
cations if we want to help users maintain their mental
map when interpreting the projection. As most ML
methods are OOS by design, they can be potentially
used to design OOS projections (Sec. 4).
Stability. Small changes in the input dataset D should
only lead to small changes in the output dataset X(D).
If not, then noise-level perturbations in D will mas-
sively affect the resulting inference X(D) thereby ren-
dering such results potentially unusable and/or mis-
leading. Note that stability is related but not the same
as OOS: An OOS algorithm needs to be stable by def-
inition but not all stable algorithms have OOS abil-
ity (Vernier et al., 2021; Espadoto et al., 2019a). Sim-
ilarly, large-scale changes in D should arguably lead
to correspondingly large changes in X(D). We discuss
this aspect in more detail when outlining the chal-
lenges of dynamic projections (Sec. 5.2).
Availability. X should be readily available to prac-
titioners in terms of documented open-source code.
While sometimes neglected, this is a key requirement
for ML and DR algorithms to become impactful in
practice.
Most ML techniques in existence comply by de-
sign with the above properties. However, not all DR
techniques do the same. As we shall see in Sec. 4,
ML can be used to construct DR techniques, thereby
making the latter techniques inherit all the desirable
properties of the former.
3 DR FOR ASSISTING ML
Given the close relation between DR and ML outlined
above, it is not surprising that DR has been used as a
visual analysis tool to assist model engineering. We
next discuss several prominent cases of such usage of
DR.
3.1 Assessing and Improving Classifiers
Arguably the most frequent use of DR for ML engi-
neering is to create a projection of a training or test
set, with points colored by class and/or correct-vs-
wrong classification, and use it to assess the model’s
working. Indeed, since (a) a projection places sim-
ilar samples close to each other and (b) a classi-
fier labels similar samples similarly, then the visual
structure of the projection should convey insights on
how easily separable are samples of different classes.
While this intuition has been long used, it is only re-
cently that a formal study of this correlation was pre-
sented (Rauber et al., 2017b). In the respective work,
the authors show that a dataset D which creates a pro-
jection P(D) in which classes are well separated (as
measured e.g. by the neighborhood hit metric) will be
far easier classifiable than a dataset whose projection
shows intermixed points of different labels. The pro-
jection P(D) thus becomes a ‘proxy’ for the ease of
classifying D regardless of the type of classifier be-
ing used. This helps one in assessing classification
difficulty before actually embarking in the expensive
cycle of classifier design-train-test.
Figure 1 illustrates the above. Images (a) and
(b) show the two-class Madelon dataset (Guyon et al.,
2004) (n = 500 features) classifier by KNN and Ran-
dom Forests (RFC) respectively, with samples pro-
jected by t-SNE (van der Maaten and Hinton, 2008)
and colored by class. The two projections show a
very poor separation of the two classes, in line with
the obtained accuracies AC = 54% and AC = 66%.
Images (c) and (d) show the same dataset where ex-
tremely randomized trees (Geurts et al., 2006) was
used to select n = 20 features. The projections show
a much higher visual separation of the two classes,
in line with the obtained accuracies AC = 88% and
AC = 89%. Numerous other examples in (Rauber
Beyond the Third Dimension: How Multidimensional Projections and Machine Learning Can Help Each Other
7

a) poor visual separation, AC=54% b) poor visual separation, AC=66%
c) good visual separation, AC=88% d) good visual separation, AC=89%
Figure 1: Classification difficulty assessment via projec-
tions (Rauber et al., 2017b).
et al., 2017b) show that projections are good predic-
tors of classification difficulty.
3.2 Pseudolabeling for ML Training
If projections are good predictors for classifica-
tion accuracy, it means that their low-dimensional
(2D) space captures well the similarity of the high-
dimensional samples. Following this, the next step is
to actually use projections to engineer classifier mod-
els. A first attempt was shown by (Benato et al., 2018)
for the task of training a classifier from a training
set having only very few labeled points: The entire
training set, including unlabeled points, is projected
and the user explores the projection to find unlabeled
points tightly packed around labeled ones. Following
visual confirmation that the packed samples are of the
same class as the surrounded label (using a tooltip
to look at the image samples), the user selects the
former and assigns them the latter’s label. The pro-
cess quickly leads to sufficiently large labeled sets for
training the desired model. More interestingly, auto-
mated label propagation in the embedded space using
state-of-the-art methods leads to poorer results than
user-driven labeling, which confirms the added value
of the human-in-the-loop and thus the projections.
However, the best results are obtained when hu-
mans and machine cooperate rather than aim to re-
place each other. (Benato et al., 2020) adapted the
above workflow to (a) use an automatic label propa-
gation for the 2D projection points where the propa-
gation confidence is high; and (b) expose the remain-
ing points to manual labeling (see Fig. 2). This way,
many ‘easy to label’ points are handled automatically
whereas the user’s effort is channeled towards the dif-
ficult case. This strategy led to increasing model ac-
curacy and, again, surpassed confidence-based label
propagation into the high-dimensional space.
supervised
auto-labeled
candidates for manual
Figure 2: Semi-automatic label propagation for construct-
ing training sets. An algorithm propagates ground-truth la-
bels from a small set of supervised samples towards neigh-
bor samples. When this algorithm is uncertain, samples are
left for manual labeling (Benato et al., 2020).
3.3 Understanding DL Models
Projections can be used not only to understand the
end-to-end behavior of classifier models but also their
internals. This become especially useful when we
consider deep learned (DL) models which, with their
millions of parameters, are among the hardest arti-
facts in ML to understand. ‘Opening the black box’
of DL models is one of the most challenging, and also
most actual, goals of explainable AI (XAI) (Shwartz-
Ziv and Tishby, 2017; Azodi et al., 2020). Visualiza-
tion has been listed early on as the technique of choice
for this endeavor (Tzeng and Ma, 2005). A recent
surve (Garcia et al., 2018) outlines a wide spectrum of
visual analytics techniques and tools used for DL en-
gineering, classified in terms of supporting the tasks
of training analysis (TA), architecture understanding
(AU), and feature understanding (FU). Given the di-
versity of these tasks, the variety of the proposed vi-
sual analytocs solutions – e.g. matrix plots, icicle
plots, parallel coordinate plots, stacked barcharts, an-
notated networks, activation maps – is not surprising.
Projections occupy a particular role among these
visualizations due to their ability to compactly cap-
ture high-dimensional data – in the limit, a projec-
tion needs a single pixel to represent an n-dimensional
point, for any n value. As such, they are very suitable
instruments to depict several aspect of a DL model.
For example, in Fig. 3a, every point denotes a high-
dimensional sample, in this case a digit image from
the SVHN dataset (Rauber et al., 2017b). The points,
VISIGRAPP 2023 - 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications
8

a) explore learned features b) explore training vs time c) explore training vs layers
Figure 3: Projections for understanding DL models. Exploring (a) activations of similar instances, (b) evolution of activations
over training epochs, and (c) evolution of activations over network layers (Rauber et al., 2017a).
colored by their ground-truth class, have as dimen-
sions all activations of the last hidden layer of a DL
model created to classify this dataset. We notice a
good separation of same-class images, which tells
that the model was successfully trained. We also see
two clusters of same-class points, which tell that the
model has learned to split images of the same digit
into two subclasses. Upon inspection, we see that
the model has learned by itself to separate dark-on-
bright-background digits from bright-on-dark back-
ground ones. Such findings would not be possible
without the insights given by visual tools such as pro-
jections. Moreover, such findings can help the ML
engineers to fine-tune their models to increase per-
formance – in this case, eliminate the ‘color con-
trast learning’ which does not help the targeted clas-
sification. Figure 3b explores a different DL aspect,
namely how the model learns. For every epoch, a
projection of all training-set samples is made of the
samples’ last hidden layer activations, similar to im-
age (a). To maintain temporal coherence, i.e., have
similar-value samples project to close locations over
the entire set of epochs, a dynamic projection algo-
rithm, in this case dt-SNE (Rauber et al., 2016), was
used. Next, same-image points from all epochs are
connected by a trail. As the last step, trails are bun-
dled in 2D (van der Zwan et al., 2016) to reduce visual
clutter. The resulting image shows how the projection
literally fans out from a dark clump (in the middle
of the image), where last-layer neurons exhibit sim-
ilar activations for all images, to separated clusters
of same-label images. This effectively summarizes
the training success – we see, for example, that the
purple bundle (digit 4) is less well separated from
the others, which indicates some challenges in clas-
sifying this digit. Finally, Fig. 3c shows a similarly-
constructed visualization but where the trails connect
projections of test-set image activations through all
network’s hidden layers. Bundles, initially dark and
wide (layer 1), fan in, indicating that the network pro-
gressively separates images of different classes as the
data flows through its layers – i.e., that the network
architecture is indeed good for the classification task
at hand.
3.4 Decision Boundary Maps
All projections shown so far visualize a discrete set
D of samples processed by a ML model f . However,
such models are, in general, designed to accept sam-
ples from a dense set Z ⊂ R
n
. Classifiers, for instance,
partition Z into so-called decision zones (dense sets
in Z whose points get the same label) separated by
decision boundaries. Such decision boundaries are
in general complex manifolds embedded into R
n
and
were, until recently, only depictable for very simple
models such as logistic regression. Ideally, the ML
engineer would like to see how f behaves on the en-
tire dense space Z and not only on the sparse sampling
thereof given by training (D
t
) or test (D
T
) sets.
Since projections perform so well for visually ex-
ploring classifiers, it makes sense to consider extend-
ing them to depict decision zones and boundaries. In-
tuitively put, such boundaries would go through the
whitespace in a projection to separate the same-color
point clusters in e.g. Fig. 3a. Seeing decision zones
and boundaries and their relations to training and/or
test samples would help ML engineers to e.g. find
where in the input space more training samples are
needed to improve a classifier or, conversely, assess
in which such areas would samples be misclassified.
Decision boundary maps (DBMs) propose such
a visual representation for both decision zones and
boundaries for any classifier. Intuitively put, DBMs
map the entire space Z (as classified by f ) to 2D rather
than the discrete sample set D, as follows. Given an
image space I ⊂ R
2
, a mapping P
−1
: I → R
n
is con-
structed to ‘backproject’ each pixel y ∈ I to a high-
Beyond the Third Dimension: How Multidimensional Projections and Machine Learning Can Help Each Other
9

dimensional point x = P
−1
(y). Next, y is colored by
the label f (x) assigned to it by a trained classifier to
be explored. Same-color areas emerging in I indicate
f ’s decision zones; pixels on the frontiers of these ar-
eas show f ’s decision boundaries. The key to DBM
construction is creating the mapping P
−1
. One way to
do this, shown in Fig. 4a, is to use distance-based in-
terpolation over the points P(D) of a parametric (that
is, OOS) projection of the training and/or test set of
f (Schulz et al., 2015; Schulz et al., 2020). Another
way, shown in Fig. 4b, is to general purpose so-called
inverse projection techniques (Rodrigues et al., 2018).
Finally, one can construct P
−1
by using deep learning
(Fig. 4c), as discussed further in Sec. 4.2.
DBMs can be further enhanced to encode, via
brightness, the classifier’s confidence at every 2D
pixel (Figs. 4a,c) or actual n-dimensional distance to
the closest decision boundary (Fig. 4b). The appear-
ing brightness gradients tell which areas in the projec-
tion space are more prone to misclassifications. Im-
portantly, this does not require actual samples to exist
in a training or test set in these areas – rather, such
samples are synthesized by P
−1
.
4 ML FOR ASSISTING DR
Section 3 has shown several examples of the added
value of projections for ML engineering. However,
as noted in Sec. 2.3, not all projection techniques sat-
isfy all desirable requirements needed for them to be
readily used in ML visualization (and, actually, in
other contexts as well). An important question is thus:
Which projection techniques are the best candidates
for such use-cases?
A recent survey (Espadoto et al., 2019a) addressed
this question at scale for the first time by comparing
44 projection techniques P over 19 datasets D from
the perspective of 6 quality metrics M, using grid-
search to explore the hyperparameter spaces of the
projection techniques. This is to date the only large-
scale survey that quantitatively assesses DR methods
over many datasets, techniques, quality metrics, and
parameter settings. Equally important, all its results –
datasets, projection techniques, quality metric imple-
mentations, study protocol – are automated and freely
available, much like similar endeavors in the ML
arena. Following the survey’s results, four projection
methods consistently scored high on quality for all
datasets (UMAP (McInnes et al., 2018), t-SNE (van
der Maaten and Hinton, 2008), IDMAP (Minghim
et al., 2006), and PBC (Paulovich and Minghim,
2006)), with several others close to them. However,
none of the top-ranked surveyed techniques also met
the OOS, computational scalability, and stability cri-
teria. As such, we can conclude that better DR tech-
niques are needed.
4.1 Deep Learning Projections
Following the analogy with ML regressors (Sec. 2.3,
it becomes interesting to consider ML for building
better projection algorithms. Autoencoders (Hinton
and Salakhutdinov, 2006) do precisely that and meet
all requirements in Sec. 2.3 except quality – the re-
sulting projections have in general poorer trustwor-
thiness and continuity than state-of-the-art methods
like UMAP and t-SNE. Figure 5 illustrates this: The
well-known MNIST dataset, which is well separable
into its 10 classes by many ML techniques, appears,
wrongly, poorly separated when projected by autoen-
coders. Following (Rauber et al., 2017b) (see also
Sec. 3.1, we can conclude that autoencoders are a
poor solution for DR.
Recently, Espadoto et al. (Espadoto et al., 2020)
proposed Neural Network Projections (NNP), a su-
pervised approach to learning DR: Given any dataset
D and its projection P(D) computed by the user’s
technique of choice P, a simple three-layer fully-
connected network is trained to learn to regress P(D)
when given D. Despite its simplicity, NNP can learn
to imitate any projection technique P for any dataset
D surprisingly well. While NNP’s quality is typically
slightly lower than state-of-the-art projections like t-
SNE and UMAP, it is a parametric method, stable as
proven by sensitivity analysis studies (Bredius et al.,
2022), OOS, linear in the sample count N and dimen-
sionality n (in practice, thousands of times faster than
t-SNE), and very simple to implement.
Figure 6 shows an example of the above-
mentioned sensitivity analysis. An NNP model is
trained to project the MNIST dataset, after which is
asked to project MNIST images where an increas-
ingly larger number of dimensions (pixel values) have
been cancelled, i.e., set to zero. Surprisingly, NNP
can capture the cluster structure of the data (10 classes
for the 10 digits) up to 40% cancelled dimensions.
The aggregated image shows the ‘movement’ of the
points in the NNP projection as increasingly more di-
mensions get dropped. Similar insights are obtained
for other input-dataset perturbations such as sample
jitter, translation, and scaling. At a higher level, we
see sensitivity analysis as a very powerful, yet under-
explored, technique – well known in the ML reper-
toire – to assess the quality of DR projections.
Subsequent refinements included k-
NNP (Modrakowski et al., 2021) which enhances
quality by learning to project sets of neighbor sam-
VISIGRAPP 2023 - 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications
10
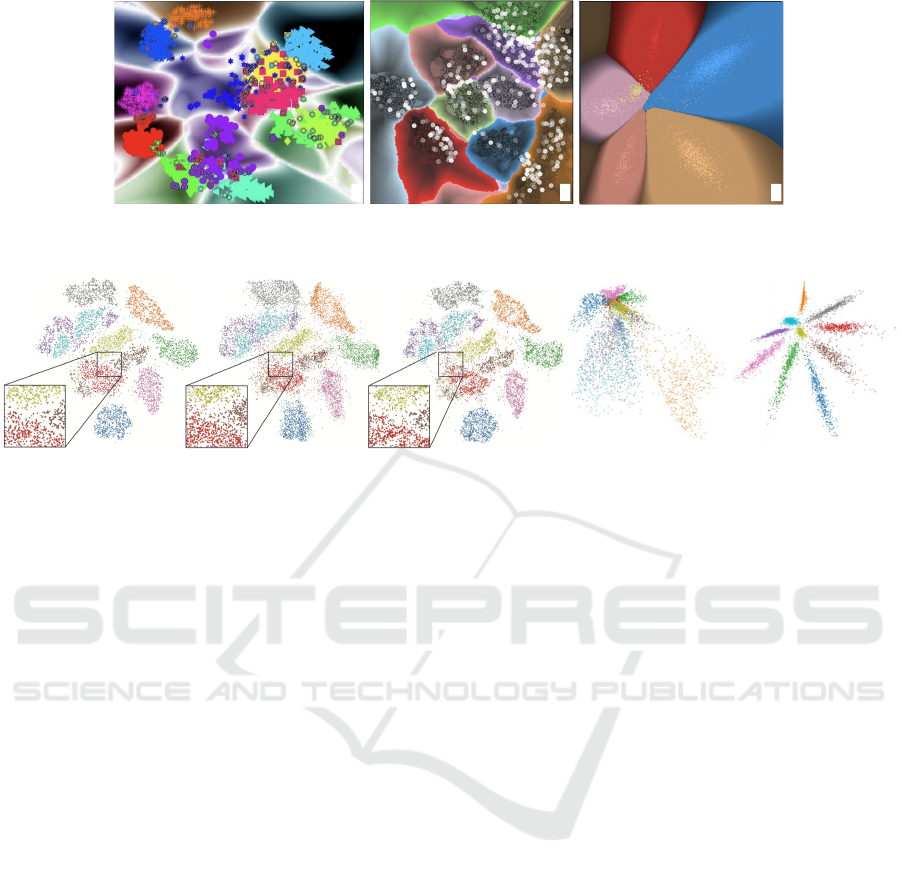
a c
b
Figure 4: Decision boundary maps for classifier analysis with luminance encoding classifier confidence (a,c) (Schulz et al.,
2015; Rodrigues et al., 2019), respectively distance-to-decision-boundary (c) (Oliveira et al., 2022).
a) t-SNE
b) NNP c) kNNP
d) autoencoder e) SSNP
Figure 5: Projection of MNIST dataset with (a) t-SNE (van der Maaten and Hinton, 2008) and with deep learning methods:
(b) NNP (Espadoto et al., 2020), (c) kNNP (Modrakowski et al., 2021), (d) autoencoders (Hinton and Salakhutdinov, 2006),
(e) SSNP (Espadoto et al., 2021b). For supervised methods, (k)NNP succeeds in well imitating t-SNE. For self-supervised
methods, SSNP yields better quality than autoencoders.
ples; SSNP (Espadoto et al., 2021b) which works
in a self-supervised way, similar to autoencoders,
thus dispensing of the need of a training projection
and also being able to create inverse projections (see
next Sec. 4.2); SDR-NNP (Kim et al., 2022) which
increases NNP’s quality by pre-sharpening the input
training set D
t
via mean shift; and HyperNP (Appleby
et al., 2022), which learns the behavior of a projec-
tion technique P for all its hyperparameter values.
Figure 5 shows several of these techniques applied
to the well-known MNIST dataset which illustrates
the qualitative comments made above. All in all, the
above results prove that DL is a serious contender
for generating projections that comply with all
requirements set forth by practice.
4.2 Deep Learning Inverse Projections
Following the success of DL for constructing projec-
tions P outlined above, it becomes immediately inter-
esting to ask if we cannot do the same to construct in-
verse projections P
−1
. Introduced in Sec. 3.4 for con-
structing DBMs, inverse projections have additional
uses, e.g., generating synthetic samples for data aug-
mentation scenarios.
Espadoto et al. (Espadoto et al., 2019b) answered
the above question positively by simply ‘switching’
the input and output of NNP, i.e., given a dataset D
that projects to a 2D scatterplot by some technique
P, train a regressor to output D when given P(D).
This technique, called NNInv, inherits all the desir-
able properties of NNP (see Sec. 2.3) and also pro-
duces higher-quality DBMs than earlier models for
P
−1
. In particular, NNInv – and also SSNP, the other
deep-learning technique able to create inverse projec-
tions introduced in Sec. 4.1 – are about two orders of
magnitude faster than other existing inverse projec-
tion techniques such as iLAMP (Amorim et al., 2012)
and RBF (Amorim et al., 2015). NNInv was further
explored in detail for visual analytics scenarios in-
volving dynamic imputation and exploring ensemble
classifiers (Espadoto et al., 2021a). Figure 7 shows
the latter use-case: In the image, each pixel is back-
projected and ran through a set of nine classifiers,
trained to separate classes 1 and 7 from the MNIST
dataset. The pixel is then colored to indicate the clas-
sifiers’ agreement. Deep blue, respectively red, zones
show areas where all classifiers agree with class 1, re-
spectively 7. Brighter areas indicate regions of high
classifier disagreement – which are thus highly diffi-
cult to decide upon and are prime candidates for ML
engineering, regardless of the used classifier.
Beyond the Third Dimension: How Multidimensional Projections and Machine Learning Can Help Each Other
11
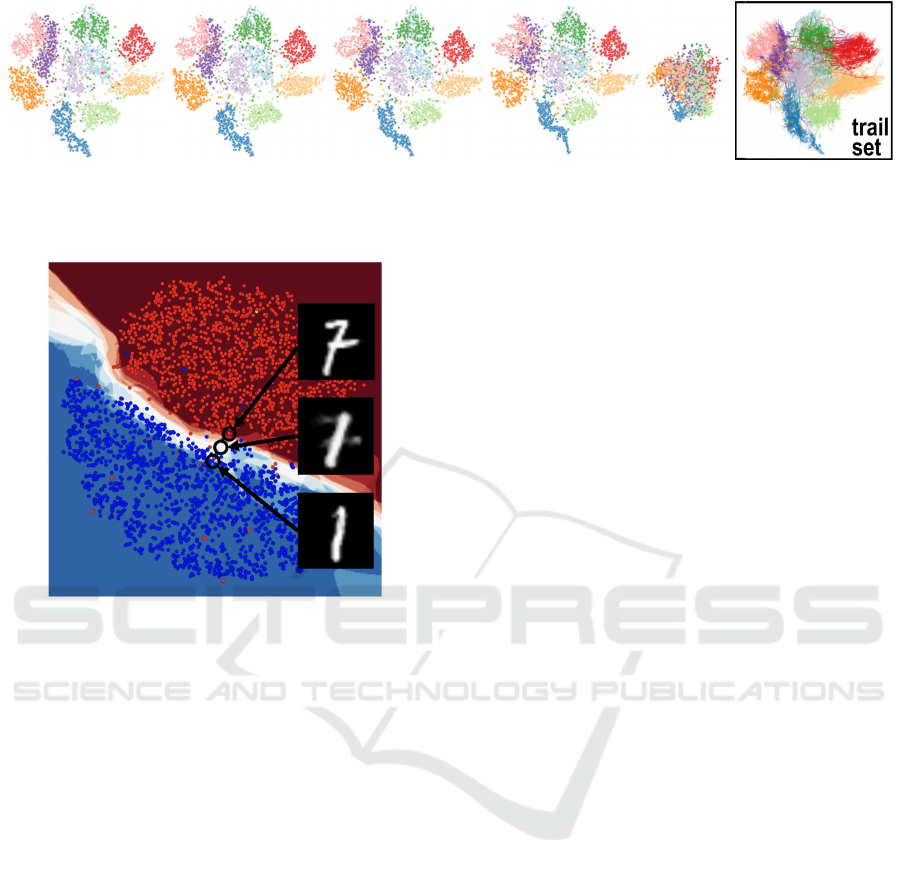
10% 20% 30% 40% 90% aggregation
Figure 6: NNP sensitivity analysis when removing between 10% and 90% of the MNIST dimensions. Surprisingly, NNP can
robustly depict the data structure even when a large part of the input information is missing (Bredius et al., 2022).
Figure 7: Classifier agreement map for 9 classifiers, MNIST
datasets digits 1 and 7. Dark colors indicate more of the 9
classifiers agreeing, at a pixel in the map, with the deci-
sion (red=1, blue=7). Brighter, desaturated, colors indicate
fewer classifiers in agreement (white=4 classifiers say 1, the
other 5 say 7, or conversely) (Espadoto et al., 2021a).
5 THE WAY FORWARD
Figure 8 summarizes the tight interaction between
ML and DR described above. The central box (blue)
depicts the typical ML pipeline which maps some
input real-valued dataset D into class labels or an-
other real-valued signal by means of a classifier,
respectively regressor. The box atop this pipeline
(green) shows various visualizations that cane used
to assist ML engineering, such as semi-automatic la-
beling (Sec. 3.2), assessing classification difficulty
(Sec. 3.1), and assessing training and deep mod-
els (Sec. 3.3). The bottom box (yellow) uses ML
regressors to build several DR techniques such as
(self-)supervised projections (Sec. 4.1) and inverse
projections (Sec. 4.2). In turn, these lead to refined
visualization methods – sensitivity analysis to assess
learned projections (Sec. 4.1) and quality analysis for
inverse projections (see Sec. 5.2 further). Finally, all
these DR methods can be used to construct the earlier-
described visualizations that assist ML engineering
(red arrow in Fig. 8).
Reflecting upon the current achievements of us-
ing ML for DR and conversely, we see a bright
future ahead for research where the two direc-
tions strengthen each other. A few selected, non-
exhaustive, examples of such potential ML-DR syn-
ergies are outlined next.
5.1 Prospects of DR Helping ML
Better DBMs. While current techniques allow the
fast creation of accurate DBMs (Sec. 3.4), some fun-
damental trade-offs still exist. Very accurate tech-
niques exist which solve the inherent ill-posedness
of inverting a projection function P which can map
different high-dimensional points to the same low-
dimensional location (Schulz et al., 2015; Schulz
et al., 2020). However, such techniques make various
assumptions on the underlying projections, are quite
complex to implement, and also computationally ex-
pensive – they are far from real-time adaptation of the
DBM upon re-training a classifier, which would be
ideal for ML engineering (see below). Conversely,
DL-based techniques like NNInv and SSNP are near-
real-time and simple to implement but may create er-
rors that ultimately mislead their users. We foresee
possibilities of using ML, and in particular DL, to im-
prove the latter to match the quality of the former.
DBMs in Use. DBMs are not a goal in themselves,
but a tool serving a goal. Apart from the scenarios
depicted in (Espadoto et al., 2021a), DBMs could be
readily used in a visual analytics explorative scenario
to drive a classifier’s training. If computable in real-
time, users could visualize the DBMs, find problem-
atic areas with respect to how the decision boundaries
wrap around samples, and next modify the training
set by e.g. adding or deleting labels, adding new aug-
mented samples, or even moving samples. We envis-
age a tool in which users could effectively ‘sculpt’ the
shape of decision boundaries by sample manipulation
much as one edits 2D shapes by manipulating spline
control points. This would offer unprecedented free-
VISIGRAPP 2023 - 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications
12
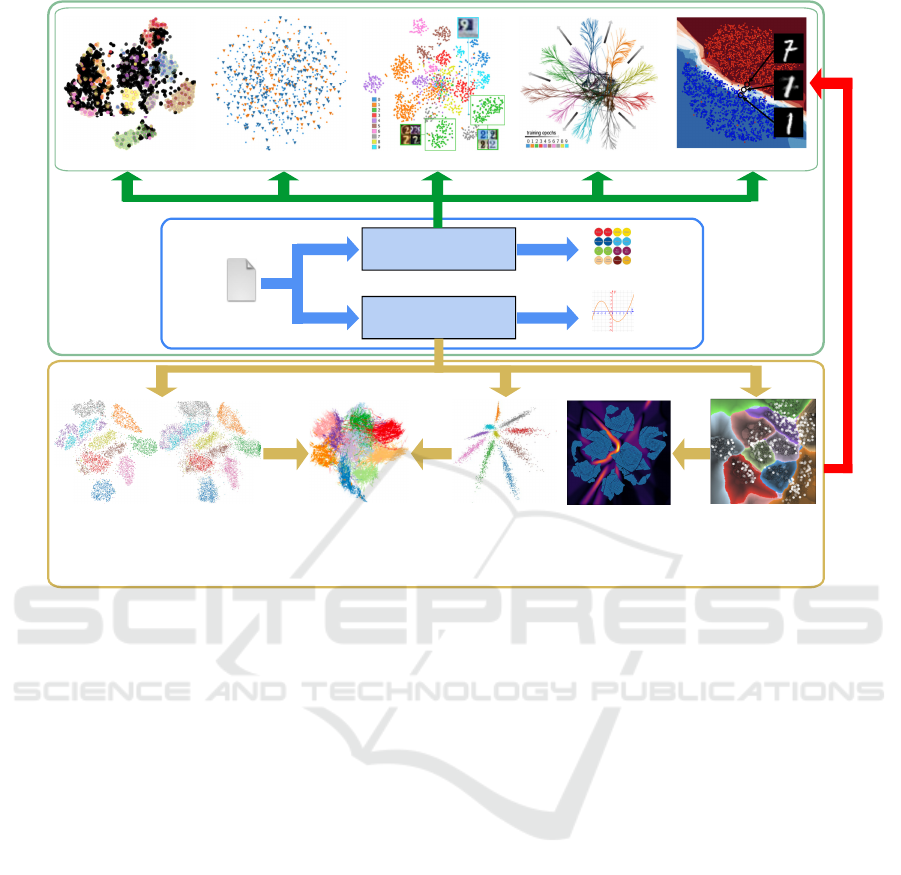
pseudolabeling classif. difficulty assessment feature understanding training assessment
classifier
regressor
input data
output labels
output signal
model assessment
supervised DR self-supervised DR inverse projectionssensitivity analysis quality analysis
Machine
learning
Dimensionality
reduction
ML
pipeline
Figure 8: Interactions between machine learning (ML) and dimensionality reduction (DR). See Sec. 5.
dom and a wholly new way of fine-tuning classifiers
to extend the approaches pioneered in (Benato et al.,
2018; Benato et al., 2020).
Visualizing Regressors. The examples shown in this
paper have arguably convinced the reader that pro-
jections are efficient and effective in visualizing both
high-dimensional data and classifier models working
on such data. However, as Sec. 2 mentions, ML is
also about a second type of technique, namely regres-
sors. A very complex, but high-potential, challenge is
to adapt and extend DR methods to visualize regres-
sors (first of the single-variate type, then the multi-
variate one). This is fundamentally hard as the 2D vi-
sual space does not readily offer the possibility of dis-
playing many values at a single point. In some sense,
it seems that a second DR pass would be needed to re-
duce the regressor’s output dimension to what could
be displayed in 2D. Generalizing DBMs from classi-
fiers to ‘regressor maps’ would open a wide spectrum
of possibilities going beyond ML, e.g., in operations
research and optimization applications. A recent at-
tempt in this direction was shown in (Espadoto et al.,
2021c). However, this approach only treated single-
variate regressors f : R
n
→ R and used a relatively
low-quality projection (PCA).
5.2 Prospects of ML Helping DR
Learning Styles. All current DL-based projection
methods use relatively simple cost functions – ei-
ther aiming to globally mimic a training projection
(NNP-class methods) or aiming to globally minimize
some reconstruction loss (autoencoder-class meth-
ods). A first extension direction would be to re-
fine this loss to e.g. create projections where the
sizes and/or shapes of clusters can be controlled by
data attributes. One high-potential direction would be
to create a hierarchy-aware projection algorithm that
would combine the advantages of treemaps and clas-
sical projections, in the wake of earlier ideas in this
class (Duarte et al., 2014). A second extension would
be to design local cost functions that attempt to con-
struct the projection by combining different criteria
for different subsets of the input data – for example,
to achieve a globally-better projection that locally be-
haves like t-SNE in some areas and like UMAP in
others. ML techniques can help here by e.g. extend-
ing the HyperNP idea (Appleby et al., 2022) to train
from a set of projection techniques run on the same
input dataset. Further inspiration can be gotten from
recent ways in which DL is used for image synthesis
and style transfer, e.g., (Luan et al., 2017).
Beyond the Third Dimension: How Multidimensional Projections and Machine Learning Can Help Each Other
13

Inverse Projection Quality. Only a handful of qual-
ity metrics exist to gauge how good inverse projec-
tion techniques are (Sec. 4.2). This is not surprising
since the main use-case of such tools is to create new
data points for locations in the 2D image where no
existing data point projects. As such, defining what
a good inverse projection should return in such areas
is conceptually hard. Yet, possibilities exist. One can
e.g. use a ML approach where an unseen test set is
kept apart from the construction of the inverse pro-
jection and is used to assess the quality of such a
trained model. For this, suitable distance approxima-
tions need to be designed, which can borrow from ex-
isting ML approaches to assess regressors. An equally
interesting question is how to design a scale, or hier-
archy, of errors. It is likely that differently inversely-
projected points x
′
= P
−1
(P(x)) that deviate from its
ground-truth location x by the same distance ∥x
′
− x∥
are not equally good, or equally bad, depending on
the application perspective. As such, inverse projec-
tion quality metrics may need to be designed in an
application-specific way.
Figure 9: Gradient map of NNInv inverse projection con-
structing from a t-SNE projection of an uniformly sam-
pled sphere. Hot map regions indicate nearby 2D points
that inversely project to far-apart nD points (green line, top
sphere). Dark map regions indicate nearby 2D points that
inversely project to close nD points (orange line, bottom
sphere). The map captures thus the joint projection-inverse
projection errors (Espadoto et al., 2021a).
Figure 9 shows another challenge of measuring in-
verse projection quality. The image shows a so-called
gradient map which encodes the gradient magnitude
of the P
−1
function (in this case constructed with
NNInv). Hot regions on this map indicate nearby 2D
points which backproject far away from each other.
However, we cannot directly say that this is an er-
ror of the inverse projection P
−1
– these regions may
well correspond to areas where the direct projection
P, in this case t-SNE, squeezed faraway data points
to fit them in the 2D space – thus areas of low con-
tinuity (Venna and Kaski, 2006). It is thus essential,
when designing inverse projection errors, to be able
to factor out errors induced by the direct projection.
Dynamic Projections. Section 3.3 has briefly intro-
duced dynamic projections. These are extensions of
the standard, static, projection techniques which aim
to handle a dataset consisting of high-dimensional
points which maintain their identity while changing
their attribute values through time. Dynamic pro-
jections have a wealth of applications – simply put,
anywhere one wants to study high-dimensional data
which changes over time. However, only a handful
of dynamic projection techniques exist (Vernier et al.,
2021; Vernier et al., 2020), and their quality – as
gauged by established quality metrics – is good in
data structure preservation or data dynamics preser-
vation but not both aspects. Designing a dynamic
projection technique that accurately maps both data
structure and dynamics is a grand challenge for the
infovis community. Following good recent results
in using ML for DR, it looks highly interesting to
explore ML (and in particular DL) for creating dy-
namic projections. A sub-challenge here is that, since
good ground-truth dynamic projections are hard to
construct, the supervised way (NNP-class methods)
may be hard to follow, so the self-supervised direc-
tion seems more promising.
6 CONCLUSIONS
For a long time, the research topics of dimensional-
ity reduction (DR) and machine learning (ML) have
evolved in parallel and with only tangential encoun-
ters. In recent years, however, the two domains have
grown increasingly close, spurred by two develop-
ments. On the ML side, and largely due to the XAI
movement aiming at opening the ‘black box’ of ML
(and in particular deep learning) models, there is in-
creasing awareness and usage of information visual-
ization techniques to explore ML artifacts. On the DR
side, increasingly better projection methods in terms
of a wide range of quality aspects (e.g., accuracy,
speed, stability, to mention just a few) have appeared,
which are readily adopted to create new visual tools
for ML exploration. More recently, the DR commu-
nity has also started to adopt ML techniques to cre-
ate better projection algorithms. Operational difficul-
ties such as poorly scalable and/or hard-to-replicate
algorithms are disappearing. As such, all is there for
cross-fertilization between ML and DR.
We see this convergence trend which unites re-
search and researchers in DR and ML growing in the
VISIGRAPP 2023 - 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications
14

near future, with both areas positively feeding each
other in terms of research questions and tasks, and
also solutions. A strong common mathematical back-
ground also unites researchers in the two fields, mak-
ing it easy to exchange research questions, ideas, and
results. We also see several high-potential research di-
rections at the crossroads of ML and DR: using dense
maps to explore and improve classifiers and regres-
sors, effectively mapping the whole high-dimensional
space to an image; using ML to create highly cus-
tomized, high-quality projections for both static and
dynamic data; and developing inverse projections to
meet all the standards that current direct projection
techniques have. Such developments, jointly enabled
by DR and ML researchers, will have impact far be-
yond these two fields.
REFERENCES
Amorim, E., Brazil, E., Daniels, J., Joia, P., Nonato, L.,
and Sousa, M. (2012). iLAMP: Exploring high-
dimensional spacing through backward multidimen-
sional projection. In Proc. IEEE VAST.
Amorim, E., Brazil, E., Mena-Chalco, J., Velho, L., Nonato,
L. G., Samavati, F., and Sousa, M. (2015). Facing the
high-dimensions: Inverse projection with radial basis
functions. Computers & Graphics, 48:35–47.
Appleby, G., Espadoto, M., Chen, R., Goree, S., Telea, A.,
Anderson, E., and Chang, R. (2022). HyperNP: Inter-
active visual exploration of multidimensional projec-
tion hyperparameters. CGF, 41(3):169–181.
Azodi, C., Tang, J., and Shiu, S. (2020). Opening the black
box: Interpretable machine learning for geneticists.
Trends Genet, 36(6):442–455.
Benato, B., Gomes, J., Telea, A., and Falc
˜
ao, A. (2020).
Semi-automatic data annotation guided by feature
space projection. Pattern Recognition, 109:107612.
Benato, B., Telea, A., and Falc
˜
ao, A. (2018). Semi-
supervised learning with interactive label propagation
guided by feature space projections. In Proc. SIB-
GRAPI, pages 392–399.
Botchkarev, A. (2019). Performance metrics (error mea-
sures) in machine learning regression, forecasting and
prognostics: Properties and typology. Interdisci-
plinary J. of Information, Knowledge, and Manage-
ment, 14:45–79.
Bredius, C., Tian, Z., and Telea, A. (2022). Visual explo-
ration of neural network projection stability. In Proc.
MLVis.
Duarte, F., Sikanski, F., Fatore, F., Fadel, S., and
Paulovich, F. V. (2014). Nmap: A novel neighborhood
preservation space-filling algorithm. IEEE TVCG,
20(12):2063–2071.
Espadoto, M., Appleby, G., A. Suh, D. C., Li, M.,
Scheidegger, C., Anderson, E., Chang, R.,
and Telea, A. (2021a). UnProjection: Lever-
aging inverse-projections for visual analyt-
ics of high-dimensional data. IEEE TVCG.
DOI:10.1109/TVCG.2021.3125576.
Espadoto, M., Hirata, N., and Telea, A. (2020). Deep learn-
ing multidimensional projections. Information Visual-
ization, 9(3):247–269.
Espadoto, M., Hirata, N., and Telea, A. (2021b). Self-
supervised dimensionality reduction with neural net-
works and pseudo-labeling. In Proc. IVAPP.
Espadoto, M., Martins, R., Kerren, A., Hirata, N., and
Telea, A. (2019a). Toward a quantitative survey
of dimension reduction techniques. IEEE TVCG,
27(3):2153–2173.
Espadoto, M., Rodrigues, F. C. M., Hirata, N., and Telea,
A. (2021c). OptMap: Using dense maps for visualiz-
ing multidimensional optimization problems. In Proc.
IVAPP.
Espadoto, M., Rodrigues, F. C. M., Hirata, N. S. T., Jr,
R. H., and Telea, A. (2019b). Deep learning inverse
multidimensional projections. In Proc. EuroVA.
Garcia, R., Telea, A., da Silva, B., Torresen, J., and Comba,
J. (2018). A task-and-technique centered survey on
visual analytics for deep learning model engineering.
Computers and Graphics, 77:30–49.
Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely
randomized trees. Machine learning, 63(1):3–42.
Guyon, I., S, S. G., and Ben-Hur, A. (2004). Result anal-
ysis of the NIPS 2003 feature selection challenge. In
Advances in Neural Information Processing Systems,
page 545?552.
Hinton, G. E. and Salakhutdinov, R. R. (2006). Reducing
the dimensionality of data with neural networks. Sci-
ence, 313(5786):504–507.
Jiang, T., Gradus, J., and Rosellini, A. (2020). Supervised
machine learning: A brief primer. Behavior Therapy,
51(5):675–687.
Kim, Y., Espadoto, M., Trager, S., Roerdink, J., and Telea,
A. (2022). SDR-NNP: Sharpened dimensionality re-
duction with neural networks. In Proc. IVAPP.
Lespinats, S. and Aupetit, M. (2011). CheckViz: Sanity
check and topological clues for linear and nonlinear
mappings. CGF, 30(1):113–125.
Luan, F., Paris, S., Shechtman, E., and Bala, K. (2017).
Deep photo style transfer. In Proc. IEEE CVPR.
McInnes, L., Healy, J., and Melville, J. (2018). UMAP:
Uniform manifold approximation and projection for
dimension reduction. arXiv:1802.03426v2 [stat.ML].
Minghim, R., Paulovich, F. V., and Lopes, A. A. (2006).
Content-based text mapping using multi-dimensional
projections for exploration of document collections.
In Proc. SPIE. Intl. Society for Optics and Photonics.
Modrakowski, T., Espadoto, M., Falcao, A., Hirata, N., and
Telea, A. (2021). Improving deep learning projections
by neighborhood analysis. In Communication in Com-
puter and Information. Springer.
Nonato, L. and Aupetit, M. (2018). Multidimensional
projection for visual analytics: Linking techniques
with distortions, tasks, and layout enrichment. IEEE
TVCG.
Beyond the Third Dimension: How Multidimensional Projections and Machine Learning Can Help Each Other
15

Oliveira, A. A. M., Espadoto, M., Hirata, R., and Telea, A.
(2022). SDBM: Supervised decision boundary maps
for machine learning classifiers. In Proc. IVAPP.
Paulovich, F. V. and Minghim, R. (2006). Text map ex-
plorer: a tool to create and explore document maps.
In Proc. IEEE IV, pages 245–251.
Rauber, P., Fadel, S. G., Falc
˜
ao, A., and Telea, A. (2017a).
Visualizing the hidden activity of artificial neural net-
works. IEEE TVCG, 23(1):101–110.
Rauber, P., Falcao, A., and Telea, A. (2016). Visualizing
time-dependent data using dynamic t-SNE. In Proc.
EuroVis – short papers, pages 43–49.
Rauber, P. E., Falc
˜
ao, A. X., and Telea, A. C. (2017b). Pro-
jections as visual aids for classification system design.
Inf Vis, 17(4):282–305.
Rodrigues, F. C. M., Espadoto, M., Jr, R. H., and Telea,
A. (2019). Constructing and visualizing high-quality
classifier decision boundary maps. Information,
10(9):280–297.
Rodrigues, F. C. M., Jr., R. H., and Telea, A. (2018). Image-
based visualization of classifier decision boundaries.
In Proc. SIBGRAPI.
Schulz, A., Gisbrecht, A., and Hammer, B. (2015). Us-
ing discriminative dimensionality reduction to visual-
ize classifiers. Neural Process. Lett., 42(1):27–54.
Schulz, A., Hinder, F., and Hammer, B. (2020). DeepView:
Visualizing classification boundaries of deep neural
networks as scatter plots using discriminative dimen-
sionality reduction. In Bessiere, C., editor, Proc. IJ-
CAI, pages 2305–2311.
Shwartz-Ziv, R. and Tishby, N. (2017). Opening the
black box of deep neural networks via information.
arXiv:1703.00810 [cs.LG].
Thiyagalingam, J., Shankar, M., Fox, G., and Hey, T.
(2022). Scientific machine learning benchmarks. Na-
ture Reviews Physics, 4:413–420.
Tzeng, F. Y. and Ma, K.-L. (2005). Opening the black box –
data driven visualization of neural networks. In Proc.
IEEE Visualization.
van der Maaten, L. and Hinton, G. E. (2008). Visualizing
data using t-sne. JMLR, 9:2579–2605.
van der Zwan, M., Codreanu, V., and Telea, A. (2016).
CUBu: Universal real-time bundling for large graphs.
IEEE TVCG, 22(12):2550–2563.
Venna, J. and Kaski, S. (2006). Visualizing gene interaction
graphs with local multidimensional scaling. In Proc.
ESANN, pages 557–562.
Vernier, E., Comba, J., and Telea, A. (2021). Guided sta-
ble dynamic projections. Computer Graphics Forum,
40(3):87–98.
Vernier, E., Garcia, R., da Silva, I., Comba, J., and Telea,
A. (2020). Quantitative evaluation of time-dependent
multidimensional projection techniques. Computer
Graphics Forum, 39(3):241–252.
VISIGRAPP 2023 - 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications
16
