Course Scheduling Under Uncertainty for Defence Workforce Training

Trudy Lam

1 a

, Vicky Mak-Hau

1 b

and Kristan Pash

School of Information Technology, Deakin University, Waurn Ponds, Geelong, Australia

Defence Science and Technology Group, Department of Defence, Fishermans Bend, Australia

Keywords:

Scheduling, Uncertainty, Simulation, Optimisation.

Abstract:

In this paper, we revisit a previously studied Defence course scheduling problem where trainees are allocated

to course sessions, the Simultaneous Sequencing and Allocation Problem. The courses have a non-linear

prerequisite structure, each course has a number of sessions, and each session has a class size limit. The

uncertainty in the planning is due to a historical pass-rate associated with each course, and a trainee will not

be able to proceed once s/he fails a course. We develop a simulation-based three-stage solution algorithm

that optimises the scheduling for each scenario using integer programming. The way pass-rates are handled

is different from previous approaches, and because of this, we are able to provide decision-makers with better

insights on best-case, average-case, and worst-case outcomes.

1 INTRODUCTION

In this paper, we study a Defence trainee course

scheduling problem with multiple business require-

ments.

Defence personnel maintain and develop their

professional skills by attending applicable courses

throughout each phase of their careers, with some

courses forming part of the requirements for promo-

tion to higher ranks.

The efﬁcient scheduling of course sessions and al-

locating personnel to sessions can reduce the number

of times each course must be sessioned, reduce wait-

ing times, give more time for individuals to practice

their learned skills, reduce time to promotion, and in-

crease morale.

1.1 Problem description

The optimisation problem concerns the allocation of

Defence trainees to course sessions in a planning hori-

zon.

The courses have a pre-requisite structure. See

Figure 1 for an example, where the course structure

of a 25-course instance is provided. Since the courses

are not linearly structured, there are multiple com-

ponents of the courses that can be taken in a differ-

ent order. Take the 25-course system as an example.

https://orcid.org/0000-0003-1412-6598

https://orcid.org/0000-0002-9306-5780

Once a trainee has successfully completed Course 2,

they can proceed to either Courses 3, 4, 6, 7, 8, 9, 10

or 17 without violating any pre-requisite requirement.

Course 13, on the other hand, can only be taken if a

trainee has successfully completed Courses 1, 2, and

4–12, but it can be taken either before or after Courses

3 and 17. Course 13 is also a direct pre-requisite for

Courses 14 and 15 and an implied pre-requisite for

Courses 16–25. Each trainee has only one chance to

complete a course. If a trainee fails a course, s/he is

most likely offered a transfer to a less complex trade

or be asked to leave the service. Each course has a

number of sessions. A trainee will only take one ses-

sion for each course. All sessions for the same course

have the same duration; however, the span of different

sessions of a course may overlap. A trainee can only

take one (course) session at a time. Each course ses-

sion has a lower limit and an upper limit on the size

of the class (i.e., the number of trainees that can be

admitted to the session).

There is a historic pass-rate associated with each

course (as shown in Figure 1). We were informed

that the pass-rates are independent of the sequence

the courses taken so far by a trainee. This means that,

for example, the probability of a trainee successfully

completing Courses 1, 2, 6, 11, and 8 will be 0.3249.

However, these ﬁve courses can be taken in one of the

following orders (1, 2, 6, 11, 8), (1, 2, 6, 8, 11), and

(1, 2, 8, 6, 11). This leads to an interesting question -

how far can each trainee reach in the system (in other

words, how many courses can a trainee complete be-

Lam, T., Mak-Hau, V. and Pash, K.

Course Scheduling Under Uncertainty for Defence Workforce Training.

DOI: 10.5220/0011924200003396

In Proceedings of the 12th International Conference on Operations Research and Enterprise Systems (ICORES 2023), pages 269-278

ISBN: 978-989-758-627-9; ISSN: 2184-4372

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

269

Figure 1: This ﬁgure illustrates the course structure of the problem instances with 25 courses. The nodes are the courses. An

arc between two courses indicates the pre-requisite relation (e.g., Course 1 is a pre-requisite of Course 2). The numbers in red

on top of each node represent the historic pass-rate of the course the node represents.

fore s/he is out of the system) and in what sequence

are these courses completed?

A mathematical description of the Simultaneous

Sequencing and Allocation Problem (SSAP) is given

below. Consider a directed graph D = (V,A), where

V represents all the course sessions and is partitioned

to |C | clusters. Each cluster represents a course, and

the vertices in each cluster represent available ses-

sions for the course. Each vertex has a capacity (class

size) and a time-window associated with it. The time-

windows for all vertices in the same cluster have the

same span; however, the time windows themselves

are different but may overlap. Precedence relations

exist between some clusters. The optimisation prob-

lem is to ﬁnd a “route” for each trainee such that no

more than one vertex from each cluster is visited. In

this aspect, the SSAP problem is similar to a gener-

alized Vehicle Routing Problem with Time-Windows

(GVRP-TW). However, the major difference is that

vehicles do not disappear mid-tour in a Vehicle Rout-

ing Problem, but in the SSAP problem, trainees will

not be able to proceed if they fail a course.

1.2 Literature Review

Optimal scheduling and timetabling problems can be

found in many industry sectors, e.g., hospital trainees

scheduling (Beli

en and Demeulemeester, 2006), mil-

itary aircraft ﬂeet management, (Looker et al., 2017),

and army training (Lee et al., 2009), among others.

Many are based on graphs and networks, for exam-

ple, timetabling problems as graph colouring prob-

lems, (de Werra, 1985). Integer programming models

that lead to further research in solution methodologies

for real-world timetabling problems can be found in,

e.g., (Carter, 1989; Costa, 1994; Burke et al., 2005).

Many heuristic approaches for timetabling- as well as

scheduling-family problems can be found in the liter-

ature. For example, (Glover and Laguna, 1997; Battiti

and Tecchiolli, 1994; Dell’Amico and Trubian, 1993;

Hertz and Widmer, 1996; Nowicki and Smutnicki,

1996). Regarding meta-heuristic algorithms, their

hybrids and hyper-heuristics have some success in

scheduling problems in various domains (Teoh et al.,

2015; Pillay, 2016). In vehicle routing-family prob-

lems, much recent research is on the “rich” optimisa-

tion version of the problems, such as (Lam and Hen-

tenryck, 2016).

In the literature of scheduling work in the educa-

tion domain, the majority of work are on examination

timetabling and course timetabling (Rudov

a et al.,

2011; Bettinelli et al., 2015; M

uller and Rudov

2016). The university course timetabling problems

are mainly about scheduling lectures, tutorials, and

so on, that recurs on a weekly basis, be it schedul-

ing classes after students have enrolled, whereas in

post-enrolment course timetabling, or the schedule of

classes are deﬁned before enrolment in curriculum-

based course timetabling. For this reason, they are

very different from the SSAP problem.

WAPAT 2023 - Special Session on Workforce Analytics - Practical Application and Theory

270

In military training, policy effects, bottlenecks,

and resource utilisation has been studied in, e.g.,

(Davenport et al., 2007; S

eguin and Hunter, 2013;

Novak et al., 2015; Nguyen et al., 2016). System

dynamics simulations in workforce planning is re-

viewed in (Wang, 2005). Heuristic approaches can

be found in (Yang and Ignizio, 1987) for peacetime

scheduling of training activities of battalions where

decisions must be made in regards to the kind of

training tasks to be performed, by which battalion,

at what time, with the objective of minimizing the

make-span. In military and other aircrew training,

heuristic methods can be found in, e.g., (Lee et al.,

2009). A hybrid heuristic-integer programming ap-

proach was used to schedule examination timetables

for cadets in (Wang et al., 2010). A two-phase heuris-

tic method is proposed for scheduling army battalion

training exercises in (Yang and Ignizio, 1987). Inte-

ger programming has been applied in (Scott, 2005)

to produce multi-year schedules at the Defence Lan-

guage Institute. In (Qi et al., 2004), a hybrid Branch

and bound method and heuristics are applied to the

scheduling of the retraining of pilots for Continen-

tal Airlines. Dynamic programming and column gen-

eration approaches were used in (Raffensperger and

Schrage, 2008) for training in a tank battalion. A re-

source scheduling problem is presented in (McGinnis

and Fernandez-Gaucherand, 1994) for the US Army’s

basic combat training program. An intra-theatre mil-

itary airlift problem was presented in (Brown et al.,

2013). In (Squires and Hoffman, 2015), a mili-

tary maintenance planning and scheduling problem is

modelled as ILPs and solved using Benders decom-

position. A logic-based Benders decomposition ap-

proach for multi-phase course timetabling is proposed

in (Esmaeilbeigi et al., 2022).

The SSAP problem has been studied in (Nguyen

et al., 2018), (Mak-Hau et al., 2021), and (Nguyen

et al., 2022). The common feature of these meth-

ods is that schedules are formed by sequencing the

course sessions either before the optimal allocation

of trainees to these schedules, or the two problems

solved simultaneously. The course pass-rates are han-

dled deterministically in the sense that the number of

trainees to be taking a particular session of a course

is obtained by multiplying the number of trainees al-

located to the session by the accumulative pass-rate

from the ﬁrst course to the course immediately before

the current course. Further details will be provided in

Section 3.

In (Nguyen et al., 2018), the timetabling problem

is solved as a generalised exact cover problem. The

set of all feasible schedules is enumerated using Don-

ald Knuth’s Dancing Links algorithms DLX.

On the other hand, multiple mixed-integer linear

programming (MILP)-based approaches are proposed

and tested in (Mak-Hau et al., 2021). The ﬁrst MILP

model considers each trainee individually as a sched-

ule. A continuous decision variable is used to repre-

sent the probability that a trainee has not failed when

s/he reaches a course, and the class size constraint

is based on the expected number of trainees attend-

ing a course session. The second method is a two-

stage approach with the Stage-one MILP using an in-

teger variable to determine the expected number of

trainees taking a schedule. Given that the Stage-one

MILP did not show signiﬁcant improvement, Stage-

two MILP was not implemented. The third method

is a column generation-based heuristic, where an in-

teger programming (IP) model is solved, with each

column as a schedule. Column generation is used

for solving the Linear Programming (LP) relaxation,

and the columns obtained are ultimately used as the

set of columns in the IP. The LP solution to all but

two instances tested are naturally integral, and for the

ones that are not, they are solved to optimality at the

root node in under 0.05 seconds due to the pre-solve,

reduction, and cutting planes implemented automati-

cally by CPLEX.

Another search algorithm is proposed in (Nguyen

et al., 2022), where schedules with minimum cost-

function values are generated by Knuth’s Dancing

Links indexing scheme with A

∗

search, and trainees

are greedily allocated until the maximum class size is

reached by one or more of sessions. This approach

is most computationally efﬁcient when compared to

(Nguyen et al., 2018) and (Mak-Hau et al., 2021).

These methods essentially provide an “expected

number” of trainees attending each course session,

and it must be within the class size’s lower and up-

per limits. Essentially this gives users insights into

an average-case outcome. If resources (such as in-

structors and equipment) are planned based on the

average-case scenario, in real-life practice, there may

be an under-resourcing issue. However, resourcing

for worst-case or somewhere between average-case

and worst-case requires the knowledge of what the

worst-case scenarios are, which previous approaches

cannot tell us unless we change the pass-rate. For this

reason, we propose an alternative approach that will

allow us to obtain insights on best-case, average-case,

and worst-case solutions, and to take them into con-

sideration in evidence-based decision-making.

1.3 Contributions and Outline of Paper

This paper proposes a new paradigm to integrate his-

torical pass-rates into our optimisation procedure, and

Course Scheduling Under Uncertainty for Defence Workforce Training

271

because of that, we obtained a new integer program-

ming formulation for the SSAP problem. We imple-

mented and extensively tested the new method on the

same set of test instances used in (Nguyen et al., 2018;

Nguyen et al., 2022; Mak-Hau et al., 2021), and pre-

sented best-case, average-case, and worst-case out-

comes in the number of distinct sessions required as

well as total make-span. We provide the Integer Pro-

gramming formulation in Section 2 and a detailed ex-

planation of pass-rate based progression simulation in

Section 3. In Section 4, we present the computational

experiments. Finally, we conclude our ﬁndings and

present future research directions in 5.

2 INTEGER PROGRAMMING

FORMULATION

First we introduce the mathematical notation used in

the rest of the paper. Let:

• S = {1,...,S} be the set of all trainees;

• C = {1, . . .,C} be the set of all courses;

• p

, the pass-rate of Course c;

• K = {1, ...,K} = {1,...,n

+ 1,..., n

1,...,n

c−1

+ 1,.. . , n

} be the set of all sessions;

• E

the time trainee s enters the training program;

• k

min

and k

max

the minimum and maximum num-

ber of trainees Session k can take;

• n

− n

c−1

the number of sessions for Course c;

with n

= 0;

• σ

and ε

the start and end time of Session k; and

• E = {(c,c

′

) | c, c

′

∈ C ,c is a pre-requisite of c

′

}

the set of all pairs of courses with a pre-requisite

relation.

We deﬁne the following decision variables.

• z

∈ {0,1} with z

= 1 indicating Session k is

scheduled and z

= 0 otherwise; and

• x

∈ {0, 1} with x

= 1 indicating trainee s is al-

located to Session k, and x

= 0 otherwise.

We now discuss the constraints used to capture the

business rules. Each trainee will take no more than 1

session for a course.

∑

k=n

c−1

≤ 1, ∀s ∈ S , c ∈ C (1)

The number of trainees enrolled in a session must be

within its lower and upper class size limit.

min

≤

∑

s∈S

≤ k

max

, ∀k ∈ K (2)

The constraint below will ensure that if Course c is a

pre-requisite of Course c

′

, then a trainee cannot take

Course c

′

unless they have taken Course c.

′

∑

k=n

′

−1

≤

∑

k=n

c−1

, ∀s ∈ S , (c,c

′

) ∈ E (3)

Now, if a trainee will take both of Courses c and c

′

then the start date of Course c

′

for this trainee can-

not be earlier than the end date of Course c for this

trainee. To model this requirement, let α

be a bi-

nary decision variable with α

= 1 if trainee s will

complete Course c and α

= 0 otherwise. We have

that

∑

k=n

c−1

, ∀s ∈ S , c ∈ C (4)

We introduce another binary decision variable β

s,c,c

′

with β

s,c,c

′

= 1 representing trainee s will take both

Courses c and c

′

, and β

s,c,c

′

= 0 otherwise (which

means that they trainee would have failed some

courses before reaching Course c

′

). These can be cap-

tured by the following constraints.

s,c

+ α

s,c

′

≤ β

s,c,c

′

+ 1, ∀s ∈ S , (c,c

′

) ∈ E (5)

s,c,c

′

≤ α

s,c

, β

s,c,c

′

≤ α

s,c

′

, ∀s ∈ S , (c, c

′

) ∈ E (6)

We have that

∑

k=n

c−1

+ 1 ≤

′

∑

k=n

′

−1

′

(1 − β

s,c,c

′

), ∀s ∈ S , (c, c

′

) ∈ E (7)

where M

′

is a large number and we used the latest

session ﬁnish time of Course c

′

Each trainee can only be taking one session at a

time. We enumerate the set of all cliques Ξ, where

each clique contains a maximal set of sessions that

cannot be taking simultaneously.

∑

k∈ξ

≤ 1, ∀s ∈ S , ξ ∈ Ξ (8)

See Figure 2 for an illustration of all cliques for Prob-

lem Instance 2repsPrYr 5courses.

3 PROGRESSION SIMULATION

BASED ON PASS-RATE

Previously, the course pass-rates are handled in the

following manner. Take the 5-course problem in-

stances as an example. The historic pass-rates of

Courses C1, C2, C3, C4, and C5 are 0.9, 0.5, 0.9, 0.8,

and 0.7, respectively. Suppose that a trainee takes the

course schedule: C1, C2, C4, C3, followed by C5, in

WAPAT 2023 - Special Session on Workforce Analytics - Practical Application and Theory

272

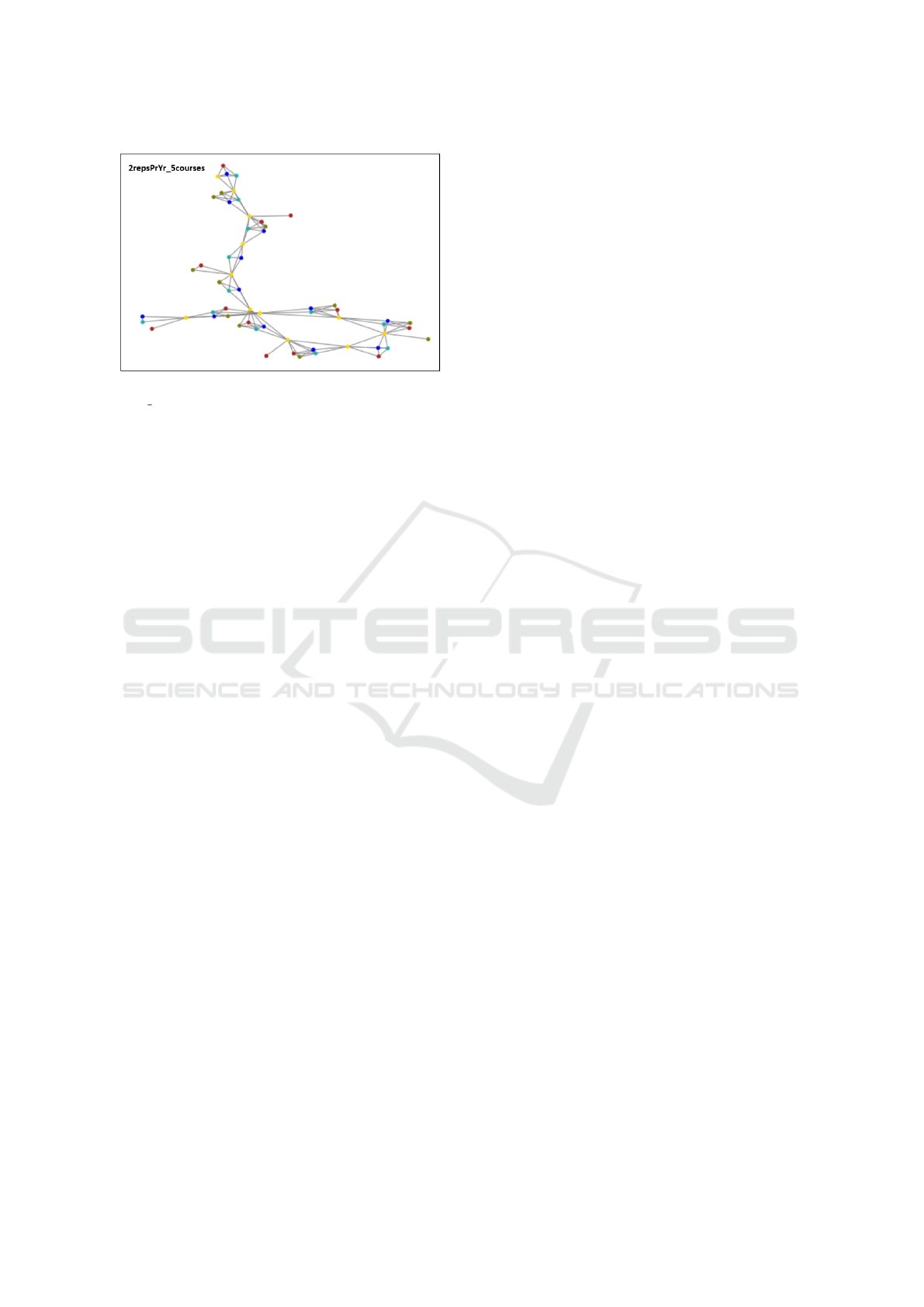
Figure 2: Illustration of the set of all cliques Ξ for the 2rep-

sPrYr 5courses problem instance. The colours represent

the course to which the nodes (i.e., sessions) belong. That

is, blue denotes Course 1, green denotes Course 2, red de-

notes Course 3, olive denotes Course 4, and yellow denotes

Course 5.

this precise order. The cumulative pass-rates will be

0.9, 0.45, 0.36, 0.324, and 0.2268. In other words,

there is a 36% chance, for example, the trainee will

pass C1, C2, and C4. Once s/he makes it to Course

C3; however, the probability of passing the course

is still 80%. Time-feasible schedules (a session for

each course, and all courses must be included ex-

actly once) are either exhaustively enumerated using

DLX (Knuth’s Dancing Links) or generated within a

mixed-integer linear program. For each course ses-

sion, all the schedules generated by DLX that con-

tain the course session are considered in the class-size

constraint.

As an example, suppose that Session 2 of Course

C3 has a lower class size limit and an upper limit of

2 and 3, respectively. Now, in a solution, Session

2 of Course C3 are only taken by Schedule 1 and

Schedule 2. Schedule 1, with the following order:

(C1, C2, C4, C3, C5), has two trainees allocated to

it. The probability that a trainee can pass courses C1,

C2, and C4 and reach C3 is 36%. Schedule 2, with

the following order: C1, C2, C3, C4, C5, has three

trainees allocated to it, and also takes Session 2 of

Course C3. The probability a trainee can pass courses

C1 and C2 and reach C3 is 45%. The expected num-

ber of trainees taking Session 2 of Course C3 will be

0.36 × 2 + 0.45 × 3 = 2.07. Since 2 ≤ 2.07 ≤ 3, the

class size constraint for Session 2 of Course C3 is sat-

isﬁed. Pass-rates handled in this manner, in a way,

provide users with an average-case outcome.

In reality, however, if we have both trainees allo-

cated to Schedule 1 and two out of three trainees allo-

cated to Schedule 2 passing the relevant prior courses

and reach Course C3, the upper class size limit of

3 would have been violated, and one of them would

have to be re-allocated to another session. This has an

impact on resourcing for the planning horizon. Re-

source planning based on an average-case scenario is

risky, and therefore being able to obtain insights into

the risk boundaries is critical.

In what follows, we propose a new approach for

handling pass-rates. The key idea of the proposed

method is the course failure simulation, which deter-

mines the course at which a trainee may fail based on

the historic pass-rates. A trainee who fails a course

will not be able to repeat the course. As a result, fail-

ing a course suggests that the trainee will not take all

other courses for which the failed course is the direct

or implied prerequisite course. Additionally, the pro-

posed method incorporates a post-processing proce-

dure in order to determine the courses to be done prior

to the failed course. This post-processing procedure

can help ﬁnd the set of to-do courses more easily for

some large problem instances. It is noted that the ex-

istence of a large number of courses that can be done

before the failed course renders the enumeration of all

possible permutations inefﬁcient. Take the 25-course

problem instance (see Figure 1) as an example. If the

trainee fails Course 3, then there are 22 other courses

(i.e., 4, 5, ..., 24, 25) that Course 3 can be among in

any position. This gives a total of 23! possible permu-

tations.

The new approach is summarised in Algorithm 1.

In this pseudocode, pred(c) denotes the set of direct

and implied prerequisite courses of c ∈ C , succ(c) de-

notes the set of all courses for which c is a direct or

implied prerequisite course.

The algorithm starts with Phase 1 (WHILE loop

lines 5 - 12), which is an iterative procedure that ﬁnds

the failed course for the considered trainee. At each

iteration, a course c is assigned a random number

r generated from uniform distribution U(0,1). If r

is not greater than the pass-rate, then the procedure

moves to the next course. Otherwise, this course c

will be considered as a failed course. In the pseu-

docode below, the failed course of trainee s is denoted

by c

∗

. This procedure terminates when a failed course

is found or when all courses have been considered.

Note that if c

∗

is 0 when the While loop completes,

this indicates that the trainee passes all courses. If

this happens, Phase 2 will not be invoked, and the al-

gorithm simply returns the set of all courses (lines 13

- 15).

Given the failed course c

∗

of trainee s, Phase 2 of

the algorithm includes a post-processing procedure,

which attempts to determine what number of courses

and exactly which courses are done before c

∗

(lines 17

- 60). When determining how many courses from the

set Parallel(c

∗

) that should be done before the failed

Course Scheduling Under Uncertainty for Defence Workforce Training

273

Algorithm 1: Simulating Trainee’s Progression.

1: Input: Trainee s ∈ S; pass-rate p

,∀c ∈ C ;

2: Output: Failed course c

∗

; set of courses that trainee s may com-

plete before the failed course R

3: Phase 1: Determine at which course the trainee may fail

4: Set c ← 1, c

∗

← 0

5: while c ≤ C do

6: Generate r ∼ U (0, 1)

7: if r ≤ P

then

8: Set c ← c + 1

9: else

10: c

∗

← c; break

11: end if

12: end while

13: if c

∗

= 0 then

14: return C

15: end if

16:

17: Phase 2: Determine which courses are done before the failed

course c

∗

18: Initialise parallel(c

∗

) ← C \ (pred(c

∗

) ∪ succ(c

∗

) ∪ {c

∗

})

19: Set n ← |parallel(c

∗

20: Calculate π

,k = 0,...,n according to (9)

21: Using π

, randomly select a number k ∈ [0, ...,n]

22: ImmediateNext ←

0, status ← True

23: for all c ∈ parallel(c

∗

) do

24: for all j ∈ pred(c) do

25: if j ∈ parallel(c

∗

) then

26: status ← False; break

27: end if

28: end for

29: if status = True then

30: ImmediateNext ← ImmediateNext ∪ {c}

31: end if

32: end for

33: R

←

34: if k ≤ |ImmediateNext| then

35: while |R

| ≤ k do

36: c

′

← randomly select a course from the set

ImmediateNext.

37: R

← R

∪ {c

′

}

38: ImmediateNext ← ImmediateNext \ {c

′

}

39: end while

40: else

41: while |R

| ≤ k do

42: c

′

← randomly select a course from the set

ImmediateNext.

43: R

← R

∪ {c

′

}

44: F ← parallel(c

∗

) \ (R

∪ ImmediateNext)

45: ImmediateNext ← ImmediateNext \ {c

′

}

46: for all i ∈ F do

47: status ← True

48: for all j ∈ pred(i) do

49: if j ̸∈ R

then

50: status ← False; break

51: end if

52: end for

53: if status = True then

54: ImmediateNext ← ImmediateNext ∪ {i}

55: end if

56: end for

57: end while

58: end if

59: Add (c,c

∗

) to E, for all c ∈ R

60: R

← R

∪ pred(c

∗

)

61: return c

∗

, R

course (lines 18 - 21), the number is chosen randomly

with non-uniform probability, i.e., larger number has

lower probability of being chosen. Speciﬁcally, the

probability of having to do exactly k courses before

the failed course is given by

n − k + 1

(n + 1)(n + 2)/2

, (9)

where n is the total number of courses in the set

Parallel(c

∗

). The rationale behind (9) is that as

there needs to be more courses done before the failed

course, hence the higher the chance a trainee would

have failed before they reach this course. A more so-

phisticated formula can be considered and we leave

this for future research. Let k be the number cho-

sen at random based on (9). The next step of the

post-processing procedure is as follows. First, a set

of courses that can be immediately taken after the

last course in pred(c

∗

), denoted by ImmediateNext,

is constructed (lines 22 - 32). Then, we initialise

a set of courses that trainee s may complete before

the failed course, denoted by R

, which is empty at

the beginning. Next, we randomly select a course

′

∈ C from the set ImmediateNext and add it into

the set R

. If the size of the set ImmediateNext

is not greater than k, this step repeats by adding

courses from ImmediateNext to R

until the size of

ImmediateNext reaches k. On the other hand, if the

size of the set ImmediateNext is greater than k, an ad-

ditional step is performed to insert courses that can

be immediately done after course c

′

, that is not al-

ready in ImmediateNext. We present an example of

the trainee’s progression simulation procedure below

using a 25-course problem instance.

Example. Suppose that the considered trainee, i.e.

s = 1, fails course 3 (see Figure 3 for an illus-

tration of the failed course). According to the

course structure in Figure 1, we have pred(3) =

{1,2} and succ(3) =

0. Thus, the set of courses

that can be completed before reaching Course 3 is

Parallel(3) = {1,...,25}\{1, 2}\{3} = {4, 5, ...,25}

and the set of courses that can be immediately taken

after the last course in pred(3), i.e., Course 2, is

ImmediateNext = {4,6,7,8,9,10,17}. Suppose that

the random number chosen is 5, which means that

the trainee may complete ﬁve courses before reach-

ing Course 3. Since the size of ImmediateNext is

greater than 5, the algorithm randomly selects ﬁve

courses from ImmediateNext and adds them to R

e.g., R

= {4,6,7,10,17}. Otherwise, if the random

number chosen is 8, which is greater than the size of

ImmediateNext. In this case, R

is constructed as fol-

lows:

• Iteration 1: Suppose that Course 6 was cho-

sen at random from ImmediateNext. Then,

WAPAT 2023 - Special Session on Workforce Analytics - Practical Application and Theory

274

we have R

= {6} and ImmediateNext =

{4,7,8,9,10,17,11}

• Iteration 2: Suppose that Course 4 was cho-

sen at random from ImmediateNext. Then,

we have R

= {6,4} and ImmediateNext =

{7,8,9,10,17,11,5}

• Iteration 3: Suppose that Course 5 was cho-

sen at random from ImmediateNext. Then,

we have R

= {6,4,5} and ImmediateNext =

{7,8,9,10,17,11}

• Iteration 4: Suppose that Course 7 was cho-

sen at random from ImmediateNext. Then,

we have R

= {6, 4, 5, 7} and ImmediateNext =

{8,9,10,17,11}

• Iteration 5: Suppose that Course 11 was cho-

sen at random from ImmediateNext. Then, we

have R

= {6,4,5,7,11} and ImmediateNext =

{8,9,10,17,12}

• Iteration 6: Suppose that Course 12 was chosen

at random from ImmediateNext. Then, we have

= {6,4,5,7,11,12} and ImmediateNext =

{8,9,10,17}

• Iteration 7: Suppose that Course 17 was chosen

at random from ImmediateNext. Then, we have

= {6, 4,5,7,11,12,17} and ImmediateNext =

{8,9,10}

• Iteration 8: Suppose that Course 10 was cho-

sen at random from ImmediateNext. Then,

we have R

= {6, 4,5,7,11,12,17,10} and

ImmediateNext = {8,9}

• Finally, R

= {6,4,5,7,11,12,17,10} ∪ {1,2},

which gives R

= {1, 2, 4, 5, 6,7,10,11,12,17}

Figure 3: Finding a course that the trainee may fail.

4 COMPUTATIONAL

EXPERIMENTS

This section presents the results of computational ex-

periments aimed at the evaluation of the new approach

to deal with course pass-rates. All computational ex-

periments were conducted on a computer with Intel

Core i5-7300U 2.60GHz and 8GB RAM. We coded

our models and algorithms in Python. IBM ILOG

CPLEX 12.10 was used to solve the mathematical

programming models.

The computational experiments use the synthetic

instances comprised of 5, 6, 15, 20, and 25 courses.

These instances are the same as in (Mak-Hau et al.,

2021). For each course, the number of sessions range

from 7 to 24 sessions, the durations range from 1 to 30

weeks, and the pass-rates range from 0.5 to 1. There

are 24 trainees in each instance. Table 1 summarizes

the main characteristics of the 14 synthetic instances.

In what follows, Section 4.1 explains a three-

stage approach to optimally allocate course-sessions

to trainees taking into account the historic pass-rate.

Section 4.2 evaluates the performance of the proposed

trainee’s progression simulation procedure.

4.1 Optimisation Procedure

In order to produce an optimal course-sessions-

trainees allocations, while considering uncertainty,

speciﬁcally, the course pass-rate, we propose a

simulation-based three-stage solution approach (see

Figure 4). The ﬁrst stage determines, for each trainee,

the course s/he fails and the set of courses that s/he

may complete before the failed course, which can be

obtained using Algorithm 1 described in Section 3.

Each trainee s ∈ S thus has the associated set of to-do

courses A

= R

∪ {c

∗

}. Given A

,∀s ∈ S , the second

stage tackles the SSAP problem, where the objective

is that the total number of course-sessions to trainees

allocations is maximised. The Integer Programming

model used in the second stage is as follows.

max : Z

stage2

∑

s∈S

∑

k∈K

(10)

s.t. (1) − (8)

= 0, ∀s ∈ S , c ∈ C \ A

k = n

c−1

+ 1,...,n

(11)

where (11) ﬁxes the x-variables to 0 for the course

sessions that the trainees cannot take. Note that the al-

location of course-sessions to trainees obtained from

the second stage is unlikely to be optimal, since we

seek for a maximum number of allocations in this

stage. The third stage attempts to improve the alloca-

tions by solving the following Integer Programming

Course Scheduling Under Uncertainty for Defence Workforce Training

275

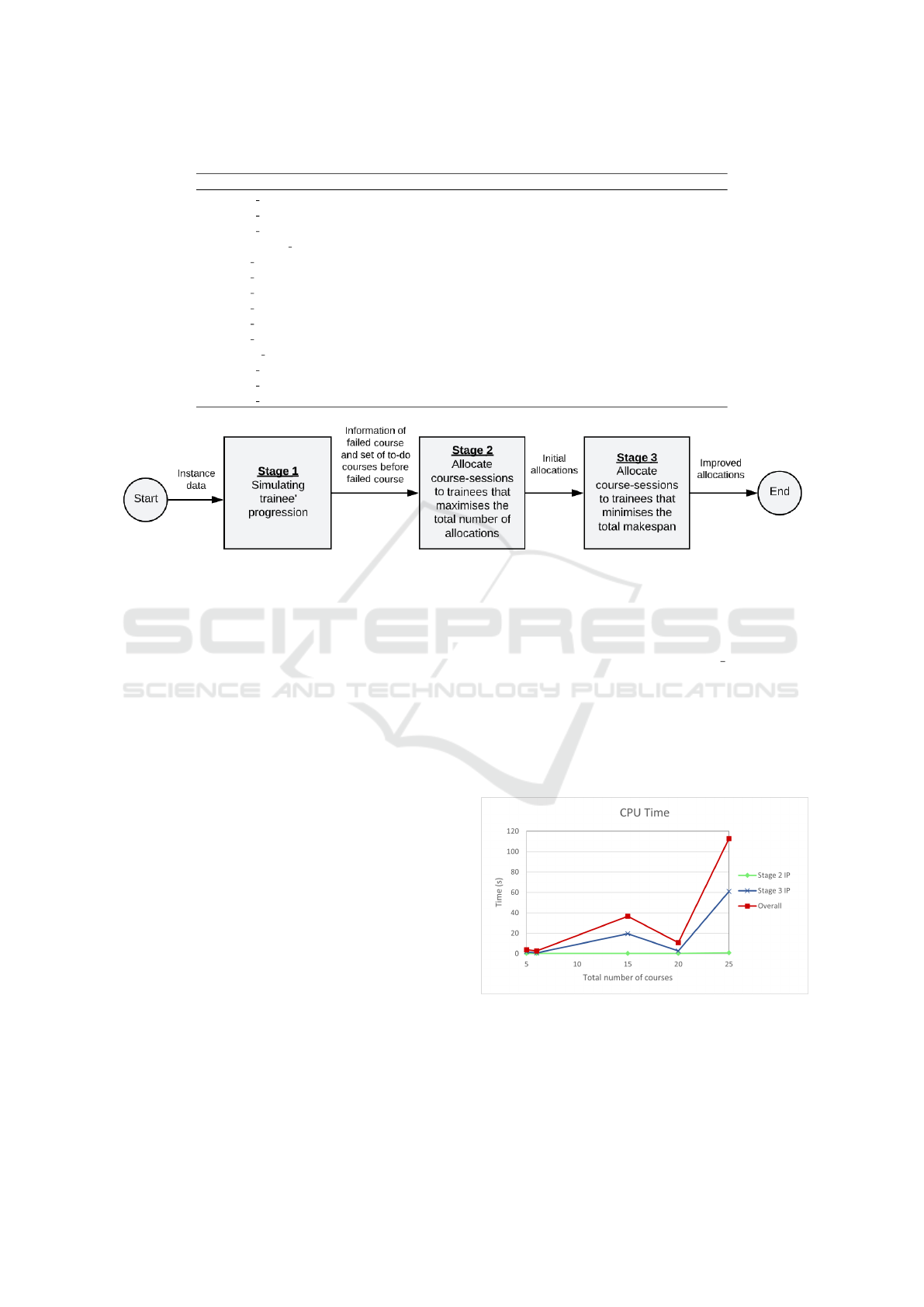
Table 1: Characteristics of the problem instances.

Problem instances Total # courses Total # sessions Total pairs of overlapping sessions Total # cliques

2repsPrYr 5courses 5 60 260 31

3repsPrYr 5courses 5 72 324 36

4repsPrYr 5courses 5 84 392 42

INS 6 6 75 806 37

2repsPrYr 15courses 15 180 2048 47

3repsPrYr 15courses 15 240 2982 47

4repsPrYr 15courses 15 300 4132 47

2repsPrYr 25courses 25 300 4246 47

3repsPrYr 25courses 25 420 7246 47

4repsPrYr 25courses 25 540 11004 48

INS 994224 20 164 1666 81

INS 1743540 20 162 1676 81

INS 2233256 20 163 1676 81

INS 3353124 20 165 1696 81

Figure 4: A high-level view of the simulation-based three-stage solution approach.

model:

min : Z

stage3

∑

s∈S

− E

) (12)

s.t. (1) − (8), (11)

∑

s∈S

∑

k∈K

≥ Z

stage2

(13)

≥

∑

k=n

c−1

, ∀s ∈ S , c ∈ A

(14)

where (13) imposes the requirement that the total

number of course sessions to trainees allocations must

be greater than or equal to Z

stage2

and (14) captures

the time the trainees ﬁnish their last course.

4.2 Computational Results

We apply the proposed simulation-based three-stage

solution approach on the 14 synthetic instances in Ta-

ble 1. For the parameter M

′

,∀(c,c

′

) ∈ E , a choice

of very large M can lead to slow progress in solv-

ing the MILP due to weak relaxation. In our imple-

mentation, we choose the value of M

′

to be the lat-

est end time among all the sessions of Course c

′

, i.e.,

′

= max

′

k=n

′

−1

The time CPLEX spent to solve the IP models in

Stage 2 (construction of feasible course sessions to

trainees allocations) and Stage 3 (improvement), as

well as the total time are shown in Figure 5. We report

the average time (in seconds) over 100 runs. In these

two ﬁgures, the total time captures the running time of

the three-stage approach from start to end. For Stage

2, the largest instance, i.e., 4repsPrYr 25courses re-

quired only 0.8 seconds to produce an optimal solu-

tion to the SSAP problem. For Stage 3, CPLEX can

solve all the instances with C ≤ 20 in less than 20 sec-

onds. When C = 25, CPLEX required, on average,

60 seconds. Overall, the time required by CPLEX

increased signiﬁcantly as the number of courses in-

creased.

Figure 5: The average time, in seconds, CPLEX spent to

solve the IP models in Stage 2 (green line) and Stage 3 (blue

line) as well as the total running time of the three-stage ap-

proach (red line).

The solution quality for Stages 2 and 3 are given

in Tables 2. In this table, we report the average value

WAPAT 2023 - Special Session on Workforce Analytics - Practical Application and Theory

276

Table 2: Summary of results for the SSAP problem. The best, average and worst values across 100 runs are reported.

Problem Instances

Stage 2 Stage 3

Avg. Distinct sessions make-span Distinct sessions make-span

SSA Best Avg. Worst Best Avg. Worst Best Avg. Worst Best Avg. Worst

2repsPrYr 5courses 71 30 35 41 30222 37927 44600 29 31 32 14878 17363 20681

3repsPrYr 5courses 72 36 43 48 33190 38212 46791 37 40 43 15508 17556 19428

4repsPrYr 5courses 71 39 45 50 31965 39214 49808 38 41 43 14325 16820 19456

INS 6 78 30 36 42 11287 15171 18273 29 29 31 6649 9142 11304

2repsPrYr 15courses 114 56 81 93 30817 40441 47869 52 75 84 16908 21698 27464

3repsPrYr 15courses 114 81 107 132 33498 41775 49220 84 105 121 17727 20495 26008

4repsPrYr 15courses 116 98 126 148 35808 41429 50970 97 127 144 17839 21108 27058

2repsPrYr 25courses 124 72 123 148 30299 39627 49052 78 120 144 18028 23090 29578

3repsPrYr 25courses 130 93 170 204 30124 38886 47750 88 165 197 15781 21520 27520

4repsPrYr 25courses 133 101 180 228 33127 40086 47484 100 176 219 16656 21945 29060

INS 994224 108 36 76 89 9460 14384 22816 30 71 83 5932 9310 15928

INS 1743540 109 26 76 92 8081 14595 21388 27 71 84 4259 9352 14738

INS 2233256 110 48 78 90 9922 14393 23390 42 73 84 5337 9439 15067

INS 3353124 111 20 76 92 8655 14266 20422 20 71 84 4791 9514 15361

of Z

stage2

over 100 runs under the column titled ‘Avg.

SSA’. We also report the best, average, and worst val-

ues of the number of distinct sessions and the total

make-span over 100 runs. For all the instances, Stage

3 was able to improve the make-span objective by

about 44% on average. While minimising the total

make-span in Stage 3, it is noted that the total num-

ber of distinct sessions was also optimised. Stage 3

was able to reduce the number of distinct sessions by

about four sessions on average.

5 CONCLUSIONS AND FUTURE

RESEARCH DIRECTIONS

In this paper, we studied a Defence trainee course

scheduling problem where every course has a his-

toric pass-rate and a trainee will not be allowed to

progress further if they fail a course. We proposed

a new approach for handling pass-rate, in which the

failed course and the courses a trainee can complete

before the failed course are determined prior to the

optimisation procedure. A simulation-based three-

stage solution approach was presented, which con-

sists of a trainee’s progression simulation stage, an

initial course-sessions to trainees allocation stage, and

an allocation improvement stage. The computational

results show that the proposed approach yields opti-

mal solutions to the 25-course instances in less than

two minutes, on average. The proposed approach

also offers information on the best-case, average-case,

and worst-case solutions that can beneﬁt managerial

decision-making.

Future research can apply the introduced solution

approach to an extended problem where geography

and language introduce additional business rules re-

garding the location of courses, and language match

between instructors and trainees.

REFERENCES

Battiti, R. and Tecchiolli, G. (1994). The reactive tabu

search. ORSA journal on computing, 6(2):126–140.

Beli

en, J. and Demeulemeester, E. (2006). Scheduling

trainees at a hospital department using a branch-and-

price approach. European Journal of Operational Re-

search, 175(1):258 – 278.

Bettinelli, A., Cacchiani, V., Roberti, R., and Toth, P.

(2015). An overview of curriculum-based course

timetabling. TOP, 23(2):313–349.

Brown, Gerald, G., Carlyle, W., M., Dell, Robert, F., and

Brau, John, W. (2013). Optimizing intratheater mili-

tary airlift in iraq and afghanistan.

Burke, E., Dror, M., Petrovic, S., and Qu, R. (2005). Hybrid

graph heuristics within a hyper-heuristic approach to

exam timetabling problems. In The next wave in com-

puting, optimization, and decision technologies, pages

79–91. Springer US.

Carter, M. W. (1989). A lagrangian relaxation approach to

the classroom assignment problem. INFOR: Informa-

tion Systems and Operational Research, 27(2):230–

246.

Costa, D. (1994). A tabu search algorithm for computing

an operational timetable. European Journal of Oper-

ational Research, 76(1):98 – 110.

Davenport, J., Neu, C., Smith, W., and Heath, S. (2007). Us-

ing discrete event simulation to examine marine train-

ing at the marine corps communication-electronics

school. In 2007 Winter Simulation Conference, pages

1387–1394.

de Werra, D. (1985). An introduction to timetabling. Eu-

ropean Journal of Operational Research, 19(2):151 –

162.

Dell’Amico, M. and Trubian, M. (1993). Applying tabu

search to the job-shop scheduling problem. Ann. Oper.

Res., 41(1-4):231–252.

Course Scheduling Under Uncertainty for Defence Workforce Training

277

Esmaeilbeigi, R., Mak-Hau, V., Yearwood, J., and Nguyen,

V. (2022). The multiphase course timetabling prob-

lem. European Journal of Operational Research,

300(3):1098–1119.

Glover, F. and Laguna, M. (1997). Tabu Search. Kluwer

Academic Publishers, Norwell, MA, USA.

Hertz, A. and Widmer, M. (1996). An improved tabu search

approach for solving the job shop scheduling problem

with tooling constraints. Discrete Applied Mathemat-

ics, 65(1):319 – 345.

Lam, E. and Hentenryck, P. V. (2016). A branch-and-price-

and-check model for the vehicle routing problem with

location congestion. Constraints, 21(3):394–412.

Lee, S.-Y., Kim, Y.-D., and Lee, H.-J. (2009). Heuristic

algorithm for a military training timetabling problem.

Asia Paciﬁc Management Review, 14(3):289–299.

Looker, J., Mak-Hau, V., and Marlow, D. (2017). Opti-

mal policies for aircraft ﬂeet management in the pres-

ence of unscheduled maintenance. In Syme, G., Hat-

ton MacDonald, D., Fulton, B., and Piantadosi, J.,

editors, Proceedings of MODSIM2017, 22nd Interna-

tional Congress on Modelling and Simulation.

Mak-Hau, V., Hill, B., Kirszenblat, D., Moran, B., Nguyen,

V., and Novak, A. (2021). A simultaneous sequenc-

ing and allocation problem for military pilot training:

Integer programming approaches. Computers & In-

dustrial Engineering, 154:107161.

McGinnis, M. L. and Fernandez-Gaucherand, E. (1994).

Resource scheduling for the united states army’s basic

combat training program. In Proceedings of IEEE In-

ternational Conference on Systems, Man and Cyber-

netics, volume 1, pages 553–558 vol.1.

uller, T. and Rudov

a, H. (2016). Real-life curriculum-

based timetabling with elective courses and course

sections. Annals of Operations Research, 239(1):153–

170.

Nguyen, V., Mak-Hau, V., Moran, B., and Novak, A.

(2022). An efﬁcient and exact algorithm for military

timetabling and trainee assignment problems. Com-

puters & Industrial Engineering, 169:108192.

Nguyen, V., Moran, B., Novak, A., Mak-Hau, V., Caelli, T.,

Hill, B., and Kirszenblat, D. (2018). Dancing links for

optimal timetabling. Military Operations Research,

23(2):61–78.

Nguyen, V., Shokr, M., Novak, A., and Caelli, T. (2016).

A reconﬁgurable agent-based discrete event simulator

for helicopter aircrew training. In International Sym-

posium on Military Operations Research (ISMOR).

Novak, A., Tracey, L., Nguyen, V., Johnstone, M., Le, V. T.,

and Creighton, D. C. (2015). Evaluation of tender so-

lutions for aviation training using discrete event simu-

lation and best performance criteria. In Winter Simu-

lation Conference.

Nowicki, E. and Smutnicki, C. (1996). A fast taboo search

algorithm for the job shop problem. Manage. Sci.,

42(6):797–813.

Pillay, N. (2016). A review of hyper-heuristics for educa-

tional timetabling. Annals of Operations Research,

239(1):3–38.

Qi, X., Bard, J. F., and Yu, G. (2004). Class scheduling for

pilot training. Operations Research, 52(1):148–162.

Raffensperger, J. F. and Schrage, L. E. (2008). Scheduling

training for a tank battalion: How to measure readi-

ness. Computers & Operations Research, 35(6):1844

– 1864. Part Special Issue: OR Applications in the

Military and in Counter-Terrorism.

Rudov

a, H., M

uller, T., and Murray, K. (2011). Complex

university course timetabling. Journal of Scheduling,

14(2):187–207.

Scott, J. (2005). Optimally scheduling basic courses at

the defense language institute using integer program-

ming. Master’s thesis, Naval Postgraduate School,

Monterey, CA.

eguin, R. and Hunter, C. (2013). 2 canadian forces ﬂying

training school (2cffts) resource allocation simulation

tool. In Winter Simulations Conference (WSC), pages

2866–2877.

Squires, R. R. and Hoffman, K. L. (2015). A military main-

tenance planning and scheduling problem. Optimiza-

tion Letters, 9(8):1675–1688.

Teoh, C. K., Wibowo, A., and Ngadiman, M. S. (2015). Re-

view of state of the art for metaheuristic techniques in

academic scheduling problems. Artiﬁcial Intelligence

Review, 44(1):1–21.

Wang, J. (2005). A review of operations research applica-

tions in workforce planning and potential modeling of

military training. Technical report, DSTO, Salisbury,

South Australia.

Wang, S., Bussieck, M., Guignard, M., Meeraus, A., and

O’Brien, F. (2010). Term-end exam scheduling at

united states military academy/west point. Journal of

Scheduling, 13(4):375–391.

Yang, T. and Ignizio, J. P. (1987). An algorithm for the

scheduling of army battalion training exercises. Com-

puters & Operations Research, 14(6):479–491.

WAPAT 2023 - Special Session on Workforce Analytics - Practical Application and Theory

278