Generalized Torsion-Curvature Scale Space Descriptor for

3-Dimensional Curves

Lynda Ayachi, Majdi Jribi and Faouzi Ghorbel

CRISTAL Laboratory, GRIFT Research Group, Ecole Nationale des Sciences de l’Informatique (ENSI),

La Manouba University, 2010, La Manouba, Tunisia

Keywords:

3D Curve Description, Invariant 3D Descriptor, Space Curves.

Abstract:

In this paper, we propose a new method for representing 3D curves called the Generalized Torsion Curvature

Scale Space (GTCSS) descriptor. This method is based on the calculation of curvature and torsion measures

at different scales, and it is invariant under rigid transformations. To address the challenges associated with

estimating these measures, we employ a multi-scale technique in our approach. We evaluate the effectiveness

of our method through experiments, where we extract space curves from 3D objects and apply our method to

pose estimation tasks. Our results demonstrate the effectiveness of the GTCSS descriptor for representing 3D

curves and its potential for use in a variety of computer vision applications.

1 INTRODUCTION

In the ﬁeld of computer vision, the ability to accu-

rately describe curves is essential for numerous ap-

plications, including object recognition, image seg-

mentation, motion estimation, and tracking. In two-

dimensional images, contours can be represented as

two-dimensional curves. Over the years, a variety of

methods and techniques have been developed for de-

scribing these curves in a concise and effective man-

ner. These curve descriptors are essential for many

computer vision tasks, as they enable the extraction

of useful information from images and enable algo-

rithms to better understand the shape and structure of

objects within an image. Two categories of methods

have been proposed in the literature: global and local.

These terms refer to the scope of the features that are

extracted from contours. Global methods typically

focus on extracting high-level, overall characteristics

of the contour, such as its length or overall shape.

Local methods, on the other hand, focus on extract-

ing more detailed, ﬁne-grained features that capture

the local structure of the contour, such as the angles

between adjacent points or the curvature at different

points along the contour. These two types of methods

have different strengths and weaknesses, and they are

often used in combination to achieve the best perfor-

mance in contour description and analysis tasks. In

the global set of algorithms, there are several meth-

ods that have been applied to the task of contour de-

scription. One such method is the Fourier descrip-

tor, which has been used in a number of works, in-

cluding (Persoon and Fu, 1977) and (Ghorbel, 1998).

These methods focus on extracting global features

of contours, but other methods have been developed

that focus on local features instead. For example, the

method proposed in (Hoffman and Richards, 1984)

partitions the curve into segments at points of neg-

ative curvature, which improves the performance of

object recognition. In a more recent work, (Yang and

Yu, 2018) introduces a multiscale Fourier descriptor

that is based on triangular features. This method com-

bines global and local features, addressing the limita-

tions of existing Fourier descriptors in terms of lo-

cal shape representation. Triangle area representation

(TAR) is a multi-scale descriptor that was introduced

in (Alajlan et al., 2007). It is based on the signed ar-

eas of triangles formed by boundary points at differ-

ent scales. Another multiscale approach is the Angle

Scale Descriptor, which was proposed in (Fotopoulou

and Economou, 2011) and is based on computing

the angles between points of the contour at different

scales. In (Sebastian et al., 2003), a method called

Curve Edit was proposed that characterizes the con-

tour using two intrinsic properties: its length and the

variations in its curvature. This method has been used

for contour registration and matching. Another no-

table method is the Shape Context algorithm, which

was introduced in (Belongie et al., 2002). (Pedrosa

et al., 2013) introduced the Shape Saliences Descrip-

tor (SSD), which is based on the identiﬁcation of

points of high curvature on the contour. These points,

known as salience points, are represented using the

relative angular position and the curvature values at

Ayachi, L., Jribi, M. and Ghorbel, F.

Generalized Torsion-Curvature Scale Space Descriptor for 3-Dimensional Curves.

DOI: 10.5220/0011895500003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 185-190

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

185

multiple scales. Another well-known local descriptor

is the Curvature Scale Space (CSS), which was intro-

duced in (Mokhtarian et al., 1997). This descriptor is

obtained by extracting the zero-crossing points of the

smoothed contour parameterizations using a series of

Gaussian functions at different scales. In , a simi-

lar approach is used, but the extrema of the Gaussian

functions are extracted instead of the zero-crossing

points. This type of descriptor has been widely used

in tasks such as shape retrieval, classiﬁcation, and

analysis, due to its good performance, robustness, and

compactness. In (BenKhlifa and Ghorbel, 2019), this

descriptor is extended to the three-dimensional case,

and the GCSS (Generalized Curvature Scale Space)

descriptor is introduced, which considers an invariant

feature on curve points with a given level of curvature.

This type of descriptor has been shown to be effective

for representing also for 3D curves. Another notable

approach for representing 3D curves is the Torsion

Scale Space representation, which was introduced by

(Yuen et al., 2000). This descriptor is based on the

torsion information of the curve, which is a local mea-

sure of its non-planarity. Geometrically, space curves

that lie on the surface of 3D objects contain valuable

information about the shape and structure of those

surfaces. (Burdin et al., 1992) proposed a method for

extracting 3D primitives, such as long bones, using

a set of 2D Fourier descriptors. This set of descrip-

tors is shown to be stable, complete, and endowed

with geometrical invariance properties. In a recent

work, (Jribi et al., 2021) introduced a novel invariant

3D face description that is invariant under the SE(3)

group. This description is based on the construction

of level curves of the three-polar geodesic represen-

tation, followed by geometric arc-length reparameter-

ization of each level curve. The principal curvature

ﬁelds are then computed on the sampled points of this

three-polar parameterization.

In this paper, we introduce a new descriptor for

3D curves called the Generalized Torsion Curvature

Scale Space (GTCSS). This descriptor is based on

the calculation of curvature and torsion measures at

different scales. According to the second fundamen-

tal theorem of geometry (Friedrich, 2002), this pair

of measures is invariant under rigid transformations.

This means that two different space curves that have

the same values of curvature and torsion should have

the same shape. In the next section, we present the

mathematical formulation of the GTCSS descriptor,

and we demonstrate its effectiveness through empiri-

cal results.

2 GENERALIZED CURVATURE

TORSION SCALE SPACE

Let Γ(u) be a parameterization of the space curve Γ.

It is a function of a continuous parameter u deﬁned

by:

Γ : [0,1] → R

u 7→ [x(u),y(u),z(u)]

(1)

Where [x(u),y(u),z(u)] are the geometric coordinates

of the curve points. It is important to note that the

parameterization of the curve is not unique because

it depends upon the starting point and the speed we

go over the curve. To get rid of this problem, the arc

length reparameterization is generally chosen as a so-

lution since it is invariant under Euclidean transfor-

mations. For a curve Γ, the arc length parameteriza-

tion is formulated as follows:

∗

(s) =





−1

(s)





−1

(s)





−1

(s)



(2)

Where ϕ

−1

(s) represents the inverse of the arc length

function deﬁned as:

ϕ(u) = s(u) −s(0) =



d (Γ(u))



du (3)

Let denote by Γ

the smoothed curve for a ﬁxed

scale σ and κ(s, σ) and τ(s,σ) its curvature and tor-

sion :

κ(s,σ) =

√

(¨z

˙y

−¨y

˙z

)

+( ¨x

˙z

−¨z

˙x

)

+( ¨y

˙x

−¨x

˙z

)

(

˙x

+ ˙y

+˙z

)

(4)

τ(s,σ) =

˙x

( ¨y

˘z

−¨z

˘y

)−˙y

( ¨x

˘z

−¨z

˘x

)+˙z

( ¨x

ˇy

−¨y

¨x

)

( ˙y

¨z

−˙z

¨y

)

+(˙z

¨x

−˙x

¨z

)

+( ˙x

¨y

−˙y

¨x

)

(5)

Let a be a substitution of x,y and z. The notation

˙a

, ¨a

and ˘a

stands for respectively the ﬁrst, second

and third derivative of a in scale σ, expressed in equa-

tion(6):







˙a

(s) = a(s) ⊗ ˙g(s,σ),

¨a

(s) = a(s) ⊗ ¨g(s,σ),

˘a

(s) = a(s) ⊗ ˘g(s,σ)

(6)

Where g is a gaussian function.

Once the curvature and torsion functions of the

smoothed curve are obtained, the next step corre-

sponds to the extrema extraction and the thresholding.

Extrema, that have signiﬁcant curvature and torsion

variations in the sense of shape information, are ex-

tracted. The number of extrema decreases after each

gaussian convolution and the space curve becomes

smoother as illustrated in Figure 1.

Therefore, a thresholding is performed in order to

eliminate local extrema that have low absolute curva-

ture and torsion variations. Curvature extrema that are

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

186

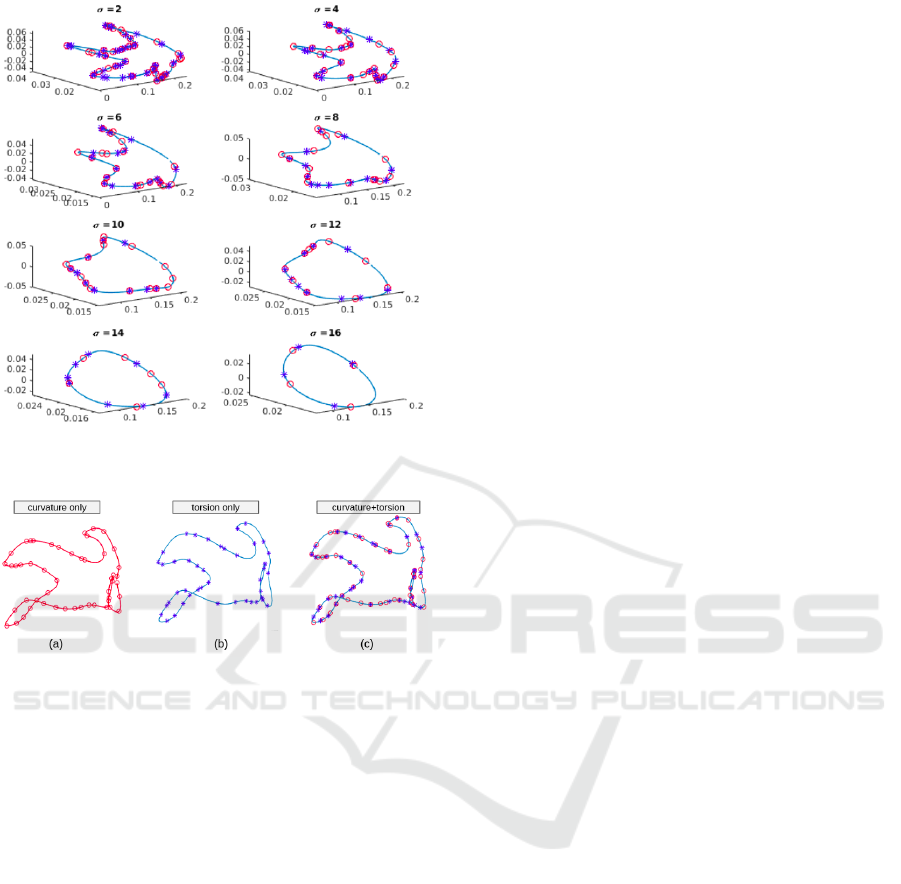
Figure 1: An example of a space curve in different levels of

smoothing, from σ = 2 to σ = 16.

Figure 2: (a) The curvature keypoints (b) The torsion key-

points (c) The curvature and torsion keypoints.

higher than the threshold ε

are kept in the set Ω

(ε

)

which can be formulated as follows:

Ω

(ε

) =

{

κ ∈ Ω

;|κ| > ε

}

(7)

The torsion extrema that are higher than the threshold

are kept in θ

(ε

)

(ε

) =

{

τ ∈ θ

;|τ| > ε

}

(8)

The next step is the generalization part. It con-

sists on seeking points of the curve having the same

curvature values as the set Ω

and the same torsion

values as the set θ

. The objective of this step is the

enrichment of the point set. It allows reaching areas

that are not selected in the previous steps but having

the same level of interest (same curvature and torsion)

as the extracted points of interest. Reciprocal images

are described as follows:

−1

(Ω

(ε

)) =

{

s ∈ [0,1] /κ

(s) ∈ Ω

(τ)

}

(9)

−1

(θ

(ε

)) =

{

s ∈ [0,1] /τ

(s) ∈ θ

(τ)

}

(10)

The previous steps are repeated a number of times

chosen empirically. The selected points at each scale

σ are stored, respectively, in F

(σ) and F

(σ). They

can be described as follows:

(σ) =



Γ(s,σ) /s ∈ κ

−1

{

Ω

(ε

)

}



(11)

(σ) =



Γ(s,σ) /s ∈ τ

−1

{

(ε

)

}



(12)

3 EXPERIMENTATIONS AND

RESULTS

In this section, we evaluate the performance of our

proposed method on 3D object datasets. As there are

currently no datasets available for space curves, we

generate them from widely used 3D object datasets in

order to validate our approach. The method we use for

extracting space curves from 3D objects allows us to

evaluate the performance of the GTCSS descriptor in

terms of pose retrieval. We demonstrate the effective-

ness of our method on simple pose estimation tasks,

and compare its performance to existing state-of-the-

art methods.

3.1 Dataset

The experiments in this paper were conducted on the

3DBodyTex dataset (Saint et al., 2018), which con-

tains 400 high-resolution 3D scans of 200 different

subjects. The subjects are captured in at least two

poses: the ”U” pose and another random pose belong-

ing to a ﬁxed set of 35 poses. The dataset provides

a useful benchmark for evaluating the performance of

our proposed method on human pose estimation tasks.

(Saint et al., 2018). The Figure 3 illustrates some ex-

amples of the dataset.

3.1.1 Space Curves Extraction

Our idea involves generating space curves from three-

dimensional objects, on which we then apply our

GTCSS descriptor. In this work, we focus on acquisi-

tions of the human body. To create a space curve for

a given object, we take the following steps:

• Identify a set of landmarks on the object, located

on the head, shoulders, elbow, wrist, hips, knees,

and ankles.

• Connect each pair of successive landmarks with a

geodesic line, as shown in Figure 5.

• Concatenate all of the geodesic lines to create the

ﬁnal space curve for the object.

The obtained 3D curve accurately represents the

shape of M and captures its global morphological

variations. As a result, it can be used for pose recog-

nition, as it lies on mobile areas of the body.

Generalized Torsion-Curvature Scale Space Descriptor for 3-Dimensional Curves

187

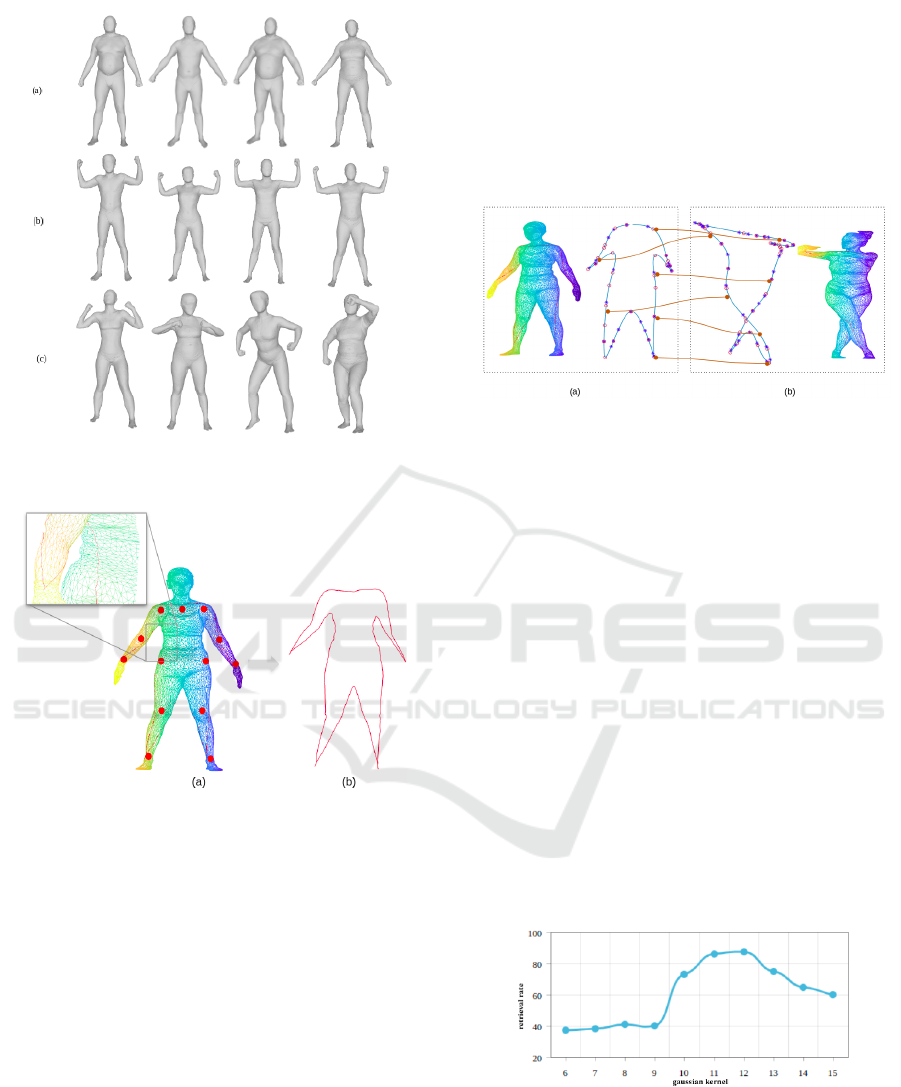
Figure 3: Samples from the 3DBodyTex dataset: (a) ”A”

pose, (b) ”U” pose, (c) random pose.

Figure 4: (a) Spots in red, the chosen landmarks (b) Space

curve generation.

3.2 Similarity Metric

Let π(σ) be the set of points, represented by their ar-

clength parametrization, and obtained by concatenat-

ing F

(σ) and F

(σ), as illustrated in Figure 2 and

expressed in the following equation:

π(σ) = F

(σ) ∪F

(σ) (13)

As a similarity metric, we employ the Dynamic

Time Warping (DTW) distance developed by Sankoff

aat al. (Sankoff and Kruskal, 1983) to compare 3D

curve descriptors as illustrated in Figure 5. As stated

in (Ratanamahatana and Keogh, 2004), the proposed

representation generates a pseudo time series, and

the DTW guarantees an invariance relatively to the

initial point. Let A and B be two space curves of

length N

and N

respectively, and represented by

two signatures S(A) =

{

S (a

),S(a

)...S (a

)

}

and

S(B) =

{

S (b

),S(b

)...S (b

)

}

. The path that min-

imizes the cumulative distance between these two se-

ries represents the distance between them and denoted

by D(S (a

),S(b

)) :

D(S(a

),S (b

)) = min







D(S(a

),S (b

j−1

))

D(S(a

i−1

),S (b

))

D(S(a

l−1

),S (b

j−1

))

+ D (S (a

),S (b

))

(14)

Figure 5: The comparaison process between two models

with different poses.

3.3 Results

We apply our method to each model in the dataset,

using the GTCSS description of each object. To de-

termine the optimal scale, we perform a study to

compute the retrieval rate using a gaussian kernel,

as shown in Figure 6. We experimentally set the

thresholds for the curvature and torsion measures to

be ε

= 10

−2

and ε

= 10

−3

, respectively, in order to

eliminate points with very low curvature and torsion.

The curvature and torsion of the obtained curves vary

signiﬁcantly. For example, a human body in a running

pose will have varying curvature and torsion values in

the arms and legs, and almost zero values elsewhere.

In contrast, a human body in a standing position (or A

pose) will have mostly monotonous or zero curvature

and torsion values. Figure 7 demonstrates the utility

of the combination of curvature and torsion measures

for pose estimation.

Figure 6: Dependency of the retrieval rates and the gaussian

kernel.

Our approach is evaluated in terms of pose re-

trieval. We use the k-nearest neighbor (kNN) algo-

rithm with k=1 to obtain the scores of the pairwise

shape matching. For each model, we compute the dy-

namic time warping (DTW) distance using a super-

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

188

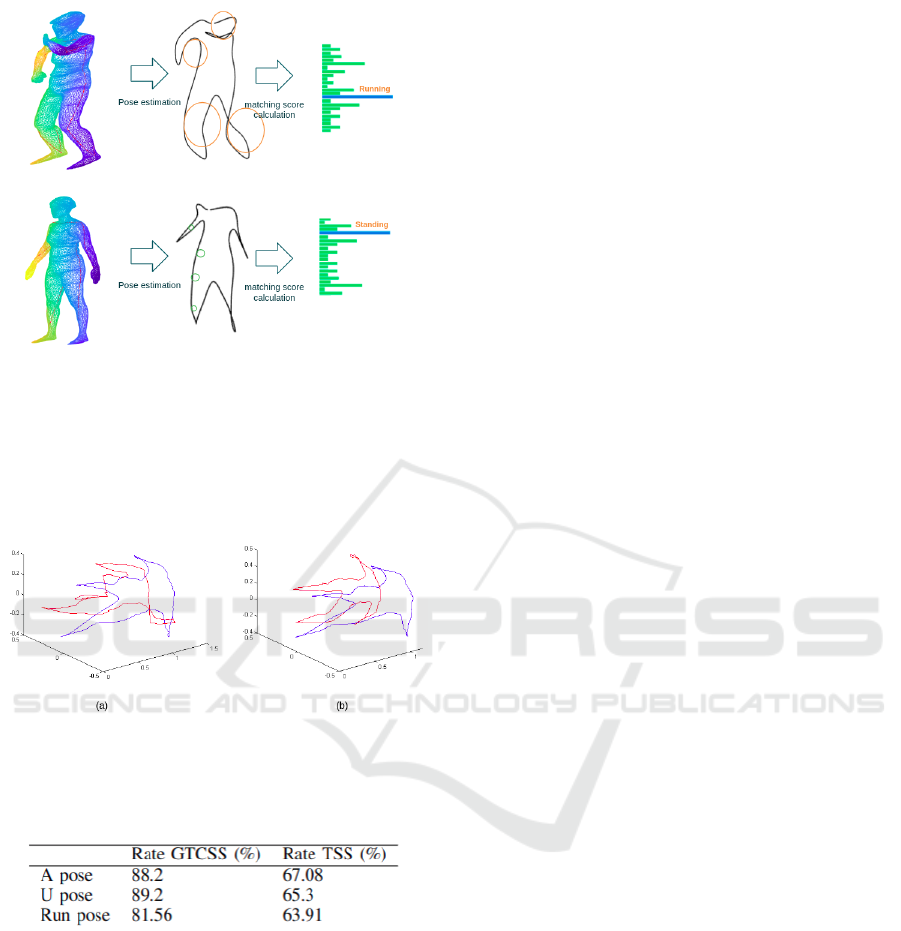
Figure 7: The decision process based on the descrimina-

tive measures of curvature and torsion in two space curves

representing two different poses. In red, zones with high

variations. In green, zones with low variations.

vised list of poses consisting of 36 descriptors: one

model descriptor for each pose. An example of a good

and bad matching is illustrated in Figure 8.

Figure 8: (a) An example of bad matching (b) An example

of a good matching.

Table 1: The obtained retrieval rate for different category of

poses.

Our proposed descriptor GTCSS is compared to

TSS (Yuen et al., 2000) with σ ranges from 0.5 to 12

with the step =0.2. Table.1 shows the retrieval results

of the GTCSS on 3DBodyTex dataset using KNN al-

gorithm, k=1 for some poses: A pose, U pose and Run

pose.

4 CONCLUSION

The problem of 3D curve description remains a sig-

niﬁcant challenge in the ﬁeld of computer vision, with

the need for robust and efﬁcient methods that can ac-

curately represent the shape of 3D curves in a man-

ner that is invariant to various transformations. In this

paper, we introduce a new descriptor for 3D curves

called the Generalized Torsion Curvature Scale Space

(GTCSS) that is based on the calculation of curvature

and torsion measures at different scales. This descrip-

tor is invariant under rigid transformations, making it

well-suited for representing the shape of 3D curves.

To address the challenges associated with estimating

these measures, we employ a multi-scale technique

in our approach. By estimating torsion and curvature

at multiple scales, we are able to mitigate the cumula-

tive errors that can arise from the computation of mul-

tiple derivatives in the torsion equation. We demon-

strate the effectiveness of our approach through exper-

iments, where we extract space curves from 3D ob-

jects and apply our method to pose estimation tasks.

In future research, we plan to reﬁne our method and

conduct further studies on the GTCSS parameters to

evaluate their effectiveness for 3D object recognition.

REFERENCES

Alajlan, N., El Rube, I., Kamel, M. S., and Freeman, G.

(2007). Shape retrieval using triangle-area representa-

tion and dynamic space warping. Pattern Recognition,

40(7):1911–1920.

Belongie, S., Malik, J., and Puzicha, J. (2002). Shape

matching and object recognition using shape contexts.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 24(4):509–522.

BenKhlifa, A. and Ghorbel, F. (2019). An almost complete

curvature scale space representation: Euclidean case.

Signal Processing: Image Communication, 75:32–43.

Burdin, V., Ghorbel, F., Tocnaye, J.-L., and Roux, C.

(1992). A three-dimensional primitive extraction of

long bones obtained from fourier descriptors. Pattern

Recognition Letters, 13:213–217.

Fotopoulou, F. and Economou, G. (2011). Multivariate an-

gle scale descriptor of shape retrieval. Proceedings of

SPAMEC, 2011.

Friedrich, T. (2002). Global Analysis: Differential Forms in

Analysis, Geometry, and Physics, volume 52. Ameri-

can Mathematical Soc.

Ghorbel, F. (1998). Towards a unitary formulation for

invariant image description: Application to image

coding. Annales des Telecommunications/Annals of

Telecommunications, 53:242–260.

Hoffman, D. and Richards, W. (1984). Parts of recognition.

Cognition, 18(1):65–96.

Jribi, M., Mathlouthi, S., and Ghorbel, F. (2021). A

geodesic multipolar parameterization-based represen-

tation for 3d face recognition. Signal Processing: Im-

age Communication, 99:116464.

Mokhtarian, F., Abbasi, S., and Kittler, J. (1997). Efﬁcient

and robust retrieval by shape content through curva-

Generalized Torsion-Curvature Scale Space Descriptor for 3-Dimensional Curves

189

ture scale space. In Image Databases and Multi-Media

Search, pages 51–58.

Pedrosa, G. V., Batista, M. A., and Barcelos, C. A. (2013).

Image feature descriptor based on shape salience

points. Neurocomputing, 120:156–163. Image Fea-

ture Detection and Description.

Persoon, E. and Fu, K.-S. (1977). Shape discrimination us-

ing fourier descriptors. IEEE Transactions on Pattern

Analysis and Machine Intelligence, PAMI-8:388–397.

Ratanamahatana, C. A. and Keogh, E. (2004). Everything

you know about dynamic time warping is wrong. In

Third Workshop on Mining Temporal and Sequential

Data, pages 22–25.

Saint, A., Ahmed, E., Cherenkova, K., Gusev, G., Aouada,

D., and Ottersten, B. (2018). 3dbodytex: Textured 3d

body dataset. In 2018 International Conference on 3D

Vision (3DV), pages 495–504. IEEE.

Sankoff, D. and Kruskal, J. B. (1983). Time warps, string

edits, and macromolecules: The theory and practice

of sequence comparison. In Sankoff, D. and Kruskal,

J. B., editors, Time Warps, String Edits, and Macro-

molecules: The Theory and Practice of Sequence

Comparison. Addison-Wesley Publication.

Sebastian, T., Klein, P., and Kimia, B. (2003). On aligning

curves. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 25:116–125.

Yang, C. and Yu, Q. (2018). Multiscale fourier descriptor

based on triangular features for shape retrieval. Signal

Processing: Image Communication, 71.

Yuen, P., Mokhtarian, F., Khalili, N., and Illingworth,

J. (2000). Curvature and torsion feature extraction

from free-form 3-d meshes at multiple scales. IEE

Proceedings-Vision, Image and Signal Processing,

147(5):454–462.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

190