Learning Preferences in Lexicographic Choice Logic
Karima Sedki
1,2 a
, Nada Boudegzdame
1,2 b
, Jean Baptiste Lamy
1,2 c
and Rosy Tsopra
3,4 d
1
LIMICS (INSERM UMRS 1142), Universit
´
e Paris 13, Sorbonne Paris Cit
´
e, 93017 Bobigny, France
2
UPMC Universit
´
e Paris 6, Sorbonne Universit
´
es, Paris, France
3
INSERM, Universit
´
e de Paris, Sorbonne Universit
´
e, Centre de Recherche des Cordeliers,
Information Sciences to Support Personalized Medicine, F-75006 Paris, France
4
Inria Paris, 75012 Paris Department of Medical Informatics, Hopital European Georges-Pompidou, AP-HP, Paris, France
Keywords:
Preferences Learning, Lexicographic Choice Logic.
Abstract:
Lexicographic Choice Logic (LCL) is a variant of Qualitative Choice Logic which is a logic-based formalism
for preference handling. The LCL logic extends the propositional logic with a new connective (⃗⋄) to express
preferences. Given a preference x⃗⋄y, satisfying both x and y is the best option, the second best option is to
satisfy only x, and satisfying only y is the third best option. Satisfying neither x nor y is not acceptable. In
this paper, we propose a method for learning preferences in the context of LCL. The method is based on an
adaptation of association rules based on the APRIORI algorithm. The adaptation consists essentially of using
variations of the support and confidence measures that are suitable for LCL semantic.
1 INTRODUCTION
Preferences can be obtained in two ways: i) by
elicitation from the user, through a sequence of
queries/answers or ii) directly learning them from
data. However, even if powerful formalisms have
been proposed, preference elicitation is in general not
an easy task especially when there are too many out-
comes. It is then more appealing to learn prefer-
ences from data which is easy to collect. Preference
learning (Johannes and H
¨
ullermeier, 2010) has re-
cently received a considerable attention in many dis-
ciplines. It aims to learn a preference model from ob-
served preference information. There are three pref-
erence learning problems (Johannes and H
¨
ullermeier,
2010): i) Object ranking problem (Waegeman and
De Baets, 2010; Joachims et al., 2005), ii) Label rank-
ing (H
¨
ullermeier et al., 2008; Vembu and G
¨
artner,
2010) , and iii) Instance ranking problem (Cohen
et al., 2011).
The purpose of this paper is to learn preferences
in the context of Lexicographic Choice Logic (LCL)
(Bernreiter et al., 2022). LCL is a variant of the
a
https://orcid.org/0000-0002-2712-5431
b
https://orcid.org/0000-0003-1409-6560
c
https://orcid.org/0000-0002-6078-0905
d
https://orcid.org/0000-0002-9406-5547
well-known preference formalism Qualitative Choice
Logic (Brewka et al., 2004). In QCL, to express pref-
erences, an ordered disjunction connective is added
to propositional logic. Intuitively, if x and y are two
options then x
⃗
×y means: “if possible x, but if x is im-
possible then at least y”. LCL allows to encode lexi-
cographic ordering over variables by using the logical
connective⃗⋄. Given a preference x⃗⋄y, satisfying both
x and y is the best option, satisfying only x is the sec-
ond best option, and the third best option is to satisfy
only y. Satisfying neither x nor y is not acceptable.
The proposed method consists in an adaptation of
association rules based on the APRIORI algorithm
(Agrawal et al., 1993). The adaptation consists es-
sentially of using variations of the support and con-
fidence measures according to the semantic of LCL.
In previous work (Sedki et al., 2022), we proposed
a method for learning preferences in the context of
QCL. It is also based on the adaptation of association
rules as for LCL. However, the method for learning
preferences in LCL requires different definitions than
those of QCL, particularly the support, the confidence
and the length of the learned formulas.
The paper is organized as follows: We start with
some useful notations, then we present a description
of some important elements of LCL. The fourth sec-
tion describes the proposed method for learning LCL
preferences. In Section 5 we present a case study in
1012
Sedki, K., Boudegzdame, N., Lamy, J. and Tsopra, R.
Learning Preferences in Lexicographic Choice Logic.
DOI: 10.5220/0011891300003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 3, pages 1012-1019
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

the front of medical domain, particularly in antibiotics
prescription where we aim to learn an LCL preference
model of medical experts that provide recommenda-
tions of antibiotics. Finally, we conclude the paper.
2 NOTATIONS
Let V be a finite set of propositional variables. An in-
terpretation I is defined as a set of propositional vari-
ables such that v ∈ I if and only if v is set to true by I.
If I satisfies a formula φ, we write I |= φ, otherwise,
we write I ̸|= φ. A model of a formula φ is an interpre-
tation I that satisfies the formula. var(φ) denotes the
variables of a formula φ. |.| denotes the cardinality of
a set. Let us give the following definition:
Definition 1. Let V be a set of variables, then:
• Each single option is built on the set of variables
V and the connective ¬.
• Each conjunctive option is built on the set of sin-
gle options and the connective ∧.
• The set of single and conjunctive options is de-
noted by X.
v
1
, ¬v
2
are examples of single options, v
1
∧¬v
2
is
a conjunctive option.
3 LEXICOGRAPHIC CHOICE
LOGIC (LCL)
Lexicographic Choice Logic (Bernreiter et al., 2022)
is a variant of Qualitative Choice Logic (Brewka et al.,
2004). It has two types of connectives: classical con-
nectives (here we use ¬, ∨, and ∧) and a new con-
nective⃗⋄, used to encode lexicographic ordering over
variables. Given a preference x⃗⋄y, satisfying both x
and y is the best option, satisfying only x is the sec-
ond best option, and the third best option is to sat-
isfy only y. Satisfying neither x nor y is not accept-
able. In this paper, we do not use the unified lan-
guage proposed in (Bernreiter et al., 2022) since we
focus only on LCL and not on the other choice logics
such as QCL (Brewka et al., 2004), PQCL (Benferhat
and Sedki, 2008) and CCL (Boudjelida and Benferhat,
2016). Note that the connective⃗⋄ of LCL is not asso-
ciative (see (Bernreiter et al., 2022) for more details).
Here, we follow the presentation given in (Bernreiter
et al., 2022), where we consider a BCF formula φ pre-
sented as follows: (x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))).
As for QCL, the LCL language is composed of three
types of formulas defined in the following.
Definition 2. Each propositional formula is built on
the set of variables V and the connectives ∧, ∨, ¬.
PROP
V
denotes the language of propositional formu-
las.
Definition 3. Basic choice formulas (BCF) allow the
expression of simple preferences. BCF
V
denotes the
language of BCF formulas and defined as follows:
a) If φ, ψ ∈ PROP
V
then φ⃗⋄ψ ∈ BCF
V
.
b) Every BCF formula is only obtained by applying
the item a) above a finite number of times.
Definition 4. General choice formulas (GCF) can
be obtained from V using connectives ⃗⋄, ∧, ∨, ¬.
The language composed of GCF formulas, denoted
GCF
V
, is defined as follows:
c) If φ, ψ ∈ BCF
V
then (φ ∧ ψ),¬(ψ), (φ ∨ ψ), (φ⃗⋄ψ)
∈ GCF
V
.
d) The language of GCF
V
is obtained by applying
the item c) a finite number of times.
Example 1. φ
1
=a ∨ b is an example of propositional
formula. φ
2
=a⃗⋄b⃗⋄c is a BCF formula, φ
3
=(a⃗⋄b) ∧
(c⃗⋄d) is a GCF formula.
3.1 Semantics and syntax of LCL
The semantics of an LCL formula is based on the
degree of satisfaction of a formula in a particular
interpretation I. The satisfaction degree of a formula
given an interpretation is a positive natural number
when a formula is satisfied by that interpretation or ∞
otherwise. The higher this degree, the less preferable
the interpretation. Unacceptable interpretations have
a degree of ∞. The set of satisfaction degrees is
denoted by D. Let us define firstly the notions of
optionality and length.
The optionality of a formula φ is a function that as-
signs to φ a strictly positive integer. It corresponds to
the greatest satisfaction degree d (d ̸= ∞) of all possi-
ble degrees of φ. The definition of optionality of LCL
formulas is given in the following.
Definition 5. The optionality in LCL is defined as fol-
lows:
1. opt(v)=1, for every v in V .
2. opt(φ⃗⋄ ψ)= (opt(φ) +1) × (opt(ψ)+ 1) −1
3. opt(φ ∧ψ)= max(opt(φ), opt(ψ)).
4. opt(φ ∨ψ)= max(opt(φ), opt(ψ)).
5. opt(¬φ) = 1.
We can observe that from Definition 5, the option-
ality of a BCF formula φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))),
opt(φ) = 2
n
−1. It corresponds to the degree ascribed
by the last preferred interpretation to φ.
Learning Preferences in Lexicographic Choice Logic
1013

Example 2. Let us consider the BCF formula φ= (a⃗⋄
(b⃗⋄ c)). From Item 2 of Definition 5, opt(φ) = 7. This
means that there an interpretation that ascribes a de-
gree 7 to φ but there is no interpretation that ascribes
a degree greater than 7 to φ.
Let us give in the following the definition of length
of LCL formulas.
Definition 6. The length of an LCL formula φ, de-
noted by len(φ) corresponds to the number of options
that φ contains.
1. len(v)=1, for every v in V .
2. len(φ⃗⋄ ψ)= len(φ) + len(ψ)
3. len(φ ∧ ψ)= max(len(φ), len(ψ)).
4. len(φ ∨ ψ)= max(len(φ), len(ψ)).
5. len(¬φ) = 1.
Example 3. Let us consider the BCF formula φ= a⃗⋄
b ⃗⋄ c. From Item 2 of Definition 6, len(φ) = 3. This
means that φ contains 3 options (a, b, and c).
Let us now define the inference relation of LCL
formulas.
Definition 7. Let v be a propositional atom in
PROP
V
, φ and ψ be two LCL formulas, I be an in-
terpretation. The satisfaction degree of a formula φ
under an interpretation I is denoted by deg(I,φ).
1. deg(I,v) =

1 i f v ∈ I
∞ i f v ̸∈ I
2. deg(I,¬φ) =

1 i f I ̸|= φ
∞ otherwise
3. deg(I,φ⃗⋄ψ) =



















(m − 1) ×opt(ψ) +n
i f I |=
m
φ,I |=
n
ψ
opt(φ) ×opt(ψ) +m
i f I |=
m
φ,I ̸|= ψ
opt(φ) ×opt(ψ) +opt(φ) + n
i f I ̸|= φ,I |=
n
ψ
∞ otherwise
4. deg(I,φ ∧ψ) =

max(m,n) i f I |=
m
φ and I |=
n
ψ
∞ otherwise
5. deg(I,φ ∨ψ) =

min(m,n) i f I |=
m
φ or I |=
n
ψ
∞ i f I ̸|= φ and I ̸|= ψ
For any propositional formula φ, there is only one
degree of satisfaction (namely 1) obtained when φ is
satisfied by I. Namely, if a propositional formula is
satisfied, then it can only be to a degree of 1, other-
wise, the degree is ∞. The formula φ ∧ ψ is assigned
the maximum degree of φ and ψ because both formu-
las need to be satisfied. φ∨ψ is assigned the minimum
degree since it is sufficient to satisfy either φ or ψ. Re-
garding a BCF formula φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))), an
interpretation I satisfies φ to a degree 1, if it satisfies
the n options of φ, namely I |= x
1
∧ ... ∧ x
n
, an in-
terpretation I satisfies φ to a degree 2, if it satisfies
the n − 1 options of φ, namely I |= x
1
∧ ... ∧ x
n−1
and
so on. The formula ¬(x
1
⃗⋄x
2
⃗⋄...⃗⋄x
n
) is equivalent to
the propositional formula ¬x
1
∧ ¬x
2
∧ ... ∧ ¬x
n
. So,
its degree of satisfaction is 1 if φ is not satisfied, ∞
otherwise.
Example 4. Let us consider the LCL formula φ = (a
⃗⋄ (b⃗⋄ c)). The satisfaction degree of φ for each inter-
pretation is given in Table 1.
Table 1: The LCL inference relation of φ.
Interpretations a b c deg(I,φ)
I
1
F F F ∞
I
2
F F T 7
I
3
F T F 6
I
4
F T T 5
I
5
T F F 4
I
6
T F T 3
I
7
T T F 2
I
8
T T T 1
With respect to the lexicographic orderings of the
variables a, b, and c in φ, the interpretation I
8
={a,
b, c} ascribes a degree of 1 to φ, the interpretation
I
7
={a, b} ascribes a degree of 2 to φ
1
, and so on. The
interpretation
/
0 ascribes a degree of ∞ to φ.
4 LEARNING PREFERENCES IN
LCL
We consider the problem of learning LCL preferences
from a preference database P containing a set of inter-
pretations described with a set of variables and each
one associating with a satisfaction degree indicating
the degree of preference for the user. In this paper, we
are restricted for learning BCF formulas. Learning
GCF formulas follows the same method since each
GCF formula can be transformed into its equivalent
BCF formula, the same thing for propositional for-
mula which corresponds to a BCF formula with only
one option. In addition, for lack of space, we lim-
ited to single and conjunctive options. Namely, BCF
formulas contains only single or conjunctive options
instead of a propositional formulas.
Definition 8. (Bernreiter et al., 2022) Let P be a pref-
erence database, I be an interpretation in P , D be a
set of satisfaction degrees s.t. I is assigned with a de-
gree in D. A degree d is LCL-obtainable from D iff
there exists an interpretation I and an LCL formula φ
s.t. deg(I,φ) = d. The set of all degrees obtainable
from P is denoted by D
LCL
.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
1014

From Definition 8, ∀ φ ∈ PROP
V
, we have
D
LCL
={1,∞}, ∀ φ ∈ BCF
V
, we have D
LCL
=N.
Proposition 1. Let P be a preference database, D be a
set of satisfaction degrees in P , d = max(D) s.t. d ̸=
∞. Then, for a smallest positive natural number n
verifying that d < 2
n
it holds that there exists an LCL
formula φ s.t. len(φ) = n.
Proof. Assume that P contains a set of interpretations
where each one is assigned with one satisfaction de-
gree d in D. Assume that D is LCL-obtainable from
D. From Definition 8, there exists a formula φ s.t.
deg(I,φ) ∈ D
LCL
.
• If φ∈ PROP
V
, then from Definition 6, len(φ) =
1. From Definition 8, D
LCL
={1,∞}. Thus, d =
max(D) = 1. For a smallest number n = 1, we
have d = 1 < 2
n=1
.
• If φ∈ BCF
V
s.t. φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))), then
from Definition 6, len(φ) = n. From Definition 8,
D
LCL
=N. According to the lexicographic ordering
over x
i
, we have ∀d ∈ D
LCL
(d ̸= ∞), we have d ≤
2
n
− 1 which means that if d≥2
n
, then there is no
LCL formula s.t. len(φ) = n so that d be LCL-
obtainable from D.
For example, assume that D={1,2, 3,4, ∞}.
∀ d∈D, d is LCL-obtainable iff d = 4 verifies
Proposition 1. A smallest positive natural number
that verifies Proposition 1 is n = 3. So, d = 4 be
LCL-obtainable, iff there exists an LCL formula
φ s.t. len(φ) = 3. Thus, D
LCL
={1,2,3, 4,∞} is
LCL-obtainable from D since there is an LCL formula
φ s.t. len(φ)=3. It is clear that if we consider ψ
s.t. len(ψ) = 2, D
LCL
={1,2,3, 4,∞} is not LCL-
obtainable from D since even if each of d = 1 (resp.
2, 3, ∞) is LCL-obtainable with ψ s.t. len(ψ) = 2,
d = 4 is not.
We aim to learn a preference model M
LC L
defined
as follows.
Definition 9. Let P be a preference data base, D be
the set of satisfaction degrees, then
M
LC L
=



φ = (x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
)))
x
i
∈ X and len(φ) = n
according to Proposition 1
Definition 9 states that the learned preference
model contains a BCF formula. Its length is equal
to n. So it contains n options which are single or
conjunctive. The length of the formula is determined
from the set D according to Proposition 1.
The question we addressed in the following sec-
tions is among all possible options in X , what are the
options x
1
, x
2
, . .., x
n
that compose φ such that φ pre-
dicts the correct satisfaction degree of each interpre-
tation in P .
Our aim is to learn an LCL preference model maxi-
mizing accuracy measure Acc with respect to P . We
choose the following simple measure that computes
the proportion of interpretations that kept their degree
of satisfaction with the learned model M
LC L
that con-
tains a formula φ. The degree of interpretation I in P
is denoted by d(I), and the degree that I ascribes to
the learned formula φ is denoted by deg(I,φ).
Acc(P ,M
LC L
) =
|{
I ∈ P | d(I) = deg(I,φ)
}|
|
P
|
(1)
4.1 Learning LCL formulas
The learned LCL model contains a formula in the
form of φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))) is a single or a
conjunctive option. For generating best options of
φ, our proposed method is inspired from Apriori
algorithm (Agrawal et al., 1993) for generating
frequent item-sets. Instead of generating all possible
options which can be very large, we generate only
frequent ones which correspond to those exceeding
a minimal fixed support and confidence. Let’s first
introduce the following proposition before defining
the support and confidence of options in LCL.
We first explain what we consider lexicograph-
ically preferred interpretation. We say that an in-
terpretation I is lexicographically preferred than an-
other interpretation I
′
with respect to the LCL formula
φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))) where x
1
> x
2
> ... > x
n
if
there is j ∈ {1, ...,n} s.t. x
i
∈ I, x
i
∈ I
′
for all i < j
and x
j
∈ I but x
j
̸∈ I
′
. For example, given a formula
φ=x
1
⃗⋄x
2
, with respect to the orderings of the variables
x
1
,x
2
in φ, the lexicographically first preferred inter-
pretation is {x
1
,x
2
} and it ascribes a degree of 1 to φ,
the second lexicographically preferred is {x
1
} and it
ascribes a degree of 2 to φ, the third preferred is {x
2
}
and it ascribes a degree of 3 to φ. The fourth interpre-
tation is
/
0, it is unacceptable and it ascribes a degree
of ∞ to φ.
Proposition 2. Let P be a preference database,
D be a set of satisfaction degrees and
φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))) be the LCL formula
to be learned, it holds that 2
n−1
lexicographically
preferred interpretations are sufficient for learning
the options x
i=1,...,n
.
Proof. Let us consider φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
))) the
LCL formula to be learned. Thus there are 2
n
possible
Learning Preferences in Lexicographic Choice Logic
1015

interpretations s.t. following the lexicographic order-
ing on the variables x
1
, x
2
, ... ,x
n
, the interpretation
/
0
ascribes a degree of ∞ to φ and the remaining 2
n
− 1
interpretations ascribe to φ a degree of 1 to 2
n
− 1.
• x
1
is the preferred variable of φ, so from the pos-
sible 2
n
interpretations, there are 2
n−1
interpreta-
tions that satisfy x
1
. From these interpretations,
the most preferred one is {x
1
,x
2
,.. ., x
n
} and it as-
cribes a degree of 1 to φ, the second preferred in-
terpretation is {x
1
,x
2
,.. ., x
n−1
} and it ascribes a
degree of 2 to φ and the last preferred interpreta-
tion is {x
1
} and it ascribes a degree of 2
n−1
to φ.
Thus, the best option for x
1
is the one that is sat-
isfied by the interpretations I that ascribe a degree
of d(I) = 1, 2,. .. ,2
n−1
to φ.
• x
2
is the second preferred variable of φ. Thus,
from the 2
n−1
interpretations that satisfy x
1
, we
have 2
n−2
interpretations that satisfy x
1
and x
2
.
From the 2
n−2
interpretations, the last preferred
interpretation that satisfies x
1
and x
2
ascribes a de-
gree of 2
n−2
to φ. Thus, the best option for x
2
is
the one verifying that the interpretations I ascrib-
ing the degree of d(I) = 1, 2,. .. ,2
n−2
to φ contain
x
1
and x
2
(i.e., x
1
∧ x
2
is satisfied by these inter-
pretations).
• The unique interpretation that satisfies x
1
,.. ., x
n
is the one ascribed the degree 1 to φ. So, the best
option for x
n
is the one verifying that the inter-
pretations I ascribing a degree of d(I) = 1 to φ
contain x
1
,.. ., x
n
(i.e., x
1
∧ ... ∧ x
n
is satisfied by
these interpretations).
Thus, we have 2
n−1
lexicographically preferred inter-
pretations that are necessary for learning x
1
. From
the 2
n−1
interpretations, 2
n−2
are necessary for learn-
ing x
2
and so on. So, 2
n−1
interpretations are nec-
essary for learning the n options of φ. To general-
ize, the best option x
i=1,...,n
is the one verifying that
x
1
∧ .. . ∧ x
i
is satisfied by interpretations I ascribed
d(I) = 1, 2,. .. ,2
n−i
.
From the result given in Proposition 2, the support
and confidence in LCL are defined as follows:
Definition 10 (Support). Let P be a preference
database, I be an interpretation in P , D be the set
of satisfaction degrees, φ be an LCL formula to be
learned s.t. len(φ)=n according to Proposition 1. The
support of an option x
i=1,...,n
= x for interpretations
I∈P is defined as:
Supp(x
i
)=



I | I |= x
1
∧ ... ∧ x
i
∧ d(I) = 1, .. ., 2
n−i



|{
I | d(I) = 1, .. ., 2
n−i
}|
Definition 11 (Confidence). Let P be a prefer-
ence database, I be an interpretation in P , D be
the set of satisfaction degrees s.t. d(I) ∈ D, φ
be an LCL formula to be learned s.t. len(φ)=n
according to Proposition 1. The confidence of an op-
tion x
i=1,...,n
= x for interpretations I∈P is defined as:
Con f (x
i
)=
|{I | I |= (x
1
∧ . .. ∧ x
i
∧ d(I) = 1,. . . ,2
n−i
∨ (I ̸|= x
1
∧ . .. ∧ x
i
∧ d(I) ̸= 1,. . . ,2
n−i
}|
|P |
Example 5. Let us consider in Table 2, 6 possible
configurations for a futur shopping center. The con-
sidered services are parking (p), shopping (s), and
restaurants (r). The global evaluation of each con-
figuration represents the satisfaction of users, 1 for
high satisfaction, 2 for medium satisfaction, 3 for low
satisfaction and ∞ for unacceptable configurations.
Table 2: A simple example of user’s preferences.
con f igurations p s r User’s satisfaction (D)
I
1
0 0 1 3
I
2
0 1 0 ∞
I
3
1 0 0 ∞
I
4
1 0 1 3
I
5
1 1 0 2
I
6
1 1 1 1
P ={I
1
, . .., I
6
}, D ={1, 2, 3,∞}. We have len(φ) =
2. We aim to learn a preference model M
LC L
s.t.
M
LC L
=

φ s.t. φ = x
1
⃗⋄x
2
,x
i=1,...,2
∈ X
and x
1
̸= x
2
The learned model contains a BCF formula φ that
contains 2 options, each one is a single or conjunctive
option built on V ={p, s, r}.
Let us consider the option x
1
= p. From data of
Table 2, we have Supp(x
1
= p)=1 (p is satisfied by
I
6
having d=1 and satisfied also by I
5
having d = 2).
Con f (x
1
= p)=4/6. We have I
3
|= p with d = ∞ and
I
4
|= p with d = 3). So, these two interpretations do
not verify the definition of confidence. This means that
p is not the best first option of φ since we aim to learn
an option with maximum support and confidence (ide-
ally 1).
The method for learning the frequent best options
is defined in the following.
4.2 Generation of Options of the LCL
Formula
For generating frequent options, we adapt the ap-
proach of association rules (Agrawal et al., 1993).
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
1016

The idea is to start with all single options, count their
support and find all single frequent options, com-
bine them to form candidate 2-conjunctive options,
go through data and count their support and find all
frequent 2-conjunctive options, combine them to form
candidate 3-conjunctive options and so on. More pre-
cisely, two principal steps are applied: i) Join Step
where candidates’ conjunctive options (CC
k
) are gen-
erated by joining frequents ones (FC
k−1
), ii) Prune
Step where any (k-1)-option that is not frequent can-
not be a subset of a frequent k-option. Once frequent
conjunctive options are generated for each x
i=1,...,n
,
we return only those exceeding a minimal confidence
θ, called final frequent options (FinalF
x
i
). Algorithm
1 summarizes these steps.
Algorithm 1: Final frequent options.
Data: The preference database P , the set of
satisfaction degrees D, d∈D,
φ=(x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
)))) the LCL
formula to be learned, a minimal support σ
and a minimal confidence θ for x
i=1...n
FC
j
: Frequent conjunctive options of size j
FC
1
: Frequent single options
FC
x
i
: Final options for x
i=1,...,n
Result: FinalF
x
i=1,...,n
: Final frequent options for
each x
i=1,...,n
with support and confidence
exceeding σ and θ
1 for each x
i=1,...,n
do
2 for j = 1; j ̸=
/
0; j + + do
3 CC
j
: candidate options of size j;
4 for each interpretation I having
d(I) = 1,. . . , 2
n−i
do
5 for each x ∈ CC
j
do
6 Compute Supp(x) according to
Definition 10
7 end
8 end
9 FC
j
={x ∈ CC
j
| Supp(x) ≥ σ}
10 end
11 FC
x
i
= ∪
j
FC
j
12 FinalF
x
i
=
/
0
13 for each x ∈ FC
x
i
do
14 if Con f (x) ≥ θ and x is minimal
according to Definition 12 then
15 FinalF
x
i
=FinalF
x
i
∪ x
16 end
17 end
18 Return FinalF
x
i
19 end
Many frequent options can be learned for a given
option of the BCF formula. To deal with this prob-
lem, we define in the following the notion of minimal
frequent option.
Definition 12. Let FC
x
i=1,...,n
be a set of frequent op-
tions for x
i
, and x in FC
x
i
. Then, x is a minimal
frequent option for x
i
iff there is no frequent option
x
′
in FC
x
i
s.t. i) Supp(x
i
= x
′
) = Supp(x
i
= x), ii)
Con f (x
i
= x
′
) = Con f (x
i
= x) and iii) x
′
⊆ x.
From Table 2, the option x = p ∧ s in FinalF
x
1
is
a minimal final frequent option.
As each final frequent option has its support and
confidence, we propose to order them as follows.
Definition 13. Let FinalF
x
i=1,...,n
be a set of final fre-
quent options for x
i=1...n
. Given x, y ∈ FinalF
x
i
.
x ≻
x
i
y iff
• Con f (x
i
= x,) > Con f (x
i
= y) or,
• Con f (x
i
= x)=Con f (x
i
= y) and Supp(x
i
= x) >
Supp(x
i
= y).
For comparing the final frequent options for a de-
gree x
i
, we consider the confidence as the most im-
portant criterion and the support the second one. This
allows to guarantee selecting interesting options for
each x
i
.
Example 6 (Example 5 continued). Let us consider
the data in Table 2. Table 3 gives final frequent op-
tions (x ∈ X) for the option x
1
of φ exceeding minimal
support σ = 0.9. FC
x
1
=FC
1
∪FC
2
={p, s, p ∧s}. With
minimal confidence θ=0.9, FinalF
x
1
={p ∧ s}.
Table 3: Final frequent options for x
1
.
The set CC
1
for x
1
x Supp(x
1
= x)
p 1
¬p 0
s 1
¬s 0
r 0.5
¬r 0.5
The set FC
1
for x
1
x Supp(x
1
= x)
p 1
s 1
The set CC
2
for x
1
x Supp(x
1
= x)
p ∧ s 1
The set FC
2
for x
1
x Supp(x
1
= x)
p ∧ s 1
FC
x
1
=FC
1
∪FC
2
x Supp(x
1
= x) Con f (x
1
= x)
p 1 0.66
s 1 0.83
p ∧ s 1 1
FinalF
x
1
with θ = 0.9
x Supp(x
1
= x) Con f (x
1
= x)
p ∧ s 1 1
Table 4 gives final frequent options for the option
x
2
of φ exceeding minimal support σ = 0.9. The set
CC
1
contains all possible single options and their sup-
port for interpretations with degree d = 1. For exam-
ple, supp(x
2
= r) is computed according to Definition
Learning Preferences in Lexicographic Choice Logic
1017

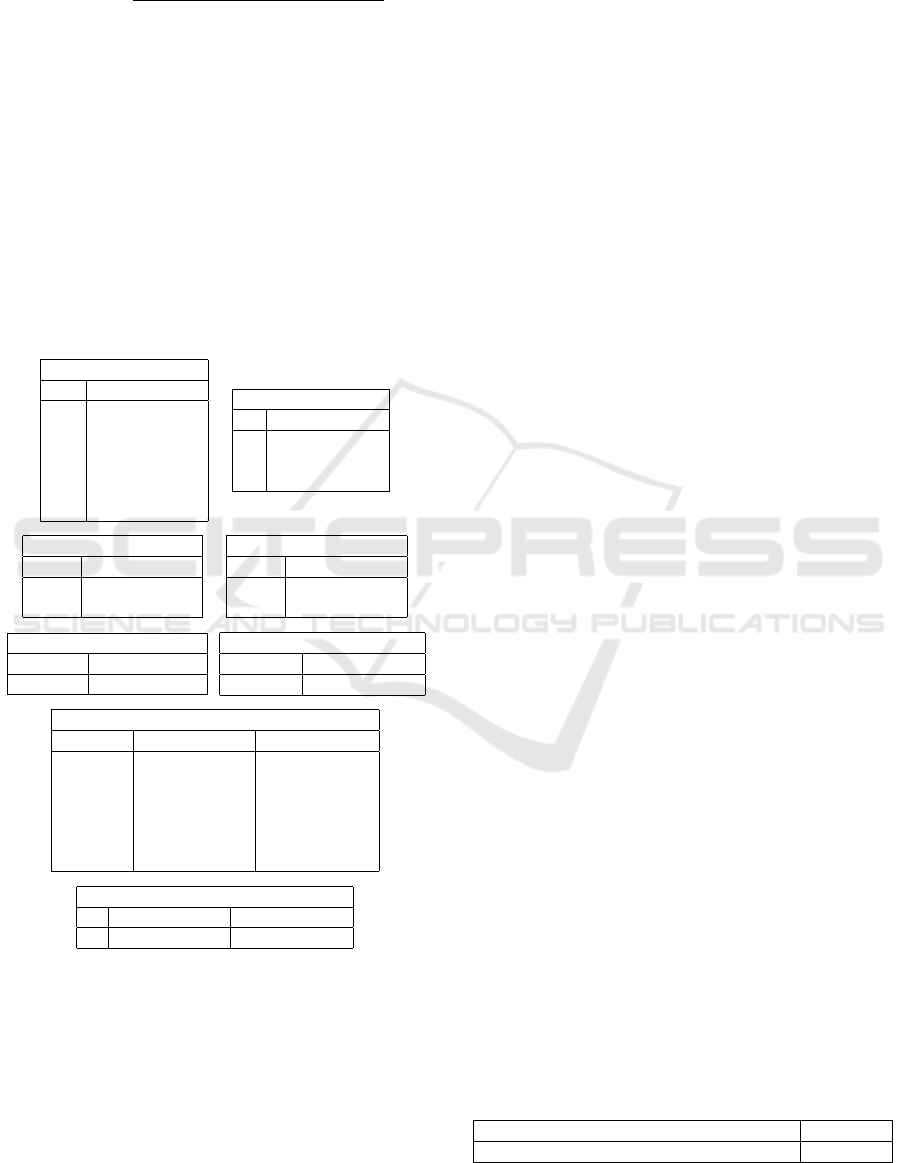
10 as follows: We have p ∧ s as the final frequent op-
tion for x
1
. So,
supp(x
2
= r) =
|{
I | I |= p ∧ s ∧ r ∧ d(I) = 1
}|
|{
I | d(I) = 1
}|
= 1
The set FC
1
contains all frequent single options
obtained from CC
1
exceeding minimal support σ =
0.9. CC
2
contains conjunctive options of size 2 that
are composed from the set FC
1
. The set FC
2
is com-
posed from CC
2
, it contains frequent conjunctive op-
tions of size 2 (p ∧ s is removed from CC
2
since it is
the unique final frequent option for x
1
, it can not be a
final frequent option for x
2
). The set FC
3
is composed
from CC
3
, it contains frequent conjunctive options of
size 3. FC
x
2
=FC
1
∪FC
2
∪FC
3
. With minimal confi-
dence θ=0.9 and applying Definition 12 to return only
minimal frequent options, FinalF
x
2
={r}.
Table 4: Final frequent options for x
2
.
The set CC
1
for x
2
x Supp(x
2
= x)
p 1
¬p 0
s 1
¬s 0
r 1
¬r 0
The set FC
1
for x
2
x Supp(x
2
= x)
p 1
s 1
r 1
The set CC
2
for x
2
x Supp(x
2
= x)
p ∧ r 1
s ∧ r 1
The set FC
2
for x
2
x Supp(x
2
= x)
p ∧ r 1
s ∧ r 1
The set CC
3
for x
2
x Supp(x
2
= x)
p ∧ s ∧ r 1
The set FC
3
for x
2
x Supp(x
2
= x)
p ∧ s ∧ r 1
FC
x
2
=FC
1
∪FC
2
∪FC
3
x Supp(x
2
= x) Con f (x
2
= x)
p 1 0.83
s 1 0.83
r 1 1
p ∧ r 1 1
r ∧ s 1 1
p ∧ s ∧ r 1 1
FinalF
x
2
with θ = 0.9
x Supp(x
2
= x) Con f (x
2
= x)
r 1 1
Given FinalF
x
i=1,...,n
be a set of final frequent op-
tions for each x
i=1,...,n
ordered following Definition
13, the LCL learned preference model is:
M
LC L
=



φ = (x
1
⃗⋄(x
2
⃗⋄(...(x
n−1
⃗⋄x
n
)))
s.t. x
i
∈ FinalF
x
i=1,...,n
and x
1
̸= x
2
̸= . .. ̸= x
n
.
Thus, the best LCL learned model contains a formula
which is composed of preferred final frequent options
for each option. The accuracy of each model is com-
puted by applying Equation 1. The best preference
model is the one that contains formula with the great-
est accuracy (ideally 1). To define the satisfaction de-
gree of new interpretations by the learned LCL prefer-
ence model that contains a formula φ, we apply Defi-
nition 7.
Example 7. Let us continue Example 6. The LCL
preference model learned from data of Table 2 is
M
LC L
=

φ = (p ∧ s)⃗⋄r
The accuracy of M
LC L
is 1. Let us consider the fol-
lowing two new interpretations I={p=0, s=0, r=0}
and I
′
={p=0, s=1, r=1}, then deg(I,φ)=∞ and
deg(I
′
,φ)=3.
5 EXPERIMENTAL RESULTS
To further test our method, we provide a case study in
the context of antibiotics prescription. The database
used here contains a list of antibiotics, each one is
described with some features (here we use 7 binary
features), and a rank of recommendation as defined
in Clinical Practice Guidelines (CPGs). It should be
noted that the complete dataset was tested using Al-
gorithm 1 implementation in Python3.
Antibiotics with recommendation rank 1 are rec-
ommended in first intention, those having a recom-
mendation rank 2 are recommended in second inten-
tion and those having recommendation rank 3 are rec-
ommended in third intention. Antibiotics having a
recommendation rank 0 are not recommended. So,
antibiotics having rank 1 are preferred to those hav-
ing rank 2 which are also preferred to those having
rank 3. Antibiotics having rank 0 are unacceptable
since they can not be prescribed for the patient. Thus,
in the context of LCL, we have D={1, 2, 3, ∞}.
Our aim is to determine what are the features so
that an antibiotic has a given recommendation rank.
Thus, we apply our method for learning an LCL pref-
erence model from the antibiotic database. The an-
tibiotic’s features are: Convenient protocol (proto),
Non precious class (Precious), serious side effects
(SideE f f ), High level of efficacy (E f f icacy), Nar-
row antibacterial spectrum (Spect), ecological ad-
verse effects (RiskResi) and Taste (Taste). The
learned LCL preference model for pharyngitis is given
in Table 5.
Table 5: M
LC L
in pharyngitis clinical situation.
M
LC L
Accuracy
(Proto ∧ ¬SideE f f )⃗⋄(Proto ∧ ¬RiskResi) 0.91
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
1018

Let us explain results of Table 5. M
LC L
contains
a BCF formula that has 2 options. The accuracy of
the model is higher which means that LCL is fully
adapted for modeling experts’ reasoning for providing
recommendations of antibiotics. The model does not
predict correctly some antibiotics. The reason is that
it is not possible to obtain a lexicographic ordering
over the two options of the BCF formula. In fact, the
learned model should verify the following conditions:
i) only antibiotics with rank 1 satisfy the two options
of the formula, ii) only antibiotics with rank 2 sat-
isfy the first option and not satisfy the second option,
and iii) only antibiotics with rank 3 satisfy the second
option and falsify the first option. There is no model
that verifies these conditions in the antibiotic database
for the considered clinical situation. The model given
here does not verify the condition iii). This is due cer-
tainly to some inconsistencies in the database (Tsopra
et al., 2018).
6 CONCLUSION
We proposed a method for learning preferences in the
context of a logic-based preference formalism, LCL.
The method is based on an adaptation of associa-
tion rules based on the Apriori algorithm. The LCL
learned model is qualitative and easily interpretable
for the user. To the best of our knowledge, this is the
first proposition for learning preferences in the con-
text of LCL.
The choice of train data plays an important role of
the learned LCL model. It can be different following
the considered train data. For example, if we consider
a preference database with D={1, 2, 3, ∞}, then the
learned model will contain an LCL formula with 2 op-
tions. However, if we consider a preference database
with D={1, 2, 3, 4, ∞}, then the learned model will
contain an LCL formula with 3 options. The formula
to be learned from D={3, 4, ∞} will be certainly dif-
ferent from the one learned from D={1, 2, 3, 4, ∞}.
The problem of learning LCL preferences is consid-
ered as an instance ranking problem where the set of
satisfaction degrees corresponds to the set of labels
and the set of outcomes corresponds to the set of in-
terpretations. In future work, we would perform some
evaluations to compare our method with other prefer-
ence learning methods, particularly those of instance
ranking problem.
REFERENCES
Agrawal, R., Imieli
´
nski, T., and Swami, A. (1993). Min-
ing association rules between sets of items in large
databases. In Proceedings of the 1993 ACM SIGMOD
International Conference on Management of Data,
SIGMOD ’93, pages 207–216, New York, NY, USA.
ACM.
Benferhat, S. and Sedki, K. (2008). Two alternatives for
handling preferences in qualitative choice logic. Fuzzy
Sets and Systems, 159(15):1889–1912.
Bernreiter, M., Maly, J., and Woltran, S. (2022). Choice
logics and their computational properties. Artif. In-
tell., 311:103755.
Boudjelida, A. and Benferhat, S. (2016). Conjunctive
choice logic. In International Symposium on Artifi-
cial Intelligence and Mathematics, ISAIM 2016, Fort
Lauderdale, Florida, USA, January 4-6, 2016.
Brewka, G., Benferhat, S., and Berre, D. L. (2004). Quali-
tative choice logic. Artif. Intell., 157(1-2):203–237.
Cohen, W. W., Schapire, R. E., and Singer, Y. (2011).
Learning to order things. CoRR, abs/1105.5464.
H
¨
ullermeier, E., F
¨
urnkranz, J., Cheng, W., and Brinker, K.
(2008). Label ranking by learning pairwise prefer-
ences. Artif. Intell., 172(16-17):1897–1916.
Joachims, T., Granka, L., Pan, B., Hembrooke, H., and Gay,
G. (2005). Accurately interpreting clickthrough data
as implicit feedback. In SIGIR’05: Proceedings of the
28th annual international ACM SIGIR conference on
Research and development in information retrieval,
pages 154–161, New York, NY, USA. ACM Press.
Johannes, F. and H
¨
ullermeier, E. (2010). Preference Learn-
ing. Springer-Verlag New York, Inc., New York, NY,
USA, 1st edition.
Sedki, K., Lamy, J., and Tsopra, R. (2022). Qualitative
choice logic for modeling experts recommendations
of antibiotics. In Proceedings of the Thirty-Fifth Inter-
national Florida Artificial Intelligence Research Soci-
ety Conference, FLAIRS 2022.
Tsopra, R., Lamy, J., and Sedki, K. (2018). Using pref-
erence learning for detecting inconsistencies in clin-
ical practice guidelines: Methods and application to
antibiotherapy. Artificial Intelligence in Medicine,
89:24–33.
Vembu, S. and G
¨
artner, T. (2010). Label ranking algo-
rithms: A survey. In Preference Learning., pages 45–
64.
Waegeman, W. and De Baets, B. (2010). A survey on roc-
based ordinal regression learning. In F
¨
urnkranz, J. and
H
¨
ullermeier, E., editors, Preference learning, pages
127–154. Springer.
Learning Preferences in Lexicographic Choice Logic
1019