Energy Consumption Optimization in Data Center with Latency Based
on Histograms and Discrete-Time MDP
L
´
ea Bayati
Laboratoire d’Algorithmique Complexit
´
e et Logique, Universit
´
e Paris-Est Cr
´
eteil (UPEC),
Keywords:
Data Center, Energy Saving, Markov Decision Process, Quality of Services, Latency.
Abstract:
This article introduces a probabilistic model for managing power dynamically (DPM) in a data center. The
model involves switching servers on and off, while considering both the time it takes for the machines to be-
come active and the amount of energy they consume. The goal of DPM is to balance energy consumption with
Quality of Service (QoS) requirements. To construct the model, job arrivals and service rates are represented
using histograms, which are discrete distributions derived from actual traces, empirical data, or measurements
of incoming traffic. The data center is modeled as a queue, and the optimization problem is formulated as a
discrete-time Markov decision process (MDP) in order to identify the optimal policy. The proposed approach
is evaluated using real traffic traces from Google, and different levels of latency are compared.
1 INTRODUCTION
The recent expansion of Clouds and Data Centers are
arising energetic and digital pollution challenges. En-
ergy consumed by data centers is estimated to be more
than 1.3% of the global energy consumption. Other-
wise, the daily CO
2
emission of one data center server
can be evaluated to more than 10 kg. Those rates are
increasing and needs for considering power manage-
ment strategy is emerging face of the energetic prob-
lems and digital pollution issues (Rajesh et al., 2008).
Data centers are conceived to hold up the peak traffic
load, however the global load is less than three quar-
ters of the peak load (Benson et al., 2010). Thus, a
considerable number of machines are not under load
and still consume more than the half of the maximal
energy consumption (Greenberg et al., 2009). Papers
like (Lee and Zomaya, 2012) show that 70% of the to-
tal cost of the data center is spent for electricity used
to run the servers and to make them cooler. Therefore,
the primary determinant of energy consumption is the
number of active servers. To reduce energy usage, a
power management strategy can be implemented to
control the on/off status of servers in a data center,
which ensures both efficient performance of the ser-
vices provided by the data center and reasonable en-
ergy consumption. Two requirements are in conflict:
(i) Saving energy, and (ii) Increasing the Quality of
the Service (QoS). To conserve energy, it is neces-
sary to activate a limited number of servers, result-
ing in lower energy consumption but longer waiting
times and a higher rate of job loss. Conversely, in or-
der to improve QoS, more servers must be activated,
which consumes more energy, but results in shorter
waiting times, a lower rate of job loss, and higher en-
ergy consumption. Additionally, turning-on a server
is not instantaneous and may cause an extra amount of
energy. The objective, therefore, is to develop power
management algorithms that consider both of these
constraints to minimize waiting times, job loss rates,
and energy consumption. In other word, it is neces-
sary to define a cost for each requirement and con-
ceive a policy that minimizes the overall cost. Notice
that each job arriving to a data center may generate a
profit. Works like in (Dyachuk and Mazzucco, 2010)
suggest that a lost job may cost 6.2 × 10
−6
$. Other-
wise, according to research published by Dell, Princi-
pled Technologies and other works as in (Rajesh et al.,
2008), running, one server costs around 300$ per year.
2 RELATED WORK
Many works as in (Gandhi et al., 2013; Aidarov et al.,
2013; Mitrani, 2013) model data centers as a theoret-
ical queuing model to evaluate the trade-off between
waiting time and energy consumption where jobs ar-
rive according to Poisson process then served accord-
98
Bayati, L.
Energy Consumption Optimization in Data Center with Latency Based on Histograms and Discrete-Time MDP.
DOI: 10.5220/0011846400003491
In Proceedings of the 12th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2023), pages 98-105
ISBN: 978-989-758-651-4; ISSN: 2184-4968
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ing to an exponentially distributed service time. They
consider specific management mechanisms to min-
imize energy consumption that leads to suboptimal
strategies like threshold policy. By conducting exper-
imental simulations and using analytical equations,
they were able to show that it is possible to achieve a
significant reduction in energy consumption (ranging
from 20% to 40%) without sacrificing a reasonable
waiting time. However works as (Maccio and Down,
2015; Bayati, 2018) were interested in finding the op-
timal policy by formalizing the energy saving models
by Markov Decision Process.
MDP (Markov Decision Process) is a model that
allows for the formalization of stochastic decision
systems. It is based on a Markov chain that is aug-
mented by a set of decision-making actions. Each ac-
tion changes the system from one state to another and
incurs a certain cost. Thus, the probability of tran-
sitioning to a new state is influenced by the selected
action. In the context of power management, the cost
of consumed energy depends on the number of active
servers and the switching-on rate of servers. On the
other hand, the cost of QoS depends on the number
of jobs that are waiting and/or rejected. Furthermore,
to find the optimal policy that minimizes the expected
total cost accumulated over a finite period of time, all
possible ways of turning off/turning on each machine
from every state of the system must be considered.
Notice that most of studies consider the latency of
servers, time latency (period needed to switch on/off
a server) as in (Mitrani, 2013; Xu and Tian, 2008), or
energetic latency (additional energy needed to switch
on/off a server) as in (Schwartz et al., 2012; Dy-
achuk and Mazzucco, 2010; Leng et al., 2016), or
both, as in (Maccio and Down, 2015; Gandhi et al.,
2013; Entezari-Maleki et al., 2017), in the case of
continuous-time framework, where arrival jobs are
modeled by a continuous time distribution obtained
by fitting the empirical data or by asserting some as-
sumptions that leads usually to a Poisson distribution
(Maccio and Down, 2015). Less work was addressed
to the context of discrete-time MDP, were arrival jobs
and service rates can be modeled by more general dis-
tributions (Benini et al., 1999).
More recent works can be found in (Chen and
Wang, 2022; Khan, 2022; Rteil et al., 2022; Peng
et al., 2022; An and Ma, 2022).
In fact, in the following we will show how MDP
can be used to include the latency of servers. No-
tice that modeling our energetic optimization prob-
lem with an MDP when including latency is not easy.
Thus, we will assume following assumptions: (i) only
latency of switching-on is considered; (ii) turning-off
a running server is instantaneous, which means that
switching-off latency is zero; (iii) all servers are ho-
mogeneous and have the same constant latency pe-
riod, which is of a duration of k units of time; (iv) the
data center is modeled by a discrete time queue, in-
cluding the set of homogeneous servers with the same
level of energy consumption and the same service ca-
pacity; (v) real incoming traffic traces are sampled
then used directly to build empirical discrete distri-
butions (histograms) to model job arrivals and service
rates. After that, our problem of energy-QoS opti-
mization is formulated by a discrete-time MDP then
the value iteration algorithm that implements the Bell-
man’s backup equations (Bellman, 1957) is used to
compute the optimal policy.
The rest of this paper is organized as follows. Sec-
tion 3 models the system by simple queue. Then,
Section 6 formulates the optimization problem as
discrete-time MDP. After that, in Section 8 we give
experimental results when analyzing a system with ar-
rivals modeled by discrete distribution obtained from
real Google traffic traces (Wilkes, 2011).
3 MODEL DESCRIPTION
In this work we consider a queue model that oper-
ates in discrete time. This model is based on a batch
arrival queue with a finite buffer capacity of size b.
Arrival jobs and service rates are modeled using his-
tograms, which are discrete probability distributions
derived from actual traces. The number of jobs arriv-
ing at the data center during a time slot is represented
by a histogram denoted H
A
, where P
A
(i) gives the
probability of having i arrival jobs per slot. The data
center comprises a maximum of max homogeneous
servers, and during a single time unit, each server can
process a certain number of jobs, which is modeled
using a histogram denoted H
D
, where P
D
(d) gives the
probability of processing d jobs. Each server can be
in one of several states:
• stopped: switched-off
• in latency since 0 unit of time and needs k unit to be
ready
• in latency since 1 unit of time and needs k −1 unit to be
ready
• ...
• in latency since i unit of time and needs k − i unit to be
ready
• ...
• in latency since k − 1 unit of time and needs 1 unit to be
ready
• ready: switched-on
Energy Consumption Optimization in Data Center with Latency Based on Histograms and Discrete-Time MDP
99

Each slot we need to know the number of servers
grouped by states given above (see Figure 1). We con-
sider the set of the following levels of latency:
L = {lat
∞
= stop, lat
k
, lat
k−1
, . . . , lat
i
, . . . , lat
2
, lat
1
, ready = lat
0
} (1)
where lat
i
denotes that the server is within the
switching-on period and need i slot to be completely
ready to work. The number of servers of level x ∈ L
is denoted by m
x
.
Stopped
Need k slot
to be ready
Need k-1 slot
to be ready
Need i slot
to be ready
Need 2 slot
to be ready
Need 1 slot
to be ready
Ready
Figure 1: Transition between stopping, sleeping, and ready
modes.
Thus, the number of operational servers is m =
m
ready
= m
lat
0
, the number of servers that will be
ready within i slot is m
lat
i
, the total number of servers
in latency is given by m
lat
=
k
∑
i=1
m
lat
i
, and finally
max = m
ready
+ m
lat
+ m
stop
is the maximal number
of operational servers (total number of servers).
The number of jobs that are currently waiting in
the queue is represented by the symbol n, while the
number of jobs that have been rejected or lost is rep-
resented by l. At the start of the simulation, we as-
sume that there are no waiting or rejected jobs, and
all servers are in the ”stopped” mode.
stopped server
stopped server
server in latency
server in latency
ready server
ready server
served jobs
i: job arrivals
l: rejected jobs
b: Buffer size
n: Waiting jobs
Figure 2: Illustration of the queuing model.
To compute the number of waiting jobs n, one can
use an induction method where the specific sequence
of events during a slot must be described. Initially,
jobs are added to the buffer, then they are executed by
the servers. Job admission is performed on a per-job
basis using the Tail Drop policy, which means that
a job is accepted if there is space in the buffer, oth-
erwise it is rejected. The equations below show the
number of waiting jobs in the buffer and the lost jobs,
where i represents the number of arrival jobs, and d
represents the service rate:

n ← min{b, max{0, n + i − m
ready
× d}}
l ← max{0, n + i − m
ready
× d − b}
(2)
Under the assumption that input arrivals are inde-
pendent and identically distributed (i.i.d.), the queue
model is represented by a time-homogeneous Dis-
crete Time Markov Chain. However, when dealing
with real traffic traces, it is necessary to ensure the
i.i.d. assumption by finding the appropriate sampled
period for which the sampled trace is i.i.d. So we use
a statistical hypothesis testing called the turning point
test (Kendall, 1973) to test the i.i.d-ness of the sam-
pled trace, then consider only the sampled period for
which the data is i.i.d.
Nonetheless, the system becomes increasingly
complex to analyze as the number of servers varies
over time. The number of servers may fluctuate based
on traffic and performance metrics. To be more pre-
cise, n, l, m
ready
are considered, then some decisions
are taken depending on a particular cost function.
4 ENERGY AND PERFORMANCE
METRIC
The energy consumption of the data center depends
on the number of active servers. When a server is
turned off, it doesn’t consume any energy, but when
it’s operational, it consumes a certain amount of en-
ergy per time slot, which incurs a cost in monetary
units (c
M
). Additionally, since it takes k units of time
for a server to switch on, it incurs an extra energy
cost that also has a monetary value (c
on
). We assume
that the energy consumed during the latency period is
uniform, i.e.,
c
on
k
per time slot. The total energy con-
sumption is the sum of all the energy units consumed
over a certain period. QoS depends on the number of
jobs that are waiting or lost. Each waiting job incurs
a cost in monetary units (c
N
), while each rejected job
has a different cost (c
L
).
Table 1: Unitary costs of energy end Qos.
Cost Meaning
c
M
∈ IR
+
energy cost for running one operational server
c
on
∈ IR
+
energy cost needed to switch-on a server
c
N
∈ IR
+
waiting cost for one job per unit of time
c
L
∈ IR
+
rejection cost of one lost job
5 OBJECTIVE COST FUNCTION
During a given period of time, a dynamic control
policy for energy efficiency involves taking action in
each slot (either turning on or turning off a specific
number of servers) to adjust the number of operational
servers in response to changes in incoming jobs. The
optimal strategy is to find the best sequence of ac-
tions that minimizes the overall monetary cost, which
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
100

is a combination of the energetic cost and the perfor-
mance cost. The cost incurred for each slot can be
expressed as:
n × c
N
+ l × c
L
+ m
ready
× c
M
+ m
lat
×
c
on
k
(3)
where n is the number of waiting jobs, l is the num-
ber of lost jobs, m
ready
is the current number of op-
erational servers, and m
lat
is the number of servers in
latency mode.
6 MARKOV DECISION PROCESS
To analyze the performance and energy consumption
of the data center under the optimal strategy, we will
utilize the concept of a Markov Decision Process to
formulate our optimization problem. It is important
to note that (n, l) and m
ready
are interdependent. De-
creasing m
ready
saves more energy, but it also leads to
an increase in both n and l, resulting in an undesirable
reduction in QoS, and vice versa.
Let (S , A, P , C ) be an MDP where S is the
state space, A is the set of actions, P is the
transition probability, and C the immediate cost
of each action. Let H
A
= (S
A
, P
A
) be the his-
togram used to model the arrival jobs, and let H
D
=
(S
D
, P
D
) be the histogram used to model the ser-
vice rate. The state of the system is defined by
the couple ((m
stop
, m
lat
k
, m
lat
k−1
, . . . , m
lat
i
, . . . , m
lat
2
,
m
lat
1
, m
ready
), (n, l)) indeed the state space S is de-
fined as:
S = {((m
x
: x ∈ L ), (n, l)) | m
x
∈ [0..max], n ∈ [0..b] and l ∈ [0.. max(S
A
)]}
(4)
The action space is defined as:
A = {α
+z
|z ∈ [1..max]} ∪ {α
0
} ∪ {α
−z
|z ∈ [1..max]}
(5)
where:
1. action α
0
consists of doing nothing;
2. action α
+z
consists in switching-on z additional
servers if the number of stopped servers is more
than z, otherwise switches-on all stopped ma-
chines;
3. action α
−z
consists in switching-off z servers if
the number of ready servers is more than z, other-
wise switches-off all the ready machines.
If the current state of the system is:
s =

(m
stop
, m
lat
k
, m
lat
k−1
, . . . , m
lat
i
, . . . , m
lat
2
, m
lat
1
, m
ready
)
(n, l)
(6)
then:
1. action α
0
move the system to the state s
0
:
s
0
=

(m
stop
, 0, m
lat
k
, m
lat
k−1
, . . . , m
lat
i
, . . . , m
lat
2
, m
lat
1
+ m
ready
)
(n
0
, l
0
)
(7)
So we have a probability of P
α
0
ss
0
and an immediate
cost of C
α
0
s
to transit from state s to state s
0
under
action α
0
:
P
α
0
ss
0
=
∑





for each i ∈ S
A
and each d ∈ S
D
satisfying:
n
0
= min{b, max{0,n +i − (m
ready
+ m
lat
1
) ×d}}
l
0
= max{0, n + a − (m
ready
+ m
lat
1
) ×d −b}
P
A
(i) × P
D
(d)
(8)
C
α
0
s
= n × c
N
+ l × c
L
+ (m
lat
1
+ m
ready
) × c
M
+
∑
k
i=2
m
lat
i
×
c
on
k
(9)
2. action α
+z
move the system to the state s
+
:
s
+
=



(max{m
stop
− z, 0}, min{z, m
stop
}, m
lat
k
, m
lat
k−1
, . . .
. . . , m
lat
i
, . . . , m
lat
2
, m
lat
1
+ m
ready
)
(n
0
, l
0
)
(10)
So we have a probability of P
α
+z
ss
+
to transit from
state s to state s
+
under action α
+z
:
P
α
+z
ss
+
=
∑





for each i ∈ S
A
and each d ∈ S
D
satisfying:
n
0
= min{b, max{0, n +i − (m
ready
+ m
lat
1
) ×d}}
l
0
= max{0, n + a − (m
ready
+ m
lat
1
) ×d −b}
P
A
(i) × P
D
(d)
(11)
And we have an immediate cost of C
α
+z
s
to transit
from state s to state s
+
under action α
+z
:
C
α
+z
s
= n × c
N
+ l × c
L
+ (m
lat
1
+ m
ready
) × c
M
+

min{z, m
stop
} +
∑
k
i=2
m
lat
i

×
c
on
k
(12)
3. action α
−z
move the system to the state s
−
:
s
−
=



(m
stop
+ min{z, m
ready
}, 0, m
lat
k
, m
lat
k−1
, . . .
. . . , m
lat
i
, . . . , m
lat
2
, m
lat
1
+ max{m
ready
− z, 0})
(n
0
, l
0
)
(13)
So we have a probability of P
α
−z
ss
−
to transit from
state s to state s
−
under action α
−z
:
P
α
−z
ss
−
=
∑





for each i ∈ S
A
and each d ∈ S
D
satisfying:
n
0
= min{b, max{0,n + i − (m
lat
1
+ max{m
ready
− z, 0}) × d}}
l
0
= max{0, n + a − (m
lat
1
+ max{m
ready
− z, 0}) × d − b}
P
A
(i) × P
D
(d)
(14)
Energy Consumption Optimization in Data Center with Latency Based on Histograms and Discrete-Time MDP
101

And we have an immediate cost of C
α
−z
s
to transit
from state s to state s
−
under action α
−z
:
C
α
−z
s
= n × c
N
+ l × c
L
+ (m
lat
1
+ max{m
ready
− z, 0}) × c
M
+
k
∑
i=2
m
lat
i
×
c
on
k
(15)
Notice that n
0
(resp. l
0
) is the new number of waiting
(resp. rejected) jobs, and the immediate cost includes
two parts. The QoS part, which includes cost due to
waiting and rejected jobs. Power part composed of
energy consumed for running operational servers and
energy used by servers which are in the switching-on
latency period. Table 2 resumes parameters of MDP
model formulation.
Table 2: Model and MDP Parameters.
Parameters Description
h duration of analysis
k latency period
b buffer size
max total number of servers
H
D
histogram modeling the processing
capacity of a server
H
A
histogram of job arrivals
m
ready
number of operational servers
m
lat
i
number of servers in latency level i
n number of waiting jobs
l number of rejected jobs
S set of all possible states
A set of all possible actions
s s = ((m
x
: x ∈ L), (n, l)) system
state
s
0
s
0
= ((max, 0, ..., 0), (0, 0)) starting
state
α
0
action to keep the same number of
operational servers
α
+z
action to switch-on z additional
server
α
−z
action to switch-off z server
P
α
ss
0
probability of transition from s to s
0
under action α
C
α
s
immediate cost from s under action
α
Theorem 1. The number of state of the MDP is in
O

b × max(S
A
) × max
k

.
Proof. Every state of the MDP includes three parts:
(i) the number of waiting jobs in the buffer which
is bounded by b, (ii) the number of rejected jobs
which can be at most equals to the maximum num-
ber of arrival jobs given by max(S
A
), and (iii) as
we deal with k level of latency, the set of number
of servers for every latency level in L. Each num-
ber is between 0 and max. So, |S| is bounded by
(b + 1) × (max(S
A
) + 1) × max
k+2
.
Theorem 2. MDP transitions number is in
O

b × |S
A
| × |S
D
| × max(S
A
) × max
k

.
Proof. From each state of the MDP we have at most
(2 × max + 1) action, and each action leads to a num-
ber of transitions equals to |S
A
| × |S
D
| (one transition
for each bin in the support of the arrivals distribution
combined with each bin in the support of the service
rate distribution).
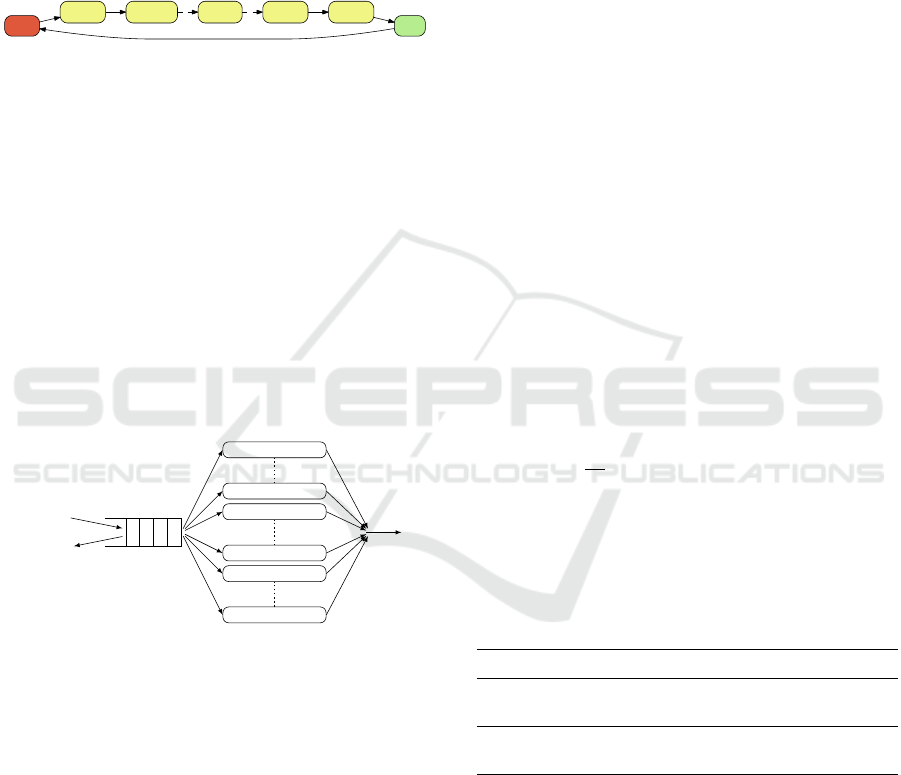
To illustrate our formalization, Figure 3 shows an
example of an MDP modeling a very simple data cen-
ter of two servers max = 2 with a latency period of
two unite of time k = 2 with a buffer size equals two
b = 2. Additionally, to keep the example simple, we
set service rate of each machine as a histogram with
only one bin: P
D
(1) = 1 (one server process one job
every slot). Also job arrivals are modeled by his-
togram with only one bin P
A
(1) = 1 (system receives
one job every slot).
7 OPTIMAL STRATEGY
By formulating our optimization problem as a
Markov Decision Process (MDP), we define an ac-
tion as the process of turning on a specific number of
servers each unit of time and turning off the rest of the
servers. The optimal strategy is determined by finding
the best sequence of actions that minimizes the over-
all cost during a finite period of time, referred to as
the horizon and denoted by h. In general, the objec-
tive of the value function V : S × [0..h] → I!R
+
is to
minimize the expected sum of costs over time:
V (s, t) = min
π
E
"
t
∑
k=0
C
π(s
k
,k)
s
k
#
(16)
The value function can be seen as a Bellman equa-
tion (Bellman, 1957):
V (s,t) = min
α
(
C
α
s
+
∑
s
0
∈S
P
α
ss
0
V (s
0
,t − 1)
)
(17)
Where α is the action taken by the system, and P
α
ss
0
is the transition probability from state s to state s
0
. In
this case the optimal policy for each state s is:
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
102

π
∗
(s,t) = argmin
α∈A
(
C
α
s
+
∑
s
0
∈S
P
α
ss
0
V (s
0
,t − 1)
)
(18)
Given that the value iteration algorithm is a power-
ful dynamic programming approach for solving the
Bellman equation, we employed it to derive the op-
timal control policy of our Markov Decision Process
(MDP).
8 CASE STUDY
This case study uses real traffic traces based on the
open cluster-data-2011-2 trace (Wilkes, 2011). As
in (Bayati, 2018), we model arrival jobs and service
rate by discrete distributions build from the job/ma-
chine events corresponding to the requests destined to
a specific Google data center for the whole month of
May 2011. This traffic trace is sampled with a sam-
pling period of 136 second that ensure the i.i.d-ness.
Listing 1: Example of PRISM specification.
1 mdp
2 const int k=2;
3 const int B;
4 const int m=5;
5 const int d=2;
6 //---------------------------------------------
7 const double cN =1;
8 const double cM =1;
9 const double cL =1;
10 const double cON=1;
11 //---------------------------------------------
12 const int A0=7;
13 const double p0=1.0;
14 //---------------------------------------------
15 module system1
16 off : [0..m ] init m;
17 set2 : [0..m ] init 0;
18 set1 : [0..m ] init 0;
19 M : [0..m ] init 0;
20 N : [0..B ] init 0;
21 L : [0..A0] init 0;
22 //---------------------------------------------
23 [a_5] M>=5
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
24 (M’=min(m,M+set1-5))&(set1’=set2)&(set2’=0)&
25 (off’=min(m,off+5))&(L’=max(0,N+A0-M
*
d-B));
26 //---------------------------------------------
27 [a_4] M>=4
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
28 (M’=min(m,M+set1-4))&(set1’=set2)&(set2’=0)&
29 (off’=min(m,off+4))&(L’=max(0,N+A0-M
*
d-B));
30 //---------------------------------------------
31 [a_3] M>=3
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
32 (M’=min(m,M+set1-3))&(set1’=set2)&(set2’=0)&
33 (off’=min(m,off+3))&(L’=max(0,N+A0-M
*
d-B));
(0,0,0,2,0,0) a0
(1,0,0,1,0,0)
a-1
(2,0,0,0,0,0)
a-2
(0,0,0,2,1,0)
a0
a-1
a-2
(0,0,0,2,2,0)
a0
(1,0,0,1,1,0)
a-1
(2,0,0,0,1,0)
a-2
(0,0,0,2,2,1)
a0
a-1
a-2
(0,0,1,1,0,0)
a0
a-1
(0,0,1,1,1,0)
a0
a-1
(0,0,1,1,2,0)
a0
(1,0,0,1,2,0)
a-1
(0,0,1,1,2,1)
a0
a-1
(0,0,2,0,2,0)
a0
(0,0,2,0,2,1)
a0
(0,1,0,1,0,0)
a0
(1,0,1,0,0,0)
a-1
(0,1,0,1,1,0)
a0
(1,0,1,0,1,0)
a-1
(0,1,0,1,2,0)
a0
(1,0,1,0,2,0)
a-1
(0,1,0,1,2,1)
a0
a-1
(0,1,1,0,2,0)
a0
(0,1,1,0,2,1)
a0
(0,2,0,0,1,0)
a0
(0,2,0,0,2,0)
a0
(0,2,0,0,2,1)
a0
a+1
a0
a-1
a+1
a0
a-1
a+1
a0
(2,0,0,0,2,0)
a-1
(1,0,0,1,2,1)
a+1
a0
a-1
a+1
a0
a+1
a0
a+1
a0
(1,0,1,0,2,1)
a+1
a0
(1,1,0,0,1,0)
a+1
a0
(1,1,0,0,2,0)
a+1
a0
(1,1,0,0,2,1)
a+1
a0
a+2
a+1
a0
a+2 a+1
a0
a+2 a+1(2,0,0,0,2,1)
a0
a+2 a+1
a0
Figure 3: MDP example for a data center of only two ma-
chine with latency k = 2 and b = 2.
34 //---------------------------------------------
35 [a_2] M>=2
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
36 (M’=min(m,M+set1-2))&(set1’=set2)&(set2’=0)&
37 (off’=min(m,off+2))&(L’=max(0,N+A0-M
*
d-B));
38 //---------------------------------------------
39 [a_1] M>=1
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
40 (M’=min(m,M+set1-1))&(set1’=set2)&(set2’=0)&
41 (off’=min(m,off+1))&(L’=max(0,N+A0-M
*
d-B));
Energy Consumption Optimization in Data Center with Latency Based on Histograms and Discrete-Time MDP
103

42 //---------------------------------------------
43 [a0] off>=0
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
44 (M’=min(m,M+set1))&(set1’=set2)&(set2’=0)&
45 (off’=off-0)&(L’=max(0,N+A0-M
*
d-B));
46 //---------------------------------------------
47 [a1] off>=1
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
48 (M’=min(m,M+set1))&(set1’=set2)&(set2’=1)&
49 (off’=off-1)&(L’=max(0,N+A0-M
*
d-B));
50 //---------------------------------------------
51 [a2] off>=2
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
52 (M’=min(m,M+set1))&(set1’=set2)&(set2’=2)&
53 (off’=off-2)&(L’=max(0,N+A0-M
*
d-B));
54 //---------------------------------------------
55 [a3] off>=3
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
56 (M’=min(m,M+set1))&(set1’=set2)&(set2’=3)&
57 (off’=off-3)&(L’=max(0,N+A0-M
*
d-B));
58 //---------------------------------------------
59 [a4] off>=4
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
60 (M’=min(m,M+set1))&(set1’=set2)&(set2’=4)&
61 (off’=off-4)&(L’=max(0,N+A0-M
*
d-B));
62 //---------------------------------------------
63 [a5] off>=5
-> p0:(N’=min(B,max(0,N+A0-M
*
d)))&
64 (M’=min(m,M+set1))&(set1’=set2)&(set2’=5)&
65 (off’=off-5)&(L’=max(0,N+A0-M
*
d-B));
66 endmodule
67 //---------------------------------------------
68 rewards "r"
69 [a_5] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
70 [a_4] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
71 [a_3] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
72 [a_2] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
73 [a_1] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
74 [a0] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
75 [a1] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
76 [a2] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
77 [a3] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
78 [a4] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
79 [a5] true : M
*
cM+N
*
cN+L
*
cL+(set1+set2)
*
cON/k;
80 endrewards
To specify, solve, and analyze energy consump-
tion in our data centers, we utilize an efficient model
checker called PRISM (Kwiatkowska et al., 2002).
PRISM is a probabilistic software that allows for the
specification of MDP models. However, writing a
specification for large-scale systems can be challeng-
ing. For instance, the PRISM program for a data
center with a latency of ten units of time consists of
thousands of lines of code, and it is difficult to write
the specification manually without making mistakes
or omitting cases. Furthermore, updating or main-
taining such a large specification is time-consuming.
Therefore, automated generation of the specification
is necessary to save time and avoid errors. (see Theo-
rems 1 and 2 ), We developed a tool to automatically
generate the PRISM specification file. For instance,
consider a basic data center with five machines and
latency k = 2, and Dirac histograms for job arrival
and service rate. The corresponding PRISM script for
this example is shown in Listing 1.
Table 3: Parameters of the numerical analysis.
b max E(H
A
) E(H
D
) c
M
c
On
c
N
c
L
k h
1-70 5 7 2 1 1 1 1 2-5 100
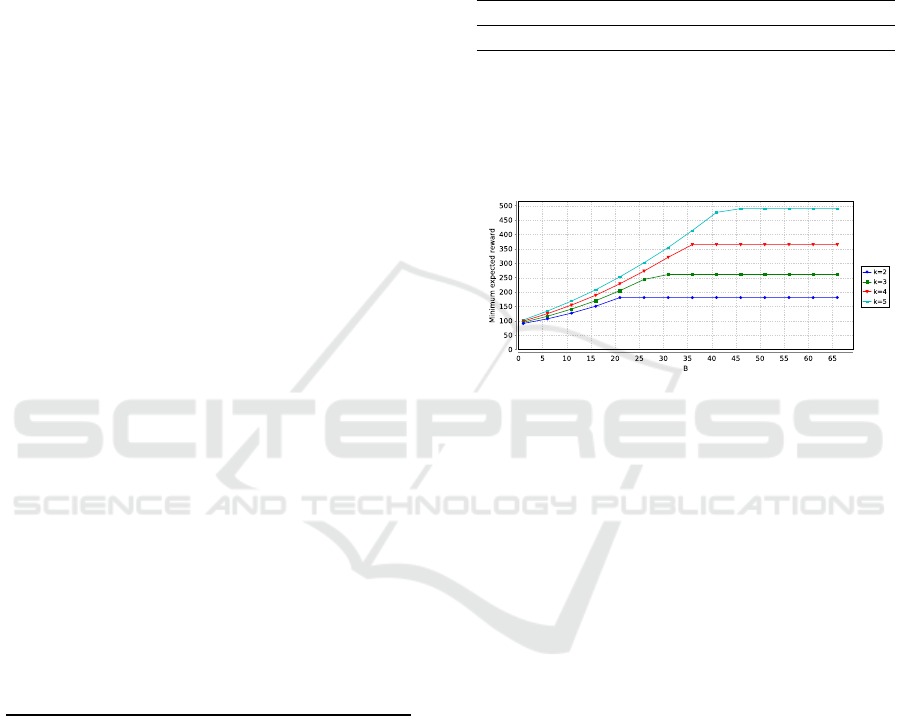
Figure 4 shows the result of experiments where
we analyze the total cost over 100 units of time when
varying the buffer size b and latency k. We observe
that in general the total cost increase when b is less
than some value b
k
that depends on k.
Figure 4: Total cost when varying buffer size b for different
level k.
When the buffer size b is greater than b
k
, the total
cost appears to converge for any configuration. This
behavior can be explained as follows: when the buffer
size is small, the number of waiting jobs is low, result-
ing in a small number of served jobs, and the system
switches on fewer servers. As a result, both the energy
consumption and the number of waiting jobs are low.
However, when the buffer size increases, the number
of waiting jobs becomes more significant, resulting in
a larger number of served jobs and more servers be-
ing switched on. This, in turn, leads to an increase
in both energy consumption and the number of wait-
ing jobs. As the number of incoming jobs is limited,
when the buffer size exceeds a certain value, the num-
ber of waiting jobs and the number of served jobs be-
come stable, resulting in a constant number of running
servers and, as a result, a constant total cost. Another
related observation is the fact that b
k
grows when k
increases. For example, for a system with k = 4, the
total cost becomes independent from the latency pe-
riod when b > b
k
= b
4
= 36, however, for a system
with k = 2, the total cost becomes independent from
the latency period when only b > b
k
= b
2
= 21. It
means that a data center with servers with longer pe-
riods of latency have to be designed with more longer
buffer size. A last observation is the fact that the to-
tal cost is more important when k increases. We can
SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems
104

explain that from the fact that the system, during the
latency period, accumulates more waiting jobs before
the complete switching-on of the servers.
9 CONCLUSION
The aim of this study is to develop a model for effi-
cient management of a data center that takes into ac-
count server latency and minimizes energy consump-
tion and Quality of Service (QoS) costs. The model
uses a discrete-time Markov decision process, with
job arrivals and service rates modeled by a discrete
probability distribution estimated from real data. To
account for switching-on latency, it is assumed that
all servers have the same constant latency period of k
units of time. The optimal control policy is computed
using the value iteration algorithm, and is used to im-
plement a Dynamic Power Management strategy that
balances energy consumption and performance. De-
spite the large size of the model (which is an expo-
nential of k), the experimental and theoretical results
demonstrate that increasing buffer size can lead to sig-
nificant energy savings when the latency is higher.
REFERENCES
Aidarov, K., Ezhilchelvan, P. D., and Mitrani, I. (2013).
Energy-aware management of customer streams.
Electr. Notes Theor. Comput. Sci., 296:199–210.
An, H. and Ma, X. (2022). Dynamic coupling real-time en-
ergy consumption modeling for data centers. Energy
Reports, 8:1184–1192.
Bayati, M. (2018). Power management policy for hetero-
geneous data center based on histogram and discrete-
time mdp. Electronic Notes in Theoretical Computer
Science, 337:5 – 22. Proceedings of the Ninth In-
ternational Workshop on the Practical Application of
Stochastic Modelling (PASM).
Bellman, R. (1957). Dynamic Programming. Princeton
University Press, Princeton, NJ, USA, 1 edition.
Benini, L., Bogliolo, A., Paleologo, G. A., and De Micheli,
G. (1999). Policy optimization for dynamic power
management. IEEE Transactions on Computer-Aided
Design of Integrated Circuits and Systems, 18(6):813–
833.
Benson, T., Akella, A., and Maltz, D. A. (2010). Network
traffic characteristics of data centers in the wild. In
Proceedings of the 10th ACM SIGCOMM conference
on Internet measurement, pages 267–280. ACM.
Chen, G. and Wang, X. (2022). Performance optimiza-
tion of machine learning inference under latency and
server power constraints. In 2022 IEEE 42nd Interna-
tional Conference on Distributed Computing Systems
(ICDCS), pages 325–335. IEEE.
Dyachuk, D. and Mazzucco, M. (2010). On allocation
policies for power and performance. In 2010 11th
IEEE/ACM International Conference on Grid Com-
puting, pages 313–320. IEEE.
Entezari-Maleki, R., Sousa, L., and Movaghar, A. (2017).
Performance and power modeling and evaluation of
virtualized servers in iaas clouds. Information Sci-
ences, 394:106–122.
Gandhi, A., Doroudi, S., Harchol-Balter, M., and Scheller-
Wolf, A. (2013). Exact analysis of the m/m/k/setup
class of markov chains via recursive renewal reward.
In ACM SIGMETRICS Performance Evaluation Re-
view, volume 41, pages 153–166. ACM.
Greenberg, A. G., Hamilton, J. R., Maltz, D. A., and Patel,
P. (2009). The cost of a cloud: research problems in
data center networks. Computer Communication Re-
view, 39(1):68–73.
Kendall, M. (1973). Time-series. Griffin.
Khan, W. (2022). Advanced data analytics modelling for
evidence-based data center energy management.
Kwiatkowska, M., Norman, G., and Parker, D. (2002).
Prism: Probabilistic symbolic model checker. In In-
ternational Conference on Modelling Techniques and
Tools for Computer Performance Evaluation, pages
200–204. Springer.
Lee, Y. C. and Zomaya, A. Y. (2012). Energy efficient uti-
lization of resources in cloud computing systems. The
Journal of Supercomputing, 60(2):268–280.
Leng, B., Krishnamachari, B., Guo, X., and Niu, Z. (2016).
Optimal operation of a green server with bursty traf-
fic. In 2016 IEEE Global Communications Confer-
ence (GLOBECOM), pages 1–6.
Maccio, V. J. and Down, D. G. (2015). On optimal con-
trol for energy-aware queueing systems. In Teletraf-
fic Congress (ITC 27), 2015 27th International, pages
98–106. IEEE.
Mitrani, I. (2013). Managing performance and power con-
sumption in a server farm. Annals OR, 202(1):121–
134.
Peng, X., Bhattacharya, T., Mao, J., Cao, T., Jiang, C., and
Qin, X. (2022). Energy-efficient management of data
centers using a renewable-aware scheduler. In 2022
IEEE International Conference on Networking, Archi-
tecture and Storage (NAS), pages 1–8. IEEE.
Rajesh, C., Dan, S., Steve, S., and Joe, T. (2008). Profiling
energy usage for efficient consumption. The Architec-
ture Journal, 18:24.
Rteil, N., Burdett, K., Clement, S., Wynne, A., and
Kenny, R. (2022). Balancing power and perfor-
mance: A multi-generational analysis of enterprise
server bios profiles. In 2022 International Conference
on Green Energy, Computing and Sustainable Tech-
nology (GECOST), pages 81–85. IEEE.
Schwartz, C., Pries, R., and Tran-Gia, P. (2012). A queuing
analysis of an energy-saving mechanism in data cen-
ters. In Information Networking (ICOIN), 2012 Inter-
national Conference on, pages 70–75.
Wilkes, J. (2011). More Google cluster data. Google re-
search blog. Posted at http://googleresearch.blogspot.
com/2011/11/more-google-cluster-data.html.
Xu, X. and Tian, N. (2008). The m/m/c queue with (e, d)
setup time. Journal of Systems Science and Complex-
ity, 21(3):446–455.
Energy Consumption Optimization in Data Center with Latency Based on Histograms and Discrete-Time MDP
105