Studying Synchronization Issues for Extended Automata
∗
Natalia Kushik
1
and Nina Yevtushenko
2
1
SAMOVAR, T
´
el
´
ecom SudParis, Institut Polytechnique de Paris, Palaiseau, France
2
Ivannikov Institute for System Programming of the Russian Academy of Sciences, Moscow, Russia
Keywords:
Extended Automata, Synchronizing Sequence, Model based Testing and Monitoring.
Abstract:
The paper presents a study of synchronization issues for one of non-classical state models, i.e., a state identifi-
cation problem widely used in the area of Model based Testing (MBT) and run-time verification / monitoring.
We consider Finite Automata (FA) augmented with the context variables and their related updates when the
transitions are executed. For such Extended Automata (EA) we define the notions of merging and synchro-
nizing sequences that serve as reset words in MBT, and show that under certain conditions and when every
context variable is defined over a ring, it is possible for the extended automata of the studied class to ‘repeat’
the necessary and sufficient conditions established for the classical automata. Otherwise, in a general case, the
problem can be reduced to deriving reset words for classical FA that represent corresponding EA slices.
1 INTRODUCTION
Finite state models are widely used as formal specifi-
cations in the testing and verification area of discrete
and hybrid systems. When deriving test suites with
the guaranteed fault coverage, in MBT, one of typical
well known problems for finite automata or finite state
machines concerns their state identification (Lee and
Yannakakis, 1994; Lee and Yannakakis, 1996). Final
state identification in some cases can be solved via
generation and application of homing and synchroniz-
ing sequences (Sandberg, 2004) to the machine under
experiment. Such sequences can serve as reset words
or checking sequence preambles, when it comes to ac-
tive testing of non-initialized implementations (Hen-
nie, 1964). At the same time, both sequences can
minimize the monitoring efforts when testing or ver-
ifying a system behavior in a passive mode (Kushik
et al., 2016). State identification problems are well
studied for classical finite automata and finite state
machines (FSMs), however when the corresponding
state model is augmented with additional parameters
/ variables, such as for example, timeouts, predicates,
input / output parameters, to the best of our knowl-
edge, the problem has not been largely investigated.
Synchronizing sequences bring a machine to a
unique final state and are usually considered for ma-
chines without outputs (Sandberg, 2004), i.e., for
*
This work is partially supported by RSF project N 22-
29-01189.
classical automata. For deterministic complete au-
tomata the length of such sequence is polynomial and
it exists whenever each state pair has a merging se-
quence.
Note also that when it comes to testing and ver-
ification of a discrete event system, be that software
or hardware component of a communicating system,
it is rather hard to obtain its formal specification as a
finite automaton or a finite state machine. Sometimes
it is more convenient to consider an extended model
augmented with parameters listed above. In this pa-
per, we state and solve a problem of the existence
check and derivation of a synchronizing sequence for
an extended automaton, which looks like a classical
FA augmented with context variables that update their
values when certain transitions are executed, as well
as special predicates guarding some transitions which
depend on context variables.
When the behavior of an Implementation Under
Test (IUT) is described by an extended machine it can
well happen that for simplifying the run-time verifi-
cation or monitoring, not only a reached state is im-
portant but rather a state together with the context.
As a motivating example, we consider a Simple Con-
nection Protocol (SCP) which is designed to ‘con-
nect’ two entities, negotiating the quality of service at
the connection establishment (Alcalde et al., 2004).
The SCP allows connecting an entity called the up-
per layer to an entity called the lower layer. The up-
per layer dialogues with the SCP for fixing the quality
338
Kushik, N. and Yevtushenko, N.
Studying Synchronization Issues for Extended Automata.
DOI: 10.5220/0011785700003464
In Proceedings of the 18th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2023), pages 338-345
ISBN: 978-989-758-647-7; ISSN: 2184-4895
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

of service (QoS) desirable for the future connection.
Later on, the upper layer comes to the lower layer re-
questing the establishment of a connection. The lower
layer accepts or refuses this connection request. If the
lower layer accepts the request, then it informs the
upper layer that the connection has been established
and the upper layer can start transmitting data which
is followed by a corresponding acknowledgment. The
reader can find an FSM describing the SCP behavior
in (Kushik et al., 2016), where a possibility of mini-
mizing the monitoring efforts through the observation
of the SCP homing sequences was discussed. In the
example below, we abstract from the negotiation step
and data transmission, i.e., when monitoring the be-
havior of the SCP implementation, our observations
will be taken at the inputs, i.e., requests, and the fol-
lowing implementation actions. The corresponding
extended automaton, describing the SCP connection
establishment, is shown in Figure 1.
s
1
s
2
req QoS TryCount = 0
conn
TryCount < 2
TryCount = TryCount + 1
req QoS
reset
TryCount == 2
Figure 1: Extended automaton for the connection establish-
ment in the SCP.
In the original FSM in (Kushik et al., 2016),
the upper layer tried to establish the connection two
times, before receiving the abort signal from the
lower layer, i.e., in fact, the context variable TryCount
in the EA in Figure 1 is defined over the group
({0,1,2},+mod3). Assume, that during the protocol
monitoring, one of the properties to be checked is the
safety of the abort signal. Indeed, we would like to
make sure not only that abort follows the connection
request but that there were at least two unsuccessful
attempts before.
That is, we would like to observe the output abort,
when the protocol reaches not only state state = s
2
but the configuration (state = s
2
,< TryCount = 2 >)
(and not (state = s
2
,< TryCount = 1 >), for exam-
ple). In other words, differently from the (Kushik
et al., 2016) result, we not only want to know the cur-
rent state of the protocol implementation when veri-
fying certain properties but even more precisely, we
would like to make sure that the configuration of in-
terest has been reached. The latter could allow mini-
mizing the number of properties to be checked, as not
all the properties are relevant at different configura-
tions, even for the same state.
In the literature, there have been proposed vari-
ous definitions of extended FAs and FSMs, see for
example (Petrenko et al., 2004; Holzmann, 2004). In
(El-Fakih et al., 2016; Petrenko et al., 1999; Petrenko
et al., 2004), the distinguishability notions for an EA
are considered. However, for the machines of the
studied classes, for identifying a final (current) con-
figuration of the machine, to the best of our knowl-
edge, there exist few papers where a homing sequence
(HS) is derived for an FSM with timed guards (Tvar-
dovskii and Yevtushenko, 2020) and a synchroniz-
ing sequence (SS) is derived for a Timed Automa-
ton (Doyen et al., 2014). In the latter paper, the au-
thors also consider the SS problem for a Weighted
Automaton (WA), that is considered as an EA where
the weight is a context variable. However, the weight
cannot be directly assigned to some integer, and due
to this fact, the authors show that in their case, an
SS never exists for a non-initialized WA, as two con-
figurations with the same location and different ini-
tial weight values cannot be synchronized. In a gen-
eral case of EA, it is not the case. The reachability
problem of WA (Bouyer-Decitre, 2016) is also rele-
vant to our studies, but on the one hand, it is differ-
ent from the SS problem, and on the other, weights
themselves do not affect the behavior of the machine
(Droste et al., 2009) which is not the case for context
variables of an EA considered in the paper.
We hereafter investigate a specific class of EA
where the values of context variables belong to a ring
and thus, the update functions are defined accordingly
using ring multiplication and addition; predicates are
used to verify if a context variable value belongs to a
certain ring subset. The provided formal definition of
such EA allows establishing the conditions for exis-
tence check and derivation of an SS.
The main contribution of the paper is a method for
the existence check and derivation of a synchronizing
sequence for an EA with the context variables which
values belong to a ring, as well as with the appropriate
predicates. For a special class of configurations, when
the context variables’ values belong to an ideal of the
ring, to have an appropriate SS, it is necessary and
sufficient that the corresponding underlying automa-
ton (context-free slice) has an SS, along with having
proper transitions from a state reached by the SS. The
same result applies to an EA with mutually exclusive
predicates at each state, that verify that a context vari-
able value belongs to an ideal of a ring. Given a set of
configurations with the same state and context vari-
ables which values belong to an ideal, we also discuss
an issue of merging the configurations of the set into
Studying Synchronization Issues for Extended Automata
339

a single configuration. If such a sequence exists then
it is used for deriving an SS for the given extended
automaton.
The structure of the paper is as follows. Section 2
contains preliminaries as well as the problem state-
ment. The existence check and derivation of a merg-
ing sequence for two sets of configurations for an
extended automaton is discussed in Section 3. Cor-
respondingly, a method for the existence check and
derivation of a transfer sequence and of an SS for an
extended automaton is presented in Section 4. Sec-
tion 5 is devoted to EA with mutually exclusive predi-
cates and the related SS derivation problem. Section 6
concludes the paper.
2 BACKGROUND AND PROBLEM
STATEMENT
In this paper, we consider one of the classical state
identification problems, namely we focus on the ex-
istence check and derivation of a synchronizing se-
quence for finite extended automata. As usual, a fi-
nite automaton, simply an automaton throughout this
paper, is a 3-tuple A = (S, M,δ) where S is a fi-
nite nonempty set of states, M is a finite nonempty
set of actions, δ ⊆ S × M × S is a set of transitions.
Note that, similar to (Ito and Shikishima-Tsuji, 2004;
Volkov, 2008), we consider automata without the non-
observable action. Moreover, in this paper, we focus
on complete deterministic automata, i.e., for each pair
(s,m), s ∈ S, m ∈ M, there exists exactly one transition
(s,m,s
′
) ∈ δ. Given a sequence / trace α ∈ M
⋆
and a
state s, α takes the automaton to the α-successor of
s. The α-successor of the subset S
′
of states is the
set of α-successors for all states of S
′
. A sequence
/ trace α ∈ M
⋆
is an SS for A if the α-successor of
the set of states S is a singleton. If the automaton
has an SS then the automaton is synchronizing. If the
automaton has the designated subset S
′
⊂ S of initial
states, i.e., is weakly initialized, then this automaton
is synchronizing if there exists a trace α such that the
α-successor of the set S
′
is a singleton. In this paper,
we consider non-initialized automata if the converse
is not explicitly stated.
A sequence α ∈ M
⋆
is a merging sequence for two
different states s and p of A if the α-successors of s
and p coincide, i.e., are the same. It is known (Epp-
stein, 1990; Natarajan, 1986) that a complete and de-
terministic automaton is synchronizing if and only if
every pair of different states has a merging sequence.
In the SCP example, given in Section 1, a merging se-
quence is a synchronizing sequence for two states s
1
and s
2
, for example, it can be a single input req QoS.
However, if we would like to take into account the
values of the context variables when synchronizing
the automaton, we need to restrict the correspond-
ing definition and in fact, merge and synchronize not
the states, but rather the configurations. That is the
reason why in this paper, we consider a special class
of extended automata and define the notion of an SS
for this class of machines. For the sake of simplicity,
we first, abstract from the predicates (or guards) that
can potentially label the transitions, only keeping the
context variables that can be updated when a transi-
tion is executed. Therefore, in this paper, an extended
automaton is augmented with a finite set of context
variables and each transition is labeled with update
functions for these variables. To formally define the
possible update functions, we furthermore turn to the
relevant algebraic structures, and consider that every
context variable is defined over a ring.
An extended automaton A is a 4-tuple A =
(S,M, T,δ) where S is a finite nonempty set of states,
M is a finite nonempty set of actions, T = {t
1
,... ,t
k
}
is a finite set of context variables which are defined
over a finite ring R = (R, +, ∗), and δ is a set of tran-
sitions between states from S such that each transition
in δ is a tuple (s,a,up, s
′
), where s,s
′
∈ S are the initial
and final states of a transition, a ∈ M is an (input) ac-
tion, up =< f
1
,... , f
k
> is a context update function
such that ∀ j = 1,..., k, the function f
j
(t
j
) : R −→ R
is a linear combination h ∗ t
j
+ b where h, b ∈ R. By
default, for identity function f
j
the context variable t
j
does not change its value after the transition is exe-
cuted and we will simply omit these functions when
defining the transitions
1
. An EA is complete and de-
terministic when at every state, there exists exactly
one transition under each input.
As an example of an abstract EA, consider an au-
tomaton A in Figure 2. This automaton has three
states and two context variables t
1
and t
2
defined over
the ring R = Z
10
= ({0,. . .,9},+mod10,∗mod10);
h
1
= 3, h
2
= 1 while b
1
= 4, b
2
= 0. All the tran-
sitions in the automaton contain the update of context
variables, except one, namely (1,a, 2) which is only
labeled by a letter a, i.e., all the context variables pre-
serve their values when the transition is executed.
As usual, a configuration is a pair (s,v) where s
is a state and v is the context, i.e., v is a vector of
values of context variables. We also consider a fi-
nite set of configurations C
s
= (s,V ) where V is a fi-
nite non-empty set of contexts. Moreover, given two
configurations (s,v
1
) and (s, v
2
) and a trace σ, the σ-
successors of (s,v
1
) and (s,v
2
) are (p,u
1
) and (p,u
2
)
1
Here we notice that in a WA in (Doyen et al., 2014), the
weight values are also defined over an infinite Abel group
R = (R, +).
ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering
340

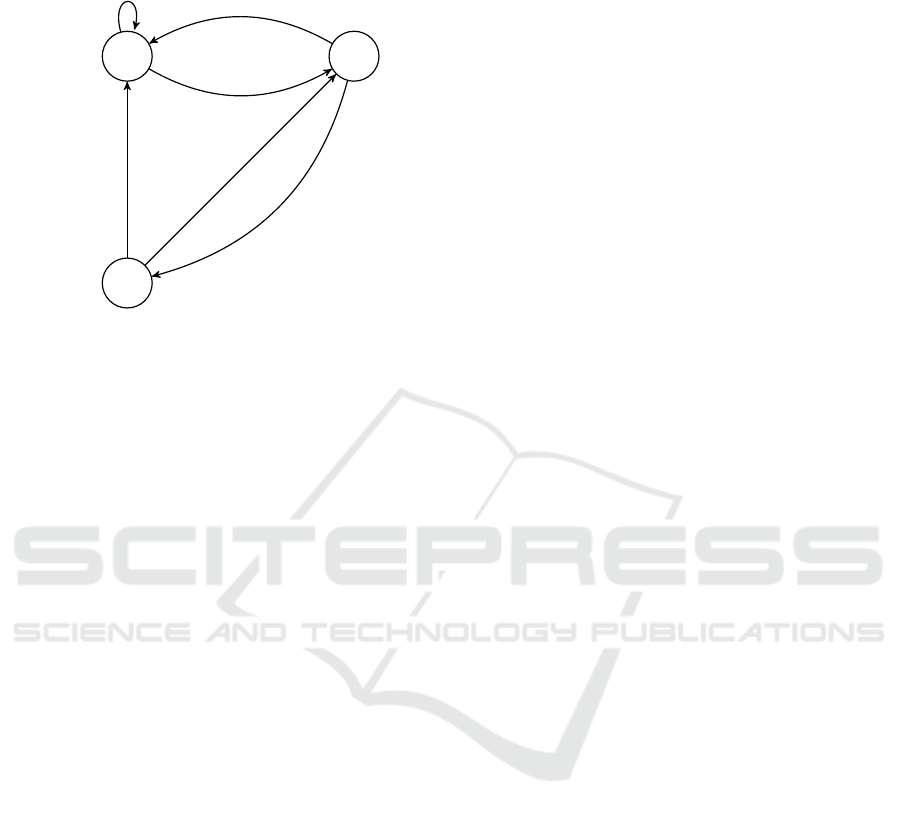
1 2
3
b
t
1
= 3 ∗ t
1
t
2
= t
2
+ 4
a
b
t
1
= t
1
+ 4
t
2
= t
2
+ 4
a
t
1
= t
1
+ 4
t
2
= 3 ∗ t
2
+ 4
a
t
1
= 3 ∗ t
1
t
2
= 3 ∗ t
2
b
t
1
= t
1
+ 4
t
2
= 3 ∗ t
2
Figure 2: An extended automaton A.
for some state p.
Given an automaton A = (S,M, T,δ) with the set
T = {t
1
,t
2
,... ,t
k
} of context variables with the values
in R, we further consider the context-free slice (El-
Fakih et al., 2008) A
aut
that is the underlying classical
automaton without the context variables, while A
sim
denotes the classical automaton that is obtained by the
simulation of A. By definition, both, A
aut
and A
sim
,
are complete and deterministic automata if an initial
EA is complete and deterministic.
Given the set A = A
1
× A
2
× · ·· × A
k
, A
j
⊆ R,
two sets of configurations C
s
= (s, A) and C
p
= (p, A)
and a set B = B
1
× B
2
× ··· × B
k
, B
j
⊆ R, of con-
texts, we would like to check if there exist a se-
quence σ of actions and a state q such that from each
configuration (s, v) ∈ C
s
and from each configuration
(p,v) ∈ C
p
the sequence σ takes the extended automa-
ton A to some configuration of the set C
q
= (q,B).
If the trace σ exists then we further refer to it as a
(q,B)-merging sequence for the sets C
s
and C
p
. A se-
quence which (q,B)-merges n sets of configurations
C
1
= (s
1
,A),.. . ,C
n
= (s
n
,A), is a (q,B)-merging se-
quence for the set of these n subsets of configurations.
A sequence which (q,R
k
)-merges n sets of con-
figurations C
1
= (s
1
,R
k
),... ,C
n
= (s
n
,R
k
) is a q-
synchronizing sequence for the automaton A. A se-
quence which merges n sets of configurations C
1
=
(s
1
,R
k
),... ,C
n
= (s
n
,R
k
) into a singleton (s, v) is a
synchronizing sequence for the automaton A.
Given a set of configurations C
s
= (s,A), if there
exist a singleton (q,v) and a sequence that takes the
automaton from each configuration of the set to (q,v),
then this sequence is a transfer sequence from C
s
to
(q,v) or a synchronizing sequence for C
s
.
In this paper, we tackle the following problems:
1. Existence check of a (q, B)-merging sequence for
two sets of configurations of a given automaton;
2. Derivation of a (q,B)-merging sequence for two
sets of configurations, whenever exists;
3. Existence check and derivation of a (q, B)-
merging sequence for an extended automaton;
4. Existence check and derivation of a transfer se-
quence for a subset C
q
= (q,B) of an extended au-
tomaton;
5. Derivation of a synchronizing sequence for an ex-
tended automaton.
3 EXISTENCE CHECK AND
DERIVATION OF A MERGING
SEQUENCE FOR TWO SETS OF
CONFIGURATIONS IN AN
EXTENDED AUTOMATON
Note that a (q,B)-merging sequence for a pair of states
{s, p} only exists if in the context-free slice A
aut
of
the extended automaton A there exists a sequence
merging states s and p into state q.
Proposition 1. 1. If for states s and p there is no
merging sequence in the slice A
aut
then there is no
(q,B)-merging sequence for any two sets of configu-
rations C
s
= (s,A) and C
p
= (p,A), A ⊆ R
k
.
2. A (q,R
k
)-merging sequence exists for the sets
C
s
= (s, A) and C
p
= (p, A) if and only if in the slice
A
aut
, there exists a sequence merging states s and p
into state q.
The first statement of the proposition establishes
the necessary conditions for the existence of a (q,B)-
merging sequence for two sets of configurations for
an arbitrary B ⊆ R
k
. However, according to the sec-
ond statement of the proposition, if B = R
k
then the
conditions become necessary and sufficient.
If B ⊂ R
k
, then the sufficient conditions for the ex-
istence of a (q,B)-merging sequence can be obtained
similar to ‘classical’ synchronizing / homing tree ap-
proaches (Sandberg, 2004). For that matter we adapt
the notion of a successor tree for such an extended au-
tomaton and later on propose the corresponding trun-
cating rules that allow deriving a (q,B)-merging se-
quence or to conclude that such a sequence does not
exist.
Given the set A = A
1
× A
2
× ·· · × A
k
, A
j
⊆ R, the
set B = B
1
× B
2
× ··· × B
k
, B
j
⊆ R, two sets of con-
figurations C
s
= (s,A) and C
p
= (p,A), the root of the
tree is labeled by the pair {C
s
,C
p
}. Edges of the tree
are labeled by possible (input) actions. Given a cur-
rent node labeled by a pair {C
x
= (x,A
′
1
× A
′
2
× · ·· ×
Studying Synchronization Issues for Extended Automata
341

A
′
k
),C
y
= (y,A
′′
1
× A
′′
2
× ··· × A
′′
k
)}, this node is adja-
cent to a node labeled by {C
q
= (q,L
′
1
× L
′
2
× · · · ×
L
′
k
),C
z
= (z,L
′′
1
× L
′′
2
× · · · × L
′′
k
)} through an arc la-
beled by m, if A contains the following transitions:
(x,m,up,q), (y, m, up,z) and L
′
j
is obtained from A
′
j
through the application of related update function f
j
for the variable t
j
for the transition (x,m, up, q), while
L
′′
j
is obtained from A
′′
j
through the application of
related update function f
j
for t
j
for the transition
(y,m,up,z), j ∈ {1, 2, ...,k}.
Truncating rules are defined as follows.
Rule 1: A node labeled by a pair {C
q
= (q, A
′
= A
′
1
×
A
′
2
× ··· × A
′
k
),C
z
= (z,A
′′
= A
′′
1
× A
′′
2
× ··· × A
′′
k
)} is
terminal if at the same level or upper in the tree there
exists a node labeled by a pair {C
x
= (q,L
′
= L
′
1
×
L
′
2
×·· · ×L
′
k
),C
y
= (z,L
′′
= L
′′
1
×L
′′
2
×·· · ×L
′′
k
)} such
that L
′
j
⊆ A
′
j
and L
′′
j
⊆ A
′′
j
, j ∈ {1,2,.. . ,k}.
Rule 2: A node labeled by a pair {C
q
= (q, A
′
),C
z
=
(z,A
′′
)} is terminal if q = z, and A
′
j
⊆ B
j
, A
′′
j
⊆ B
j
,
j ∈ {1,2,... , k}.
Proposition 2. A sequence α is a (q,B)-merging se-
quence for sets C
s
= (s,A) and C
p
= (p,A) of con-
figurations of the extended complete deterministic au-
tomaton A if and only if it labels a path to a node
truncated using Rule 2. If all the nodes in the tree
are truncated using Rule 1 then there no SS for the
automaton A.
Note that by definition, α is a (q,B)-merging se-
quence for the sets (C
s
,A) and (C
p
,A) if and only if
the automaton A is taken by α from any configuration
of the set (C
s
,A) to a configuration of the set (q,B)
and the same holds for any configuration of (C
p
,A).
In the successor tree, it is exactly the case when α
labels a path to a node that is terminal due to Rule 2.
Note also that rules 1 and 2 provide an estimation
of the length of a shortest (q,B)-merging sequence
for the sets C
s
= (s,A) and C
p
= (p, A). Indeed,
it is limited by the number of pairs {C
q
= (q,A
′
=
A
′
1
×A
′
2
×· ··×A
′
k
),C
z
= (z, A
′′
= A
′′
1
×A
′′
2
×· ··×A
′′
k
)}
and thus can be estimated as O (n
2
|R|
2k
) but in reality
is much shorter when it exists. We would like to high-
light the fact that the (q,B)-merging sequence deriva-
tion strategy can be also applied in the case of infi-
nite ring R, however another truncating rule should
be then added; the latter should define the maximal
desirable length of a merging sequence in question.
Proposition 3. A sequence α is a (q,B)-merging se-
quence for the complete deterministic extended au-
tomaton A if and only if α is a (q,B)-merging se-
quence for each pair of different sets of configurations
C
s
= (s,R
k
) and C
p
= (p,R
k
). If there is no (q,R
k
)-
merging sequence for the extended automaton A then
there is no SS for the automaton A.
Consider a slightly modified automaton in Fig-
ure 2 when the update functions at the transition from
state 1 to state 2 under input a are not identities but
t
1
= 2 and t
2
= 2. By direct inspection one can assure
that there is an SS bba that takes the automaton from
any configuration to the configuration (2,< 2, 2 >).
4 EXISTENCE CHECK AND
DERIVATION OF A TRANSFER
AND A SYNCHRONIZING
SEQUENCE FOR EXTENDED
AUTOMATA
Note that, differently from classical automata, for the
existence check of an SS it is not sufficient to have
the merging sequences for all pairs of states of the
underlying context-free automaton; nor it is sufficient
to have the merging sequences for all pairs of sets of
configurations. The reason is that the configurations
of the obtained sets should be brought into the set of
configurations for which there exists a sequence that
transfers this set to a single configuration.
4.1 (q,B)-Merging Sequence Derivation
Under certain conditions over the automaton A, ex-
isting necessary and sufficient conditions for classical
automata can be somehow ‘repeated’. Below, as be-
fore, we consider that the EA A is complete and de-
terministic.
Proposition 4. Given an ideal I of the ring R, let for
every context variable t
j
and its update function h
j
∗
t
j
+b
j
, it holds that b
j
is in I. Then {C
s
= (s, I
k
),C
p
=
(p,I
k
)} has a (q,I
k
)-merging sequence if and only if
{s, p} has a merging sequence in the related context-
free slice A
aut
.
Indeed, by definition of update functions, after up-
dating the value of any context variable, it still be-
longs to I, and thus the context-free slice A
aut
defines
the existence of the I
k
-merging sequence.
Corollary 1. Given an ideal I of the ring R, let for ev-
ery context variable t
j
and its update function h
j
∗t
j
+
b
j
, it holds that b
j
is in I. Then the automaton A with
the initial set of configurations (s
1
,I
k
),... , (s
n
,I
k
) has
a (s
j
,I
k
)-merging sequence for some j ∈ {1, ...,n}, if
and only if each state pair {s, p} in its context-free
slice has a merging sequence.
As an example, consider again the automaton in
Figure 2 and an ideal I = {0, 2,4,6,8}.
A sequence ba is the (2,I
2
)-merging sequence in
this case. Note that the two sets (1, I
2
) and (3,I
2
) are
ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering
342

(2,I
2
)-merged by a single input a, and ba is a (2,I
2
)-
merging sequence for the whole automaton A.
4.2 Deriving an SS for a Set (q, B) of an
Extended Automaton
We now study whether given a pair (q,I
k
), there exists
a configuration (p,v) and an input sequence β such
that β takes the automaton from each configuration of
the set (q,I
k
) to (p,v). We refer to such sequence as
a transfer sequence from (q,I
k
) to (p,v). Suppose
that a transfer sequence β = x
1
...x
n
exists and for a
context variable t
j
of the configuration we have the
following updates: h
1
∗ t
j
+ b
1
,... , h
n
∗ t
j
+ b
n
when
applying this input sequence. Consider now two con-
figurations of the set with the initial value of context
variable t
j
equal to z
1
and z
2
. In order to get the same
value of this variable after applying the sequence β it
has to be held that h
1
∗···∗h
n
∗z
1
= h
1
∗···∗h
n
∗z
2
. To
prove this, consider the formulas h
n
∗(h
n−1
∗(. ..z
1
)+
b
n−1
) + b
n
and h
n
∗ (h
n−1
· (...z
2
) + b
n−1
) + b
n
. If the
results of the corresponding functions are equal then
b
n
can be deleted as well as all the products of the
type h ∗ b as they belong to the ideal I. The results of
two functions are equal if and only if h
n
∗ h
n−1
∗ · · · ∗
h
1
∗ z
1
= h
n
∗ h
n−1
··· ∗ h
1
∗ z
2
.
Therefore, there exists z
′
∈ I such that for any item
z ∈ I, the product h
n
∗h
n−1
∗·· · ∗h
1
∗z is z
′
. Thus, this
z
′
can be only 0.
Correspondingly, given a ring R without zero di-
visors, a transfer sequence exists if and only if there
is a path to some state such that for each context vari-
able t
j
there is a transition of the path with the update
function t
j
= b
j
. If the ring has zero divisors then the
conditions become only sufficient, since in this case,
the above product has to be a proper zero divisor. For
instance, in the above example (Figure 2) it can hap-
pen when the product equals 5.
Proposition 5. 1. Given a ring R without zero divi-
sors and a set (s,I
k
) of configurations, there exists a
transfer sequence for (s,I
k
) if and only if there exist a
state p and a path from state s to p such that for each
context variable t
j
there is a transition of the path with
the update function t
j
= b
j
.
2. Given an arbitrary ring R and a set (s,I
k
) of config-
urations, let there exist a state p and a path from state
s to p such that for each context variable t
j
there is a
transition of the path with the update function t
j
= b
j
.
Then the sequence labeling the path is a transfer se-
quence for the set (s,I
k
).
Indeed, consider two configurations (s,t
′
1
...t
′
k
)
and (s,t
′′
1
...t
′′
k
) of the set (s,I
k
). For a transfer se-
quence β and j = 1, ..., k, we have the update function
k
j
∗t
j
+b
j
. Therefore, h
n
∗(h
n−1
∗(...t
′
j
)+b
n−1
)+b
n
= h
n
∗ (h
n−1
∗ (. . .t
′′
j
) + b
n−1
) + b
n
. Then b
n
can be
deleted as well as all the products of the type h ∗ b as
they belong to the ideal I. Correspondingly, by in-
duction, the results of two functions are equal if and
only if h
n
∗ h
n−1
∗ ··· ∗ h
1
∗ t
′
j
= h
n
∗ h
n−1
··· ∗ h
1
∗ t
′′
j
.
Since the same holds for t
′
j
= 0, the latter means that
h
n
∗ h
n−1
∗ ··· ∗ h
1
= 0. At the same time, once in
the path there exists an update function t
j
= b
j
, in the
postfix of the path we get the same t
j
value indepen-
dently of the initial value of this variable.
Here we note that the conditions of part 2 of
Proposition 5 can be modified when the ring has zero
divisors. In this case, the product h
n
∗h
n−1
∗· · ·∗ h
1
=
h can have only non-zero items but at least one of
them is a zero divisor.
SS Derivation. The process of deriving an SS for a
complete deterministic extended automaton described
above, i.e., where the values of context variables be-
long to an ideal I of a finite ring R, can be performed
in two steps.
Step 1: To check whether the underlying automaton
(context-free slice) A
aut
has an SS. If there is no SS
then the extended automaton A has no SS. Otherwise,
derive the set of all states {s
1
,... , s
l
} such that there
exists an SS to these states.
Step 2: Let the automaton have an (q,I
k
)-merging
sequence to the set (p,I
k
) of configurations. If there
exist a state s
j
∈ {s
1
,... , s
l
}, a state p and a path from
state s
j
to p such that for each context variable t
j
there is a transition of the path with the update func-
tion t
j
= b
j
, then there exists a transfer sequence for
(s
j
,I
k
) and thus, there exists an SS for the extended
automaton with the initial set of (s
1
,I
k
),... , (s
n
,I
k
) of
configurations. This SS is obtained by prolonging an
(q,I
k
)-merging sequence to state s
j
by a transfer se-
quence from (s
j
,I
k
).
Note that for the EA in Fig. 2 the conditions of
Proposition 5 do not hold and by direct inspection,
one can assure that the EA does not possess an SS.
However, if we change an update function at state 1
for input b for t
2
as t
2
= 4 and an update function at
state 2 for input b as t
1
= 4 then the EA has an SS
baab.
It is also important to underline that if the ring has
no zero divisors and there are no such states s
j
and
p at Step 2, there is no guarantee that the extended
automaton has no SS. The reason is that at Step 1,
there can exist an (q,(I
′
)
k
)-merging sequence where
I
′
is a proper subset of I for which a corresponding
transfer sequence can exist.
We also notice that every context variable t
j
can
be defined over a proper ring R
j
and correspondingly,
Studying Synchronization Issues for Extended Automata
343

the context v will be defined not over R
k
but over the
ring that is the Cartesian product of R
j
. In this case,
the statements of the paper should be slightly modi-
fied.
5 SYNCHRONIZATION ISSUES
FOR AUTOMATA WITH
PREDICATES
We now add simple predicates to an EA and show
that some results of the previous section still hold.
We assume that an extended automaton has predi-
cates where a predicate P
j
is a function defined over
the context variable t
j
; P
j
is a mapping P
j
: R −→
{True,False} of the type t
j
∈ B, B ⊆ R or its nega-
tion.
The transition is unconditional if the predicate P
j
is True for any value of t
j
; then by default, we do not
associate any predicate with such a transition. Due to
the definition of predicates, every two predicates are
mutually exclusive, i.e., the automaton A
sim
again is
complete and deterministic. However, if an EA A has
predicates then the context-free slice A
aut
of the deter-
ministic EA can be non-deterministic. Nevertheless,
the definition of merging sequences and a synchroniz-
ing sequence stay the same for an automaton with the
above predicates.
Fig. 3 contains an example automaton A aug-
mented with predicates. Note that for this augmented
automaton, ba is not a (2,I
2
)-SS anymore. In fact, a
(q,I
2
)-SS cannot start with input b due to the non-
determinism of the slice A
aut
. There is however a
longer (q,I
2
)-synchronizing sequence, for example
aba.
Proposition 6. Given a set of configurations C
s
=
(s,W ) and a sequence σ, if the σ-successor of s in the
context-free slice A
aut
of the automaton A is a set Q
of states then the σ-successor of C
s
in A is contained
in the union of some sets C
q
over all q ∈ Q.
Corollary 2. If the context-free slice A
aut
is synchro-
nizing then the automaton A is (q,R
k
)-synchronizing.
The corollary establishes the sufficient condition
for the existence of a (q, R
k
)-synchronizing sequence
for an extended automaton. Note that this condition is
not necessary even for a complete and deterministic
EA. However, there is a proper case of an extended
automaton with predicates when the conditions of the
corollary become necessary and sufficient.
Similar to the results of the previous section, let
I be an ideal of the ring R. Consider a complete ex-
tended automaton A with the following features. A
transition of the EA can have a predicate P(t
j
) which
1 2
3
b
t
1
= 3 ∗ t
1
t
2
= t
2
+ 4
a
t
1
/∈ I
a
t
2
= 2 ∗ t
2
b
t
1
= t
1
+ 4
t
2
= t
2
+ 4
t
1
∈ I
a
t
1
= t
1
+ 4
t
2
= 3 ∗ t
2
+ 4
a
t
1
= 3 ∗ t
1
t
2
= 3 ∗ t
2
t
2
/∈ I
b
t
2
= 4 ∗ t
2
+ 2
t
2
∈ I
b
t
1
= t
1
+ 4
t
2
= 3 ∗ t
2
Figure 3: An extended automaton A augmented with predi-
cates.
is True if t
j
is in I or its negation. Moreover, there are
the update functions of the kind h ∗ x + b where h,b
are in I.
Proposition 7. Given a set of configurations C
s
=
(s,R
k
) and an action m, the set where the automa-
ton A is taken from any configuration of the set C
s
by
action m is a subset of a set (s,I
k
).
Due to the above proposition, after applying any
input (action) at the initial configuration we will reach
a configuration where the context is in I
k
. Therefore,
the problem should be solved for a submachine with
subsets of such configurations from which there exist
only unconditional transitions. That is, the results of
the previous section can be directly applied.
6 CONCLUSION
In this paper, we studied a problem of the existence
check and derivation of synchronizing sequences for
extended finite automata that are widely used in MBT
and monitoring. We investigated a particular class of
those when the context variables are defined over a
finite ring and in this case, the conditions for the ex-
istence check of an SS can be established. In fact,
when the updates are represented by linear functions
for which the coefficients belong to an ideal, an SS
can be derived based on merging sequences for pairs
of sets of configurations combined with a correspond-
ing transfer sequence. We established the conditions
for the existence of such a transfer sequence. The
ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering
344

same results hold for a particular class of the extended
automata with predicates, which we also described in
the paper.
As a future work, we plan to extend the stud-
ied EA classes, by adding input/output parameters,
and considering other update functions and predi-
cates. Synchronizing sequences with appropriate fea-
tures can also be studied, similar to safe synchroniz-
ing sequences in (Doyen et al., 2014) when an SS
does not traverse appropriate (unsafe) states.
Finally, all the fundamental results presented in
the paper need a thorough experimental evaluation,
concerning their performance when it comes synchro-
nization issues in MBT and monitoring. We plan to
perform such experimental study with various (dis-
tributed) networking systems in the future.
REFERENCES
Alcalde, B., Cavalli, A. R., Chen, D., Khuu, D., and Lee, D.
(2004). Network protocol system passive testing for
fault management: A backward checking approach. In
de Frutos-Escrig, D. and N
´
u
˜
nez, M., editors, Formal
Techniques for Networked and Distributed Systems -
FORTE 2004, 24th IFIP WG 6.1 International Con-
ference, Madrid Spain, September 27-30, 2004, Pro-
ceedings, volume 3235 of Lecture Notes in Computer
Science, pages 150–166. Springer.
Bouyer-Decitre, P. (2016). Optimal reachability in
weighted timed automata and games. In Faliszewski,
P., Muscholl, A., and Niedermeier, R., editors, 41st
International Symposium on Mathematical Founda-
tions of Computer Science, MFCS 2016, August 22-
26, 2016 - Krak
´
ow, Poland, volume 58 of LIPIcs,
pages 3:1–3:3. Schloss Dagstuhl - Leibniz-Zentrum
f
¨
ur Informatik.
Doyen, L., Juhl, L., Larsen, K. G., Markey, N., and Shir-
mohammadi, M. (2014). Synchronizing words for
weighted and timed automata. In Raman, V. and
Suresh, S. P., editors, 34th International Conference
on Foundation of Software Technology and Theoreti-
cal Computer Science, FSTTCS 2014, December 15-
17, 2014, New Delhi, India, volume 29 of LIPIcs,
pages 121–132. Schloss Dagstuhl - Leibniz-Zentrum
f
¨
ur Informatik.
Droste, M., Kuich, W., and Vogler, H. (2009). Handbook of
Weighted Automata. Springer Publishing Company,
Incorporated, 1st edition.
El-Fakih, K., Kolomeez, A., Prokopenko, S., and Yev-
tushenko, N. (2008). Extended finite state machine
based test derivation driven by user defined faults.
In First International Conference on Software Test-
ing, Verification, and Validation, ICST 2008, Lille-
hammer, Norway, April 9-11, 2008, pages 308–317.
IEEE Computer Society.
El-Fakih, K., Yevtushenko, N., Bozga, M., and Bensalem,
S. (2016). Distinguishing extended finite state ma-
chine configurations using predicate abstraction. J.
Softw. Eng. Res. Dev., 4:1.
Eppstein, D. (1990). Reset sequences for monotonic au-
tomata. SIAM J. Comput., 19(3):500–510.
Hennie, F. C. (1964). Fault detecting experiments for se-
quential circuits. In 5th Annual Symposium on Switch-
ing Circuit Theory and Logical Design, Princeton,
New Jersey, USA, November 11-13, 1964, pages 95–
110.
Holzmann, G. J. (2004). The SPIN Model Checker - primer
and reference manual. Addison-Wesley.
Ito, M. and Shikishima-Tsuji, K. (2004). Some results on
directable automata. In Theory Is Forever, Essays
Dedicated to Arto Salomaa on the Occasion of His
70th Birthday, pages 125–133.
Kushik, N., L
´
opez, J., Cavalli, A. R., and Yevtushenko, N.
(2016). Improving protocol passive testing through
”gedanken” experiments with finite state machines.
In 2016 IEEE International Conference on Software
Quality, Reliability and Security, QRS 2016, Vienna,
Austria, August 1-3, 2016, pages 315–322. IEEE.
Lee, D. and Yannakakis, M. (1994). Testing finite-state
machines: State identification and verification. IEEE
Trans. Computers, 43(3):306–320.
Lee, D. and Yannakakis, M. (1996). Principles and methods
of testing finite state machines-a survey. Proceedings
of the IEEE, 84:1090–1123.
Natarajan, B. K. (1986). An algorithmic approach to the
automated design of parts orienters. In Proceedings
of Symposium on Foundations of Computer Science
(SFCS), pages 132–142.
Petrenko, A., Boroday, S., and Groz, R. (1999). Confirm-
ing configurations in EFSM. In Wu, J., Chanson,
S. T., and Gao, Q., editors, Formal Methods for Pro-
tocol Engineering and Distributed Systems, FORTE
XII / PSTV XIX’99, IFIP TC6 WG6.1 Joint Interna-
tional Conference on Formal Description Techniques
for Distributed Systems and Communication Proto-
cols (FORTE XII) and Protocol Specification, Testing
and Verification (PSTV XIX), October 5-8, 1999, Bei-
jing, China, volume 156 of IFIP Conference Proceed-
ings, pages 5–24. Kluwer.
Petrenko, A., Boroday, S., and Groz, R. (2004). Confirming
configurations in EFSM testing. IEEE Trans. Software
Eng., 30(1):29–42.
Sandberg, S. (2004). Homing and synchronizing sequences.
In Model-Based Testing of Reactive Systems, Ad-
vanced Lectures [The volume is the outcome of a re-
search seminar that was held in Schloss Dagstuhl in
January 2004], pages 5–33.
Tvardovskii, A. S. and Yevtushenko, N. V. (2020). Deriving
homing sequences for finite state machines with timed
guards. Model. Anal. Inform. Sist., 27(4):376–395.
Volkov, M. V. (2008). Synchronizing automata and the
ˇ
cern
´
y conjecture. In Language and Automata Theory
and Applications, Second International Conference,
LATA 2008, Tarragona, Spain, March 13-19, 2008.
Revised Papers, pages 11–27.
Studying Synchronization Issues for Extended Automata
345