BigGraphVis: Visualizing Communities in Big Graphs Leveraging

GPU-Accelerated Streaming Algorithms

Ehsan Moradi

and Debajyoti Mondal

Department of Computer Science, University of Saskatchewan, Canada

Keywords:

Graph Visualization, Big Graphs, Community Detection, GPGPU, Streaming Algorithms, Count-Min Sketch.

Abstract:

Graph layouts are key to exploring massive graphs. Motivated by the advances in streaming community detec-

tion methods that process the edge list in one pass with only a few operations per edge, we examine whether

they can be leveraged to rapidly create a coarse visualization of the graph communities, and if so, then how

the quality would compare with the layout of the whole graph. We introduce BigGraphVis which combines a

parallelized streaming community detection algorithm and probabilistic data structure to leverage the parallel

processing power of GPUs to visualize graph communities. To the best of our knowledge, this is the ﬁrst

attempt to combine the potential of streaming algorithms coupled with GPU computing to tackle community

visualization challenges in big graphs. Our method extracts community information in a few passes on the

edge list, and renders the community structures using a widely used ForceAtlas2 algorithm. The coarse layout

generation process of BigGraphVis is 70 to 95 percent faster than computing a GPU-accelerated ForceAtlas2

layout of the whole graph. Our experimental results show that BigGraphVis can produce meaningful layouts,

and thus opens up future opportunities to design streaming algorithms that achieve a signiﬁcant computational

speed up for massive networks by carefully trading off the layout quality.

1 INTRODUCTION

Graph visualization has been one of the most useful

tools for studying complex relational data. A widely

used algorithm for computing a graph layout is force-

directed layout (Kobourov, 2012), where forces on

the nodes and edges are deﬁned in a way such that

in an equilibrium state, the distances between pairs

of nodes become proportional to their graph-theoretic

distances. As a result, such layouts can reveal dense

subgraphs or communities in a graph. Here, a com-

munity is considered as a subgraph where nodes have

more edges with each other than with the rest of the

nodes in the graph. Constructing meaningful visual-

izations for big graphs (with millions of nodes and

edges) is challenging due to the long computing time,

memory requirements and display limitations. To

cope with the enormous number of nodes and edges,

researchers often ﬁrst detect the communities in the

graph and then visualize a smaller coarse graph (Wal-

shaw, 2000; Hachul and J

unger, 2004; Riondato et al.,

2017), where communities are merged into supern-

odes. Other approaches include layout computation

https://orcid.org/0000-0001-6689-4711

https://orcid.org/0000-0002-7370-8697

based on distributed architecture (Perrot and Auber,

2018) or GPUs (Brinkmann et al., 2017), computa-

tion of graph thumbnails (Yoghourdjian et al., 2018),

interactive ﬁltering by approximating the node rank-

ing (Huang and Huang, 2018; Nachmanson et al.,

2015; Mondal and Nachmanson, 2018), or retrieval of

a pre-computed visualization based on machine learn-

ing (Kwon et al., 2018).

This paper focuses on visualizing a supergraph

(Fig. 1), i.e., a coarse or compressed graph com-

puted from a large graph. We can construct such

a compressed graph in various ways (Von Landes-

berger et al., 2011; Abello et al., 2006; Hu et al.,

2010). For example, one can examine a sampled or

ﬁltered graph (Leskovec and Faloutsos, 2006), or ex-

amine only the densest subgraph (Gallo et al., 1989)

(a vertex-induced subgraph with the maximum aver-

age degree), or several dense subgraphs (communi-

ties) of the original graph (Gibson et al., 2005; New-

man, 2004). Sometimes nodes and edges are aggre-

gated (Elmqvist et al., 2008) (merged into some su-

pernodes) based on node clusters or attributes. Since

a supergraph retains major relational structures of

the original graph, the hope is that the visualization

might reveal the crucial relations between communi-

ties. Most algorithms for computing a supergraph run

Moradi, E. and Mondal, D.

BigGraphVis: Visualizing Communities in Big Graphs Leveraging GPU-Accelerated Streaming Algorithms.

DOI: 10.5220/0011783700003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 3: IVAPP, pages

195-202

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

195

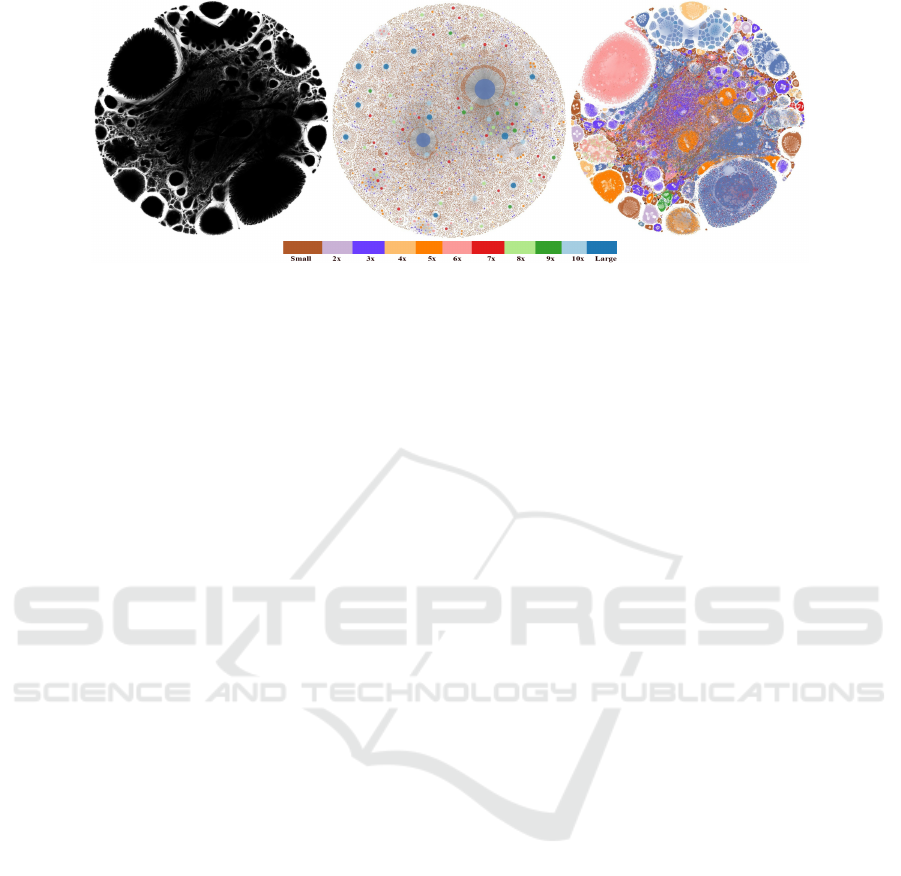
Figure 1: Different layouts computed for a graph (web-BerkStan (Leskovec and Krevl, 2014a)): (left) A layout produced

by the traditional ForceAtlas2 algorithm. (middle) The graph layout produced by our approach — BigGraphVis, where the

communities are shown with colored nodes of varying radii based on the community sizes. (right) The ForceAtlas2 layout,

where nodes are colored by the color assignment computed through BigGraphVis community detection. A qualitative color

scale is used to provide an idea of the node size distribution and to illustrate a detailed mapping of the nodes between

BigGraphVis and ForceAtlas2 visualizations.

in linear time on the number of vertices and edges of

the graph. However, even linear-time algorithms turn

out to be slow for big graphs if the constant factor hid-

den in the asymptotic notation is large. A bold idea in

such a scenario is to design a parallel streaming al-

gorithm that processes the edge list in one pass, takes

only a few operations to process each edge, and ren-

ders the graph as soon as it ﬁnishes reading the edge

list. Note that the graph does not need to be tempo-

ral or streamed, one can read the graph from exter-

nal or local memory. The idea of a parallel stream-

ing algorithm is to limit the number of passes the in-

put elements are being looked at. To achieve high

computational speed, realizing such an approach for

big graphs would require streaming edges in parallel.

Such streaming algorithms naturally come with sev-

eral beneﬁts, e.g., fast computing and limited mem-

ory requirement, and with a cost of losing quality.

However, to the best of our knowledge, no such one-

pass parallel algorithm for big graph visualization is

known to date.

Understanding whether we can effectively visual-

ize big graphs in a streaming or one-pass model pre-

dominantly relies on our knowledge of whether we

can extract a meaningful structure in such a model.

In this paper we take a ﬁrst step towards achieving

the goal by bringing the streaming community de-

tection into the scene, which allows us to create an

edge-weighted supergraph by merging the detected

communities into single nodes (i.e., supernodes). We

then visualize the supergraph using the known graph

layout algorithm. Although visualizing a supergraph

is not a new idea (e.g., see (Batagelj et al., 2010;

Batagelj et al., 2010; Abello et al., 2006)), integrating

streaming community detection for big graph visual-

ization is a novel approach and brings several natural

and intriguing questions: How fast can we produce

a supergraph visualization using streaming commu-

nity detection? Is there a reasonable GPU-processing

pipeline? Do we lose the quality signiﬁcantly us-

ing streaming community detection, when compared

with the traditional force-based visualization algo-

rithms (Jacomy et al., 2014)? Can we meaningfully

stylize traditional graph layouts by coloring the com-

munities without increasing the time overhead?

To keep the whole pipeline of community detec-

tion, graph aggregation, and visual rendering mean-

ingful and fast (in a few minutes), we propose Big-

GraphVis, which is a GPU-accelerated pipeline that

seamlessly integrates streaming community detection

and visual rendering. The availability of an increased

number of computer processing units and GPUs with

hundreds of cores have inspired researchers to imple-

ment force-based visualization algorithms that lever-

age these computing technologies (Frishman and Tal,

2007; Brinkmann et al., 2017). Although GPUs

can allow massive parallelization via a high num-

ber of cores and low-cost task dispatching, they are

structured processing units that suit structured data

like matrices (Shi et al., 2018; Frishman and Tal,

2007). Hence, designing parallel graph processing al-

gorithms often turns out to be challenging, especially

for graphs (Moradi et al., 2015). Integrating stream-

ing community detection and force-based visualiza-

tion algorithms becomes even more challenging since

the supergraph between these two processes needs to

be handled with care retaining as much quality as pos-

sible.

Our Contribution. Our ﬁrst contribution is to adapt

streaming community detection algorithms to visu-

alize communities in a graph and to examine the

trade-offs between speed and layout quality. We

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

196

propose a pipeline BigGraphVis that combines the

idea of GPU-powered parallel streaming community

detection and probabilistic data structures to com-

pute and visualize supergraphs, which can be com-

puted 70 to 95 times faster than computing a layout

of the whole graph using GPU-accelerated ForceAt-

las2 (Brinkmann et al., 2017). This can potentially

be useful in time-sensitive applications if the qual-

ity of the detected communities in the coarse layout

is reasonable when compared with the layout of the

whole graph. Although BigGraphVis trades off the

layout resolution (the amount of details to be visu-

alized) to achieve such high speed, we indicate (by

comparing with the ForceAtlas2 outputs) that it can

still detect large communities in the graph. Thus, Big-

GraphVis creates a stronghold for exploring the op-

portunity for designing one-pass graph drawing algo-

rithms in the future. Note that one-pass community

detection algorithms are several orders of magnitude

faster than GPU-accelerated community detection al-

gorithms (Hollocou et al., 2017). Thus, any pipeline

based on a typical GPU-accelerated community de-

tection (e.g., Louvain, Walktrap, etc.) followed by a

force-directed layout algorithm is much slower than

BigGraphVis.

We observe that the relative community sizes in a

ForceAtlas2 visualization may sometimes be difﬁcult

to interpret. Since the size of a community is deter-

mined by a complex force simulation, communities

that are visually similar regarding to the space they

occupy, demonstrate different behaviors: One may

contain a large number of nodes but fewer edges, and

the other may contain many edges but fewer nodes.

A community with a high average degree with fewer

nodes may take a signiﬁcantly large space (due to

node repulsion) than another community with numer-

ous nodes but fewer edges. Therefore, when we em-

ploy the community detection algorithm, we maintain

an approximate size (number of edges) for each com-

munity, and the supernodes are drawn with circles of

various radii based on the community sizes. We pro-

vide empirical evidence that BigGraphVis can reveal

communities of good quality, which is crucial for lay-

out interpretation.

Our second contribution is to leverage GPUs to

parallelize streaming community detection and prob-

abilistic data structures to fast approximate commu-

nity sizes to be used by the force layout algorithms.

To compute the supergraph, we ﬁrst detect commu-

nities and then merge each of them into a supernode.

Since community detection algorithms take a consid-

erable amount of time, we adopt a streaming com-

munity detection algorithm (SCoDA (Hollocou et al.,

2017)) that ﬁnds the communities in linear time by

going over the edges in one pass. To accelerate the

procedure, we propose a GPU-accelerated version of

SCoDA that allows for hierarchical community detec-

tion.

We use GPUs to manage millions of threads that

keep the speed of the whole process. However, com-

puting a supergraph using community detection is

challenging in a parallel environment, since we need

to compute each community’s size (i.e., the number

of edges). However, counting is an atomic opera-

tion, which means that if we want to count the com-

munities’ sizes in parallel, each thread assigned to a

community should examine the whole network. We

indicate how one can use a probabilistic data struc-

ture count-min sketch (Cormode and Muthukrishnan,

2005) to approximately compute the size of each

community in parallel to be used in the subsequent

force layout algorithm.

2 TECHNICAL BACKGROUND

Here we describe the building blocks that will be

leveraged to implement BigGraphVis.

ForceAtlas2. We were inspired to choose ForceAt-

las2 due to its capability and popularity (Bastian

et al., 2009) for producing aesthetic layout for large

graphs (Jacomy et al., 2014), and also its speed when

implemented via GPU (Brinkmann et al., 2017). The

ﬁrst step of ForceAtlas2 is reading the edge list and

putting each node in a random position. After the

initialization step, it calculates several variables, as

follows: A gravity force that keeps all nodes in-

side the drawing space (we distribute nodes among

threads). An attractive force to attract the neigh-

bor nodes (edges are distributed among threads and

atomic operations are used to avoid race conditions).

A body repulsion force to move nodes that are not re-

lated further apart from each other. A variable that

controls the node displacements at each iteration. A

‘swinging’ strategy to optimize the convergence (cal-

culate different update speeds for different nodes).

The algorithm displaces the nodes based on the forces

and the update speed. The forces are updated over a

number of iterations for better convergence.

SCoDA. To attain fast speed, BigGraphVis uses a par-

allel streaming algorithm for community detection. A

streaming algorithm takes a sequence of edges as in-

put and produces the output by examining them in

just one or a few passes. A streaming algorithm is

not necessarily for real-time streaming data, but any

graph can be read as a list of edges. SCoDA, pro-

posed by Hollocou et al. (Hollocou et al., 2017), is a

streaming community detection algorithm, which was

BigGraphVis: Visualizing Communities in Big Graphs Leveraging GPU-Accelerated Streaming Algorithms

197

implemented using sequential processing. SCoDA

is based on the key observation that a random edge

picked is highly likely to be an intra-community edge

(i.e., an edge connecting two nodes in the same com-

munity) rather than an inter-community edge (i.e.,

an edge between two different communities). Let

e(C,C) and e(C,C) be the intra and inter-community

edges of a community C, respectively. Assume that

e(C) = e(C,C) + e(C,C). Then if we draw k edges

from e(C), then the probability that they are all intra-

community edges of C is as follows.

P[intra

(C)] =

k−1

∏

l=0

|e(C,C)| − l

|e(C)| − l

k−1

∏

l=0

(1 − φ

(C)),

where φ

|e(C,C)|

2|e(C,C)|+|e(C,C)|−l

. For a well-deﬁned

community, φ

as k is small, the chance for picking edges within the

community C is large. The algorithm starts with all

nodes having degree 0 and a degree threshold. It then

updates the node degrees as it examines new edges.

For every edge, if both its vertices are of degree less

than D, then the vertex with a smaller degree joins the

community of the vertex with a larger degree. Other-

wise, the edge is skipped. The degree threshold en-

sures that only the ﬁrst few edges of each community

are being considered for forming the communities.

Count-Min Sketch. BigGraphVis computes a super-

graph based on the detected communities. We present

the communities as ‘supernodes’ with weights corre-

sponding to their number of edges. However, comput-

ing frequencies (community sizes) is highly costly for

a parallel algorithm (each thread needs to go through

the whole data, which is not efﬁcient). The commonly

used method will be an atomic operation, which is

very time-consuming for big graphs. Therefore, we

exploit an approximate method, which is reasonable

since we are interested in presenting supergraphs and

thus can avoid computing ﬁner details. A simple so-

lution is to use a hash table to map the data to their

occurrences. However, for big graphs, to get a good

approximation with this method, one needs to allo-

cate a massive space in the memory. Hence we use

a data structure named count-min sketch (Cormode

and Muthukrishnan, 2005), which can keep the oc-

currences in a limited space with a better guarantee

on solution quality.

The count-min sketch algorithm maintains an r ×c

matrix M, where r, c are determined based on the tol-

erance for error. Each row is assigned a hash function,

and the columns keep an approximate count deter-

mined by that hash function. To count the frequency

of events, for each event j and for each row i, the en-

try M[i, hash

( j)] is increased by 1, where hash

(·) is

the hash function associated to the ith row. The value

min

1≤i≤r

M[i, hash

( j)] determines the number of oc-

currences of j. Having more pairwise independent

hash functions ensures less collision and thus pro-

vides more accurate results. Since the hash functions

are independent of each other, this naturally allows

for parallel processing.

3 ALGORITHM OVERVIEW

The proposed algorithm reads an edge list stream as

the input. We then detect the communities based on a

GPU-accelerated version of SCoDA, as follows.

Modiﬁed and GPU-Accelerated SCoDA. Although

SCoDA processes each edge once with two compar-

isons, we need to deal with graphs with millions of

edges. Consequently, we design a GPU-accelerated

version of the SCoDA, where we read the edges in

parallel and use atomic operations for the degree up-

date. We run SCoDA in multiple rounds such that the

communities converge and the number of communi-

ties becomes small. This can also be seen as hier-

archical community detection. The pseudocode for

this process is illustrated in Algorithm 1 (lines 8–22).

At the end of the ﬁrst round, some communities are

detected, but the number of detected communities is

very large. Furthermore, the degree of each node is

at most the initial degree threshold. In the subsequent

rounds, communities with large average degrees ab-

sorb the smaller ones. However, due to the increase

in node degrees, a bigger threshold is needed. There-

fore, we increase the degree threshold at each round

by a multiplicative factor. One can choose a factor for

the threshold based on the nature of the graph.

Leveraging Count-Min Sketch to Approximate

Community Sizes. After SCoDA, we compute a su-

pergraph that represents the communities as supern-

odes, where each node is weighted proportional to

the number of edges it contains. Although one can

calculate the community sizes in the community de-

tection process, it would require adding more atomic

counters and signiﬁcantly slow down the computa-

tion. Hence we leveraged count-min sketch.

We took the sum of the vertex degrees (equiv-

alently, twice the number of edges) within a com-

munity as the weight of the corresponding supern-

ode. To compute this, for each node v, we increment

M[i, hash

(com(v))] by the degree of v, where 1 ≤ i ≤

r, com(·) is the community number, and hash

(·) is

the hash function associated to the ith row. The value

min

1≤i≤r

M[i, hash

(com(v))] determines the approxi-

mate size for com(v).

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

198

Drawing the Supergraph Using GPU-Accelerated

ForceAtlas2. Finally, we leveraged the GPU-

accelerated ForceAtlas2 (Section 2) to draw the ag-

gregated nodes. When drawing a supernode, we

choose the radius proportional to the square root of

its size. For dense communities, the space occu-

pied by a supernode is thus proportional to the num-

ber of vertices that it contains. If a visualization for

the whole graph is needed (instead of a supergraph),

then we ﬁrst compute a layout for the whole graph

using GPU-accelerated ForceAtlas2 and then color

the nodes based on the communities detected using

SCoDA. The details of such coloring are in Section 3.

Count-Min Sketch Parameters. The error in the

count-min sketch can be controlled by choosing the

size of the sketch matrix, i.e., the number of hash

functions and the number of columns w. For a partic-

ular hash function, the expected amount of collision

, where N is the total number of items and they

are mapped to {1,2, . . . , w} by the hash function. Cor-

mode and Muthukrishnan (Cormode and Muthukrish-

nan, 2005) observed that the probability of seeing a

collision of more than an expected amount is bounded

, and for d hash functions, the probability of hav-

ing a large error is bounded by

. This indicates that

a larger number of hash functions is a better choice

when accuracy is important. However, this also in-

creases the size of the count-min sketch matrix. In our

experiment, we choose the number of hash functions

to be four and the number of columns to be a fraction

−4

of the number of edges, which is bounded by our

available GPU memory. Choosing a larger number of

columns can further improve the count-min sketch ac-

curacy as more collisions can be avoided.

Community Detection Parameters. For stream-

ing community detection, we need to deﬁne two pa-

rameters: the degree threshold and the number of

rounds. The streaming community detection algo-

rithm is based on the idea that the probability of

intra-community edges appearing before the inter-

community edges is very high when a community

is being formed. Therefore, the degree threshold

could be very sensitive since a very small threshold

might miss some intra-community edges, which can

break communities into sub-communities (Hollocou

et al., 2017). Similarly, if the degree threshold is se-

lected too high, it may lose granularity, i.e., it can

merge too many communities into a single commu-

nity. Thus, as suggested in the original SCoDA (Hol-

locou et al., 2017), we have chosen the most common

degree (mode degree δ) in the graph as the degree

threshold. However, if the user wants to have big-

ger communities with a larger number of nodes, then

choosing a slightly bigger degree will produce such

results. In our experiment, we observed a few rounds

sufﬁce to have a high modularity score. The modular-

ity is a metric to measure the quality of the commu-

nities (Newman, 2006). The modularity Q ranges be-

tween −0.5 and 1, where 1 denotes the highest qual-

ity. After achieving high modularity, the communi-

ties become stable, and hence choosing a big num-

ber of rounds does not affect the running time. Since

the degrees of the supernodes increases at each round,

we choose the δ

to be the threshold at the ith round,

where i runs from 1 to 10.

Convergence. The node positions in the ForceAt-

las2 algorithm are updated in several rounds so that

the energy of the system is minimized. To achieve

convergence, one needs to choose a large number

of iterations for big graphs. For the graphs with

millions of nodes and edges, the GPU-accelerated

ForceAtlas2 with 500 iterations showed a good per-

formance (Brinkmann et al., 2017). However, in our

method, much fewer rounds are enough since we have

a much smaller network for drawing after community

detection. We observed that for visualizing the super-

graph, 100 iterations is more than enough to obtain a

stable layout for all graphs we experimented with.

Coloring Communities. When visualizing super-

graph, we create 11 node groups and color them us-

ing a qualitative color scheme (Brewer and Harrower,

2001). Speciﬁcally, we ﬁrst compute the sum α of the

sizes of all communities, then sort the communities

based on their sizes, and color the smaller communi-

ties that take 50% of α with a brown color. The rest

of the supernodes are partitioned into 10 groups and

colored using (from small to big) brown, light pur-

ple, purple, light orange, orange, light red, red, light

green, green, light blue, blue (Fig. 1). Such coloring

provides a sense of the community size distribution in

the layout.

Note that the above coloring scheme assigns a

color to each supernode. If visualization of the whole

graph is needed (instead of a supergraph), then we

color the layout of the whole graph computed by the

GPU-accelerated ForceLayout2, where each node is

drawn with the color of its corresponding supernode.

Such a compatible coloring provides us a way to ex-

amine the quality of ForceAtlas2 from the perspective

of community detection and vice versa.

4 EXPERIMENTS

For our experiments, we used an Nvidia Tesla k20c

with 5GB of VRAM. It is based on the Kepler archi-

tecture, which has 2496 CUDA cores. The compiler

that we used is a CUDA 11.0.194.

BigGraphVis: Visualizing Communities in Big Graphs Leveraging GPU-Accelerated Streaming Algorithms

199

Algorithm 1: BigGraphVis Layout.

Input: Edge list (src, dst)

1: D ← ModeDegree

2: #GPUthreads ← #edges

3: EachThread i do

4: C

← i, Csize

← 0

5: end EachThread

6: EachThread j = 1 . . . Number o f Rounds do

7: EachThread i do

8: if deg(src) ≤ D and deg(dst) ≤ D then

9: if deg(src) > deg(dst) then

10: C

dst

← C

src

11: atomic(deg(dst) + +)

12: else

13: if deg(dst) > deg(src) then

14: C

src

← C

dst

15: atomic(deg(src) + +)

16: end if

17: end if

18: end if

19: end EachThread

20: D ← multiplicative f actor

21: end EachThread

GPUdo Find community sizes Csize

via Count-

Min Sketch

GPUdo C

x,C

y ← FA2(Csrc,Cdst,Csize)

GPUdo Draw(C

x,C

y,Csize

)

The implementation of ForceAtlas2 that we

are using is the same as that of Brinkmann et

al. (Brinkmann et al., 2017), which provides a

grayscale layout. BigGraphVis leverages commu-

nity detection to color the nodes. Furthermore, the

node repulsion in BigGraphVis considers the node

weights (i.e., supernode sizes), which provides the

space needed to draw the supernode. For a proper

comparison of the speed up, we choose the ForceAt-

las2 force parameters similar to Brinkmann et al.’s

work. Thus the gravitational and repulsive force pa-

rameters remain the same as 1 and 80 for all networks.

Note that Brinkmann et al. mentioned that tuning

these variables does not have any major inﬂuence on

the algorithm’s performance. The source code of our

implementation is available as a GitHub repository

Data. We choose multiple real-world datasets for our

work (Leskovec and Krevl, 2014b). Whereas most of

these graphs have millions of edges, they also have

millions of nodes. Hence to examine dense graphs,

we choose a graph Bio, created from bio-mouse-gene

network (Rossi and Ahmed, 2015), and another graph

called Authors. The Authors graph is created by tak-

ing authors of 15 journals as nodes, where an edge

https://github.com/Ehsan486/GraphVis

represents that the corresponding authors published in

the same journal (Tang et al., 2008).

Running Time. Table 1 compares the running

time of BigGraphVis (visualizing supergraph) and

GPU-accelerated ForceAtlas2 (visualizing the whole

graph). For BigGraphVis, we report both the run-

ning time (in milliseconds) and the size of the su-

pergraph (number of supernodes or communities de-

tected), whereas for GPU-accelerated ForceAtlas2,

we report the running time. We also compute the

speedup in percentage for all the networks, which

ranges between 70 to 95. The results are repeated 20

times to see if there is any difference in speedup; and

the least speedup is reported. Table 1 also reports sep-

arately the time taken by BigGraphVis to detect the

communities using 10 rounds. This is to provide an

idea of time required to stylize a ForceAtlas2 visual-

ization using a color mapping based on community

sizes. We noticed that for all graphs this overhead is

only a few seconds. For all our graphs, the outputs

were seen to converge in 3 rounds, which indicates

that the number of rounds could be lowered to achieve

yet a smaller overhead.

Quantity Measure (Modularity). We examined

modularity of the detected communities. For ﬁve of

the 10 graphs, the modularity scores were very high

(above 0.7 and upto 0.9), and for none of them was

below 0.55. This indicates reliable detection of the

communities.

Visual Comparison. We now visually examine

the ForceAtlas2 and BigGraphVis layouts on various

datasets. Fig. 2 illustrates three layouts for github,

eu-2005, web-BerkStan and soc-LiveJournal graphs

: (left) GPU-accelerated ForceAtlas2, (middle) Big-

GraphVis supergraph, and (right) ForceAtlas2 layout

colored by BigGraphVis. It is noticeable that Big-

GraphVis were able to reveal big communities. One

can access the members of each community using the

dataset created at hierarchical community detection

rounds. ForceAtlas2 layouts, which are colored by

BigGraphVis, take more time but show a higher level

of detail. However, the community sizes seen in a

ForceAtlas2 output may not always show their true

sizes (i.e., the number of nodes or edges are not clear).

On the other hand, the BigGraphVis supergraph can

provide us with a quick understanding of the number

of big communities in a graph and some idea of their

relative sizes. Although true communities for these

graphs are either unknown or not well-deﬁned, for the

graph Authors Fig. 3, we know the authors are from

15 journals. Both the BigGraphVis supergraph and

the ForceAtlas2 output colored by BigGraphVis, re-

veal about 15 big visual blobs. This provides an indi-

cation that even in cases when the streaming commu-

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

200

Table 1: BigGraphVis speed up when compared with GPU-accelerated ForceAtlas2 (time is in milliseconds). DT, SS, SN,

SE, M are the degree threshold, sketch size, super nodes, super edges, and modularity, respectively. SG time is the time to

compute supergraph. BGV time is the total time taken by BigGraphVis.

Network Name Nodes Edges DT SS SN SE FA2 time BGV Time SG Time Speedup M

Wiki-Talk 2.39M 5.02M 5 5K 112K 122K 400K 28K 3854 92 0.64

bio-mouse-gene 45101 14506195 5 14500 193 196 50016 8937 7941 82 0.88

as-Skitter 1696414 11095298 7 11000 136597 300779 350141 58750 7128 83 0.55

web-ﬂickr 105938 2316948 43 2000 1094 26170 25251 3280 1497 87 0.61

github 1471422 13045696 11 13000 71166 91345 181538 17519 9115 90 0.90

com-Youtube 1157827 2987624 4 3000 211192 232266 233915 43666 2198 81 0.73

eu-2005 333377 4676079 15 4500 9181 20263 52268 5145 2827 90 0.66

web-Google 916427 5105039 11 5000 75443 125287 131792 13863 3415 89 0.80

web-BerkStan 685230 6649470 11 6500 31213 57382 138000 6565 4566 95 0.81

soc-LiveJournal 3997962 34681189 17 34500 248188 566160 3862325 315072 21344 91 0.62

Authors 12463 10305446 2 10000 4315 1398089 146443 42541 6382 70 0.62

Figure 2: ForceAtlas2 layout, BigGraphVis layout and stylized ForceAtlas2 layout for four graphs: (top-left) github, (top-

right) eu-2005, (bottom-left) web-BerkStan and (bottom-right) soc-LiveJournal.

Figure 3: (top) Visualization for the graph — Authors. (bot-

tom) Illustration for the effect of different rounds of com-

munity detection.

nity detection may be a coarse approximation, Big-

GraphVis can produce a meaningful layout since it

employs ForceAtlas2 to visualize the supergraph.

5 CONCLUSION

In this paper, we propose BigGraphVis that visual-

izes communities in big graphs leveraging streaming

community detection and GPU computing. Our com-

puting pipeline uses probabilistic data structures to

produce a coarse layout of the graph that is fast, yet

can reveal major communities. Through a detailed

experiment with the real-world graphs (the biggest

graph, soc-LiveJournal, had about 34 million edges),

we observed that BigGraphVis can produce a mean-

ingful coarse layout within a few minutes (about ﬁve

minutes for soc-LiveJournal). We also showed how

the graph summary produced by BigGraphVis can be

used to color ForceAtlas2 output to reveal meaningful

graph structure for the whole graph. Exploring user

interactions while visualizing graphs from streamed

edges would be an interesting directions for future

work. We believe that our work will inspire future re-

search on leveraging streaming algorithms and GPU

computing to visualize massive graphs.

ACKNOWLEDGEMENTS

The research is supported in part by the Natural Sci-

ences and Engineering Research Council of Canada

(NSERC), and by a Research Junction Grant with the

University of Saskatoon and the Saskatoon Transit di-

vision of the City of Saskatoon.

BigGraphVis: Visualizing Communities in Big Graphs Leveraging GPU-Accelerated Streaming Algorithms

201

REFERENCES

Abello, J., van Ham, F., and Krishnan, N. (2006). Ask-

graphview: A large scale graph visualization system.

IEEE Trans. Vis. Comput. Graph., 12(5):669–676.

Bastian, M., Heymann, S., and Jacomy, M. (2009). Gephi:

An open source software for exploring and manipulat-

ing networks. In Proc. of the Int. AAAI Conf. on Web

and Social Media, volume 3.

Batagelj, V., Didimo, W., Liotta, G., Palladino, P., and Pa-

trignani, M. (2010). Visual analysis of large graphs

using (X, Y)-clustering and hybrid visualizations. In

IEEE Paciﬁc Visualization Symposium, pages 209–

216.

Brewer, C. and Harrower, M. (2001). Colorbrewer 2.0.

https://colorbrewer2.org/.

Brinkmann, G. G., Rietveld, K. F., and Takes, F. W. (2017).

Exploiting GPUs for fast force-directed visualization

of large-scale networks. In 2017 46th Int. Conf. on

Parallel Processing (ICPP), pages 382–391. IEEE.

Cormode, G. and Muthukrishnan, S. (2005). An improved

data stream summary: the count-min sketch and its

applications. Journal of Algorithms, 55(1):58–75.

Elmqvist, N., Do, T.-N., Goodell, H., Henry, N., and Fekete,

J.-D. (2008). Zame: Interactive large-scale graph vi-

sualization. In 2008 IEEE Paciﬁc visualization Symp.,

pages 215–222. IEEE.

Frishman, Y. and Tal, A. (2007). Multi-level graph layout

on the GPU. IEEE Transactions on Visualization and

Computer Graphics, 13(6):1310–1319.

Gallo, G., Grigoriadis, M. D., and Tarjan, R. E. (1989). A

fast parametric maximum ﬂow algorithm and applica-

tions. SIAM Journal on Computing, 18(1):30–55.

Gibson, D., Kumar, R., and Tomkins, A. (2005). Discover-

ing large dense subgraphs in massive graphs. In Int.

Conf. on Very large data bases, pages 721–732. Cite-

seer.

Hachul, S. and J

unger, M. (2004). Drawing large graphs

with a potential-ﬁeld-based multilevel algorithm. In

Graph Drawing, pages 285–295. Springer.

Hollocou, A., Maudet, J., Bonald, T., and Lelarge, M.

(2017). A linear streaming algorithm for commu-

nity detection in very large networks. arXiv preprint

arXiv:1703.02955.

Hu, Y., Gansner, E. R., and Kobourov, S. G. (2010). Visu-

alizing graphs and clusters as maps. IEEE Computer

Graphics and Applications, 30(6):54–66.

Huang, X. and Huang, C. (2018). NGD: ﬁltering graphs for

visual analysis. IEEE Trans. Big Data, 4(3):381–395.

Jacomy, M., Venturini, T., Heymann, S., and Bastian, M.

(2014). Forceatlas2, a continuous graph layout algo-

rithm for handy network visualization designed for the

gephi software. PloS one, 9(6):e98679.

Kobourov, S. G. (2012). Spring embedders and force

directed graph drawing algorithms. arXiv preprint

arXiv:1201.3011.

Kwon, O., Crnovrsanin, T., and Ma, K. (2018). What would

a graph look like in this layout? A machine learning

approach to large graph visualization. IEEE Trans.

Vis. Comput. Graph., 24(1):478–488.

Leskovec, J. and Faloutsos, C. (2006). Sampling from large

graphs. In ACM SIGKDD Int. Conf. on Knowledge

discovery and data mining, pages 631–636.

Leskovec, J. and Krevl, A. (2014a). Snap datasets: Stanford

large network dataset collection.

Leskovec, J. and Krevl, A. (2014b). SNAP Datasets: Stan-

ford large network dataset collection. http://snap.

stanford.edu/data.

Mondal, D. and Nachmanson, L. (2018). A new approach to

GraphMaps, a system browsing large graphs as inter-

active maps. In Proceedings of the 13th International

Joint Conference on Computer Vision, Imaging and

Computer Graphics Theory and Applications (VISI-

GRAPP), pages 108–119. SciTePress.

Moradi, E., Fazlali, M., and Malazi, H. T. (2015). Fast par-

allel community detection algorithm based on modu-

larity. In Int. Symp. on Comp. Architecture and Digital

Systems (CADS), pages 1–4. IEEE.

Nachmanson, L., Prutkin, R., Lee, B., Riche, N. H., Hol-

royd, A. E., and Chen, X. (2015). Graphmaps: Brows-

ing large graphs as interactive maps. In Graph Draw-

ing and Network Visualization (GD), volume 9411 of

LNCS, pages 3–15. Springer.

Newman, M. E. (2004). Fast algorithm for detecting com-

munity structure in networks. Physical review E,

69(6):066133.

Newman, M. E. (2006). Modularity and community struc-

ture in networks. Proc. of the national academy of

sciences, 103(23):8577–8582.

Perrot, A. and Auber, D. (2018). Cornac: Tackling huge

graph visualization with big data infrastructure. IEEE

Transactions on Big Data, 6(1):80–92.

Riondato, M., Garc

ıa-Soriano, D., and Bonchi, F. (2017).

Graph summarization with quality guarantees. Data

mining and knowledge discovery, 31(2):314–349.

Rossi, R. A. and Ahmed, N. K. (2015). The network data

repository with interactive graph analytics and visual-

ization. In AAAI Conf. on Artiﬁcial Intelligence, pages

4292–4293.

Shi, X., Zheng, Z., Zhou, Y., Jin, H., He, L., Liu, B., and

Hua, Q.-S. (2018). Graph processing on GPUs: A

survey. ACM Computing Surveys, 50(6):1–35.

Tang, J., Zhang, J., Yao, L., Li, J., Zhang, L., and Su, Z.

(2008). Arnetminer: extraction and mining of aca-

demic social networks. In ACM SIGKDD Int. Conf.

on Knowledge discovery and data mining, pages 990–

998.

Von Landesberger, T., Kuijper, A., Schreck, T., Kohlham-

mer, J., van Wijk, J. J., Fekete, J.-D., and Fellner,

D. W. (2011). Visual analysis of large graphs: state-

of-the-art and future research challenges. In Computer

graphics forum, volume 30, pages 1719–1749. Wiley

Online Library.

Walshaw, C. (2000). A multilevel algorithm for force-

directed graph drawing. In Graph Drawing, pages

171–182. Springer.

Yoghourdjian, V., Dwyer, T., Klein, K., Marriott, K., and

Wybrow, M. (2018). Graph thumbnails: Identifying

and comparing multiple graphs at a glance. IEEE

Trans. Vis. Comput. Graph., 24(12):3081–3095.

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

202