Separation of Concerns in an Edge-Based Compartmental Modeling

Framework

A. Yvan Guifo Fodjo

1,2 a

, Jerry Lacmou Zeutouo

2,3 b

and Samuel Bowong

4,5

CNRS, UMR 7606, LIP6, Sorbonne Universit

e, Paris, France

URIFIA, Universit

e de Dschang, Dschang, Cameroon

Inria Avalon, LIP,

Ecole Normale Sup

erieure de Lyon, University of Lyon, France

IRD, UMI 209, UMMISCO, Bondy, France

epartement de Math

ematiques, Universit

e de Douala, Douala, Cameroon

Keywords:

Separation of Concerns, Compartmental Models, Contact Network, Epidemiology Modeling Tool, Edge-

Based Compartmental Network.

Abstract:

A well-known framework with strong potential for epidemic prediction and the ability to incorporate realistic

contact structures is edge-based compartmental modeling (EBCM). However, models built from this frame-

work lead to a multiplication of ordinary differential equations and many parameters to be estimated, which

make the models complex and difﬁcult to extend or to reuse. The Kendrick approach has shown promising re-

sults in generalizing compartmental models to take into account aspects of contact networks while preserving

the separation of concerns, thus allowing to deﬁne modular, extensible and reusable models. But this general-

ization of compartmental models to contact network aspects is still limited to a few contact networks. In this

paper, we present an attempt to extend Kendrick’s approach from an approximation of EBCM models to fur-

ther support aspects of contact networks, thereby improving the predictive quality of models with signiﬁcant

heterogeneity in contact structure, while maintaining the simplicity of compartmental models. This extension

consists of an integration of the basic reproductive number R

into the compartmental SIR framework. This

attempted is validated using Miller’s mass action and the approximation of EBCM conﬁguration model.

1 INTRODUCTION

Mathematical modeling and computer simulation

have been widely used in epidemiology to ﬁnd appro-

priate control strategies and means of control (Levin

and Durrett, 1996). One of the most common mod-

els in mathematical modeling using the compartmen-

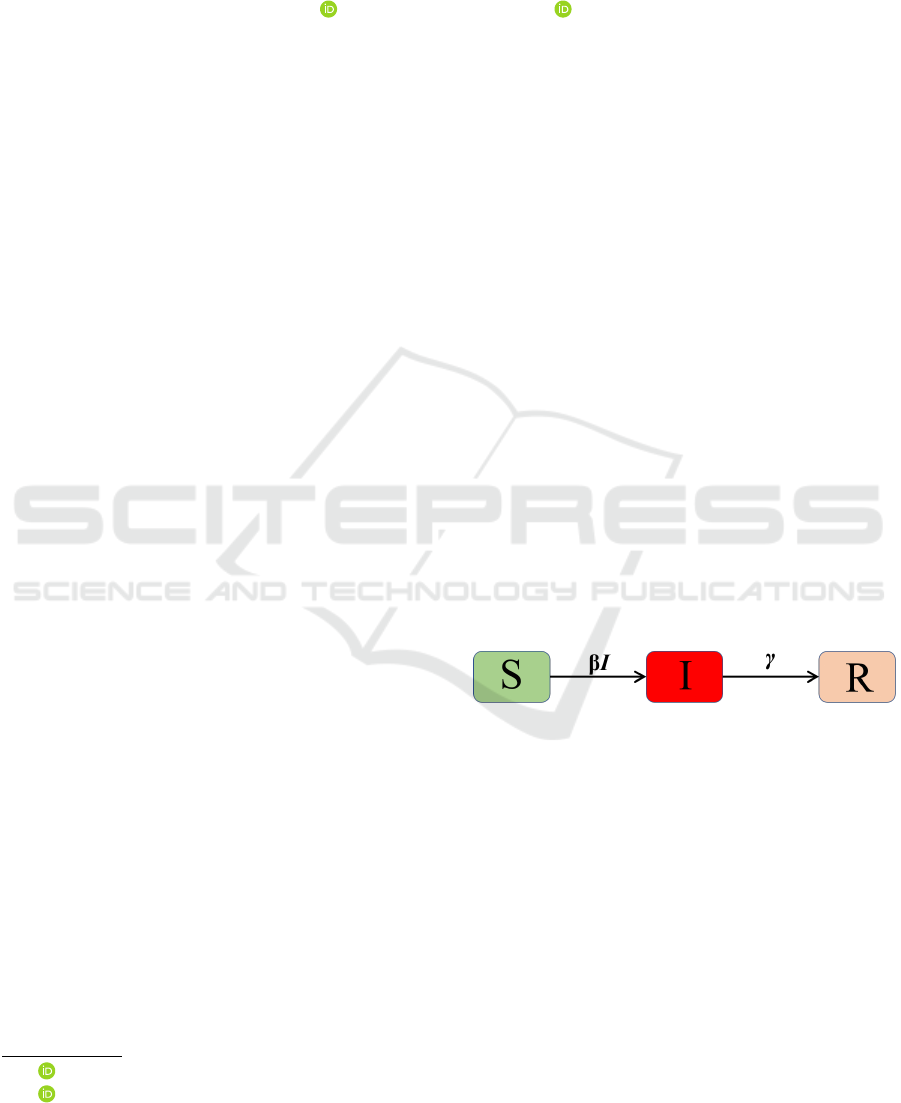
tal framework is the mass action model (see Figure

1). The basic assumption in this model is that sus-

ceptible and infectious individuals meet at random

and can spread the disease (Cuddington and Beisner,

2005; Keeling and Rohani, 2011). Susceptible indi-

viduals (S) can become infected from the force of in-

fection

λ(S,I,N) = βI where β is the contact trans-

mission rate and N is the population size. Infectious

individuals (I) can be recovered at the recovery rate γ.

https://orcid.org/0000-0002-0714-6737

https://orcid.org/0000-0003-4414-7453

This is the rate at which susceptible individuals be-

come infected.

Figure 1: Flow diagram of the mass action mathematical

model.







′

= −βIS

′

= βIS − γI

′

= γI

(1)

Compartmental models are typically ﬁrst deﬁned

as ordinary differential equations (ODEs) such as

Equation 1. These models can be studied ana-

lytically and/or simulated using algorithms such as

RungeKutta. However, it is considered more real-

istic to adopt a stochastic viewpoint on these mod-

els considering them as Continuous-Time Markov

Chains (CTMCs). The latter can be derived from the

ODEs modulo some widely accepted, albeit simplify-

ing, probabilistic assumptions.

Although the mass action model is known largely

for its conceptual and mathematical simplicity (Ker-

mark and Mckendrick, 1927), it has been found to

262

Guifo Fodjo, A., Zeutouo, J. and Bowong, S.

Separation of Concerns in an Edge-Based Compartmental Modeling Framework.

DOI: 10.5220/0011780200003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 3: BIOINFORMATICS, pages 262-269

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

have some shortcomings, including the fact that it in-

correctly assumes that all individuals have the same

contact rate and implicitly assumes that all partner-

ships are inﬁnitely short (Miller et al., 2012; Wang

et al., 2018).

(Miller et al., 2012; Kiss et al., 2017; Wang et al.,

2018) built on these limitations of the mass action

model to introduce the edge-based compartmental

modelling (EBCM) framework. It is a compartment-

based model extension approach where the contacts

between individuals are materialized by the edges

(Miller et al., 2012; Wang et al., 2018). The main idea

is to integrate the heterogeneous mixture by consider-

ing the population as a network of individuals where

the contacts follow a given probability distribution.

Thus, it consists in incorporating into the ordinary dif-

ferential equations of the mass action model, a kind

of social heterogeneity (heterogeneous contact rate),

while taking into account the impact of the partner-

ship duration

The results obtained from this incorporation have

enabled realistic and more predictable contact struc-

tures to be considered. However, the modiﬁcation of

the compartmental framework of mass action results

in more and more multiple and complex differential

equations, especially when new concerns (age, sex,

control strategy, etc.) and parameters are taken into

account (Balde et al., 2019). Moreover, another dif-

ﬁculty of the EBCM framework is that the models it

contains are not easily scalable, extensible and there-

fore not reusable.

Kendrick’s approach (Bui et al., 2016; Bui et al.,

2019) has shown its ability to deﬁne concerns (age,

sex, spatial heterogeneity, etc.) as independent (pos-

sibly incomplete) models that are then combined

into stochastic automata networks (SANs) (Plateau

and Stewart, 2000) using a tensorial sum operator.

Stochastic dependencies between concerns are then

introduced in a second phase so that independent con-

cerns can be reused and combined in other models

much more easily. In (Fodjo et al., 2022), the authors

showed that this approach, based on compartmental

models, could be extended to take into account cer-

tain aspects of contact networks while enabling the

building of reusable models. But this generalization

of compartmental models to contact network aspects

is still limited to a few contact networks (Poisson, Ex-

ponential and Scale free).

While it is well known that taking into account as-

pects of contact networks in compartmental models

leads to more realistic and predictive models, there

The notion of partnership, materializes here the exis-

tence of a contact (edge), between two individuals. In this

case, we say that these individuals are partners.

is also a large body of work that recognizes the cru-

cial importance of the basic reproductive number R

in predicting epidemics (Meyers et al., 2005; Danon

et al., 2011; Molina and Stone, 2012; Heesterbeek

et al., 2015; Zhang et al., 2015; Trapman et al., 2016;

Yang and Xu, 2019). This parameter refers to the

number of new cases caused by a single randomly in-

fected individual in a completely susceptible popula-

tion. When R

< 1, epidemics are impossible, while

when R

> 1, they are possible. (Aparicio and Pas-

cual, 2007) suggest modifying the SIR compartmen-

tal framework to incorporate the parameter R

into the

ordinary differential equations. In this study, in order

to take the aspects of contact networks, R

is approx-

imated to Poisson, Exponetial and Scale free contact

networks.

In this work, we propose an attempt to extend

Kendrick’s approach from an approximation of the

EBCM approach while maintaining the separation of

concerns and preserving the simplicity of compart-

mental models. This approximation consists in con-

structing a concern in the sense of Kendrick’s ap-

proach (i.e. as a stochastic automaton that can then

be combined) from the R

of each EBCM model. The

extension of the Kendrick approach is done by incor-

porating the base reproduction rate R

into the com-

partmental SIR framework. The simulation results

obtained are similar to those of the EBCM conﬁgu-

ration model presented in (Miller et al., 2012).

2 MILLER ET AL.’S MASS

ACTION MODEL AND

EDGE-BASED

COMPARTMENTAL

CONFIGURATION MODELS

In this section, and for the purposes of this work,

we will restrict ourselves to the standard mass ac-

tion model of (Miller et al., 2012) and the edge-based

compartmental conﬁguration model.

2.1 Miller et Al.’s Mass Action Model

This model is constructed like the system of Equa-

tions 1) with some modiﬁcations. Such as the fact

that the authors of (Miller et al., 2012) assume that an

infected individual causes new infections at the rate

βS(t), where

β is the transmission rate per infected

Separation of Concerns in an Edge-Based Compartmental Modeling Framework

263

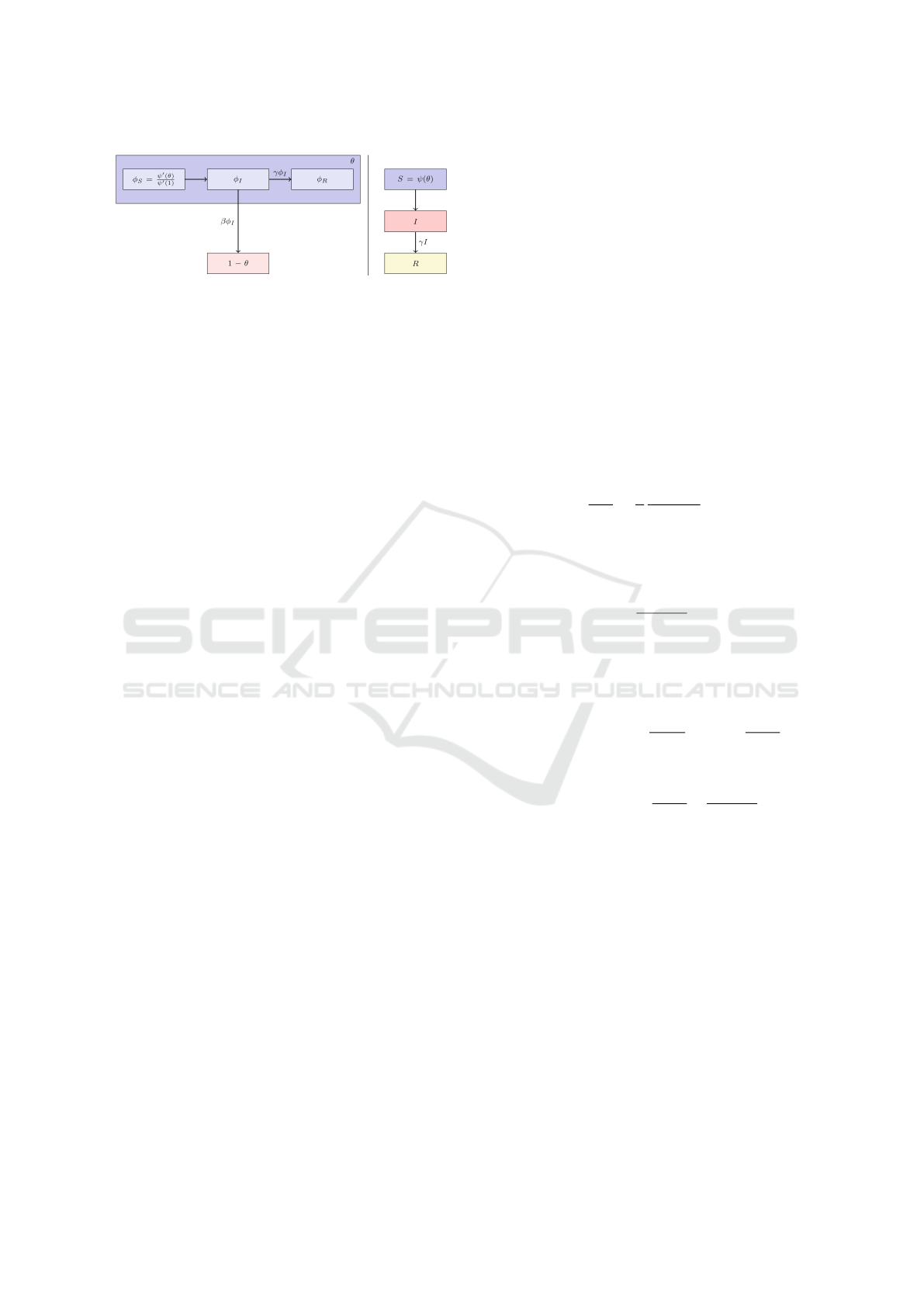
Figure 2: Flow diagram of the EBCM conﬁguration model

of (Miller et al., 2012).

individual. Recovery occurs at the rate of γ.







′

= −

βIS

′

βIS − γI

′

= γI

(2)

Moreover, when building the mass action model (see

system of Equations 1), many works (Cuddington and

Beisner, 2005; Keeling and Rohani, 2011; Martcheva,

2015) interpret the transmission rate β as the product

of the contact rates and the transmission probability.

But in the speciﬁc case of the mass action model of

Miller et al.’s, the authors assume that the transmis-

sion rate per infected person

β = β⟨k⟩ where ⟨k⟩ is

the average degree of the contact network considered.

2.2 EBCM Conﬁguration Model

The ﬂow diagram of the EBCM conﬁguration model

is shown in Figure 2. The compartments S, I, and R

represent the proportions of susceptible, infected, and

recovered, respectively, as in the case of the mass ac-

tion model in section 2.1. To calculate S(t), I(t), and

R(t), the authors note that these are the probabilities

that a random test node u is in each compartment. We

calculate S(t) noting that this is also the probability

that none of u’s partners has yet transmitted to u. The

probability that a randomly selected partner v has not

yet transmitted the infection to u.

For large networks, (Miller et al., 2012; Wang

et al., 2018) assumed that the neighbors of the node

test u are independent. Given a degree k, u is sus-

ceptible at time t with probability s(k,θ(t)) = θ(t)

Thus, S(t) =

∑

P(k)s(k,θ(t)) = ψ(θ(t)). The ODEs

of the EBCM conﬁguration model are obtained in (3).



S = ψ(θ)

I = 1 − S − R

(3)

The φ

, φ

and φ

compartments of Figure 2 repre-

sent respectively the probabilities that a partner v is

susceptible, infected and recovered but has not yet

transmitted the infection to u. The compartment 1−θ,

represents the probability that there is infection (it is

done with the rate βφ

between the compartment φ

and 1 − θ).

In order to determine θ, consider that (θ = φ

+ φ

). At time t = 0, θ = φ

≃ 1. Because we

consider that there has not yet been an infection, so

= φ

≃ 0.

The central parameter of this calculation is the de-

termination of φ

. Thus,

= θ − φ

− φ

(4)

It remains to calculate φ

and φ

explicitly to obtain

. If we ﬁnally consider that the v is infected and that

there was an infection, then

′

= −βφ

(5)

To determine φ

, the authors use the fact that in Figure

2 the ﬂuxes from φ

to φ

and from φ

to (1 − θ) are

proportional to one another. Both φ

and (1 − θ) are

equal to zero at time zero since we assume that no

infection or recovery events can occur prior to time

zero. By integrating the relation

dφ

d(1 − θ)

(6)

and using the initial condition

(0) = (1 − θ(0)) = 0 (7)

Thus,

γ(1 − θ)

(8)

To determine φ

, the authors rely on the fact that

a partner v has a degree k with probability P

(k) =

kP(k)/⟨k⟩. Given a degree k, v is susceptible with

probability θ

(k−1)

. This allows us to obtain

∑

(k)θ

(k−1)

∑

kP(k)

⟨k⟩

(k−1)

′

(θ)

′

(1)

(9)

Therefore, from the relation 4, they obtain

= θ − φ

− φ

= θ −

′

(θ)

′

(1)

−

γ(1 − θ)

(10)

While it is easy to recognize that the EBCM conﬁg-

uration model captures much more population struc-

ture than the mass action model, it is also important

to note that the complexity and number of differential

equations increases signiﬁcantly. As we have seen,

to obtain Equation (10), the authors of (Miller et al.,

2012) had to develop new Equations 4, 5, 6, 7, 8, 9 in

addition to the one of the system of (3).

3 GENERALIZING KENDRICK’S

APPROACH

The challenge of this work is to show that Kendrick’s

approach can be extended to support aspects of con-

tact networks using an approximation of the EBCM

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

264

approach. This would improve the predictive qual-

ity of models with signiﬁcant heterogeneity in the

structure of contacts while preserving the separation

of concerns. This would result in modular models,

easily extensible and reusable. The idea is to avoid

the designers/modelers/developers having to build a

model with a multitude of ordinary differential equa-

tions, having to build an explicit contact network and

having to estimate many parameters.

(Fodjo et al., 2022) showed that it was possible

to extend the compartmental framework in order to

integrate some aspects of contact network models.

Their idea was to make the force of infection a cen-

tral parameter that could be redeﬁned from the exten-

sion points (α

gen

, it

gen

, τ

gen

) and according to the

concerns that one wished to model. Thus, from the

idea of (Bansal et al., 2007) and the application of

the Template Method Design Pattern (Gamma et al.,

1995), they proposed a generic deﬁnition to the force

of infection named λ (see Equation 11). (Fodjo et al.,

2022) insisted on the fact that the index ”gen” of the

extension points α

gen

, it

gen

and τ

gen

is intended to sig-

nify that they are applied to a model based on a net-

work of contacts and to indicate that they are generic

points, i.e. variable points.

λ = α

gen

(11)

For our modeling and simulation purposes, we use

the same convention as the authors of (Fodjo et al.,

2022). Thus we use names with the subscript ”gen”

in the ﬁnal generic deﬁnitions of the models and in

the Kendric code.

The force of infection of the mass action model

given by (2) described in section 2.1 is given by the

relation 12.

λ =

βI = β⟨k⟩I (12)

From the relations 11 and 12 the identiﬁcation of the

extension points α

gen

, it

gen

and τ

gen

gives :







gen

= ⟨k⟩

gen

= I

gen

= β

(13)

In section 2.2, we have presented the EBCM conﬁg-

uration model and the array of ODEs and parameters

to be estimated from the model. This constitutes more

effort of understanding, programming for the model

designers/modelers/developers. Our goal is to cope

with the complexity of ordinary differential equations

It is the average number of individuals with whom a

susceptible individual is in contact or the average degree of

nodes in a contact network.

This is the proportion of contacts that are infectious.

The rate per contact at which disease is transmitted be-

tween an infectious individual and a susceptible individual.

in the EBCM framework while deﬁning extensible

and reusable models.

In order to cope with the complexity of the or-

dinary differential equations of the EBCM frame-

work while deﬁning extensible and reusable models,

we propose to use an approximation of each EBCM

model from the mathematical formulation of R

Indeed, (Aparicio and Pascual, 2007) showed that

it was possible to modify the simple compartmental

framework in order to integrate the parameter R

into

the model equations.

We propose to this effect to approximate the

EBCM models, by incorporating each R

of EBCM

model in the compartmental framework SIR (Suscep-

tible, Infected, Recovered) as shown in (Aparicio and

Pascual, 2007), so as to deﬁne these EBCM model ap-

proximations as concerns in the sense of the Kendrick

approach (i.e. a stochastic automaton that can be com-

posed) as illustrated in (Fodjo et al., 2022) and then to

be able to determine the force of infection 11, which

it would then be possible to decompose into different

points of extensions α

gen

, it

gen

and τ

gen

Thus, the results of this incorporation of R

into

the SIR compartmental framework would give (14) :







′

= −R

′

= R

SI − γI

′

= γI

(14)

(Miller et al., 2012) gave the following formulation in

the case of the EBCM conﬁguration model :

(β + γ)

⟨k

− k⟩

⟨k⟩

(15)

From (14), the force of infection of the EBCM ap-

proximation is given by the relation

λ = R

I =

(β + γ)

⟨k

− k⟩

⟨k⟩

I (16)

Thus from the relation 11 the identiﬁcation of the ex-

tension points allows us to obtain :











gen

⟨k

− k⟩

⟨k⟩

gen

= I

gen

(β + γ)

(17)

In the relationship 17, the term α

gen

⟨k

− k⟩

⟨k⟩

is ob-

tained from the python code of the EoN module

for

This parameter was an approximation of the different

contact networks considered.

https://epidemicsonnetworks.readthedocs.io/en/latest/

GettingStarted.html

Separation of Concerns in an Edge-Based Compartmental Modeling Framework

265

each degree distribution (Homogeneous, Poisson, Bi-

modal and PowerLaw) speciﬁed for the graph gen-

eration. For example, the code to obtain α

gen

from

the conﬁguration model generated from a Bimodal

degree distribution

. We proceed in a similar way

for distributions of degree Homogeneous

and Power-

Law degree distribution

, but for the particular case

of the Poisson degree distribution, ⟨k

− k⟩ = ⟨k⟩

(Miller et al., 2012) thus, α

gen

⟨k

− k⟩

⟨k⟩

⟨k⟩ .

4 VALIDATION AND

DISCUSSION

To validate our approach, we replicated the EBCM

conﬁguration model experiments of (Miller et al.,

2012) using the approximation of the EBCM conﬁg-

uration model on the distributions

(Homogeneous,

Poisson, Bimodal, and PowerLaw) in Kendrick (Bui

et al., 2019; Fodjo et al., 2022). In our implementa-

tions, the variable points of the λ parameter of (11) are

named ”alphagen”, ”itgen” and ”taugen”. The models

are built in different entities that are easy to deﬁne in

modules, extensible and reusable. Indeed, each model

generally includes an entity of deﬁnition of the con-

cerns then of composition of model (see Figure 6),

an entity of initialization of parameters (see Figure 7)

and ﬁnally an entity of simulation (lines 36 to 41) and

visualization (lines 43 to 49) (see Figure 8).

The challenge was to check if Kendrick’s ap-

proach to separation of concerns could capture ap-

proaches such as Miller et al.’s mass action model or

the approximation of the EBCM conﬁguration model

while maintaining the familiar compartmental frame-

work.

The implementation of the mass action model (see

(2)) allowed us to obtain the black curve of Figure 9.

For this implementation, the code is subdivided into

two major parts. The ﬁrst one is the deﬁnition of the

basic concern SIR (Susceptible, Infected and Recov-

https://github.com/YvanGuifo/EBCM-

ConﬁgurationModel/blob/main/generate heterogeneity CM

Bimodal.py

https://github.com/YvanGuifo/EBCM-

ConﬁgurationModel/blob/main/generate heterogeneity CM

Homogeneous.py

https://github.com/YvanGuifo/EBCM-

ConﬁgurationModel/blob/main/generate heterogeneity CM

PowerLaw.py

The Python and Kendrick code of our experi-

ments is available under https://github.com/YvanGuifo/

EBCM-ConﬁgurationModel

Figure 3: Deﬁnition of the classical concern SIR where λ

and the extension points are deﬁned in lines 9 to 10.

Figure 4: Deﬁnition of the concern of mass action in lines

16 to 22. Then composition of the classic concern and the

mass action concern in line 24.

Figure 5: Composition of the basic SIR concern and the

approximation concern of the EBCM conﬁguration model

on a Bimodal degree distribution.

Figure 6: Deﬁnition of the concern of the approximation of

the EBCM conﬁguration model on a Bimodal degree distri-

bution.

ered) where λ is deﬁned (see Figure 3). In this imple-

mentation, λ is deﬁned in a general way (see lines 9 to

10). The second part of the code, is the implementa-

tion of the mass action concern named here ”maCon-

cern” as shown in Figure 4. In this deﬁnition, lines

16 to 22 allow to redeﬁne the extension points ”al-

phagen”, ”itgen” and ”taugen”. Then in line 24 we

compose the basic concern and the mass action con-

cern.

As for the implementation of the approximation

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

266

of the EBCM conﬁguration model in Kendrick, we

proceed in a similar way to the mass action model.

But in the case of this model (see Figure 6), the ex-

tension point ”alphagen” is obtained according to the

speciﬁed degree distribution. In the case of the Bi-

modal degree distribution for example, the value of

”alphagen” is given in line (17 to 18) of Figure 6.

Note that in our implementations, for approximation

of the EBCM conﬁguration model what varies from

one degree distribution to another is the value of ”al-

phagen”. After having deﬁned the concerns of the ba-

sic SIR model (see Figure 3) and the approximation

of the EBCM conﬁguration model (see Figure 6), we

compose the different concerns as illustrated in Fig-

ure 5. The results obtained enable us to have in Fig-

ure 9 the curves of the various distributions of degrees

of the model of conﬁguration EBCM implemented in

Kendrick.

It can be seen that, whether it is the mass action

model of Miller et al.’s. or the approximation of the

EBCM conﬁguration model, Kendrick’s approach al-

lows us to easily deﬁne the concerns (”maConcern”

and ”cmBimodal” in the case of the approximation

of the EBCM conﬁguration model on a Bimodal de-

gree distribution) in a way that is separate from the

basic SIR concern ”sirConcern”. Therefore, the basic

concern ”sirConcern” can be reused without ”maCon-

cern” or ”cmBimodal”. Kendrick’s approach enabled

us to deﬁne ”myConcern” and ”cmBimodal” as inde-

pendent models that can then be composed.

Regarding the results obtained while implement-

ing the EBCM conﬁguration model on the Power-

law degree distributions (see orange curves of Fig-

ures 9 and 9), the same dynamics are observed but

with a difference regarding the infectious. This can

be explained by the fact that some individuals (super-

spreaders) have an abnormally high number of con-

tacts at the beginning of the epidemic. We often note a

strong propensity of individuals to attach themselves

preferentially to the individual with more contacts in

this type of network. We also note that the moment of

the epidemic peak is reached at the same time.

EBCM conﬁguration model simulations on homo-

geneous, Poisson, and bimodal degree distributions

using our EBCM model approximation approach (see

Figure 9) yield improved curve heights (lower curves)

compared to a typical conﬁguration model approach

on homogeneous, Poisson, and bimodal degree distri-

butions simulated with EoN (see Figure 9). Further-

more, we note that the curves of Figure 9 have the

same dynamics as those seen in Figure 9 and signif-

icantly improve the predictive quality that one would

expect from a mass action model (black curve). We

also note that the timing of the epidemic peak of the

Figure 7: Initialization of simulation parameters.

Figure 8: Simulation and visualization of the conﬁguration

model.

homogeneous, Poisson and bimodal curves in Figure

9 is slightly slower compared to the respective homo-

geneous, Poisson, and bimodal curves in Figure 9.

Our approach to approximating EBCM models

can be applied to mean ﬁeld social heterogeneity

(MFSH) algorithms

and a ﬁxed-degree dynamic

model (DFD)

(Miller et al., 2012; Istvan et al.,

2019).

5 CONCLUSION

In this paper, we proposed to generalize Kendrick’s

approach to the consideration of realistic contact

structures from the edge-based compartmental mod-

eling (EBCM) framework while preserving the sepa-

ration of concerns in compartmental epidemic models

(Bui et al., 2016). To do this, we applied the solution

of (Fodjo et al., 2022) which involved deﬁning the

usual λ parameter of epidemic models as a kind of

model method with three extension points, which al-

lowed us to easily capture aspects of contact network

models.

It’s model where contact rates in the population are as-

signed using a P(k) or ρ(k) distribution, while considering

that the contact duration is negligible.

It’s model in which each node in the dynamic network

has a constant-valued degreed, assigned using the P(k) dis-

tribution.

Separation of Concerns in an Edge-Based Compartmental Modeling Framework

267

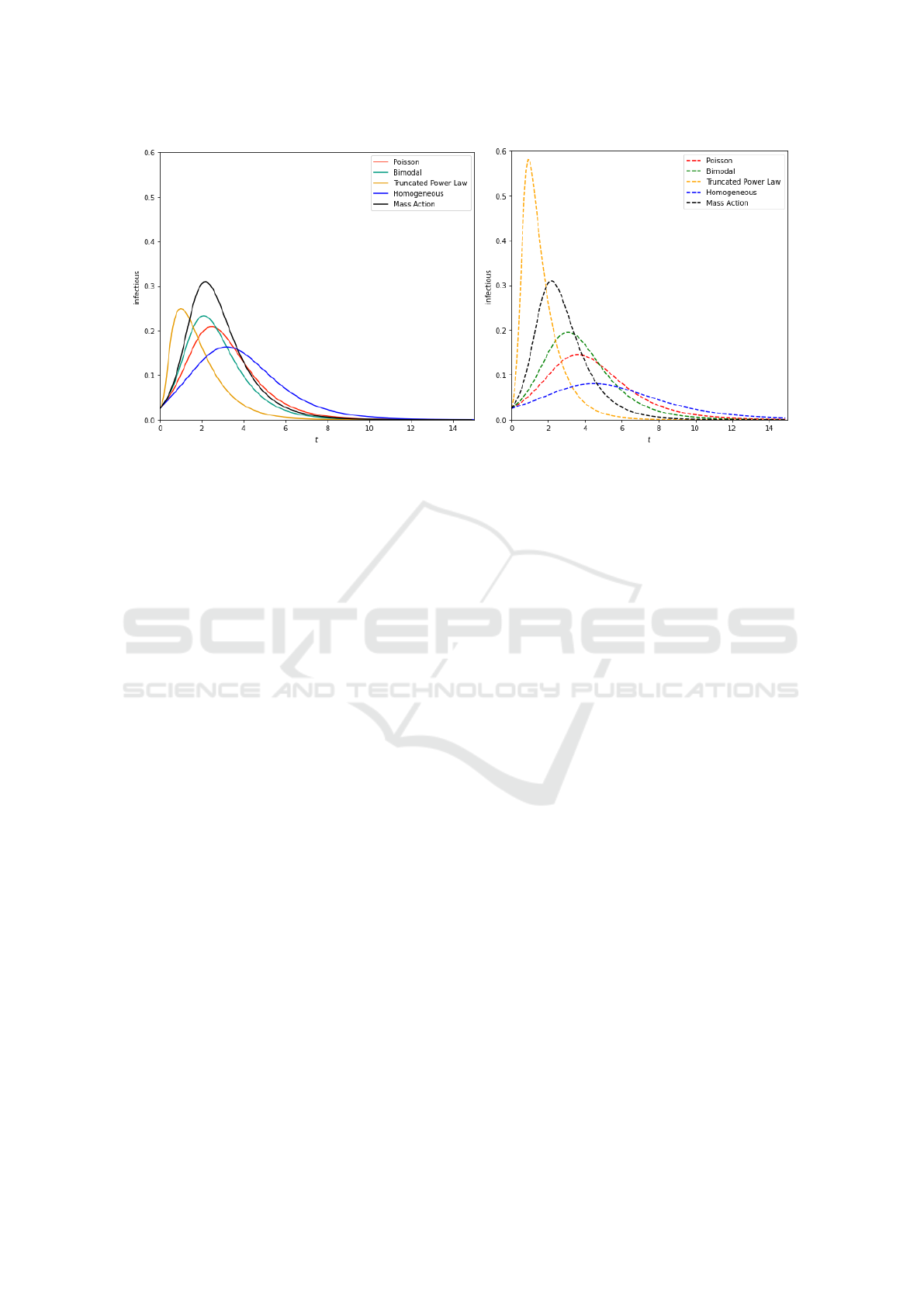
(a) EoN simulations. (b) Kendrick simulations.

Figure 9: EoN and Kendrick simulations of the mass action model (black curve) and the EBCM conﬁguration model on four

different degree distributions : Homogeneous (blue curve), Poisson (red curve), Bimodal (green curve) and Truncated Power

Law (orange curve). Each contact network has 500,000 nodes and an average degree of 5. The Poisson degree distribution

has an average of 5, half of the nodes have a degree of 2 and the other half a degree of 8 for the bimodal distribution, and

ﬁnally a truncated Powerlaw distribution in which P(k) ∝ k

−v

−k/40

where v = 1.418.

In order to validate this integration, we applied the

approach of (Fodjo et al., 2022) to the mass action and

the approximation of the EBCM conﬁguration model

of (Miller et al., 2012) and we were able to obtain

similar results close to those of (Miller et al., 2012).

Both models (mass action model and the approxima-

tion of the EBCM conﬁguration model) were deﬁned

as a very simple and distinct concern of the basic SIR

model in Kendrick.

If it is obvious that we were able to obtain simi-

lar results from the EBCM conﬁguration model from

the approximation of the EBCM conﬁguration model

in Kendrick, it is still a bit limiting. This is because

it requires to have beforehand a mathematical formu-

lation of R

of each EBCM model that we wish to

implement as a concern in the Kendrick sense and to

be able to ﬁnd the appropriate decomposition of the

extension points of the relation 11. However, the ap-

proach we propose avoids having to build an explicit

contact network, and moreover we do not have to de-

ﬁne a multitude of differential equations. Another en-

couraging aspect is the fact that most of the EBCM

models proposed in the literature have a mathemati-

cal formulation of R

, which gives us a wide range of

models to explore for future work. In the same way,

we also think that in the future, it would be interesting

to be able to implement typical EBCM models (with-

out model approximation approach) as concerns that

could be composed when adding new concerns.

REFERENCES

Aparicio, J. P. and Pascual, M. (2007). Building epidemio-

logical models from r0: an implicit treatment of trans-

mission in networks. Proceedings of the Royal Society

B: Biological Sciences, 274(1609):505–512.

Balde, C., Lam, M., and Bowong, S. (2019). Contact vacci-

nation study using edge based compartmental model

(ebcm) and stochastic simulation: An application to

oral poliovirus vaccine (opv). In International Sym-

posium on Mathematical and Computational Biology,

pages 81–96. Springer.

Bansal, S., Grenfell, B. T., and Meyers, L. A. (2007). When

individual behaviour matters: homogeneous and net-

work models in epidemiology. Journal of the Royal

Society Interface, 4(16):879–891.

Bui, T., Papoulias, N., Stinckwich, S., Ziane, M., and

Roche, B. (2019). The Kendrick modelling platform:

language abstractions and tools for epidemiology [+

correction art. no 439, 1 p.]. BMC Bioinformatics, 20.

Bui, T. M. A., Ziane, M., Stinckwich, S., Ho, T. V., Roche,

B., and Papoulias, N. (2016). Separation of concerns

in epidemiological modelling. In Companion pro-

ceedings of the 15th international conference on mod-

ularity, pages 196–200.

Cuddington, K. and Beisner, B. E. (2005). Ecological

paradigms lost: routes of theory change. Elsevier

Academic Press New York.

Danon, L., Ford, A. P., House, T., Jewell, C. P., Keeling,

M. J., Roberts, G. O., Ross, J. V., and Vernon, M. C.

(2011). Networks and the epidemiology of infectious

disease. Interdisciplinary perspectives on infectious

diseases, 2011.

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

268

Fodjo, A. Y. G., Ziane, M., Stinckwich, S., Anh, B. T. M.,

and Bowong, S. (2022). Separation of concerns in

extended epidemiological compartmental models. In

Proceedings of the 15th International Joint Confer-

ence on Biomedical Engineering Systems and Tech-

nologies - Volume 3: BIOINFORMATICS,, pages

152–159. INSTICC, SciTePress.

Gamma, E., Helm, R., Johnson, R., Vlissides, J., and Pat-

terns, D. (1995). Elements of reusable object-oriented

software, volume 99. Addison-Wesley Reading, Mas-

sachusetts.

Heesterbeek, H., Anderson, R. M., Andreasen, V., Bansal,

S., De Angelis, D., Dye, C., Eames, K. T., Edmunds,

W. J., Frost, S. D., Funk, S., et al. (2015). Modeling

infectious disease dynamics in the complex landscape

of global health. Science, 347(6227):aaa4339.

Istvan, Z., Miller, K., Joel, C. S., and Peter, L. (2019). Math-

ematics of Epidemics on Networks: From Exact to Ap-

proximate Models. Springer.

Keeling, M. J. and Rohani, P. (2011). Modeling infectious

diseases in humans and animals. Princeton university

press.

Kermark, M. and Mckendrick, A. (1927). Contributions to

the mathematical theory of epidemics. part i. Proc. r.

soc. a, 115(5):700–721.

Kiss, I. Z., Miller, J. C., Simon, P. L., et al. (2017). Math-

ematics of epidemics on networks. Cham: Springer,

598.

Levin, S. A. and Durrett, R. (1996). From individu-

als to epidemics. Philosophical Transactions of the

Royal Society of London. Series B: Biological Sci-

ences, 351(1347):1615–1621.

Martcheva, M. (2015). An introduction to mathematical epi-

demiology, volume 61. Springer.

Meyers, L. A., Pourbohloul, B., Newman, M. E., Skowron-

ski, D. M., and Brunham, R. C. (2005). Network the-

ory and sars: predicting outbreak diversity. Journal of

theoretical biology, 232(1):71–81.

Miller, J. C., Slim, A. C., and Volz, E. M. (2012). Edge-

based compartmental modelling for infectious dis-

ease spread. Journal of the Royal Society Interface,

9(70):890–906.

Molina, C. and Stone, L. (2012). Modelling the spread of

diseases in clustered networks. Journal of theoretical

biology, 315:110–118.

Plateau, B. and Stewart, W. J. (2000). Stochastic automata

networks. In Computational Probability, pages 113–

151. Springer.

Trapman, P., Ball, F., Dhersin, J.-S., Tran, V. C., Wallinga,

J., and Britton, T. (2016). Inferring r 0 in emerging

epidemics—the effect of common population struc-

ture is small. Journal of The Royal Society Interface,

13(121):20160288.

Wang, Y., Cao, J., Li, X., and Alsaedi, A. (2018). Edge-

based epidemic dynamics with multiple routes of

transmission on random networks. Nonlinear Dynam-

ics, 91(1):403–420.

Yang, J. and Xu, F. (2019). The computational approach for

the basic reproduction number of epidemic models on

complex networks. IEEE Access, 7:26474–26479.

Zhang, Z., Wang, H., Wang, C., and Fang, H. (2015). Mod-

eling epidemics spreading on social contact networks.

IEEE transactions on emerging topics in computing,

3(3):410–419.

Separation of Concerns in an Edge-Based Compartmental Modeling Framework

269