Intrinsic-Dimension Analysis for Guiding Dimensionality Reduction in

Multi-Omics Data

Valentina Guarino

, Jessica Gliozzo

1,2

, Ferdinando Clarelli

, B

eatrice Pignolet

4,5

, Kaalindi Misra

Elisabetta Mascia

, Giordano Antonino

3,6

, Silvia Santoro

, Laura Ferr

3,6

, Miryam Cannizzaro

3,6

Melissa Sorosina

, Roland Liblau

, Massimo Filippi

6,7,8,9

, Ettore Mosca

, Federica Esposito

3,6

Giorgio Valentini

1,11

and Elena Casiraghi

1,11,12

AnacletoLab - Computer Science Department, Universit

a degli Studi di Milano, Via Celoria 18, 20135, Milan, Italy

European Commission, Joint Research Centre (JRC), Ispra, Italy

Laboratory of Neurological Complex Disorders, Division of Neuroscience, Institute of Experimental Neurology (INSPE),

IRCCS San Raffaele Scientiﬁc Institute, 20132 Milan, Italy

CRC-SEP, Neurosciences Department, CHU Toulouse, France

Inﬁnity, CNRS, INSERM, Toulouse University, UPS, Toulouse, France

Neurology and Neurorehabilitation Unit, IRCCS San Raffaele Scientiﬁc Institute, 20132 Milan, Italy

Vita-Salute San Raffaele University, 20132 Milan, Italy

Neurophysiology Unit, IRCCS San Raffaele Scientiﬁc Institute, 20132 Milan, Italy

Neuroimaging Research Unit, Division of Neuroscience, Institute of Experimental Neurology (INSPE), IRCCS San

Raffaele Scientiﬁc Institute, 20132 Milan, Italy

Institute of Biomedical Technologies, National Research Council, Segrate (Milan), Italy

CINI, Infolife National Laboratory, Roma, Italy

Environmental Genomics and Systems Biology Division, Lawrence Berkeley National Laboratory, Berkeley, CA, U.S.A.

Keywords:

Dimensionality Reduction, Intrinsic Dimensionality, Feature Selection, Feature Clustering, Omics Datasets.

Abstract:

Multi-omics data are of paramount importance in biomedicine, providing a comprehensive view of processes

underlying disease. They are characterized by high dimensions and are hence affected by the so-called ”curse

of dimensionality”, ultimately leading to unreliable estimates. This calls for effective Dimensionality Reduc-

tion (DR) techniques to embed the high-dimensional data into a lower-dimensional space. Though effective

DR methods have been proposed so far, given the high dimension of the initial dataset unsupervised Feature

Selection (FS) techniques are often needed prior to their application. Unfortunately, both unsupervised FS

and DR techniques require the dimension of the lower dimensional space to be provided. This is a crucial

choice, for which a well-accepted solution has not been deﬁned yet. The Intrinsic Dimension (ID) of a dataset

is deﬁned as the minimum number of dimensions that allow representing the data without information loss.

Therefore, the ID of a dataset is related to its informativeness and complexity. In this paper, after proposing a

blocking ID estimation to leverage state-of-the-art (SOTA) ID estimate methods we present our DR pipeline,

whose subsequent FS and DR steps are guided by the ID estimate.

1 INTRODUCTION

Many human diseases arise from the interplay of vari-

ations in multiple genes and environmental factors.

While disease diagnosis can be performed based on

similarities of symptoms, disease subtype identiﬁca-

tion based on biomolecular proﬁles can lead to deeper

understanding of underlying disease mechanisms, di-

agnosis/prognosis, and to personalized treatments (as

aimed by Precision Medicine). In this context, the ad-

vent of high-throughput techniques recently allowed

acquiring unprecedented amounts of multi-omics data

that, when opportunely integrated, may provide a

comprehensive description of genetic, biochemical,

metabolic, proteomic, and epigenetic processes un-

derlying a disease (Nicora et al., 2020).

The past decade has experienced an increasing in-

terest in the development of multi-view integration

methods integrating datasets as complex as multi-

omics ones, and some effective approaches have been

proposed (Meng et al., 2016; Gliozzo et al., 2022).

Nevertheless, most of them cannot handle the di-

Guarino, V., Gliozzo, J., Clarelli, F., Pignolet, B., Misra, K., Mascia, E., Antonino, G., Santoro, S., Ferré, L., Cannizzaro, M., Sorosina, M., Liblau, R., Filippi, M., Mosca, E., Esposito, F.,

Valentini, G. and Casiraghi, E.

Intrinsic-Dimension Analysis for Guiding Dimensionality Reduction in Multi-Omics Data.

DOI: 10.5220/0011775200003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 3: BIOINFORMATICS, pages 243-251

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

243

mension of the considered views, which is often

much larger than the available sample size (small-

sample-size problem). This results in largely sparse

datasets, where the “curse of dimensionality” (Trunk,

1979; Lv, 2013; Hughes, 1968) causes unreliable es-

timates of pairwise-distances (Franc¸ois et al., 2007;

odergren, 2011; Ceruti et al., 2014). In this context,

the samples are assumed to be drawn from an original

lower-dimensional manifold that has been twisted and

curved by a smooth mapping bringing to the observed

high-dimensional space. Hence, the true information

can be outlined by many fewer coordinates than those

of the high-dimensional space. Under this assump-

tion, DR techniques have become essential in the

bioinformatics ﬁeld, and several (linear/non-linear)

methods have been proposed in literature (Nanga

et al., 2021) to embed the data into a space where re-

dundancy and noise are removed while salient infor-

mation is emphasized (Erichson et al., 2016; Halko

et al., 2011), or the local and global topological struc-

ture of the dataset is preserved (Van der Maaten and

Hinton, 2008; McInnes et al., 2018). Most DR

techniques showed impressive results but they often

base their analysis on pairwise-point relationships,

which are biased when incurring small-sample-size

and curse of dimension. An unsupervised FS step is

therefore required prior to their application (Solorio-

Fern

andez et al., 2020) to obtain a more tractable (re-

duced) space. However, both FS and DR techniques

need the dimension of the lower-dimensional space as

input. This value should be carefully chosen (Nguyen

and Holmes, 2019); excessively large values would

bring to the computation of still sparse, noisy, and re-

dundant datasets, while excessively low values would

cause the loss of salient information. Such a choice is

still an open problem.

The ID of a dataset is deﬁned as the minimum

number of dimensions needed to represent the data

without information loss (Ceruti et al., 2014; Facco

et al., 2017). We propose an FS and DR approach

that exploits a novel and robust estimate of the dataset

ID as a crucial description of the dataset informative-

ness, which should be maintained and targeted by the

proposed pipeline. We use our approach to reduce

the dimension of each view in a multi-omics dataset.

However, the generality of the method allows its ap-

plication to any type of data.

2 MULTIPLE SCLEROSIS

DATASET

Multiple Sclerosis (MS) is a chronic disease of the

Central Nervous System, characterized by inﬂamma-

tion, demyelination and axonal loss. It currently

affects more than 2.8 million people globally, be-

ing the most common cause of non-traumatic neu-

rologic disability in young adults. MS is an highly

heterogeneous disease in terms of clinical presen-

tation and treatment response and its precise aeti-

ology is unknown, although it is widely accepted

that it implicates an interplay between genetic, en-

vironmental, and lifestyle factors. With the advent

of high throughput assays, an important contribu-

tion can be derived from their integration to iden-

tify (through unsupervised clustering) disease sub-

phenotypes, which would be an important step to-

wards stratiﬁed medicine. To obtain reliable in-

tegrative unsupervised clustering results from high-

dimensional multi-omics views, a well-designed prior

step of DR is needed.

We tested our ID-based DR method on both

miRNA and mRNA data of a private multi-omics

dataset describing the genome proﬁle of MS pa-

tients, which were sampled before the start of a

ﬁrst-line treatment, with further exclusion of those

who had been treated with highly-active immunosup-

pressive or second-line drugs. These criteria were

adopted in order to minimize the impact of drugs on

-omics values. The transcriptome was generated us-

ing the Truseq stranded mRNA kit and sequenced on

the Illumina HiSeq4000, whereas miRNA libraries

were generated using SMARTer smRNA kit Sequenc-

ing on Illumina NOVAseq6000. Both assays were

performed on peripheral mononuclear blood cells

(PBMC). Quality control, normalization and ﬁltering

for the two -omics was performed in order to mini-

mize possible technical artifacts and to discard fea-

tures deemed as not expressed, yielding D = 502 and

D = 20745 features for miRNA and mRNA, respec-

tively. Overall, for 170 patients both miRNA and tran-

scriptomics values were available.

3 METHODS

Our ID-based DR method processes each view of the

MS dataset by applying four consecutive steps (Fig-

ure 1). After each step, we monitor the ID to un-

derstand whether important information has been re-

moved.

1. Min-max Normalization Step followed by

Global ID estimation (Sections 3.1.1 and 3.1.2)

to obtain a ﬁrst estimate of the dataset informa-

tiveness. Though the ID estimated at this step

is most probably affected by the curse of dimen-

sionality, it can be used as an input parameter for

computing the blocking-ID estimate we propose

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

244

in this paper.

2. High Pairwise-correlation Filtering to remove

redundancy. Pairs of features showing a high pair-

wise correlation (i.e. Spearman correlation > 0.8)

are ﬁltered to remove the feature having the higher

mean correlation with all the other features in the

dataset

. The parallel algorithm we implemented

to perform this task is outlined in Appendix A.

3. Blocking ID Estimation (Section 3.1.3). This

estimation approach is inspired by the blocking

analysis applied in (Facco et al., 2017) to com-

pute an ID estimate less affected by noise in the

data samples. In this paper, we revisit it in order

to provide an ID estimate (hereafter referred to as

blocking-ID) robust with respect to the curse of

dimensionality (affecting datasets characterized

by an extremely large dimensionality compared to

the limited sample cardinality). Furthermore, we

use it to identify the minimum number of features,

C , that should be kept by the next unsupervised

FS approach (Step 4 below) to ensure that, with

a certain degree of conﬁdence, most of the salient

information is kept, while noise and redundancies

are minimized.

4. Unsupervised FS via Hierarchical Clustering

(Solorio-Fern

andez et al., 2020; Gagolewski,

2021) to select C features that are the medoids of

the corresponding C feature clusters (Section 3.2

and Appendix B).

5. Blocking ID Estimation in order to monitor po-

tential retained noise and information loss.

6. Dimensionality Reduction: The representative

feature set is ﬁnally embedded to a lower-

dimensional space, whose dimensionality is cho-

sen based on the blocking-ID estimate computed

in Step 3. To this aim, we compare four differ-

ent DR techniques (UMAP, t-SNE, RPCA and

RCUR) and choose the one that allows obtain-

ing a global ID estimate that is comparable to the

blocking-ID computed in Step 3.

3.1 ID Estimation

The ID (Johnsson, 2011; Campadelli et al., 2015)

of a dataset is the minimum number of parameters

Is worth mentioning that, from a biological perspec-

tive, the correlation between omics variables could often be

meaningful: for example, correlated variables in expression

data could relate to the same molecular pathway (Allocco

et al., 2004), and thus to coregulated genes. However, from

a statistical point of view, highly-correlated variables may

affect the reliability of estimates leading to inﬂated values.

Thus, their removal is often advisable.

needed to maintain its characterizing structure; in

other words, the ID is the minimum number of di-

mensions of a lower dimensional space where the

data can be projected (by a smooth mapping) in or-

der to minimize the information loss. When a dataset

= {x

}

i=1

⊂ R

has ID equal to d, the D- dimen-

sional samples are assumed to be uniformly drawn

from a manifold with topological dimension equal to

d, that has been embedded in a higher D-dimensional

space through a nonlinear smooth mapping. Unfor-

tunately, the estimation of the topological dimension

of a manifold using a limited set of points uniformly

drawn from it is a challenging, not yet solved task. All

the SOTA ID estimation techniques exploit differing

underlying theories, according to which they are of-

ten grouped into the following four main categories:

Projective ID estimators, Topological-based ID esti-

mators, Fractal ID estimators, and Nearest-Neighbors

(NN) based ID estimators.

In the bioinformatics ﬁeld, the available datasets

are often noisy and complex. In this context, Pro-

jective, Topological-based and Fractal ID estimators

are often outperformed by NN estimators; Fractal ID

estimators fail when the points are noisy and/or not

uniformly drawn from the underlying manifold, while

Projective and Topological-based ID estimators pro-

duce reliable estimates for data drawn from mani-

folds with mainly low curvature and low ID values.

On the other hand, NN estimators have shown their

robustness on not-uniformly drawn, noisy and com-

plex datasets, where the two main assumptions at the

base of Fractal, Topological-based, and Projective ID

estimators are often violated. Indeed, (1) the points

cannot be assumed to be uniformly drawn from the

manifold where they are assumed to lie, and (2) the

complexity of the available datasets allows assuming

that the points lie on more-than-one, eventually in-

tersecting manifolds, each characterized by a speciﬁc

topological dimension.

To account for the aforementioned issues, NN es-

timators often compute a reliable “global” ID estima-

tor by integrating all the “local” IDs estimated over

point-neighborhoods. Based on these remarks, in this

work we estimated the ID of the available multi-omics

views by comparing two NN ID estimators, namely

DANCo (see subsection 3.1.1) and TWO-NN (see

subsection 3.1.2).

3.1.1 DANCo

DANCo (Ceruti et al., 2014) estimates the (potentially

high) ID of a dataset by comparing the joint probabil-

ity density functions (pdfs) characterizing the point-

neighborhood distributions in the input dataset to a set

of pdfs, each characterizing the point-neighborhood

Intrinsic-Dimension Analysis for Guiding Dimensionality Reduction in Multi-Omics Data

245

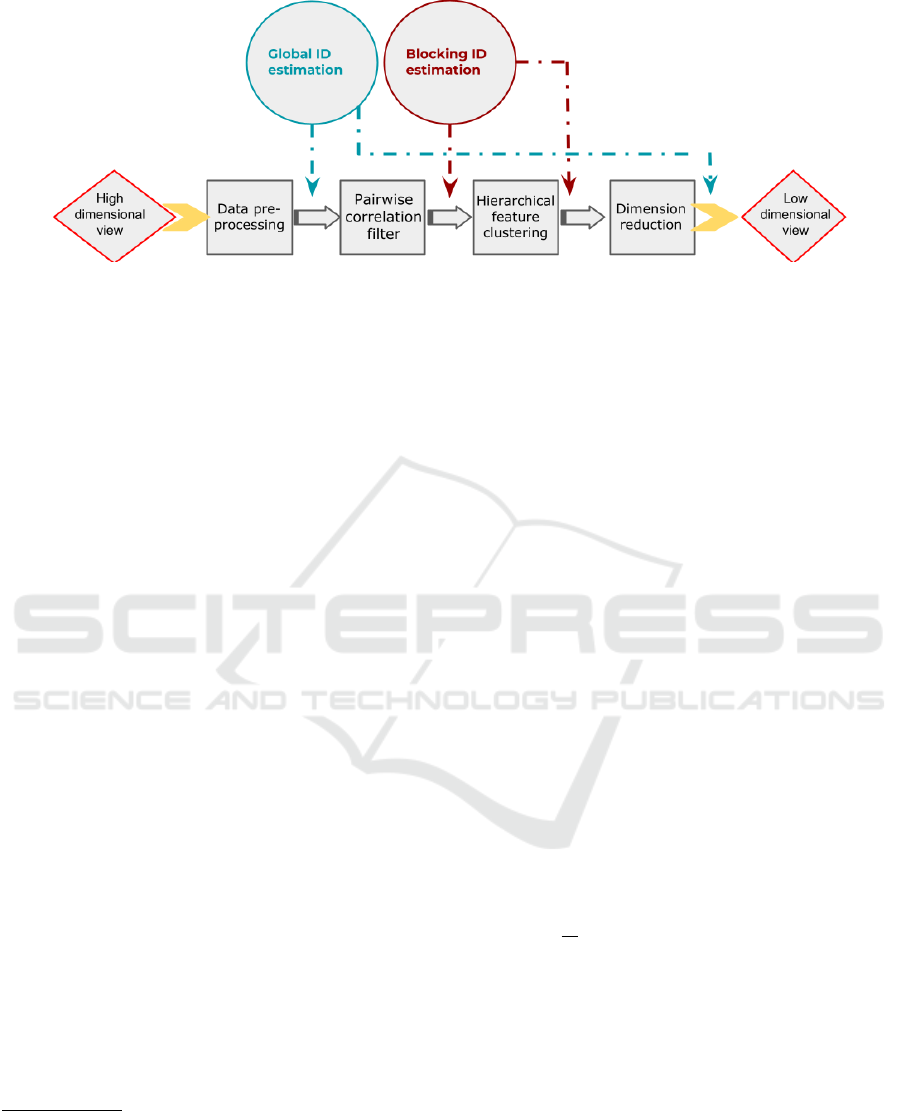
Figure 1: Workﬂow of our ID-based approach.

distribution in a synthetic dataset uniformly drawn

from a manifold of known (candidate) ID

. More pre-

cisely, the Kullback-Leibler (KL) divergence is used

to compare the pdf estimated on the input dataset to

each of the pdfs estimated on the synthetic datasets

and the input-dataset ID is estimated as the dimen-

sionality of the synthetic manifold minimizing the KL

divergence.

DANCo has proven its effectiveness when tested

both on synthetic and real, noisy datasets, composed

of points for which the assumption of uniform sam-

pling from the underlying manifold does not hold.

However, our preliminary tests performed to under-

stand its behaviour (when applied to both the available

views and in some views from the TCGA dataset

- data not shown due to shortage of space) clearly

showed its dependency from the size of the consid-

ered point-neighborhoods that are used to estimate

the joint pdfs (deﬁned by the number k of NNs to

be considered). More precisely, in order to pursue

the assumption of local uniformity of point distribu-

tions, k should not be too high (e.g. it could be set so

that the neighborhoods contain less than the 1/10 of

the sample-cardinality). However, choosing a ﬁxed k

value for different views may lead to unreliable esti-

mates. Indeed, on less sparse, “twisted”, and curved

datasets, (i.e. less affected by small-sample-sizes as in

the available miRNA data - Figure 2 -left) the ID esti-

mate increases together with k. On the other side, on

more sparse datasets (cursed by high-dimensions and

small-sample-sizes, as in the available mRNA data

- Figure 2 -right) a low neighborhood size (k = 6)

produces a peak in the ID estimate, after which we

note a drop. This may be due to the fact that, being

The joint pdf characterizing the distribution of neigh-

borhoods in a given dataset is the product of two indepen-

dent (parameterized) terms namely g(r; k, d) and q(θ; ν,τ)

that characterize, respectively, the normalized NN distance

distribution and the pairwise-angle distribution.

https://www.cancer.gov/about-nci/organization/ccg/

research/structural-genomics/tcga

the dataset more twisted and curved, local uniformity

(and consequent reliable estimates) may be assumed

only when considering small neighborhoods.

The strong dependency of DANCo estimates from

the k parameter requires choosing its value by a care-

ful and objective analysis of each individual view of

a multi-omics dataset. To automatize this choice we

propose selecting the value of k that minimizes the

distance between the DANCo and the ID estimate ob-

tained by the following TWO-NN estimator.

3.1.2 TWO-NN

TWO-NN (Facco et al., 2017) is a NN ID estimator

that has been developed by considering that several

SOTA ID estimators compute estimates that are either

inﬂuenced by the cardinality of the considered point

neighborhoods, or are not robust with respect to not-

uniformly distributed point-neighborhoods, which is

often the case of real-world bioinformatics datasets.

To tackle the aforementioned problems, the authors

proposed theories that highlight how, assuming local

uniformity across 2-NN neighborhoods, the volume

of the shell between the ﬁrst and the second NNs of

each point in a manifold is dependent on the (local)

manifold ID. This ultimately brings to a Pareto law

relationship linking the (true) manifold ID, d, and the

ratio, µ

of the distances between the i−th point

and its second and the ﬁrst NN: L (µ

;d) = dµ

(d−1)

Based on this relationship an ID estimate,

d, can be

derived by ﬁtting the empirical cumulative distribu-

tion of the µ

s through a maximum likelihood estima-

tor.

Note that the TWO-NN formulation requires as-

suming a uniform distribution only across 2-NN

neighborhoods, and it should be therefore less af-

fected by more twisted and curved datasets. When

compared to DANCo (Figure 2), the TWO-NN esti-

mator has a lower variance of the estimates; however,

DANCo has proven to be more robust than TWO-

NN in the presence of boundary points (Facco et al.,

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

246

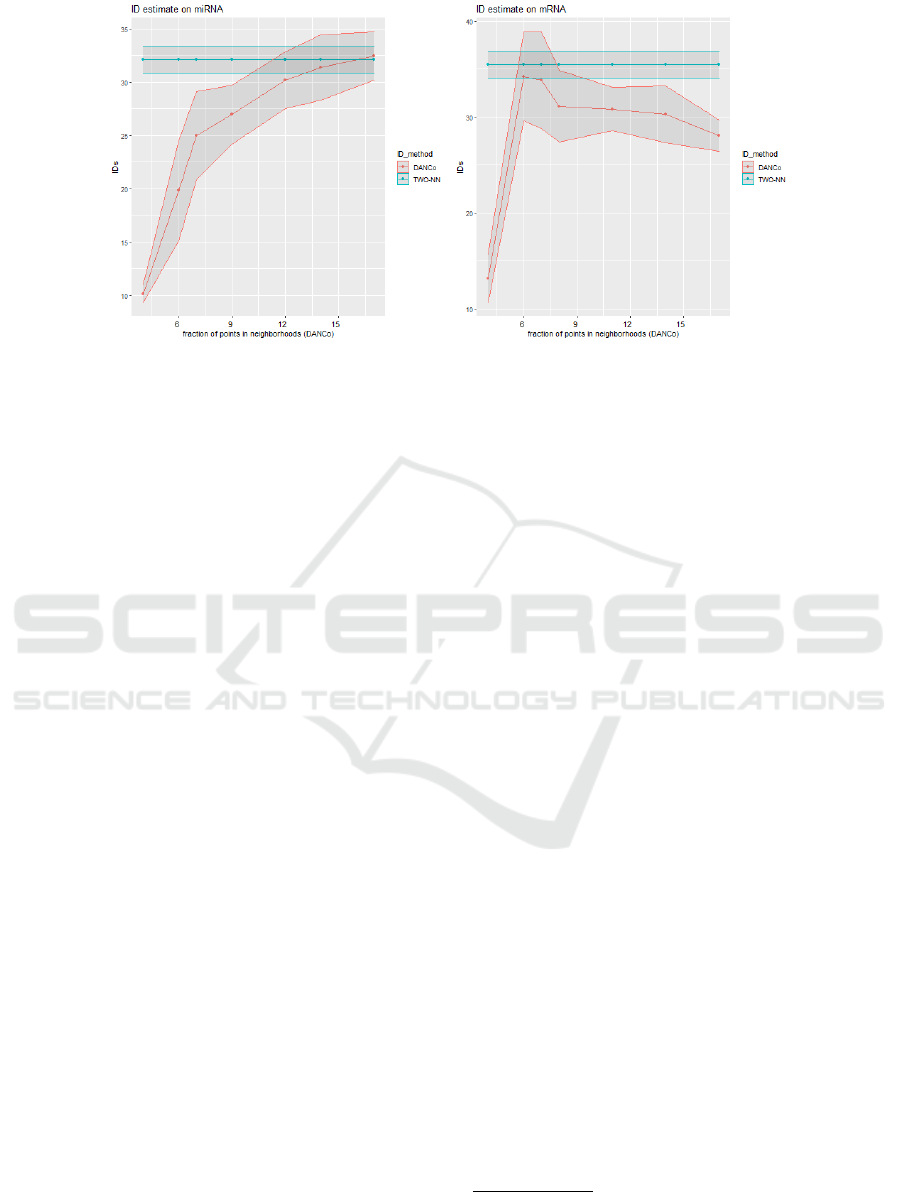
Figure 2: Comparison among IDs computed by DANCo estimator and the TWO-NN estimator. Shaded areas mark the

standard deviation of the ID estimates computed by the two methods. On the miRNA view (left) the chosen neighborhood

size for DANCo is k = 14. On mRNA the chosen neighborhood size for DANCo is k = 6.

2017), often characterizing datasets where the imbal-

ance between dimension and sample cardinality is ex-

tremely large. Considering also the previously docu-

mented (Campadelli et al., 2015) robustness and accu-

racy of DANCo, we chose it for the evaluation of the

ID. However, given the appealing properties of TWO-

NN estimator, we considered it a valid aid to auto-

matically set the best neighborhood size k to be con-

sidered when using the DANCo estimator. In detail,

among all the neighborhood sizes that contain less

than 1/10 of the cases, we choose the value minimiz-

ing the distance between the DANCo and the TWO-

NN estimates.

3.1.3 Blocking-ID Estimate

The dimension of the lower dimensional space where

the data should be projected to avoid the curse of

dimensionality should be deﬁned based on the esti-

mated dataset ID. However, as highlighted also in the

previous sections, several ID estimators produce un-

stable global estimates on sparse and noisy datasets

affected by the curse of dimensionality (Ceruti et al.,

2014; Campadelli et al., 2015; Facco et al., 2017).

This is particularly true for NN estimators, which of-

ten suffer from high variance or overestimation when,

e.g., the considered neighborhood size increases. Fur-

thermore, since all the ID estimators contain some

randomness, most of them suffer from an added fac-

tor of variance, particularly evident when working in

high dimensions.

To account for such variance and obtain more re-

liable estimates a classical blocking method may be

used (Facco et al., 2017). Under the ID estimation set-

ting, the blocking can be applied feature-wise by: (1)

considering randomly sampled feature sets (blocks)

of increasing size; (2) estimating the ID on each

block, and (3) estimating a global blocking-ID (and

its standard deviation) as the mean (and total standard

deviation) of all the block IDs (and their standard de-

viations). In more detail, to compute the blocking-ID

we ﬁrst deﬁne the dimension of the smallest block as

L(0) =

d ∗ 2, being

d the DANCo ID estimate com-

puted on the input dataset. Though we are aware that

the ﬁrst ID estimate might be biased, it can be a valid

aid to guarantee that also smaller blocks can contain

enough information. Next, we iterate over the block

dimensions and, at the j

iteration, we increase the

considered block dimension to L( j) = L(0) ∗ j and

we estimate a mean ID (and its standard deviation)

for blocks composed of L( j) features by the follow-

ing steps:

1. compose n

try

(random) blocks, each with L( j)

randomly drawn features;

2. estimate the DANCo ID of each random block;

3. compute the mean and the (within) standard devi-

ation of the obtained estimates, which essentially

provide an estimate of the ID that would be ob-

tained if the data was represented by L( j) ran-

domly selected features

We keep increasing the block dimension and es-

timating each mean block-ID with its within-block

standard-devation for n

blocks

iterations, until the con-

sidered block includes the whole feature-set. An

unbiased blocking-ID for the whole dataset may be

then computed by averaging all the block-IDs com-

puted during each iteration, and by computing the to-

We set n

try

= 51 to reduce time costs of the algorithm;

however, the higher the value, the higher the precision of

the estimate.

Intrinsic-Dimension Analysis for Guiding Dimensionality Reduction in Multi-Omics Data

247

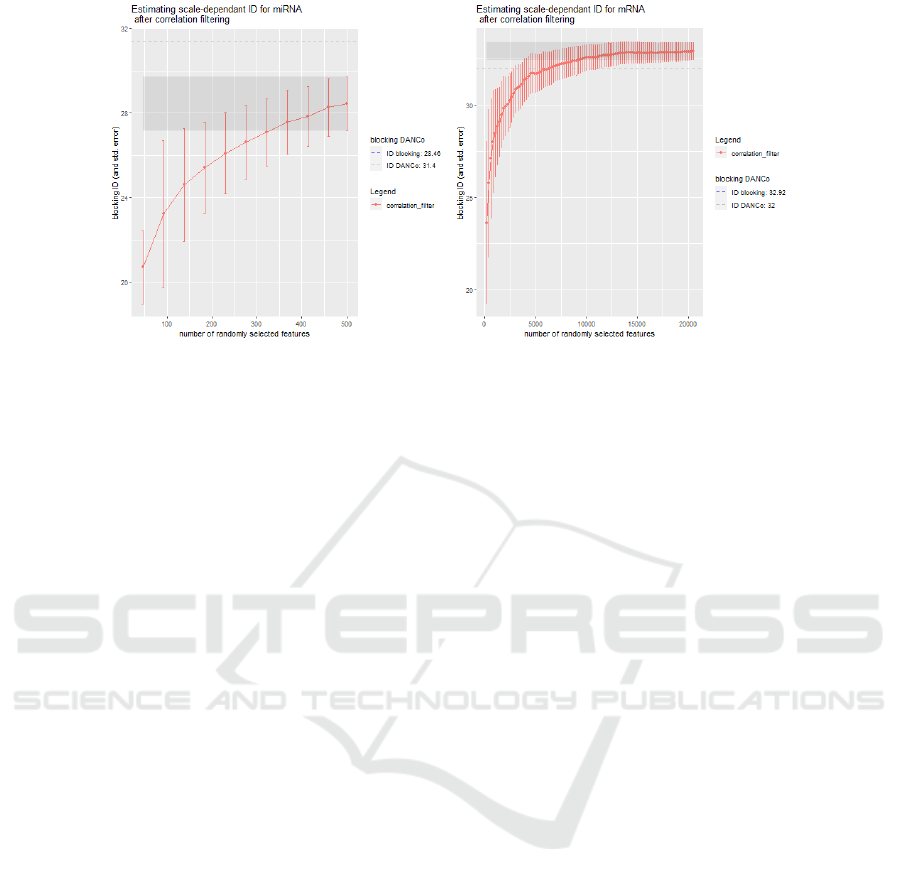
Figure 3: Cumulative mean and total standard deviation of the Block-IDs computed by using the DANCo estimator (left:

miRNA, right: mRNA view). The grey dashed line shows the initial global ID estimate computed by DANCo on the entire

dataset. The shaded area highlights the ID values that are one standard deviation away from the global blocking-ID (cor-

responding to the last point of the cumulative distribution). Observing the shaded area, we note that, for e.g. the miRNA

view, randomly selected feature-blocks with dimensions higher than ≈ 330 obtain ID estimates that are less than one standard

deviation away from the blocking ID estimate. The cumulative mean distribution on mRNA (and its total standard deviation)

conﬁrms that the data may be represented by a much smaller feature set (that the available one) without losing too much

information. Indeed, as we start from the smallest blocks (≈ 200 randomly selected features), the cumulative mean keeps

increasing until the block dimension becomes approximately equal to 9000. At this stage, the feature set contains enough

feature to properly represent the data-structure. Indeed, the block ID remains stable and the total standard deviation at each

point has a small reduction, suggesting that the addition of more features does not improve informativeness.

tal standard deviation to account for both the within

and the between-blocks variance. This value is es-

sentially representing the mean ID estimate (and its

ﬂuctuation) that would be obtained on a dataset com-

posed by randomly sampling a number of features

that is equal to (or lower than) the dimension of the

whole dataset. The idea behind the blocking method

is that, assuming that some features are mostly carry-

ing noise and/or redundant information, the random

under-sampling of features that is performed to com-

pose blocks with varied and increasing dimensions,

as well as the evaluation of the ID for different block

dimensions, is able to reduce (by averaging) biasing

effects due to noise and redundancy. Thus, instead of

limiting our analysis to the global blocking-ID esti-

mate, we compute the cumulative mean of the block-

IDs and the corresponding total standard deviation.

Figure 3 shows the distributions we obtained on the

miRNA and mRNA views in our dataset. The j

point in the plot shows the mean (and its total stan-

dard deviation) computed over all the blocks with di-

mension lower or equal to L( j). In practice, for each

block dimension, we obtain an estimate of the ID (and

its variability) that would be obtained if we randomly

selected blocks of dimension equal to L( j). Hence,

the comparison between the ﬁnal blocking-IDs (the

last point on the cumulative curve) and the cumula-

tive means computed for smaller blocks allows choos-

ing the number of features that should be (even ran-

domly) retained in order to obtain an ID estimate that

is no more than one standard deviation away from

the global blocking-ID estimated. In simpler words,

we automatically analyze the cumulative mean plot to

ﬁnd the number of features that sufﬁces to represent

the information in the dataset.

This dimension is used as the target dimension for

the FS step described in the following Section 3.2.

3.2 Hierarchical Feature Clustering

Though correlation ﬁltering removes redundancy in

the data, the number of retained features may be still

high, so that any (linear and non-linear) dimension-

ality reduction step would incur in the curse of di-

mensionality. To further reduce data dimensionality,

feature clustering can be an insightful step, which not

only allows exploring the relationships between fea-

tures, but also selects a lower dimensional subspace

composed of representative features that are either

cluster medoids or singletons (that is, features that

do not belong to any cluster). Feature clusters were

composed by an agglomerative hierarchical clustering

method (Cai et al., 2014) named Genie (Gagolewski,

2021). Genie guarantees robustness with respect to

noise and boundary points by computing pairwise-

points distances by the mutual reachability distance

(Campello et al., 2013). It applies a Single Link-

age (SL) criterion (Nielsen, 2016) to merge closer

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

248

clusters but provides a strategy to penalize the for-

mation of small clusters. Indeed, at each iteration of

the algorithm, the inequality between the cluster car-

dinalities is evaluated by the Gini index. If the in-

equality is above a certain threshold Genie starts fa-

voring the merge of the smallest clusters with their

NN clusters. In high dimension the computational

costs of Genie becomes impracticable; hence we im-

plemented a distributed-hierarchical algorithm (Ap-

pendix B) using Genie to extract a number of fea-

ture clusters (i.e. the dimension of the reduced space)

equal to the smaller block dimension whose block-

ID estimate is within one standard deviation from the

global block-ID.

3.3 Dimensionality Reduction

The lower-dimensional dataset can now be obtained

by embedding the dataset derived by feature cluster-

ing into a lower-dimensional space whose dimension

is set to be equal to 2· target ID, being target ID

the blocking-ID estimated by DANCo after correla-

tion ﬁltering. In bioinformatics, the method com-

monly used for DR is the Principal Component Anal-

ysis - PCA (Gerbrands, 1981), generally solved in

high-dimensional spaces by its approximated Singu-

lar Value Decomposition - SVD (Gerbrands, 1981).

Both PCA and SVD projections are often ineffec-

tive (Mahmud and Fu, 2019) due to their sensitivity

to noise and outliers. Moreover, the linear projec-

tion of PCA onto a space with dimension much lower

than (or equal to) the sample size causes loss of in-

formation. Finally, the computation of PCA/SVD on

massive datasets may be prohibitive. To avoid all the

aforementioned problems, randomized PCA (RPCA)

exploits the theories of randomness and probabilis-

tic matrix algorithms (Drineas and Mahoney, 2016;

Erichson et al., 2016) to derive a smaller space catch-

ing all the relevant information. Considering that

both PCA and RPCA compute novel dimensions

whose meaning is difﬁcult to interpret (Erichson et al.,

2016), the CUR decomposition (and its more promis-

ing randomized version RCUR) has been proposed

(Mahoney and Drineas, 2009; Halko et al., 2011;

Voronin and Martinsson, 2017) as an interpretable DR

alternative to PCA and RPCA. It factorizes the ini-

tial matrix A ∈ R

n×p

into 3 matrices: C ∈ R

n×k

,U ∈

k×k

,R ∈ R

k×p

where C and R are formed by a small

subset of columns and rows from the original dataset,

which are chosen based on their capability of main-

taining the original structure of the dataset. Com-

pletely different DR approaches are UMAP (McInnes

et al., 2018) and t-SNE (Van der Maaten and Hin-

ton, 2008), which ﬁnd a non-linear embedding into

a lower dimensional space that maintains the original

(local and global) dataset structure, by optimizing a

function that preserves the distances within the data

neighborhoods.

Since RPCA, RCUR, UMAP, and t-SNE have

shown their promise, we compared them for DR.

Among the computed projected views we then se-

lected the one whose DANCo-ID is most similar to

the target ID.

4 PRELIMINARY RESULTS

Table 1: ID estimates (and standard deviations) for the

views in our dataset. Asterisks (*) refer to the blocking-ID

estimate, while the red values refer to the target ID.

View Corr* Clust* DR

miRNA 28.46 28.83 23.73

± 1.27 ± 2.35 ± 1.49 (RCUR)

mRNA 32.92 36.3 30.27

± 0.49 ± 0.55 ± 3.95 (RCUR)

In Table 1 the IDs estimated after all the consecutive

steps of our algorithm are shown, highlighting that,

for both the views, the ID remains approximately sta-

ble

. In Figure 4 we show the scatter plots of the

ﬁrst two components of the different embedded space

computed by the four DR algorithms. For both the

views, RCUR is the DR method that produces an ID

estimation more consistent with the previously com-

puted ID. Indeed, for the miRNA view we have an

agreement with the target ID within ≈ 2 standard de-

viations, while for the mRNA view the ﬁnal ID esti-

mate is within 1 standard deviation of the target ID,

showing a signiﬁcant consistency of our pipeline,

even for largely sparse datasets. Remarkably, RCUR

is the only DR method that completely preserves data

interpretability for it ﬁnds a reduced space that is a

subset of the original features. While our prelimi-

nary results show the promise of our proposal, fu-

ture works are aimed at its thorough comparison with

SOTA DR approaches, and at the evaluation of dif-

ferent ID-estimation methods within our blocking-ID

It’s worth mentioning that the blocking-ID estimate for

mRNA view after clustering, higher than the target one, can

be addressed to the fact that in the hierarchical clustering

step we used the correlation matrix as similarity measure,

and thus dismissing highly similar (i.e. correlated) tran-

scriptomic features, signiﬁcant from a biological perspec-

tive (Allocco et al., 2004), could slightly increase noise.

However, hierarchical clustering for reducing correlation

bias in mRNA data is an efﬁcient method already proposed

in previous analysis (Park et al., 2007).

Intrinsic-Dimension Analysis for Guiding Dimensionality Reduction in Multi-Omics Data

249

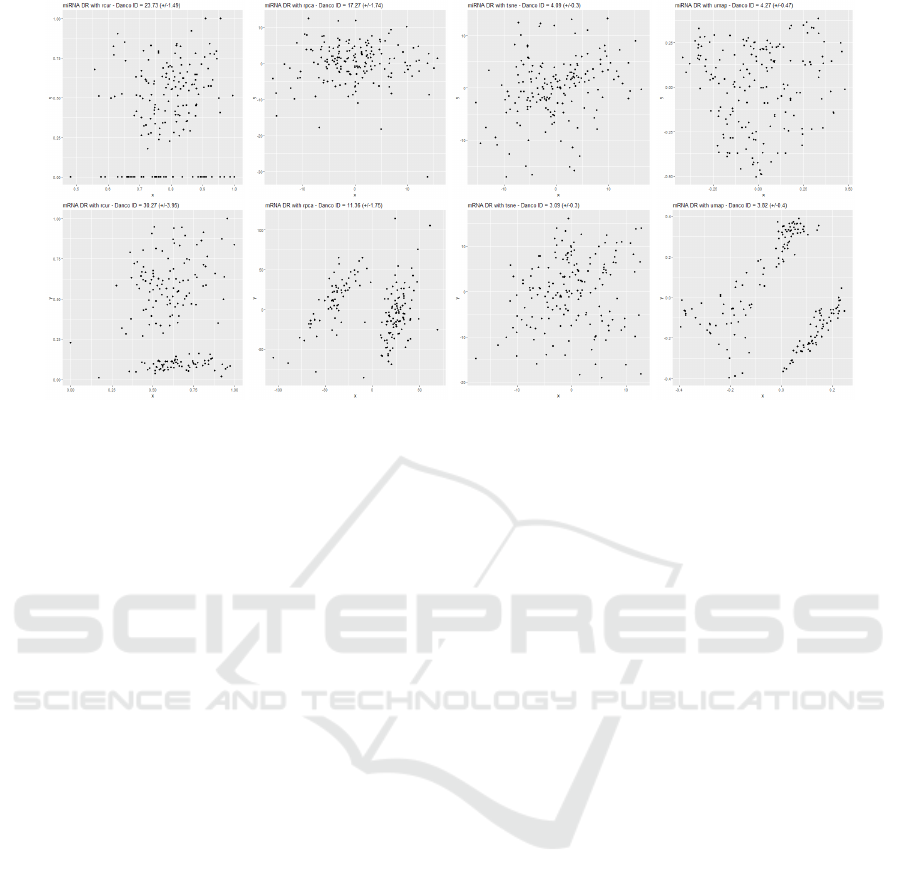
Figure 4: Plot of the ﬁrst 2 components of miRNA (top) and mRNA (bottom) embedded views. In the case of RCUR these

are two features from the original dataset (therefore for better visualizing the reduced space, a RPCA transformation can be

applied on RCUR reduction).

estimation. The aim is to choose the most performant

ID-estimation approach to produce tractable multi-

views, to be used for patient subtypes identiﬁcation.

Furthermore, the computational complexity strongly

depends on the blocking-ID step and thus has an es-

timated lower bound of Ω(n

blocks

· n

try

· D

· NlogN).

This requires future works to improve code optimiza-

tion and parallelization.

REFERENCES

Allocco, D., Kohane, I., and Butte, A. (2004). Quantifying

the relationship between co-expression, co-regulation

and gene function. BMC bioinformatics, 5:18.

Cai, R., Zhang, Z., Tung, A. K., Dai, C., and Hao, Z. (2014).

A general framework of hierarchical clustering and its

applications. Information Sciences, 272:29–48.

Campadelli, P., Casiraghi, E., Ceruti, C., and Rozza, A.

(2015). Intrinsic dimension estimation: Relevant tech-

niques and a benchmark framework. Mathematical

Problems in Engineering, 2015.

Campello, R. J. G. B., Moulavi, D., and Sander, J. (2013).

Density-based clustering based on hierarchical den-

sity estimates. In Pei, J., Tseng, V. S., Cao, L., Mo-

toda, H., and Xu, G., editors, Advances in Knowledge

Discovery and Data Mining, pages 160–172, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Ceruti, C., Bassis, S., Rozza, A., Lombardi, G., Casiraghi,

E., and Campadelli, P. (2014). Danco: An intrinsic

dimensionality estimator exploiting angle and norm

concentration. Pattern recognition, 47(8):2569–2581.

Drineas, P. and Mahoney, M. W. (2016). Randnla: random-

ized numerical linear algebra. Communications of the

ACM, 59(6):80–90.

Erichson, N. B., Voronin, S., Brunton, S. L., and Kutz, J. N.

(2016). Randomized matrix decompositions using r.

arXiv preprint arXiv:1608.02148.

Facco, E., d’Errico, M., Rodriguez, A., and Laio, A. (2017).

Estimating the intrinsic dimension of datasets by a

minimal neighborhood information. Scientiﬁc reports,

7(1):1–8.

Franc¸ois, D., Wertz, V., and Verleysen, M. (2007). The con-

centration of fractional distances. IEEE Transactions

on Knowledge and Data Engineering, 19(7):873–886.

Gagolewski, M. (2021). genieclust: Fast and robust hierar-

chical clustering. SoftwareX, 15:100722.

Gerbrands, J. J. (1981). On the relationships between svd,

klt and pca. Pattern recognition, 14(1-6):375–381.

Gliozzo, J., Mesiti, M., Notaro, M., Petrini, A., Patak, A.,

Puertas-Gallardo, A., Paccanaro, A., Valentini, G.,

and Casiraghi, E. (2022). Heterogeneous data integra-

tion methods for patient similarity networks. Brieﬁngs

in Bioinformatics.

Halko, N., Martinsson, P.-G., and Tropp, J. A. (2011).

Finding structure with randomness: Probabilistic al-

gorithms for constructing approximate matrix decom-

positions. SIAM review, 53(2):217–288.

Hughes, G. (1968). On the mean accuracy of statistical pat-

tern recognizers. IEEE transactions on information

theory, 14(1):55–63.

Johnsson, K. (2011). Manifold Dimension Estimation for

Omics Data Analysis: Current Methods and a Novel

Approach. Lund University.

Lv, J. (2013). Impacts of high dimensionality in ﬁnite sam-

ples. The Annals of Statistics, 41(4):2236–2262.

Mahmud, M. S. and Fu, X. (2019). Unsupervised classiﬁca-

tion of high-dimension and low-sample data with vari-

ational autoencoder based dimensionality reduction.

In 2019 IEEE 4th International Conference on Ad-

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

250

vanced Robotics and Mechatronics (ICARM), pages

498–503. IEEE.

Mahoney, M. W. and Drineas, P. (2009). Cur matrix decom-

positions for improved data analysis. Proceedings of

the National Academy of Sciences, 106(3):697–702.

McInnes, L., Healy, J., and Melville, J. (2018). Umap: Uni-

form manifold approximation and projection for di-

mension reduction. arXiv preprint arXiv:1802.03426.

Meng, C., Zeleznik, O. A., Thallinger, G. G., Kuster, B.,

Gholami, A. M., and Culhane, A. C. (2016). Di-

mension reduction techniques for the integrative anal-

ysis of multi-omics data. Brieﬁngs in bioinformatics,

17(4):628–641.

Nanga, S., Bawah, A. T., Acquaye, B. A., Billa, M.-I.,

Baeta, F. D., Odai, N. A., Obeng, S. K., and Nsiah,

A. D. (2021). Review of dimension reduction meth-

ods. Journal of Data Analysis and Information Pro-

cessing, 9(3):189–231.

Nguyen, L. H. and Holmes, S. (2019). Ten quick tips for ef-

fective dimensionality reduction. PLoS computational

biology, 15(6):e1006907.

Nicora, G., Vitali, F., Dagliati, A., Geifman, N., and Bel-

lazzi, R. (2020). Integrated multi-omics analyses in

oncology: a review of machine learning methods and

tools. Frontiers in oncology, 10:1030.

Nielsen, F. (2016). Introduction to HPC with MPI for Data

Science. Undergraduate Topics in Computer Science.

Springer.

Park, M., Hastie, T., and Tibshirani, R. (2007). Averaged

gene expressions for regression. Biostatistics (Oxford,

England), 8:212–27.

odergren, A. (2011). On the distribution of angles between

the n shortest vectors in a random lattice. Journal of

the London Mathematical Society, 84(3):749–764.

Solorio-Fern

andez, S., Carrasco-Ochoa, J. A., and

Mart

ınez-Trinidad, J. F. (2020). A review of unsuper-

vised feature selection methods. Artiﬁcial Intelligence

Review, 53(2):907–948.

Trunk, G. V. (1979). A problem of dimensionality: A sim-

ple example. IEEE Transactions on pattern analysis

and machine intelligence, PAMI-1(3):306–307.

Van der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of machine learning research,

9(11).

Voronin, S. and Martinsson, P.-G. (2017). Efﬁcient al-

gorithms for cur and interpolative matrix decompo-

sitions. Advances in Computational Mathematics,

43(3):495–516.

APPENDIX

A. Pairwise Correlation Analysis

For the computation of pairwise correlations, we pre-

ferred the Spearman correlation coefﬁcient since its

assumption of monotonic relationships between vari-

ables is weaker than Pearson’s requirement of lin-

ear relationships. We considered as highly-correlated

pairs of features with a correlation coefﬁcient > 0.8.

Between correlated variables, we discarded the one

whose mean absolute pairwise-correlation with re-

spect to all the other features is higher. Since the

application of pairwise-correlation ﬁltering is com-

putationally demanding, we implemented a parallel-

distributed algorithm that (1) splits the feature-set into

subsets, (2) ﬁlters each subset, (3) recomposes the ﬁl-

tered feature-set, (4) shufﬂes the remaining features

and reiterates until a maximum number of iterations

has been reached or no high correlation has been re-

moved from any of the feature subsets. This pro-

cedure allows distributing the ﬁltering of the feature

subset into multiple cores.

B. Distributed-Clustering Through Genie

To optimize the feature clustering, we apply a parallel

algorithm to iteratively cluster the feature set until the

space dimension is greater than the desired number

of clusters, C . In more detail, the following steps are

applied.

1. To limit the computational cost of Genie, the

current D-dimensional data X ∈ ℜ

m×D

(being

m the number of cases) is randomly split into

N lower-dimensional subsets subX

∈ ℜ

m×d

, i ∈

{

1,. .., N

}

, d = 1000, N = ⌊

⌋. The subsets are

distributed across multiple cores.

2. On each core, Genie is applied to cluster the fea-

ture space and obtain c clusters and the relative

medoids (c is chosen at the beginning of the al-

gorithm in order to ensure a maximum number of

iterations are applied).

3. The N × c medoids are recollected to recompose

the reduced feature space X ∈ ℜ

m×(N×c)

. If the

new dimension is still (N × c) > C , the process

restarts from step 1 to apply a further reduction.

Intrinsic-Dimension Analysis for Guiding Dimensionality Reduction in Multi-Omics Data

251