A Bi-Level Genetic Algorithm to Solve the Dynamic Flexible Job Shop

Scheduling Problem

Mohamed Dhia Eddine Saouabi

1 a

, Houssem Eddine Nouri

1,2 b

and Olfa Belkahla Driss

1,3 c

Univ. Manouba, ENSI, LARIA UR22ES01, Campus Universitaire Manouba, 2010, Tunisia

Univ. Gabes, ISGG, Rue Omar Ibn Khattab, 6029, Gabes, Tunisia

Univ. Manouba, ESCT, Campus Universitaire Manouba, 2010, Tunisia

Keywords:

Flexible Job Shop Scheduling Problem, Dynamic Scheduling, Genetic Algorithm, Bi-Level Optimization,

Job insertion, Rescheduling.

Abstract:

The dynamic ﬂexible job shop scheduling problem (DyFJSP) is an extension of the ﬂexible job scheduling

problem (FJSP) as the production environment is characterized by a set of disturbances that require a method

capable of reacting in real time in order to generate an efﬁcient schedule in case of production failure. In

this paper, we propose a bi-level genetic algorithm (BLGA) to solve the DyFJSP in order to minimize the

maximum completion time (Makespan). The dynamic scenario taken into account in this work is job insertion.

To evaluate the performance of our approach, we carry out experiments on Brandimarte benchmark instances.

The results of the experiments show that the BLGA is characterized by its efﬁciency and performance in

comparison with other methods published in the literature.

1 INTRODUCTION

With the great evolution of the production environ-

ment characterized by competition and the strict de-

mands of customers, the improvement of industrial

managing tools has become a persistent need to meet

the limits of traditional disciplines (Martinsons and

Davison, 2007). One of the most important manage-

ment instruments in the decision-making of manufac-

turing is the production scheduling. This tool is con-

sidered as a vital link that transfers the ﬂow between

the operational and tactical levels within the company.

Indeed, the scheduling function manages all the avail-

able resources and resolves conﬂicts caused by the

implementation of product lines over the estimated

time horizon. For this reason, studying this problem

in the ﬁeld of optimization is becoming increasingly

important and it is interesting to implement practical

solutions and manage the expectations of decision-

makers in various areas (Wiers, 1997) such as the lo-

gistic ﬁeld in order to schedule a list of operations

to produce a set of jobs, or in the ﬁeld of health-

care in order to affect resources with the aim of carry

https://orcid.org/0000-0003-3272-513X

https://orcid.org/0000-0003-0901-1278

https://orcid.org/0000-0003-3077-6240

out a list of medical operations. One of the schedul-

ing problems that has been studied extensively in re-

cent years is the ﬂexible job shop scheduling prob-

lem. This type of workshop problem is an exten-

sion of the classic job shop problem, it is character-

ized by the ability to perform each operation by one

or more alternative machines with different process-

ing times, whose objective is to determine the order

of operations and assigning them to machines (Xie

et al., 2019). Because of the high complexity of the

FJSP, known as NP-hard (Garey et al., 1976), sev-

eral approaches are proposed as optimization tools of

this type of problems, with the aim of minimize one

or more objectives considered as performance crite-

ria in each study. We cite the following studies to

solve the FJSP, a hybrid metaheuristics-based multi-

agent model (Nouri et al., 2018), multi-agent model

based on combination of chemical reaction optimiza-

tion metaheuristic with tabu search (Marzouki et al.,

2018) and a genetic algorithm combined with tabu

search in a holonic multi-agent model (Nouri et al.,

2015). Although these scheduling methods prove

their performance when offered for the static work-

shop, they lose their efﬁciency when applied in a dy-

namic production environment characterized by dis-

turbances like the insertion or cancellation of jobs, the

breakdowns or conﬂicts between machines, and the

752

Saouabi, M., Nouri, H. and Belkahla Driss, O.

A Bi-Level Genetic Algorithm to Solve the Dynamic Flexible Job Shop Scheduling Problem.

DOI: 10.5220/0011773300003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 752-759

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

problems related to the workers such as their fatigue

and absences (Mohan et al., 2019). In this paper, we

are interested in dynamic ﬂexible job shop scheduling

problem (DyFJSP), which is deﬁned as a production

environment characterized by the job insertion during

the production process. which require the implemen-

tation of an effective model to ensure the continuity of

the production process in the ﬂexible job shop. In the

literature, several studies which focus on the mono-

objective optimization of the DyFJSP are published.

To minimize the makespan, (Zhang and Wong, 2017)

proposed a multi agent system combined with an ant

colony optimization method to solve this problem in

a dynamic workshop described by the rush orders,

the job cancellation, and the machine breakdown or

repair. (Li et al., 2017) used a hybrid artiﬁcial bee

colony algorithm in a workshop characterized by job

insertion, machine failure, and job cancellation. In

addition, (Long et al., 2022), (Mihoubi et al., 2021)

and (Ali et al., 2020) focused on the job insertion sce-

nario and proposed a dynamic self learning artiﬁcial

bee colony, genetic algorithm combined with a hy-

brid neuronal surrogate and an improved genetic algo-

rithm as a scheduling algorithm respectively. And to

minimize the mean weighted tardiness in the DyFJSP

with the job insertion scenario, (Fan et al., 2021) used

a genetic programming based hyper heuristic as a

scheduling algorithm. We notice that the makespan is

the most important objective studied in the literature.

For this reason, we are interested in this work to min-

imize this criterion when solving the dynamic ﬂexi-

ble job shop scheduling problem. We also notice that

dynamic events related to jobs are the most disrup-

tive in the production system. The remainder of this

article is organized as follows. Section 2 formulates

the DyFJSP with new job insertion, the model pro-

posed to optimize this problem is described in section

3. Next, an application of the proposed approach to

solve the DyFJSP is presented in section 4. Then, the

experimental study is shown in section 5 to verify the

efﬁciency of our proposed approach and compare its

performance with other existing algorithms. Finally,

some conclusions and perspectives are presented in

section 6.

2 PROBLEM FORMULATION

In this paper, we aim to solve the dynamic and ﬂex-

ible job shop scheduling problem (DyFJSP) which is

an extension of the ﬂexible job shop scheduling prob-

lem (FJSP). The FJSP is formulated as follow. There

is a set of n jobs J= {J

,...,J

} to be realized by a set

of m machines M={M

,...,M

}, such as each job J

deﬁned by a sequence of k operations {O

i,1

,...,O

i,k

}

to be executed successively. We notice that each op-

eration can be performed by a list of alternative ma-

chines with different processing times p

i, j,m

, where i

is the index of the job, j is the index of the operation

and m is the index of the machine. The main objective

of this problem is to minimize the maximum comple-

tion time which is the makespan. This performance

criterion is deﬁned by C

max

. (See (1)), where C

is the

completion time of the job J

minC

max

= max

1<i<n

) (1)

The FJSP problem is composed by two sub-problems

which are the determination of the optimal sequenc-

ing of operations and the assignment of machines for

the execution of operations. In a dynamic production

environment, the ﬂexible job shop scheduling prob-

lem becomes dynamic and will be characterized by

the possibility of inserting jobs at a random time be-

fore the makespan. So the assumptions considered in

the DyFJSP are the following:

• All the machines are available at time zero.

• The independence of machines between them-

selves.

• Machines are available until the end of the sched-

ule.

• A machine can only perform one operation at a

given moment.

• The deﬁnition of jobs is determined before the

start of the schedule.

• Jobs are independent of each other.

• The execution of a job can only be on one machine

at a time.

• A running operation cannot be interrupted

• Jobs are allowed to wait for resources as long as

necessary.

• The production environment is characterized by

the insertion of new jobs.

• Disturbances are characterized by their timing.

3 THE BI-LEVEL GENETIC

ALGORITHM

To solve the DyFJSP, we propose a Bi-Level Genetic

Algorithm, denoted by BLGA, based on the bi-level

optimization design, which is deﬁned as a speciﬁc

type of optimization where a problem is integrated

(nested) within another. The outer optimization task

A Bi-Level Genetic Algorithm to Solve the Dynamic Flexible Job Shop Scheduling Problem

753

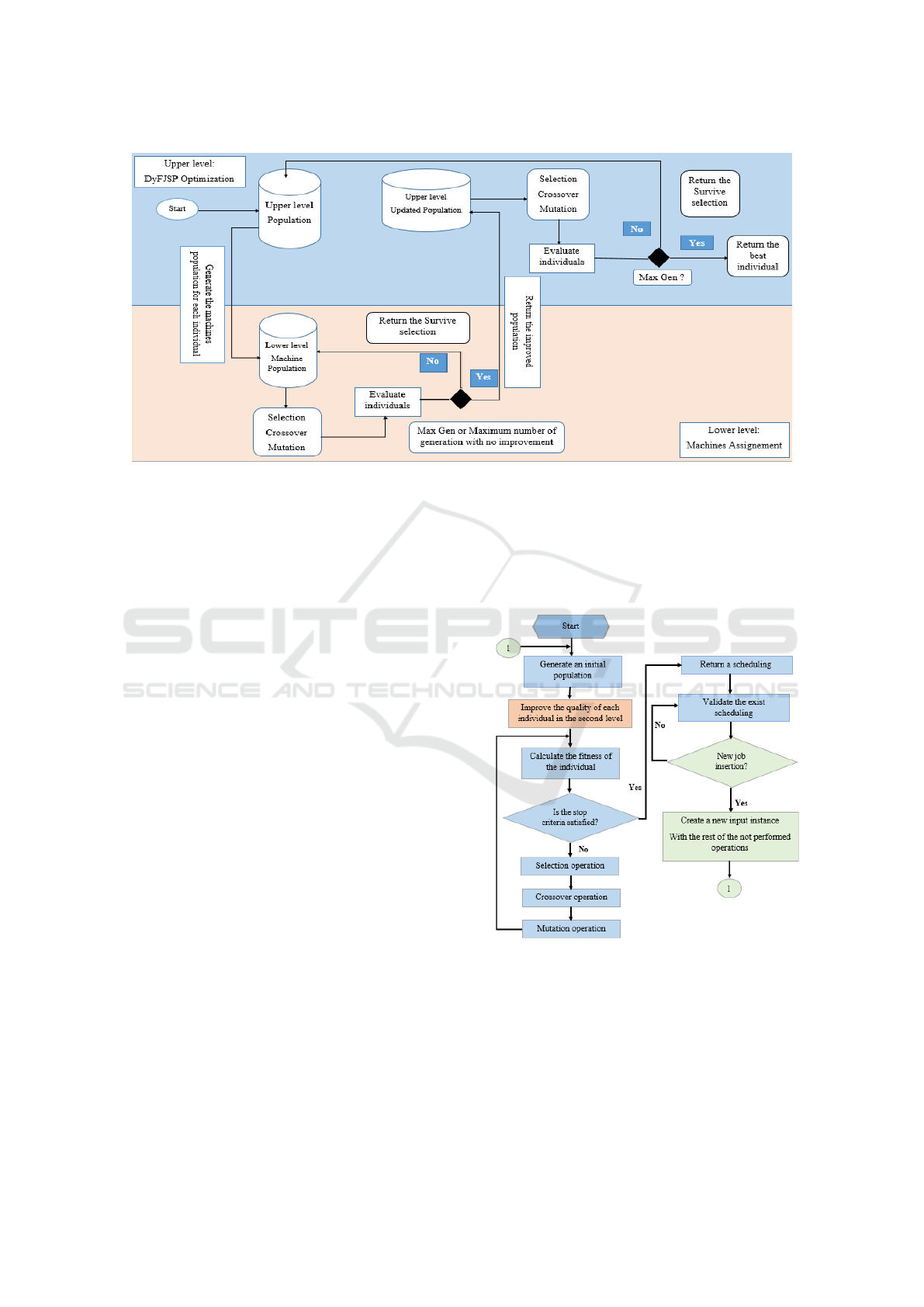
Figure 1: The description of bi-level genetic algorithm.

is commonly referred to as the upper-level optimiza-

tion task, and the inner optimization task is commonly

referred to as the lower-level optimization task (Zadeh

et al., 2018). We note that each level has its objec-

tives, constraints, and variables.

Our method BLGA can be deﬁned by modeling two

levels of optimization as shown in Figure 1. In each

level, we use the genetic algorithm. In the upper level,

we seek the optimization of the general problem, and

in the lower level, our objective is the optimal allo-

cation of machines to carry out the workshop opera-

tions.

The upper level can be described as follows:

• A randomly generated initial population. Such as

each individual of the population is deﬁned with

the operations sequence chromosome (OS) and

the machines sequence chromosome (MS).

• Application of the selection, two points crossover,

and mutation operators.

• Return the best scheduling.

The lower level is included just before the selection

phase and it allows us to improve the quality of each

individual generated randomly in the previous phase.

In this level, the OS chromosome of operations is

ﬁxed and improvements are made on the MS chro-

mosome of machines. This improvement is described

as follows for each individual:

• Removal of the initial MS chromosome.

• Generation of a new machines population.

• Application of the selection, two points crossover,

and mutation operators.

• Return the improved individual.

We present two ﬂowcharts, see Figures 2 and 3, that

illustrate the general approach and the lower level al-

gorithm successively.

Figure 2: The ﬂowchart of the bi-level genetic algorithm.

4 APPLICATION OF THE BLGA

We consider the dynamic ﬂexible job shop, which is

composed by four Jobs J

, J

, and J

and ﬁve ma-

chines M

, M

, and M

. The jobs are deﬁned

as follows: J

: [O

, O

]

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

754

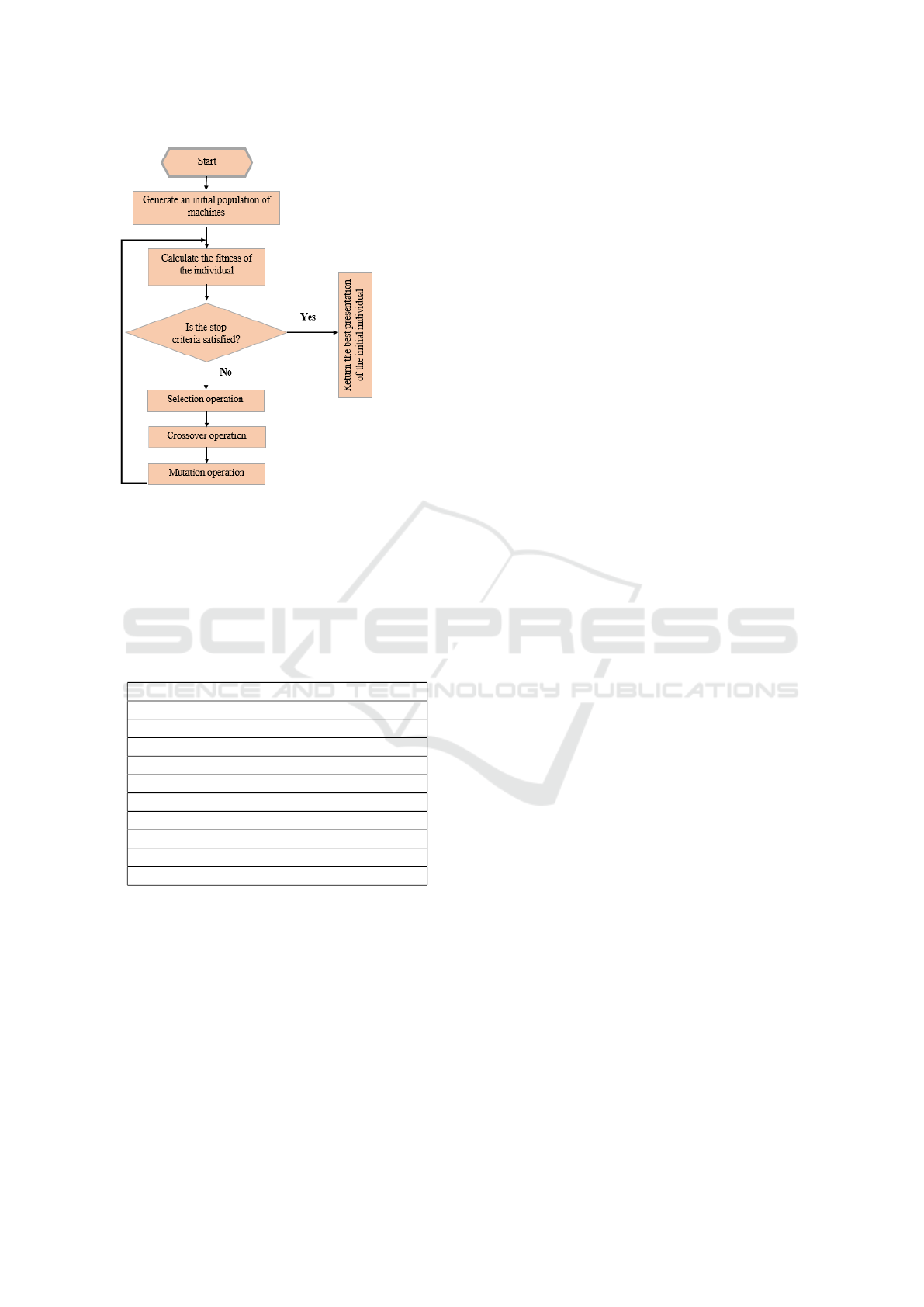
Figure 3: The ﬂowchart of the lower level.

: [O

, O

]

: [O

, O

]

: [O

, O

]

We present below in Table 1 the list of the alternative

machines for each operation and the processing time

required for each operation on that machine.

Table 1: List of the alternative machines for each operation.

Operations List of alternatives machines

{ M

(4), M

(3)}

{ M

(3), M

(5), M

(2)}

{ M

(2), M

(1)}

{ M

(4), M

(3)}

{ M

(5)}

{ M

(1), M

(2), M

(1)}

{ M

(2), M

(3)}

{ M

(3), M

(5)}

{ M

(4), M

(3), M

(2)}

{ M

(5), M

(6)}

4.1 Solution Encoding

For the encoding of the solution, we choose two chro-

mosomes called MS and OS, as MS is the chromo-

some that represents the assignment of machines for

each operation, and the OS chromosome for the rep-

resentation of the order of operations.

4.1.1 MS Chromosome

As each Job is composed of operations assigned to

machines to be performed. The MS chromosome is

constructed as follows:

We start by assigning machines to the operations of

the ﬁrst job while respecting the order of the opera-

tions of this job, and we redo the same procedure job

by job. We note that each machine is represented by

its index in the list of machines allocated to perform

the operation. See Figure 4.

4.1.2 OS Chromosome

The OS chromosome is reserved for the represen-

tation of the sequencing of operations and is con-

structed as follows, see Figure 5:

• Each gene on the chromosome contains a number

that symbolizes a job.

• Each job appears in the chromosome k times such

as k is the number of their operations.

• The operations of the job J are presented in the

chromosome by the order of appearance of the job

J index.

4.2 Implementation of The BLGA

We demonstrate in the rest of this section the imple-

mentation of the algorithm with the example shown

above:

Step 1 (Upper Level): We suppose a population P of

size 3 individuals:

= {OS

, MS

}, I

= {OS

, MS

} and I

= {OS

}. See Figure 6.

i = 0

While i < 3

Do: Step 1 (Lower Level): Generation of 3 machines

individuals for the individual (i=0) generate in the ﬁrst

step of the upper level. I

= {MS

, MS

} I

= {OS

, MS

} (See Figure 7).

= {OS

, MS

} (See Figure 8).

= {OS

, MS

} (See Figure 9).

Step 2 (Lower Level):

• Calculate ﬁtness for each individual.

• Application of the selection operator:

We select I

and I

Step 3 (Lower Level): Application of the two points

crossover operator. (See Figure 10).

Step 4 (Lower Level): Application of the mutation

operator. (See Figure 11).

Step 5 (Lower Level): Calculate ﬁtness value and

return the best individual for the ﬁrst individual of the

A Bi-Level Genetic Algorithm to Solve the Dynamic Flexible Job Shop Scheduling Problem

755

Figure 4: The representation of the MS chromosome.

Figure 5: The representation of the OS chromosome.

Figure 6: OS & MS chromosomes of the three individuals

, I

Figure 7: The ﬁrst MS

chromosome of the ﬁrst individual

generate in the upper level.

Figure 8: The second MS

chromosome of the ﬁrst indi-

vidual I

generate in the upper level.

Figure 9: The third MS

chromosome of the ﬁrst individual

generate in the upper level.

upper level to be saved as an element of the population

i++ Step 2 (Upper level):

• Calculate the ﬁtness value for each individual of

the new population improved in lower level.

• Application of the selection operator: We select I

and I

Figure 10: Application of the two points crossover in the

lower level.

Figure 11: Application of the mutation in the lower level.

Step 3 (Upper Level): Application of the two points

crossover operator.

Step 4 (Upper Level): Application of the mutation

operator.

Step 5 (Upper Level): Evaluate each individual of

the population and return the best scheduling.

5 EXPERIMENTAL STUDY

In this section, we present the experiments carried

out on the DyFJSP in order to minimize the objective

function C

max

(Makespan).

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

756

5.1 Experiment Design

The proposed BLGA is implemented in java language

on a 2.00 GHz Intel® Core (TM) i3-5005U and 6GB

of RAM memory, where we use the integrated devel-

opment environment (IDE) “IntelliJ”. As a parameter

for the algorithm used to solve the DyFJSP, the values

of population size, crossover and mutation probabil-

ity, number of generations, perturbation probability,

and maximum generation with no improvement are

adjusted experimentally. The appropriate parameters

of the two levels are shown below in Table 2.

Table 2: The appropriate parameters for our approach.

Levels Parameters

Population Size = 300

Crossover probability = 0.98

Upper

Mutation probability = 0.01

Generations = 500

max generation with no improvement = 80

Perturbation probability = 0.40

Population Size = 300

Crossover probability = 0.98

Lower

Mutation probability = 0.01

Generations = 100

max generation with no improvement = 20

5.2 Performance of the BLGA

In this subsection, we will present the experimental

results developed using the BLGA. First, we will fo-

cus on the performance of our approach by comparing

their result with other approaches in the literature, and

then we will test the ability of our method to solve the

dynamic scenario in the next subsection.

5.2.1 Benchmark Instances

For the performance tests of the proposed approach,

we worked on the Brandimarte (Brandimarte, 1993)

benchmark instances. This benchmark is used for the

FJSP. But due to the absence of speciﬁc benchmarks

for dynamic and ﬂexible problems, we worked on

this benchmark and we insert a new job at a given

moment T for the job insertion scenario based on

the work of (Long et al., 2022). To measure the

performance of our approach in minimizing the C

max

criterion, we will compare the results of BLGA with

other algorithms.

5.2.2 Comparison of the BLGA Results With

Other Algorithms

To test the performance of our approach, we will

compare the results of BLGA obtained in the ﬂexi-

ble scheduling phase with those of other algorithms

used in the existing literature which worked with

the Brandimarte benchmark, including SLABC (Long

et al., 2022), IPSO (Ding and Gu, 2020), SLGA (Chen

et al., 2020), MACROG (Marzouki et al., 2017),

MAPSO (Nouiri et al., 2018) and GATS+HM (Nouri

et al., 2015).

The next Table 3, presents the best values obtained

by these algorithms cited above to resolve the Brandi-

marte benchmark instances. Such as the HOV repre-

sents the optimal historical value of each instance. We

note that the scale of each instance is deﬁned by the

number of jobs (n) and the number of machines (m).

By analyzing the Table 3 we note that the use of

the BLGA gives more optimized results in 5 instances

of the Brandimarte benchmark compared to the other

algorithms used for comparison in this paper.

5.3 Experimental Results of the BLGA

on Job Insertion Scenario

This part is reserved for the presentation of the test

performed on dynamic event characterized by the in-

sertion of a new job that require a rescheduling of the

initial scheduling.

We will use a scenario posed by (Long et al., 2022)

which consists in inserting an 11

job to the MK02

instance of the Brandimarte benchmark at the moment

T= 12. This job is deﬁned in Table 4.

First, we will start with an initial scheduling of

the MK02 instance. This scheduling is presented in

Figure 12.

In Figure 13, we present the ﬁnal scheduling of

the MK02 instance with the insertion of job 11.

The BLGA application generates a C

max

= 30 for

dynamic scheduling characterized by the insertion of

a new job in the MK02 instance of the Brandimarte

benchmark. In the other side the DSLABC (Long

et al., 2022) returns a C

max

= 38, so we notice that

our approach is more appropriate for optimizing this

type of problem.

6 CONCLUSIONS AND

PERSPECTIVES

Over the past decade, many research efforts have been

devoted to dynamic scheduling. The objective is to

A Bi-Level Genetic Algorithm to Solve the Dynamic Flexible Job Shop Scheduling Problem

757

Table 3: The best value obtained by seven algorithms to solve 10 Brandimarte instances.

Instance Scale (n ∗ m) HOV

Algorithms

SLABC IPSO SLGA MACROG MAPSO GATS+HM BLGA

MK01 10 x 6 36 42 40 40 40 41 40 40

MK02 10 x 6 24 29 29 27 32 26 27 27

MK03 15 x 8 204 204 204 204 204 207 204 204

MK04 15 x 8 48 67 66 60 64 65 64 62

MK05 15 x 4 168 175 175 172 179 171 173 173

MK06 10 x 15 33 80 77 69 85 61 65 64

MK07 20 x 5 133 155 145 144 172 173 144 142

MK08 20 x 10 523 523 523 523 552 523 523 523

MK09 20 x 10 299 364 320 320 421 307 311 310

MK10 20 x 15 165 283 239 254 358 312 222 220

Figure 12: The initial scheduling of MK02.

Figure 13: The ﬁnal scheduling of MK02 with job insertion.

Table 4: The operations of the new job.

Operations M1 M2 M3 M4 M5 M6

11−1

2 - 5 3 3 -

11−2

- 3 - 3 5 4

11−3

- 6 3 5 - -

11−4

4 1 - 2 5 3

11−5

- 5 2 4 - 3

11−6

5 6 3 2 - 4

contribute to a more productive and efﬁcient func-

tioning of a manufacturing company in the face of

an ever-changing market environment. In this paper,

we present a bi-level genetic algorithm, called BLGA,

for the dynamic ﬂexible job shop scheduling problem

(DyFJSP). In this approach, we used two levels for the

optimization of the DyFJSP by the upper level and

the optimization of the assignment of the machines

by the lower level respectively. The main objective

of this paper is to minimize the makespan in a dy-

namic ﬂexible job shop characterized by the insertion

of jobs. The experimental results show that the pro-

posed approach is efﬁcient in comparison with other

approaches used to solve the FJSP and also show that

the BLGA can resolve the perturbation in the DyFJSP.

As future work, we plan to work towards optimiz-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

758

ing other objectives. To achieve this, a method dedi-

cated to solving multi-objective problems should be

applied in order to produce more useful results in

terms of the objectives that will be considered in fu-

ture work on this production environment. Another

perspective to consider is the improvement of our ap-

proach to be capable to solve scheduling problems

with transportation in a dynamic environment char-

acterized by other dynamic events such as machines

or robot breakdowns.

REFERENCES

Ali, K. B., Telmoudi, A. J., and Gattouﬁ, S. (2020).

Improved genetic algorithm approach based on new

virtual crossover operators for dynamic job shop

scheduling. IEEE Access, 8:213318–213329.

Brandimarte, P. (1993). Routing and scheduling in a ﬂex-

ible job shop by tabu search. Annals of Operations

research, 41(3):157–183.

Chen, R., Yang, B., Li, S., and Wang, S. (2020). A self-

learning genetic algorithm based on reinforcement

learning for ﬂexible job-shop scheduling problem.

Computers & Industrial Engineering, 149:106778.

Ding, H. and Gu, X. (2020). Improved particle swarm opti-

mization algorithm based novel encoding and decod-

ing schemes for ﬂexible job shop scheduling problem.

Computers & Operations Research, 121:104951.

Fan, H., Xiong, H., and Goh, M. (2021). Ge-

netic programming-based hyper-heuristic approach

for solving dynamic job shop scheduling problem

with extended technical precedence constraints. Com-

puters & Operations Research, 134:105401.

Garey, M. R., Johnson, D. S., and Sethi, R. (1976).

The complexity of ﬂowshop and jobshop scheduling.

Mathematics of operations research, 1(2):117–129.

Li, X., Peng, Z., Du, B., Guo, J., Xu, W., and Zhuang, K.

(2017). Hybrid artiﬁcial bee colony algorithm with

a rescheduling strategy for solving ﬂexible job shop

scheduling problems. Computers & Industrial Engi-

neering, 113:10–26.

Long, X., Zhang, J., Zhou, K., and Jin, T. (2022). Dynamic

self-learning artiﬁcial bee colony optimization algo-

rithm for ﬂexible job-shop scheduling problem with

job insertion. Processes, 10(3):571.

Martinsons, M. G. and Davison, R. M. (2007). Strategic de-

cision making and support. Decision support systems,

43(1):284–300.

Marzouki, B., Driss, O. B., and Gh

edira, K. (2017). Multi

agent model based on chemical reaction optimization

with greedy algorithm for ﬂexible job shop scheduling

problem. Procedia Computer Science, 112:81–90.

Marzouki, B., Driss, O. B., and Gh

edira, K. (2018). Multi-

agent model based on combination of chemical reac-

tion optimisation metaheuristic with tabu search for

ﬂexible job shop scheduling problem. International

Journal of Intelligent Engineering Informatics, 6(3-

4):242–265.

Mihoubi, B., Bouzouia, B., and Gaham, M. (2021). Reac-

tive scheduling approach for solving a realistic ﬂexi-

ble job shop scheduling problem. International Jour-

nal of Production Research, 59(19):5790–5808.

Mohan, J., Lanka, K., and Rao, A. N. (2019). A review

of dynamic job shop scheduling techniques. Procedia

Manufacturing, 30:34–39.

Nouiri, M., Bekrar, A., Jemai, A., Niar, S., and Ammari,

A. C. (2018). An effective and distributed particle

swarm optimization algorithm for ﬂexible job-shop

scheduling problem. Journal of Intelligent Manufac-

turing, 29(3):603–615.

Nouri, H. E., Belkahla Driss, O., and Gh

edira, K. (2018).

Solving the ﬂexible job shop problem by hybrid

metaheuristics-based multiagent model. Journal of In-

dustrial Engineering International, 14(1):1–14.

Nouri, H. E., Driss, O. B., and Gh

edira, K. (2015). Genetic

algorithm combined with tabu search in a holonic

multiagent model for ﬂexible job shop scheduling

problem. In ICEIS (1), pages 573–584.

Wiers, V. C. (1997). A review of the applicability of or

and ai scheduling techniques in practice. Omega,

25(2):145–153.

Xie, J., Gao, L., Peng, K., Li, X., and Li, H. (2019). Review

on ﬂexible job shop scheduling. IET Collaborative

Intelligent Manufacturing, 1(3):67–77.

Zadeh, P. M., Fakoor, M., and Mohagheghi, M. (2018). Bi-

level optimization of laminated composite structures

using particle swarm optimization algorithm. Journal

of Mechanical Science and Technology, 32(4):1643–

1652.

Zhang, S. and Wong, T. N. (2017). Flexible job-shop

scheduling/rescheduling in dynamic environment: a

hybrid mas/aco approach. International Journal of

Production Research, 55(11):3173–3196.

A Bi-Level Genetic Algorithm to Solve the Dynamic Flexible Job Shop Scheduling Problem

759