MAGAN: A Meta-Analysis for Generative Adversarial Networks’ Latent

Space

Frederic Rizk

1 a

, Rodrigue Rizk

2 b

, Dominick Rizk

1 c

and Chee-Hung Henry Chu

1,3 d

The Center for Advanced Computer Studies, University of Louisiana at Lafayette, Lafayette, LA, U.S.A.

Department of Computer Science, University of South Dakota, Vemillion, SD, U.S.A.

Informatics Research Institute, University of Louisiana at Lafayette, Lafayette, LA, U.S.A.

Keywords:

Generative Adversarial Networks, GAN, Meta-Analysis, Latent Space, Data Augmentation.

Abstract:

Generative Adversarial Networks (GANs) are an emerging class of deep neural networks that has sparked

considerable interest in the ﬁeld of unsupervised learning because of its exceptional data generation perfor-

mance. Nevertheless, the GAN’s latent space that represents the core of these generative models has not been

studied in depth in terms of its effect on the generated image space. In this paper, we propose and evaluate

MAGAN, an algorithm for Meta-Analysis for GANs’ latent space. GAN-derived synthetic images are also

evaluated in terms of their efﬁciency in complementing the data training, where the produced output is em-

ployed for data augmentation, mitigating the labeled data scarcity. The results suggest that GANs may be used

as a parameter-controlled data generator for data-driven augmentation. The quantitative ﬁndings show that

MAGAN can correctly trace the relationship between the arithmetic adjustments in the latent space and their

effects on the output in the image space. We empirically determine the parameter ε for each class such that

the latent space is insensitive to a shift of ε × σ from the mean vector, where σ is the standard deviation of a

particular class.

1 INTRODUCTION

Due to its remarkable data generating capabilities, the

generative models have attracted signiﬁcant interest

in the ﬁeld of unsupervised learning via a novel and

useful framework called Generative Adversarial Net-

works (GAN). The use of generative models offers

hope for the unsupervised learning of data representa-

tion. One of the most widely used frameworks in this

ﬁeld is called Generative Adversarial Nets (GAN),

initially proposed by (Goodfellow et al., 2014). The

fundamental concept behind GANs is to pair together

two deep neural networks with antagonistic target

functions to compete against each other. The Dis-

criminator (D) neural network, which is trained to

distinguish between fake and real data, is tricked by

the Generator (G), a neural network that creates false

data. These two networks will be trained in an al-

ternative fashion. While D ultimately develops the

https://orcid.org/0000-0001-7443-7254

https://orcid.org/0000-0002-4392-4188

https://orcid.org/0000-0001-8078-4420

https://orcid.org/0000-0002-5817-8798

capacity to learn the data representations in an unsu-

pervised manner, G ﬁnally learns to produce data that

are remarkably similar to real data throughout this

process. In recent years, Generative Adversarial Net-

works (GANs) (Goodfellow et al., 2014) have consid-

erably enhanced picture synthesis. Through adversar-

ial training, the system will master mapping samples

from the latent space to real data distribution. Af-

ter acquiring the required skills, GAN will be able

to produce plausible images by taking samples from

a random distribution. Previous works mainly con-

centrated on identifying a more accurate distribution

from ground-truth in order to enhance synthesis qual-

ity (Karras et al., 2017; Zhang et al., 2018), but lit-

tle attempts have been made to investigate what GAN

truly learns in terms of the latent space. For instance,

in face synthesis, even though the latent code controls

which face to generate, it is still ambiguous the way

the latent code relates to diverse semantic properties

of the ﬁnal face picture, such as age and gender. Sev-

eral approaches for controlling the generated images

are proposed (Chen et al., 2016; Mirza and Osindero,

2014), but still their quality is signiﬁcantly inferior to

that reached by unconditioned GANs (Karras et al.,

488

Rizk, F., Rizk, R., Rizk, D. and Chu, C.

MAGAN: A Meta-Analysis for Generative Adversarial Networks’ Latent Space.

DOI: 10.5220/0011771900003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 488-494

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2017; Karras et al., 2021). According to a study made

by (Radford et al., 2016), exploring the arithmetic

property of the vector in the latent space indicates

that GAN learns some semantics in the earliest hidden

space. Prior study (Bau et al., 2019) demonstrates that

the generator synthesizes some visual traits through

its intermediate layers. Despite that, there is still a

dearth of knowledge regarding the concept of how

changing in the latent space can affect a desired gen-

erated output.

In this paper, we present and evaluate a meta-

analysis of GAN’s latent space. We propose MA-

GAN, an algorithm for Meta-Analysis of GANs’ la-

tent space. We explore the GAN latent space by

studying the arithmetic beyond the vectors in the la-

tent space and discovering how can a modiﬁcation in

this vector affect the generated output. We discovered

that feeding the system with a speciﬁc vector in the

latent space as an input for the generator can give us

an insight about what would be the generated output.

In other words, we can control ahead of time the out-

put and generate the desired output such as generating

coats or trousers.

The organization of this paper is as follows. In

the ﬁrst part of this paper, we give a brief introduction

about GANs, literature review, and the contributions

accomplished in this work. Section 2 introduces a

background about GANs and discusses the motivation

behind using GANs. Section 3 presents the proposed

MAGAN algorithm as well as the model components.

Section 4 presents the meta-analysis of latent space

and the experimental results. Finally, Section 5 con-

cludes the paper by summarizing the discussed work.

2 BACKGROUND AND

MOTIVATION

In this section, we give a brief overview of the fun-

damental concepts and key notions of GANs. GAN

is a neural network framework used for unsupervised

learning. It consists of two components that compete

against each other via a min-max game. One of the

components is called discriminator (D) distinguish-

ing between real samples and fake samples while the

other one is called generator (G) producing samples

that look like the real data trying to fool D. The con-

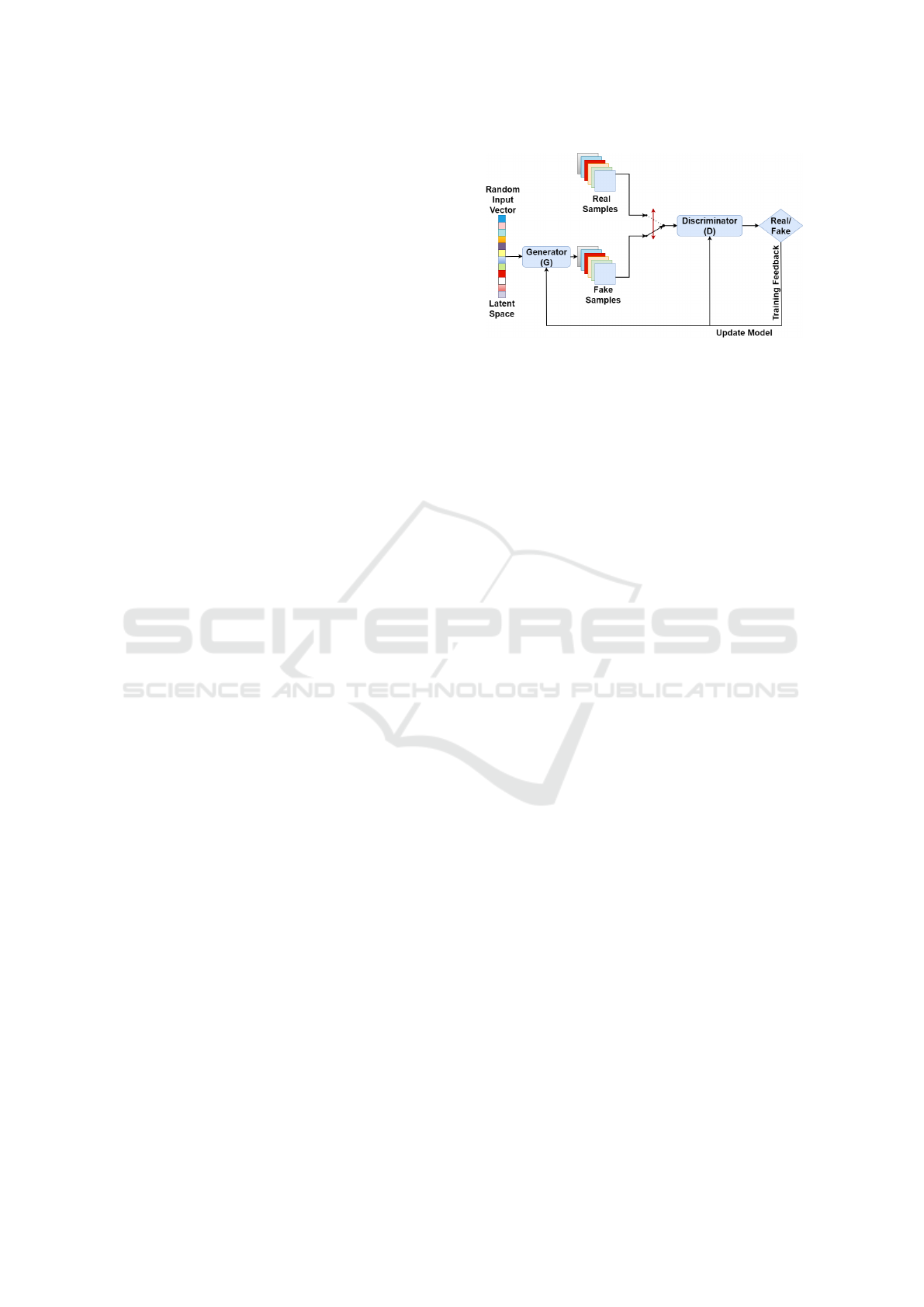
cept of GAN is summarized in Figure 1 where G takes

sample from the latent space as its input and generate

fake samples. However, D receives two inputs: real

samples (dataset) and fake samples (generated by G).

The role of D is to separate between real and fake

samples. GANs train in an alternative way, the two

models ought to always have similar skill levels.

Figure 1: Design of the GAN architecture.

Since both networks have distinct goal functions,

they both attempt to optimize themselves in order to

achieve those functions. G wants to lower its cost

value, whereas D wants to maximize it, so that the

overall optimization is:

min

max

V (D, G) = E

x∼pdata(x)

[logD(x)]+

z∼pz(z)

[log (1 –D(G(z)))]

(1)

GANs have gained exponentially expanding atten-

tion in the deep learning ﬁeld due to various bene-

ﬁts over more conventional generative models. Us-

ing conventional generative models face some limita-

tions on the generator architecture; however, GANs

can train any kind of generator network (Doersch,

2016; Goodfellow, 2017; Kingma and Welling, 2013).

Compared to other conventional generative models,

GANs can generate improved output. While VAE is

unable to produce perfect images, GANs can produce

any form of probability density (Goodfellow, 2017).

Lastly, there are no limitations on the latent variable’s

dimension.

These beneﬁts have allowed GANs to produce

synthetic data at the highest possible level, partic-

ularly for picture data. Adding to all these advan-

tages, GANs can be used for data augmentation and

especially in the case of scarce data. Furthermore,

the interpolation in the latent space is one of the

most intriguing results of the GAN training. Sim-

ple vector arithmetic features appear, and when they

are altered, the resultant pictures’ semantic qualities

change (Radford et al., 2015). Dimensionality reduc-

tion and novel applications are both made possible by

the latent space of GANs. A robust classiﬁer might

be created by using adversarial examples that are de-

termined by changes in the latent space (Jalal et al.,

2017). Hence, the ability of performing interpolation

and interpretability in the latent space raise our moti-

vation to accomplish this work: Meta-analysis of the

latent space and study the effects of arithmetic mod-

iﬁcations in the latent space with its impacts on the

generated output.

MAGAN: A Meta-Analysis for Generative Adversarial Networks’ Latent Space

489

3 PROPOSED ALGORITHM

The proposed algorithm is presented in three parts,

viz. training the GAN, training a classiﬁer to specify

the label for each generated image, and experiment-

ing with the latent space. We illustrate the algorithm

in the following using the Fashion-MNIST set as the

training set, without loss of generality in the sense that

the method can be applied to any other data set. The

Fashion-MNIST dataset consists of 70k images of a

variety of types of fashion products. Each data sam-

ple is a 28 × 28 grayscale image, associated with a

label from 10 classes. We trained the GAN model for

100 epochs with a batch size of 128.

Figure 2 shows the architecture of the generator

where 1000 samples of 100-dimensional vectors are

fed to the generator to generate images that look like

the real ones of the Fashion-MNIST dataset.

Figure 2: Generator architecture.

On the other side, the discriminator receives

grayscale images of size 28 × 28 from both the

Fashion-MNIST dataset (real images) and the gener-

ated images coming from the output of the genera-

tor (fake images) trying to distinguish between them.

The architecture for the discriminator is shown in Fig-

ure 3. Both models are trained in parallel and should

Figure 3: Discriminator architecture.

always be at a similar skill level. Once the training is

done, the generator model is ready to be used to gen-

erate images of a variety of types of fashion products.

Figure 4 shows the architecture of a classiﬁer used

to predict the label for the generated images. This

classiﬁer is trained on Fashion-MNIST dataset for

100 epochs.

Once all the models are well-trained, the gener-

ator and the classiﬁer are used together to form one

model for exploring the latent space. In Figure 5, X

Figure 4: Classiﬁer architecture.

represents the 1000 samples of 100-dimensional vec-

tors in the latent space, with each variable drawn from

a Gaussian distribution. I denotes the grayscale gen-

erated images of shape 28×28; L stands for the labels

for the 1000 generated images.

Figure 5: Flow diagram of the proposed model.

We propose MAGAN, an algorithm for Meta-

Analysis for GANs’ latent space which is depicted

in Figure 6. The MAGAN algorithm performs well

Figure 6: The MAGAN algorithm.

for meta-analysis on the latent space of GAN. It can

be replicated to other applications because of the sys-

tematic approach applied. In order to use this algo-

rithm, N samples of vector X are drawn from a Gaus-

sian distribution. Let X = {x

: i = 0, · ·· , m − 1} be

an m-dimensional vector drawn from the latent space,

where x

is the value of the i

dimension of X. As il-

lustrated in Figure 5, X should be fed to the model so

that each vector X is assigned to one of the C classes

of the dataset. We group together all the vectors that

have the same label L so that we have C groups of

vectors each where k ∈ {0, 1, · ·· ,C − 1}. For each

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

490

group, we calculate the mean µ

and the standard de-

viation σ

for all classes. We calculate C mean vectors

(µ

, µ

, ..., µ

C−1

) that, when fed into the model in Fig-

ure 5, will generate images with the following labels

, L

, · ·· , L

C−1

), respectively. We compute the Eu-

clidean distance d(µ

, µ

) between each pair of mean

vectors for all classes, where i, j ∈ {0, 1, · ·· ,C − 1}.

Furthermore, we obtain the shortest distance between

all the permutations of all the mean vectors. In other

words, we iterate across C classes to ﬁnd the mini-

mum distance d

min

[i] for each class label as deﬁned in

Equation 2:

min

[i] = min

C−1

j=0

(d (µ

, µ

)) (2)

where i ∈ {0, 1, · ·· ,C − 1}.

The computational task is to determine the param-

eter εinR that satisﬁes the condition:

min

[i] > distance(µ

, µ

± ε × σ

) (3)

for the ith class, i = 0, ·· · ,C − 1.

The purpose of parameter ε is to create various

vectors (µ

± p ×σ

) that can be used for data aug-

mentation, where p ∈ [0, ε]. The function f used for

the classiﬁcation of the vectors that once the vectors

are fed to the model shown in Figure 5, it ensures that

the label L will be equal to i.

f (ε) =

(

i, d

min

[i] > distance(µ

, µ

± ε × σ

)

j, otherwise

(4)

where i, j ∈ {0, 1, ·· · ,C − 1}.

4 EVALUATION

In our work, Fashion-MNIST dataset is used. It

consists of 70k images, each of which is a 28 × 28

grayscale image, associated with a label from 10

classes. We trained the GAN model for 100 epochs

with a batch size of 128. The latent space con-

sists of 1000 samples of 100-dimensional vectors

with each variable drawn from a Gaussian distri-

bution. The meta-analysis is made on 1000 sam-

ples {X

, X

, · ·· , X

999

} from the latent space. We

feed the model with 1000 samples from the latent

space, generate images and classify the output im-

ages. Therefore, each vector will have a label from

0 to 9 representing the class labels for the fashion-

MNIST dataset. Then, we group the vectors that have

the same label together so that we can ﬁnd the mean

and the standard deviation for each group. We set up

ten mean vectors (µ

, µ

, · ·· , µ

) that once fed to the

model in Figure 5, will generate images with the cor-

responding labels (L

, L

, · ·· , L

). Next, we calculate

the Euclidean distance d(µ

, µ

) between each pair of

the mean vectors for all the classes as shown in Fig-

ure 7. For instance, the Euclidean distance d(µ

, µ

)

Figure 7: Representation of the Euclidean distance between

each pair of vectors for all the classes.

between the two mean vectors µ

and µ

is 2.26.

We apply agglomerative clustering to the ten class

mean vectors using single, average, complete, and

Ward linkages to illustrate the clusters of the differ-

ent classes. The dendrograms are shown in Figure 8.

Figure 8: The dendrograms of the class mean vectors (x-

axis) vs the distances in the 100-dimensional space (y-axis)

using the single (upper left), average (upper right), com-

plete (lower left), and Ward (lower right) linkages.

We compute the minimum distance of the permu-

tation of all the mean vectors. The results are sum-

marized in Figure 9. For instance, the closest vec-

tor to µ

is µ

with a distance of 2. We would like

to visualize the structure of the mean vectors, which

are in a 100-dimensional space, by projecting them to

a two-dimensional space (Figure 10). We use multi-

dimensional scaling (MDS) to take advantage of the

MDS property that it preserves the relative distances

from the higher (100) dimensional space when pro-

jected onto the lower (2) dimensional space.

The mapping of class labels {0, 1, ·· · , 9} to class

contents is shown in Table1. From the dendro-

gram that uses the Ward linkage in Figure 8, we can

MAGAN: A Meta-Analysis for Generative Adversarial Networks’ Latent Space

491

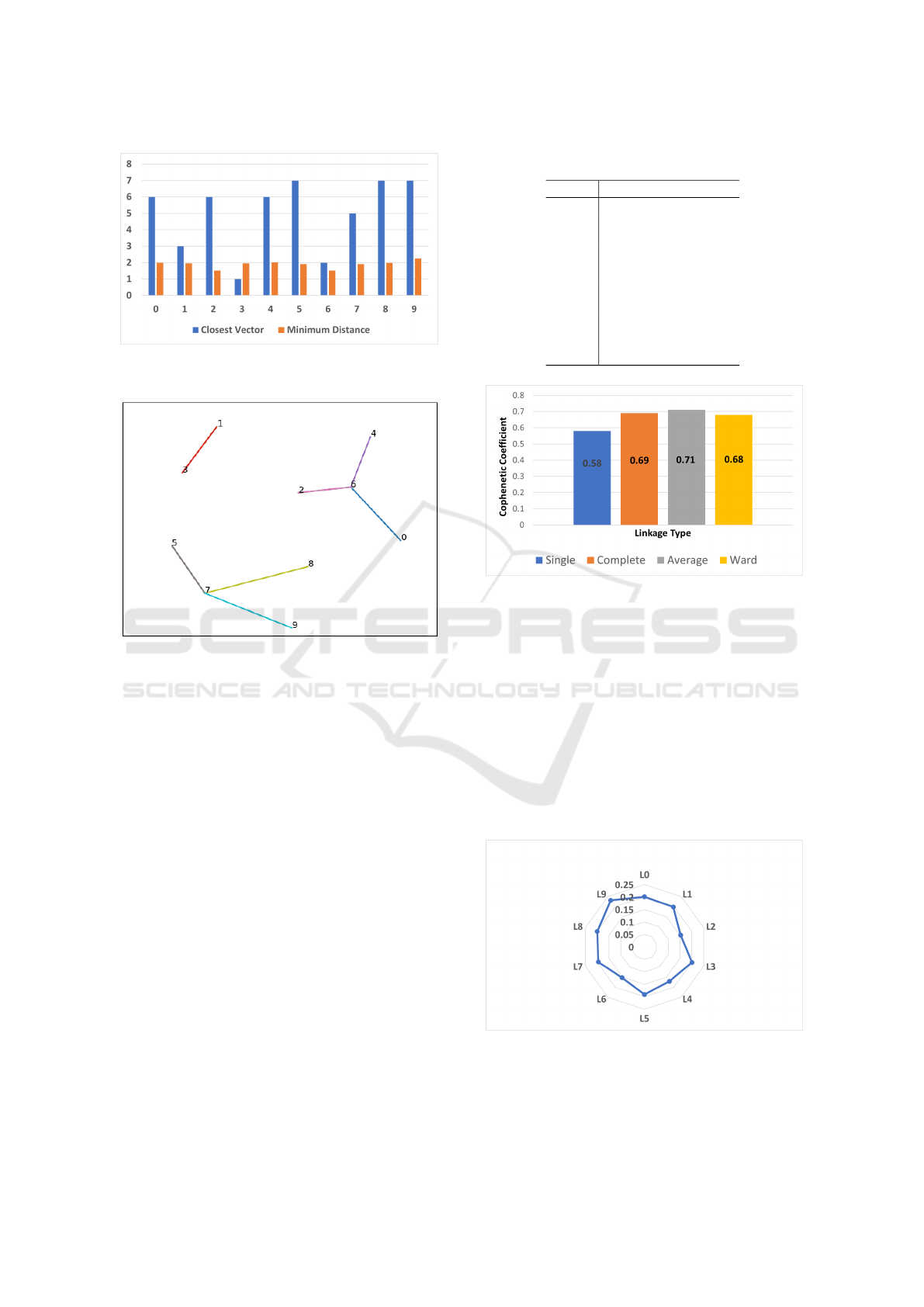
Figure 9: The distance between the source vector and the

closest vector.

Figure 10: Projection of the class mean vectors from the

100-dimensional latent space to a 2D canvas. Closest neigh-

bor pairs in the original latent space are joined by lines.

see that a stable clustering has 3 hierarchical clus-

ters: C

ward

= ((ankle boot, (bag, (sandal, sneaker))),

(coat, (pullover, shirt)), (top, (trousers, dress))). Al-

ternatively, using MDS, we can see three clusters:

MDS

= ( (trousers, dress), (shirt, pullover, coat, top),

(sneaker, sandal, ankle boot, bag)). Of the two, C

MDS

appears to be more aligned with the contents than

ward

Figure 8 demonstrates that the choice of linkage

method has crucial effect on the cluster formation.

It is challenging and time-consuming to inspect each

dendrogram in order to identify which clustering con-

nection works best. To address this, we use the cophe-

netic coefﬁcient to determine which linkage method

results in a dendrogram that best preserves the pair-

wise distance of the mean vectors in the latent space.

Figure 11 illustrates the cophenet index for each link-

age method. We can conclude that average linkage

performs the best with a cophenetic correlation coef-

ﬁcient equals to 0.71. Furthermore, the complete and

the Ward linkage methods perform reasonably well.

In contrast, the single linkage is the worst choice to

be used to get a satisfactory clustering.

Table 1: The 10 classes in the Fashion-MNIST data set.

Label Content Description

0 T-shirt/top

1 Trousers

2 Pullover

3 Dress

4 Coat

5 Sandal

6 Shirt

7 Sneaker

8 Bag

9 Ankle boot

Figure 11: Cophenet index of different linkage methods in

hierarchical clustering.

After calculating the minimum distance, we de-

termine the value of ε for all the mean vectors using

the equation in Line 10 of Algorithm 1. Any value of

the {0, ·· · , ε} set will generate outputs of the same

class. Figure 12 shows the values of ε where the

vector (µ

± ε

× σ

) , which has never been sampled

during the training phase, will be classiﬁed as class

. For instance, we can still get images classiﬁed as

Class 0 if we move in both directions from the mean

vector of Class 0 until 0.2010 times the standard de-

viation vector of Class 0.

Figure 12: The values of the parameter ε for each class la-

bel.

Figure 13 illustrates the output images that are

generated by the model using (µ

− ε

× σ

) (ﬁrst col-

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

492

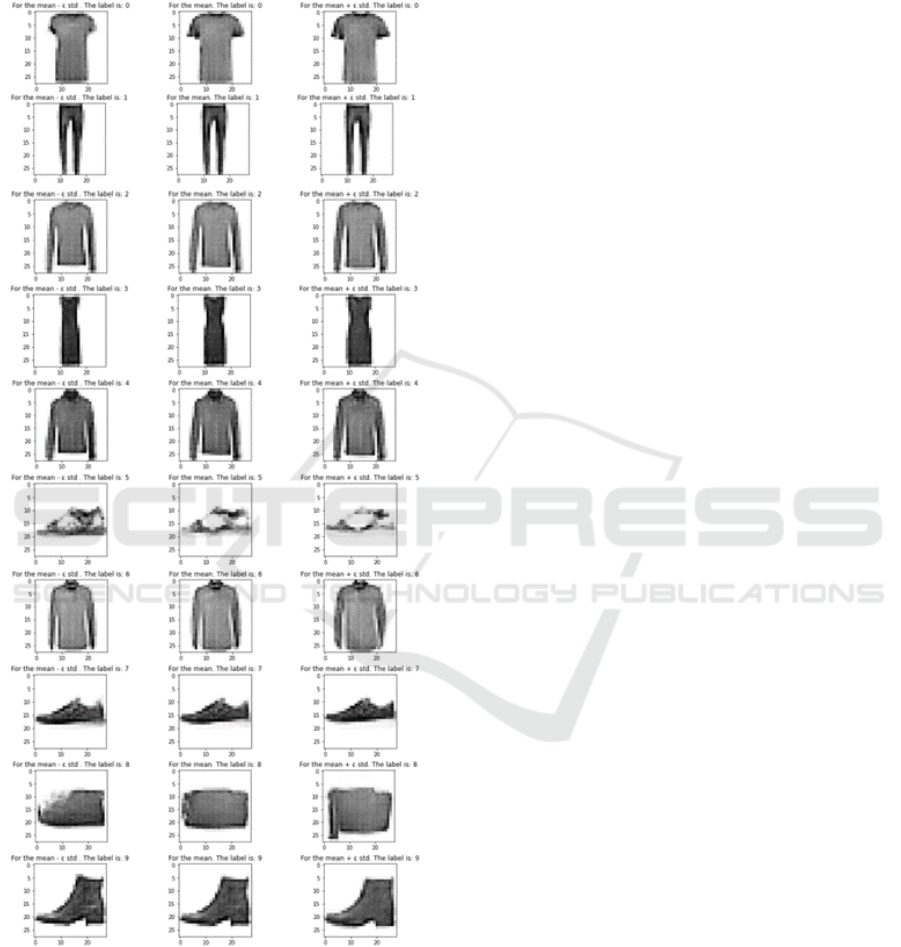
umn), (µ

) (second column), and (µ

+ ε

× σ

) (third

column) as input vectors. We can notice that shifting

from the mean vector by up to (ε

×σ

) will still result

in an image of the same class of the original one.

Figure 13: Generated output.

5 CONCLUSIONS

GAN’s latent space analysis is still an ongoing re-

search problem. In this paper, MAGAN, an algo-

rithm for Meta-Analysis for GANs’ latent space is

proposed and evaluated. GAN’s derived synthetic im-

ages are also examined to supplement training the

data addressing the issue of labeled data’s scarcity

where the generated output is used for data augmen-

tation. The results show that GANs may subsequently

be employed to be a parameter-controlled data gener-

ator as a further data-driven source of augmentation.

The quantitative results demonstrate that MAGAN

can perfectly map the relation between the arithmetic

modiﬁcations in the latent space and their impacts on

the resulting output in the image space. We can con-

clude that the latent space is invariant to a ε

×σ

shift

from the mean vector. With the completion of this

work, we pave the way for future research avenues in

GAN’s latent space analysis and provide a blueprint

for a deterministic GAN-based models that can be

used in distinct applications including data augmen-

tation and annotations generation.

ACKNOWLEDGMENTS

The authors are grateful to the reviewers whose sug-

gestions helped to improve the clarity of our paper.

This work was supported in part by the U.S. Na-

tional Science Foundation under grant number OIA-

1946231 and the Louisiana Board of Regents for the

Louisiana Materials Design Alliance (LAMDA).

REFERENCES

Bau, D., Zhu, J.-Y., Strobelt, H., Zhou, B., Tenenbaum,

J. B., Freeman, W. T., and Torralba, A. (2019). On

the units of GANs (extended abstract).

Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever,

I., and Abbeel, P. (2016). Infogan: Interpretable rep-

resentation learning by information maximizing gen-

erative adversarial nets.

Doersch, C. (2016). Tutorial on variational autoencoders.

Goodfellow, I. (2017). NIPS 2016 tutorial: Generative ad-

versarial networks.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In Ghahra-

mani, Z., Welling, M., Cortes, C., Lawrence, N., and

Weinberger, K., editors, Advances in Neural Infor-

mation Processing Systems, volume 27. Curran Asso-

ciates, Inc.

Jalal, A., Ilyas, A., Daskalakis, C., and Dimakis, A. G.

(2017). The robust manifold defense: Adversarial

training using generative models.

Karras, T., Aila, T., Laine, S., and Lehtinen, J. (2017). Pro-

gressive growing of gans for improved quality, stabil-

ity, and variation.

MAGAN: A Meta-Analysis for Generative Adversarial Networks’ Latent Space

493

Karras, T., Laine, S., and Aila, T. (2021). A style-based

generator architecture for generative adversarial net-

works. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 43(12):4217–4228.

Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-

ational bayes.

Mirza, M. and Osindero, S. (2014). Conditional generative

adversarial nets.

Radford, A., Metz, L., and Chintala, S. (2015). Unsuper-

vised representation learning with deep convolutional

generative adversarial networks.

Zhang, H., Goodfellow, I., Metaxas, D., and Odena, A.

(2018). Self-attention generative adversarial net-

works.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

494