Quantum Clustering on Streaming Data: A Novel

Method for Analyzing Big Data

Rebecca Hofer

and Kevin Mallinger

1,2

SBA Research gGmbh, Vienna, Austria

Technical University Vienna, Vienna, Austria

Keywords:

Quantum Clustering, Data Stream Clustering, Intrusion Detection, CIDDS-001 Dataset, IoTDI20 Dataset.

Abstract:

Quantum Clustering is an efﬁcient unsupervised machine learning method that exploits models of quantum

mechanics to discover clusters in data points. We applied an adaption of the algorithm on the CIDDS-001

and IoTID20 network intrusion datasets to distinguish malicious from benign network activity. For this pur-

pose, we integrated Quantum Clustering into the framework of DenStream, adjusting it to the streaming data

conditions required for analyzing network data. We found that this signiﬁcantly improved running time and

memory requirements compared to the original version of Quantum Clustering, which is known to have high

computational complexity. We also found that the accuracy with which the proposed version detected patterns

in network activity was comparable to established methods, conﬁrming the algorithm’s applicability for intru-

sion detection.

1 INTRODUCTION

1.1 Background

Novel advances in data collection methods increased

data availability tremendously over the past years.

Data that is generated and processed at fast rates is

also called data stream (C. Aggrawal, 2003). This

vast accessibility opens up many areas of application,

such as intrusion detection, stock market analysis, so-

cial network analysis, or observation of environmen-

tal systems. As analyzing big data is a challenge due

to limited computational resources, storage, and pro-

cessing time, there is a growing interest in increasing

the efﬁciency of methods while still producing con-

ﬁdent results for processing and managing massive

data (J. A. Silva, 2013).

In common data mining techniques, a ﬁnite

amount of data with a stationary probability distribu-

tion is assumed, and the data analysis method is per-

formed over the entire dataset. However, a core issue

with data streams is that new objects arrive continu-

ously, and the stream size is potentially unbounded.

Formally, a data stream can be described as a se-

quence of objects x

, x

,...,x

arriving at times T

,..., T

where each of these objects represents a

m × 1 - dimensional feature vector x

= (x

, x

,...

). Because of this continuous arrival of new data

and non-stationary data generation processes, the un-

derlying probability distribution is not stable but dy-

namically evolves (J. A. Silva, 2013). In network traf-

ﬁc analysis, for instance, patterns of user connections

are not stable but gradually change over time. In en-

vironmental monitoring, data can be subject to an ex-

ternal inﬂuence such as forest ﬁre, which will subse-

quently change its data distribution (C. Feng, 2006).

Considering the properties mentioned above, methods

that provide fast analysis are needed and can have a

valuable contribution to the research areas and appli-

cations where real-time monitoring and fast response

due to time-critical processes are needed.

The Internet-of-Things (IoT) is an ever-growing

source of data streams, attracting attention from

the industry as well as the academic ﬁelds

(D.E. Kouicern, 2018). As such, it is vulnerable

to security attacks in hardware and network com-

ponents. The heterogeneity, resource constraints,

physical coupling, and complex environment of the

devices make it especially hard for traditional net-

work or internet security approaches to ensure safety

(M.M. Noor, 2019). Security solutions for networks

can be grouped into three main components: pre-

vention, detection, and mitigation. When preven-

tion methods fail, intrusion detection comes into play

(I. Butun, 2014). Our research focuses on implement-

ing a new clustering approach to detect malicious be-

Hofer, R. and Mallinger, K.

Quantum Clustering on Streaming Data: A Novel Method for Analyzing Big Data.

DOI: 10.5220/0011764200003482

In Proceedings of the 8th International Conference on Internet of Things, Big Data and Security (IoTBDS 2023), pages 17-28

ISBN: 978-989-758-643-9; ISSN: 2184-4976

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

havior through scanning network data produced in

a simulated business environment and a network of

Internet-of-Things devices. Since the types of attacks

can vary, our approach solely relies on detecting at-

tacks, assuming that those patterns are distinguish-

able from malign network behavior but without prior

knowledge about the speciﬁc attack type.

1.2 State-of-the-Art

Clustering is a widely used technique for process-

ing data streams (A. Zubaroglu, 2021), (C. Aggrawal,

2003), (C. Feng, 2006), (T. Zhang, 1997). It is an

unsupervised machine-learning technique that groups

data according to a well-deﬁned similarity. Cluster-

ing algorithms adapted for streaming data differ from

static methods because they have to consider this dy-

namic evolution of the data probability distribution.

Algorithms handling data streams need to discard his-

torical data after a certain period to capture actual

patterns when clustering is performed and to ensure

memory accessibility (J. A. Silva, 2013). To address

this issue, a common approach of data stream cluster-

ing methods is separating the clustering process into

an online and ofﬂine process. In the online com-

ponent, statistical summary information of the data

is stored. At the same time, the ofﬂine component

takes this summary information as input for the ac-

tual clustering (C. Feng, 2006). The most relevant and

cited data stream clustering algorithms are BIRCH

(T. Zhang, 1997), CluStream (C. Aggrawal, 2003),

StreamKM++ (M.R. Ackermann, 2012), which are

based on the K-means algorithm, DenStream (F. Cao,

2006), D-Stream (Y. Chen, 2006), that are based

on DBSCAN, ClusTree (P. Kranen, 2011) as a hy-

brid method of k-means and DBSCAN, or Dynami-

cal Gaussian Mixture model, based on Gaussian Mix-

ture model clustering, to name a few (J. Diaz-Rozo,

2018). A commonly known problem with k-means

adaptions is the infeasibility of detecting complex and

arbitrarily shaped clusters (J. Diaz-Rozo, 2018). As

stream data only can be read once and the number

and shape of clusters are unknown in advance, meth-

ods need to be able to adapt to these data complexities

without prior speciﬁcations (L. Wan, 2009). Although

density-based clustering methods, such as the State-

of-the-Art algorithm DBSCAN, often perform very

well (A. Zubaroglu, 2021), there is a need to adapt and

ﬁne-tune methods to speciﬁc use cases. For network

intrusion analysis, algorithms need to be able to detect

and discriminate attack patterns of varying intensities.

It was shown that k-means, as well as DBSCAN, lack

sensitivity to detect those patterns in the context of

streaming data (P. Casas, 2012). This is why we pro-

pose a new method that is tailored to the speciﬁc chal-

lenges of network intrusion detection. Nevertheless,

taking DenStream as an extension of DBSCAN as a

comparison algorithm in this study, we compare our

method to a well-performing and widely established

stream clustering algorithm, highlighting the beneﬁts

our new method brings to the ﬁeld.

We analyze our algorithm for processing data

streams in the context of network intrusion detec-

tion. Currently, no research was conducted to in-

vestigate the application of Quantum Clustering for

streaming data or network anomaly detection. As

Quantum technology and, thus, new possibilities in

computation and analysis are on the rise, quantum-

inspired machine learning is bridging the gap where

quantum hardware computations are not commer-

cially available. However, the conceptual or mathe-

matical framework can already be used and mapped

to traditional computation tasks. Case studies us-

ing quantum-inspired machine learning techniques

are found in the context of analyzing high-energy

physics data (T. Felser, 2020), the analysis of 6G net-

works (T.Q. Duong, 2022), or recommendation sys-

tems (Tang, 2019) to name a few. Some of the studies

simulate the behavior of qubits or quantum states, in

general, (Y. Mahmoudi, 2020) as processing units and

use these approaches in the development of new meth-

ods, while others exploit the mathematical framework

to solve classical computation tasks in a new way

(K.H. Han, 2002). Quantum Clustering is a technique

inspired by the description and evolution of states de-

scribed as wavefunctions under the Schr

odinger equa-

tion. It works with a Parzen-window estimator as

a Gaussian wave packet over data points, viewing

those as the Eigenfunctions of the Schr

odinger equa-

tion (Y. Mahmoudi, 2020). Studies have shown the

strength of the method in several applications such as

asteroid spectrum taxonomy (Deutsch, 2017), docu-

ment analysis (D. Liu, 2016), or ﬁnancial data anal-

ysis (Shaked, 2013). Furthermore, (D. Liu, 2016)

showed the feasibility of the method for detecting

outliers in datasets, which makes it an exciting can-

didate for the application of network data analysis.

They showed that the algorithm could capture subtle

changes in the density of the data and outperformed

standard methods such as DBSCAN and conventional

Parzen-window methods (D. Liu, 2016). A signiﬁ-

cant advantage of Quantum Clustering is that it does

not require a predeﬁned number of clusters as con-

ventional methods like k-means, which makes it par-

ticularly practicable for automated analysis of data

streams. The data partition and sensitivity can be var-

ied with the length scale of sigma - the width param-

eter of the Gaussian kernel - where a bigger value

IoTBDS 2023 - 8th International Conference on Internet of Things, Big Data and Security

of sigma increases the width of the Gaussian func-

tion. As a framework for ﬁnding the optimal hyperpa-

rameter value, (R.V. Casana-Eslava, 2020) suggested

an approach that considers selecting the kernel width

as the mean distance between the data points and its

k-nearest neighbors. A detailed explanation of the

method can be found in (R.V. Casana-Eslava, 2020).

As Quantum Clustering comes with the challenge of

having a high time and space complexity O(n

) due to

the computation of distances between each data point

with all the other data points and the gradient of the

potential function (P. Jim

enez, 2022), (Shaked, 2013)

(see Eq. 3), studies deployed the original Quantum

Clustering mostly to small datasets (D. Liu, 2016),

(D. Horn, 2001), (R.V. Casana-Eslava, 2020). To

tackle the complexity problem, (Shaked, 2013) sug-

gested using Approximate Quantum Clustering to re-

duce the number of data points for calculating the

probability function. In this approach, the dataspace

gets divided into an n-dimensional grid, where one

unit is called a voxel. The data points falling within

a voxel are approximated as one data point. This re-

duces the problem’s dimensionality, but the method is

not directly applicable to analyzing data streams, as it

does not consider the dynamic changes in the under-

lying probability distribution of data.

To overcome the mentioned limitations, this paper

investigates the implementation of Quantum Cluster-

ing into the framework for handling large data streams

while combining the beneﬁts of fast and accurate

cluster detection and the detection of small groups

of irregularities, without prior knowledge of cluster

amounts. With this, we present a new method in data

stream analysis and propose an approach to address

the complexity problem of Quantum Clustering. The

suggested approach builds on the work of (C. Feng,

2006) and the DenStream algorithm, as an extension

of DBSCAN for handling large data streams. The

model is based on a density clustering approach seek-

ing to partition the data space into high and low-

density regions.

In the following, some preliminary concepts will

be described. We will then introduce the adapted ver-

sion of Quantum Clustering for streaming data and

evaluate it in terms of clustering quality, space, and

time complexity.

2 METHODS

2.1 Quantum Clustering

The method of Quantum Clustering was developed by

David Horn, and Assaf Gottlieb (D. Horn, 2001). It

uses a Gaussian kernel to generate a probability dis-

tribution from the data points given by:

Ψ(x) =

∑

(x−x

)

2σ

(1)

The probability distribution results as the sum of

Gaussians computed over the data points. Embedded

in the Quantum framework, we interpret the probabil-

ity distribution as a wave function and insert it into

the stationary Schr

odinger equation:

Hψ ≡



−

∇

+V (x))Ψ(x) = EΨ(x) (2)

where H is the Hamiltonian, E is the energy eigen-

value, σ is the width parameter of the Gauss func-

tion, ∇ denotes the Laplacian operator and V (x) is the

potential function. We denote the ground state en-

ergy eigenvalue with E =

as the lowest possible en-

ergy in the system. When solving the Schr

odinger

equation, we usually look for solutions for the wave-

functions as evolving in the system described by the

Hamiltonian, from which the probability of ﬁnding

a particle in a certain state can be calculated. The

Hamiltonian, specifying this evolution, is composed

of a kinetic term and the potential V . In the case of

Quantum Clustering, we look at the problem from the

opposite side - given the probability distribution of

data points, we want to calculate the potential func-

tion V , which results from the Gaussians over the data

distribution. We then interpret the local minima of

this function as our cluster centers. Rewriting Eq. (2),

we arrive at the expression for the potential function

of the form:

V (x) = E +

∇

= E −

2σ

∑

(x − x

)

−

(x−x

)

2σ

(3)

Setting E = −min

∇

, the potential function V

can be determined uniquely. To arrive at the clusters,

we apply the Gradient descent algorithm to our po-

tential function, with η as the learning rate. Deﬁn-

ing y

(0) = x

the data points get clustered by moving

them along the gradient from their initial position to

the local minima of the potential function, i.e. the

cluster centers, in discrete steps y

(t + ∇t):

(t + ∇t) = y

(t) − η(t)∇V (y

(t)) (4)

The time complexity for calculating the potential

function is O(n), where n is the number of data points,

whereas the time complexity for each complete step

of the gradient descent is O(n

). The complete cal-

culation of Quantum Clustering, therefore, is of the

order O(m · n

) with m being the number of itera-

tions in the gradient descent (Shaked, 2013). For large

Quantum Clustering on Streaming Data: A Novel Method for Analyzing Big Data

datasets, the complexity of the algorithm makes cal-

culations unfeasible. Therefore, we propose an adap-

tation of the algorithm integrating it into an existing

framework for streaming data.

2.2 DenStream

In this study, we draw on the method of DenStream

(C. Feng, 2006). It uses a damped window model,

which considers the latest information given by data

points by assigning weights, whereas more recent ob-

jects have higher weights than older objects. The

weight ω of each data point decreases with time, fol-

lowing an exponentially decreasing function f (x) =

−λt

, in which λ is the decay constant. A high value

of λ results in a faster decrease of old information.

Clustering in the data stream can be divided into

two steps: the online component, also known as the

data abstraction step, and the ofﬂine component at

which the actual clustering is performed. In the data

abstraction step, summary statistics of the data in the

stream are stored in a feature vector. In the case

of DenStream, data points get sampled into micro-

clusters of outlier-micro-clusters (o-micro-cluster) or

potential-micro-clusters (p-micro-cluster). An arriv-

ing data point gets merged into a p-micro-cluster if the

resulting cluster radius after adding this data point lies

within a maximum radius of ε. If this is not the case,

the data point is tried to be merged into an existing

o-micro-cluster. If the radius of this cluster then suc-

ceeds the maximum radius, ε, a new o-micro-cluster

is created. The algorithm continuously checks the up-

dated weights of the clusters after a deﬁned time pe-

riod. When a given threshold ω > βµ for the weight is

reached (the hyper-parameters β and µ have to be set

respectively), o-micro-clusters evolve into p-micro-

clusters. Due to the decay function, when no new

points get clustered into an existing p-micro-cluster, it

will become an o-micro-cluster since its weight ω will

fall under the given threshold and subsequently be

deleted from the outlier buffer. With this, DenStream

reduces the required space in memory and takes care

of the dynamical evolution of the probability distribu-

tion of the data stream. The ofﬂine component data

get clustered in the original version by the DBSCAN

algorithm. When a clustering request arrives, the p-

micro-cluster-centers given at that time are treated as

virtual data points with an assigned weight.

2.3 Quantum Clustering Implemented

in DenStream Framework

Instead of DBSCAN, in this study, we apply Quan-

tum Clustering as an ofﬂine clustering method, treat-

ing the p-micro-cluster-centers as data points for cal-

culating the probability function. On the one hand,

this approach is valuable as we overcome the high

computational complexity of Quantum Clustering,

ﬁnding a way to apply it to the use case of net-

work intrusion detection. On the other hand, Quan-

tum Clustering shows comparable to increased per-

formance over the traditionally used DBSCAN. In

the following, we will refer to the new method as

DenStream

for the adapted version of Quantum

Clustering and DenStream

DBSCAN

for the conven-

tional method. When a clustering request arrives on

the data stream, the potential function gets calculated

over the p-cluster-centers, and the algorithm clusters

the p-micro-cluster-centers. After this clustering step,

the data points get assigned the label of their near-

est p-cluster center, following the distance-based ap-

proach suggested in the original framework. Using

Quantum Clustering to cluster the data in the ofﬂine

phase is a novel approach to fasten its computation

time. The number of data points in calculating the

potential function and the gradient descent gets re-

duced since we only consider the p-cluster-centers.

Furthermore, through the dynamic calculation of the

cluster centers, the clustering result reﬂects a real-

time picture of the underlying data distribution. As

with the DBSCAN algorithm DenStream uses, Quan-

tum Clustering does not require a predeﬁned number

of clusters, which is important for the clustering data

stream, as the number of clusters might change over

time (C. Feng, 2006).

2.4 Experimental Design

In the ﬁrst step, we compare the original

DenStream

DBSCAN

with our new approach

DenStream

for cluster quality, calculating the

metrics Purity and F1-Score over different time-

windows for both methods for the CIDDS-001 and

the IoTID20 dataset. To simulate a natural streaming

data environment, the data is fed into the clustering

algorithms in the order of the instances given by

the data set. Employing the decay function, which

decreases the cluster weights when no new data is

assigned to that cluster, we further ensure that old

data points get discarded when the clustering request

arrives.

To evaluate the feasibility of our method for

anomaly detection, we analyzed the results for each

attack class respectively and calculated Precision, Re-

call, and Accuracy. We could do this since both

datasets were labeled for the respective attack classes.

We then analyze the method in terms of mem-

ory requirement and running time compared with the

IoTBDS 2023 - 8th International Conference on Internet of Things, Big Data and Security

original Quantum Clustering to show the increased

computational performance. All test runs were con-

ducted on the same hardware, a 64-bit operating sys-

tem with a CPU with 1.80 GHz and an available RAM

of 8.00 GB.

2.5 Datasets

2.5.1 CIDDS-001 Dataset

The ﬁrst dataset used in this study is the CIDDS-001

dataset (M. Ring, 2017). It is a labeled, ﬂow-based

dataset generated for anomaly-based intrusion evalu-

ation. It consists of four weeks of network trafﬁc data

in total, generated through OpenStack and an Exter-

nal Server respectively. The data is labeled for ﬁve

different classes: normal data trafﬁc, attack, victim,

suspicious, and unknown. Each ﬂow instance is as-

signed to one class. The labeling of the ﬂows hap-

pened as follows, according to the authors: ﬂows that

come from the OpenStack environment were only be-

nign and therefore labeled as normal, ﬂows coming

from port 443, and 80 could be normal trafﬁc or in-

trusion attempts categorized as unknown. The attacks

came from three controlled servers; those ﬂows were

labeled as either attack or victim, respectively. All

remaining trafﬁc was labeled suspicious, leaving the

class relatively broad and undeﬁned (M. Ring, 2017).

In this study, we used the dataset of the third week,

captured at the external server. We chose this set be-

cause of the variety of employed attacks: week 1 on

the external server had no executed attacks and was

therefore not interesting for our analysis, whereas our

dataset had the most attacks executed, 12 in total, 5 of

which were PortScan and 7 Brute Force. The set con-

sists of 153026 instances and 8 attributes used for fur-

ther processing: Source IP Address, Source Port, Des-

tination IP Address, Destination Port, Proto, Dura-

tion, TCP-Flags, and Packets. Flows with class labels

attack or victim are further categorized into the types

of attacks. We use this distinction for our ground truth

labeling for our analysis, resulting in seven class la-

bels. Table (1) shows a summary of the dataset. We

can see that the dominant class is the class labeled

suspicious with more than half of the instances be-

longing to it. What is apparent is the imbalance in the

dataset, with comparatively small classes Brute Force

attack and victim.

2.5.2 IoTID20 Dataset

The second dataset used is the IoTID20 (I. Ullah,

2020), which is more focused on the context of the

Internet of Things and contains a combination of IoT

devices with interconnections. The data was gener-

Table 1: CIDDS-001 dataset external server week 3.

Class Total Flows Label

bruteForce Attack 700 0

portScan Attack 8555 1

Normal 6180 2

Suspicious 97852 3

Unknown 33837 4

bruteForce Victim 700 5

portScan Victim 5202 6

ated in a smart home environment consisting of SKT

NGU devices and an EZVIZ Wiﬁ camera that is con-

nected to a router. Other devices connected to that

network include laptops, smartphones, and tablets.

The SKT NGU and EZVIZ Wiﬁ camera act as vic-

tim devices, whereas all the other devices in the ar-

chitecture are attacking devices. The dataset consists

of 80 network features and is labeled according to the

attack classes DoS, MITM, Mirai, Normal, and Scan.

In total, it contains 625783 ﬂow instances, whereas

we only took 150000 to test our model. As in the

CIDDS-001 dataset, we used a categorical encoding

method for the features’ Source and Destination IP

addresses. The other numerical features were normal-

ized. Features contained in the dataset were Protocol

Type, Duration, Packets, and Flag, to name a few. For

further details about the data, we point the reader to

the original paper (I. Ullah, 2020). For our analysis,

we used the mutual information score as a feature se-

lection method, reducing the number of features from

80 to 41. In Table (2), we depict a summary of the la-

beled instances, as well as the assigned label that we

use in the result section to display the cluster results

of the respective classes.

Table 2: IoTID20 dataset; normal and attacked instances.

Class Total Flows Label

DoS 14149 0

MITM 8381 1

Mirai 99811 2

Normal 9519 3

Scan 18140 4

2.6 Metrics

Because both datasets contained labeled instances, we

were able to use classiﬁcation metrics for the clus-

tering analysis. To quantify our results and compare

it to the given label classes, we labeled the resulting

clusters according to their most frequently occurring

class. The Purity of the clustering is then calculated

by summing the correct assigned data points in each

class and dividing it by the number of total data points

Quantum Clustering on Streaming Data: A Novel Method for Analyzing Big Data

purity(Ω,C) =

∑

max

|ω

∩ c

| (5)

here Ω = {ω

, ω

, ..., ω

} is the set of predicted clus-

ters and C= {c

, c

, ..., c

} is the set of classes (Stan-

ford, 2008).

Purity alone is not a good indicator of cluster qual-

ity since a high number of clusters automatically re-

sults in a higher Purity - if each data point is sepa-

rately clustered in one class, the Purity is 1 (Stanford,

2008). We, therefore, additionally evaluate the clus-

tering result with the Precision, Recall, Accuracy, and

F1-Score, as described in Equations (6)-(9). Here T P

is the true positive, T N is the true negative, FP is the

false positive and FN is the false negative:

Precision =

T P

T P + FP

(6)

Recall =

T P

T P + FN

(7)

Accuracy =

T P + T N

T P + T N + FP + FN

(8)

F1 − Score = 2 ·

Precision ∗ Recall

Precision + Recall

(9)

3 RESULTS

In this section, we test the performance of the stream-

ing adapted version DenStream

by evaluating its

ability to detect patterns in the datasets, as well as its

space and running time requirements in comparison

to the original Quantum Clustering.

3.1 Cluster Quality

3.1.1 CIDDS-001 Dataset

We test the Purity and F1-Score for different peri-

ods of stream execution for the conventional Den-

Stream algorithm using DBSCAN as its method for

the clustering step and our version using Quantum

Clustering. As the weights of the data points gradu-

ally decrease and are thus erased from memory and no

longer available for clustering, we compute the cluster

metrics for deﬁned windows starting from the present

time. Since lambda is the decisive parameter for how

fast this decrease happens, the one for the compari-

son was chosen to be the same for both algorithms.

We have chosen the parameters for both algorithms

to achieve the highest possible Purity and F1-Score.

Figure (1) and Figure (2) show that the performance

for both metrics of DenStream

DBSCAN

is slightly bet-

ter than that of DenStream

across the windows.

For both, DenStream

and DenStream

DBSCAN

, the

values of Purity and F1-score are around 0.95 with

a minimum F1-Score of 0.87 for DenStream

and

0.89 for DenStream

DBSCAN

. For DenStream

DBSCAN

both values remain relatively constant across the win-

dows, with Purity and F1-Score decreasing slightly

for DenStream

for larger periods of stream execu-

tion.

As the attack clusters are highly underrepresented,

the generalized metrics do not adequately indicate

the cluster quality. We, therefore, added Tables (3)-

(6) to compare the ability of the algorithms to detect

small clusters. Figures (3) and (4) show the cluster

results for DenStream

and DenStream

DBSCAN

, re-

spectively, for the whole dataset. On the horizontal

axis, we can see the detected classes. As described

in the methods section, these have been labeled based

on the most common class found in them. The verti-

cal axis shows the ground truth class to which the data

points actually belong. Tables (4) and (5) show that

both algorithms detect the majority classes (e.g., sus-

picious, unknown) well, whereas DenStream

DBSCAN

has a slightly higher detection rate for this data set.

On the other side, underrepresented classes, as its

most common in network intrusion sets, could not be

detected at all by DBSCAN. Therefore, the classes

that stand out in the result of both methods are brute-

Force attacker and victim. With DenStream

DBSCAN

none of the ﬂows could be clustered correctly, but

nearly entirely fell into the class suspicious. In the

case of DenStream

, the ﬂows of bruteForce at-

tacker were clustered either as normal or suspicious,

and the ﬂows belonging to ground truth label brute-

Force victim were nearly entirely clustered as suspi-

cious.

In the case of DenStream

DBSCAN

, adapting the hy-

perparameters did not improve the clustering result

for the class bruteForce - varying the parameters only

led to an overall deterioration in cluster quality. For

DenStream

, however, we enhanced the clustering

result of bruteForce attacker and victim for smaller

values of ε. Figure (5) and Table (6) show the cluster-

ing result for a value of the maximum micro-cluster

radius ε = 0.1 for DenStream

. This resulted in

a signiﬁcantly better cluster detection for bruteForce

attacker and victim of 47% respectively in compari-

son to 0% for DenStream

DBSCAN

. The ﬂows which

could not be assigned to the correct classes again

predominantly fell into the category suspicious. We

will discuss this result in more detail in the next sec-

IoTBDS 2023 - 8th International Conference on Internet of Things, Big Data and Security

Figure 1: Purity for different window sizes for

DenStream

CIDDS-001 dataset.

Figure 2: F1-Score for different window sizes for

DenStream

and DenStream

DBSCAN

CIDDS-001 dataset.

tion. Table (3) further shows the summary results of

DenStream

and DenStream

DBSCAN

of the metrics

Precision, Recall, and Accuracy. For the CIDDS-

001 dataset, DenStream

achieved an accuracy of

0.91 for the clustering displayed in Figures (3) and

(5), and DenStream

DBSCAN

an accuracy of 0.93. The

methods for network intrusion detection must be tai-

lored to the reliable detection of attacks. An assign-

ment of instances as False-Positive is often more cost-

effective than False-Negative, i.e., a non-detection of

attack patterns can have more severe consequences

than a slightly too sensitive attack analysis method.

Figure (5) shows that after epsilon’s ﬁne-tuning, only

104 data ﬂows were incorrectly clustered as normal

from DenStream

. With DenStream

DBSCAN

, 237

ﬂows were not detected as attacks or potential attacks

but clustered as normal network behavior. This ob-

servation is also reﬂected in the values for Recall.

For DenStream

this is 90% after ﬁne-tuning; for

DenStream

DBSCAN

, 88% is the best case.

Figure 3: Result DenStream

with ε = 0.4 CIDDS-001

dataset.

Figure 4: Clustering result DenStream

DBSCAN

CIDDS-001

dataset.

Figure 5: Result DenStream

with ε = 0.1 CIDDS-001

dataset.

3.1.2 IoTID20-Dataset

For the IoTID20 dataset, we see that the Quantum

clustering method achieves much better results than

Quantum Clustering on Streaming Data: A Novel Method for Analyzing Big Data

Table 3: Metrics Clustering Results DenStream

Data Precision Recall Accuracy

Fig. 3 DenStream

CIDDS-001/ 0.9034 0.8419 0.9142

Fig. 5 DenStream

CIDDS-001 0.8461 0.9037 0.9157

Fig. 4 DenStream

DBSCAN

CIDDS-001 0.9176 0.8845 0.9377

Fig. 8 DenStream

IoTID20 0.5939 0.9521 0.7301

Fig. 9 DenStream

DBSCAN

IoTID20 0.5747 0.8658 0.7033

Table 4: Summary results DenStream

with ε = 0.4

CIDDS-001; Figure 3.

Class correctly clustered instances

bruteForce attacker 0 ≡ 0%

portScan attacker 8538 ≡ 99%

Normal 6094 ≡ 98%

suspicious 89722 ≡ 92%

unknown 30357 ≡ 90%

bruteForce victim 0 ≡ 0%

portScan victim 5183 ≡ 99%

Table 5: Summary results DenStream

DBSCAN

CIDDS-001;

Figure 4.

Class correctly clustered instances

bruteForce attacker 0 ≡ 0%

portScan attacker 8538 ≡ 99%

Normal 6092 ≡ 98%

suspicious 91866 ≡ 94%

unknown 31814 ≡ 94%

bruteForce victim 0 ≡ 0%

portScan victim 5183 ≡ 99%

Table 6: Summary results DenStream

with ε = 0.1

CIDDS-001; Figure 5.

Class correctly clustered instances

bruteForce attacker 332 ≡ 47%

portScan attacker 4636 ≡ 54%

Normal 6048 ≡ 97%

suspicious 93516 ≡ 95%

unknown 31006 ≡ 91%

bruteForce victim 300 ≡ 47%

portScan victim 4291 ≡ 82%

the original DenStream

DBSCAN

algorithm. The over-

all performance of the methods for the second dataset

is not as good as for CIDDS-001, indicating the

complexity of the data produced in an IoT environ-

ment. For the Purity and F1-measure, DenStream

shows a constant performance over window sizes,

with an average score of 0.7 in both metrics, whereas

DenStream

DBSCAN

only achieves an average result of

around 0.65.

Similar to the CIDDS-001 dataset, some attack

classes tend to be overpredicted by the clustering;

in the IoTID20 dataset, it is the class Mirai. In the

case of DenStream

DBSCAN

, the class DoS was over-

predicted as well - in the end, the method only clus-

tered the instances into these two classes. Again this

is probably because of the imbalance in the dataset,

where the majority of instances belong to this attack

class, and especially DenStream

DBSCAN

has problems

detecting the small clusters in the large dataset. Our

method shows very good results for the differentia-

tion of the DoS attack class, with a correct prediction

of 99% of the instances belonging to this category,

and predicted in total only 13 instances False-Positive

for this class. Also, DenStream

detected the Scan

attack much better with 41% compared to 0% for

DenStream

DBSCAN

. The Accuracy of DenStream

for clustering the data into the different attack classes

was 0.73, as shown in Table (3). We see that al-

though DenStream

DBSCAN

performed very badly for

this dataset, its accuracy is still higher than one would

expect. That is because it overpredicted the classes

with the most instances, which distorts the result.

Therefore the analysis and comparison of individ-

ual cluster assignments are important for imbalanced

data.

Other studies that analyzed the IoTID20 dataset

using clustering techniques didn’t report on individ-

ual results of the respective attack class categories,

which is why a comparison in this regard is difﬁcult.

In fact, most studies we found deploying IoTID20

used a supervised learning approach (R. Qaddoura,

2021), (A.Y. Hussein, 2021), (H. Alkahtani, 2021),

(S. Bajpai, 2021), (T.V. Ramana, 2022). For real-

world data, such approaches remain often unfeasible,

as attack patterns are often not known beforehand, or

no prior attack data is available. Quantum Cluster-

ing is able to recognize some classes with high accu-

racy, which is a promising result and can be used as

a benchmark result for other clustering studies in the

domain of anomaly detection.

Table 7: Summary results DenStream

with ε = 0.8

IoTID20; Figure 9.

Class correctly clustered instances

Normal 6108 ≡ 64%

DoS 14030 ≡ 99%

Mirai 90104 ≡ 90%

MITM 1393 ≡ 16%

Scan 7366 ≡ 41%

IoTBDS 2023 - 8th International Conference on Internet of Things, Big Data and Security

Figure 6: Purity for different window sizes for

DenStream

and DenStream

DBSCAN

IoTID20 dataset.

Figure 7: F1-Score for different window sizes for

DenStream

and DenStream

DBSCAN

IoTID20 dataset.

Table 8: Summary results DenStream

DBSCAN

IoTID20;

Figure 10.

Class correctly clustered instances

Normal 0 ≡ 0%

DoS 11536 ≡ 82%

Mirai 93774 ≡ 94%

MITM 0 ≡ 0%

Scan 0 ≡ 0%

3.2 Runtime and Memory Analysis

In this section, we compare the runtime and mem-

ory requirement of our new method and the original

Quantum Clustering. We only do this for the CIDDS-

001 dataset, which is sufﬁcient since the size of both

datasets is almost the same.

Figure 8: Clustering result DenStream

with ε = 0.8

IoTID20 dataset.

Figure 9: Clustering result DenStream

DBSCAN

IoTID20

dataset.

In the original version of Quantum Clustering, the

computational complexity makes the algorithm infea-

sible for large streaming datasets. Therefore, one of

the main foci of our study was to ﬁnd a way to im-

prove the runtime performance and memory space re-

quirement of the clustering. We could not test the

original version of Quantum Clustering for the whole

dataset as the computational demand exceeded the

available RAM capacities. We only used the ﬁrst forty

percent of the dataset. As expected, there were no

memory capacity problems for the version adapted for

streaming data, so we used the complete dataset.

In the graphs for the running time (Figures 10 and

11), we see the time measured on the hardware re-

quired to run the algorithm for different numbers of

instances. In the graphs showing the memory require-

ments, we executed one run for the complete dataset

for DenStream

(Figure 12) and one run using only

forty percent of the data for the original Quantum

Clustering (Figure 13). The graphs show the RAM

required for different time points in the algorithm

execution and highlight the high computational de-

mand of the original Quantum Clustering approach in

Quantum Clustering on Streaming Data: A Novel Method for Analyzing Big Data

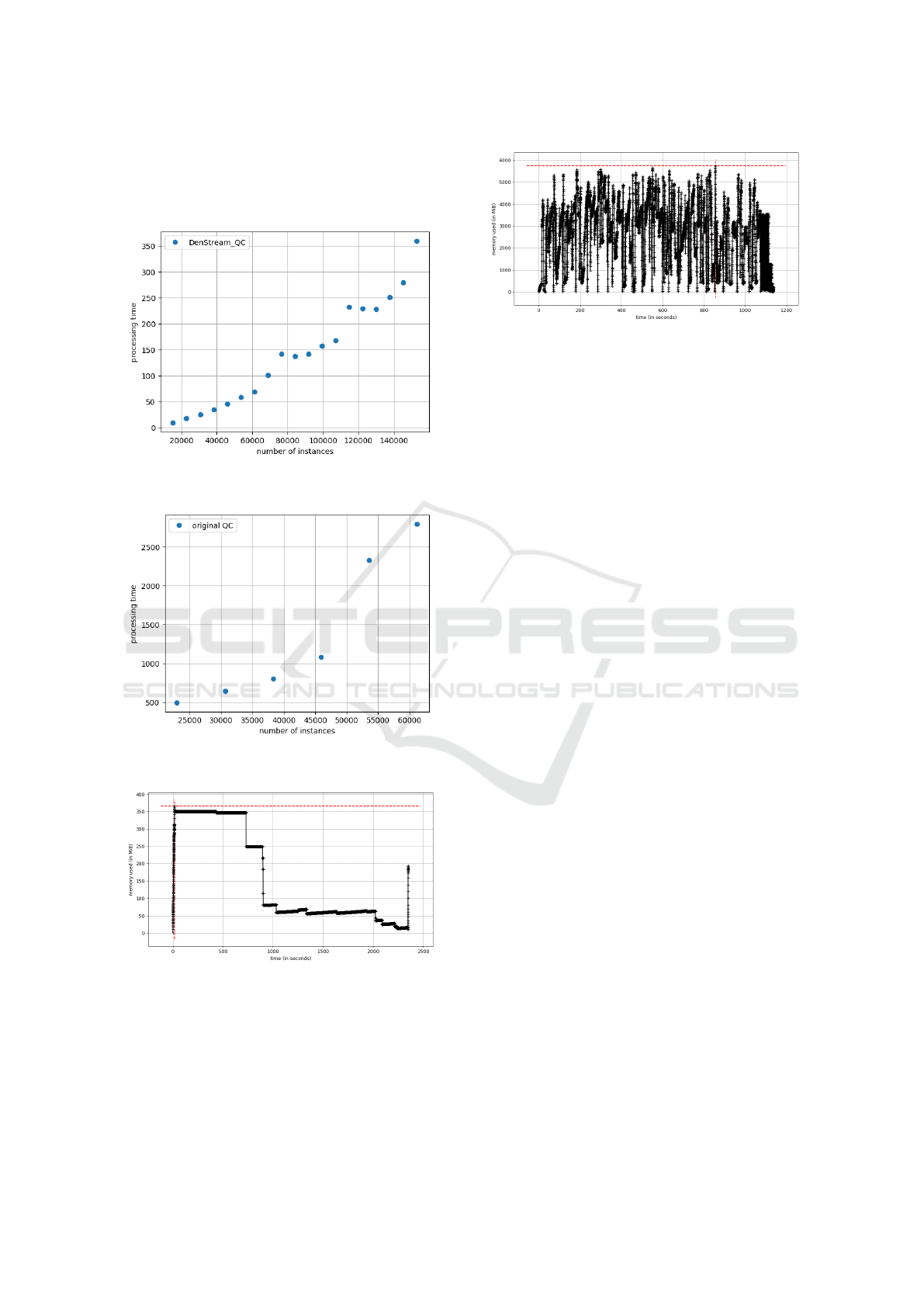
comparison to DenStream

. In the original Quan-

tum Clustering, we are already close to the maximum

RAM capacity available for the test run by only using

a fraction of the data.

Figure 10: Running time DenStream

for all instances of

the dataset CIDDS-001.

Figure 11: Running time for the original Quantum Cluster-

ing for 40% instances of the dataset CIDDS-001.

Figure 12: Memory requirement in DenStream

for all

instances of the dataset CIDDS-001.

4 DISCUSSION

The implementation of Quantum Clustering into the

framework of DenStream for streaming data leads to a

Figure 13: Memory requirement in the original Quantum

Clustering for 40% instances of the dataset CIDDS-001.

signiﬁcant reduction in runtime and memory require-

ments. Although runtime and memory consumption

is not stable for different hardware, we want to illus-

trate the improved performance by highlighting the

clear difference between the streaming adapted ver-

sion DenStream

compared to the original method.

This reduction is achieved as the potential function,

and the subsequent clustering is not performed over

all data points of the dataset but only on those who

are present in memory at the time when clustering

is requested. We could only evaluate forty percent

of the dataset for the original version of Quantum

Clustering because of exhausted RAM capacity. We

have therefore refrained from comparing the clus-

ter results of Quantum Clustering with Denstream

The small number of data ﬂows to be evaluated and

the high computation time excludes the original algo-

rithm from being applied to streaming data. As far as

we know, our proposed method DenStream

is the

ﬁrst use case where it was possible to use Quantum

Clustering to analyze data streams and further extend

its applicability to intrusion detection.

We are interested in detecting malign network be-

havior and attack patterns in real time for this use

case. From Table (4), we can see that our streaming

adopted method could assign all classes except brute-

Force attacks and bruteForce victims very well for the

CIDDS-001 dataset, with a 90%-99% match for each

of the labels, respectively.

Overall, 91% of the instances were clustered cor-

rectly. When false clustering happens, the ﬂows are

most often assigned to the class suspicious for both

methods, DenStream

and DenStream

DBSCAN

. This

tendency of disproportionately frequent assignment

to these categories could also be observed after the

adaptation of the hyperparameters. From these re-

sults, we can conclude that this class seems to be

not clearly deﬁned and distinguishable for machine

learning models, i.e., ﬂows that fall into this cate-

gory are not as clearly delineated as those of the other

classes. This was also pointed out in (M. Ring, 2017)

and (J. Carneiro, 2022) and comes from the labeling

IoTBDS 2023 - 8th International Conference on Internet of Things, Big Data and Security

process described above. The class suspicious repre-

sents a broad container term for ﬂows that are neither

attacks, ﬂows from the OpenStack environment, nor

ﬂows coming from ports 80 and 443. Another reason

for the overabundant assignment to the class suspi-

cious is the imbalance in the dataset, where it is by far

the largest in the number of ﬂows.

On the other hand, this imbalance makes it

hard for the algorithm to identify the classes brute-

Force victim and bruteForce attacker. Both classes

represent the smallest number of ﬂows, making it

difﬁcult for the algorithm to detect their patterns.

Comparing our method with the performance of

DenStream

DBSCAN

leads to similar results in purity

and F1-Score. However, DenStream

was better at

detecting the small-sized clusters of bruteForce victim

and bruteForce attacker in the data. By choosing ap-

propriate parameters, it was possible to obtain a bet-

ter delimitation of these classes, which was not pos-

sible for DenStream

DBSCAN

. Further research has to

be done to test DenStream

’s sensitivity to data pat-

terns and to various hyperparameters settings. Nev-

ertheless, the observations show the possibility of us-

ing DenStream

in a combination with variable hy-

perparameter settings when dealing with imbalanced

data to make hardly discernible patterns visible. Fur-

thermore, the better Recall value makes it a promis-

ing tool, especially in the context of intrusion detec-

tion, where sensitivity to pattern changes and outliers

is needed.

Similar conclusions can be drawn from the analy-

sis of the IoTID20 dataset. Also, this dataset has an

imbalance in the classes, where the class Mirai is the

biggest one with 99811 instances. Since also for this

dataset, the majority of wrong-clustered instances fall

into this category, we can conclude that DenStream

still needs to be ﬁne-tuned for imbalances in data

and the detection of outliers. Still, in comparison

to the original DenStream

DBSCAN

method, Quantum

Clustering shows good performance for both datasets.

DenStream

is able to locate clusters that are difﬁ-

cult to delineate for DenStream

DBSCAN

. This is espe-

cially evident for the IoTID20 dataset. The method of

constructing the potential function to estimate the data

density distribution allows quantum clustering to pick

up dynamic patterns in the data. As studies have pre-

viously shown, quantum clustering shows superiority

in ﬁnding outliers, compared to DBSCAN (D. Liu,

2016). Our results in a direct comparison of the two

methods in the framework of stream clustering con-

ﬁrm this trend.

We also point to the need for more data stream

clustering studies using this dataset. Hence, a quanti-

tative comparison of our method with other standard

streaming methods in terms of cluster quality was out

of the scope of this study.

Overall, the results suggest that DenStream

an exciting new method in the repertoire of stream-

ing algorithms that brings the advantages of the orig-

inal Quantum Clustering shown in previous studies

(D. Liu, 2016), (D. Liu, 2020), (Deutsch, 2017), (R.V.

Casana-Eslava, 2020), (Shaked, 2013) to the context

of big data. The reduced memory and running time

requirements of the method can beneﬁt applications

on devices that cope with limited resources but must,

at the same time, ensure secure data analysis. Con-

strained devices can be found in the context of the

internet of things a lot, pointing to an important use

case area of DenStream

- especially in the context

of security and resilience, where continuous moni-

toring and real-time analysis of systems are required,

and standard solutions fail to deliver the desired per-

formance (N. Ntuli, 2016). With this study, we ad-

dress the question of how security aspects in the IoT

can be ensured despite limited capacities, suggesting

a method that can provide fast, reliable, and computa-

tionally effective results.

5 CONCLUSION

This paper proposed a variation of the original al-

gorithm Quantum Clustering as an implementation

into the framework of DenStream. We show that

the Quantum Clustering approach achieves solid re-

sults compared to State-of-the-Art algorithms like

DBSCAN. It was able to detect small clusters in an

unbalanced dataset, which was not possible for DB-

SCAN. This makes the Quantum Clustering approach

particularly suitable for data consisting of small clus-

ters, such as the network intrusion domain. It could

also be shown, by comparing the runtime and mem-

ory costs, that the adapted quantum clustering ap-

proach could be signiﬁcantly enhanced in processing

speed, rendering it a suitable application for various

network domains. This advancement allows the use

of optimization methods of hyperparameters to detect

different network anomalies. These results make us

conﬁdent that DenStream

can be used for further

streaming data analysis applications.

REFERENCES

A. Zubaroglu, V. A. (2021). Data Stream Clustering: A

review. In: Artiﬁcial Intelligence Review), 54.

A.Y. Hussein, P. Falcarin, A. S. (2021). Enhancement per-

formance of random forest algorithm via one hot en-

Quantum Clustering on Streaming Data: A Novel Method for Analyzing Big Data

coding for IoT IDS. Periodicals of Engineering and

Natural Sciences, 9.

C. Aggrawal, J. Han, J. W. P. Y. (2003). A framework

for clustering evolving data streams. Proceedings of

the 29th International Conference on Very Large Data

Bases, 29.

C. Feng, M. Ester, W. Q. A. Z. (2006). Density-Based Clus-

tering over an Evolving Data Stream with Noise. In:

Proceedings of the 2006 SIAM International Confer-

ence on Data Mining, SDM.

D. Horn, A. G. (2001). The method of Quantum Clustering.

In: Proceedings of the 14th International Conference

on Neural Information Processing Systems: Natural

and Synthetic, NIPS 01.

D. Liu, H. L. (2020). Outlier Detection Using a Novel

method. Arxiv.

D. Liu, M. Jiang, X. Y. H. L. (2016). Analyzing documents

with Quantum Clustering: A novel pattern recogni-

tion algorithm based on quantum mechanics. Pattern

Recognition Letters, 77.

D.E. Kouicern, A. Bouabdallah, H. L. (2018). Internet of

things security: A top-down survey. Computer Net-

works, 141.

Deutsch, L. (2017). Quantum Clustering and its Application

to Asteroid Spectral Taxonomy. Tel Aviv University.

F. Cao, M. Ester, W. Q. A. Z. (2006). Density-based cluster-

ing over an evolving data stream with noise. Proceed-

ings of the 2006 International Conference on Data

Mining, 6.

H. Alkahtani, T. A. (2021). Intrusion Detection System

to Advance Internet of Things Infrastructure-Based

Deep Learning Algorithms. Complexity, 2021.

I. Butun, S.D. Morgera, R. S. (2014). A Survey of Intru-

sion Detection Systems in Wireless Sensor Networks.

IEEE Communications Survey & Tutorials, 16.

I. Ullah, Q. M. (2020). A Scheme for Generating a Dataset

for Anomalous Activity Detection in IoT Networks.

Advances in Artiﬁcial Intelligence: 33rd Canadian

Conference on Artiﬁal Intelligence.

J. A. Silva, E.R. Faria, R. B. E. H. (2013). Data Stream

Clustering: A Survey. In: ACM Computing Surveys,

46.

J. Carneiro, N. Oliveira, N. S. E. M. I. P. (2022). Machine

Learning for Network-based Intrusion Detection Sys-

tems: an Analysis of the CIDDS- 001 Dataset. In:

Distributed Computing and Artiﬁcial Intelligence, 1.

J. Diaz-Rozo, C. Bielza, P. L. (2018). Clustering of Data

Streams with Dynamic Gaussian Mixture Models. An

IoT Application in Industrial Processes. Internet of

Things Journal, Special Issue on Real-Time Data Pro-

cessing for Internet of Things.

K.H. Han, J. K. (2002). Quantum-inspired evolutionary

algorithm for a class of combinatorial optimization.

IEEE Transactions on Evolutionary Computation, 6.

L. Wan, W. N. (2009). Density based Clustering of Data

Streams at Multiple Resolutions. ACM Transactions

on Knowledge Discovery from Data, 3.

M. Ring, S. Wunderlich, D. G. (2017). Technical Report

CIDDS-001 data set. In: Proceedings of the 16th

European Conference on Cyber Warfare and Security

(ECCWS), ACPI.

M.M. Noor, W. H. (2019). Current research on Internet of

Things (IoT) security: A survey. Computer Networks,

148.

M.R. Ackermann, M. M

artens, C. R. K. S. C. L. C. S.

(2012). StreamKM++: A clustering algorithm for data

streams. Journal of Experimental Algorithmics, 17.

N. Ntuli, A. A.-M. (2016). A Simple Security Architecture

for Smart Water Management System. In: Procedia

Computer Science, 83.

P. Casas, J. Mazel, P. O. (2012). Unsupervised Network

Intrusion Detection Systems: Detecting the Unknown

without Knowledge. Computer Communications, 7.

P. Jim

enez, J.C. Rold

an, R. C. (2022). A hybrid quantum

approach to leveraging data from HTML tables. In:

Knowledge and Information Systems, 64.

P. Kranen, I. Assent, C. B. T. S. (2011). The ClusTree:

indexing micro-clusters for anytime stream mining.

Knowledge and Information Systems, 29.

R. Qaddoura, A.M. Al-Zoubi, I. A. H. F. (2021). A Multi-

Stage Classiﬁcation Approach for IoT Intrusion De-

tection Based on Clustering with Oversampling. Ap-

plied Scineces, 11.

R.V. Casana-Eslava, P. Lisboa, S. O.-M. I. J. J. M.-

G. (2020). Probabilistic Quantum Clustering.

Knowledge-Based Systems, 194.

S. Bajpai, K. S. (2021). A Framework for Intrusion Detec-

tion Models for IoT Networks using Deep Learning.

Research Square, 2021.

Shaked, G. (2013). Quantum Clustering for Large Data

Sets. Tel Aviv University.

Stanford, N. (2008). Evaluation of clustering. https:// nlp.st

anford.edu/IR-book/ html/htmledition/evaluation-of-c

lustering-1.html.

T. Felser, M. Trenti, L. S. A. G. D. Z. D. L.-S. M. (2020).

Quantum inspired machine learning on high-energy

physics data. npj Quantum Inf, 7.

T. Zhang, R. Ramakrishan, M. L. (1997). BIRCH: A new

data clustering algorithm and its applications. Data

Mining and Knowledge Discovery, 1.

Tang, E. (2019). A quantum-inspired classical algorithm

for recommendation systems. STOC 2019: Proceed-

ings of the 51th Annual ACM SIGACT Symposium on

Theory of Computing.

T.Q. Duong, J.A. Ansere, B. N. (2022). Quantum-Inspired

Machine Learning for 6G: Fundamentals, Security,

Resource Allocations, Challenges, and Future Re-

search Directions. IEEE Open Journal of Vehicular

Technology, 3.

T.V. Ramana, M. Thirunavukkarasan, A. M. G. D. S. N.

(2022). Ambient intelligence approach: Internet of

Things based decision performance analysis for intru-

sion detection. Computer Communications, 195.

Y. Chen, L. T. (2006). Density-based clustering for real-

time stream data. Proceeding of the 2006 Interna-

tional Conference on Data Mining, 6.

Y. Mahmoudi, N. Zioui, H. B. (2020). A new quantum-

inspired clustering method for reducing energy con-

sumption in IOT networks. npj Quantum Inf, 7.

IoTBDS 2023 - 8th International Conference on Internet of Things, Big Data and Security