Study on Decentralized Anytime Evolutionary Algorithm for DCOPs

Containing Adversarial Agents

Toshihiro Matsui

Nagoya Institute of Technology, Gokiso-cho Showa-ku Nagoya Aichi 466-8555, Japan

Keywords:

Multiagent System, Distributed Constraint Optimization, Cooperative Problem Solving, Adversarial,

Evolutionary Algorithm, Sampling.

Abstract:

The Distributed Constraint Optimization Problem (DCOP) is a fundamental optimization problem that repre-

sents the cooperation of multiple agents. An extended class of DCOPs contains potentially adversarial agents

that can select arbitrary decisions or the worst one, and the goal is to ﬁnd a safe solution under the worst case

by emulating adversarial agents. Such problems are important for addressing risky situations in real world

applications. Although several exact solution methods based on distributed asynchronous game-tree search

for the case have been studied, their scalability is limited by the tree-width of constraint graphs that represent

the DCOPs. We study the application of decentralized optimization methods based on an anytime evolutionary

algorithm for DCOPs to the cases containing adversarial agents. We employ solution methods to minimize

upper bound cost values, investigate several heuristic unbounded methods, and experimentally evaluate our

proposed approach.

1 INTRODUCTION

The Distributed Constraint Optimization Problem

(DCOP) is a fundamental optimization prob-

lem that represents the cooperation of multiple

agents (Fioretto et al., 2018). With DCOP, the

cooperation of agents is formalized as a constraint

optimization problem distributed among agents and

cooperatively solved using a distributed optimization

algorithm performed by the agents.

Different types of solution methods have been

applied to DCOPs, including tree search, dynamic

programming, belief propagation, stochastic local

search, stochastic sampling and Lagrangian primal-

dual method (Fioretto et al., 2018). Recently, sev-

eral solution methods based on soft computing tech-

niques have also been proposed for large-scale prob-

lems (Mahmud et al., 2020; Choudhury et al., 2020).

Various cooperation problems of resource alloca-

tion and collaboration on multiagent systems have

been modeled using the DCOP framework, including

sensor networks, smart grids, disaster response and

meeting scheduling (Fioretto et al., 2018). DCOP has

been extended by introducing several additional prop-

erties to address more practical cases, such as spe-

https://orcid.org/0000-0001-8557-8167

ciﬁc resource requirements (Matsui et al., 2008), dy-

namic environments (Hoang et al., 2022), and fairness

among agents (Matsui et al., 2018).

An extended class of DCOPs contains potentially

adversarial agents that can select arbitrary decisions

or the worst one, and the goal is to ﬁnd a safe so-

lution under the worst case by emulating adversar-

ial agents (Matsui et al., 2010). Such problems

are important for addressing risky situations in real

world applications. Although several exact solution

methods based on distributed asynchronous game-

tree search for the case have been studied, their time

complexity is exponential for the tree-width of con-

straint graphs that represent the DCOPs.

For relatively large-scale DCOPs including adver-

sarial agents that resembles the previous work, we

study the application of decentralized optimization

methods based on an anytime evolutionary algorithm

for DCOPs (Mahmud et al., 2020). We employ solu-

tion methods that minimize the upper bound cost val-

ues by extending the processing and protocols of the

existing solution method. We also investigate several

heuristic unbounded methods to experimentally cap-

ture the inﬂuence of search strategies for the problem.

The effect of the proposed approaches is experimen-

tally evaluated.

338

Matsui, T.

Study on Decentralized Anytime Evolutionary Algorithm for DCOPs Containing Adversarial Agents.

DOI: 10.5220/0011758800003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 1, pages 338-346

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 BACKGROUND

2.1 Distributed Constraint

Optimization Problem

A Distributed Constraint Optimization Problem

(DCOP) is deﬁned by hA, X, D, Fi, where A is a set of

agents, X is a set of variables, D is a set of domains of

the variables, and F is a set of functions that represent

the cost values of constraints. In a common funda-

mental case, agent a

∈ A has single decision variable

∈ X that takes a discrete value from D

∈ D. Func-

tion f

i, j

, x

) ∈ F represents the relationship among

two variables, x

and x

, and returns non-negative in-

teger cost values. Global assignment A is the as-

signment to all the variables, and the assignment to

a subset of variables is called a partial assignment.

Globally optimal solution A

∗

stands for the globally

minimum cost: A

∗

= arg min

∑

i, j

∈F

i, j

↓x

, A

↓x

The fundamental DCOP is represented by a constraint

graph where the nodes and edges represent agent/vari-

able and functions. The set of neighborhood agents

relating agent a

with the functions are denoted by N

Although the number of agents’ variables and the ar-

ity of functions can be generalized, we employ the

above common setting as did the related studies.

Agents search for assignments to their own vari-

ables in a decentralized manner with their related

agents. The solution methods for DCOPs (Fioretto

et al., 2018) are categorized into complete meth-

ods (Petcu and Faltings, 2005; Yeoh et al., 2008)

for the optimal solution and incomplete meth-

ods (Nguyen et al., 2019; Mahmud et al., 2020;

Choudhury et al., 2020) for quasi-optimal solutions.

Since complete methods cannot be applied to large-

scale and densely constrained problems, incomplete

solution methods have been developed. We focus on

a decentralized anytime evolutionary algorithm (Mah-

mud et al., 2020) due to its relatively good search ef-

ﬁciency.

2.2 DCOP With Adversarial Agents

In several classes of problems, some agents can

choose arbitrary assignments to their variables, repre-

senting the situation where the agents’ behavior is ad-

versarial in the worst case. To address such situations,

agents cooperatively minimize the worst case cost

value by emulating potentially adversarial agents.

In a related study, the Quantiﬁed DCOP (Matsui

et al., 2010) derived from Quantiﬁed DCSP (Baba

et al., 2010), which is a decentralized Quantiﬁed

Constraint Satisfaction Problem (Chen, 2004), em-

ploys universal and existential quantiﬁers to catego-

rize agents/variables. The deﬁnitions of the agents,

variables, and cost functions in a Quantiﬁed DCOP

are identical to the original DCOP, and a sequence

of quantiﬁed variables of form Q.C = q

·· · q

is additionally deﬁned. Q is a sequence of variables

where q

are existential quantiﬁer ∃ or universal quan-

tiﬁer ∀. The semantics of a QDCOP Q.C is recur-

sively deﬁned as follows. If C is empty, Q.C takes

a zero cost value. If Q has form ∃x

·· · q

.C,

then x

can take any assignment, and Q.C takes a cost

value for any d ∈ D

under q

·· · q

.C. If Q has

form ∀x

·· · q

.C, then Q.C takes the minimal

cost value for all d ∈ D

under q

·· · q

.C. The

problem deﬁnition yields the upper and lower bound

of the optimal cost value, and a practical major is-

sue is the worst case that represents a risky situation.

In the previous study, several exact solution meth-

ods based on an asynchronous game-tree search and

partial dynamic programming for Quantiﬁed DCOPs

were studied. However, such methods are inapplica-

ble to large-scale and densely constrained problems

due to the combinational explosion caused by the

large tree-width on constraint graphs.

We focus on a similar problem where the sequence

of quantiﬁers is relaxed as a general case. Here the

agents are categorized into ally agents that cooper-

ate for the minimization and adversarial agents that

might choose the worst assignment to their variables.

The goal of the problem is to ﬁnd the minimum up-

per bound cost value, which is also desired to ﬁnd

a relatively robust solution for the adversarial agents.

Due to the complexity of the problem in general cases,

we investigate the application of an evolutionary algo-

rithm for DCOPs.

2.3 AED: Decentralized Anytime

Evolutionary Algorithms for

DCOPs

The Anytime Evolutionary DCOP algorithm

(AED) (Mahmud et al., 2020) is a synchronized

and decentralized algorithm. In its process, neigh-

boring agents on a constraint graph exchange the

information of their solution sets, and the globally

best solution is synchronized at each iteration using

a rooted best-ﬁrst-search (BFS) tree on a constraint

graph. Agents maintain their sets (populations) of

individuals (solutions), and each individual I consists

of a complete assignment to all the variables and its

ﬁtness (cost) value I. f itness. Fig. 1 shows the pseudo

code of AED. Here IN and ER are the parameters

for the number of individuals, and MI is the period

between two iterations of migration phases.

In the preprocessing, a BFS tree on a constraint

Study on Decentralized Anytime Evolutionary Algorithm for DCOPs Containing Adversarial Agents

339

1 Construct a BFS tree on a constraint graph.

2 Share an initial population of IN individuals P

by a protocol

on the BFS tree.

3 Itr ← 0.

4 until Itr is within a cutoff cycle do begin

5 P

sel

← a set of |N

| × ER individuals sampled from P

allowing duplication.

6 Partition P

sel

into sets of the same size {P

new

, ..., P

new

7 for n

in N

do begin

8 Update individuals in P

j,i

new

by sampling each assignment

to a

’s variable.

9 Send P

j,i

new

to n

. end

10 for P

i, j

new

received from n

in N

do begin

11 Update individuals in P

i, j

new

by selecting each best

assignment to a

’s variable.

12 Return P

i, j

new

to n

. end

13 for P

j,i

new

returned from n

in N

do begin P

← P

∪ P

j,i

new

end

14 B ← argmin

I∈P

I. f itness.

15 Update and commit the globally best solution using B by a

protocol on the BFS tree performing in background.

16 P

← a set of |N

| × ER individuals sampled from P

disallowing duplication.

17 if Itr is MI

iteration after the previous migration phase or

the initialization then begin

18 for n

in N

do begin

19 Send a set of ER individuals, sampled from P

disallowing duplication, to n

. end

20 for P

i, j

mig

received from n

in N

do begin P

← P

∪ P

i, j

mig

end end

21 Itr ← Itr + 1. end

Figure 1: AED (agent a

)

graph is constructed, and a population of initial in-

dividuals is generated as follows (Fig. 1, Lines 1-

2). First, each agent a

generates IN individuals

that contain only an assignment to x

. Then the in-

dividuals are shared among neighboring agents, and

partial assignments A

of the aggregated individuals

are locally evaluated in each agent a

as I. f itness =

∑

j∈N

i, j

i↓x

, A

i↓x

). The partial individuals are ag-

gregated in a bottom-up manner based on the BFS

tree. Here the k-th partial individuals in the initial sets

are integrated into a new k-th individual by unifying

the identical assignments, and the corresponding to-

tal ﬁtness value is computed. Finally, the root agent

knows the initial population of the individuals with

complete assignments and their ﬁtness values. At this

point, the same initial ﬁtness values, which were eval-

uated by two neighboring agents, have been doubly

aggregated. Therefore, the root agent adjusts the ﬁt-

ness value by dividing by two, and the initial popula-

tion is duplicated to initial one P

for each agent a

a top-down manner on the BFS tree.

Each agent a

iteratively performs the following

main process to update its P

and its assignment to

. First, agent a

selects P

j,i

new

for each neighboring

agent n

∈ N

by sampling the individuals from P

(Lines 5-6). Then a

updates the assignment to its

own variable contained in each individual in P

j,i

new

sampling the assignment from D

and sends P

j,i

new

to its

neighboring agent n

(Lines 7-9). Receiver agent n

updates the assignment to its own variable contained

in each individual in P

j,i

new

by locally minimizing the

ﬁtness values and returns P

j,i

new

to a

(Lines 10-12). Fi-

nally, the returned P

j,i

new

is aggregated into P

(Line

13), and the currently best individual B with the mini-

mum ﬁtness value is selected from P

(Line 14). If B

is the globally best individual, it is propagated to all

the agents using a decentralized snapshot algorithm

based on the BFS tree in the background (Line 15),

and the currently best assignment to all the variables

is updated. Then P

is sampled to maintain its size

(Line 16).

While the above stochastic local search reduces

the diversity of the individuals, a migration process,

where each agent imports a part of the individuals

from its neighboring agents, is performed at every MI

iteration to maintain the diversity (Lines 17-20). See

the literature (Mahmud et al., 2020) for details, in-

cluding the sampling equations and parameters.

3 APPLYING AED TO

ADVERSARIAL DCOP

3.1 Basic Approach

Here we employ an approach where agents cooperate

to ﬁnd a robust solution to adversarial agents by em-

ulating the adversarial ones. It is assumed that adver-

sarial agents can be identiﬁed, and virtual agents em-

ulating them are operated by their neighborhood ally

agents in a decentralized manner to preserve their pri-

vate information. We inherit these assumptions from

the related work (Matsui et al., 2010).

A method to ﬁnd a solution considering adver-

sarial agents is the application of an existing solu-

tion method with modiﬁcations to minimize the up-

per bound cost value. The upper bound should be re-

duced from a trivial upper bound cost value: g

UB0

∑

i, j

∈F

max

∈D

i, j

, d

). Although several

solution methods can be employed to reduce the up-

per bound, an issue here is the scalability of the meth-

ods. The original AED, which handles the globally

best cost value, can be modiﬁed to handle the glob-

ally best upper bound cost value.

Although a solution standing for the best upper

bound cost value explains a limit of the worst case,

the true cost value for the solution is generally smaller

than the upper bound value. To experimentally es-

timate the possible worst case from a solution by a

solver, we perform post-processing to solve a maxi-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

340

mization problem where only the assignment to the

variables of adversarial agents can be reassigned. The

aim of this procedure is to evaluate the actual robust-

ness of the solutions. Due to the common issue of

scalability, we employ another maximization version

of AED under a partially ﬁxed assignment. Below,

we propose two bounded approaches with AED. We

also investigate unbounded approaches with a heuris-

tic method.

3.2 Standard AED With Upper Bound

Cost Functions

For ally agent a

and adversarial agent a

, original

cost function f

i, j

can be approximated to the repre-

sent upper bound cost values:

UB1

i, j

, d

) = max

∈D

i, j

, d

) . (1)

Note that, for a pair of adversarial agents, it uniformly

takes the maximum cost value for all assignments.

The original AED can be simply applied to the ap-

proximated functions without any modiﬁcation. Only

an additional preprocessing is introduced to compute

the approximated function. We employ this version

of AED as a baseline of the bounded approach. How-

ever, the gap between the upper bound cost value and

the truly worst one for the possible solutions will be

relatively large, since it only considers each function

separately.

3.3 Dedicated AED With Locally

Aggregated Upper Bound Cost

Values

For adversarial agent a

and assignment A, the up-

per bound cost value for its related cost functions is

represented as follows:

UB2

(A) = max

∈D

∑

i∈N

i, j

↓x

, d

) . (2)

Although this upper bound is also relatively simple, it

is not straightforward to modify AED when it remains

in a decentralized manner. This is indeed a reason-

able range of modiﬁcation for AED, since aggregat-

ing the upper bound cost value for a greater number of

agents increases the computation/communication cost

and the difﬁculty of designing an algorithm/protocol.

Therefore, we mainly concentrate on this extension as

a bounded approach in this study.

To adjust AED to compute the upper bound, sev-

eral steps of the original algorithm must be modiﬁed.

First, we note that the assignment to the adversarial

agents’ variables are now substantially dummy val-

ues, although they are adjusted as much as possible

to reasonable values. This is because f

UB2

(A) does

not refer to the assignment to the adversarial agents’

variable in A.

3.3.1 Approximated Asymmetric Cost Function

In addition, the upper bound cost values can only be

computed by adversarial agents, and it requires the

modiﬁcation of problems to those with asymmetric

cost functions. In the following, we distinguish agent

’s function f

i, j

from f

j,i

, which is for agent a

. For

a pair of ally agents, its related cost function is still

symmetrically deﬁned: f

i, j

= f

j,i

= f

i, j

. On the other

hand, for a pair of ally and adversarial agents, its re-

lated function is asymmetrical. While f

i, j

= 0 for ally

agent a

, the other is deﬁned as f

j,i

= f

i, j

for adver-

sarial agent a

. For a pair of adversarial agents, its re-

lated function is symmetrical but uniformly takes the

maximum cost value for any assignments. This re-

sembles the above case of f

UB1

. The common max-

imum cost value enables the evaluation of an adver-

sarial agent that is independent from its neighboring

adversarial ones. The asymmetric cost functions are

prepared in the preprocessing, and the original AED

is modiﬁed to evaluate them.

3.3.2 Construction of Initial Population

In the ﬁrst step to construct initial individuals, each

adversarial agent selects a dummy assignment to its

own variable for each partial individual. After the

partial individuals are received from neighborhood

agents, each adversarial agent a

locally computes

its upper bound cost value f

UB2

as a partial ﬁtness

value. Note that now all agents evaluate their asym-

metric cost functions. Then the partial individuals and

related ﬁtness values are aggregated in a bottom up

manner based on a BFS tree. Here adversarial agents

perform a dedicated aggregation of ﬁtness values dif-

ferent from those of the ally agents. For f

UB2

adversarial agent a

also aggregates corresponding

partial summation f

−UB2

) for its neighboring ad-

versarial agents. Then adversarial agent a

adds its

local ﬁtness value 2 f

UB2

J) − f

−UB2

J) to a ﬁt-

ness value of a corresponding individual. Then the

population of aggregated individuals are sent to a

’s

parent. As the result, the cost values for any asym-

metric cost functions are doubly aggregated at the

root agent of a BFS tree, and the aggregated ﬁtness

is halved to be the correct value.

Study on Decentralized Anytime Evolutionary Algorithm for DCOPs Containing Adversarial Agents

341

...

fit.

...

dif.

...

dif.

...

dif.

fit.

previous d

...

dif.

fit.

(a) Sending common individual

(b) Aggregation of returned individuals

Adversarial

Open-Ally

Closed-Ally

Figure 2: Interaction among open-ally agent and its neigh-

borhood agents (one of individuals in transferred popula-

tions).

3.3.3 Adversarial Agents

The interaction among agents in AED is also mod-

iﬁed for the asymmetric cost functions. Since the

assignments to adversarial agents’ variables are sub-

stantially dummy values, they do not prepare their

new population to be sent to neighboring agents at

every iteration. Namely, adversarial agents only re-

spond to their neighborhood ally agents.

Ally agent a

that sends its new population to ad-

versarial agent a

cannot evaluate the update of ﬁtness

value of f

( j, i), while f

(i, j) is always zero. There-

fore, agent a

attaches the previous assignment to a

’s

variable for each new individual. Then adversarial

agent a

evaluates the update of ﬁtness values by com-

paring the new and previous assignments. Optionally,

adversarial agent a

can adjust the assignment to its

own variable so that it is consistent with a new up-

per bound cost value although it is not employed in

the solver. In our experiment, the assignment to the

variables of the adversarial agents is employed to ver-

ify the true cost value with the original cost functions.

The updates are returned to the sender agents.

Note that neighboring adversarial agents can in-

dependently perform this interaction process without

any contradiction because the cost function related to

the agents has been modiﬁed to asymmetric ones that

always return the common maximum cost value as

mentioned above.

3.3.4 Ally Agents

Here ally agents are categorized into open-ally agents

that have at least one adversarial neighborhood agent

and closed-ally agents without any adversarial neigh-

borhood agents. While a closed-ally agent can com-

pletely evaluate the modiﬁcation of the assignment to

its own variable, an open-ally one has to ask adversar-

ial agents to evaluate its modiﬁcation. This requires

an adjustment in several steps of interaction.

First, open-ally agents do not receive new popu-

lations from their neighborhood ally agents to avoid

incorrectly updating ﬁtness values that depend on ad-

versarial agents. Second, each open-ally agent a

pre-

pares only one common set of its new population, be-

cause each individual in the population requires up-

dating ﬁtness value by at leas one adversarial agent

in addition to other closed-ally/adversarial agents.

Namely, for each individual of open-ally agent a

general cases, multiple neighborhood agents evaluate

ﬁtness values for the same individual, whose updates

should be aggregated by agent a

. Therefore, open-

ally agent a

multi-casts its new common population

to its neighborhood closed-ally/adversarial agents and

receives feedback from the neighborhood agents (Fig-

ure 2). In this case, the neighborhood agents return

their new updated assignments and related differen-

tial ﬁtness values.

The aggregation of the information returned to

the sender open-ally agent a

is also technical (Fig-

ure 2(b)). Open-ally agent a

locally duplicates a

common new population for each neighborhood agent

before the aggregation. For each new individual of

closed-ally neighborhood agent a

, the new returned

assignment to a

’s variable and the related differential

ﬁtness value are applied. Moreover, for each individ-

ual of all neighborhood agents a

, and for all neigh-

borhood adversarial agents a

, the new returned as-

signment to a

’s variable and the related differential

ﬁtness value are simultaneously applied to a

’s indi-

vidual. As mentioned above, the update of assign-

ments to adversarial agents’ variables is optional, and

the update of ﬁtness values is necessary.

3.3.5 Other Related Operations

To maintain the set of individuals, agents perform the

necessary part of sampling of individuals even in the

case of adversarial agents. Migration phases are per-

formed by all types of agents as in the original AED.

Due to the limited operation regarding the open-

ally and adversarial agents, the exploration for assign-

ments is also affected. On the other hand, the limita-

tion also reduces the interaction costs among several

pairs of agents.

3.4 Unbounded Heuristic Methods for

Investigation

The solution methods that optimize upper bound cost

values take the most pessimistic strategy that ignores

the true cost value for assignments. We also eval-

uate an unbounded heuristic approach to investigate

whether there is room to adjust a strategy between op-

timistic and pessimistic ones.

The approach experimentally maximizes the

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

342

worst cost values for several candidate solutions. We

employ two modiﬁed versions of AED that repeat

the minimization and maximization phases. In the

ﬁrst version, ally agents minimize the solutions in the

populations in the minimization phase, while the as-

signment to the adversarial agents’ variables does not

change. Then in the maximization phase, the adver-

sarial agents maximize the solutions under a ﬁxed as-

signment to the variables of the ally agents. In another

version, adversarial agents cooperate with ally agents

in the minimization phase to further reduce the cost

values.

For this modiﬁcation, each individual in a popula-

tion stores its best solution depending on both phases,

and the best one is inherited to each individual in the

next alternative phase. In addition, a snapshot algo-

rithm for the best solution in the original AED is ap-

plied to the best individual with the lowest cost at the

last iteration in each maximization phase. We vary the

lengths of both phases in our experiment.

4 EVALUATION

4.1 Settings

We experimentally evaluated our proposed approach.

The benchmark problems of the extended DCOPs

consist of n variables and c cost functions, and each

variable takes a value from its domain whose size is

d. We varied the number a of the adversarial agents.

We evaluated the following types of cost func-

tions. Uniform: random integer values in [1, 100]

based on uniform distribution. Gamma: rounded ran-

dom integer values in [1, 100] based on gamma distri-

bution with α = 9 and β = 2.

We compared the following methods.

• AED: the original AED.

• UB1: an AED with approximated cost functions

prepared in preprocessing as Equation (1).

• UB2: a modiﬁed AED that computes the upper

bound cost value as Equation (2).

• Alt-x-y: a modiﬁed AED shown in Section 3.4

that alternatively performs the minimization and

maximization phases, where adversarial agents do

not cooperate in the latter. Here x and y are the

number of 10

iterations for each minimization

and maximization process.

• AltAM-x-y: another version of Alt, where adver-

sarial agents cooperate in the minimization.

The parameters below were employed based on

the literature (Mahmud et al., 2020) and our prelimi-

nary experiment: IN = 5, ER = 5, α = 1, R

max

= 5,

β = 5, and O

max

= 5, where α, R

max

, β, and O

max

are

sampling parameters (Mahmud et al., 2020).

The cut-off iteration was set to 10000. The re-

sults were averaged over 10 instances for each prob-

lem setting and 10 trials with different seed values of

the pseudo-stochastic process.

As mentioned in Section 3.1, we ﬁrst performed

the above solution methods and then performed the

post maximization process under the ﬁxed assign-

ments to the ally agents’ variables found by the solu-

tion methods. We evaluated upper bound cost value

FitUB, true cost value FitTrue for the assignment

found by the solution methods, cost value FitPst max-

imized by the post process, gap GapUB = FitUB −

FitPst, increment FitInc = FitPst −FitTrue, and the

execution time.

4.2 Results

Tables 1 and 2 show the ﬁtness values for the Uniform

problems. In all cases, UB2 reduced upper bound cost

values FitUB more than UB1. Although true ﬁtness

values FitTrue for UB1 and UB2 were greater than

those of the other unbounded methods, increased ﬁt-

ness values FitPst by the post maximization process

were less than those of the other unbounded methods.

The results suggest that the solutions related to the

upper bounds are more robust than the others.

Regarding UB1 and UB2, GapUB between the

upper bound cost value and the cost value maximized

by the post process was also relatively small in the

case of UB2. Increment FitInc from the true cost

value to the maximized cost value by the post process

was also smallest in the case of UB2.

Comparing unbounded methods, in several set-

tings, increased ﬁtness value FitPst by the post max-

imization process was relatively large in the order of

AED, AltAM and Alt; this order is the same as that

of optimism. In the case of larger number a of ad-

versarial agents, upper bound cost value FitUB and

increased ﬁtness value FitPst were relatively large.

Regarding Alt and AltAM, increased ﬁtness value

FitPst was affected by the ratio of iterations for the

minimization and maximization phases, but a com-

mon correlation cannot be identiﬁed. In total, our

result conﬁrmed that the strategies containing some

optimism cannot be easily tuned, and the pessimistic

methods with the upper bound are effective, even with

a relatively wider bound.

Tables 3 and 4 show the ﬁtness values for the

Gamma problems. The result resembles the Uniform

case, alghough the scales of the cost values are dif-

ferent due to probabilistic distribution. In addition,

Study on Decentralized Anytime Evolutionary Algorithm for DCOPs Containing Adversarial Agents

343

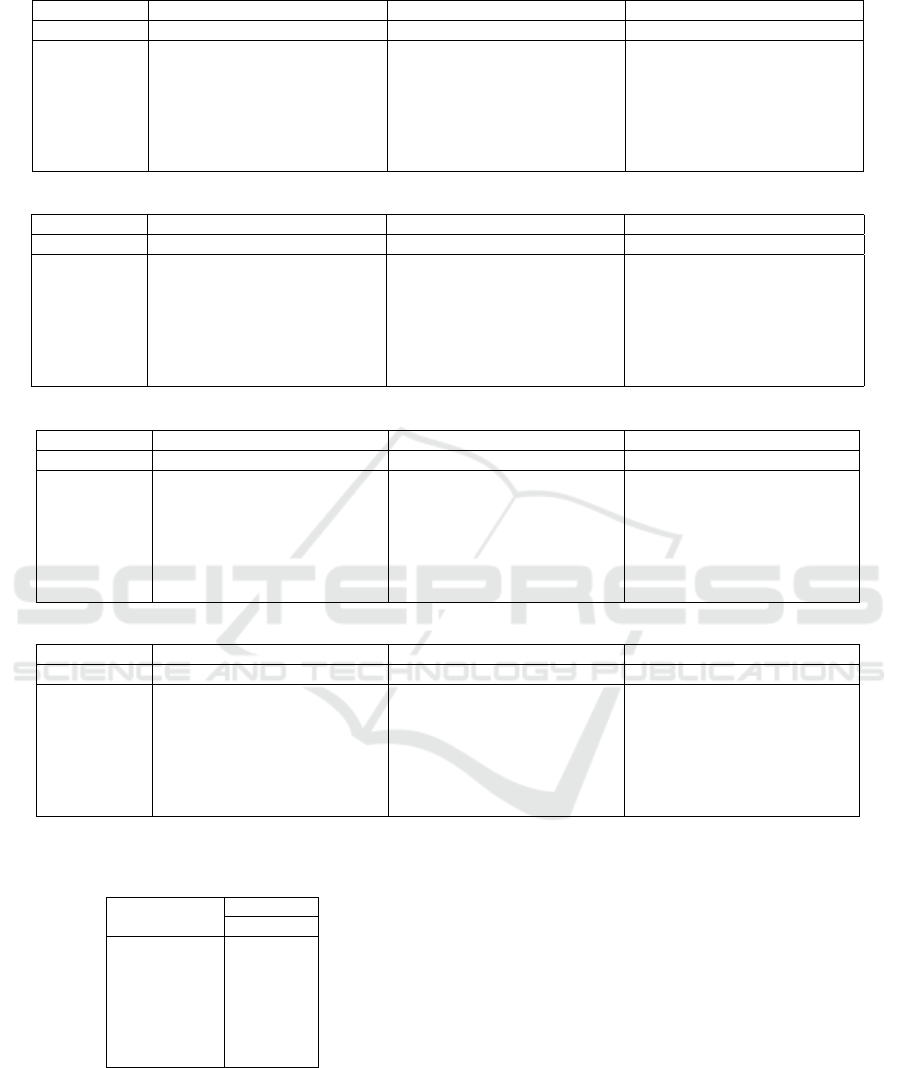
Table 1: Fitness values (Uniform, n = 50, d = 3, c = 250).

a 10 25 40

Alg. FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc

AED 8970 11000 2030 8970 13389 4418 8970 15310 6340

UB1 12304 9933 10723 1581 791 16577 11178 12939 3639 1760 20439 12245 15153 5287 2908

UB2 10992 10621 10739 253 118 14704 12304 12904 1800 599 19632 13137 15016 4616 1879

Alt-0.5-2 9546 10934 1388 10487 13281 2794 11474 15231 3757

Alt-1.25-1.25 9544 10932 1388 10488 13283 2795 11474 15226 3752

Alt-2-0.5 9545 10930 1385 10487 13280 2792 11474 15235 3761

AltAM-0.5-2 9215 10959 1744 9682 13364 3681 10463 15287 4824

AltAM-1.25-1.25 9176 10955 1780 9618 13333 3715 10389 15285 4896

AltAM-2-0.5 9175 10953 1779 9582 13350 3767 10358 15287 4929

Table 2: Fitness values (Uniform, n = 100, d = 5, c = 300).

a 20 50 80

Alg. FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc

AED 7944 12219 4275 7944 17097 9153 7944 20789 12845

UB1 13757 10084 11612 2145 1528 20707 12527 16369 4338 3842 26235 14574 20268 5966 5695

UB2 11832 11277 11502 330 225 18305 14766 16180 2125 1414 25315 16379 20239 5076 3861

Alt-0.5-2 9108 12172 3064 11019 16977 5957 13159 20682 7524

Alt-1.25-1.25 9101 12176 3075 11021 16979 5958 13158 20704 7545

Alt-2-0.5 9098 12177 3079 11020 16973 5953 13158 20699 7540

AltAM-0.5-2 8379 12262 3883 9284 17045 7761 11116 20754 9638

AltAM-1.25-1.25 8269 12218 3949 9035 17051 8016 10747 20744 9997

AltAM-2-0.5 8239 12205 3966 8941 17051 8110 10628 20756 10128

Table 3: Fitness values (Gamma, n = 50, d = 3, c = 250).

a 10 25 40

Alg. FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc

AED 3643 4045 402 3643 4548 905 3643 4954 1311

UB1 4275 3840 3981 294 142 5226 4105 4460 766 355 6217 4290 4911 1306 621

UB2 4038 3965 3980 58 15 4879 4304 4452 426 148 6073 4514 4905 1168 392

Alt-0.5-2 3756 4037 281 3932 4546 613 4139 4943 805

Alt-1.25-1.25 3756 4037 281 3932 4544 612 4139 4944 806

Alt-2-0.5 3756 4037 281 3932 4544 612 4139 4945 806

AltAM-0.5-2 3679 4051 371 3765 4552 787 3926 4946 1020

AltAM-1.25-1.25 3676 4051 375 3756 4558 802 3913 4947 1034

AltAM-2-0.5 3675 4051 376 3752 4556 804 3904 4947 1043

Table 4: Fitness values (Gamma, n = 100, d = 5, c = 300).

a 20 50 80

Alg. FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc FitUB FitTrue FitPst GapUB FitInc

AED 3853 4684 831 3853 5713 1860 3853 6485 2632

UB1 5004 4268 4576 428 308 6692 4762 5535 1157 773 8301 5110 6382 1918 1273

UB2 4641 4487 4541 101 53 6213 5185 5514 699 329 8105 5487 6373 1732 886

Alt-0.5-2 4067 4692 625 4440 5703 1263 4850 6493 1642

Alt-1.25-1.25 4066 4692 626 4440 5703 1263 4850 6492 1642

Alt-2-0.5 4066 4692 626 4440 5703 1262 4850 6495 1645

AltAM-0.5-2 3927 4692 765 4091 5702 1611 4423 6486 2064

AltAM-1.25-1.25 3911 4682 771 4051 5714 1662 4359 6487 2128

AltAM-2-0.5 3906 4685 778 4031 5709 1678 4333 6488 2155

Table 5: Execution times [s] (Gamma, n = 100, d = 5, c =

300).

Alg. a

20 50 80

AED 169 169 166

UB1 175 167 164

UB2 91 63 39

Alt-0.5-2 64 76 86

Alt-1.25-1.25 193 188 184

Alt-2-0.5 220 185 158

AltAM-0.5-2 68 82 96

AltAM-1.25-1.25 195 210 230

AltAM-2-0.5 226 227 224

FitPst for Alt and AltAM were not good in compari-

son to that for the original AED in several cases.

Table 5 shows the execution times of the main

part of the solution methods for the Gamma prob-

lems. The experiment was performed on a computer

with g++ (GCC) 8.5.0 -O3, Linux version 4.18, Intel

(R) Core (TM) i9-9900 CPU @ 3.10 GHz and 64GB

memory. As shown in the result for AED, there was

some ﬂuctuation of the execution time. The execution

time for UB2 was less than the other methods partic-

ularly in the case of the large number of adversarial

agents because this method reduces some interaction

relating the adversarial agents. The other extended

version needed overhead. Considering the quality of

the ﬁtness values and the computational costs, UB2 is

reasonable one for this class of algorithms.

5 DISCUSSION

In this study, we addressed the extended class of

DCOPs containing adversarial agent as an investiga-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

344

tion to apply a decentralized evolutionary algorithm

to the class of problems with risks. Even though our

extension of the algorithm is based on a relatively

simple boundary of cost values, it is not straightfor-

ward and requires many adjustments of the algorithm

in decentralized cases. While we investigated limited

types of upper bound cost values that can be com-

puted with reasonable computation and communica-

tion costs, several opportunities exist for to tighten-

ing boundaries by employing additional interaction

among agents. Such boundaries with some reason-

able processing cost will be investigated in a future

study.

Other classes of problems represent different

types of risks, including the absence of several agents

and the probabilistic cost functions. Although the

generality of evolutionary algorithms might allow

several extensions, additional investigation is neces-

sary for dedicated optimization criteria that are ag-

gregated in a decentralized manner. Even though

sampling-based solution methods for DCOPs are rel-

atively scalable, they are still affected by the density

of the neighboring agents and the large-size domain

of variables. Approximating such huge-scale prob-

lems considering the feature of sampling methods re-

mains as an issue. We concentrated on a standard

case of DCOPs where each agent has a single deci-

sion variable. For real-world problems, there are sev-

eral extension techniques to handle multiple variables

for each agent (Fioretto et al., 2018).

6 CONCLUSION

We applied a decentralized anytime evolutionary al-

gorithm to a class of DCOPs containing potentially

adversarial agents, and extended the processing and

protocol of the existing solution method to minimize

the upper bound cost value for the worst case. We also

investigated several heuristic unbounded methods to

experimentally capture the inﬂuence of search strate-

gies for the problems. We experimentally evaluated

the effect of the proposed approach, and the result re-

vealed that the minimization of the upper bound cost

value also found relatively robust solutions for adver-

sarial agents. Our future work will include more so-

phisticated methods for better upper bound cost val-

ues, as well as the approximation of a large domain of

variables and more dense functions toward practical

huge-scale problems.

ACKNOWLEDGEMENTS

This work was supported in part by JSPS KAKENHI

Grant Number JP22H03647.

REFERENCES

Baba, S., Iwasaki, A., Yokoo, M., Silaghi, M. C., Hirayama,

K., and Matsui, T. (2010). Cooperative Problem Solv-

ing against Adversary: Quantiﬁed Distributed Con-

straint Satisfaction Problem. In Proceedings of the 9th

International Conference on Autonomous Agents and

Multiagent Systems, volume 1, page 781–788.

Chen, H. M. (2004). The computational complexity of quan-

tiﬁed constraint satisfaction. PhD thesis, Ithaca, NY,

USA. Adviser-Kozen, Dexter.

Choudhury, M., Mahmud, S., and Khan, M. M. (2020). A

Particle Swarm Based Algorithm for Functional Dis-

tributed Constraint Optimization Problems. In Pro-

ceedings of the 34th AAAI Conference on Artiﬁcial In-

telligence, volume 34, pages 7111–7118.

Fioretto, F., Pontelli, E., and Yeoh, W. (2018). Distributed

constraint optimization problems and applications: A

survey. Journal of Artiﬁcial Intelligence Research,

61:623–698.

Hoang, K. D., Fioretto, F., Hou, P., Yeoh, W., Yokoo, M.,

and Zivan, R. (2022). Proactive Dynamic Distributed

Constraint Optimization Problems. Journal of Artiﬁ-

cial Intelligence Research, 74:1076–9757.

Mahmud, S., Choudhury, M., Khan, M. M., Tran-Thanh,

L., and Jennings, N. R. (2020). AED: An Anytime

Evolutionary DCOP Algorithm. In Proceedings of the

19th International Conference on Autonomous Agents

and MultiAgent Systems, pages 825–833.

Matsui, T., Matsuo, H., Silaghi, M., Hirayama, K., and

Yokoo, M. (2018). Leximin asymmetric multiple

objective distributed constraint optimization problem.

Computational Intelligence, 34(1):49–84.

Matsui, T., Matsuo, H., Silaghi, M. C., Hirayama, K.,

Yokoo, M., and Baba, S. (2010). A Quantiﬁed Dis-

tributed Constraint Optimization Problem. In Pro-

ceedings of the 9th International Conference on Au-

tonomous Agents and Multiagent Systems, volume 1,

pages 1023–1030.

Matsui, T., Silaghi, M., Hirayama, K., Yokoo, M., and Mat-

suo, H. (2008). Resource constrained distributed con-

straint optimization with virtual variables. In 23rd

AAAI Conference on Artiﬁcial Intelligence, pages

120–125.

Nguyen, D. T., Yeoh, W., Lau, H. C., and Zivan, R. (2019).

Distributed Gibbs: A Linear-Space Sampling-Based

DCOP Algorithm. Journal of Artiﬁcial Intelligence

Research, 64(1):705–748.

Petcu, A. and Faltings, B. (2005). A Scalable Method for

Multiagent Constraint Optimization. In Proceedings

of the 19th International Joint Conference on Artiﬁcial

Intelligence, pages 266–271.

Study on Decentralized Anytime Evolutionary Algorithm for DCOPs Containing Adversarial Agents

345

Yeoh, W., Felner, A., and Koenig, S. (2008). BnB-ADOPT:

an asynchronous branch-and-bound DCOP algorithm.

In Proceedings of the 7th International Joint Confer-

ence on Autonomous Agents and Multiagent Systems,

pages 591–598.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

346