An Empirical Heuristic Algorithm for Solving the Student-Project
Allocation Problem with Ties
Hoang Huu Bach
1
, Nguyen Thi Thuong
2
and Son Thanh Cao
2 a
1
Faculty of Information Technology, University of Engineering and Technology (UET), Vietnam National University, Hanoi
144 Xuan Thuy, Cau Giay, Hanoi, Vietnam
2
Faculty of Information Technology, School of Engineering and Technology, Vinh University
182 Le Duan, Vinh city, Nghe An, Vietnam
Keywords:
Student-Project Allocation Problem, Matching Problem, Heuristic Search.
Abstract:
In this paper, we propose a simple heuristic algorithm to deal with the Student-Project Allocation problem
with lecturer preferences over Projects with Ties (SPA-PT). The aim of such a problem is to find a maximum
stable matching of students and projects to meet the constraints on students’ and lecturers’ preferences over
projects, and the maximum numbers of students given by lecturers for each lecturer and her/his projects. Our
algorithm starts from an empty matching and iteratively constructs a maximum stable matching of students
and projects. For each iteration, our algorithm chooses the most ranked project of an unassigned student to
assign for her/him. If the assigned project or the lecturer who offers the assigned project is over-subscribed,
our algorithm removes a worth student assigned the project, where a worth student is a person corresponding
to the maximum value of the proposed heuristic function. Experimental results illustrate the outperformance
of the proposed algorithm w.r.t. the execution time and solution quality for solving the problem.
1 INTRODUCTION
The problem of finding a suitable project together
with a desired lecturer has been of great interest to
students at universities. Many university departments
assign a student to a random lecturer for doing the
lecturer’s project without any common interest be-
tween them. To deal with this problem, there are sev-
eral approaches have been proposed over the years.
In 2003, Abraham et. al. studied the problem of al-
locating students to projects called Student-Project
Allocation problem (SPA) (Abraham et al., 2003),
which is a generalization of the classical Hospitals-
Residents problem (HR) (Gale and Shapley, 1962). In
SPA, a lecturer will normally (i) offer a non-empty list
of projects, and (ii) propose a preference list over stu-
dents that he/she wants to supervise in a strict order,
whilst each student proposes a strictly ordered prefer-
ence list over available projects. There is no overlap
of projects among lecturers. Moreover, there are also
limitations on the number of students assigned to a
given project as well as a given lecturer (i.e., capac-
ity constrains). Solving this problem means to find a
matching, which is an assignment between students
a
https://orcid.org/0000-0002-4771-7856
and projects w.r.t. given preference lists so that each
student can only be assigned to at most one project
without violating the capacity constraints for projects
and lecturers. A property for a matching to satisfy is
stability (Roth, 1984). Informally, a matching is stable
(i.e., stable matching) if there are no student and lec-
turer that would both prefer to be matched with each
other instead of their current partners in the matching.
In 2007, Abraham et. al. (Abraham et al., 2007)
presented two optimal linear-time algorithms for find-
ing a stable matching of a given instance of SPA.
The first algorithm is student-oriented, which finds
the best-possible stable matching for all students.
Besides, the second algorithm is lecturer-oriented,
which finds the best-possible stable matching for all
lecturers.
In 2008, Menlove et. al. (Manlove and O’Malley,
2008) considered a variant of SPA, referred to SPA-P
(SPA with preferences over Projects), in which both
students and lecturers have preference lists over
projects in a strict order. The authors also showed
that stable matchings for an SPA-P instance can have
different sizes, and the problem of finding a max-
imum cardinality stable matching, referred to MAX-
SPA-P, is NP-hard (even in the special case that each
Bach, H., Thuong, N. and Cao, S.
An Empirical Heuristic Algorithm for Solving the Student-Project Allocation Problem with Ties.
DOI: 10.5220/0011731800003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 3, pages 665-672
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
665

project and lecturer can accommodate only one stu-
dent). Therefore, to solve the MAX-SPA-P problem ef-
fectively, researchers often focus on using the approx-
imation solutions. In (Manlove and O’Malley, 2008),
authors presented a polynomial-time 2-approximation
algorithm for MAX-SPA-P, named SPA-P-approx. In
2012 (Iwama et al., 2012), Iwama et. al. proposed
an
3
2
-approximation algorithm, named SPA-P-approx-
promotion, which is a combination of ideas from
Manlove’s algorithm (Manlove and O’Malley, 2008)
and the approximation algorithm of Kir
´
aly (Kir
´
aly,
2011) for MAX-SPA-P. In 2018 (Manlove et al., 2018),
Manlove at. al. proposed
3
2
-approximation algorithm
to find stable matchings that are very close to having
maximum cardinality for MAX-SPA-P by using Integer
Programming model. Recently, Viet et. al. proposed
a local search strategy based on the min-conflicts
heuristic, named SPA-P-MCH algorithm, to find a max-
imum weakly stable matching for the SPA-P prob-
lem (Viet et al., 2020).
A variant of SPA that involves lecturer preferences
over students, which is known as SPA-S (the SPA with
lecturer preferences over Students). SPA-S requires
ranking in strict order of preferences. However, this
might not fair in practical applications. For example,
a lecturer may be willing to rank two or more students
equally in a tie. In 2022 (Olaosebikan and Manlove,
2022), Olaosebikan et. al. studied a variant of SPA-S
with Ties, referred to SPA-ST. The authors also pro-
posed a polynomial-time algorithm to find a supper-
stable matching for an instance of SPA-ST or to report
that no such matching exists.
As far as we are concerned, there is no research
related to the problem of SPA-P with Ties. It is worth
doing further research on the topic because this prob-
lem has many practical applications, especially for the
cases with ties. In this work, we propose a simple
heuristic algorithm to find a maximum stable match-
ing for an instance of SPA-P with Ties, denoted by
SPA-PT. The aim is to find a maximum stable match-
ing of students and projects with the following con-
straints: (i) the ranking in a strict order of students’
and lecturers’ preferences list over projects, and (ii)
the limitations on the number of students assigned to
a given project and a given lecturer.
The rest of this paper is structured as follows. Sec-
tion 2 reminds the SPA-PT problem. Section 3 de-
scribes our proposed algorithm. Section 4 presents
our experimental results, and concluding remarks are
given in Section 5.
2 SPA-P WITH TIES
In this section, we present the formal notions and
definitions related to the Student-Project Allocation
problem with preferences over Project with Ties, de-
noted by SPA-PT. For convenience, the notions used
for SPA-PT are similar to the ones given in (Manlove
and O’Malley, 2008). An instance of SPA-PT con-
sists of the following sets: S = {s
1
,s
2
,...,s
n
}
of students, P = {p
1
, p
2
,..., p
q
} of projects, and
L = {l
1
,l
2
,...,l
m
} of lecturers. Each lecturer l
k
pro-
vides a non-empty set P
k
of projects and ranks these
projects in a preference list (with ties allowed). We
assume that, there is no overlap of projects among
lecturers (i.e., P
k
partitions P , where k = 1,2,...,m).
Also, each student s
i
∈ S suggests a set of projects
A
i
⊆ P and ranks A
i
in a preference list (with ties al-
lowed). Moreover, each l
k
∈ L (resp. p
j
∈ P ) has
an associated capacity to specify the maximum num-
ber of students that l
k
can supervise (resp. that can be
assigned to p
j
), denoted by d
k
∈ Z
+
(resp. c
j
∈ Z
+
).
We denote A = {(s
i
, p
j
) ∈ S × P } by a set of ac-
ceptable pairs, where p
j
is given by l
k
, s
i
(resp. l
k
)
ranks p
j
in the s
i
’s (resp. l
k
’s) preference list, de-
noted by rank(s
i
, p
j
) (resp. rank(l
k
, p
j
)). If a student
s
i
strictly (resp. equally) prefers a project p
j
to (resp.
and) a project p
t
, then we denote by rank(s
i
, p
j
) <
rank(s
i
, p
t
) (resp. rank(s
i
, p
j
) = rank(s
i
, p
t
)). We use
notations for rank(l
k
, p
j
) similarly.
An assignment M is a subset of A. If (s
i
, p
j
) ∈ M,
then we say that s
i
is assigned to p
j
in M and vice
versa. If s
i
is assigned to p
j
in M, then we denote
M(s
i
) = p
j
, otherwise, we denote M(s
i
) = ∅ (i.e.,
unassigned). Consequently, if l
k
is the lecturer offer-
ing p
j
and s
i
is assigned to p
j
, then we can also say
that s
i
is assigned to l
k
and vice versa. Similarly, for
any project p
j
∈ P (resp. lecturer l
k
∈ L ), we denote
M(p
j
) (resp. M(l
k
)) by the set of students assigned to
p
j
(resp. l
k
) in M. We also say that, a project p
j
∈ P
(resp. lecturer l
k
∈ L ) is under-subscribed, full or
over-subscribed in M if |M(p
j
)| < c
j
, |M(p
j
)| = c
j
,
or |M(p
j
)| > c
j
(resp. |M(l
k
)| < d
k
, |M(l
k
)| = d
k
, or
|M(l
k
)| > d
k
), respectively.
Definition 1 (Matching). A matching M is an assign-
ment such that |M(s
i
)| ≤ 1 for each s
i
∈ S , |M(p
j
)| ≤
c
j
for each p
j
∈ P , and |M(l
k
)| ≤ d
l
for each l
k
∈ L
(i.e., each student is assigned to at most one project,
and no project or lecturer is over-subscribed in M). ◁
Definition 2 (Blocking Pair). An acceptable pair
(s
i
, p
j
) ∈ (S × P )\M is a blocking pair of a match-
ing M, if all the following conditions are fulfilled:
1. p
j
∈ A
i
(i.e., s
i
find p
j
acceptable);
2. Either M(s
i
) = ∅ or s
i
prefers p
j
to M(s
i
);
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
666

3. |M(p
j
)| < c
j
and either
(a) s
i
∈ M(l
k
) and l
k
prefers p
j
to M(s
i
), or
(b) s
i
/∈ M(l
k
) and |M(l
k
)| < d
k
, or
(c) s
i
/∈ M(l
k
), |M(l
k
)| = d
k
, and l
k
prefers p
j
to
l
k
’s worst non-empty project, where l
k
is the
lecturer offering p
j
. ◁
We say that a matching M is stable if it admits no
blocking pair, otherwise, it is unstable. Given a stable
matching M, we denote by |M| the number of students
assigned in M. We also say that M is a perfect match-
ing if |M| = n, otherwise, it is a non-perfect matching.
Example 1. To make these definitions clearer, in
this example, we considers an instance of SPA-PT,
which involves a set of six students S = {s
1
, s
2
, s
3
,
s
4
, s
5
, s
6
}, a set of two lecturers L = {l
1
,l
2
} with
P
1
= {p
1
, p
2
, p
3
, p
4
} and P
2
= {p
5
, p
6
}, and a set of
six projects P = {p
1
, p
2
, p
3
, p
4
, p
5
, p
6
}. Further de-
tails are described in Table 1, where ties in students’
and lecturers’ preference lists are presented in round
brackets. In the lecturers’ preference list, let’s con-
sider the first row for the lecturer l
1
, the meaning of
l
1
: p
3
p
4
(p
1
p
2
) is that, l
1
strictly prefers p
3
to
p
4
, and p
4
to (p
1
and p
2
), also in this case, l
1
prefers
p
1
and p
2
equally. In particular, rank(l
1
, p
3
) = 1,
rank(l
1
, p
4
) = 2, and rank(l
1
, p
1
) = rank(l
1
, p
2
) = 3.
We use the same notations in the students’ preference
list. Rank lists corresponding to the students’ and lec-
turers’ preference lists presented on the left-hand side
of Table 1 are shown on the right-hand side of that ta-
ble. From now on, we use the term students’ list (resp.
lecturers’ list) instead of students’ (resp. lecturers’)
rank list, for short. We say that, s
i
’s list is empty if
rank(s
i
, p
j
) = 0 for all p
j
∈ P .
The matching M = {(s
1
, p
2
), (s
2
, p
6
), (s
3
, p
5
),
(s
4
,∅), (s
5
, p
5
), (s
6
, p
4
)} is unstable since there ex-
ists some blocking pairs {(s
2
, p
2
), (s
2
, p
3
), (s
4
, p
2
),
(s
4
, p
3
)} for M. The matching M = {(s
1
,∅), (s
2
, p
6
),
(s
3
, p
3
), (s
4
, p
2
), (s
5
, p
6
), (s
6
, p
4
)} is stable because
there exists no blocking pair for M, and M is a non-
perfect matching since |M| = 5. The matching M =
{(s
1
, p
3
), (s
2
, p
6
), (s
3
, p
5
), (s
4
, p
2
), (s
5
, p
4
), (s
6
, p
5
)}
is stable since there exists no blocking pair for M. Ad-
ditionally, in this case, M is a perfect matching since
|M| = 6. ◁
3 PROPOSED ALGORITHM FOR
SPA-PT
In this section, we propose an algorithm for finding
maximum stable matching of SPA-PT instances using
a heuristic strategy, named SPA-PT-heuristic, which is
described in Algorithm 1. For initialization, we set
Algorithm 1: SPA-PT-heuristic Algorithm.
Input : An instance of SPA-PT with
S = {s
1
,s
2
,...,s
n
};
P = {p
1
, p
2
,..., p
q
};
L = {l
1
,l
2
,...,l
m
};
M := ∅;
active(s
i
) := 1, ∀s
i
∈ S ;
h(l
k
,s
i
) := 0, ∀l
k
∈ L and ∀s
i
∈ S ;
Output: A maximum-size stable matching M
for SPA-PT
1 while ∃s
i
such that active(s
i
) > 0 do
2 if IsEmpty(s
i
’s list) then
3 active(s
i
) := 0;
4 continue;
5 end
6 A
+
i
:= argmin(rank(s
i
, p
t
) > 0), ∀p
t
∈ A
i
;
7 p
j
:= argmax(c
t
− |M(p
t
)|), ∀p
t
∈ A
+
i
;
8 l
k
:= lecturer offering p
j
;
9 M := M ∪ {(s
i
, p
j
)};
10 active(s
i
) := 0;
11 y(v) := number of projects of rank v in s
i
’
list (v = 1,2,...);
12 h(l
k
,s
i
) := rank(l
k
, p
j
) + (q ∗ sum(y) +
max(y))/(q ∗ q + q + 1);
13 if p
j
is over-subscribed then
14 s
r
:= argmax(h(l
k
,s
r
)), ∀s
r
∈ M(p
j
);
15 M := M \ {(s
r
, p
j
)};
16 rank(s
r
, p
j
) := 0;
17 active(s
r
) := 1;
18 h(l
k
,s
r
) := 0;
19 end
20 if l
k
is over-subscribed then
21 s
r
:= argmax(h(l
k
,s
r
)), ∀s
r
∈ M(l
k
);
22 p
t
:= M(s
r
);
23 M := M \ {(s
r
, p
t
)};
24 rank(s
r
, p
t
) := 0;
25 active(s
r
) := 1;
26 h(l
k
,s
r
) := 0;
27 end
28 end
29 return M;
M = ∅; active(s
i
) = 1 for all s
i
∈ S with the meaning
that all students are active for the first time; and an
array h(l
k
,s
i
) = 0, for all l
k
∈ L (1 ≤ k ≤ m) and s
i
∈
S (1 ≤ i ≤ n), to store a heuristic value for the pair
(l
k
,s
i
) at each iteration.
When there exists an active student s
i
, if there is no
more project in s
i
’s list, then s
i
becomes inactive for-
ever (i.e., active(s
i
) = 0, line 3), and therefore in this
case s
i
is unassigned in M. Otherwise, s
i
is assigned
to the project p
j
with the minimum value of rank, and
An Empirical Heuristic Algorithm for Solving the Student-Project Allocation Problem with Ties
667

Table 1: An instance of SPA-PT.
Students’ preference list Lecturers’ preference list Students’ rank list Lecturers’ rank list
s
1
: (p
1
p
2
) (p
3
p
5
) l
1
: p
3
p
4
(p
1
p
2
) s
1
: 1 1 2 0 2 0 l
1
: 3 3 1 2 0 0
s
2
: p
2
p
3
(p
5
p
6
) l
2
: p
6
p
5
s
2
: 0 1 2 0 3 3 l
2
: 0 0 0 0 2 1
s
3
: (p
1
p
4
p
5
) p
2
p
3
s
3
: 1 2 3 1 1 0
s
4
: (p
2
p
3
) p
5
s
4
: 0 1 1 0 2 0
s
5
: (p
4
p
5
) p
1
(p
2
p
6
) s
5
: 2 3 0 1 1 3
s
6
: p
5
p
4
s
6
: 0 0 0 2 1 0
Lecturers’ capacities: d
1
= 3,d
2
= 3; Projects’ capacities: c
1
= c
3
= c
4
= 1,c
2
= c
5
= 2,c
6
= 3
the maximum remaining capacity on the s
i
’s list (i.e.,
the pair (s
i
, p
j
) is added to M, lines 6-9). In this case,
s
i
becomes inactive (line 10), and the heuristic value
h(l
k
,s
i
) is updated based on the following heuristic
function, where y is an array and each y(v) stores the
number of project of rank v in s
i
’s list (i.e., the fre-
quency of rank v in s
i
’s list with v = 1,2,...):
h(l
k
,s
i
) := rank(l
k
, p
j
) + (q ∗ sum(y) +
max(y))/(q ∗ q + q + 1).
The intuition behind the heuristic function h(l
k
,s
i
)
is that, the student s
i
, who has the most opportuni-
ties to choose his/her projects based on s
i
’s list, will
be selected to remove from M for the cases either p
j
is over-subscribed, or l
k
is over-subscribed. Particu-
larly, instead of choosing an arbitrary assigned stu-
dent s
i
to remove, the heuristic function is used to
eliminate the student with the most opportunity and
keep the students in M who have the least opportunity
to be reassigned to some project in their lists at the
next iterations.
In the case p
j
is over-subscribed, the student
s
r
∈ M(p
j
) corresponding to the maximum value of
h(l
k
,s
r
) is removed from M (lines 14-15), where l
k
is the lecturer offering p
j
. Also in this case, p
j
is
deleted from s
r
’s list (line 16) and s
r
is now active
again (line 17).
Similarly, in the case l
k
is over-subscribed, the
student s
r
∈ M(l
k
) corresponding to the maximum
value of h(l
k
,s
r
) is removed from M (lines 21-23).
Also in this case, p
t
is deleted from s
r
’s list (line 24)
and s
r
is now active again (line 25), where p
t
is the
project assigned to s
r
in the earlier step. We set the
heuristic value h(l
k
,s
r
) to zero when a student s
r
is
remove from M (lines 18 and 26). If there is no stu-
dent in the active state, the algorithm terminates and
returns a maximum stable matching in M.
Example 2. This example illustrates the running of
Algorithm 1 by using the SPA-PT instance given in Ta-
bles 1. Algorithm 1 starts with M = ∅, active(s
i
) = 1,
∀s
i
∈ S (i.e., all students are assigned to active), and
h(l
k
,s
i
) = 0, ∀l
k
∈ L and ∀s
i
∈ S . The i
th
iteration of
running Algorithm 1 is performed in detail as follows:
(1) s
1
is assigned to p
2
since p
2
has the minimum
value of rank with the maximum remaining ca-
pacity on the s
1
’s list (there are two projects p
1
and p
2
with rank(s
1
, p
1
) = rank(s
1
, p
2
) = 1, and
the current capacity for p
1
is 1, whilst p
2
is 2).
Consequently, M = {(s
1
, p
2
)} and s
1
is now inac-
tive (i.e., active(s
1
) = 0).
(2) s
2
is assigned to p
2
since p
2
is the unique min-
imum value of rank on the s
2
’s list and p
2
is
under-subscribed. As the result, M = {(s
1
, p
2
),
(s
2
, p
2
)} and s
2
is now inactive.
(3) s
3
is assigned to p
5
since projects p
1
, p
4
and p
5
have the minimum value of rank on the s
3
’s list,
but p
5
has the maximum current capacity. Conse-
quently, M = {(s
1
, p
2
), (s
2
, p
2
), (s
3
, p
5
)} and s
3
becomes inactive.
(4) Similarly, s
4
is assigned to his/her most preferred
project p
3
and becomes inactive. Consequently,
M = {(s
1
, p
2
), (s
2
, p
2
), (s
3
, p
5
), (s
4
, p
3
)}.
(5) s
5
is assigned to his/her most preferred project p
4
and becomes inactive. However, in this case l
1
is
over-subscribed and h(l
1
,s
1
) is maximum, there-
fore the pair (s
1
, p
2
) is eliminated from M, s
1
is
now active again. As the result, M = {(s
2
, p
2
),
(s
3
, p
5
), (s
4
, p
3
), (s
5
, p
4
)}.
(6) Similarly, s
6
is assigned to p
5
and becomes
inactive. Consequently, M = {(s
2
, p
2
), (s
3
, p
5
),
(s
4
, p
3
), (s
5
, p
4
), (s
6
, p
5
)}. After this step, we
have only s
1
in active state.
(7) s
1
is assigned to p
1
and becomes inactive since p
1
is the unique minimum value of rank on the s
1
’s
list. However, in this case l
1
is over-subscribed
and h(l
1
,s
2
) is maximum, therefore the pair
(s
2
, p
2
) is eliminated from M, s
2
is now active
again. As the result, M = {(s
1
, p
1
), (s
3
, p
5
),
(s
4
, p
3
), (s
5
, p
4
), (s
6
, p
5
)}.
(8) s
2
is assigned to his/her most preferred project p
3
and becomes inactive. However, in this case p
3
is over-subscribed and the pair (s
2
, p
3
) ∈ M has
the maximum value of h(l
1
,s
2
), therefore the pair
(s
2
, p
3
) is eliminated from M, and s
2
is now ac-
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
668

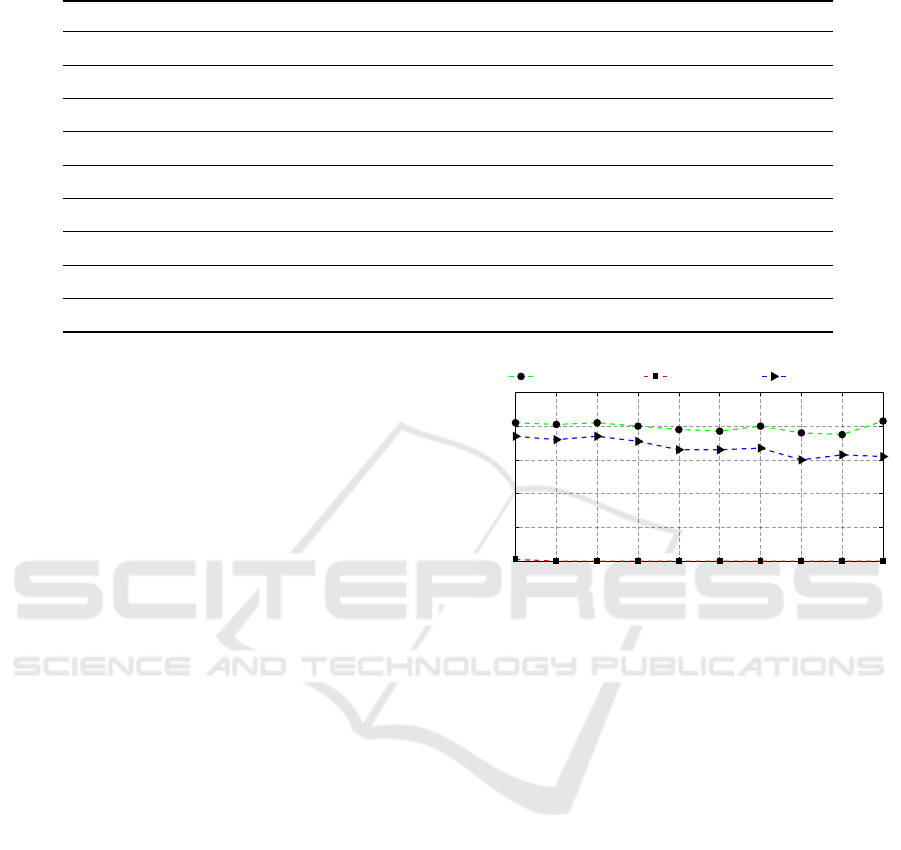
Table 2: The step-by-step of running Algorithm 1 for the instance given in Table 1.
# s
i
p
j
l
k
Matching M (M = M ∪ (s
i
, p
j
)) M \(s
r
, p
t
)
1 s
1
p
2
l
1
{(s
1
, p
2
)}
2 s
2
p
2
l
1
{(s
1
, p
2
),(s
2
, p
2
)}
3 s
3
p
5
l
2
{(s
1
, p
2
),(s
2
, p
2
),(s
3
, p
5
)}
4 s
4
p
3
l
1
{(s
1
, p
2
),(s
2
, p
2
),(s
3
, p
5
),(s
4
, p
3
)}
5 s
5
p
4
l
1
{(s
2
, p
2
),(s
3
, p
5
),(s
4
, p
3
),(s
5
, p
4
)} {(s
1
, p
2
)}
6 s
6
p
5
l
2
{(s
2
, p
2
),(s
3
, p
5
),(s
4
, p
3
),(s
5
, p
4
),(s
6
, p
5
)}
7 s
1
p
1
l
1
{(s
1
, p
1
),(s
3
, p
5
),(s
4
, p
3
),(s
5
, p
4
),(s
6
, p
5
)} {(s
2
, p
2
)}
8 s
2
p
3
l
1
{(s
1
, p
1
),(s
3
, p
5
),(s
4
, p
3
),(s
5
, p
4
),(s
6
, p
5
)} {(s
2
, p
3
)}
9 s
2
p
6
l
2
{(s
1
, p
3
),(s
2
, p
6
),(s
3
, p
5
),(s
4
, p
2
),(s
5
, p
4
),(s
6
, p
5
)}
tive again. As the result, M = {(s
1
, p
1
), (s
3
, p
5
),
(s
4
, p
3
), (s
5
, p
4
), (s
6
, p
5
)}.
(9) Finally, s
2
is assigned to his/her most preferred
project p
6
and becomes inactive. After this step,
all students are inactive, the algorithm termi-
nates and returns a stable matching M = {(s
1
, p
3
),
(s
2
, p
6
), (s
3
, p
5
), (s
4
, p
2
), (s
5
, p
4
), (s
6
, p
5
)}. ◁
The running steps of Algorithm 1 in Example 2
are summarized in Table 2.
4 EXPERIMENTS
In this section, we present several experiments to eval-
uate the performance of our SPA-PT-heuristic algo-
rithm. We implemented our algorithm and the com-
pared algorithms by Matlab R2019a software on a
laptop computer with Core i7-8550U CPU 1.8 GHz
and 16 GB RAM, running on Windows 11.
Datasets. To run experiments, we extend the ran-
dom problem generator algorithm for SMTI prob-
lem (Gent and Prosser, 2002) to generate random
SPA-PT instances. Specifically, we generated random
SPA-PT instances with four parameters (n, m, q, τ),
where n is the number of students, m is the number
of lecturers, and q is the number of projects, and τ is
the probability of ties in both preference lists of stu-
dents and lecturers.
4.1 Experiments for SPA-P
In this section, we chose the well-known SPA-P-
approx (Manlove and O’Malley, 2008) and SPA-P-
approx-promotion (Iwama et al., 2012) (for short, we
call it SPA-P-promotion) algorithms to compare their
solution quality and execution time with those of SPA-
200 400 600 800 1000 1200 1400 1600 1800 2000
Number of students
0
20
40
60
80
100
Percentage of perfect matchings
SPA-PT-heuristic SPA-P-approx
SPA-P-promotion
Figure 1: Percentage of perfect matchings found by SPA-
PT-heuristic, SPA-P-promotion, and SPA-P-approx algo-
rithms for the Experiment 1.
PT-heuristic algorithm. Since SPA-P-approx and SPA-P-
promotion algorithm are used for SPA-P, so we chose
τ = 0.0, meaning that SPA-PT becomes SPA-P.
Experiment 1. In this experiment, we chose n ∈
{200,400,··· ,2000}. For each value of n, we gener-
ated 100 instances of SPA-PT of parameters (n,m, q),
where m and q are random integer numbers bound
by 0.02n ≤ m ≤ 0.1n and 0.1n ≤ q ≤ 0.5n, respec-
tively. This means that the student-to-lecturer ratio is
from 10 to 50, the student-to-project ratio is from 2
to 10, and each lecturer offers from 1 to 25 projects
randomly. In each instance, we let each student ran-
domly rank from 1 to 20 (i.e., |A
i
| ∈ [1,20]) projects in
the set P of projects offered by all lecturers. Besides,
we generate the capacity c
j
of each project p
j
∈ P
such that 2 ≤ c
j
≤ 11 and
∑
q
j=1
c
j
= n. Finally, we set
the capacity d
k
of each lecturer l
k
to the total capac-
ity of projects offered by l
k
, i.e. d
k
=
∑
c
j
, where c
j
is
the capacity of project p
j
∈ P
k
. These conditions mean
that the total capacity of the projects proposed by all
lecturers is the same as that with the total number of
students (i.e., the total capacity of the projects is just
enough to assign to the given number of students n).
An Empirical Heuristic Algorithm for Solving the Student-Project Allocation Problem with Ties
669

200 400 600 800 1000 1200 1400 1600 1800 2000
Number of students
0
0.1
0.2
0.3
Average execution time (sec.)
SPA-PT-heuristic SPA-P-approx
SPA-P-promotion
Figure 2: Execution time of SPA-PT-heuristic, SPA-P-
promotion, and SPA-P-approx algorithms for the Experi-
ment 1.
Figure 1 shows the percentage of perfect
matchings found by SPA-PT-heuristic, SPA-P-promotion,
and SPA-P-approx algorithms. SPA-PT-heuristic finds
from 75% to 83% of perfect matchings, SPA-P-approx-
promotion finds from 60% to 74% of perfect match-
ings, while SPA-P-approx finds only 1% of perfect
matchings at n = 200.
Table 3 shows the average of unassigned students
found by SPA-PT-heuristic, SPA-P-promotion, and SPA-P-
approx algorithms. For every n from 200 to 2000, SPA-
PT-heuristic finds a smaller number of unassigned stu-
dents in non-perfect matchings than SPA-P-promotion
and SPA-P-approx do. Especially, when n is larger, the
average of unassigned students in non-perfect match-
ings found by SPA-PT-heuristic is much smaller than
that found by SPA-P-promotion and SPA-P-approx. This
means that the stable matchings found by SPA-PT-
heuristic are larger than those found by SPA-P-promotion
and SPA-P-approx in terms of size.
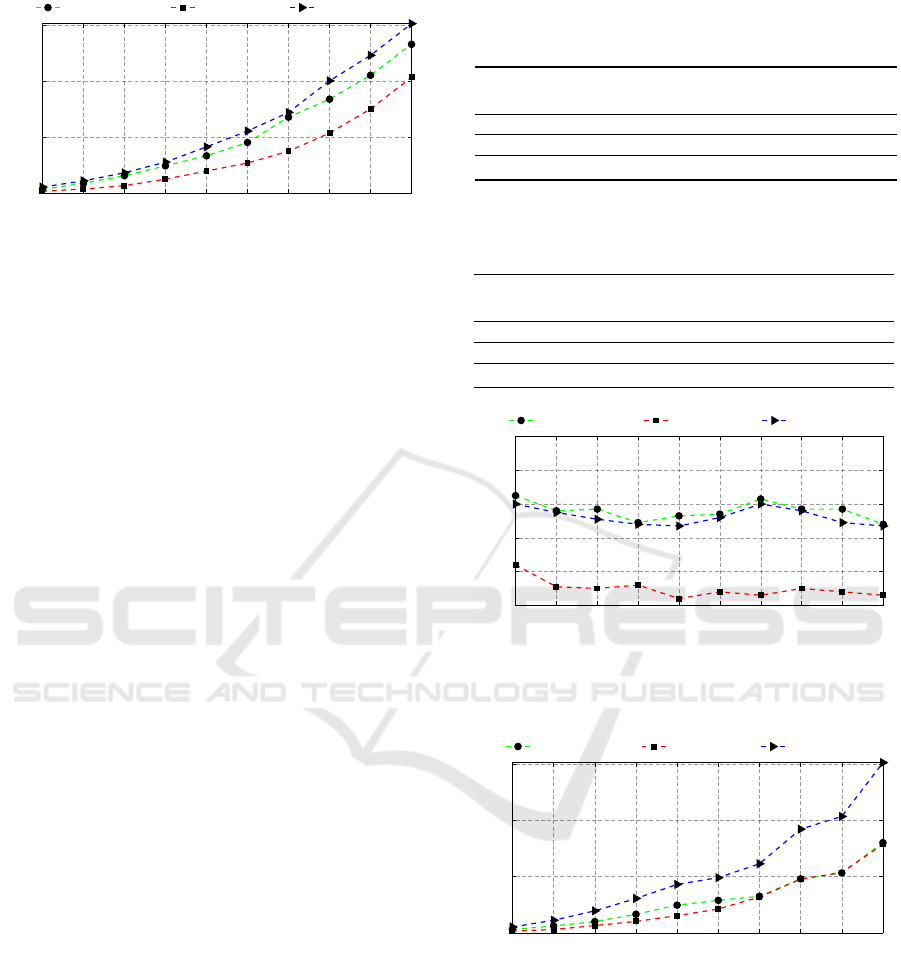
Figure 2 shows the average execution time of
found by SPA-PT-heuristic, SPA-P-promotion, and SPA-
P-approx algorithms. We see that SPA-PT-heuristic runs
faster than SPA-P-promotion, but slower than SPA-P-
approx. As mentioned above, the problem of finding a
maximum cardinality stable matching is NP-hard. By
using the approximation solutions, these algorithms
run approximately in 3 seconds with n = 2000. That
is, they are possible for using in practical applications
w.r.t. the execution time.
Experiment 2. In this experiment, we chose val-
ues of parameters n, m, and q as in Experiment 1.
In each instance, we let each student randomly rank
from 1 to 10 (i.e., |A
i
| ∈ [1,10]) projects in the set P
of projects offered by all lecturers. Besides, we gen-
erate the capacity c
j
of each project p
j
∈ P such that
2 ≤ c
j
≤ 11 and n ≤
∑
q
j=1
c
j
≤ 1.5n. Finally, we set
the capacity d
k
of each lecturer l
k
to be a random inte-
ger number such that 0.8 ×
∑
c
j
≤ d
k
≤
∑
c
j
, where c
j
is the capacity of project p
j
∈ P
k
. This means that each
lecturer l
k
chooses from 80% to 100% students in the
Table 3: Average of unassigned students found by SPA-PT-
heuristic (A1), SPA-P-promotion (A2), and SPA-P-approx
(A3) algorithms for the Experiment 1.
Number of students n
200 400 600 800 1000 1200 1400 1600 1800 2000
A1 13.2 16.4 23.9 42.6 77.0 62.4 55.1 91.4 97.8 86.8
A2 14.1 17.1 26.4 44.4 79.0 65.0 59.3 95.1 102.9 96.5
A3 29.2 49.3 75.7 107.4 151.9 157.0 170.1 210.6 240.1 255.2
Table 4: Average of unassigned students found by SPA-PT-
heuristic (A1), SPA-P-promotion (A2), and SPA-P-approx
(A3) algorithms for the Experiment 2.
Number of students n
200 400 600 800 1000 1200 1400 1600 1800 2000
A1 9.4 19.6 27.8 33.0 43.5 36.8 67.6 64.0 76.0 78.2
A2 9.7 19.8 28.6 33.7 43.6 37.5 67.6 66.1 77.3 79.0
A3 17.1 36.0 50.8 64.9 81.1 82.7 124.3 130.2 149.8 151.8
200 400 600 800 1000 1200 1400 1600 1800 2000
Number of students
0
20
40
60
80
100
Percentage of perfect matchings
SPA-PT-heuristic SPA-P-approx
SPA-P-promotion
Figure 3: Percentage of perfect matchings found by SPA-
PT-heuristic, SPA-P-promotion, and SPA-P-approx algo-
rithms for the Experiment 2.
200 400 600 800 1000 1200 1400 1600 1800 2000
Number of students
0
0.1
0.2
0.3
Average execution time (sec.)
SPA-PT-heuristic SPA-P-approx
SPA-P-promotion
Figure 4: Execution time of SPA-PT-heuristic, SPA-P-
promotion, and SPA-P-approx algorithms for the Experi-
ment 2.
total of capacities of projects offered by her/him.
Figure 3 shows the percentage of perfect match-
ings found by SPA-PT-heuristic, SPA-P-promotion, and
SPA-P-approx algorithms. Again, we see that SPA-PT-
heuristic finds many perfect matchings than SPA-P-
promotion and SPA-P-approx do.
Table 4 shows the average of unassigned students
found by SPA-PT-heuristic, SPA-P-promotion, and SPA-P-
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
670

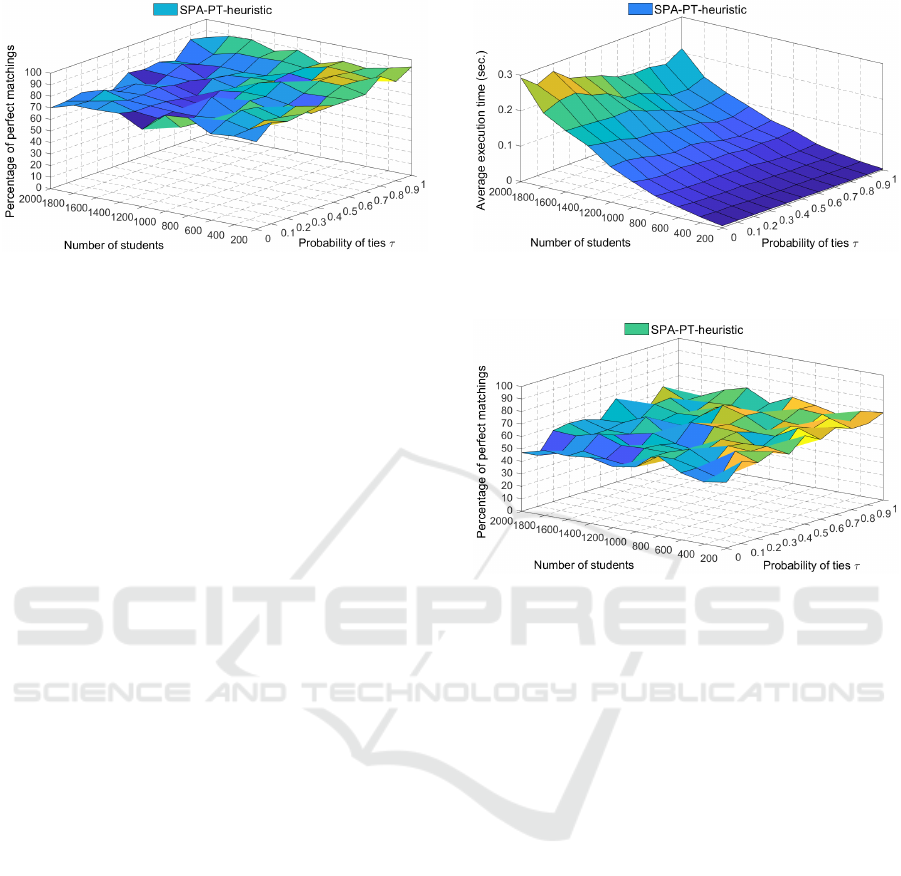
Figure 5: Percentage of perfect matchings found by SPA-
PT-heuristic algorithm for the Experiment 3.
approx algorithms. Again, we see that SPA-PT-heuristic
finds a smaller number of unassigned students in non-
perfect matchings than SPA-P-promotion and SPA-P-
approx. This means the stable matchings found by
SPA-PT-heuristic is larger than those found by SPA-P-
promotion and SPA-P-approx.
Figure 4 shows the average execution time of
found by SPA-PT-heuristic, SPA-P-promotion, and SPA-P-
approx algorithms. We see that when n is larger, SPA-
PT-heuristic runs much faster than SPA-P-promotion, but
equally fast as SPA-P-approx.
In brief, in the two above experiments, SPA-PT-
heuristic not only outperforms both SPA-P-promotion
and SPA-P-approx in terms of solution quality but also
the execution time.
4.2 Experiments for SPA-PT
In this section, we present two experiments to con-
sider the behavior of SPA-PT-heuristic for SPA-PT when
the probability of ties τ varies from 0.0 to 1.0.
Experiment 3. In this experiment, we let all the
settings be the same as in Experiment 1. However,
we allow ties to appear in the preference lists of
both students and lecturers with the probability of ties
τ ∈ {0.0,0.1,··· ,1.0}.
Figure 5 shows the percentage of perfect match-
ings found by SPA-PT-heuristic algorithm. For n from
200 to 2000, SPA-PT-heuristic found more than 70% of
perfect matchings. Moreover, as n increases from 200
to 2000 the percentage of perfect matchings found by
SPA-PT-heuristic decreases. As τ increases from 0.0 to
1.0 the percentage of perfect matchings found by SPA-
PT-heuristic increases.
Figure 6 shows the execution time of SPA-PT-
heuristic algorithm. As τ increases from 0.0 to 1.0,
the execution time of SPA-PT-heuristic decreases. As
n increases from 200 to 2000, the execution time of
SPA-PT-heuristic increases. As mentioned earlier, with
n = 2000, our algorithm runs approximately in 3 sec-
Figure 6: Execution time of SPA-PT-heuristic algorithm for
the Experiment 3.
Figure 7: Percentage of perfect matchings found by SPA-
PT-heuristic algorithm for the Experiment 4.
onds, thus, it can be applied easily in practical appli-
cations.
Experiment 4. In this experiment, we let all the
settings be the same as in Experiment 2 and τ ∈
{0.0,0.1,··· ,1.0}.
Figure 7 shows the percentage of perfect match-
ings found by SPA-PT-heuristic algorithm. As τ in-
creases from 0.0 to 1.0 the percentage of perfect
matchings found by SPA-PT-heuristic slightly increases.
As n increases from 200 to 2000 the percentage of
perfect matchings found by SPA-PT-heuristic decreases.
Figure 8 shows the execution time of SPA-PT-
heuristic algorithm. As τ increases from 0.0 to 1.0, the
execution time of SPA-PT-heuristic slightly increases.
As n increases from 200 to 2000, the execution time
of SPA-PT-heuristic increases.
5 CONCLUSIONS
In this paper, we proposed a heuristic algorithm to
find maximum stable matching of SPA-PT instances.
Starting at an empty matching, our algorithm itera-
tively constructs a maximum stable matching of stu-
dents and projects. At each iteration, our algorithm
An Empirical Heuristic Algorithm for Solving the Student-Project Allocation Problem with Ties
671

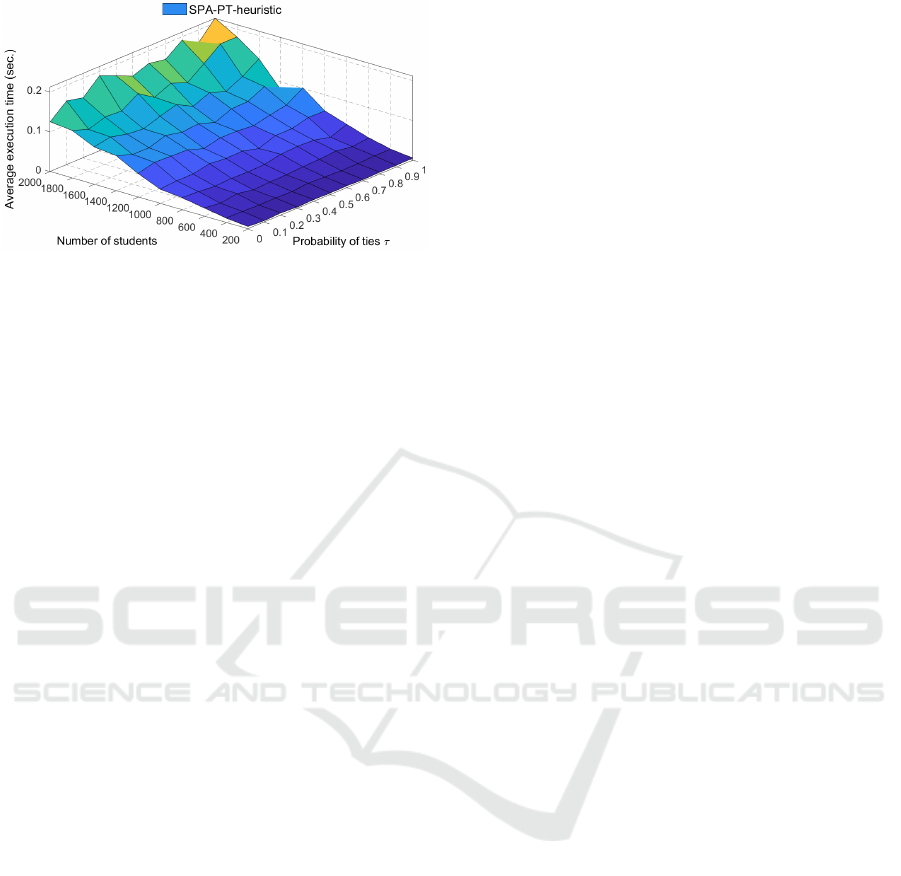
Figure 8: Execution time of SPA-PT-heuristic algorithm for
the Experiment 4.
chooses the most ranked project of an unassigned stu-
dent to assign for her/him. If the assigned project or
the lecturer who offers the assigned project is over-
subscribed, instead of choosing an arbitrary assigned
student to remove, our algorithm removes the stu-
dent corresponding to the maximum value of the pro-
posed heuristic function (i.e., we want to keep the
students who have the least opportunity to be reas-
signed to some project in their lists at the next it-
erations). Experiment results showed that our algo-
rithm not only outperforms the SPA-P-approx and SPA-
P-approx-promotion algorithms for the SPA-P problem
w.r.t. the execution time and solution quality, but also
efficient for the SPA-PT problem.
REFERENCES
Abraham, D. J., Irving, R. W., and Manlove, D. F. (2003).
The Student-Project Allocation Problem. In Proceed-
ing of ISAAC’2003, Lecture Notes in Computer Sci-
ence, page 474–484.
Abraham, D. J., Irving, R. W., and Manlove, D. F.
(2007). Two algorithms for the student-project al-
location problem. Journal of Discrete Algorithms,
5(1):73–90.
Gale, D. and Shapley, L. S. (1962). College admissions and
the stability of marriage. The American Mathematical
Monthly, 69(1):9–15.
Gent, I. P. and Prosser, P. (2002). An empirical study of the
stable marriage problem with ties and incomplete lists.
In in Proceedings of the 15th European Conference on
Artificial Intelligence, pages 141–145, Lyon, France.
Iwama, K., Miyazaki, S., and Yanagisawa, H. (2012). Im-
proved approximation bounds for the student-project
allocation problem with preferences over projects.
Journal of Discrete Algorithms, 13(1):59–66.
Kir
´
aly, Z. (2011). Better and simpler approximation algo-
rithms for the stable marriage problem. Algorithmica,
60:3–20.
Manlove, D., Milne, D., and Olaosebikan, S. (2018). An
Integer Programming Approach to the Student-Project
Allocation Problem with Preferences over Projects. In
Proceeding of ISCO’2018, Lecture Notes in Computer
Science, page 313–325.
Manlove, D. F. and O’Malley, G. (2008). Two algorithms
for the student-project allocation problem. Journal of
Discrete Algorithms, 5(4):553–560.
Olaosebikan, S. and Manlove, D. (2022). Super-stability in
the student-project allocation problem with ties. Jour-
nal of Combinatorial Optimization, 43:1203–1239.
Roth, A. E. (1984). The evolution of the labor mar-
ket for medical interns and residents: a case study
in game theory. Journal of Political Economy,
92(6):991–1016.
Viet, H. H., Tan, L. V., and Cao, S. T. (2020). Finding Max-
imum Stable Matchings for the Student-Project Allo-
cation Problem with Preferences Over Projects. In
Proceeding of FDSE’2020, Communications in Com-
puter and Information Science, page 411–422.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
672