Integrated Optimization of Vehicle Trajectories and Traffic Signal

Timings

Hao Chen

and Hesham A. Rakha

Charles E. Via, Jr. Department of Civil and Environmental Engineering, Virginia Tech Transportation Institute,

Virginia Polytechnic Institute and State University, 3500 Transportation Research Plaza, Blacksburg, VA 24061, U.S.A.

Keywords: Integrated Controller, Signal Time Optimization, Vehicle Speed Control, Signalized Intersections,

Energy-Optimized Solution, Connected and Automated Vehicles, Microscopic Traffic Simulation.

Abstract: This research develops a bi-level optimizer that provides energy-optimal control for vehicles and traffic

signals. The first level optimizes the traffic signal timings to minimize the total energy consumption of

approaching vehicles. The traffic signal optimization can be easily implemented in real-time traffic signal

controllers and overcomes the shortcomings of the traditional Webster method, which overestimates the cycle

length when the traffic volume-to-capacity ratio exceeds 50 percent. The lower-level optimizer is the vehicle

speed controller, which calculates the optimal vehicle brake and throttle levels to minimize the energy

consumption of individual vehicles. The proposed integrated controller is first tested on an isolated signalized

intersection, and then on an arterial network with multiple signalized intersections to investigate the

performance of the proposed controller under various traffic demand levels. The test results demonstrate that

the proposed integrated controller can greatly improve energy efficiency producing fuel savings of up to

17.7%. It can also enhance traffic mobility by reducing traffic delays by up to a 47.2% and reducing vehicle

stops by up to 24.8%.

1 INTRODUCTION

The United States is one of the world’s prime

petroleum consumers, burning more than 20% of the

planet’s total refined petroleum. The surface

transportation sector alone accounts for around 69%

of the United States’ total petroleum usage and 33%

of the nation’s CO

emissions (Administration,

2018). This presents the transportation sector with

three important challenges: availability of fuel to

drive vehicles, emissions of greenhouse gases, and

vehicular crashes. It is, therefore, important to reduce

petroleum consumption and greenhouse gas

emissions to make surface transportation safer, more

efficient, and more sustainable (Kamalanathsharma,

2014).

Studies have shown that stop-and-go traffic near

signalized intersections can greatly increase traffic

delays, energy consumption, and emission levels on

arterial roads since vehicles are forced to stop ahead

of traffic signals when encountering red indications,

https://orcid.org/0000-0001-8272-734X

https://orcid.org/0000-0002-5845-2929

producing shock waves within the traffic stream

(Barth & Boriboonsomsin, 2008). Starting from the

1980s, many studies have focused on optimizing

traffic signal timings using measured traffic data to

improve the operation of arterial roads (Gartner,

Assman, Lasaga, & Hou, 1991; Park, Messer, &

Urbanik, 1999). In the past decade, the advanced

communication power in CVs ensures rapid

information sharing, which enables researchers to

develop eco-driving strategies to optimize vehicle

trajectories in real-time using signal phase and timing

(SPaT) data. This has the potential to greatly improve

traffic mobility and reduce energy consumption and

emissions (Almannaa, Chen, Rakha, Loulizi, & El-

Shawarby, 2019; Chen & Rakha, 2020; Chen, Rakha,

Loulizi, El-Shawarby, & Almannaa, 2016). Recently,

a few studies have attempted to simultaneously

optimize vehicle trajectories and traffic signal timings

to further improve transportation efficiency and fuel

economy on arterial roads. For instance, an integrated

optimization method was developed to optimize

Chen, H. and Rakha, H.

Integrated Optimization of Vehicle Trajectories and Trafﬁc Signal Timings.

DOI: 10.5220/0011709900003479

In Proceedings of the 9th International Conference on Vehicle Technology and Intelligent Transpor t Systems (VEHITS 2023), pages 27-34

ISBN: 978-989-758-652-1; ISSN: 2184-495X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

vehicle platoons and traffic signal timings using a

mixed integer linear programming model (C. Yu,

Feng, Liu, Ma, & Yang, 2018). However, this method

uses some unrealistic assumptions, such as assuming

all vehicles are homogeneous and lane changes are

instantaneous, which limit the method’s applicability.

A simplified simulation with one intersection was

designed to validate the performance of the proposed

method. In addition, another study developed a

cooperative method of traffic signal and vehicle speed

optimization at isolated intersections (Xu et al.,

2018). This method entails a two-level controller –

the first level calculates the optimal signal timings

and vehicle arrival times to minimize the total travel

time; the second level optimizes the engine power and

brake force to minimize the fuel consumption of

individual vehicles. However, the proposed method

assumes a 100% market penetration of CAVs, so it

cannot be used for CVs that are controlled by human

drivers. In addition, the optimization problem is

solved using an enumeration method, which results in

a heavy computational cost. Thereafter, a dynamic

programming and shooting heuristic approach is

proposed to optimize CAV trajectories and the traffic

signal controller at the same time (Guo et al., 2019).

A shooting heuristic algorithm was used to compute

near-optimal vehicle trajectories to save

computational costs. Numerical tests were conducted

that demonstrated that the proposed method

outperforms adaptive signal control. Although the

algorithm can be used with a mixture of CAVs and

CVs, the developed controller only optimizes CAVs

which can fully follow the speed control but does not

provide optimized speed for CVs.

According to the aforementioned studies,

optimizing both vehicle trajectories and signal

timings is a promising method to improve

transportation system efficiency and fuel economy on

arterial roads. However, there are several issues in

these studies. First, the developed methods are

generally very complicated with high computational

costs, and thus there is a need to develop a simpler

approach with low computational cost so that it can

be easily implemented in real-time applications.

Second, existing studies only validated the developed

methods either in numerical tests or simplified

simulation tests with only one intersection. This is

also because these methods are very complicated to

implement into simulation software or field tests. So,

there is a need to test the approach using microscopic

traffic simulation software and validate the

performances under various conditions, such as

different traffic demand levels on the arterial network

with multiple signalized intersections.

This study considers these issues in the previous

literature to develop an integrated vehicle speed and

traffic signal controller. In the proposed system, we

develop a two-layer optimization approach that is

computationally fast to provide energy-optimal

control for vehicles and traffic signal controllers.

These two optimizers will work in tandem by sharing

information. The optimizer in the first layer computes

the traffic signal timings to minimize the total energy

consumption levels of approaching vehicles from

upstream traffic. The traffic signal optimization can

be easily implemented into the real-time signal

controller, and it overcomes the issues in the

traditional Webster’s method of overestimating the

cycle length when the traffic volume-to-capacity ratio

exceeds 50 percent. The second layer optimizer is the

vehicle speed controller which calculates the optimal

vehicle brake and throttle levels to minimize the

energy consumption of individual vehicles. The

proposed integrated controller is first tested in an

isolated signalized intersection. An arterial network

with multiple intersections is then used to investigate

the performance of the proposed controller under

various traffic demands. The test results demonstrate

that the proposed integrated controller outperforms

other methods and produces the most savings in fuel

consumption, traffic delay, and vehicle stop under

various traffic demands.

The remainder of this paper is presented as

follows. The integrated controller is described in the

next section, including the traffic signal optimization,

and the vehicle speed controller. The proposed bi-

level controller is then tested in an isolated signalized

intersection. This is followed by implementing the

proposed controller on a simulated arterial network in

the town of Blacksburg, VA to test the network-level

performance under different traffic demands. The last

section provides the study conclusions.

2 PROPOSED INTEGRATED

CONTROLLER

The proposed integrated controller includes two

levels of optimization: one for traffic signals and the

other for vehicle trajectories. The traffic signal

controller optimizes the signal cycle length and

timing according to the incoming traffic flow rate

from the upstream links of the signalized intersection.

The individual vehicle speed controller optimizes the

vehicle trajectories using the data from traffic signals

and surrounding vehicles through V2I and V2V

communications. The integrated controller computes

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

the optimized signal timing and vehicle trajectory to

minimize the energy consumption of the entire traffic

network. The details of the two-layer control

strategies are provided below.

2.1 Traffic Signal Optimization

The traditional goal of optimizing traffic signal cycle

length usually focuses on minimizing vehicle delay

and increasing throughput at the intersection. The

classic method is designed by British researcher F.V

Webster, who developed an optimal cycle length

formulation that approximates the signal timings

necessary to minimize vehicle delay (Webster, 1958),

as seen in Equation (1). This formulation has been

used in traffic analysis for years and is still one of the

prevailing methodologies used to determine the

optimal cycle length for traffic signals.

𝐶



1.5𝐿+ 5

1−𝑌

(1)

where,

opt

= cycle length to minimize delay in seconds.

L = total lost time for cycle in seconds.

Y = sum of flow ratios for critical lane groups.

However, several studies have found that the

optimal signal timing for minimizing delays is not

necessarily identical to the timing plans that minimize

energy consumption and emissions. For instance, a

generalized formulation was developed in (Akcelik,

1981) to compute optimal cycle time for signalized

intersections by different performance measures

including fuel consumption, cost and delay. An

additional parameter was introduced into the

equation, and different values were calibrated to

optimize cycle length for fuel consumption and delay.

The study in (Ma, Jin, & Lei, 2014) proposed and

compared various traffic signal optimization methods

using VISSIM and SUMO. The test results indicated

that there are apparent trade-offs between the goal of

mobility and sustainability. Moreover, researchers

studied the emissions at isolated intersections and

found that the goal of decreasing delays at

intersections and reducing emissions is not simply

equivalent (Li, Wu, & Zou, 2011). Delays at

intersections will increase if the number of vehicle

stops decrease, which will help reduce the pollution

at intersections. In addition, the study in (Liao, 2013)

considers a fuel-based signal optimization model,

which describes the stochastic effects of vehicle

movements that consume excess fuel. The proposed

model was compared with the results from Webster’s

model, TRANSYT 7F, and Synchro, demonstrating

the greatest efficiency among all the methods with

fuel consumption reductions of up to 40%.

Recent studies in (Calle-Laguna, Du, & Rakha,

2019; Calle Laguna, 2017) improved the traditional

equation recommended by Webster by using the data

obtained from microscopic traffic simulation

software. The improved model, represented in

Equation (2), has also outperformed Webster’s

equation to further reduce traffic delay, especially

during higher traffic demand volumes. Since

optimizing traffic signal to minimize traffic delay

doesn’t mean the fuel consumption is also minimized,

another new formulation in Equation (3) is computed

by optimizing the signal cycle length to minimize

vehicle fuel consumption levels. A case study has

shown that the improved equations overcome the

issues in the traditional Webster’s method of

overestimating the cycle length when the traffic

volume-to-capacity ratio exceeds 50 percent, the

detailed test results can be found in (Calle-Laguna et

al., 2019; Calle Laguna, 2017). First, the optimal

cycle length is obtained, thereafter the signal timings

are computed by considering the green times using

the critical lane traffic ratio (Urbanik et al., 2015).

Eventually, the optimal signal timings can be

computed according to the traffic flow rates from

upstream links of the signalized intersections at each

interval, e.g., five minutes.

𝐶

,

0.33𝐿+ 8.56

1−𝑌

+3.8

)

𝐶

,

0.82𝐿

1−𝑌

+ 40

)

2.2 Vehicle Trajectory Optimization

In this study, the vehicle trajectory is optimized by the

connected eco-driving controller, named eco-

cooperative adaptive cruise control at intersections

(Eco-CACC-I), previously developed in (Almannaa

et al., 2019; Chen & Rakha, 2020; Chen et al., 2016)

to compute real-time fuel/energy-optimized vehicle

trajectories in the vicinity of signalized intersections.

The control region was defined from a distance

upstream of the signalized intersection (d

) to a

distance downstream of the intersection (d

down

) in

which the Eco-CACC-I controller optimizes the

vehicle trajectories approaching and leaving

signalized intersections. Upon approaching a

signalized intersection, the vehicle may accelerate,

decelerate, or cruise (maintain a constant speed)

based on several factors, such as vehicle speed, signal

timing, phase, distance to the intersection, road grade,

headway distance, etc. We assumed no leading

Integrated Optimization of Vehicle Trajectories and Trafﬁc Signal Timings

vehicle ahead of the subject vehicle so that we could

compute the energy-optimized vehicle trajectory for

the subject without considering the impacts of other

surrounding vehicles. The computed optimal speed

was used as a variable speed limit, denoted by v

(t),

which is one of the constraints on the subject

vehicle’s longitudinal motion. When a vehicle travels

on the roadway, there are other constraints to be

considered, including the allowed speed constrained

by the vehicle dynamics model, steady-state car

following model, collision avoidance constraints, and

roadway speed limit. All these constraints work

together to control the vehicle speed. In this way, the

proposed controller can also be used in the situation

that the subject vehicle follows a leading vehicle, and

the vehicle speed can be computed by v(t) = min(v

(t),

(t), v

(t)) using the following constraints:

• The maximum speed v

(t) allowed by the vehicle

acceleration model for a given vehicle throttle

position.

• The maximum speed v

(t) constrained by the

steady-state vehicle spacing in the simulation

software.

• The speed v

(t) to avoid a rear-end vehicle

collision.

• The road speed limit v

(t).

Within the control region, the vehicle’s behavior

can be categorized into one of two cases: (1) the

vehicle can proceed through the signalized

intersection without decelerating or (2) the vehicle

must decelerate to proceed through the intersection.

Given that vehicles drive in different manners for

cases 1 and 2, the Eco-CACC-I control strategies

were developed separately for the two cases.

Case 1 does not require the vehicle to decelerate to

traverse the signalized intersection. In this case, the

cruise speed for the vehicle to approach the

intersection during the red indication can be

calculated using Equation (4) to maximize the

average vehicle speed within the control region.

When the vehicle enters the control region, it should

adjust its speed to u

by following the vehicle

dynamics model developed in (K. Yu, Yang, &

Yamaguchi, 2015). After the traffic signal indication

turns from red to green, the vehicle accelerates from

the speed u

to the maximum allowed speed (speed

limit u

) by following the vehicle dynamics model

until it leaves the control region.

𝑢



=𝑚𝑖𝑛

𝑑



𝑡



,𝑢





(4)

Figure 1: Vehicle optimum speed profile.

In case 2, the vehicle’s energy-optimized speed

profile is illustrated in Figure 1. After entering the

control region, the vehicle with the initial speed of

u(t

) needs to brake at the deceleration level denoted

by a, then cruise at a constant speed of u

to approach

the signalized intersection. After passing the stop bar,

the vehicle should increase speed to u

per the vehicle

dynamics model and then cruise at u

until the vehicle

leaves the control region. In this case, the only

unknown variables are the upstream deceleration rate

a and the downstream throttle f

. The following

optimization problem is formulated to compute the

optimum vehicle speed profile associated with the

least energy consumption.

Assuming a vehicle enters the Eco-CACC-I

control region at time t

and leaves the control region

at time t

+T, the objective function entails

minimizing the total energy consumption as

𝑚𝑖𝑛 𝐸𝐶𝑢

(

𝑡

)













·𝑑𝑡

(5)

where EC denotes the energy consumption at instant

t. The energy models for internal combustion engine

vehicles (ICEVs) are presented in Equations (8) ~ (9).

The constraints to solve the optimization problem can

be built according to the relationships between

vehicle speed, location, and acceleration/deceleration

as presented below:

𝑢

(

𝑡

)

⎩

⎪

⎨

⎪

⎧

𝑢

(

𝑡

)

=𝑢

(

𝑡



)

−𝑎𝑡

𝑢

(

𝑡

)

=𝑢



𝑡



≤𝑡≤𝑡



𝑡



<𝑡≤𝑡



𝑢

(

𝑡+∆𝑡

)

=𝑢

(

𝑡

)

















(



)





∆𝑡

𝑢

(

𝑡

)

=𝑢



𝑡



<𝑡≤𝑡



𝑡



<𝑡≤𝑡



+𝑇

(6)

𝑢

(

𝑡



)

·𝑡−

𝑎𝑡



+𝑢



(

𝑡



−𝑡



)

=𝑑



𝑢



=𝑢

(

𝑡



)

−𝑎

(

𝑡



−𝑡



)

𝑢

(

𝑡

)









𝑑𝑡 +𝑢



(

𝑡



+𝑇−𝑡



)

=𝑑



𝑢

(

𝑡



)

=𝑢



𝑎



<𝑎≤𝑎



𝑓



≤

𝑓



≤

𝑓



𝑢



(7)

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

where u(t) is the velocity at instant t; m is the vehicle

mass; 𝑎

(

𝑡

)

=𝑑𝑣(𝑡)𝑑𝑡

⁄

is the acceleration of the

vehicle in [m/s

] (𝑎

(

𝑡

)

takes negative values when the

vehicle decelerates); function F denotes vehicle

tractive force, and function R represents all the

resistance forces (aerodynamic, rolling, and grade

resistance forces). Note that the maximum

deceleration is limited by the comfortable threshold

felt by average drivers (Kamalanathsharma, 2014).

The throttle value f

ranges between f

min

and f

max

. An

A-star dynamic programming approach is used to

solve the problem by constructing a graph of the

solution space by discretizing the combinations of

deceleration and throttle values and calculating the

corresponding energy consumption levels; the

minimum path through the graph computes the

energy-efficient trajectory and optimum parameters

(Guan & Frey, 2013; Kamalanathsharma, 2014).

𝐹𝐶



(𝑡)



𝑎



+𝑎



𝑃

(

𝑡

)

+𝑎



𝑃(𝑡)



∀ 𝑃(𝑡)≥0

𝑎



∀ 𝑃(𝑡)<0

(8)

𝑃

(

𝑡

)

=(𝑚𝑎

(

𝑡

)

+ 𝑚𝑔 ∙

𝐶



1000

(

𝑐



𝑢

(

𝑡

)

+𝑐



)

+𝜌



𝐴



𝐶



𝑢



(

𝑡

)

⁄

+𝑚𝑔 𝜃)𝑢(𝑡)

(9)

where FC

ICEV

(t) is the fuel consumption rate for

ICEV; α



, α



and α



are the model parameters that

can be calibrated for a particular vehicle using public

available vehicle specification information from the

manufacturer, and the details of calibration steps can

be found in (Rakha, Ahn, Moran, Saerens, & Van den

Bulck, 2011); P(t) is the instantaneous total power

(kW); 𝑔 [m/s

] is the gravitational acceleration; 𝜃 is

the road grade; 𝐶



,𝑐



and 𝑐



are the rolling resistance

parameters that vary as a function of the road surface

type, road condition, and vehicle tire type; 𝜌



[kg/m

] is the air mass density; 𝐴



] is the frontal

area of the vehicle, and 𝐶



is the aerodynamic drag

coefficient of the vehicle.

3 CASE STUDY

In order to test the performance of the proposed

control strategies, we implement the controllers in the

microscopic traffic simulation software and conduct

two tests using an isolated signalized intersection and

an arterial traffic network with multiple signalized

intersections, respectively.

INTEGRATION is used as the simulation tool to

simulate the traffic network in the case study.

INTEGRATION is an integrated simulation and

traffic assignment model that creates individual

vehicle trip departures based on an aggregated time-

varying O-D matrix. In consideration of traffic

control devices and gap acceptance, INTEGRATION

moves vehicles along the network in accordance with

embedded preset traffic assignment models and the

Rakha-Pasumarthy-Adjerid (RPA) car-following

model. A more detailed description of

INTEGRATION is provided in the literature (M. V.

Aerde & Rakha, 2007a, 2007b).

3.1 Isolated Intersection Test Case

This test considers the simplest case of a single-lane

signalized intersection to validate the performance of

using the proposed controller. The traffic stream

parameters on the major road are free flow speed of

40 mph, a speed at capacity of 30 mph, a saturation

flow rate of 1600 veh/h/lane, and a jam density of 160

veh/km/lane. The total simulation time is 60 minutes,

and the traffic signal timing is optimized every 5

minutes. The vehicle speed is optimized within the

control region: 200 meters upstream and 200 meters

downstream of the intersection. Three levels of traffic

demand volumes are considered in the test using the

volume over capacity values of 0.1, 0.5, and 1,

respectively. Five test scenarios described below are

compared in the test.

• Scenario 1 (S1): Base

This is the base scenario without signal

optimization and vehicle speed control. The fixed-

time signals (cycle length and green times) were

obtained by using the final optimized signal timings

in scenario 2 after running for 60 minutes.

• Scenario 2 (S2): Signal Optimization – Webster

The traffic signal is optimized using Webster’s

method as shown in Equation (1).

• Scenario 3 (S3): Signal Optimization – Delay

The traffic signal is optimized using the modified

method to minimize traffic delay as shown in

Equation (2).

• Scenario 4 (S4): Signal Optimization – Fuel

The traffic signal is optimized using the modified

method to minimize fuel consumption as shown in

Equation (3).

• Scenario 5 (S5): Integrated Controller (Signal

Optimization – Fuel + Eco-CACC-I)

The traffic signal is optimized using the modified

method to minimize fuel consumption as shown in

Equation (3), and vehicle speed is optimized using the

Eco-CACC-I controller within the control region.

Integrated Optimization of Vehicle Trajectories and Trafﬁc Signal Timings

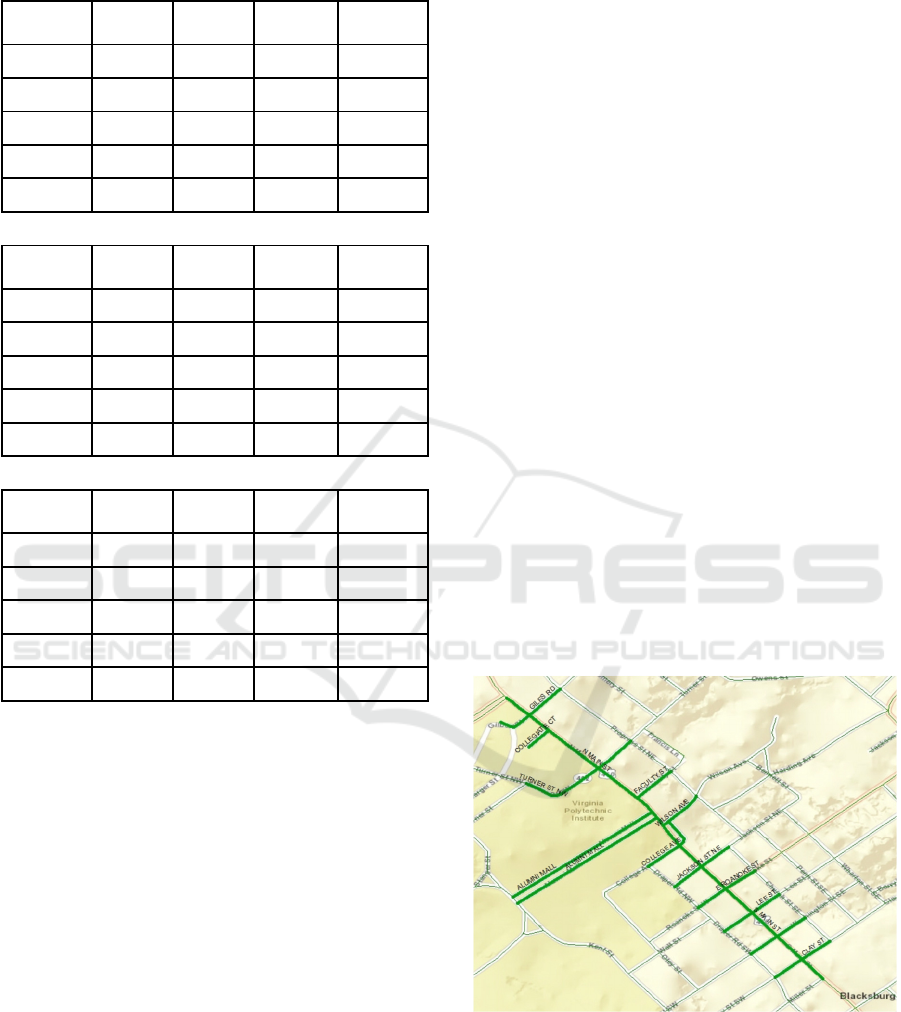
Table 1: Test results on isolated signalized intersection.

Uncon

ested

(

v/c=0.1

)

Scenario

(liter)

saving

Delay

(sec)

Delay

saving

S1 0.1012 11.4

S2 0.0979 -3.3% 10.9 -4.8%

S3 0.0972 -3.9% 10.8 -5.4%

S4 0.0955 -5.6% 11.5 1.1%

S5 0.0932 -7.9% 11.8 3.6%

Medium (v/c=0.5)

Scenario

(

liter

)

savin

Delay

(

sec

)

Delay

savin

S1 0.1054 12.8

S2 0.1021 -3.1% 12.4 -3.4%

S3 0.1019 -3.3% 12.2 -4.7%

S4 0.0998 -5.3% 12.3 -3.9%

S5 0.0979 -7.1% 13.0 1.0%

Con

ested

(

v/c=1

)

Scenario

(

liter

)

savin

Delay

(

sec

)

Delay

savin

S1 0.1089 32.7

S2 0.1056 -3.0% 32.5 -0.7%

S3 0.1052 -3.4% 31.9 -2.3%

S4 0.1032 -5.2% 32.3 -1.3%

S5 0.1018 -6.5% 36.0 10.0%

The test results of the five scenarios for various

traffic demand levels are summarized in Table 1. For

uncongested traffic conditions, both the modified

signal optimization methods in S3 and S4 outperform

Webster’s method (S2) by producing more fuel

savings. But the total delay in S4 is higher than

S1~S3, which matches with findings in previous

studies stating that the optimal signal timing for

minimizing delays is not necessarily identical to the

timing plans that aim at minimizing energy

consumption and emissions. The proposed integrated

controller in S5 produces the most fuel savings of

7.9% compared to the base scenario without any

controller. However, it also produces an increased

total delay of 3.6% compared to S1. Similar trends

can be found in the medium and congested traffic

conditions. For the medium traffic demand, the fuel

consumption continues to decrease from S1 to S5.

The integrated controller produces the most fuel

savings of 7.1%, but the corresponding total delay is

increased by 1.0% compared to S1. For congested

traffic conditions, the integrated controller in S5

reduces fuel consumption by 6.5%, but it also greatly

increases the traffic delay by 10.0% compared to S1.

Overall, the test results demonstrate the proposed

integrated controller can effectively reduce fuel

consumption at isolated signalized intersections.

3.2 Arterial Traffic Network Test Case

The proposed integrated controller is further tested on

an arterial network located in the heart of downtown

Blacksburg, as shown in Figure 2. The O-D demand

matrices were generated using QueesOD software

(M. Aerde & Rakha, 2010) and were based on traffic

counts collected during the afternoon peak period (4

~ 6 pm) at 15 minutes intervals for the year 2012

(Abdelghaffar, Yang, & Rakha, 2017). The

simulations were conducted using the following

parameter values: free-flow speed of 40 km/h based

on the roadway speed limit, speed-at-capacity of 29

km/h, jam density of 160 veh/km/lane, and saturation

flow rate of 1800 veh/h/lane. In the simulation,

vehicles were allowed to enter the links in the first 2

hours, and the simulation ran for an extra 15 minutes

to guarantee that all vehicles exited the network.

Three different traffic demand volumes are

investigated during this test. 100% demand represents

the O-D demand matrices calibrated by the field data

during afternoon peak hours. Then we also consider

25% and 50% demand to investigate the

performances of the different controllers.

Figure 2: The arterial roadways in the city of Blacksburg,

VA.

In this test, the same five different scenarios as

described in the isolated intersection test are also

considered. The test results of five scenarios for three

traffic demand levels are summarized in Table 2. For

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

Table 2: Test results on arterial network.

25% Demond

Sc.

(liter)

FC saving

Delay

(sec)

Delay

saving

Stops

saving

S1 0.0751 33.4 1.49

S2 0.0688 -8.4% 22.7 -32.0% 2.08 39.6%

S3 0.0692 -7.9% 21.3 -36.2% 2.01 34.9%

S4 0.0675 -10.1% 23.2 -30.5% 2 34.2%

S5 0.0646 -14.0% 22.9 -31.4% 1.13 -24.2%

50% Demond

Sc.

(liter)

FC saving

Delay

(sec)

Delay

saving

Stops

saving

S1 0.0757 34.6 1.53

S2 0.0675 -10.8% 20.9 -39.6% 1.97 28.8%

S3 0.0681 -10.0% 20.1 -41.9% 1.94 26.8%

S4 0.0664 -12.3% 21.6 -37.6% 1.92 25.5%

S5 0.0643 -15.0% 20.9 -39.6% 1.15 -24.8%

100% Demond

Sc.

(liter)

FC saving

Delay

(sec)

Delay

saving

Stops

saving

S1 0.0791 39 1.61

S2 0.0671 -15.2% 19.4 -50.3% 1.86 15.5%

S3 0.0679 -14.2% 18.5 -52.6% 1.84 14.3%

S4 0.0668 -15.6% 20.9 -46.4% 1.82 13.0%

S5 0.0651 -17.7% 20.6 -47.2% 1.24 -23.0%

25% traffic demand, the delay-optimized method in

S3 outperforms Webster’s method in S2 and the fuel-

optimized method in S4 by producing the greatest

reduction in delay at 36.2%. The fuel-optimized

method in S4 outperforms Webster’s method in S2

and the delay optimized method in S3 by producing

the most fuel savings at 10.1%. These findings are

consistent with the test results in (Calle-Laguna et al.,

2019; Calle Laguna, 2017) and prove that Webster’s

method represented in Equation (1) is indeed

improved by the modified methods in Equations (2)

and (3). However, the scenarios of S2, S3 and S4

result in more than a 34% increase in vehicle stops on

the arterial network. Among all five scenarios, the

integrated controller in S5 produces the greatest

reduction in vehicle stops compared to S1, at 24.2%.

S5 also produces the most fuel savings (14.0%) of all

five scenarios. The test results under 25% demand

indicate that the integrated controller can greatly

enhance traffic mobility with a 31.4% reduction in

total delay and a 24.2% reduction in vehicle stops, at

the same time improving the energy efficiency with a

14.0% reduction in fuel consumption. Similar trends

can be observed for the 50% and 100% demand

levels. In both cases, the integrated controller

produces the most savings in fuel consumption and

vehicle stops while significantly reducing traffic

delay. Overall, the test results on the arterial network

indicate that the proposed controller can greatly

improve energy efficiency with 17.7% fuel savings

and enhance traffic mobility with up to a 47.2%

reduction in total delay and 24.8% reduction in

vehicle stops.

4 CONCLUSIONS

This paper develops a bi-level controller that provides

energy-optimal traffic signal and vehicle trajectory

control. At the upper level, the controller computes

the traffic signal timings to minimize the total energy

consumption levels of approaching vehicles. The

traffic signal optimization can be easily implemented

in real-time signal controllers and overcomes the

problems with the traditional Webster’s method of

overestimating the cycle length when the traffic

volume-to-capacity ratio exceeds 50 percent. At the

lower level, the controller optimizes the vehicle brake

and throttle levels to minimize the energy

consumption of individual vehicles. The proposed

integrated controller is first tested in an isolated

signalized intersection, and then on an arterial

network with multiple signalized intersections to test

the controller under various traffic demand levels.

The test results demonstrate that the proposed

integrated controller can greatly improve energy

efficiency with up to 17.7% fuel savings, at the same

time enhancing the traffic mobility by reducing total

delay by 47.2% and vehicle stops by 24.8%. More

tests on city-level traffic networks will be considered

in future work. We will also consider expanding the

integrated control strategies to different vehicle types

such as battery electric and hybrid electric vehicles.

ACKNOWLEDGEMENTS

This work was funded by the Urban Mobility &

Equity Center at Morgan State University under the

University Transportation Center(s) Program of the

U.S. Department of Transportation.

Integrated Optimization of Vehicle Trajectories and Trafﬁc Signal Timings

REFERENCES

Abdelghaffar, H. M., Yang, H., & Rakha, H. A. (2017).

Developing a de-centralized cycle-free nash bargaining

arterial traffic signal controller. Paper presented at the

2017 5th IEEE International Conference on Models and

Technologies for Intelligent Transportation Systems

(MT-ITS).

Administration, U. S. E. I. (2018). Oil: crude and petroleum

products explained. Retrieved from https://www.eia.

gov/energyexplained/oil-and-petroleum-products/use-

of-oil.php

Aerde, M., & Rakha, H. A. (2010). QUEENSOD Rel.

2.10—User’s Guide: Estimating Origin—Destination

Traffic Demands from Link Flow Counts. Tech. Rep.

Release 2.30 for Windows: User's Guide – Volume I:

Fundamental Model Features. M. Van Aerde & Assoc.,

Ltd., Blacksburg.

Release 2.30 for Windows: User's Guide – Volume II:

Advanced Model Features. M. Van Aerde & Assoc.,

Ltd., Blacksburg.

Akcelik, R. (1981). Traffic signals: capacity and timing

analysis: Australian Road Research Board.

Almannaa, M. H., Chen, H., Rakha, H. A., Loulizi, A., &

El-Shawarby, I. (2019). Field implementation and

testing of an automated eco-cooperative adaptive cruise

control system in the vicinity of signalized

intersections. Transportation Research Part D:

Transport and Environment, 67, 244-262.

Barth, M., & Boriboonsomsin, K. (2008). Real-world

carbon dioxide impacts of traffic congestion.

Transportation Research Record: Journal of the

Transportation Research Board(2058), 163-171.

Calle-Laguna, A. J., Du, J., & Rakha, H. A. (2019).

Computing optimum traffic signal cycle length

considering vehicle delay and fuel consumption.

Transportation Research Interdisciplinary

Perspectives, 3, 100021.

Calle Laguna, A. J. (2017). Isolated Traffic Signal

Optimization Considering Delay, Energy, and

Environmental Impacts. (Unpublished thesis), Virginia

Tech.

Chen, H., & Rakha, H. A. (2020). Battery Electric Vehicle

Eco-Cooperative Adaptive Cruise Control in the

Vicinity of Signalized Intersections. Energies, 13(10),

2433.

Chen, H., Rakha, H. A., Loulizi, A., El-Shawarby, I., &

Almannaa, M. H. (2016). Development and

Preliminary Field Testing of an In-Vehicle Eco-Speed

Control System in the Vicinity of Signalized

Intersections. IFAC-PapersOnLine, 49(3), 249-254.

Gartner, N. H., Assman, S. F., Lasaga, F., & Hou, D. L.

(1991). A multi-band approach to arterial traffic signal

optimization. Transportation Research Part B:

Methodological, 25(1), 55-74.

Guan, T., & Frey, C. W. (2013). Predictive fuel efficiency

optimization using traffic light timings and fuel

consumption model. Paper presented at the Intelligent

Transportation Systems-(ITSC), 2013 16th

International IEEE Conference on.

Guo, Y., Ma, J., Xiong, C., Li, X., Zhou, F., & Hao, W.

(2019). Joint optimization of vehicle trajectories and

intersection controllers with connected automated

vehicles: Combined dynamic programming and

shooting heuristic approach. Transportation Research

Part C: Emerging Technologies, 98

, 54-72.

Kamalanathsharma, R. K. (2014). Eco-Driving in the

Vicinity of Roadway Intersections - Algorithmic

Development, Modeling, and Testing. (Doctor of

Philosophy), Virginia Polytechnic Institute and State

University.

Li, J.-Q., Wu, G., & Zou, N. (2011). Investigation of the

impacts of signal timing on vehicle emissions at an

isolated intersection. Transportation Research Part D:

Transport and Environment, 16(5), 409-414.

doi:http://dx.doi.org/10.1016/j.trd.2011.03.004

Liao, T.-Y. (2013). A fuel-based signal optimization model.

Transportation Research Part D: Transport and

Environment, 23(1), 1-8.

Ma, X., Jin, J., & Lei, W. (2014). Multi-criteria analysis of

optimal signal plans using microscopic traffic models.

Transportation Research Part D: Transport and

Environment, 32(0), 1-14.

doi:http://dx.doi.org/10.1016/j.trd.2014.06.013

Park, B., Messer, C. J., & Urbanik, T. (1999). Traffic signal

optimization program for oversaturated conditions:

genetic algorithm approach. Transportation Research

Record, 1683(1), 133-142.

Rakha, H. A., Ahn, K., Moran, K., Saerens, B., & Van den

Bulck, E. (2011). Virginia tech comprehensive power-

based fuel consumption model: model development and

testing. Transportation Research Part D: Transport

and Environment, 16(7), 492-503.

Urbanik, T., Tanaka, A., Lozner, B., Lindstrom, E., Lee, K.,

Quayle, S., . . . Gettman, D. (2015). Signal timing

manual (Vol. 1): Washington, DC: Transportation

Research Board.

Webster, F. V. (1958). Traffic Signal Settings. Road

Research Technical Paper No. 39.

Xu, B., Ban, X. J., Bian, Y., Li, W., Wang, J., Li, S. E., &

Li, K. (2018). Cooperative method of traffic signal

optimization and speed control of connected vehicles at

isolated intersections. IEEE Transactions on Intelligent

Transportation Systems, 20(4), 1390-1403.

Yu, C., Feng, Y., Liu, H. X., Ma, W., & Yang, X. (2018).

Integrated optimization of traffic signals and vehicle

trajectories at isolated urban intersections.

Transportation Research Part B: Methodological, 112,

89-112.

Yu, K., Yang, J., & Yamaguchi, D. (2015). Model

predictive control for hybrid vehicle ecological driving

using traffic signal and road slope information. Control

theory and technology, 13(1), 17-28.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems