Shrinking the Inductive Programming Search Space with

Instruction Subsets

Edward McDaid

and Sarah McDaid

Zoea Ltd., 20-22 Wenlock Road, London, N1 7GU, U.K.

Keywords: Inductive Programming, State Space Search, Knowledge Representation.

Abstract: Inductive programming frequently relies on some form of search in order to identify candidate solutions.

However, the size of the search space limits the use of inductive programming to the production of

relatively small programs. If we could somehow correctly predict the subset of instructions required for a

given problem then inductive programming would be more tractable. We will show that this can be

achieved in a high percentage of cases. This paper presents a novel model of programming language

instruction co-occurrence that was built to support search space partitioning in the Zoea distributed

inductive programming system. This consists of a collection of intersecting instruction subsets derived from

a large sample of open source code. Using the approach different parts of the search space can be explored

in parallel. The number of subsets required does not grow linearly with the quantity of code used to produce

them and a manageable number of subsets is sufficient to cover a high percentage of unseen code. This

approach also significantly reduces the overall size of the search space - often by many orders of magnitude.

https://orcid.org/0000-0001-8684-0868

https://orcid.org/0000-0001-7643-6722

1 INTRODUCTION

The use of AI to assist in the production of computer

software is an active area of research (e.g. Xu et. al.,

2022; Nguyen & Nadi, 2022). Many current systems

are based on deep learning and recent work includes

the use of large language models such as GPT-3

(Brown et. al., 2020). These involve training on

large quantities of code although this can also raise

ethical concerns (Lemley & Casey, 2021).

Work also continues on approaches not

traditionally associated with training (Cropper et al.,

2020; Petke et. al., 2018). Inductive programing (IP)

aims to generate code directly from a specification

such as test cases (Flener & Schmid, 2008). Various

IP techniques exist but fundamentally many of these

utilise search (Kitzelmann, 2010).

Aside from trivial cases it is not possible to

determine the outcome of a computation directly

from source code without executing it. Some kind of

generate-and-test approach is therefore unavoidable.

The size of the search space has limited

IP systems to the production of relatively small

programs (Galwani et. al., 2015). A major source of

combinatorial growth in IP is the number of

instructions, comprising core language and standard

library functions, and operators. This number varies

by programming language but is frequently around

200 or more. It has been suggested that if we could

predict the subset of instructions required for a given

program then IP would be more tractable (McDaid

& McDaid, 2019).

One way to produce slightly larger programs in a

given time period is to distribute the work across

many computers. This requires the search space to

be partitioned. Partitioning on the instruction set is

attractive as most programs use a relatively small

subset of instructions. But how do we define the

subsets?

This paper presents the results of a study that

was carried out to define instruction subsets for the

Zoea IP system (McDaid & McDaid, 2021). Zoea

employs a distributed blackboard architecture

comprising many knowledge sources that operate in

parallel. Activations can already be partitioned by

instruction subsets although currently these are

coarse grained and manually specified.

578

McDaid, E. and McDaid, S.

Shrinking the Inductive Programming Search Space with Instruction Subsets.

DOI: 10.5220/0011706900003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 578-585

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

At present, Zoea can efficiently utilise up to

around 100 cores in solving a problem. Using larger

numbers of cores requires finer-grained partitioning

of the instruction set. This will also enable Zoea to

better leverage cloud-based deployment.

The strategy of deriving subsets from existing

code was seen as a potential way to make subsets

more representative of human originated software. It

was also apparent that any such subsets would need

to intersect with one another to some extent.

The number of subsets required to provide

sufficient coverage for a wide variety of programs

was unknown in advance. Based on experience in

tuning the current system hundreds to thousands of

subsets would result in acceptable performance.

The target size of the instruction subsets is an

important consideration. Smaller subsets make it

possible to find programs with fewer instructions in

in less time. However, we also need to be able to

produce programs with larger numbers of

instructions. This suggests the use of multiple sets of

instruction subsets of different sizes. The subset

sizes studied were 10 to 100 in increments of 10.

The following sections describe our approach to

the production and evaluation of instruction subsets.

We then go on to discuss some significant findings

that became apparent after this work was completed.

2 PRELIMINARIES

Let C be a source code program in a high level

imperative programming language L. C is composed

of one or more program units U - corresponding to

procedures, functions or methods. L provides a set of

instructions IL comprising built in operators, core

and standard library functions. Each U contains a set

of instructions IU where IU ⊆ IL ∧ IU ≠ Ø.

Given a collection of programs SP1 we can

enumerate the corresponding family of program unit

instruction subsets SIU where SIU ∈ P(IL) ∧ SIU

≠ Ø. (Here P refers to the power set.)

IU is said to cover U if IU is the instruction

subset for U or IU is the instruction subset for a

different U and a superset of the IU for U. Each IU

trivially covers the corresponding U. We can also

say that SIU covers SP1. Coverage for a set of

programs is quantified as the number of covered

program units divided by the total number of

program units expressed as a percentage.

Any IU that is a subset of another IU can be

removed from SIU without affecting the overall

coverage of SIU wrt SP1. Two or more IUs can be

combined to form a new derived instruction subset

ID. ID provides the same aggregate coverage as its

component IUs wrt SP1.

SID is a family of instruction subsets comprising

all IUs (that have not been removed or merged)

union all IDs. SID provides the same coverage as the

original SIU wrt SP1. We can enforce an upper limit

M1 on |IU| and an upper limit M2 on |ID| during the

creation of SID. Any U where |IU| > M1 is silently

ignored. M2 constrains which subsets of SIU (IUs)

can be combined to form IDs. Any number of IDs

can be created providing their respective component

IUs are also removed and |ID| <= M2. Once created

SID can then be evaluated in terms of the coverage it

provides wrt a different set of programs SP2.

3 APPROACH

3.1 Objectives

The primary goal of this work was to define a set of

instruction subsets to support efficient clustering in

the Zoea IP system.

Evaluation of subsets was also necessary to

ensure that they were capable of generating a wide

range of programs. The approach selected involved

cross-validating subsets generated using part of the

code sample with the entire code sample.

3.2 Method

This work began as a piece of analysis and without a

specific research question. The methodology

followed can best be characterised as descriptive

with some similarities to exploratory data analysis.

A large quantity of code was required for

instruction subset creation to ensure sufficient

variety. Ideally it should be the product of many

different developers from a variety of contexts. The

code also needs to be legally and ethically available.

GitHub (Microsoft, 2022) was identified as a

suitable source of software and it has been used in

the past for similar analyses of code (Ray et. al.,

2014). We used the largest 1,000 repositories on

GitHub (as of 13 May 2022) and limited our analysis

to Python (Martelli et al., 2017) programs only.

Python was selected on the basis that it is a fairly

popular language and the available instructions are

representative of similar languages.

In each case the complete repository was

downloaded as a zip file, extracted and non-Python

files were discarded. Each Python program was split

into program units (classes, methods, functions and

Shrinking the Inductive Programming Search Space with Instruction Subsets

579

mains) and tokenised using simple custom code

based on regular expressions. Two of the

repositories were excluded due to parsing errors.

From the identified tokens the occurrences of each

of a specific set of instructions were counted.

Instructions that have no meaning in Zoea, such as

those relating to variable assignment, were either

mapped to an equivalent instruction if possible or

else excluded. (E.g. '+=' is mapped to '+' while '=' is

excluded.) No code or other information was used in

any other way. This step output a list of instruction

names in alphabetical order for each program unit.

The analysis included 71,972 Python files

containing 15,749,416 lines of code or 580,476,516

characters. From this 886,421 program units were

identified. For each program unit the subset of

instructions it contains was recorded. Many of the

instruction subsets so identified were duplicates and

when these were removed 345,120 unique

instruction subsets remained.

During processing the instruction subsets were

filtered to remove any that are proper subsets of

another instruction subset. This left 33,823

instruction subsets. These varied in size between 1

and 74 instructions (median: 3, standard deviation:

3.67). Many of the unique instruction subsets were

very similar to one another, differing by only one or

two instructions.

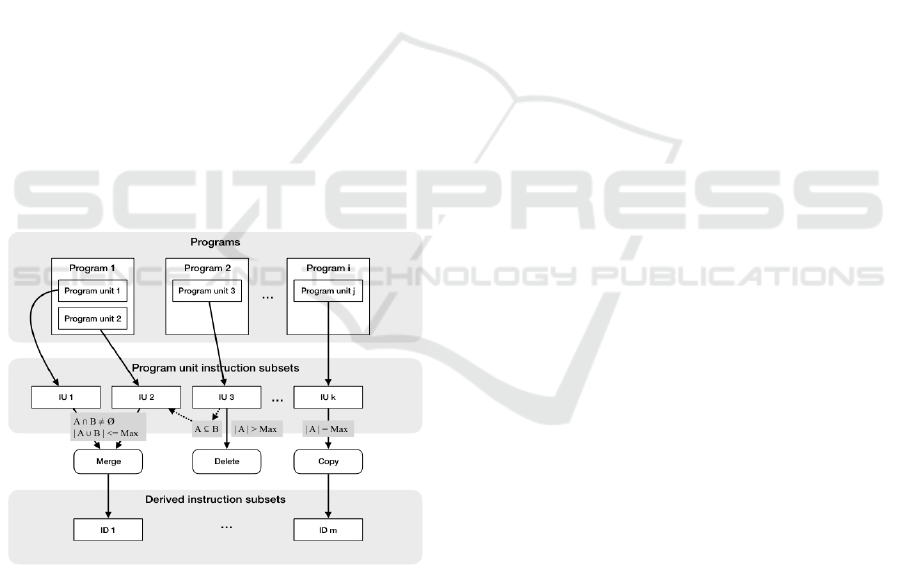
Figure 1: Overview of subset creation process.

3.3 Clustering Algorithm

Figure 1 gives a conceptual overview of the subset

creation process. Producing derived instruction

subsets (IDs) from program unit instruction subsets

(IUs) is a clustering problem. A number of different

clustering algorithms were developed and evaluated.

The end result incorporates the two most successful

of these together with some pre- and post-

processing. Pseudo-code for the software is shown

in Algorithm 1.

Every derived instruction subset is created with

respect to a specified maximum subset size. This

size limit also impacts the number of derived subsets

as described in more detail later in this section.

delete any duplicate IUs

amplify IUs (see section 3.4)

delete IUs that are subsets of IU’

foreach IU do

find Instr, Subsets where

Instr is not a subset of IU and

length(IU ∪ Instr) is maximum

Let IU = IU ∪ { Instr }

delete all IUs in Subsets

end foreach

create NumIDs empty IDs

foreach IU do

if exists( empty ID ) then

Let ID = IU

else

find IDs with max( | ID ∩ IU | )

choose ID with min( | ID | )

Let ID = ID ∪ IU

end if

end foreach

merge IDs where size <= MaxIdSize

return set of IDs

Algorithm 1: Clustering algorithm.

Input subsets are processed in decreasing order

of size. In order to improve performance all

instruction subsets are internally sorted at all times.

Pre-processing involves de-duplication,

amplification and subset removal. Amplification is

described in the next section. Many input subsets are

duplicates of which set one is retained. Any input

subset that is wholly contained within another input

subset is also removed.

The first clustering stage attempts to subsume the

largest number of near subsets by adding a single

additional instruction to each IU in turn. In choosing

which instruction to add the algorithm determines

how many other IUs will become subsets of the

current IU if that instruction is added. The

instruction that results in the removal of the greatest

number of other IUs is selected.

The second clustering stage tries to merge each

IU with the ID with which it has the greatest

intersection. This involves pre-creating a specified

number of empty IDs and then either populating the

empty IDs or else merging the IU into the ID with

both the largest intersection and the most remaining

capacity. If all IDs are at their maximum capacity

then additional empty IDs are created.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

580

Post-processing involves merging any remaining

small IUs and non-full IDs together. This is driven

entirely by subset size and ignores similarity.

As noted already, the algorithm allows for the

specification of both a maximum subset size and a

target number of subsets. However, the number of

subsets requested is not honoured if this proves

impossible, in which case a minimal number of

additional subsets are created. For each subset size

the approximate number of subsets required is

determined in advance by code that iterates over

possible values in ascending order. The number of

subsets required is detected when the number of

subsets created equals the number of subsets

requested. Given this requires considerable time the

process has only been done in increments so the

figures obtained are approximate, within the size of

the increment.

The derived subset size that is enforced is

allowed to be somewhat larger than the maximum

by a small configurable amount – typically 10%.

Without this headroom program unit subsets of the

same size could not be merged.

3.4 Amplification

Initially, the process of merging subsets was seen as

a way to reduce the number of derived subsets and

standardize their sizes. However, it was observed

that coverage against unseen code improved

significantly after merging. This is partly because

larger subsets provide better coverage than do small

ones. Also, merging introduces additional intra-

subset instruction co-occurrence variety that would

not otherwise be present. It is interesting to note that

adding an equivalent number of random instructions

rather than merging does not give any detectable

benefit.

In order to take advantage of this phenomenon an

amplification step was introduced whereby smaller

input subsets are merged with one another before

clustering to create additional artificial program

subsets. This was not explored systematically but the

benefits do not seem to continue to accrue beyond a

50% increase in the number of subsets. Further work

in this area may be fruitful.

4 RESULTS

4.1 Input Data

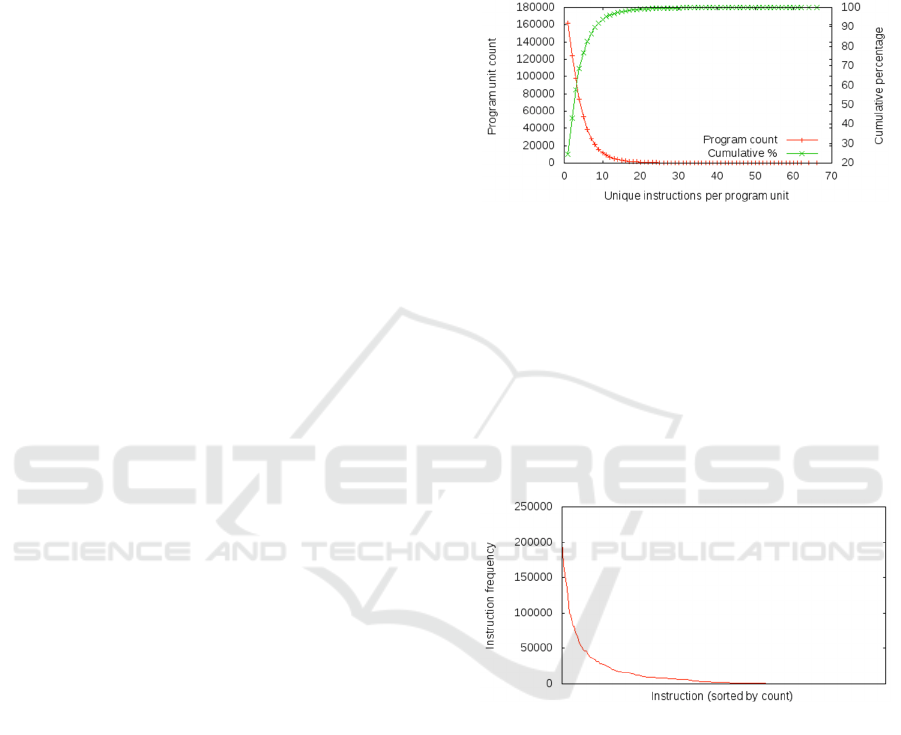
Figure 2 shows the size frequency distribution of the

program unit instruction subsets. This provides both

the numbers of subsets of different sizes and the

cumulative percentage of program units for each

subset size. From this it can be seen that around 90%

of program units have instruction subsets containing

10 or fewer unique instructions. Only 2% of

program units contain 20 or more instructions.

Figure 2: Program unit instruction subset size frequency

distribution.

Figure 3 gives the frequency distribution for

instructions across all of the code used. Here

instructions are ranked in order of descending

frequency. This shows that a small number of

instructions are used very frequently and that many

instructions are seldom used. This is similar to a

Zipfian distribution that is often associated with

human and artificial languages (Louridas et al.,

2008).

Figure 3: Ranked instruction frequency distribution.

The ranked frequency distribution for co-

occurring instruction pairs is similar to that for

instructions although it is more pronounced. Very

few instruction pairs co-occur frequently while most

occur infrequently or not at all.

4.2 Coverage of Unseen Code

By definition the derived subsets will always give

100% coverage of the code that was used to create

them. In other words, all of the instructions in each

program unit instruction subset will be found

together in at least one single derived instruction

subset. However, this is not the purpose for which

the derived subsets are created.

Shrinking the Inductive Programming Search Space with Instruction Subsets

581

To be useful the derived subsets should also

provide a high level of coverage for code that was

not used for their creation. The level of coverage for

unseen code was determined by nominating a

percentage of the input code as a training set from

which the derived subsets were then produced. The

derived subsets could then either be tested against a

different section of the input codebase or all of it.

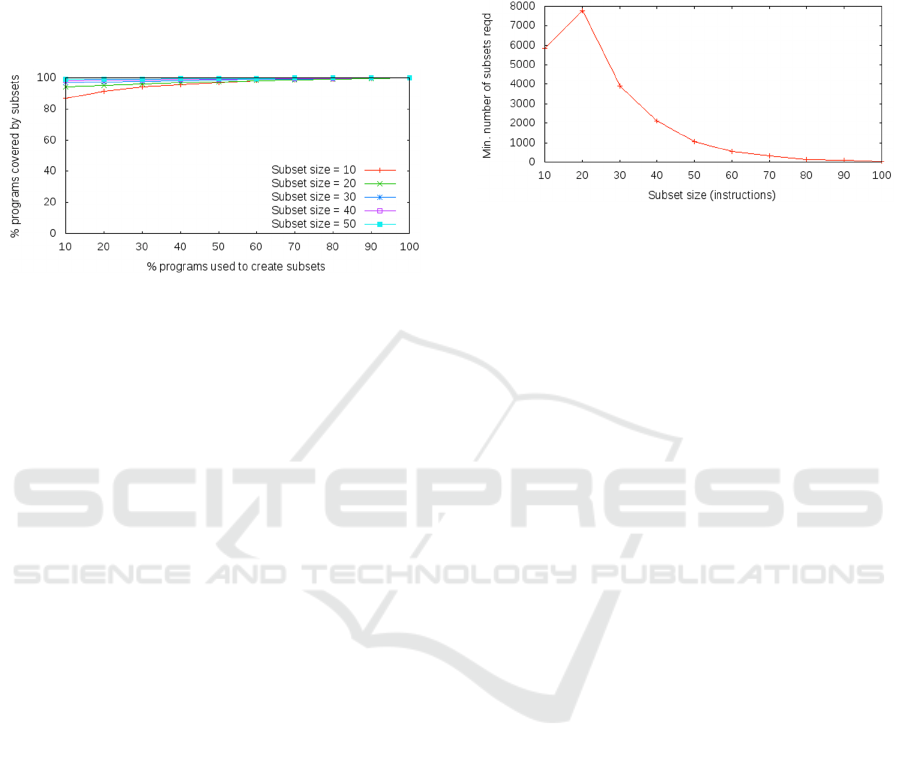
Figure 4: Unseen code coverage for different training set

percentages and subset sizes.

To understand the relative coverage that was

achieved using training sets of different sizes,

subsets were produced using 10% to 100% of the

available code in 10% increments. In each case the

derived subsets were then evaluated against the

entire codebase. These results are shown in Figure 4.

These tests were executed over 50 times and it was

soon clear that subsets produced using a relatively

small percentage of the code sample can provide

high coverage. For subset size 10 just 1% of the

code produces subsets that provide 77.31%

coverage.

Other tests - that are not reported here - were

carried out to ensure the particular section of code

from which the training set was taken had no

adverse impact on the results.

4.3 Number of Subsets

As we have already noted the number of derived

subsets required depends to a large extent on the

maximum derived subset size. Figure 5 shows the

numbers of derived subsets for various maximum

sizes. Generally, the number of subsets reduces

exponentially with increasing maximum subset size.

That the number for maximum size 10 is less than

20 is probably due to the fixed size of the derived

subset headroom in combination with the skewed

subset size distribution.

The numbers of derived subsets are acceptable in

order to support Zoea clustering. It is possible to

reduce the number of subsets further by various

means although this will also reduce the coverage

for unseen code. For example, some of the subsets

are redundant when considered solely in terms of

coverage of the training set. In addition, many

individual instructions can be removed from subsets

on the same basis.

Figure 5: Number of subsets required by subset size.

Another important factor is how the number of

required subsets grows as the size of the training set

is increased. This growth is not linear but instead

decreases with each increment. The decreasing rate

of growth suggests that subset size eventually

stabilizes rather than growing indefinitely.

4.4 Search Space Reduction

The original motivation for using instruction subsets

is to distribute work across many worker nodes in a

cluster. An unanticipated benefit is that the size of

the search space is also significantly reduced. It is

easy to see why this is the case.

The search space for code approximates to a tree

of a given depth with a branching factor largely

determined by the number of instructions. Various

approaches have been published for estimating the

size of such a search tree (Kilby et. al., 2006).

However, the reality is more complicated. Different

instructions have different numbers of arguments

and the data flows may span any number of levels

forming a graph rather than a tree.

A more accurate estimate of cumulative search

space size instead considers the number of values

generated as successive layers of instructions are

added. Inputs exist at level zero. If all instructions

are applied at each level then single argument

instructions must take their input from the previous

level whereas two argument instructions only

require one value from the previous level and

another from any level. In this approach the number

of search space nodes at a given level is the current

total number of values excluding inputs.

Figure 6 shows the impact of different subset

sizes on the size of the search space. This shows

very large reductions in search space size –

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

582

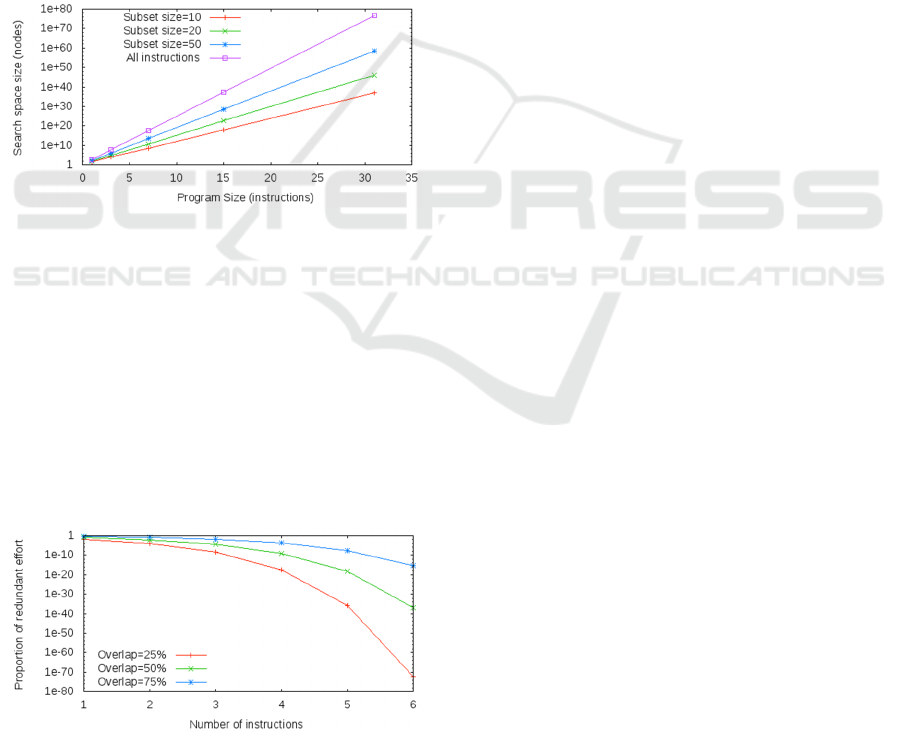
particularly for subsets of size 10. This is largely due

to the reduction in branching factor from around 200

to 10. The results in Figure 6 take account of the

number of subsets, although this makes little

difference to the relative scale of the results.

It is clear that distributing the work across a

number of nodes in this manner does not just enable

the work to be completed more quickly. It also

reduces the amount of work that needs to be done.

People seem to get by using a relatively small

proportion of all possible instruction subsets. This

means there are a great many subsets that are not

used very often - if at all. Every instruction subset,

that does not include all instructions, accounts for a

different and somewhat overlapping part of the

complete search space. Effectively it is the

instruction subsets that are not used that account for

the reduction in the size of the search space.

Figure 6: Search space reduction for different instruction

subset sizes.

4.5 Subset Overlap

Instruction subsets often overlap. This is intentional

and reflects the fact that instructions used in

different program units frequently intersect. It is also

partly due to the clustering process. The median

overlap for subset size 10 is around 20% and for size

50 is around 40%. As a result there might be a

concern that an excessive amount of effort may be

wasted when using the subsets to partition work.

Figure 7: Proportion of redundant activity for different

subset overlap percentages.

Estimation of duplicate effort uses the same

approach outlined earlier for search space size.

Duplicated work at a given level corresponds to the

size of the search space subtree for overlapping

instructions only, divided by the size of the tree for

the subset size number of instructions. Results are

shown in Figure 7.

As the search tree grows, any values that have

been produced using any non-duplicated instruction

are distinct. Thus the proportion of values at each

level that are produced exclusively from duplicated

instructions quickly becomes insignificant.

4.6 Meaning of Results

The concept of coverage is a proxy for IP success or

failure in finding a particular solution. High levels of

coverage mean that for a given set of instruction

subsets there is a correspondingly high probability

that at least one worker in the cluster will encounter

a particular IP solution.

Using only a subset of instructions rather than all

of them significantly reduces the time Zoea takes to

produce a solution. This, together with the overall

reduction in search space size and the ability to run

hundreds or possibly thousands of workers in

parallel will certainly yield a dramatic improvement

in response times. The size of programs that can be

generated in a given time are also certain to increase.

4.7 Comparative Evaluation

It would be interesting to compare our results with

other approaches such as various forms of heuristic

search and generic algorithms (Mart et al., 2018).

Distance metrics and fitness functions can be used to

guide best first search for some specific types of

program. However, no known set of distance metrics

or fitness functions covers all possible programs. In

many kinds of software the distance between a target

value and successive intermediate values has no

discernable pattern. Bi-directional search is also

impractical as the number of possible input values

for a given output can often be infinite. As a result

only comparisons with various kinds of uninformed

search can be made.

Consider a search space of size S with a

maximum depth (and upper bound on program size)

M. The simplest version of a specific program X is

known to exist within that space at depth D. Sd is the

cumulative size of the search space up to and

including D. There also exist a number N of larger

but functionally equivalent variants Vn of X between

depths D+1 and M. The task is to find X or

Shrinking the Inductive Programming Search Space with Instruction Subsets

583

alternatively any Vn using different kinds of search

and estimate the size of the space. See Table 1.

Depth first and breadth first search are well

known. Iterative deepening depth first search

(IDDFS) approximates the behaviour of breadth first

but although it requires less memory this is at the

cost of repeating some work.

S is considerably larger than Sd so in this case

depth first performs poorly. It can be seen that the

use of instruction subsets results in a huge reduction

in search space size. The corresponding running

time can also be expected to be considerably less.

Table 1: Comparison of search techniques.

Depth

first

IDDFS Breadth

first

Instr.

subsets

Always

finds

solution

Yes Yes Yes Yes

Best

solution

first

No Yes Yes No

Approx.

size

S /

(N+1)

>Sd Sd Between

Sd/10^5

and

Sd/10^40

5 DISCUSSION AND FUTURE

WORK

Much of this work was conducted as an exercise in

static code analysis rather than as a scientific

investigation. However, that does not detract from

the validity or potential significance of the results.

The frequency distributions of individual

instructions and instruction pairs can be seen as tacit

forms of software development knowledge. These

distributions are highly skewed yet it is not clear

why, or whether it has to be this way. Neither of

these topics have attracted much attention to date.

In conducting this work it became clear that

there is a key trade-off between clustering and

merging/amplification. While it is possible to

produce many fewer subsets through more

aggressive clustering this comes at the price of less

generality. We do not claim to have identified the

optimum position on this continuum and more work

in this area would be useful. However, the current

results are sufficient to support the on-going

operational deployment of this approach in Zoea.

By conceding that candidate solutions will only

come from defined subsets of instructions we are

accepting a compromise. We are willing to take any

solution, potentially produced much faster, but there

may be a small percentage of cases for which this

approach might not succeed. More work will be

required to quantify operational success in terms of

generated solutions that meet the specification.

Other approaches to producing instruction

subsets and alternative clustering algorithms are

possible. Some of these may produce smaller sets of

subsets and/or deliver greater coverage.

The authors believe that the results would also

hold for other imperative programming languages.

Most mainstream languages are very similar at the

instruction level. Intuitively, the approach should

also benefit different software development

paradigms such as logic programming. Built-in

predicates serve much the same role as instructions.

The authors also believe that the code sample

used should be representative of other code. The

sample used was large and came from many

different repositories. Additional verification with

code from other hosting sites would of course be

useful.

Some instructions occur very frequently in the

instruction subsets. One option would be to remove

the most frequent instructions from the subsets and

assume they always apply. This would have a

dramatic effect on the size and number of the

subsets. Since no clear boundary exists any

threshold could be chosen.

It is worth noting that instruction subsets are

capable of generating many more programs than

those from which they were derived. Also, lack of

coverage does not mean that an equivalent program

cannot be produced. There are many different ways

to produce a functionally equivalent program –

sometimes using different instructions.

Some of the individual subsets provide much

more program coverage than others. This

information could be used to prioritise the

assignment of cluster jobs to increase the probability

that a solution is found early.

This approach should be useful in any problem

that involves searching a program configuration

space. Integration should be a simple matter in any

software that utilises a defined list of instructions. It

is also worth considering whether a similar approach

might be useful in domains beyond IP.

Combinatorial problems are common as is the need

to partition work within clusters.

The current work considers subset construction

as an offline activity. In operational deployment this

could alternatively be a continuous process.

The only information extracted from the input

source code was an alphabetic list of instruction

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

584

names. In most cases these lists of instructions are

not unique to the code they came from. Instead they

are exceptionally common both as literal copies and

also as subsets of one another. As such there can be

no sense in which intellectual property rights or the

terms of any license have been violated.

6 CONCLUSIONS

We have described a technique for partitioning the

IP search space using instruction subsets. This

enables us to distribute IP work across many

computer cores by assigning each a distinct but

overlapping subset of instructions. Testing suggests

the subsets generalise quickly, particularly when

they are merged. Cross-validation shows they should

work well with unseen code. The approach

significantly reduces the size of the search space.

Any duplication of effort due to subset overlap

quickly becomes insignificant as program size

increases. We also believe that our approach is

ethical and does not exploit open source developers.

ACKNOWLEDGEMENTS

This work was supported by Zoea Ltd. Zoea is a

trademark of Zoea Ltd. Other trademarks are the

property of their respective owners.

REFERENCES

Brown, T. B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan,

J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry,

G.; Askell, A.; Agarwal, S.; Herbert-Voss, A.;

Krueger, G.; Henighan, T.; Child, R.; Ramesh, A.;

Ziegler, D. M.; Wu, J.; Winter, C.; Hesse, C.; Chen,

M.; Sigler, E.; Litwin, M.; Gray, S.; Chess, B.; Clark,

J.; Berner, C.; McCandlish, S.; Radford, A.; Sutskever,

I.; Amodei, D. (2020). Language Models are Few-Shot

Learners. arXiv pre-print. arXiv:2005.14165 [cs.CL].

Ithaca, NY: Cornell University Library.

Cropper‚ A.; Dumancic, S.; Muggleton, S. H. (2020).

Turning 30: New Ideas in Inductive Logic

Programming. In Proceedings of the Twenty−Ninth

International Joint Conference on Artificial In-

telligence‚ IJCAI 2020. ijcai.org. pp. 4833–4839.

doi.org/10.24963/ijcai.2020/673.

Flener, P., Schmid, U. (2008). An introduction to

inductive programming. Artificial Intelligence Review

29(1), 45-62. doi.org/10.1007/s10462-009-9108-7.

Galwani, S.; Hernandez-Orallo, J.; Kitzelmann, E.;

Muggleton, S. H.; Schmid, U.; Zorn, B. (2015).

Inductive Programming Meets the Real World.

Communications of the ACM 58(11), 90–99. doi.org/

10.1145/2736282.

Kilby, P.; Slaney, J. K.; Thiébaux, S.; Walsh, T. (2006).

Estimating Search Tree Size. In Proceedings of the

Twenty-First National Conference on Artificial

Intelligence AAAI 2006. AAAI Press. 1014-1019.

Kitzelmann, E. (2010). Inductive programming: A survey

of program synthesis techniques. Approaches and

Applications of Inductive Programming. Lecture

Notes in Computer Science 5812, 50–73. Springer-

Verlag.

Lemley, M. A., Casey B. (2021). Fair Learning. Texas

Law Review 99(4): 743-785.

Louridas, P.; Spinellis, D.; Vlachos. V. (2008). Power

laws in software. ACM Transactions on Software

Engineering and Methodology 18(1): 1-26.

doi.org/10.1145/1391984.1391986.

Mart, R., Pardalos, P. M., Resende, M. G. C. (2018)

Handbook of Heuristics. Springer Publishing

Company. 1

edition.

Martelli, A.; Ravenscroft, A.; Holden, S. (2017). Python in

a Nutshell. O'Reilly Media, Inc. 3

edition.

Microsoft. (2022). GitHub. https://www.github.com.

Accessed: 2022-11-06.

McDaid, E., McDaid, S. (2019). Zoea – Composable

Inductive Programming Without Limits. arXiv

preprint. arXiv:1911.08286 [cs.PL]. Ithaca, NY:

Cornell University Library.

McDaid, E., McDaid, S. (2021). Knowledge-Based

Composable Inductive Programming. In Proceedings

Artificial Intelligence XXXVIII: 41st SGAI

International Conference on Artificial Intelligence, AI

2021, Cambridge, UK, December 14–16, 2021,

Springer-Verlag. doi.org/10.1007/978-3-030-91100-

3_13.

Nguyen, N., Nadi, S. (2022). An Empirical Evaluation of

GitHub Copilot's Code Suggestions. In Proceedings of

the IEEE/ACM 19th International Conference on

Mining Software Repositories (MSR), 2022, 1-5.

doi.org/10.1145/3524842.3528470.

Petke, J.; Haraldsson, S.; Harman, M.; Langdon, W. B.;

White, D.; Woodward, J. (2018). Genetic

Improvement of Software: a Comprehensive Survey.

IEEE Transactions on Evolutionary Computation.

22(3): 415-432. doi.org/10.1109/TEVC.2017.

2693219.

Ray, B.; Posnett, D.; Filkov, V.; Devanbu, P. (2014). A

large scale study of programming languages and code

quality in github. In Proceedings of the 22nd ACM

SIGSOFT International Symposi-um on Foundations

of Software Engineering (FSE 2014). Association for

Computing Machinery. 155–165. doi.org/10.1145/

2635868.2635922.

Xu, F. F.; Alon, U.; Neubig, G.; Hellendoorn, V. J. (2022).

A systematic evaluation of large language models of

code. In Proceed-ings of the 6th ACM SIGPLAN

International Symposium on Machine Programming.

Association for Computing Machinery. 1–10. doi.

org/10.1145/3520312.3534862.

Shrinking the Inductive Programming Search Space with Instruction Subsets

585