Ethical Considerations for the Deployment of Logic-Based Models of

Reasoning

Aaron Hunter

Department of Computing, British Columbia Institute of Technology, Burnaby, Canada

Keywords:

AI Ethics, Logic-Based AI, Belief Change.

Abstract:

Ethical considerations in the development of Artiﬁcial Intelligence systems need to be addressed as more

systems are deployed in practice. Much of the current work in this area is focused on Machine Learning

systems, with an emphasis on issues such as fairness and bias. However, there are also fundamental ethical

problems to be addressed in simple logic-based systems, and we do not have solid methods in place to handle

these issues. In this paper, we discuss ethical problems that are implicitly introduced in the deployment of

systems that formalize reasoning in logic. As a speciﬁc example, we focus on logic-based models of belief

change. We consider the way belief change operators are deﬁned, and how unintended behaviour can emerge

in operators deﬁned with respect to well-known rationality postulates. Preventative measures and potential

solutions are discussed.

1 INTRODUCTION

Considerations around the ethics of Artiﬁcial Intel-

ligence (AI) have become increasingly important, as

more AI systems are deployed in practice. There have

generally been two lines of work in this area. One

type of work is related to general, forward-looking

concerns about the ethical behaviour of machines that

make decisions using human-level intelligence (Malle

et al., 2019). The other type of work that is commonly

seen is explicitly focused on issues around bias and

responsibility for systems based on Machine Learn-

ing (ML) (Mehrabi et al., 2021). However, it is likely

that future AI systems will actually be hybrid sys-

tems, that use a combination of learning technology

together with models of formal reasoning. For this

reason, it is important that we also examine the ethics

and biases embedded in traditional logic-based mod-

els of reasoning.

In this paper, we look in detail at one speciﬁc

logic-based model of reasoning: the theory of belief

change. We view this as kind of a case study, high-

lighting different ethical issues that occur in a logi-

cal formulation. Note that we are not concerned with

broad philosophical concerns about the relationship

between logic and ethics. Our concern here is the

manner in which simple, logically-defensible choices

introduce problems with ethical decision making. The

focus is on providing a pathway to move forward with

the deployment of hybrid systems that use learning

technology and logic in concert.

2 PRELIMINARIES

2.1 Motivating Example

The following example is a variation on a well-known

problem originally presented by Darwiche and Pearl

(Darwiche and Pearl, 1997). The example here is

modiﬁed by changing the context to make the con-

nection with moral decision making more clear.

Consider a situation where we have an intelligent

system that is processing job applications for a po-

sition in engineering. A given applicant is initially

identiﬁed as being part of a disadvantaged group (D)

that should get priority for job interviews; so the sys-

tem believes D to be the case. On further examina-

tion of the application materials, it appears that the

applicant is registered as a professional engineer (E),

so this is also believed. However, a second system

is consulted to verify the credentials, and it indicates

that the school the applicant attended is not properly

accredited. This leads the system to reject E.

The question at this stage is what happens to the

previous beliefs, such as the belief that the applicant

belongs to a disadvantaged group. This might be im-

portant to maintain, because there might actually be

Hunter, A.

Ethical Considerations for the Deployment of Logic-Based Models of Reasoning.

DOI: 10.5220/0011704500003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 565-569

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

565

other suitable opportunities for this applicant. We will

see that some formal models of belief change will ac-

tually reject the ﬁrst information, as if it had never

been obtained. On the other hand, some models will

actually keep the older information. In the present ex-

ample, this is appropriate. However, we argue that

this can also be a problem in different contexts.

The fundamental problem is that the well-known

postulates that describe rational belief change can be

satisﬁed by signiﬁcantly different processes, in a way

that may introduce unintended bias into a system that

is intended to provide a normative model. While the

problems introduced through biased data sets in ML

approaches are now being increasingly recognized,

this kind of bias in an axiomatic reasoning system

needs to be put under the same scrutiny.

2.2 Belief Revision

Broadly, the study of belief revision is concerned with

the manner in which agents incorporate new informa-

tion with their pre-existing beliefs. The most inﬂuen-

tial approach to belief revision is the AGM approach,

in which a set of rationality postulates is speciﬁed to

deﬁne the essential features of the revision process

(Alchourr

on et al., 1985). This framework is deﬁned

in the context of propositional logic. So we assume

a ﬁxed vocabulary V , which is just a set of proposi-

tional variables. Formulas over V are deﬁned using

the usual logical connectives ¬, ∧. The beliefs of an

agent are represented by a logically closed set of for-

mulas.

An AGM revision operator is a function ∗ that

maps a belief set K and a formula φ to a new belief

set K ∗ φ. The new belief set represents what an agent

should believe after incorporating φ. Informally, we

want to add φ to the belief set, and remove as little as

possible while maintaining consistency. An AGM re-

vision operator must satisfy a set of postulates, which

we do not list here in the interest of space. However,

as an example, one straightforward postulate is the so-

called success postulate:

K ∗ φ |= φ.

This simply says that new information should be be-

lieved; this postulate encapsulates the fundamental

assumption of the AGM approach that new infor-

mation is provided by a reliable source. It is well-

known that the semantics of AGM belief revision can

be deﬁned with respect to plausibility orderings over

propositional interpretations (Katsuno and Mendel-

zon, 1992).

In this paper, we are not directly concerned with

AGM revision. It has a known limitation in that it

can not be used for iterated belief change. The most

inﬂuential approach to iterated belief change is an ex-

tension of AGM called DP revision (Darwiche and

Pearl, 1997). The main difference is that the beliefs

of an agent are now represented by an epistemic state

E, which is essentially a total pre-order over possible

interpretations. The minimal elements of this order-

ing are considered the most plausible states, and we

let B(E) denote the set of formulas that are true in all

of the minimal states. At the level of formulas, there

is a set of postulates for DP revision that essentially

guarantee that they behave like AGM revision opera-

tors. But then there are four additional postulates that

explicitly deal with iterated change:

Darwiche-Pearl Postulates

[DP1] If β |= α, then B(E ∗ α ∗ β) = B(E ∗ β).

[DP2] If β |= ¬α, then (κ ∗ β) ∗ α = κ ∗ α.

[DP3] If α ∈ B(E ∗ β), then α ∈ B(E ∗ α ∗ β).

[DP4] If ¬α 6∈ B(E ∗ β), then ¬α 6∈ B(E ∗ α ∗ β).

It turns out that there are many different DP operators

that satisfy all of the postulates. We mention the two

most extreme examples:

• Natural Revision: After revision by φ, B(E) be-

comes the set of states where φ is true. For all

other states the ordering deﬁned by E is preserved.

• Lexicographic Revision: After revision by φ, all

states where φ is true are moved before the states

where φ is false. The relative ordering between

φ-states and ¬φ-states is preserved.

Figure 1 gives a schematic depiction of how these op-

erators work. We remark that there are known is-

sues with these operators, and improvements have

been proposed (Booth and Meyer, 2006; Jin and

Thielscher, 2007). However, for the purposes of this

paper, the signiﬁcant feature is simply that these two

extreme examples satisfy the raitionality postulates.

3 ETHICAL CONSIDERATIONS

3.1 On Prescriptive Theories

For the ethical evaluation of formal belief change, we

will consider several approaches: Kant’s categorical

imperative, utilitarianism, and virtue ethics. These are

all well-known approaches, and we refer the reader to

(Hill, 2009; Rosen, 2003; Hursthouse, 2001) for a de-

scription of each approach, as well as comparisons

between them. For the purposes of this paper, the in-

tention is not to draw hard ethical conclusions; our

primary intention is simply to highlight where ethical

issues can creep into formal models of reasoning.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

566

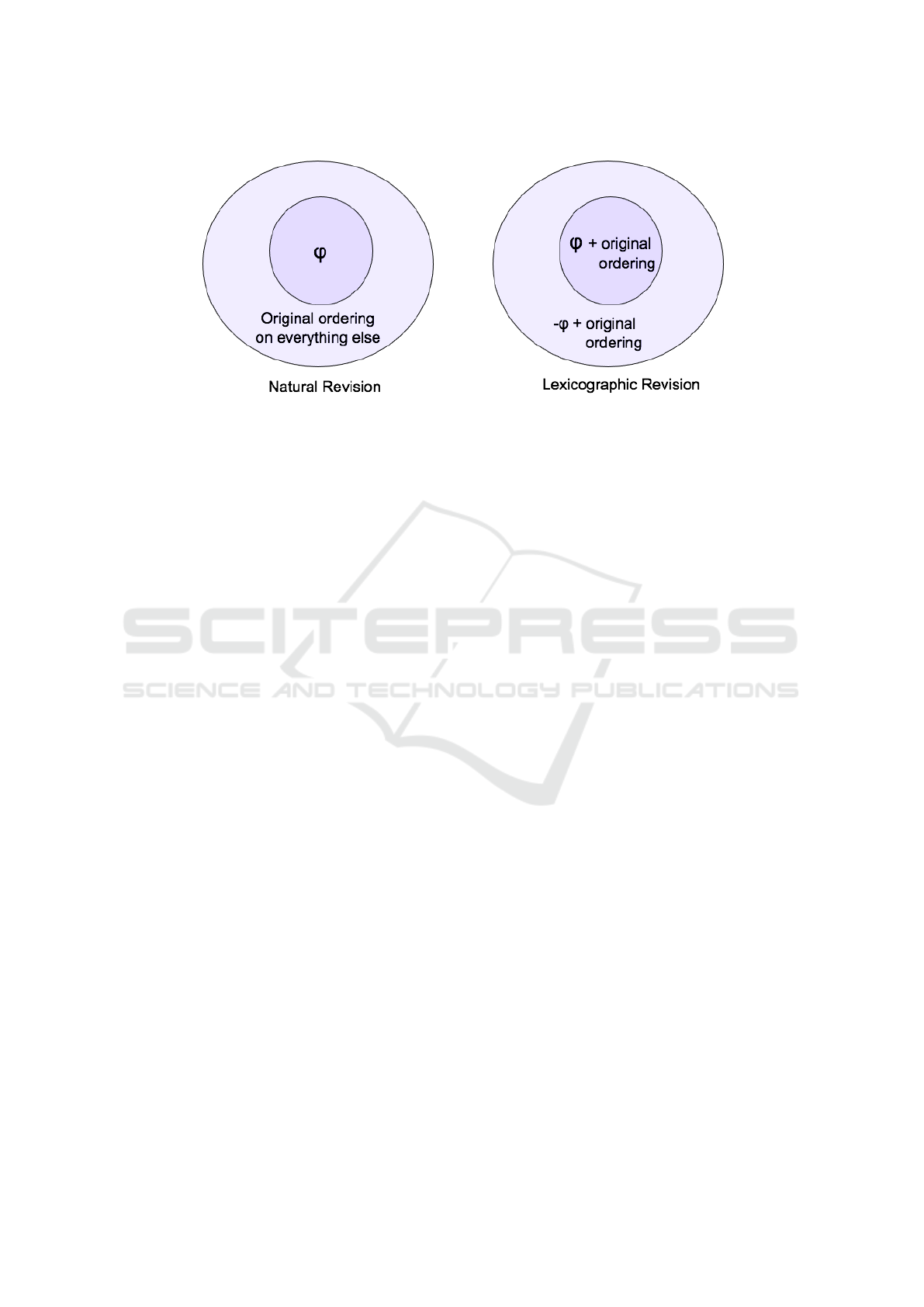
Figure 1: Two Revision Operators.

A distinguishing feature of belief change research

is that it is prescriptive rather than descriptive. It is

clear that real humans do not follow AGM-type ratio-

nality postulates when they revise their beliefs. For

example, human agents do not generally have logi-

cally closed belief sets. The fundamental view is that

a fully rational agent should obey the principles, and

it is therefore a human failing to some extent that we

do not.

There are clearly ethical concerns around human-

deﬁned postulates dictating how beliefs “should” be

revised. In most work on belief change theory, the

postulates are justiﬁed through small sets of motivat-

ing examples. The selection and design of these ex-

amples can introduce bias, or unjustiﬁed assumptions

for a general reasoner. This is certainly a problem,

although it is not one a particularly novel one. In

any scientiﬁc endevour, we need to be careful about

the consideration of biases of the researcher. We are

more concerned with problems that are hidden in the

formalism, irrespective of the intentions of the re-

searchers.

3.2 Problems with Ethical Decision

Making

We return to our motivating example, regarding the

system that is vetting job applicants. It is easy to

demonstrate that natural revision will give the follow-

ing result:

1. After seeing the applicant is from a disadvantaged

group (D), the agent believes D.

2. After seeing the engineering degree, the agent be-

lieves E.

3. After learning the program is not accredited, the

agent revises by ¬E. The agent disregards the ob-

servation D, as if it had never happened.

This result is ethically problematic:

• Kantian view: The applicant in this case pro-

vided information about their status in a desig-

nated group, because they wanted that informa-

tion to be considered. By disregarding this in-

formation, the sequence of revisions here is not

treating this applicant as an end to themselves;

they would presumably like to be considered for

all available positions.

• Utilitarian view: Rules around improving oppor-

tunities for disadvantaged groups are generally ac-

cepted as being good for society overall. This re-

vision process is therefore leading to a harmful

result.

• Virtue ethics view: As a general principle, it is a

virtuous property to look for all opportunities suit-

able for a qualiﬁed candidate - taking into account

all relevant factors. This has not occurred here.

Hence, it is very easy to argue that the system in

this case is performing in a way that is ethically prob-

lematic. The reason it is problematic is simple: in

this particular context, older information is important

- yet it is being disregarded. We remark that this ap-

proach to revision does respect a large set of ratio-

nality postulates, but this problematic behaviour has

been observed and addressed previously (Booth and

Meyer, 2006). However, the solution in most cases is

to introduce more logical postulates. It is difﬁcult to

guarantee that operators satisfying the new postulates

will be immune to similar problems.

Another important point is that the behaviour of

this revision operator is not inherently bad. The re-

sult of this revision is problematic for this particular

context. However, there are other contexts where it

is ethically preferable to ignore earlier reports. Con-

sider, for example, a situation where a particular view

has been discredited. The view could be a social view

Ethical Considerations for the Deployment of Logic-Based Models of Reasoning

567

from an early era, or perhaps a scientiﬁc theory that

has been proved false. In such cases, we may actu-

ally want to disregard previous revisions in line with

the natural revision approach. The problem is not that

this model of revision is “wrong”; the problem is that

it can be ethically problematic in certain contexts.

3.3 The Problem with Iteration

In general, the problem with formal models of iter-

ated belief revision is the fact that they need to ascribe

value to information from the past. The formal mod-

els have to explicitly answer this question: how much

weight should be given to past information that has

been discredited?

The problem here is not easily addressed. The

general approach of the discipline is to use rational-

ity postulates that specify minimum requirements for

a suitable operator. But the rationality postulates do

not describe a deﬁnite approach. Instead, the rational-

ity postulates describe a set of operators. The person

that is interested in modelling a particular problem is

able to choose the speciﬁc operator that is appropriate

for their context.

However, we argue that this approach is unlikely

to be successful beyond very limited and precisely de-

scribed contexts. In this paper, we have only looked

at the two extreme cases of iterated revision. In nat-

ural revision, information obtained in the past carries

little weight as compared to new information. On the

other hand, in lexicographic revision, the full impact

of past revisions is maintained as new information is

received. But these are not the only examples. There

are many different operators that each value past in-

formation differently; each operator may lead to ethi-

cal problems in particular contexts.

We need more than rationality postulates. These

postulates are excellent for establishing the mathe-

matical properties of the system, but they do little to

help determine where particular operators can be de-

ployed. For this reason, we propose that a fundamen-

tal new direction for research would be useful. With

any formal model of reasoning, one would like to

have a precise characterization of the contexts where

that model can be trusted to avoid ethically problem-

atic decision making.

4 CHALLENGES

4.1 Discussions with Non-Specialists

One of the challenges with the deployment of logic-

based reasoning systems is the fact that the postulates

and the logics are not accessible to non-specialists.

While the literature focuses on formal characteriza-

tion results and proofs of correctness, these kinds of

results are of little interest to most users of an AI sys-

tem. All a user would like is a simple tool that mod-

els how an agent makes decisions, without worrying

about the details.

But this is a problem when there are several differ-

ent formal models that might behave poorly in differ-

ent contexts. In order to deploy logic-based reasoning

tools in an ethical manner, we therefore propose the

following steps:

• Knowledge acquisition. We must consult with do-

main experts to understand the context where the

reasoning system will be used. In the case of be-

lief revision systems, one aspect of this process

would be to determine how past information is

perceived and valued.

• Validation. We need to formally validate that the

reasoning system we propose behaves well in the

given context. This means that we need to move

away from the hand-crafted examples produced

by AI scientists, and focus on validation with re-

spect to real examples where the system is likely

to be employed.

Step 1 here is similar the interview process one might

do in the development of an expert system. This is

challenging, but necessary. For example, we have

seen that some logic-based resasoning systems can

lead to unethical behaviour when used in the wrong

context. If we want to develop such systems to be de-

ployed in hybrid AI systems, we need to be able to ex-

plain to communicate effectively with a non-specialist

user.

4.2 Formalizing the Goal

Discussing the deployment setting is an important

step, but it will not address the problem. If we look

towards AI ethics research in ML as a guide, we can

see that issues of bias emerged over time as systems

were deployed. As a result, there has been signiﬁcant

effort to address the problem. There are clear prin-

ciples around key notions of fairness and ethics for

learning systems (Mehrabi et al., 2021). These prin-

ciples might not always be followed, but at least they

are speciﬁed and under discussion.

On the logic side, the situation is quite differ-

ent. In many cases, logical reasoning systems are de-

ﬁned with respect to explicit principles that capture

some aspect of rational decision making. For exam-

ple, the rationality postulates in the theory of belief

change are speciﬁed by a person based on intuition

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

568

and simple examples. This is clearly a problem in

terms of implicit bias. The validation of the system is

generally a mathematical validation addressing issues

around syntax, semantics, and efﬁciency. To some ex-

tent it is assumed that a particular belief change oper-

ator should only be used in a restricted context, but

that context is not speciﬁed. We remark that this sit-

uation is not unique to the theory of belief change,

similar patterns can be seen in other areas of formal

AI.

We propose that the solution is to develop a mech-

anism for specifying context and communicating it to

practitioners for deployment. We need to be be able to

precisely specify the characteristics of the reasoning

problems that can be tackled with a particular model,

without running into clear ethical problems. This

mechanism will be helpful to those choosing frame-

works and models in software, but it is also essential

on the theoretical side to formally demonstrate prop-

erties around fairness and bias for particular logical

models.

5 CONCLUSION

In this position paper, we have outlined a particu-

lar challenge for AI ethics. Much of the work on

AI ethics today has focused on subtle, difﬁcult prob-

lems related to bias in learning systems. However,

we argue that there is a much less subtle problem on

the logic side, where models are developed by hand

and it is easy to ﬁnd examples where such models do

not make ethically sound decisions. We have demon-

strated this through a concrete example, looking at

formal belief change operators. While the problems

in this setting are much easier to see, the solutions are

not obvious. We have proposed that explicitly work-

ing with domain experts and formalizing context may

be an important step towards the eventual safe deploy-

ment of hybrid systems that involve formal reasoning.

REFERENCES

Alchourr

on, C., G

ardenfors, P., and Makinson, D. (1985).

On the logic of theory change: Partial meet func-

tions for contraction and revision. Journal of Symbolic

Logic, 50(2):510–530.

Booth, R. and Meyer, T. (2006). Admissible and restrained

revision. Journal of Artiﬁcial Intelligence Research,

26:127–151.

Darwiche, A. and Pearl, J. (1997). On the logic of iterated

belief revision. Artiﬁcial Intelligence, 89(1-2):1–29.

Hill, T. (2009). The Blackwell Guide to Kant’s Ethics. John

Wiley and Sons.

Hursthouse, R. (2001). On Virtue Ethics. Oxford University

Press.

Jin, Y. and Thielscher, M. (2007). Iterated belief revision,

revised. Artiﬁcial Intelligence, 171(1):1–18.

Katsuno, H. and Mendelzon, A. (1992). Propositional

knowledge base revision and minimal change. Arti-

ﬁcial Intelligence, 52(2):263–294.

Malle, B. F., Bello, P., and Scheutz, M. (2019). Require-

ments for an artiﬁcial agent with norm competence.

In Conitzer, V., Hadﬁeld, G. K., and Vallor, S., edi-

tors, Proceedings of the 2019 AAAI/ACM Conference

on AI, Ethics, and Society, pages 21–27. ACM.

Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K., and

Galstyan, A. (2021). A survey on bias and fairness in

machine learning. ACM Comput. Surv., 54(6).

Rosen, F. (2003). Classical Utilitarianism from Hume to

Mill. Routledge.

Ethical Considerations for the Deployment of Logic-Based Models of Reasoning

569