GPTree: Generator of Phylogenetic Trees with Overlapping and

Biological Events for Supertree Inference

Aleksandr Koshkarov

and Nadia Tahiri

epartement d’Informatique, Universit

e de Sherbrooke, 2500 Boulevard de l’Universit

e, Sherbrooke,

Keywords:

Bioinformatics, Phylogenetics, Simulation, Tree Generator, Supertrees.

Abstract:

Summary: More and more evolutionary and molecular biologists are interested in building alternative su-

pertrees. Often, developing new approaches or testing new metrics requires relevant datasets that are not

always easy to obtain. In order to solve this problem of lack of data, we propose a new approach and devel-

oped a program in Python to generate overlapping phylogenetic trees with biological events to simplify the

process of obtaining this type of data. The new tool takes the number of phylogenetic trees the user wants to

generate, the maximum number of leaves per tree to generate, and the average level of leaf overlap between

phylogenetic trees as input parameters. The program returns to the user a set of phylogenetic trees in Newick

format, respecting the parameters given as input, in order to use them to infer a supertree (or supertrees). This

data can be an important resource for research; the user can download the generated data and use it later in

their relevant application tasks.

Availability and implementation: The generator is freely and publicly available to the entire scientiﬁc com-

munity on the GitHub platform, without any registration, https://github.com/tahiri-lab/gptree under the MIT

licence. The pipeline is written in Python 3.7.

1 INTRODUCTION

More and more phylogenetic researchers are deal-

ing with phylogenetic supertrees in order to improve

our understanding of species evolution. A supertree

is assembled from individual gene trees, but these

trees can be deﬁned in different, but mutually overlap-

ping, sets of taxa. Studies on supertrees are essential

to reconstructing the phylogenetic trees of all living

species (i.e., the OpenTree Online project (Hinchliff

et al., 2015)). Among the unsolved problems, clas-

siﬁcation problems play an important role and have

several practical applications, i.e., the creation of the

tree of life in order to know and understand the biodi-

versity of species.

The reliability of species phylogeny can be vali-

dated through the merging of related gene trees, con-

sidering the present topological conﬂicts (Maddison

et al., 2007). As part of this aspect, it is possible to ex-

amine the consensus tree issue, where trees for merg-

ing are constructed for the same set of taxa, or the su-

pertree issue, where trees for merging are constructed

https://orcid.org/0000-0002-3630-2911

https://orcid.org/0000-0002-1818-208X

for different but overlapping sets of taxa. There are

a number of methods for inferring a consensus tree,

examples of which are the majority-rule consensus

trees, the extended majority-rule consensus tree, and

the strict consensus tree (Bryant, 2003). It is worth

noting that, in practice, researchers do not often work

with phylogenies on the same set of taxa, and, there-

fore, the issue of inferring a supertree becomes im-

portant (Bininda-Emonds, 2004). One approach is to

combine a collection of small phylogenetic trees with

a partial level of overlap between them into complex

supertrees (Wilkinson et al., 2007).

We should also highlight the aspects of tree clus-

tering in situations, where combining the overlapping

trees into a supertree can be performed for the iden-

tiﬁed clusters. There are a number of approaches

to tree clustering that include k-means (Stockham et

al., 2002), k-medoids (Tahiri et al., 2018), MultiPolar

Consensus (MPC) method (Bonnard et al., 2006), and

Multiple Consensus Trees (MCT) method (Gu

enoche,

2013). Recently, (Tahiri et al., 2022a) have intro-

duced a method for building alternative consensus

trees and supertrees using k-means and the Robinson

and Foulds (RF) distance alongside with adaptation of

212

Koshkarov, A. and Tahiri, N.

GPTree: Generator of Phylogenetic Trees with Overlapping and Biological Events for Supertree Inference.

DOI: 10.5220/0011697100003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 3: BIOINFORMATICS, pages 212-219

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

several popular cluster validity indices.

Researchers who work with phylogenetic trees

and supertrees may experience a lack of availability

of datasets that they can use to test their solutions, for

example, classiﬁcation, clustering, and testing new

metrics for comparing trees ((Swenson et al., 2010);

(Tahiri et al., 2022b)). In this context, the creation

of software for generating overlapping phylogenetic

trees to infer supertrees that can be used later by sci-

entists, i.e., in biology, medicine, ecology, bioinfor-

matics, may become a relevant tool for phylogenetic

studies.

Generation of a supertree through its inference

from a set of trees as the core of the solution should

have the functionality to generate phylogenetic trees

with a certain set of features, including the different

number of leaves in trees, the presence of overlap-

ping between trees, and the incorporation of biolog-

ical events, which provide the generated set with the

property of approximation to the processes of evolu-

tion rather than randomness.

2 RELATED WORK

There are various software solutions for the genera-

tion of individual phylogenetic trees based on differ-

ent approaches and with additional features incorpo-

rated. An overview of some of these implementations

is shown in Table 1.

We analyzed and tested these generators and eval-

uated the possibility of using them for the speciﬁed

task. Some applications are aimed at random tree gen-

eration, and such solutions are usually part of a larger

software product with broader functionality (e.g., a

web service (T-Rex) or a library for working with

phylogenetic trees in Python (ete3)). Most of these

simulators are capable of introducing additional fea-

tures into the generated trees, which include birth

and death events (e.g., based on the Gillespie algo-

rithm (Gillespie, 1977)) and horizontal gene transfer

(HGT). The most popular languages for the genera-

tors considered are Python, Java, and C.

None of the existing tree simulators provides the

functionality to generate phylogenetic tree sets with

partially overlapping sets of taxa, so there is a need to

propose an approach to get this kind of data (with the

possibility to use the existing simulator as a base gen-

erator). We chose the AsymmeTree library (Schaller

et al., 2022) version 2.2 as the basic simulator for gen-

erating a single tree (or a pair of species trees and

gene trees), since it is the closest option according

to the requirements we set for the tree: the availabil-

ity of evolutionary scenarios (duplication, loss, and

horizontal gene transfer events), the possibility of set-

ting additional parameters (such as loss, duplication,

and HGT rates), and the Python programming lan-

guage (this is the programming language that com-

monly used to prototype solutions using a wide range

of data and algorithm libraries for bioinformatics and

machine learning). We use ete3 library as an addi-

tional tool for working with generated trees (using the

features available in Python). It provides a possibility

to visualize the data, calculate comparison parameters

of two trees (including RF distances), and save the

generated trees in Newick format. More information

about this is in the following sections.

Special attention should be given to horizontal

gene transfer, which plays an essential role in evolu-

tion ((Dav

ın et al., 2018); (Wolfe and Fournier, 2018);

(Bapteste et al., 2004)) and its incorporation into the

dataset makes the data closer to realistic. Since each

gene has its own evolutionary history, which can be

represented by its own phylogenetic tree, it (the gene)

can demonstrate evolutionary patterns based, in par-

ticular, on horizontal gene transfer events (Tahiri et

al., 2022a). HGT in AsymmeTree is implemented as

follows (Schaller et al., 2022):

1. A species tree is generated.

2. A copy of a gene present at time t in any branch

of the species tree is moved to another branch of

the species tree. This branch, where the copy of

the gene is placed, is chosen uniformly among the

branches available at time t, but without consider-

ing the branch with the parent gene.

Visualization of the presence of HGT in the gener-

ated dataset will be shown in the Results and Discus-

sion section. The selected generator of a single phy-

logenetic tree with the presence of duplication, loss,

and horizontal gene transfer events was used as the

basis for the pipeline, which is described in the next

section.

3 METHODS

Several basic conditions have to be fulﬁlled to gen-

erate a phylogenetic tree dataset in order to obtain a

phylogenetic supertree:

1. Generation of trees with different numbers of

leaves in each tree;

2. Presence of simulated biological events in trees

(in particular, horizontal gene transfer);

3. Presence of overlaps between trees.

The level of overlap of the two trees we determine

GPTree: Generator of Phylogenetic Trees with Overlapping and Biological Events for Supertree Inference

213

Table 1: Overview of phylogenetic tree simulators. Several solutions for generating species and gene trees with the inclusion

of additional features (such as horizontal gene transfer) are presented in the table in alphabetical order (by package name).

Package name Incorporation of additional features

(in simulators)

Programming

Language

Reference

AsymmeTree Speciation, duplication, loss, gene

conversion, and horizontal gene

transfer events

Python (Schaller et al., 2022)

Castor Horizontal gene transfers, gene

duplication, and gene loss events

R (Louca and Doebeli, 2018)

ete3 (populate()

function)

Random generation Python (Huerta-Cepas et al., 2016)

GenPhyloData Gene duplication, gene loss, lateral

gene transfer, clock models, and

sequence evolution

Java (Sj

ostrand et al., 2013)

HGT-gen Horizontal gene transfer Perl (Horiike et al., 2011)

HybridSim Divergence speciation, hybrid

speciation, and introgression

Java (Woodhams et al., 2016)

Ngesh Birth and death models, mutation,

and horizontal gene transfer

Python (Tresoldi, 2021)

SaGePhy Gene birth, speciation, gene

duplications, horizontal gene

transfers, and gene losses

Java (Kundu and Bansal, 2019)

SimPhy Lineage sorting, gene duplication

and loss, and horizontal gene

transfer

C (Mallo et al., 2016)

TreeSim Speciation and extinction R (Stadler, 2011)

TreeSim GM Bellman–Harris models with

lineage-speciﬁc shifts of speciation

and extinction

R (Hagen and Stadler, 2018)

T-Rex (Random

tree generator

module)

Random generation C++, web

service

(Makarenkov, 2001); (Boc

et al., 2012)

Zombi Birth-death model Python (Dav

ın et al., 2020)

by the following formula 1:

OL(T

, T

) =

n(T

, T

)

n(T

) + n(T

) − n(T

, T

)

, (1)

where, OL(T

, T

) is the overlap level between tree 1

(denoted T

) and tree 2 (denoted T

), n(T

, T

) is the

number of common leaves between T

and T

, n(T

)

is the number of leaves in T

, n(T

) is the number of

leaves in T

As mentioned above, an analysis of current solu-

tions in phylogeny and bioinformatics did not detect

the availability of dataset “generators” with the above

conditions. In this work, we propose a dataset gener-

ation pipeline of phylogenetic trees for use in gener-

ating supertrees. A scheme of the pipeline is shown

in Figure 1.

The main steps in the proposed workﬂow are as

follows:

1. Input step. The user enters the initial values:

• L

min

is the minimum possible number of leaves

for each tree;

• L

max

is the maximum possible number of leaves

for each tree;

• N

gen

is the number of trees to be generated;

• p

level

is the average level of overlap (common

leaves) between the trees in the set.

2. Validation step. The input values should satisfy

the following constraints: L

min

is an integer and

5 ≤ L

min

< 500; L

max

is an integer and L

min

max

≤ 500; N

gen

is an integer and N

gen

≤ 500;

level

is a ﬂoating-point number in the range from

0.2 to 0.7 in increments of 0.05 (which corre-

sponds to the range from 20% to 70%).

3. Original tree step. Generate the ﬁrst tree with L

max

leaves. Each tree is generated in 2 steps: ﬁrst,

a species tree is generated, and then a gene tree

(with HGT) is generated on its basis. We distin-

guish separately the generation of the ﬁrst tree as

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

214

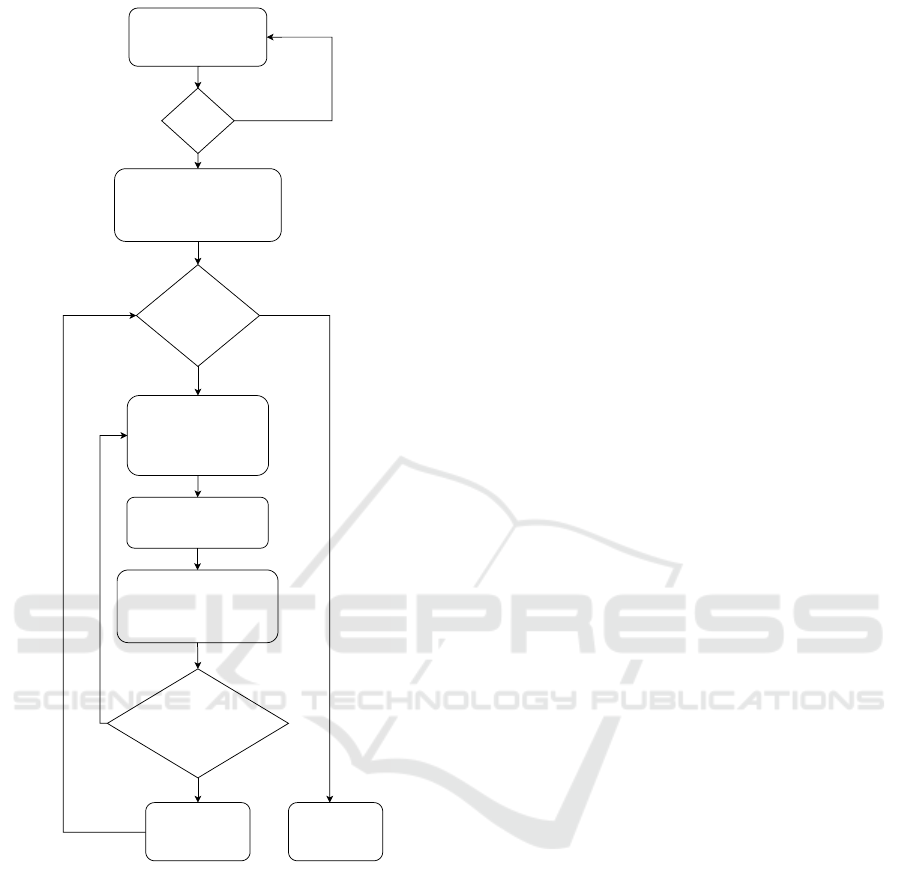
Inputs:

min

, L

max

, N

gen

, p

level

Generate the first tree (with initial

parameters)

N < Ngen?

Generate the number of

leaves n

as a random

number in the range

min

, L

max

)

Generate another tree

with n

leaves

Calculate the average pairwise

(without repetitions) level of

overlaps

Level of overlap

in range

level

-0.01;

level

+0.01)?

Add trees into the

dataset of generated

trees

Save generated

data (trees in

Newick format) to

text files

Yes

Validation

Error

Figure 1: The scheme of data generation. The following

values are used in this workﬂow: L

min

is the minimum pos-

sible number of leaves for each tree; L

max

is the maximum

possible number of leaves for each tree; N is the current

number of generated trees; N

gen

is the number of trees to

be generated; p

level

is the average level of overlap (com-

mon leaves) between the trees in the set; n

is the number of

leaves. The workﬂow uses HGT rate = 0.2 by default (this

value is within the range estimated in (Koonin et al., 2001)

based on biological data), but the user can change this pa-

rameter depending on their experience and objectives. The

principle of HGT implementation is described in the ”Re-

lated work” section. As a result, the user will get a dataset

of N

gen

gene trees, each with a number of leaves from the

range (L

min

, L

max

) with HGT incorporated. The user can

save both sets of species trees and gene trees in Newick for-

mat as text ﬁles and download them for their own purposes.

the base tree, which is used to calculate the level

of overlap with the subsequent tree. The L

max

value is used to provide a large spread in the com-

parison of leaves in trees during calculations.

4. Pairwise tree step. Generate the next tree with a

random number of leaves from the range (L

min

max

5. Overlap level evaluation step. Calculate the aver-

age pairwise (without repetitions) level of overlap

between trees and check how the new tree affects

the average level of overlap. If they overlap in the

speciﬁed range (p

level

− 0.01; p

level

+ 0.01), this

new tree is saved to the dataset (the user can ad-

just the size of this range). If not, return to step

6. Repeat steps 4 and 5 until the dataset includes the

required number of trees (N

gen

7. Output step. Save the generated data (trees in

Newick format) to a text ﬁle.

The user can save two datasets as a result of this

workﬂow: the ﬁrst dataset (main dataset) is a set of

gene trees, the second dataset is a set of species trees

(for individual purposes). In both datasets, the tree

positions in the ﬁles correspond to each other. We will

use individual pairs of trees to analyze the presence of

horizontal gene transfer events.

This workﬂow can be extended for the case of in-

ferring a single or multiple supertrees based on the

generated data using additional packages. One of the

most popular solutions for supertree inference is the

CLANN tool (Creevey and McInerney, 2005), which

is freely available on GitHub and widely used by a

large number of researchers. In order to perform it,

the user needs to follow several steps:

1. Dataset preparation (input): Generating phyloge-

netic trees deﬁned on different, but partially over-

lapping sets of species, based on GPTree.

2. Prepare the input data: it can be data generated

from the GPTree generator of phylogenetic trees

with a different number of overlapping leaves.

3. Prepare a text ﬁle with commands: basic recom-

mendations are provided in the tool documenta-

tion.

4. Run CLANN.

5. Save the output data.

A sample command ﬁle with recommended parame-

ters is available on the project’s GitHub repository.

GPTree: Generator of Phylogenetic Trees with Overlapping and Biological Events for Supertree Inference

215

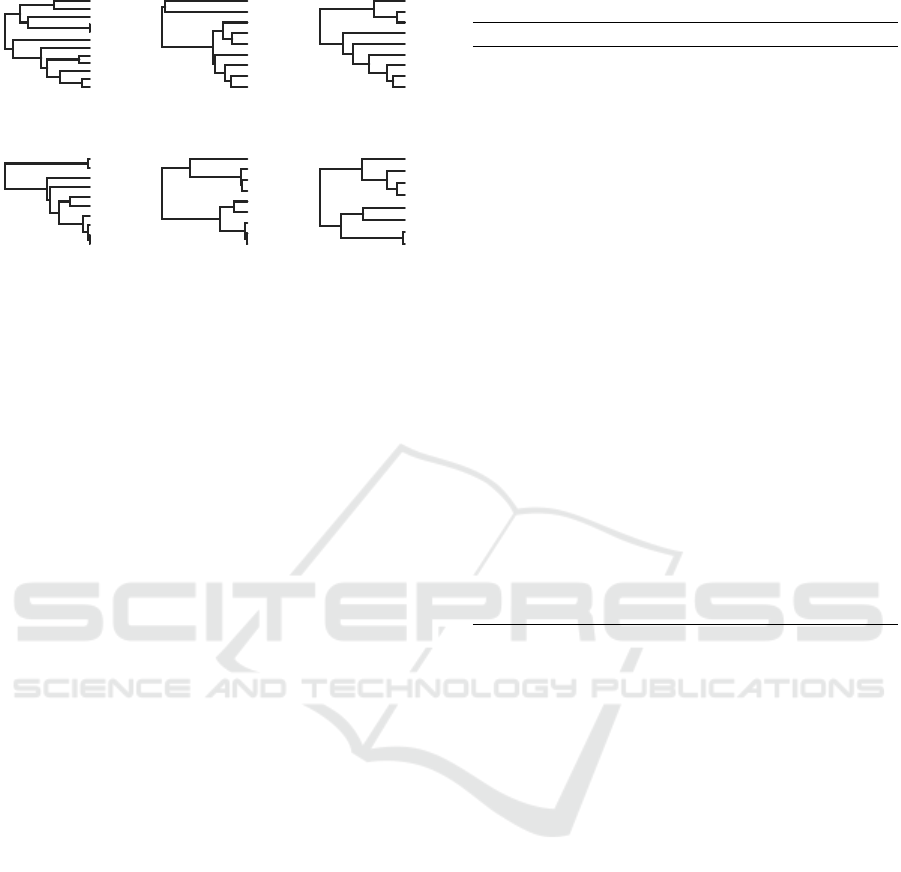
Figure 2: Visualization of 6 trees from the generated

dataset with the following parameters: L

min

=7, L

max

=12,

level

=0.5. Basic visual analysis shows that these trees have

different numbers of leaves (one tree has 8 leaves, three

trees have 9 leaves, one tree has 10 leaves, and one tree

has 12 leaves), and they are within the given parameters. In

addition, these trees have a certain proportion of common

leaves, and, in fact, the average level of overlap is 0.5 with

a small margin of error.

4 RESULTS AND DISCUSSION

This solution is implemented in Python and struc-

tured as an interactive Jupiter Notebook (in .ipynb for-

mat). The generator was tested in Google Colabora-

tory (Google Colab with a basic free version).

First, we generated and visualized a small number

of trees in order to show their structure (Figure 2).

The resulting image reﬂects the basic parameters set

by the user.

Second, we tested the functionality of the phylo-

genetic tree dataset generator with relation to three

basic parameters: the number of generated trees with

different set of leaves from the deﬁned range, evalua-

tion of the level of overlap between trees, and analysis

of the presence of HGTs. The identiﬁed parameters

and the basic results are shown in Table 2.

Figure 3 shows a visualization of the results by the

level of overlap between trees. It should be noted that

the distribution resembles a normal distribution. The

bell-shaped curve can show us the degree of diversity

in the number of common leaves belonging to pairs of

trees. In parts (a) and (b), we may see a small number

of rare values (left and right), which actually are out-

liers. Part (b) may also help to evaluate the standard

deviation, which can be relatively large for a ﬂat bell-

shaped distribution. The boundaries in the left and

right tails region are also estimable using formula 1

(for the cases of L

min

and L

max

number of leaves) and

considering the initial parameters set by the user.

We analyzed for the presence of horizontal gene

transfer in the generated dataset. For this purpose,

we used a random pair of species and gene trees

Table 2: Dataset generation parameters and basic results.

Actions Values

Setting parameters

• L

min

= 15;

• L

max

= 25;

• N

gen

= 50;

• plevel = 0.5

Checking the ﬁnal

number of trees in the

generated dataset

• Desired number of

trees = 50;

• Real number of trees

= 50;

• Number of unique

trees in the dataset =

Calculation of the ac-

tual average level of

overlap between trees

• Desired level of over-

lap = 0.5;

• Average level of

overlap between

each pair of trees =

0.5

and checked for the presence of HGT using the T-

Rex web service (Boc et al., 2012). The results are

shown in Figure 4. This service utilizes a polynomial-

time algorithm with the possibility to choose between

several optimization criteria (in particular, biparti-

tion dissimilarity, Robinson and Foulds distance, and

least-squares) and a bootstrap HGT detection (Boc et

al., 2010). To infer a horizontal gene transfer sce-

nario, the user needs to provide a pair of species and

gene trees.

We observe that the generated dataset corresponds

to our criteria. It should be noted that the genera-

tor works slower for overlap levels less than 0.2 and

greater than 0.7, and therefore in the current version

of the generator the recommended value of the over-

lap level is in the range (0.2, 0.7). In future releases

of this generator, we plan to expand this range.

A version of Jupiter Notebook with code to

analyze the generated dataset and examples can

be found in the project repository on GitHub

(https://github.com/tahiri-lab/GPTree).

The inference of supertrees based on the generated

dataset is also an important subject. Depending on the

objectives of the study, we can refer to the clustering

approach, when the supertree inference is performed

on the basis of a cluster of trees. The ﬁrst option is to

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

216

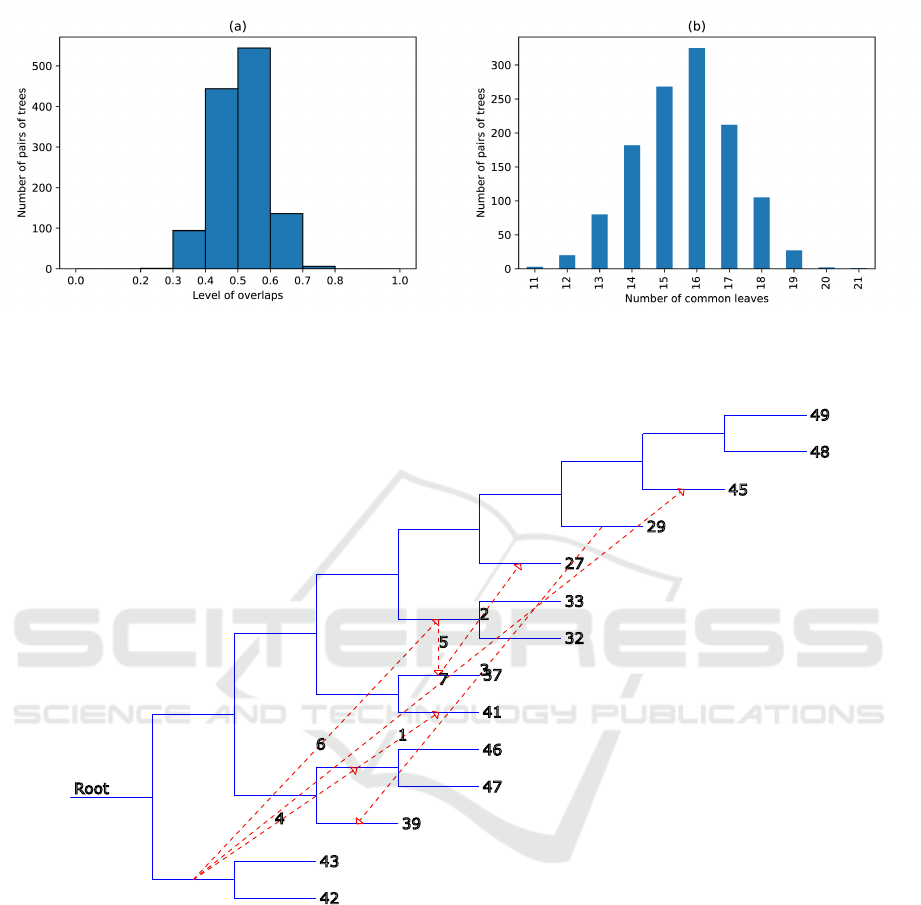
Figure 3: Visual analysis of the level of overlap in the dataset. Part (a) shows the level of overlap relative to the number of

pairs of trees. It may be observed that most of it is around 0.5 (as set by the user as initial parameters) with a slight deviation

left and right. Part (b) shows the distribution according to the number of common leaves in possible pairs of trees (without

overlaps). It can be seen that this visualization is bell-shaped with peaks in the center of the indicated range.

Root

Figure 4: Analysis of the presence of HGT. The results of the analysis are as follows: HGT 1: from subtree (46, 47) to subtree

(41); HGT 2: from subtree (37) to subtree (27); HGT 3: from subtree (29) to subtree (39); HGT 4: from subtree (42, 43) to

subtree (41, 46, 47); HGT 5: from subtree (32, 33) to subtree (27, 37); HGT 6: from subtree (41, 42, 43, 46, 47) to subtree

(27, 32, 33, 37); HGT 7: from subtree (27, 32, 33, 37, 41, 42, 43, 46, 47) to subtree (45). Total number of HGTs = 7. The

analysis was performed using T-Rex web service (Boc et al., 2012).

generate a large dataset, then cluster this dataset using

existing algorithms (e.g., k-means or k-medoids, see

(Tahiri et al., 2022a)) to build a supertree for each

cluster that is found. The second option is to use the

generator in a loop and generate several datasets of

clusters for each set of parameters to infer a supertree.

One of the use cases of the developed tool is the

generation of data to test new distance measures be-

tween phylogenetic trees deﬁned on different, but mu-

tually overlapping, sets of taxa, or supertrees. Al-

though metrics between trees have been studied for

more than 40 years, the story is different for su-

pertrees since most distances were introduced in the

last decade or so. The Robinson and Foulds distance

is the most popular phylogenetic tree distance, but no

such standard is known for supertrees. On the one

side, it is possible to adapt existing metrics to com-

pare phylogenetic trees (with overlapping leaves) in

the context of clustering. This can help to effectively

use phylogenetic tree clusters to infer supertrees. On

GPTree: Generator of Phylogenetic Trees with Overlapping and Biological Events for Supertree Inference

217

the other side, this foundation can help to evaluate,

adapt and improve metrics for comparing phyloge-

netic supertrees relying on distance properties. Re-

searchers can use simulated data with incorporated bi-

ological events in such tasks.

5 CONCLUSION

The analysis and comparison of several phylogenetic

tree simulators did not reveal phylogenetic tree gener-

ators with partially overlapping taxon sets, which can

be used in problems using phylogenetic supertrees.

This paper proposes a new approach for generating

a dataset of phylogenetic trees for further use in the

building of phylogenetic supertrees. The generator

takes the minimum possible number of leaves for each

tree, the maximum possible number of leaves for each

tree, the number of trees to be generated, and the av-

erage level of overlap (common leaves) between the

trees in the set as input parameters. The output is a

dataset consisting of gene trees with incorporated bi-

ological events, including duplication, loss, and hori-

zontal gene transfer events. The trees in the generated

dataset are in Newick format.

The generator presented in this paper can be use-

ful for biologists, bioinformaticians, ecologists, and

computer scientists to conduct experiments with phy-

logenetic trees and supertrees, for example, in the

problems of developing new metrics of distance be-

tween supertrees, clustering, and classiﬁcation prob-

lems. This solution is freely available in the reposi-

tory on GitHub, where there are also additional scripts

for testing the generated dataset with detailed com-

ments, and sample datasets. The possibility to run the

generator in Google Colaboratory makes it easier and

more accessible for the scientiﬁc community.

ACKNOWLEDGEMENTS

The authors would like to thank the Department of

Computer Science, University of Sherbrooke, Que-

bec, Canada for providing the necessary resources to

conduct this research.

FUNDING

The authors thank the reviewers for their valuable

comments on this paper. This work was supported

by the Natural Sciences and Engineering Research

Council of Canada, the University of Sherbrooke

grant, and the Centre de recherche en

ecologie de

l’UdeS (CREUS).

Conﬂict of Interest: none declared.

REFERENCES

Bapteste, E., Boucher, Y., Leigh, J., and Doolittle,

W. (2004). Phylogenetic reconstruction and lat-

eral gene transfer. Trends in microbiology, 12(9),

406-411.

Bininda-Emonds, O. (2004). Phylogenetic supertrees:

combining information to reveal the tree of life.

Springer Science & Business Media.

Boc, A., Philippe, H., and Makarenkov, V. (2010).

Inferring and validating horizontal gene transfer

events using bipartition dissimilarity. Systematic

biology, 59(2), 195-211.

Boc, A., Diallo, A. B., and Makarenkov, V. (2012). T-

REX: a web server for inferring, validating and

visualizing phylogenetic trees and networks. Nu-

cleic Acids Research, 40(W1), W573-W579.

Bonnard, C., Berry, V., and Lartillot, N. (2006). Mul-

tipolar consensus for phylogenetic trees. System-

atic Biology, 55(5), 837-843.

Bryant, D.(2003). A classiﬁcation of consensus meth-

ods for phylogenetics. DIMACS series in dis-

crete mathematics and theoretical computer sci-

ence, 61, 163-84.

Creevey, C. and McInerney, J. (2005). Clann: inves-

tigating phylogenetic information through su-

pertree analyses. Bioinformatics, 21(3), 390-

392.

Dav

ın, A., Tannier, E., Williams, T., Boussau, B.,

Daubin, V., and Sz

oll

osi, G. (2018). Gene trans-

fers can date the tree of life. Nature ecology &

evolution, 2(5), 904-909.

Dav

ın, A., Tricou, T., Tannier, E., de Vienne, D., and

oll

osi, G. (2020). Zombi: a phylogenetic sim-

ulator of trees, genomes and sequences that ac-

counts for dead linages. Bioinformatics, 36(4),

1286-1288.

Gillespie, D. (1977). Exact stochastic simulation of

coupled chemical reactions. The journal of phys-

ical chemistry, 81(25), 2340-2361.

enoche, A.(2013). Multiple consensus trees: a

method to separate divergent genes. BMC Bioin-

formatics, 14, 1-7.

Hagen, O. and Stadler, T. (2018). TreeSim GM: Sim-

ulating phylogenetic trees under general Bell-

man–Harris models with lineage-speciﬁc shifts

of speciation and extinction in R. Methods in

ecology and evolution, 9(3), 754-760.

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

218

Hinchliff, C., Smith, S., Allman, J., Burleigh, J.,

Chaudhary, R., Coghill, L., ... and Cranston, K.

(2015). Synthesis of phylogeny and taxonomy

into a comprehensive tree of life. Proceedings

of the National Academy of Sciences, 112(41),

12764-12769.

Horiike, T., Miyata, D., Tateno, Y., and Minai, R.

(2011). HGT-Gen: a tool for generating a phylo-

genetic tree with horizontal gene transfer. Bioin-

formation, 7(5), 211.

Huerta-Cepas, J., Serra, F., and Bork, P. (2016). ETE

3: reconstruction, analysis, and visualization of

phylogenomic data. Molecular biology and evo-

lution, 33(6), 1635-1638.

Koonin, E., Makarova, K., and Aravind, L. (2001).

Horizontal gene transfer in prokaryotes: quan-

tiﬁcation and classiﬁcation. Annual Reviews in

Microbiology, 55(1), 709-742.

Kundu, S. and Bansal, M. (2019). SaGePhy: An

improved phylogenetic simulation framework

for gene and subgene evolution. Bioinformatics,

35(18), 3496-3498.

Louca, S. and Doebeli, M. (2018). Efﬁcient compara-

tive phylogenetics on large trees. Bioinformatics,

34(6), 1053-1055.

Maddison, D., Schulz, K., and Maddison, W. (2007).

The tree of life web project. Zootaxa, 1668(1),

19-40.

Makarenkov, V. (2001.) T-REX: reconstructing and

visualizing phylogenetic trees and reticulation

networks. Bioinformatics, 17(7), 664-668.

Mallo, D., de Oliveira Martins, L., and Posada, D.

(2016). SimPhy: phylogenomic simulation of

gene, locus, and species trees. Systematic biol-

ogy, 65(2), 334-344.

Philippe, H. and Douady, C. (2003). Horizontal gene

transfer and phylogenetics. Current opinion in

microbiology, 6(5), 498-505.

Schaller, D., Hellmuth, M., and Stadler, P. (2022).

AsymmeTree: A Flexible Python Package for

the Simulation of Complex Gene Family Histo-

ries. Software, 1(3), 276-298.

ostrand, J., Arvestad, L., Lagergren, J., and

Sennblad, B. (2013). GenPhyloData: realistic

simulation of gene family evolution. BMC bioin-

formatics , 14(1), 1-5.

Stadler, T. (2011). Simulating trees with a ﬁxed num-

ber of extant species. Systematic biology, 60(5),

676-684.

Stockham, C., Wang, L., and Warnow, T. (2002). Sta-

tistically based postprocessing of phylogenetic

analysis by clustering. Bioinformatics, 18, S285-

S293.

Swenson, M., Barbanc¸on, F., Warnow, T., and Lin-

der, C. (2010). A simulation study comparing

supertree and combined analysis methods using

SMIDGen. Algorithms for Molecular Biology,

5(1), 1-16.

Tahiri, N., Willems, M., and Makarenkov, V. (2018).

A new fast method for inferring multiple con-

sensus trees using k-medoids. BMC Evolution-

ary Biology, 18, 1-12.

Tahiri, N., Fichet, B., and Makarenkov, V. (2022).

Building alternative consensus trees and su-

pertrees using k-means and Robinson and Foulds

distance. Bioinformatics, 38(13), 3367-3376.

Tahiri, N., Veriga, A., Koshkarov, A., and Morozov,

B. (2022). Invariant transformers of Robinson

and Foulds distance matrices for convolutional

neural network. Journal of bioinformatics and

computational biology, 2250012-2250012.

Tresoldi, T. (2021). Ngesh: a Python library for syn-

thetic phylogenetic data. Journal of Open Source

Software, 6(66), 3173.

Wilkinson, M., Cotton, J., Lapointe, F., and Pisani,

D. (2007). Properties of supertree methods in

the consensus setting. Systematic Biology, 56(2),

330-337.

Wolfe, J. and Fournier, G. (2018). Horizontal gene

transfer constrains the timing of methanogen

evolution. Nature ecology & evolution, 2(5),

897-903.

Woodhams, M., Lockhart, P., and Holland, B. (2016).

Simulating and summarizing sources of gene

tree incongruence. Genome biology and evolu-

tion, 8(5), 1299-1315.

GPTree: Generator of Phylogenetic Trees with Overlapping and Biological Events for Supertree Inference

219