Automatic Facility Layout Design System Using Deep Reinforcement

Learning

Hikaru Ikeda, Hiroyuki Nakagawa and Tatsuhiro Tsuchiya

Institute of Information Science and Technology, Osaka University, 1-5 Yamadaoka, Suita, Osaka, Japan

Keywords:

Deep Reinforcement Learning, Machine Learning, Layout Design, Facility Layout Problem, Analytic

Hierarchy Process.

Abstract:

Facility layout designing aims to deploy functional objects in appropriate locations within the logistics facil-

ities and production facilities. The designer’s ability to create a layout is a major factor in the quality of the

layout because they need to satisfy functional requirements like lead time, relations among functional objects

to deploy and material handling costs. In this paper, a deep reinforcement learning (RL) based automatic lay-

out design system is developed. Deep Q-Networt (DQN) is introduced to solve facility layout problem (FLP)

by the adaptability of RL with the expression of deep neural networks. We apply the developed system to the

existing FLP and compare the layout result with conventional RL based system. Consequently, the perfor-

mance improvement was conﬁrmed in terms of the relations among units in the created layout comparing to

the RL based system.

1 INTRODUCTION

Facility layout designing aims to create high work

efﬁciency layouts in facilities. The designer’s abil-

ity to create a layout is a major factor in the quality

of the layout. This problem is known as the facility

layout problem (FLP) (Kusiak and S.Heragu, 1987).

FLP is optimization problems of deploying equip-

ment and machines in logistics facilities and produc-

tion facilities with consideration of lead time, rela-

tions among functional objects to deploy and mate-

rial handling costs. The computational complexity of

FLP is NP-hard. Therefore meta-heuristic methods

like genetic algorithms or simulated annealing are the

mainstream.

In this study, we developed a layout design sys-

tem that can create layouts using deep reinforcement

learning (RL). RL (Kaelbling et al., 1996) is a ma-

chine learning method that learns behavior through

trial-and-error interactions by the system itself. Ma-

chine learning methods are generally classiﬁed into

three types: supervised learning, unsupervised learn-

ing and reinforcement learning. While supervised and

unsupervised learning methods’ agents require train-

ing data for learning, reinforcement learning agents

obtain the data generated from its own experience.

Lately self-supervised learning and semi-supervised

learning become major methods. Developers of re-

inforcement learning system create a high learning

efﬁciency model instead of preparing learning data.

Reinforcement learning agents learn the behavior to

maximize the objective score in the environment. The

series of actions in the learning follow the Markov

decision process (Liu et al., 2017). The Markov deci-

sion process has the characteristic that the probability

distribution of the future state depends only on the

current state and not on all past states, which is called

the Markov property.

Deep RL (Arulkumaran et al., 2017) is a learning

method that combines deep learning and reinforce-

ment learning. Deep learning learns by using neural

networks that reproduce human brain cells with high

processing power. Deep RL can handle more com-

plex problems than RL because of using the Neural

Network. Convolutional Neural Network (CNN) is a

type of deep learning model for processing data that

has a grid pattern, such as images (Yamashita et al.,

2018). DQN (Lee et al., 2021) is the most common

deep RL method using CNN.

The object of this study is to clarify the effective-

ness of DQN for FLP compared with RL. More efﬁ-

cient layouts can be created by using DQN method.

We conducted some experiments to demonstrate the

effectiveness of the developed system. Consequently,

the performance improvement was conﬁrmed in terms

of the relations among units in the created layout com-

Ikeda, H., Nakagawa, H. and Tsuchiya, T.

Automatic Facility Layout Design System Using Deep Reinforcement Learning.

DOI: 10.5220/0011678500003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 2, pages 221-230

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

221

paring to the RL based system.

The structure of this paper proceeds as follows.

Section 2 explains deep RL, the layout design, current

problems, and Analytic Hierarchy Process (AHP) as

the background of this study. Section 3 explains the

layout design mechanism using DQN and AHP. Sec-

tion 4 describes the results of the experiments. Sec-

tion 5 describes the discussion according to the exper-

iments presented in Section 4. Section 6 concludes

the paper.

2 BACKGROUND

2.1 Deep RL

Deep learning has signiﬁcantly inﬂuenced many ar-

eas in machine learning and dramatically improved

in speech recognition, visual object recognition, ob-

ject detection and many other domains such as drug

discovery and genomics (LeCun et al., 2015). Deep

learning has become advance in RL, with the use

of deep learning algorithms within RL deﬁning the

ﬁeld of Deep RL. Many of the successes in Deep

RL have been based on scaling up prior works in RL

to high dimensional problems. This is due to the

learning of low-dimensional feature representations

and the powerful function approximation properties

of neural networks. Neural networks can be used as

components of RL agents, allowing them to learn di-

rectly from high dimensional inputs. In general, Deep

RL is based on training deep neural networks to ap-

proximate the policy or value functions (Arulkumaran

et al., 2017). In the ﬁeld of DRL, there have been

outstanding success cases. Volodymyr et al. (Mnih

et al., 2015) developed an algorithm that could learn

to play Atari 2600 video games at a extraordinary

level. David et al. (Silver et al., 2016) developed Al-

phaGo and defeated a human world champion in Go.

2.2 Layout Design

The FLP is a combinatorial optimization problem

which arises in a variety of problems such as layout

design of the deployment and ﬂow lines of equipment,

materials, parts, work-in-process, workers, circuit

board design, warehouses, backboard wiring prob-

lems (S.P.Singh and R.R.K.Sharma, 2006). Creating

an appropriate layout can improve material handling

costs and lead time. Facility layout design has been

studied for a long time (Tam, 1992). GA (Thengade

and Dondal, 2012) and GP (Espejo et al., 2010) based

studies are generally conducted. GA is a program-

ming technique which forms its basis from the bio-

logical evolution. GA uses the principles of selection

and evolution to produce several solutions to a given

problem. GP is considered to be a variant of GA,

and used to evolve abstractions of knowledge. Jos

et al. (Gonc¸alvesa and G.C.Resende, 2015) intro-

duced biased random-key GA for the unequal area fa-

cility layout problem where a set of rectangular facil-

ities with given area requirements has to be deployed,

without overlapping. The role of GA is to evolve the

encoded parameters that represent the facility deploy-

ment sequence, the vector of facility aspect ratios, and

the position of the ﬁrst facility. Venkatesh and Jim

(Dixit and Lawlor, 2019) use GA to reduce the sum of

the product of the three factors of material handling

cost: the volume of material handling (frequency of

journeys), the cost of material handling, and the dis-

tance travelled. Singh et al. (D.Meller and A.Bozer,

1997) introduced a layout generating method using

the space-ﬁlling curve. The space-ﬁlling curve de-

scribes plane spaces based on the trajectory of an in-

dividual curve. The layout was created by allocating

the required area using the space-ﬁlling curve of the

site. Stanislas (Chaillou, 2019) introduced to apply

AI to ﬂoor plans analysis and generation. His ultimate

goal is three-fold: to generate ﬂoor plans, to qualify

ﬂoor plans and to allow users to browse through gen-

erated design options. He have chosen nested Gener-

ative Adversarial Neural Networks or GANs. Luisa

et al. (Vargas-Pardo and Giraldo-Ramos, 2021) in-

troduced Fireﬂy algorithm (FA), which is designed

to solve continuous optimization problems. From the

map of the layout that contains the (x, y) coordinates

corresponding to the location of each of the nodes

or workstations that are distributed on the plant, and

paths between nodes, the system solves layout prob-

lem as traveling salesman problem (TSP). Jing et al.

(fa and JunLiu, 2019) introduced the ant colony op-

timization (ACO) algorithm, which is a bio-inspired

optimization algorithm based on the behavior of nat-

ural ants that succeed in ﬁnding the shortest paths

from their nest to food sources by communicating via

pheromone trails.

Several studies have been conducted on RL and

space control problems, including FLP. Peter et al.

(Burggraf et al., 2021) described the recent surge of

research interest in Artiﬁcial Intelligence. They re-

gard machine learning techniques including RL as

the most promising approach to facility layout re-

search. In our previous study (Ikeda et al., 2022),

we developed facility layouts creation mechanism us-

ing Monte Carlo (MC) method, which is a method of

RL. In our mechanism, states are represented by the

size and the maximum rectangular in the remaining

area, and actions are represented by the size of the

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

222

unit that ﬁts the site. The mechanism was applied to

existing layout problem and the effectiveness of RL

to FLP is demonstrated. Richa et al. (Verma et al.,

2019) introduced RL framework for selecting and se-

quencing containers to load onto ships in ports. Their

goal is to minimize the number of crane movements

required to load a ship. We can regard the problem

as an assignment problem in which the order of as-

signments is important and therefore the reward is

dependent of the order. Azalia et al. (Mirhoseini

et al., 2021) introduced a graph deployment method

using RL, and demonstrate latest results on chip ﬂoor-

planning. They show that their method can generate

chip ﬂoor-plans that are comparable or superior to hu-

man experts in under six hours, whereas humans take

months to produce acceptable ﬂoor-plans for modern

accelerators. Ruizhen et al. (Hu et al., 2020) intro-

duced the transport-and-pack (TAP) problem, a fre-

quently encountered instance of real-world packing.

They developed a neural optimization solution using

RL. Given an initial spatial conﬁguration of boxes,

they seek an efﬁcient method to iteratively transport

and pack the boxes compactly into a target container.

Amine et al. (Izadinia et al., 2014) developed a Mixed

Integer Programming (MIP) robust model for a form

of multi-ﬂoor layout problem. In the experiment, they

created facility layouts considering the relation be-

tween the cellar containing main storages and upper

ﬂoors in which departments will be located in prede-

termined locations.

Some studies about space control using deep RL

have also been conducted. Matthias et al. (Klar et al.,

2021) study the layout for four functional units next

to the logistic lane where the material is transported

by vehicles using double deep Q-learning (DDQL)

method. Their layout is generated to be optimized

regarding a single planning objective, i.e., the trans-

portation time. Xinhan et al.(Di et al., 2021) intro-

duced a method of searching for an appropriate de-

ployment while moving furniture in a room using a

deep Q-Network (DQN). This method can arrange

one piece of furniture so as not to interfere with the

function of the room. They also explore the interior

graphics scenes design task as a Markov decision pro-

cess using deep RL (Di and Yu, 2021). Their goal is to

generate an accurate layout for the furniture in the in-

door graphics scenes simulation. L

opez et al. (L

opez

et al., 2020) developed a virtual reality application

that creates a production line for electric drills in a vir-

tual space using deep RL. Their PCG method can re-

duce the resources required for development and can

personalize the 3-Dimentional virtual environments.

Goal

Evaluation

criterion 1

Evaluation

criterion 2

Evaluation

criterion N

Alternative

・・・

Alternative

・・・

Goal

Evaluation

criteria

Alternatives

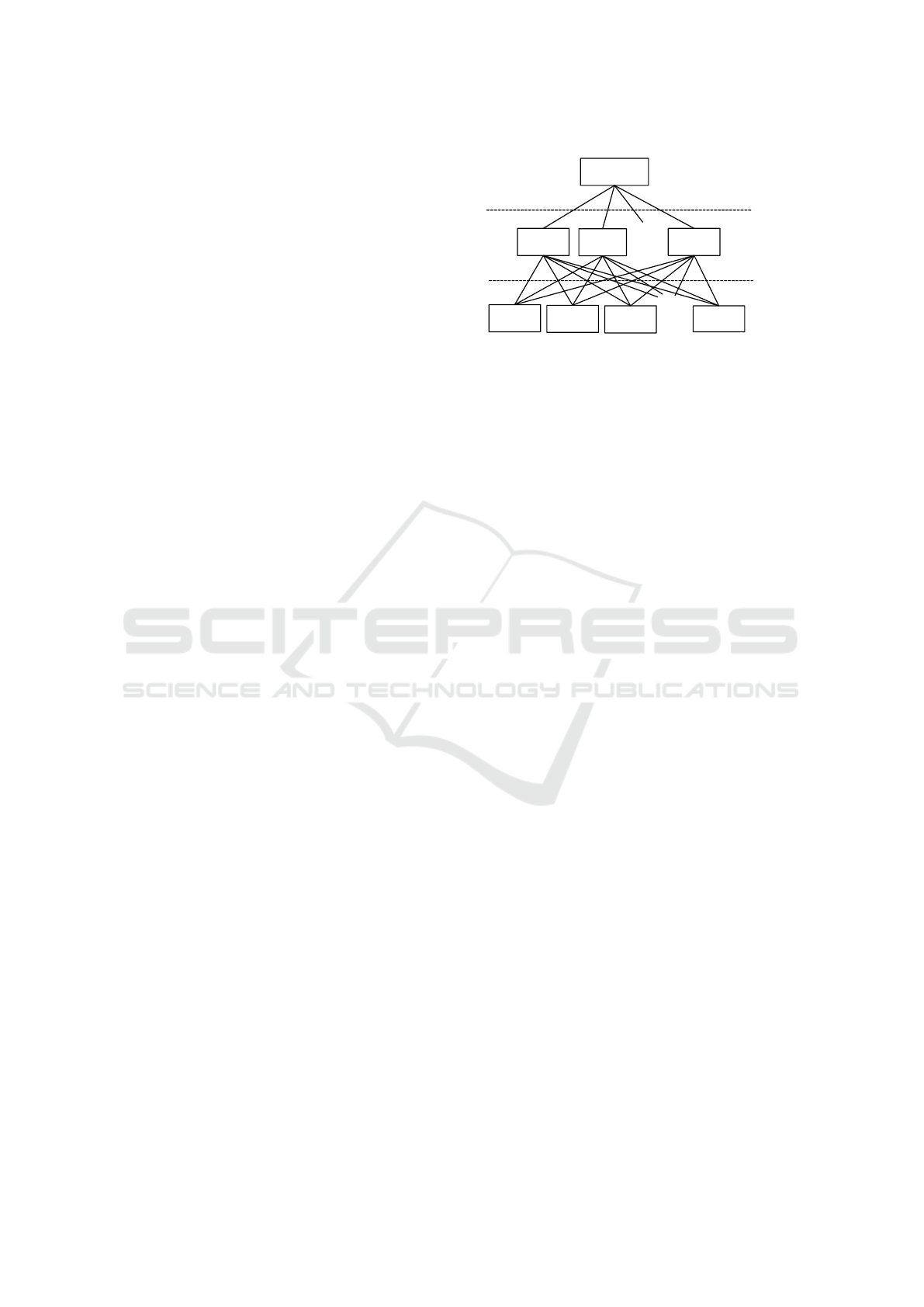
Figure 1: General example of AHP hierarchy.

2.3 Analytic Hierarchy Process (AHP)

Analytic Hierarchy Process (AHP) (Lima et al.,

2019), originally proposed by Saaty (1980), is one of

Multi-Criteria Decision Making (MCDM) procedures

that create a hierarchy for the decision divided into

levels. AHP is used widely in various ﬁelds because

of its simplicity. First, the decision criteria are hier-

archized by dividing them into three elements: goals,

evaluation criteria, and alternatives. Second, the im-

portance of each evaluation criterion in terms of the

goals is calculated and the importance of the alterna-

tives in terms of the evaluation criteria is calculated.

Finally, from these calculations, the importance of the

alternative in terms of the goals is calculated and the

weight of each alternative can be determined. The

scale for comparison is called the Saaty scale and is

quantitatively rated between 1 and 9. 1 is of equal im-

portance and the closer to 9, the more important it is.

The closer it gets to 1/9, the less important it becomes.

Fig.1 shows a general example of an AHP hierarchy.

A goal, N evaluation criteria and K alternatives are

set. First, which evaluation criteria are prioritized for

the goal is calculated. Second, which alternative is su-

perior in each evaluation criterion is calculated. These

two priorities are used to calculate the weight of each

alternative in terms of the goal. The feature of AHP is

that the priority of each alternative can be easily cal-

culated even if the number of evaluation criteria and

alternatives increases.

Several studies have been widely conducted on

combinatorial optimization problems using AHP. Es-

pecially, AHP is often used together with GA. Lin-

feng et al. (Bai et al., 2009) introduced AHP and GA

for agile supply chains. They use AHP to evaluate

the each supplier using the weigh value of time, cost,

quality and service. Ying et al. (Zeng et al., 2010) in-

troduced AHP and GA for Electric power equipment

maintenance schedule optimization. They use AHP

to evaluate the maintenance items based on reliability

object and economic object. Ke et al. (Wang et al.,

2022) AHP and GA for robotic polishing process

Automatic Facility Layout Design System Using Deep Reinforcement Learning

223

sequencing aiming at satisfying polishing sequence

rules and the shortest polishing time simultaneously.

They use 4 levels hierarchy AHP to generate a ﬁtness

function to evaluate both polishing time and polish-

ing rules. Hossein et al. (Youseﬁ et al., 2021) studied

the integration of a hybrid combined cooling, heating

and power CCHP system into a commercial building.

They considered three objective functions to cost sav-

ing, energy saving and emission reduction, and con-

sidering each objective function, the GA optimization

is applied in three approaches as a single objective op-

timization problem. Then, the most proﬁtable answer

is determined from the three answers achieved in the

optimization process using AHP.

Besides, some studies used AHP with Deep RL

methods to solve the problems. Guoqing et al. (Wang

and Wang, 2020) introduced AHP combined with

DQN (AHP-DQN) because if reinforcement learning

is adopted, there will be too many state action groups

(S, A), and the traversal is very difﬁcult, which leads

to the failure of the algorithm. Jianxi and Liutao

(Chen et al., 2020) introduced AHP-DQN framework

to solve low terminal storage capacity and diversifed

network service problems of mobile edge computing

tasks.

In this study, AHP is introduced to create a layout

that considers the relations among the units.

3 LAYOUT DESIGN SYSTEM

We develop a layout design system using a DQN as

a solution for FLP. An agent in the system arranges

units on a ﬂat site and creates a layout. This section

explains the environment settings and algorithms of

the system.

Variables used in the paper are deﬁned as follows:

• s

: state.

• a

: action.

• u

: unit.

• r(s

): reward.

• return

: return.

• V

): Action-value when the agent take ac-

tion a

in state s

• γ: discount factor.

• relation

: relation.

• d

: Manhattan Distance between units with rela-

tion Relation

• intensity

: intensity of relation of Relation

• AHP

eva

): AHP evaluator.

1 1 0 0→3 0→3

2 2 2 0→3 0→3

2 2 2 0 0

0 0 0 0 0

3 3

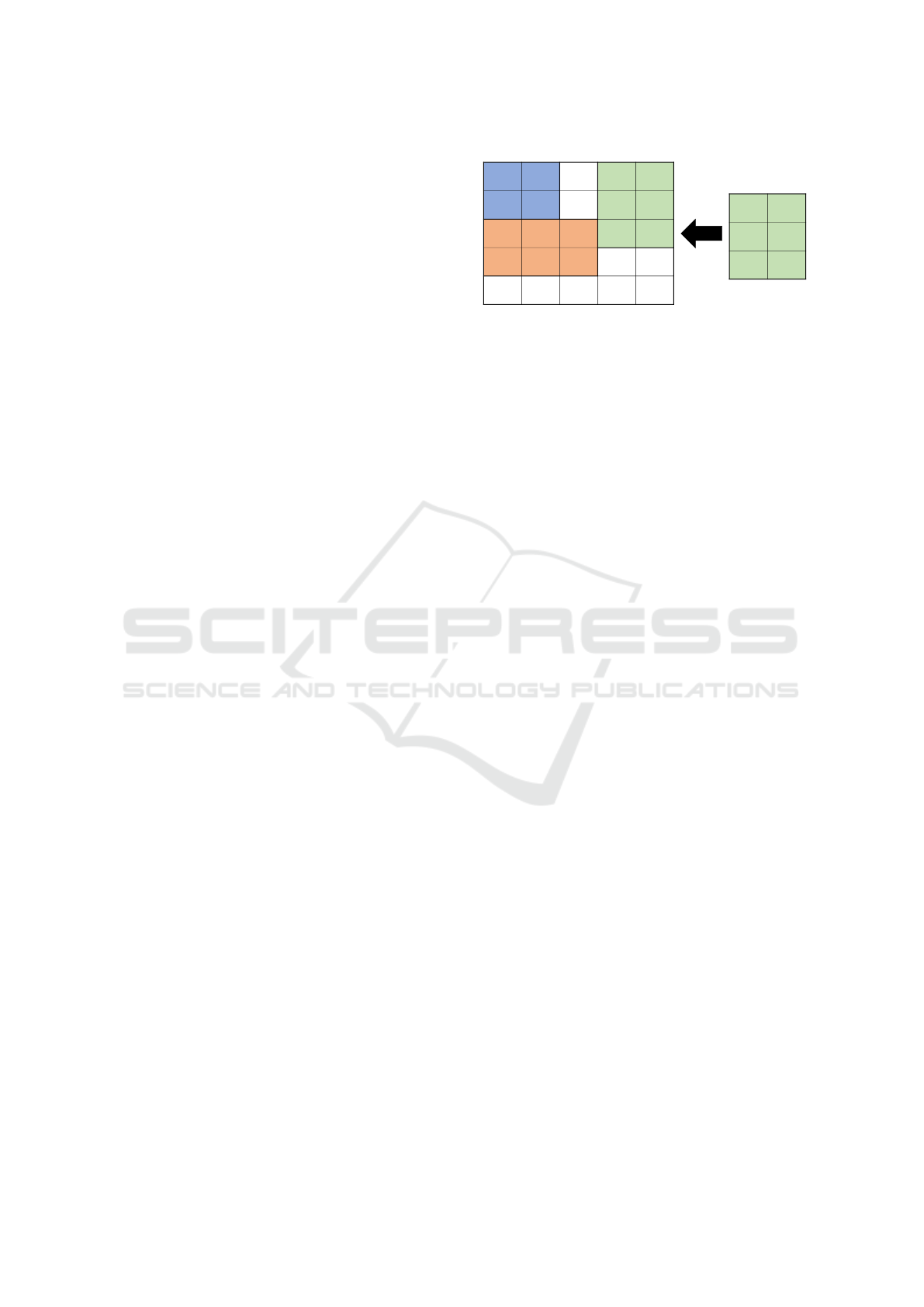
Figure 2: A 2*3 unit deployment on a 5*5 site.

• val(u

): evaluation value of u

• w: combination rate

The system assumes the following constraints.

1. Each functional space of the facility is modeled as

a unit.

2. All of the units are represented as rectangles. The

agent creates one-ﬂoor layout, not multi-ﬂoor lay-

out.

3. The state of the site is represented as shown in

Fig. 2. Deployed areas are represented by a

number that identiﬁes the deployed unit, and non-

deployed areas are represented by 0. Fig. 2 rep-

resent an example of a 2*3 unit deployment on a

5*5 site. Areas where Unit 3 (green unit) is de-

ployed will be changed from 0 to 3.

4. Units can be deployed with a 90-degree-rotated.

5. The relation relation

is expressed in the form

(u1

, u2

, intensity

) and is given in advance

when creating the layout.

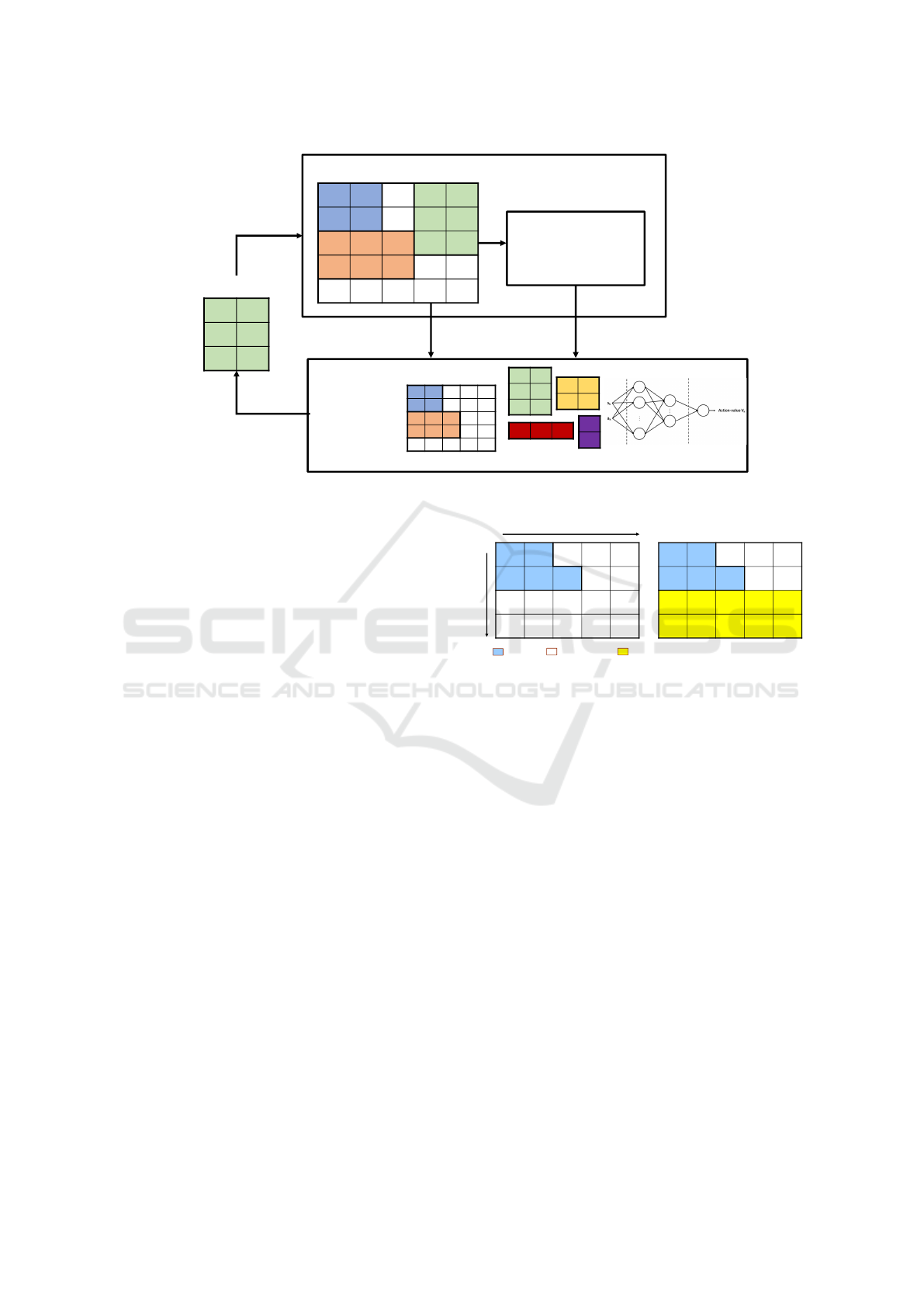
3.1 Learning Environment

The learning environment provides the necessary

learning situations to the agent. Learning environ-

ment for the agent is represented in Fig. 3. The learn-

ing agent includes the following elements:

• state: situation which the agent is located.

• action: what the agent does in a state.

• action-value function: a function that represents

the value of actions in the current state.

• reward: value obtained by an action of the agent.

• return: sum of rewards that can be earned in the

future.

• policy: guidelines for choosing actions.

States are represented by the deployment of the units

on the site, and a site with length n and width m is

represented by a grid with n ∗ m positions. Actions

are represented by units to be deployed. In DQN,

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

224

1 1 0 0→3 0→3

2 2 2 0→3 0→3

2 2 2 0 0

0 0 0 0 0

Selected action

3 3

Learning environment

1 1 0 0 0

2 2 2 0 0

0 0 0 0 0

State

Reward and return

calculation

return

= r

k+1

+ γ ∗ return

k+1

New state

Return

Agent

3 3

4 4

5 5 5

Non-deployed unit

Action-value function

ε-greedy method

Policy

Figure 3: Learning environment and agent in the proposed system.

Action-value function is approximated by the CNN.

The CNN consists of an input layer with two inputs,

an output layer with one output, and two hidden lay-

ers. The two inputs are state and action, and the

output is the action-value. Eight 5*5 size convolu-

tional ﬁlters are prepared, and the rectiﬁed linear unit

(ReLU) function, which simply computes the func-

tion: f(x) = max(0, x), is used as activation function.

In general, the more hidden layers increase, the more

complex the analysis is. In our system, the number of

nodes in the ﬁrst hidden layer is 512 and in the second

hidden layer is 256.

The action-value is updated using the return com-

puted by the formula 1.

return

= r

k+1

+ γ ∗ return

k+1

(1)

γ is a discount factor which means a parameter that

express the inﬂuence on the return in future state. Re-

wards is determined according to the total size of de-

ployed units. If a 2*3 unit is deployed, 6 is given

as a reward. ε-greedy method (Yang et al., 2021) is

used as unit selection policy. In the ε-greedy method,

the agent selects a random unit with a probability of

ε, which is called exploration, and selects a unit with

the highest action-value with a probability of 1 - ε,

which is called exploitation. The ε-greedy method

can choose unlearned actions in exploration that will

never choose in exploitation.

Unlike Go (Silver et al., 2016) or Shogi (Gold-

waser and Thielscher, 2018), it is difﬁcult to deter-

mine the deployment of units on a site because there

are various sizes of units. We use a starting point to

solve this problem. The starting point is set according

(0,0)

: deployed : non-deployed : maximum rectangle

(0,0)

(0,2)

Starting

Point

Starting point

• The agent searches the site and defines the next

starting point as the point that forms the maximum

rectangle with no units located

Figure 4: The start point decision in the present site.

to the current states, and the units are deployed based

on the starting point. The agent searches the site and

deﬁnes the next starting point as the point that forms

the largest rectangle with no units located. The ﬁrst

starting point is set to the origin (0, 0). Fig. 4 shows

an example of the starting point change. The blue area

is already deployed, and the white area is empty. In

Fig. 4 the point (0, 2) is chosen as the next starting

point because the largest rectangle 2*5 can be formed

starting from the point (0, 2).

The following evaluation function P

sum

calculates

distance-intensity in the created layout.

sum

= Σ

k=1

intensity

∗ d

(2)

intensity

is the intensity of relation

between u1

and u2

. d

is the Manhattan distance between u1

and u2

. Minimizing the evaluation function optimize

the unit deployment in considering relations.

3.2 Learning Mechanism

In this section, we explain the learning procedure of

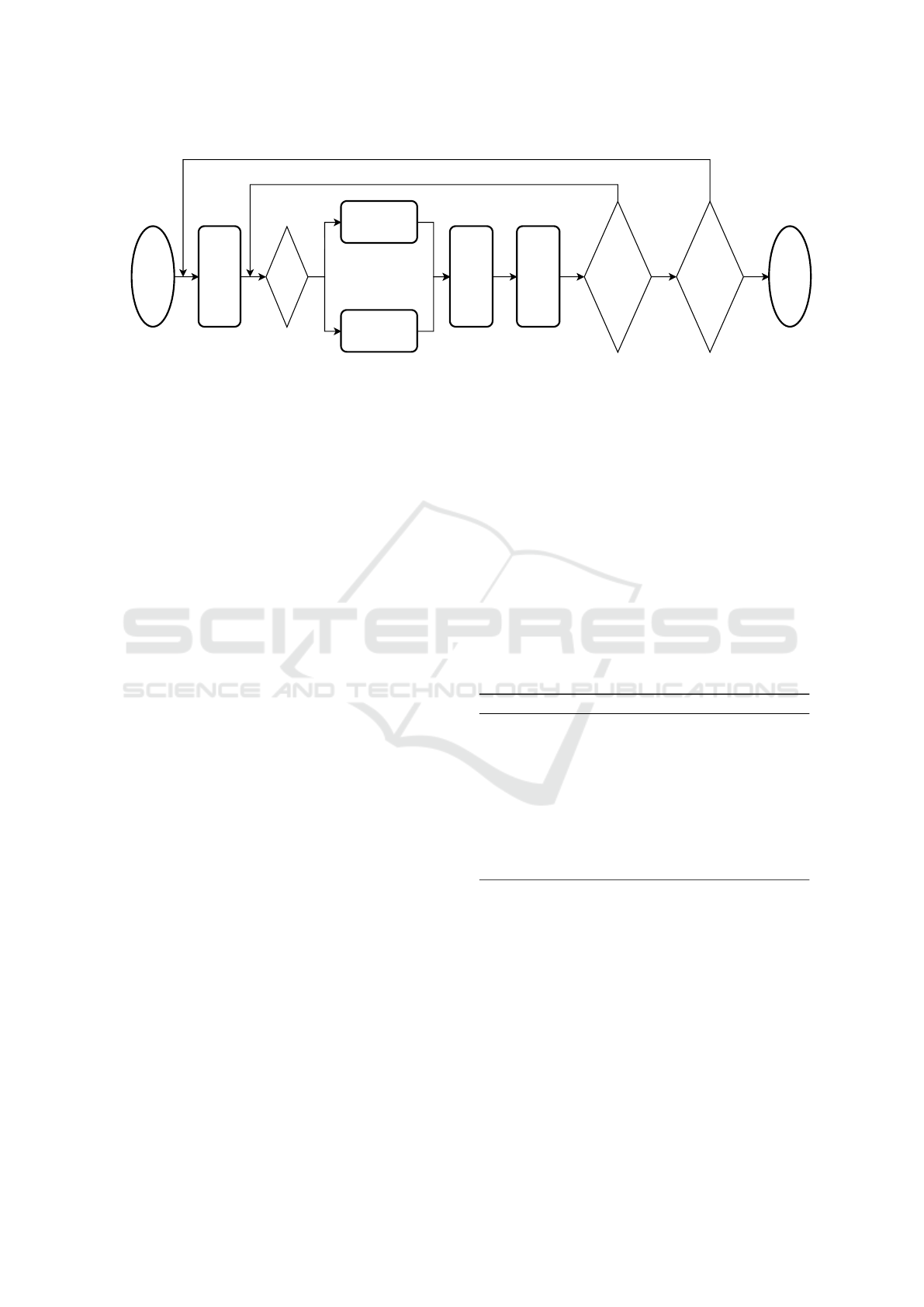
the proposed system. Fig. 5 shows the ﬂow of a learn-

Automatic Facility Layout Design System Using Deep Reinforcement Learning

225

Start

Generate

units for

learning

Yes

N<=ε

Exploration

Exploitation

Deploy

the

selected

unit

Update

the CNN

using the

gained

reward

Yes

Did the

agent try to

deploy

all units?

Yes

Did the

agent repeat

a specified

number of

trials?

End

Figure 5: Flow of a learning episode.

ing episode. First, the agent generates a set of units.

The agent then chooses a unit to be deployed from

the set using ε-greedy method. The agent generates a

random number N and selects exploration or exploita-

tion according to the threshold ε. When exploration is

selected, the agent selects a unit randomly. When ex-

ploitation is selected, the agent selects a unit with the

highest action-value. Third, the agent deploys the unit

based on the present starting point, and changes the

staring point according to the new state. Finally, the

agent updates the action-value function correspond-

ing to the current state and the chosen action using

the gained reward. The agent continues this proce-

dure until all of the units are tried to be deployed.

3.3 Layout Creation Mechanism

In this section, we explain the layout creation proce-

dure of the proposed system. Fig.6 shows the ﬂow of

a layout creation. First, the agent generates an AHP

evaluator for each non-deployed unit. The AHP eval-

uator corresponds to the function of evaluating each

alternative in AHP. In the proposed system, the AHP

evaluator is generated to determine the deployment

priority of unit regarding the relation among units.

The AHP structure in the system is shown in Fig. 7.

The AHP is hierarchized into goals, evaluation crite-

ria, and alternatives. The goal is to ﬁnd the unit that

has the strongest relation to deployed units. The eval-

uation criterion is the sum of distance-intensity ob-

tained when that unit is deployed. The alternative is

the non-deployed unit. Algorithm 1 generates an AHP

evaluator called AHP

eva

for ﬁnding the most suitable

unit to be deployed at the current state. N is the num-

ber of relations and U is the number of units. First, the

agent calculates for relation

(u1

, u2

, intensity

) be-

tween the deployed unit u1

and a non-deployed unit

. The agent evaluates the deployment of u2

at the

current starting point by the formula listed in line 3 of

Algorithm 1. The evaluation is realized by calculating

the sum of the product of the Manhattan distance be-

tween u1

and u2

, denoted as d

, and the intensity of

the relation between them, donated as intensity

. The

value of AHP

eva

(u2

), which is the sum of evaluation

of u2

, calculated according to the formula listed in

line 7 of Algorithm 1.

The agent combines the evaluation of learning re-

sult and the evaluation of the AHP evaluator in ra-

tio of w to 1 - w. The unit with the highest evalua-

tion is selected, and deployed on the current starting

point. The agent continues this procedure until all of

the units are deployed. By following the above proce-

dure, the agent created a layout that fulﬁlls the given

site. The layout reﬂects the learning result and the

relations among units.

Algorithm 1: Generate the AHP evaluator.

1: for i = 0 to N − 1 do

2: if relation

is the relation between deployed

unit u1

and non-deployed unit u2

then

3: val(u2

)+ = intensity

∗ d

4: end if

5: end for

6: for k = 0 to U − 1 do

7: AHP

eva

) =

∑

U−1

j=0

val(u

)/val(u

)

8: end for

4 EXPERIMENT

We conducted an experiment to demonstrate the ef-

fectiveness of developed system for solving FLP. We

applied two systems to the sets of units and relations

in the benchmark problems (D.Meller and A.Bozer,

1997) and compared the results:

• DQN

• Q-leaning

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

226

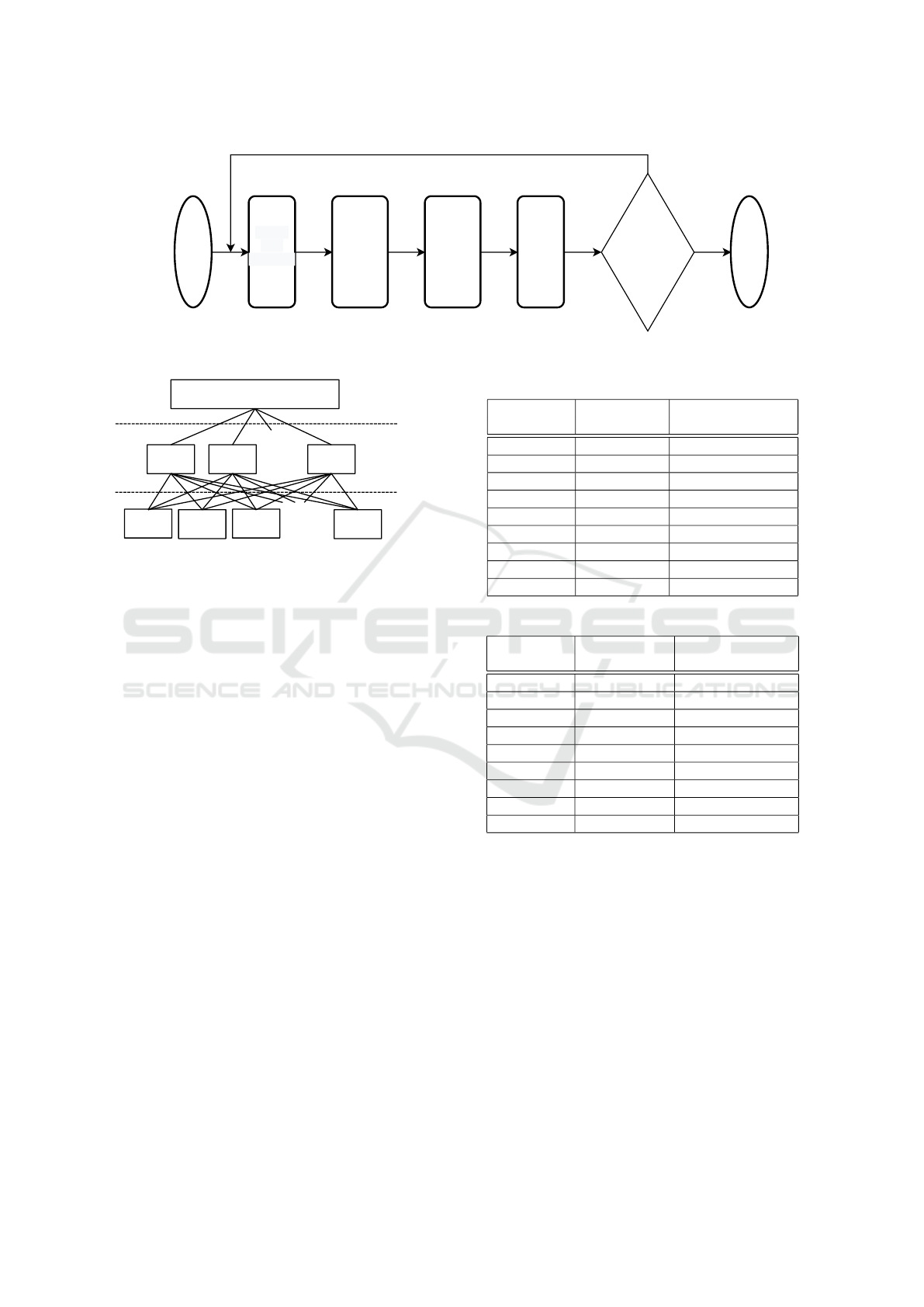
Start

Create

AHP

evaluator

Combine

AHP

evaluator

and

action-

value

function

Select

units using

combined

values

Deploy

the unit

Yes

Did the

agent try to

deploy

all units?

End

Figure 6: Flow of one layout creation.

Finding a unit that has the strongest

relation to other non-deployed units

Relation

Unit 2 Unit K

・・・

Unit 3Unit 1

・・・

Goal

Evaluation

criteria

Alternatives

Figure 7: AHP structure of the system.

The system using Q-leaning is mechanism in our pre-

vious study based system that uses Q-leaning method

(WATKINS and DAYAN, 1992) instead of Monte

Carlo method. Russell and Yavuz’s study (D.Meller

and A.Bozer, 1997) illustrates layouts that deploy

units using a space-ﬁlling curve (R.Butz, 1969). The

space-ﬁlling curve describes plane spaces based on

the trajectory of an individual curve. For this exper-

iment, we used python 3.9 and tensorﬂow 2.10. The

variables ε used in the ε-greedy method and the dis-

count factor γ used in the learning value calculation

are ε = 0.9 and γ = 0.9, respectively.

The result of layout creation of each method is

shown in Figures 8 and 9. Table 1 shows the values of

the evaluation function P

um for each layout. In Fig.

9 and 8, units of the same color in a layout represent

that they are strongly related to each other. Both sys-

tem create layouts that fulﬁll the site with a given set

of units.

To compare the learning systems of DQN and

RL in another method, we measured the success rate

when the order of set of units is changed. Layout cre-

ation was performed in 100 different orders of units.

Fig. 10 and Table 2 shows the number of trials layouts

that fulﬁll the site were created.

Table 1: The values of the evaluation function.

combination P

sum

of P

sum

rate w DQN method Q-Learning method

0.1 165,415.0 199,616.0

0.2 156,648.0 201,721.5

0.3 152,243.5 191,852.0

0.4 149,327.0 190,114.5

0.5 146,259.5 188,282.5

0.6 150,178.5 183,905.0

0.7 142,791.5 185,510.5

0.8 144,332.0 180,138.0

0.9 139,525.0 175,487.5

Table 2: Success rate in each combination rate.

combination success rate of success rate of

rate w DQN method Q-learning method

0.1 0.34 0.21

0.2 0.34 0.24

0.3 0.32 0.17

0.4 0.27 0.17

0.5 0.31 0.16

0.6 0.26 0.13

0.7 0.25 0.16

0.8 0.22 0.14

0.9 0.21 0.14

5 DISCUSSION

In Table 1, the Psum value of developed system is

smaller than the system using Q-leaning. This result

shows that DQN improved performance in consider-

ing the relations among the units. The agent can set

the unit deployment of the site to state by approx-

imating the action-value function by the CNN. The

learning results with CNN presume to be able to se-

lect units that are more suited to the situation than Q-

leaning. At the same time, Fig. 10 shows that the

um values decrease as w is increased. As the Psum

value is smaller, relations among units are better con-

sidered in the layout. Accordingly, the experimental

Automatic Facility Layout Design System Using Deep Reinforcement Learning

227

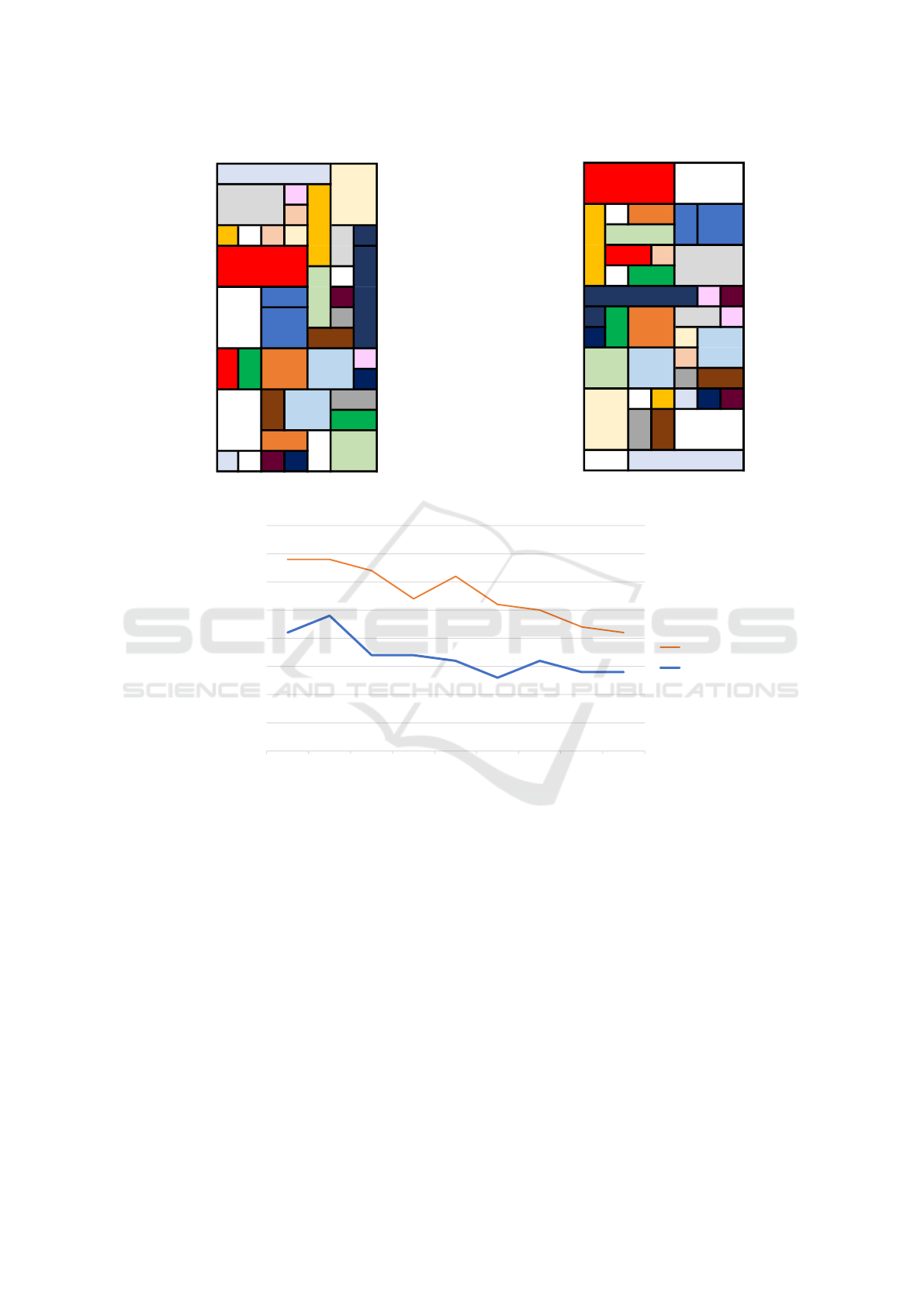
22 22 22 22 22 23 23

24 24 24 37 6 23 23

24 24 24 38 6 23 23

12 36 39 35 6 7 20

40 40 40 40 6 7 21

40 40 40 40 25 9 21

29 29 3 3 25 34 21

29 29 2 2 25 8 21

29 29 2 2 16 16 21

26 11 13 13 18 18 32

26 11 13 13 18 18 31

1 1 17 19 19 14 14

1 1 17 19 19 4 4

1 1 10 10 28 27 27

15 5 33 30 28 27 27

Figure 8: Created layout using QL method.

40 40 40 40 1 1 1

6 9 10 10 3 2 2

6 25 25 25 3 2 2

6 26 26 38 24 24 24

6 36 11 11 24 24 24

21 21 21 21 21 32 33

20 4 13 13 7 7 37

31 4 13 13 35 19 19

27 27 18 18 39 19 19

27 27 18 18 8 16 16

23 23 5 12 15 30 34

23 23 14 17 29 29 29

28 28 22 22 22 22 22

Figure 9: Created layout using DQN method.

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

The success rate of creating layouts

that fulfill the site.

Combination ratio w

DQN

Q-learning

Figure 10: Success rate in each combination rate.

results indicate that AHP is effective for considering

the relations among units in the layout.

In Russell and Yavuz’s (D.Meller and A.Bozer,

1997) study, users cannot specify the shape of the unit

because the agent assigns and deploys the location of

the unit on the site using the value of the unit. On the

other hand, our developed system can deploys units

using their shape speciﬁed by the user.

A comparison of the two graphs in Fig. 10 and

table 2 shows that DQN improves the success rate of

layout at all combination rates. This result may be at-

tributed to the high expressive power of CNN, which

can express action-values more relevant to the agent’s

states and actions.

On the other hand, some limitations exist in this

study. First, we only tried to apply our developed sys-

tem to the sets of units and relations in the benchmark

problems. Therefore, our developed system may not

create layouts in larger and more complicated condi-

tions, such as a real factory. We need to develop a

system that can adapt to multi-ﬂoored sites and much

larger sites. Second, the developed system cannot

create a layout under a layout environment using the

agent trained under the another environment. We have

to change the agent’s state and CNN settings to adapt

to different layout environments from learning one.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

228

6 CONCLUSION

In this study, layout design system that can design lay-

outs for various units and sites using DQN and AHP

is developed. Experimental results conﬁrmed that the

system is able to create a layout that can consider the

relations among units better than the Q-learning based

system. In addition, the result of the success rate of

layout by changing the unit order shows that DQN im-

proves at all combination rates comparing with RL.

Consequently, the experiment shows that the facil-

ity layout is improved by the adaptability of DQN.

In the future, we will solve some challenges of sys-

tems. First, we will expand the scope of application of

the system to improve the performance like generat-

ing the layout at the multi-ﬂoor site. Second, we will

measure the parameter conﬁguration of the CNN and

the structure of the AHP evaluator that are adopted

to the learning. Finally, we will make the developed

system able to create layouts under a layout condition

using the agent trained under another condition. We

would like to focus on these problems in future stud-

ies.

ACKNOWLEDGEMENTS

Kajima Corporation supported this work. We would

like to thank Hiromasa Akagi and Fumi Sekimoto,

who work with Kajima Corporation, for helpful dis-

cussions.

REFERENCES

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and

Bharath, A. A. (2017). A brief survey of deep rein-

forcement learning. In IEEE Signal Processing Mag-

azine, pages 1–4.

Bai, L., Qu, P., and Wang, Y. (2009). Optimal model

of agile supply chain based on fuzzy ahp genetic

algorithm. In Scientiﬁc research, pages 278–280.

978-1-935068-01-3.

Burggraf, P., Wagner, J., and Heinbach, B. (2021). Biblio-

metric study on the use of machine learning as resolu-

tion technique for facility layout problems. pages 1–7.

10.1109/ACCESS.2021.3054563.

Chaillou, S. (2019). Ai and architecture an experimental

perspective. In The Routledge Companion to Artiﬁ-

cial Intelligence in Architecture, pages 1–22. hISBN:

9780367824259.

Chen, G., Cai, Q., Fu, X., and Lai, Y. (2020). Research

on algorithms of computing ofﬂoading and resource

allocation based on dqn. In Journal of Physics: Con-

ference Series, pages 1–7. 10.1088/1742-6596/1748/

3/032047.

Di, X. and Yu, P. (2021). Multi-agent reinforcement learn-

ing of 3d furniture layout simulation in indoor graph-

ics scenes. pages 1–6. https://doi.org/10.48550/arXiv.

2102.09137.

Di, X., Yu, P., Company, I., and Research, I. (2021). Deep

reinforcement learning for producing furniture lay-

out in indoor scenes. pages 1–10. https://doi.org/10.

48550/arXiv.2101.07462.

Dixit, V. and Lawlor, J. (2019). Modiﬁed genetic algo-

rithm for automated facility layout design. In Inter-

national Journal of Advance Research, pages 1803–

1807. ISSN:2454-132X.

D.Meller, R. and A.Bozer, Y. (1997). Alternative ap-

proaches to solve the multi-ﬂoor facility layout prob-

lem. In Journal of Manufacturing Systems, pages

192–195. https://doi.org/10.1016/S0278-6125(97)

88887-5.

Espejo, P. G., Ventura, S., and Herrera, F. (2010). A survey

on the application of genetic programming to classiﬁ-

cation. In IEEE Transactions on Systems, Man, and

Cybernetics, Part C (Applications and Reviews, pages

1212–134. 10.1109/TSMCC.2009.2033566.

fa, J. and JunLiu, L. (2019). Applying multi-objective ant

colony optimization algorithm for solving the unequal

area facility layout problems. In Applied Soft Com-

puting, pages 167, 168. https://doi.org/10.1016/j.asoc.

2018.10.012.

Goldwaser, A. and Thielscher, M. (2018). Deep rein-

forcement learning for general game playing. In The

Thirty-Fourth AAAI Conference on Artiﬁcial Intelli-

gence (AAAI-20), pages 1701–1708. https://doi.org/

10.1609/aaai.v34i02.5533.

Gonc¸alvesa, J. F. and G.C.Resende, M. (2015). A biased

random-key genetic algorithm for the unequal area fa-

cility layout problem. In European Journal of Op-

erational Research, pages 86–90. https://doi.org/10.

1016/j.ejor.2015.04.029.

Hu, R., Xu, J., Chen, B., Gong, M., Zhang, H., and Huang,

H. (2020). Tap-net: Transport-and-pack using rein-

forcement learning. pages 1–8. https://doi.org/10.

1145/3414685.3417796.

Ikeda, H., Nakagawa, H., and Tsuchiya, T. (2022). Towards

automatic facility layout design using reinforcement

learning. In Fedscis 2022, pages 1–10.

Izadinia, N., Eshghi, K., and Salmani, M. H. (2014). A ro-

bust model for multi-ﬂoor layout problem. In Com-

puters and Industrial Engineering, pages 127–134.

http://dx.doi.org/10.1016/j.cie.2014.09.023.

Kaelbling, L., Littman, M., and Moore, A. (1996). Rein-

forcement learning: A survey. In JAIR, pages 237–

241. https://doi.org/10.1613/jair.301.

Klar, M., Glatt, M., and Aurich, J. C. (2021). An imple-

mentation of a reinforcement learning based algorithm

for factory layout planning. In Manufacturing Letters,

pages 1–4. https://doi.org/10.1016/j.mfglet.2021.08.

Kusiak, A. and S.Heragu, S. (1987). The facility layout

problem. In European Journal of Operational Re-

search 29, pages 229–230. https://doi.org/10.1016/

0377-2217(87)90238-4.

Automatic Facility Layout Design System Using Deep Reinforcement Learning

229

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. In Nature 521, pages 436–444.

Lee, S., Seon, J., Kyeong, C., Kim, S., Sun, Y., and Kim, J.

(2021). Novel energy trading system based on deep-

reinforcement learning in microgrids. In Energies,

pages 1–14. https://doi.org/10.3390/en14175515.

Lima, E., Gorski, E., Loures, E. F. R., Santos, E. A. P.,

and Deschamps, F. (2019). Applying machine learn-

ing to ahp multicriteria decision making method to as-

sets prioritization in the context of industrial mainte-

nance 4.0. In IFAC Papers On Line, pages 2152–2157.

https://doi.org/10.1016/j.ifacol.2019.11.524.

Liu, Y.-J., Cheng, S.-M., and Hsueh, Y.-L. (2017). enb se-

lection for machine type communications using rein-

forcement learning based markov decision process. In

eNB Selection for Machine Type Communications Us-

ing Reinforcement Learning Based Markov Decision

Process, pages 11330–11338.

opez, C. E., Cunningham, J., Ashour, O., and Tucker, C. S.

(2020). Deep reinforcement learning for procedural

content generation of 3d virtual environments. In J.

Comput. Inf. Sci. Eng., pages 1–9. https://doi.org/10.

1115/1.4046293.

Mirhoseini, A., Goldie, A., Yazgan, M., Jiang, J. W.,

Songhori, E., Wang, S., Lee, Y.-J., Johnson, E.,

Pathak, O., Nazi, A., Pak, J., Tong, A., Srinivasa, K.,

Hang, W., Tuncer, E., Le, Q. V., Laudon, J., Ho, R.,

Carpenter, R., and Dean, J. (2021). A graph place-

ment methodology for fast chip design. pages 207–

212. https://doi.org/10.1038/s41586-021-03544-w.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-

ness, J., Bellemare, M. G., Graves, A., Riedmiller,

M., Fidjeland, A. K., Ostrovski, G., Petersen, S.,

Beattie, C., Sadik, A., Antonoglou, I., King, H., Ku-

maran, D., Wierstra, D., Legg, S., and Hassabis, D.

(2015). Human-level control through deep reinforce-

ment learning. In Nature volume 518, pages 529–533.

R.Butz, A. (1969). Convergence with hilbert’s space ﬁll-

ing curve. In Journal of Computer and System

Sciences, pages 128–131. https://doi.org/10.1016/

S0022-0000(69)80010-3.

Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,

van den Driessche, G., Schrittwieser, J., Antonoglou,

I., Panneershelvam, V., Lanctot, M., Dieleman, S.,

Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I.,

Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel,

T., and Hassabis, D. (2016). Mastering the game of

go with deep neural networks and tree search. In Na-

ture volume 529, pages 484–489.

S.P.Singh and R.R.K.Sharma (2006). A review of differ-

ent approaches to the facility layout problems. In

The International Journal of Advanced Manufactur-

ing Technology, page 425. https://doi.org/10.1007/

s00170-005-0087-9.

Tam, K. Y. (1992). Genetic algorithms, function optimiza-

tion, and facility layout design. In European Jour-

nal of Operational Research, pages 322–330. https:

//doi.org/10.1016/0377-2217(92)90034-7.

Thengade, A. and Dondal, R. (2012). Genetic algorithm

– survey paper. In MPGI National Multi Conference

2012, pages 25–29. ISSN:0975-8887.

Vargas-Pardo, L. F. and Giraldo-Ramos, F. N. (2021). Fire-

ﬂy algorithm for facility layout problemoptimization.

In Visi

on electr

onica, pages 33–38. https://doi.org/10.

14483/issn.2248-4728.

Verma, R., Saikia, S., Khadilkar, H., Agarwal, P., Shrof,

G., and Srinivasan, A. (2019). A reinforcement learn-

ing framework for container selection and ship load

sequencing in ports. In AAMAS, pages 2250–2252.

Wang, J. and Wang, L. (2020). Mobile edge comput-

ing task distribution and ofﬂoading algorithm based

on deep reinforcement learning in internet of vehi-

cles. In Journal of Ambient Intelligence and Human-

ized Computing, pages 1–7. https://doi.org/10.1007/

s12652-021-03458-5.

Wang, K., Ding, L., Dailami, F., and Matthews, J.

(2022). Ga-ahp method to support robotic polishing

process planning. In Digital Manufacturing Tech-

nology, pages 23–31. http://doi.org/10.37256/dmt.

2220221513.

WATKINS, C. J. and DAYAN, P. (1992). Q-learning. In

Machine Learning, pages 279–292. https://doi.org/10.

1007/BF00992698.

Yamashita, R., Nishio, M., Do, R. K. G., and Togashi,

K. (2018). Convolutional neural networks: an

overview and application in radiology. In Insights

Imaging 9, pages 611–620. https://doi.org/10.1007/

s13244-018-0639-9.

Yang, T., Zhang, S., and Li, C. (2021). A multi-objective

hyper-heuristic algorithm based on adaptive epsilon-

greedy selection. In Complex Intell. Syst., pages 765–

767. https://doi.org/10.1007/s40747-020-00230-8.

Youseﬁ, H., Ghodusinejad, M. H., and Noorollahi, Y.

(2021). Ga/ahp-based optimal design of a hybrid

cchp system considering economy, energy and emis-

sion. In Manufacturing Letters, pages 309–313. https:

//doi.org/10.1016/j.enbuild.2016.12.048.

Zeng, Y., Liu, W., Liu, Z., Zhang, J., and Niu, W.

(2010). Improved genetic algorithm and ana-

lytic hierarchy process for electric power equip-

ment maintenance schedule optimization. In Power

and Energy Engineering Conference, pages 491–495.

978-1-935068-17-4.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

230