Compressing UNSAT Search Trees with Caching
Anthony Blomme
a
, Daniel Le Berre
b
, Anne Parrain
c
and Olivier Roussel
d
Univ. Artois, CNRS, Centre de Recherche en Informatique de Lens (CRIL), F-62300 Lens, France
Keywords:
SAT, Explainable AI, Solver.
Abstract:
In order to provide users of SAT solvers with small, easily understandable proofs of unsatisfiability, we present
caching techniques to identify redundant subproofs and reduce the size of some UNSAT proof trees. In a search
tree, we prune branches corresponding to subformulas that were proved unsatisfiable earlier in the tree. To
do so, we use a cache inspired by model counters and we adapt it to the case of unsatisfiable formulas. The
implementation of this cache in a CDCL and a DPLL solver is discussed. This approach can drastically reduce
the UNSAT proof tree of several benchmarks from the SAT’02 and SAT’03 competitions.
1 INTRODUCTION
SAT solvers have been commonly used to solve NP-
complete problems since two decades, and thus have
become commonplace in many computing applica-
tions (Biere et al., 2021). As an AI application, SAT
solvers are now also expected to provide explanations.
When an instance is satisfiable, the model found can
be given as an explanation, and compressed by re-
ducing it to a prime implicant (D
´
eharbe et al., 2013).
When the instance is unsatisfiable, giving a good ex-
planation is harder as we have to show that no solu-
tion can be found. Some forms of explanation were
proposed to prove the unsatisfiability of a formula.
For example, we may consider giving to the user a
Minimal Unsatisfiable Subset (MUS) (Ignatiev et al.,
2015), which gives the origin of the unsatisfiability,
or a certificate of unsatisfiabiliy expressed in a partic-
ular format such as DRAT (Wetzler et al., 2014). The
latter registers the important steps of a solver and can
then be verified by an independent checker. However,
these techniques may be of limited interest to the user
because, in the first case, there is no guarantee that
a MUS is smaller than the complete formula and, in
the second case, a certificate can have an exponential
number of steps. In both cases, these kinds of proofs
cannot be easily understood by a user.
In our case, we only consider unsatisfiable for-
mulas and our goal is to significantly compress the
a
https://orcid.org/0000-0001-5395-1625
b
https://orcid.org/0000-0003-3221-9923
c
https://orcid.org/0000-0001-7115-8022
d
https://orcid.org/0000-0002-9394-3897
search tree of a solver in order to obtain a proof that
is small enough to be given as explanation to the user.
We shall focus on finding recurring patterns because
of their potentially huge impact on the tree size, and
also because they can be explained individually and
independently to the user. A cache can be used to rec-
ognize these patterns. If the current subformula was
already explored and proved unsatisfiable, the current
branch can be pruned. Our actual goal is to reduce the
size of the explanation, and we do not mind spending
much time for this task if in the end we can achieve a
good compression. Therefore we do not reject costly
techniques such as NP oracles, as long as they let us
reduce the proof size.
This paper is organized as follows. In Section 2,
we introduce fundamental notions. In Section 3, after
an example dedicated to the Pigeon Hole Principle
(PHP) problem, we discuss the integration of a cache
for unsatisfiable formulas into SAT solvers, consider-
ing two solver architectures. Then, we present some
experimental results in Section 4. Finally, we con-
clude and present some future works.
2 PRELIMINARIES
A Boolean variable v can be either true or false. A lit-
eral is either a variable v or its negation ¬v. A clause
is a disjunction (or a set) of literals and a formula in
Conjunctive Normal Form (CNF) is a conjunction (or
a set) of clauses. An assignment is a function from
a set of variables to the truth values 0 (for false) or 1
(for true). A clause is satisfied by an assignment if it
358
Blomme, A., Le Berre, D., Parrain, A. and Roussel, O.
Compressing UNSAT Search Trees with Caching.
DOI: 10.5220/0011671800003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 3, pages 358-365
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

contains at least one literal l which is assigned true.
A formula is satisfied by an assignment if and only
if all its clauses are satisfied. Deciding if there exists
an assignment that satisfies a given formula in CNF
is known as the satisfiability problem (SAT), which is
NP-complete (Cook, 1971). The formula is SAT if it
is possible to find such an assignment and it is UN-
SAT otherwise. Given an assignment I, F
|I
denotes
the formula simplified by I: satisfied clauses are re-
moved from the formula and falsified literals are re-
moved from the remaining clauses. Given an assign-
ment I, a unit clause is a clause c which contains only
one non falsified literal l, therefore l must be assigned
true. Clause c can then be considered as the reason
for the assignment of l and will be denoted reason(l).
Applying this operation until there remains no unit
clause is called unit propagation. Extending an as-
signment with a literal assignment without reason is
called a decision. A function DL(l) provides the level
at which the literal l has been decided or propagated.
SAT solvers are computer programs able to solve
the satisfiability problem. Early SAT solvers able to
prove unsatisfiability relied on the Davis Putnam Lo-
gemman Loveland (DPLL) architecture (Davis and
Putnam, 1960; Davis et al., 1962). Two decades ago, a
new architecture called Conflict Driven Clause Learn-
ing (CDCL) (Silva and Sakallah, 1999; Moskewicz
et al., 2001; E
´
en and S
¨
orensson, 2003) appeared and
made SAT solvers commodity software oracles for
solving NP-Complete problems (Biere et al., 2021).
SAT solvers explore a search tree, in which a path
from the root to the leaves is a partial assignment,
and leaves correspond to falsified clauses (so called
a conflict) when the formula is unsatisfiable. While
DPLL approaches explore a binary tree by branch-
ing on variables truth values, CDCL solvers use con-
flict analysis and clause learning to drive the search
(Marques-Silva et al., 2021).
3 REDUNDANCY IN SEARCH
Detecting common subtrees in a search tree is not
new: in model counters for instance (Thurley, 2006;
Sang et al., 2004), common subtrees are used to cache
already computed number of models. In this work, we
want to implement a similar idea, but targeting un-
satisfiable formulas. In this context, the cache will
contain proven UNSAT formulas, which we expect to
recognize during the search. An element of the cache
is called an entry. The time needed to perform the
compression is not important at this stage. We rather
investigate the compression capabilities.
3.1 Motivating Example
Pigeon Hole formulas are a classic unsatisfiable prob-
lem famous for being hard for solvers and for featur-
ing lots of symmetries (Haken, 1985). The problem
is to assign n + 1 pigeons to n holes with the con-
straints that a pigeon has to be associated with one
hole and a hole cannot contain more than one pigeon.
For this problem, we define the variables x
i,k
, with
i ∈ {1,... n + 1} and k ∈ {1,.. .n}, that state that pi-
geon i is assigned hole k. The first constraint can then
be encoded by using a clause of size n for each pi-
geon: C
1,n
=
V
1≤i≤n+1
(x
i,1
∨ ··· ∨ x
i,n
). For the sec-
ond one, we may create all the mutual exclusions be-
tween two different pigeons and for a specific hole:
C
2,n
=
V
1≤i< j≤n+1
V
1≤k≤n
(¬x
i,k
∨ ¬x
j,k
). With these
considerations, a PHP problem for a value n (PHP
n
)
is defined as PHP
n
= C
1,n
∧C
2,n
.
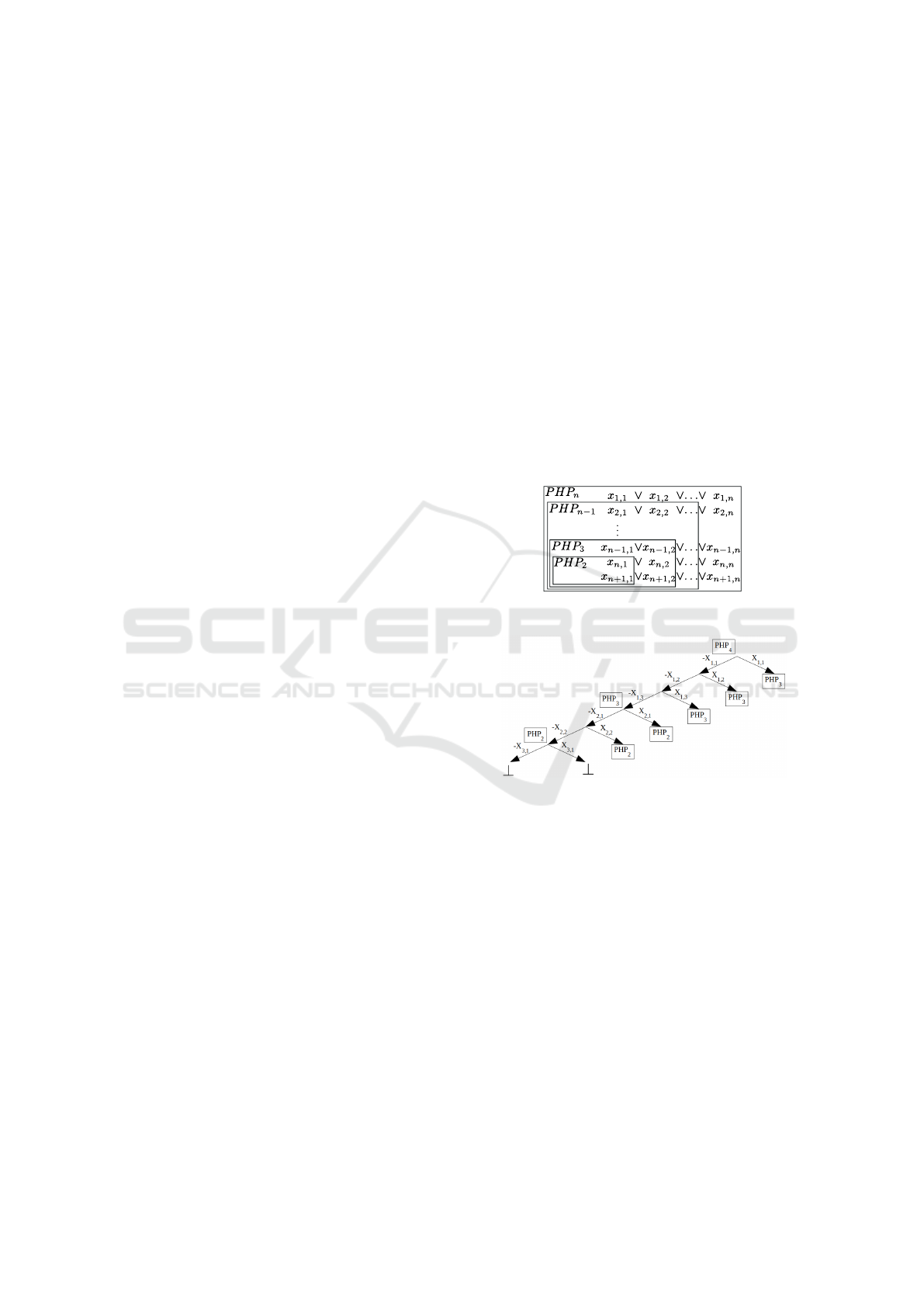
Figure 1: Pigeon Hole Principle problem of size n.
Figure 2: Expected single branch when solving the problem
PHP
4
. The propagations have been omitted.
When variable x
1,k
is assigned true and propa-
gated, we end up with a PHP problem of size n − 1.
This occurs when we explore the n ways to place the
first pigeon. Once the first PHP
n−1
subproblem has
been explored, it can be added to a cache and the n −1
other subproblems can be recognized. This method
can be repeated recursively until the problem PHP
2
is encountered. The latter only needs two branches, a
decision and its negation, to be fully explored. Figure
1 illustrates the imbricated PHP subproblems.
As an example, take the problem PHP
4
and a
heuristics that negatively decides the first unassigned
variable. This heuristics will start by assigning ¬x
1,1
,
¬x
1,2
and ¬x
1,3
. After these three decisions, the
clause x
1,1
∨ x
1,2
∨ x
1,3
∨ x
1,4
will propagate x
1,4
. This
last assignment will also propagate the literals ¬x
2,4
,
Compressing UNSAT Search Trees with Caching
359

¬x
3,4
, ¬x
4,4
and ¬x
5,4
. We have now to explore the
problem PHP
3
. The heuristics will now decide ¬x
2,1
and ¬x
2,2
and this will propagate x
2,3
thanks to the
clause x
2,1
∨ x
2,2
∨ x
2,3
∨ x
2,4
. This will also prop-
agate ¬x
3,3
, ¬x
4,3
and ¬x
5,3
. We end up now with
the problem PHP
2
. The latter will be fully explored
by deciding ¬x
3,1
and then by flipping this decision.
The two branches will lead to a conflict. As we have
proved the problem PHP
2
UNSAT, we can register it
in the cache. When we flip the decision ¬x
2,2
and then
¬x
2,1
, we will obtain each time a problem PHP
2
based
on different variables. By looking up the cache, we
know that we have already explored the same prob-
lem up to a renaming of variables and we can di-
rectly conclude that these two branches are unsatisfi-
able. We can now store the problem PHP
3
and a simi-
lar behaviour will happen when flipping the decisions
¬x
1,3
, ¬x
1,2
and ¬x
1,1
. After that, the search will fin-
ish and the instance will be considered unsatisfiable.
Figure 2 shows the tree obtained with this method. It
can be noticed that it contains a single branch with all
decisions. In the end, we have 5 isomorphism detec-
tions for a total of 7 branches in the search tree.
With this method, it is possible to have a total of
∑
n−1
y=2
y = ((n − 2)(n + 1))/2 isomorphism detections
for PHP
n
. Counting the two branches of PHP
2
, we
have a total of (((n − 2)(n +1))/2) + 2 branches.
3.2 Caching for UNSAT
To generalize the result on the PHP problem, we need
to find a way to detect that a given subformula was
already found in the search tree. Model counters
(Gomes et al., 2021) use such feature to avoid com-
puting again the number of models of a subformula
(including the UNSAT case, for which the number of
models is 0). To do so, they use a normalized rep-
resentation of the subformula. The one implemented
in the model counter Cachet (Sang et al., 2004) en-
sures that two subformulas with the same clauses can
be considered identical even if the clauses are not in
the same order or if they do not have the same index.
However, this technique is not going to work on our
PHP example. Indeed, in that case, the subformulas
are not identical, they are based on different variables.
So we need to support the notion of equality modulo
a renaming. There is also a specific issue related to
caching UNSAT formulas: a formula is UNSAT if it
contains an UNSAT subformula. So we are not just
looking for identical formulas, but also for formulas
subsumed by one entry in the cache. In that context,
the cache can no longer be implemented by a map.
We have to check sequentially all the entries which
have at least as many clauses of each size as the con-
sidered formula. Both features (inclusion and renam-
ing) can be implemented by solving an NP-complete
Subgraph Isomorphism problem when querying our
cache. To do so, formulas are encoded as graphs in
a classical way: literals are mapped to nodes of the
same color, and clauses are mapped to nodes with a
color corresponding to their size. An edge connects
opposite literals and a clause is connected to each of
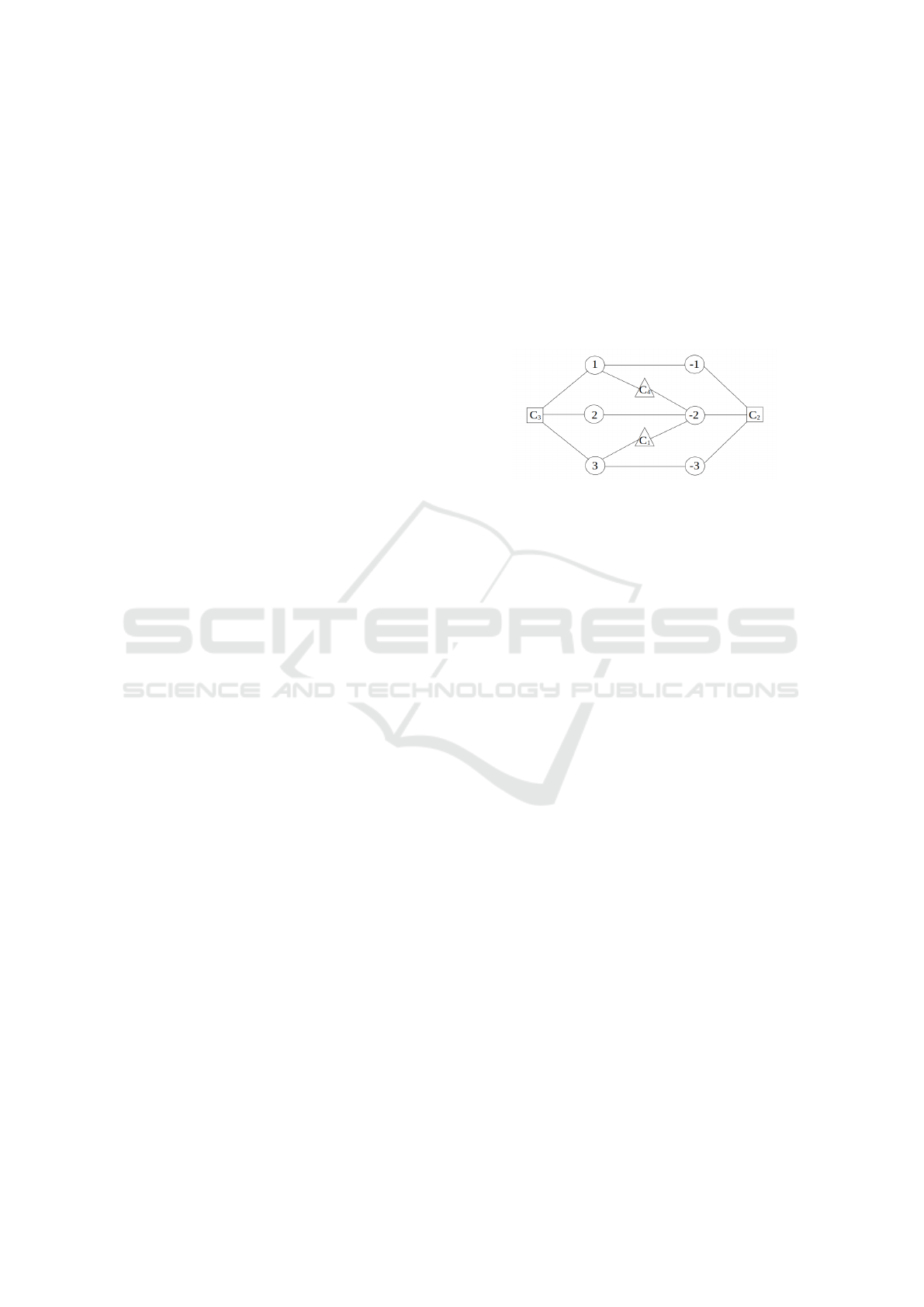
its literals. Figure 3 shows an example of this graph
representation. Each color is represented here by a
different shape.
Figure 3: Graph corresponding to F = (¬x
2
∨x
3
)∧(¬x
3
∨
¬x
2
∨ ¬x
1
) ∧ (x
1
∨ x
2
∨ x
3
) ∧ (x
1
∨ ¬x
2
). Literals are shown
as circles, binary/ternary clauses as triangles/squares.
3.3 Sources of Inconsistency
A node of the search tree is identified by the interpre-
tation I of variables that lead to that node. When the
subformula F
|I
obtained at a node is inconsistent, our
goal is to record it in the cache. But obviously, we do
not want to store the whole subformula in the cache,
but only a hopefully small subset of F
|I
which is in-
consistent. In other words, we want to record an un-
satisfiable subset of F
|I
, but not necessarily a minimal
one (MUS) because this would be too costly. Modern
SAT solvers are able to provide one source of unsatis-
fiability of a formula F when it is UNSAT (a so called
UNSAT core (Zhang and Malik, 2003)). However,
such a core is generally given at the end of search
and it corresponds to the complete formula. In con-
trast, we must generate an unsatisfiable core locally
for any node of the tree such that F
|I
is unsatisfiable.
To obtain this unsatisfiable subset, we need to collect
the clauses that were identified as conflicts or used
in the propagation leading to these conflicts. In the
rest of the paper, we shall call sources of an unsatis-
fiable subformula F
|I
the initial clauses of F used by
the solver to prove the unsatisfiability of F
|I
. This set
will be denoted S(F, I). These sources are easily ob-
tained in the solver by gathering recursively the rea-
son of each propagation leading to the conflicts. This
process is in essence the same as conflict analysis in
a CDCL solver, except that no resolution step is per-
formed. One important point is that the sources may
only contain clauses of the initial formula. In a CDCL
solver, if a learned clause appears in the sources, it is
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
360

replaced by the set of initial clauses that generated it.
Formally, sources can be defined as follows.
Definition 1. We first define the source of a clause
S(C). When C is an initial clause, S(C) = {C}. When
L is a learned clause, S(L) is the set of initial clauses
of F that appear in the derivation of L by resolution.
Let F
|I
be an unsatisfiable subformula and let
{I
1
,.. .I
m
} be the set of branches developped by the
solver to prove this inconsistency. Each F
|I
j
con-
tains a conflict C
j
. We define S
0
(F,I
j
) = {C
j
}
and S
i+1
(F,I
j
) = S
i
(F,I
j
) ∪ {S(reason(l))|l ∈ c ∧ c ∈
S
i
(F,I
j
) ∧ DL(l) ≥ DL(I
j
)}. This sequence has a
least fixed-point denoted S(F,I
j
). At last, the sources
S(F, I) of F
|I
are defined as S(F,I) = ∪
j
S(F, I
j
).
By construction, S(F,I)
|I
is unsatisfiable because
it contains all the initial clauses used by the solver
to prove the inconsistency of F
|I
. We also have
S(F, I)
|I
⊆ F
|I
. Therefore S(F,I)
|I
is an unsatisfiable
core of F
|I
. In a DPLL-like solver, S(F, I) can be ob-
tained by collecting the sources of the two children
nodes S(F, I ∪ {l}) and S(F,I ∪ {¬l}) and adding the
clauses that propagated from l a literal that appears in
the sources of the children nodes. This point will be
discussed in section 3.5. In a CDCL solver, sources
are obtained by collecting all clauses used in con-
flict analysis, and replacing each learned clauses by
its sources (i.e. the clauses collected at the conflict
that generated this learned clause).
3.4 CDCL Case
CDCL architecture is currently the state-of-the-art
approach for practical SAT solving (Marques-Silva
et al., 2021). It thus makes sense to implement the
cache on that architecture. However, this raises sev-
eral issues. CDCL solvers explore the search space in
a non chronological way, since each time it learns a
new clause, the solver backtracks to the decision level
which propagates a literal thanks to that clause. The
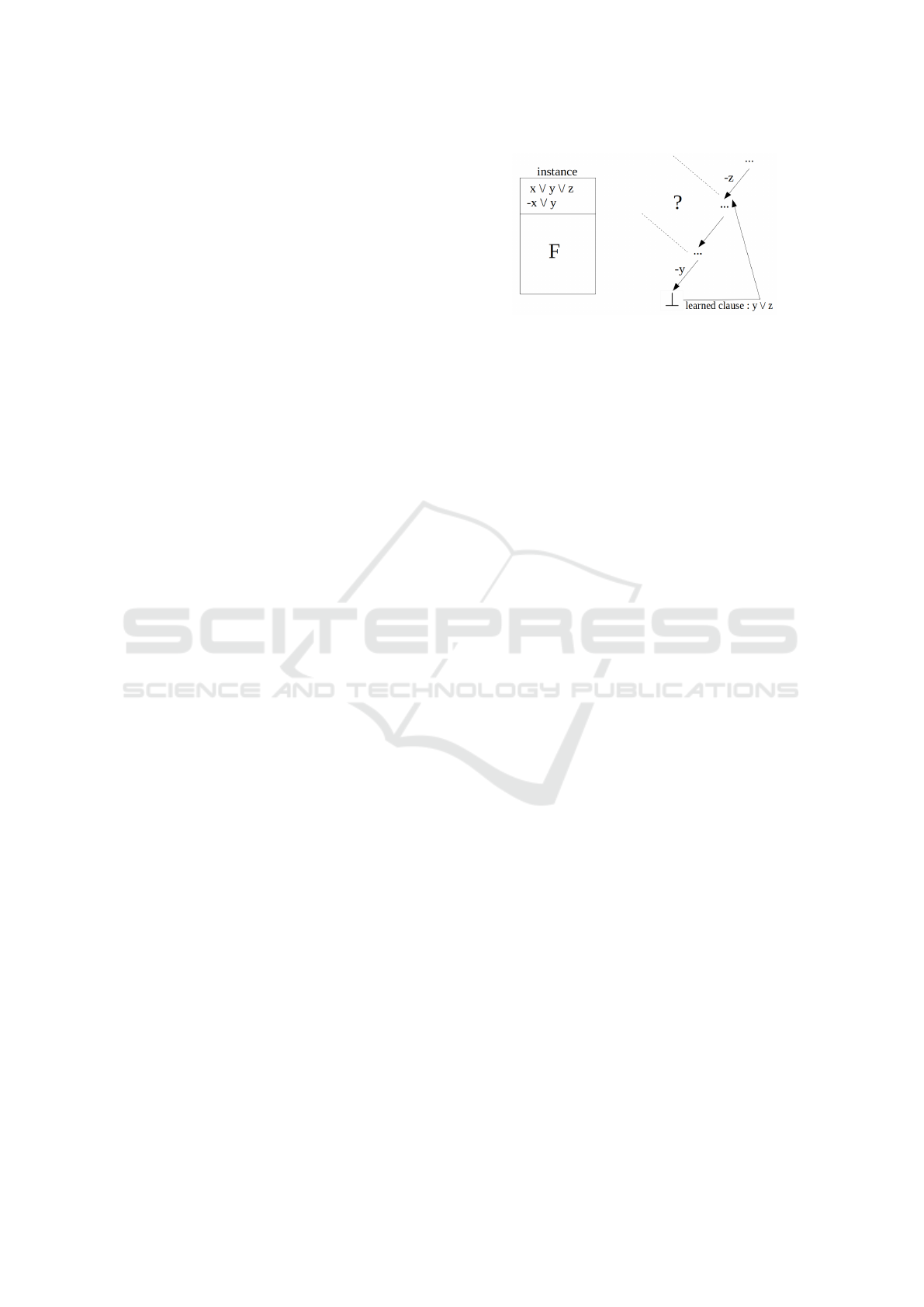
example in Figure 4 shows such behavior. Let us con-
sider a propositional formula F
′
= {x ∨y ∨z, ¬x∨y}∪
F. It is not known if F is satisfiable or not. Let us sup-
pose that the CDCL solver takes some decisions over
any variables but x,y,z, then the decision ¬z which
deletes the literal z in the first clause. After that, some
other decisions are taken and then the solver decides
¬y, which deletes the literal y in the first two clauses.
At this point, a conflict will be derived by unit prop-
agation, as we have to satisfy both x and ¬x. After
conflict analysis, the solver learns the clause y ∨ z,
which is the resolvent of the two first clauses, and
backtracks to decision ¬z and directly propagates lit-
eral y, which satisfies the two first clauses. Note that
the non chronological search will ignore the nodes
Figure 4: Example to illustrate the problem induced by
CDCL non chronological search.
between decisions ¬y and ¬z. Hence, the satisfia-
bility of the corresponding subformulas remains un-
known. In other words, the backtrack step in CDCL
does not indicate that the subformulas associated to
unexplored nodes are unsatisfiable. This is clear on
our example. The decision y could have been taken
at any level between the decisions ¬z and ¬y. In that
case, the first two clauses would have been satisfied
and the satisfiability of the subformula would only de-
pend on the satisfiability of F. This has a consequence
in the way we feed our cache: we may add an entry to
the cache only when we are assured that the current
simplified formula is UNSAT and when this has been
proved by the solver. In a CDCL solver, this only oc-
curs when we are at the leaves of the tree, when we
meet a conflicting clause. The sources of inconsis-
tency are computed by performing a graph traversal in
the implication graph from the conflict clause. Com-
pared to the classical conflict analysis procedure, the
information stored in learned clauses is expressed in
terms of original clauses. In some ways, the sources
we compute ”unfold” the learned clauses into origi-
nal clauses. In practice, as the search progresses, the
size of the sources found increases. We create entries
in our cache by computing the sources of the leaves
simplified using the current decisions and unit prop-
agation. During this simplification, we exclude the
literals propagated by a learned clause, otherwise we
would always get an empty clause.
We made some initial experiments with this set-
ting. We could retrieve a small tree for PHP bench-
marks similar to the one shown in Figure 2 by adapt-
ing the decision heuristics to branch first positively
on variables occurring more frequently in the formula
(instead of negatively as in Minisat default heuristics).
However, such heuristics does not perform well on
the considered benchmarks. Furthermore, we were
limited to use our cache in a postprocessing step, be-
cause CDCL requires a reason to backtrack. Chang-
ing the way the reason is computed changes the ex-
ploration of the search space, so may increase the fi-
nal search tree. Therefore we have considered also
Compressing UNSAT Search Trees with Caching
361

the older DPLL approach, which does not suffer from
that problem.
3.5 DPLL Case
In a DPLL-like solver, when the two children of a
node corresponding to interpretation I have been ex-
plored (one branch for decision l, another one for de-
cision ¬l) and both were unsatisfiable, F
|I
is known
to be unsatisfiable and the sources S(F, I) can be ob-
tained as presented in Section 3.3. S(F,I) simplified
by I is unsatisfiable and is added to the cache. When
a new node identified by interpretation I is explored,
the first step is to look up in the cache if there ex-
ists an entry E which is contained in the current for-
mula F
|I
up to a renaming of literals. If there exists
E in the cache and σ a renaming of literals such that
σ(E) ⊆ F
|I
, then F
|I
is necessarily unsatisfiable since
E is unsatisfiable. This test can be translated to the
subgraph isomorphism problem (see Section 3.2). If
one is found, the set F
′
of clauses of F
|I
that map
to clauses of E is easily obtained by mapping back
nodes to clauses. F
′
|I
is unsatisfiable but in general
F
′
may be satisfiable. Indeed, F
′
has to be supple-
mented with the clauses required to propagate liter-
als erased in F
′
at the current decision level to ob-
tain an unsatisfiable formula. As an example, let us
assume a PHP problem P is encoded with clauses
{C
1
,C
2
,.. .,C
n
} and let us consider the formula F de-
fined as {¬x ∨ y,¬x ∨ ¬y,x ∨ C
1
,C
2
,.. .,C
n
}. Let us
also assume the PHP instance P is already present
in the cache. Starting from F, when we branch on
y, ¬x is propagated, and the simplified formula now
contains P which is recognized as an entry of the
cache. The clauses of F corresponding to P are
F
′
= {x ∨C
1
,C
2
,.. .,C
n
}. When branching on ¬y, we
also obtain F
′
= {x ∨C
1
,C
2
,.. .,C
n
} in the same way.
However, F
′
is satisfiable because the first clause of
P can be neutralized by x. To recover an unsatis-
fiable formula, we have to add all the clauses used
to propagate ¬x on both branches, which means we
must add {¬x ∨ y, ¬x ∨ ¬y} to F
′
to get an unsatisfi-
able formula, which is the source S(F,
/
0) and there-
fore F can now be added as an entry in the cache.
It must be emphasized that looking up in the cache
has a high cost: we are solving several times an NP-
complete problem. However, since our goal is not
to speed up the resolution time but instead to reduce
the size of the search tree, it is acceptable to spend a
long time in looking up the cache if, in the end, the
generated tree is small enough. When a new entry is
added in the cache, we can use the greatest decision
level present in the sources to perform a backjump.
The idea here is to avoid backtracking to the deci-
sions that were not involved in the conflict. These
nodes would give us the same entry to add in the
cache as the current one. We can then go back to
the decision level found that way. If we are back to
a decision that has not been flipped already, we flip
that decision and otherwise, we add another new en-
try to the cache and we repeat this procedure. As
an example, let us consider a formula that contains
clauses {a ∨ b ∨ c,a ∨ b ∨ ¬c,a ∨ ¬b ∨ c,a ∨ ¬b ∨ ¬c}
and the interpretation I = ⟨¬a,x, y, z⟩. Then branch-
ing on b and ¬b will both yield a conflict, which
means that F
|I
is unsatisfiable as well as S(F,I) =
{a ∨ b ∨ c,a ∨ b ∨ ¬c,a ∨ ¬b ∨ c,a ∨ ¬b ∨ ¬c}. As
long as a is not flipped, these unsatisfiable clauses
remain in the formula, therefore we may backtrack
to decision level 1. Note that, even if this backjump
technique is similar to the conflict analysis of CDCL
solvers, there are still some differences. First we do
not perform any resolution step, hence have no cut
in the implication graph (UIP). Second, we are only
allowed to skip the subtrees that are known to be un-
satisfiable. Another difference here is the fact that the
clauses used during a conflict analysis are an explana-
tion of the learned clause whereas the sources are an
explanation of the unsatisfiability of the subformula.
4 EXPERIMENTAL RESULTS
We implemented the proposed approaches on top of
Minisat (E
´
en and S
¨
orensson, 2003). We disabled
database simplification to keep the original clauses
during the whole search. We also disabled restarts
which build a sequence of search trees. For the DPLL
approach, we also disabled clause learning and con-
flict analysis. The latter is replaced by a dedicated
procedure used to collect the sources. The activity
of a variable, which is updated for each new learned
clause in classical CDCL solver, is updated each time
a new clause is added to the sources in our con-
text. For the CDCL approach, we have both the con-
flict analysis procedure and the sources computation
procedure (the heuristics and clause learning is un-
changed compared to Minisat). The Glasgow Sub-
graph Solver (GSS for short) (McCreesh et al., 2020)
is called to compute subgraph isomorphism, i.e. to
query our cache. We used benchmarks from the the
SAT’02 (submitted part) (Simon et al., 2005) and
SAT’03 (handmade and industrial parts) (Le Berre
and Simon, 2003) competitions. We selected those
benchmarks because we needed “easy” benchmarks
for Minisat since our approach has a high computa-
tional complexity. A summary of our results is found
in Table 1. Minisat is obviously much more effi-
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
362

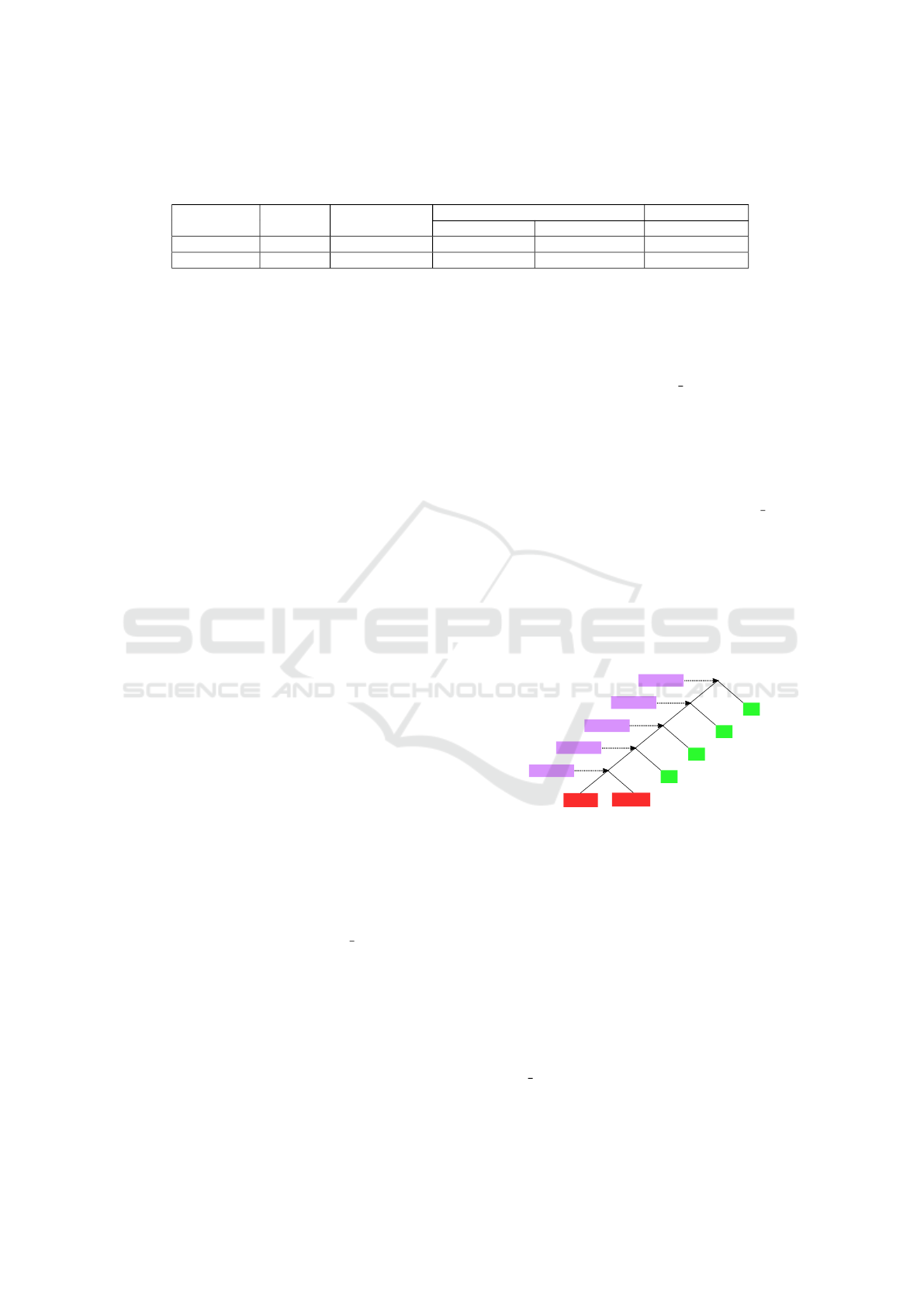
Table 1: Summary of our experiments. For each competition, we give the number of instances known to be UNSAT and the
number of instances solved by MiniSat within 1 minute (easy instances). Then, we give the number of instances solved in
each experiment. The number between parenthesis indicates the number of single branch search trees that were found.
Competition #UNSAT Minisat (1min) DPLL-like (15min) CDCL (15min)
Postprocessing Integrated cache Postprocessing
SAT’02 381 276 40 (4) 106 (42) 78 (11)
SAT’03 198 78 15 (13) 87 (53) 39 (28)
cient than our postprocessing/integrated caching ap-
proaches (described later) due to the high cost of our
cache. DPLL with postprocessing is clearly less effi-
cient than CDCL with postprocessing on those bench-
marks. However, integrating the cache directly inside
the DPLL solver provides significantly better results
than CDCL with postprocessing. It even allows to
solve benchmarks that Minisat cannot solve in 4 hours
(e.g. instances from the Urquhart families).
4.1 Postprocessing Traces
In this section, we are interested in the compression
potential of our approach. It is thus necessary to com-
pare the tree with and without caching. The only way
to do so is to first solve the problem and to store the
search tree and second to run the caching mechanism
on the stored tree. That way, it is easy to compare
the original tree and the tree obtained using caching.
In practice, storing the search tree can lead to huge
files, so we simulate the postprocessing directly on
the solver. We impose a timeout of 2 seconds for each
call to GSS when trying to identify a subgraph iso-
morphism. We ran both DPLL and CDCL approaches
with a timeout of 15 minutes on our benchmarks.
Some individual results of these experiments on a few
families of benchmarks can be seen in Table 2. We
compare the numbers of conflicts, thus the number
of branches, of both search trees. The ratio between
these two numbers represents the compression power
of our approach. The size of an instance is the sum
of its clauses length. A distribution of the ratios ob-
tained by both approaches can be found in Table 3.
The compression ratio can be very good (less than
10
−3
), especially for the CDCL approach. Unfortu-
nately, it only happens on a small subset of the bench-
marks, mainly marg, Urquhart and xor chain families,
which are highly structured. For the DPLL approach,
the postprocessor behaved on PHP problems mainly
as expected and described in section 3.1. The only
difference comes from the heuristics used in Minisat,
which negatively decides the first variable and then
negatively decides the variables starting by the last
one and in decreasing order. So, after the problem
PHP
n−1
has been added into the cache, it is recog-
nized n − 1 times with the first variable assigned (this
problem has been added just before PHP
n−1
). This
problem is also recognized when flipping the first de-
cision. This behaviour creates an additional branch
and so, the number of branches found differs by one
from the expected number of branches. Concerning
the instances from the SAT competitions, from the
families marg, Urquhart and xor chain, we have often
obtained a single branch search tree as shown in Fig-
ure 2. For these instances, when the solver adds a new
entry to the cache after a certain decision, it is often
recognized after the negation of that decision. This al-
lows us to prune a lot of branches and this explains the
good ratios we have obtained. It is not strictly the case
for some instances (e.g. marg2x6.cnf and x1 16.cnf)
but we have obtained very short trees for them. As an
example, Figure 5 shows the search tree obtained by
our approach when the cache system is used in both
the DPLL and CDCL approaches. The purple boxes
represent the addition of a new entry in the cache and
the green boxes correspond to the recognition of an
entry. The label ”i x” means that the element regis-
tered at ”cache x” has been recognized.
6 7 11
-6 -7 11
-9
9
-10
10
-11
11
-12
12
-1
1
i1
i2
i3
i4
cache 1
cache 2
cache 3
cache 4
cache 5
Figure 5: Search tree for marg2x2.cnf with caching.
4.2 Solver with Integrated Cache
As a second experiment, we used the cache during the
search itself. We could only provide a DPLL imple-
mentation, since generating a conflict clause from a
cache hit is an open question at this stage. We con-
sidered the same instances as before and still with a
timeout of 15 minutes per benchmark. A relevant ex-
cerpt of the results is shown in Table 4. In a total
of 95 instances, the solver develops a single branch
tree as shown in Figure 2. The good compression
previously obtained for the families marg, Urquhart
and xor chain is still found, also on larger instances.
We observed that the DPLL solver with integrated
cache can solve in less than 15 minutes some in-
Compressing UNSAT Search Trees with Caching
363

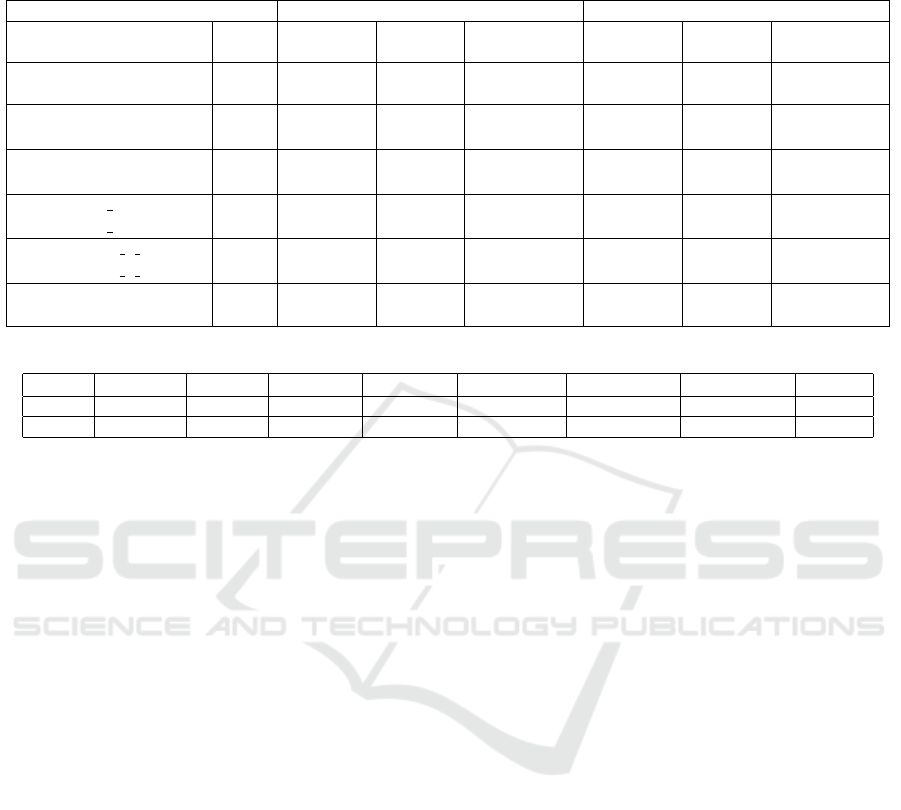
Table 2: Experimental results about the compression power of our approach. For each instance, we provide its size in number
of literals, and the number of conflicts found with and without caching for both DPLL and CDCL approaches. A dash denotes
a timeout. The compression ratio is the number of conflicts with caching divided by the number of conflicts without caching.
DPLL-like (postprocessing) CDCL (postprocessing)
Instance Size Conflicts Conflicts Compression Conflicts Conflicts Compression
(no cache) (cache) Ratio (no cache) (cache) Ratio
PHP
7
448 6.8 10
3
23 3.4 10
−3
5.6 10
3
853 1.5 10
−1
PHP
12
2,028 - - - - - -
marg2x6.sat03-1444 528 5.2 10
5
21 4.0 10
−5
3.0 10
4
20 6.6 10
−4
marg3x3add8.sat03-1449 1,056 - - - 1.8 10
5
32 1.8 10
−4
Urquhart-s3-b9 1,240 5.1 10
5
20 3.9 10
−5
1.9 10
4
21 1.1 10
−3
Urquhart-s3-b3 2,152 - - - 1.6 10
6
29 1.8 10
−5
x1 16 364 6.0 10
4
18 3.0 10
−4
2.2 10
3
20 9.1 10
−3
x1 24 556 - - - 2.0 10
5
78 3.9 10
−4
3col20 5 6 646 33 20 6.0 10
−1
27 27 1
3col40 5 5 1,286 756 198 2.6 10
−1
118 72 6.1 10
−1
homer06 1,800 5.1 10
5
195 3.8 10
−4
- - -
homer17 3,718 - - - - - -
Table 3: Distribution of the ratios for the postprocessing techniques for the DPLL and CDCL approaches.
Ratio Unsolved [1;0.75[ [0.75;0.5[ [0.5;0.25[ [0.25;10
−1
[ [10
−1
;10
−2
[ [10
−2
;10
−3
[ ≤ 10
−3
DPLL 524 4 5 11 11 5 6 13
CDCL 462 38 13 5 3 6 7 45
stances that Minisat is unable to solve in more than
4 hours. This is the case for some SAT’02 Urquhart
crafted instances for example. Stopping the search
as soon as a cache entry is detected allows to solve
much more instances than the original DPLL, notably
in the families tested in the first experiment. However,
the size of the cache only increases and as it becomes
bigger and bigger during the search, trying to recog-
nize an entry of the cache can become very expensive,
even with the timeout of 2 seconds. Moreover, as the
subformulas can be very big as well, finding an iso-
morphism may take more time than the imposed limit.
On large instances, some calls to GSS may be aborted
and we may miss some existing isomorphisms, hence
some possible compression. This occurs for example
on problems bigger than PHP
16
.
5 CONCLUSION
Our goal in this work is to prune as much as possible
the branches of an UNSAT search tree to reduce its
size. To do so, we have proposed a cache inspired by
what already exists for model counters. The idea is to
register some UNSAT subformulas and to try to rec-
ognize them later in the search tree in order to avoid
exploring several similar subparts of the tree. We have
presented a syntactic method based on the detection
of subgraph isomorphisms. We have seen that it is
possible to obtain rather good compression ratios and
short proof sizes and even a single branch search tree
for some families of instances, notably those with a
lot of symmetries or similarities but it is still unclear
if this approach may work on a wide set of instances.
We proposed an implementation of this cache on both
the DPLL and CDCL architectures. If the latter pro-
vided promising results, it currently does not scale
well because we could only implement it as a postpro-
cessing step. The integration of the cache directly in
the DPLL solver allowed to reduce drastically many
more search trees, including some cases for which
Minisat could not even solve the problem. Unfortu-
nately, generating a conflict clause from a cache hit
is an open question at this stage. Some ways to im-
prove our approach can be considered. First of all, we
have considered an approach based on the manage-
ment of a cache but we do not have implemented the
possibility to delete entries that do not seem useful.
This operation is also available in model counters to
avoid exceeding a specific memory limit. This could
be a good addition to our approach. We have only
considered two heuristics (the one of Minisat and a
variant). But some other heuristics could be tried, for
instance the ones used in model counters. Concerning
the detection of subgraph isomorphisms, it may be in-
teresting to collect some information during a call to
GSS and try to use it in future calls. Moreover, we
are interested in detecting entries of the cache where
some literals are falsified, since these are unsatisfi-
able too. Indeed, one of the reason why CDCL does
not often produce a single branch tree is that the cur-
rent subformula is not directly an entry in the cache
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
364

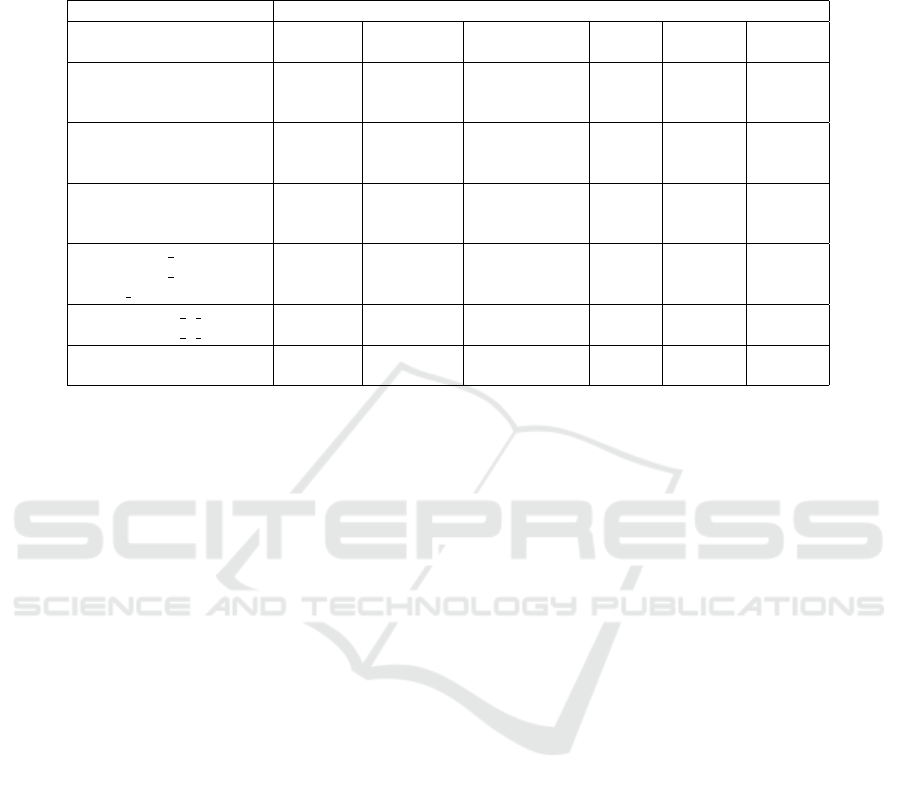
Table 4: Experimental results when the cache is used during the search. For each instance, we give the numbers of conflicts,
of entries of the cache, of calls to GSS that found an isomorphism as well as the total number of calls. The number between
parenthesis indicates the number of different entries of the cache recognized by isomorphism. We also provide the time spent
by the solver (without isomorphism detection) and the cumulated time of all the calls to GSS. All times are in seconds.
DPLL-like (integrated cache)
Instance Conflicts Cache size Subgraph Calls Time Time
Isomorphisms (Search) (GSS)
PHP
7
23 22 21 (6) 21 0.007 0.180
PHP
12
68 67 66 (11) 66 0.071 5.728
PHP
16
122 121 120 (15) 120 0.274 63.741
marg2x6.sat03-1444 21 20 17 (17) 18 0.004 0.162
marg3x3add8.sat03-1449 26 25 22 (22) 24 0.024 0.813
marg6x6.sat03-1456 86 85 84 (84) 84 0.134 7.446
Urquhart-s3-b9 20 19 18 (18) 18 0.009 0.175
Urquhart-s3-b3 29 28 27 (27) 27 0.024 0.486
Urquhart-s5-b5 94 93 92 (91) 101 0.292 36.967
x1 16 18 17 14 (14) 42 0.005 0.419
x1 24 25 24 23 (23) 23 0.037 0.779
x2 80.sat03-1605 395 394 393 (318) 2,257 0.919 427.492
3col20 5 6 12 11 6 (3) 31 0.004 0.178
3col40 5 5 357 319 235 (41) 52,583 1.451 564.310
homer06 111 105 98 (27) 420 0.495 116.096
homer17 363 348 352 (92) 1,691 3.249 712.465
but one with falsified literals. Finally, we are looking
for other forms of redundancy in order to compress
UNSAT trees in a more general situation.
ACKNOWLEDGEMENTS
The first author is partly funded by region “Hauts-de-
France”. This work has been supported by the project
CPER Data from the region “Hauts-de-France”.
REFERENCES
Biere, A., Heule, M., van Maaren, H., and Walsh, T., editors
(2021). Handbook of Satisfiability - Second Edition.
Cook, S. A. (1971). The complexity of theorem-proving
procedures. In 3rd Annual ACM, pages 151–158.
Davis, M., Logemann, G., and Loveland, D. W. (1962).
A machine program for theorem-proving. Commun.
ACM, 5(7):394–397.
Davis, M. and Putnam, H. (1960). A computing procedure
for quantification theory. J. ACM, 7(3):201–215.
D
´
eharbe, D., Fontaine, P., Le Berre, D., and Mazure, B.
(2013). Computing prime implicants. In FMCAD
2013, pages 46–52.
E
´
en, N. and S
¨
orensson, N. (2003). An extensible sat-solver.
In SAT 2003, pages 502–518.
Gomes, C. P., Sabharwal, A., and Selman, B. (2021). Model
counting. In Handbook of Satisfiability - Second Edi-
tion, pages 993–1014.
Haken, A. (1985). The intractability of resolution. Theor.
Comput. Sci., 39:297–308.
Ignatiev, A., Previti, A., Liffiton, M. H., and Marques-Silva,
J. (2015). Smallest MUS extraction with minimal hit-
ting set dualization. In CP 2015, pages 173–182.
Le Berre, D. and Simon, L. (2003). The essentials of the
SAT 2003 competition. In SAT 2003, pages 452–467.
Marques-Silva, J., Lynce, I., and Malik, S. (2021). Conflict-
driven clause learning SAT solvers. In Handbook of
Satisfiability - Second Edition, pages 133–182.
McCreesh, C., Prosser, P., and Trimble, J. (2020). The glas-
gow subgraph solver: Using constraint programming
to tackle hard subgraph isomorphism problem vari-
ants. In ICGT 2020, pages 316–324.
Moskewicz, M. W., Madigan, C. F., Zhao, Y., Zhang, L.,
and Malik, S. (2001). Chaff: Engineering an efficient
SAT solver. In Proc. of DAC 2001, pages 530–535.
Sang, T., Bacchus, F., Beame, P., Kautz, H. A., and Pitassi,
T. (2004). Combining component caching and clause
learning for effective model counting. In SAT 2004.
Silva, J. P. M. and Sakallah, K. A. (1999). GRASP: A search
algorithm for propositional satisfiability. IEEE Trans.
Computers, 48(5):506–521.
Simon, L., Le Berre, D., and Hirsch, E. A. (2005). The
SAT2002 competition. Ann. Math. Artif. Intell.,
43(1):307–342.
Thurley, M. (2006). sharpsat - counting models with ad-
vanced component caching and implicit BCP. In SAT
2006, pages 424–429.
Wetzler, N., Heule, M., and Jr., W. A. H. (2014). Drat-
trim: Efficient checking and trimming using expres-
sive clausal proofs. In SAT 2014, pages 422–429.
Zhang, L. and Malik, S. (2003). Validating SAT solvers
using an independent resolution-based checker: Prac-
tical implementations and other applications. In DATE
2003, pages 10880–10885.
Compressing UNSAT Search Trees with Caching
365