UMVpose++: Unsupervised Multi-View Multi-Person 3D Pose

Estimation Using Ground Point Matching

ogenes Wallis de Franc¸a Silva

, Jo

ao Paulo Silva do Monte Lima

1,2 a

Diego Gabriel Francis Thomas

3 b

, Hideaki Uchiyama

4 c

and Veronica Teichrieb

1 d

Voxar Labs, Centro de Inform

atica, Universidade Federal de Pernambuco, Recife, PE, Brazil

Visual Computing Lab, Departamento de Computac¸

ao, Universidade Federal Rural de Pernambuco, Recife, PE, Brazil

Faculty of Information Science and Electrical Engineering, Kyushu University, Japan

Graduate School of Science and Technology, Nara Institute of Science and Technology, Nara, Japan

Keywords:

3D Human Pose Estimation, Unsupervised Learning, Deep Learning, Reprojection Error.

Abstract:

We present UMVpose++ to address the problem of 3D pose estimation of multiple persons in a multi-view

scenario. Different from the most recent state-of-the-art methods, which are based on supervised techniques,

our work does not need labeled data to perform 3D pose estimation. Furthermore, generating 3D annotations is

costly and has a high probability of containing errors. Our approach uses a plane sweep method to generate the

3D pose estimation. We deﬁne one view as the target and the remainder as reference views. We estimate the

depth of each 2D skeleton in the target view to obtain our 3D poses. Instead of comparing them with ground

truth poses, we project the estimated 3D poses onto the reference views, and we compare the 2D projections

with the 2D poses obtained using an off-the-shelf method. 2D poses of the same pedestrian obtained from the

target and reference views must be matched to allow comparison. By performing a matching process based

on ground points, we identify the corresponding 2D poses and compare them with our respective projections.

Furthermore, we propose a new reprojection loss based on the smooth L

norm. We evaluated our proposed

method on the publicly available Campus dataset. As a result, we obtained better accuracy than state-of-the-art

unsupervised methods, achieving 0.5% points above the best geometric method. Furthermore, we outperform

some state-of-the-art supervised methods, and our results are comparable with the best-supervised method,

achieving only 0.2% points below.

1 INTRODUCTION

3D human pose estimation is an active research area

in computer vision. Over the last decade, several

methods have been proposed for human 3D pose es-

timation from single or multiple views, with com-

pelling results. 3D poses are beneﬁcial and can

be used in several applications: augmented reality,

surveillance systems, and intelligent sports. When we

talk about 3D pose estimation, we can consider sev-

eral kinds of scenarios: one-view one-person, one-

view multi-person, and multi-view multi-person. In

this paper, we focus our attention on the case of a

multi-view, multi-person scenario; that is, we have

more than one camera, and we estimate the 3D pose

https://orcid.org/0000-0002-1834-5221

https://orcid.org/0000-0002-8525-7133

https://orcid.org/0000-0002-6119-1184

https://orcid.org/0000-0003-4685-3634

of more than one person captured by these cameras.

One advantage of having a multi-view conﬁguration

is avoiding ambiguities when using only one camera

to get 3D poses from 2D data.

Considering the multi-view multi-person sce-

nario, the literature has different approaches, starting

with geometric methods (Belagiannis et al., 2014a),

(Belagiannis et al., 2015), (Belagiannis et al., 2014b),

(Dong et al., 2019) and now achieving the state-of-

the-art with supervised techniques using neural net-

works (Huang et al., 2020), (Lin and Lee, 2021),

(Tu et al., 2020). Methods that follow the ﬁrst ap-

proach use the 3D pictorial structure (3DPS) method

such as (Belagiannis et al., 2014a), (Belagiannis et al.,

2015), (Belagiannis et al., 2014b). Improvements

were made by (Dong et al., 2019) in the Mvpose

method; however, the supervised techniques based on

neural networks (Huang et al., 2020), (Lin and Lee,

2021), (Tu et al., 2020) came to achieve the top and

outperformed the geometric methods. Starting with a

Silva, D., Lima, J., Thomas, D., Uchiyama, H. and Teichrieb, V.

UMVpose++: Unsupervised Multi-View Multi-Person 3D Pose Estimation Using Ground Point Matching.

DOI: 10.5220/0011668800003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 4: VISAPP, pages

607-614

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

607

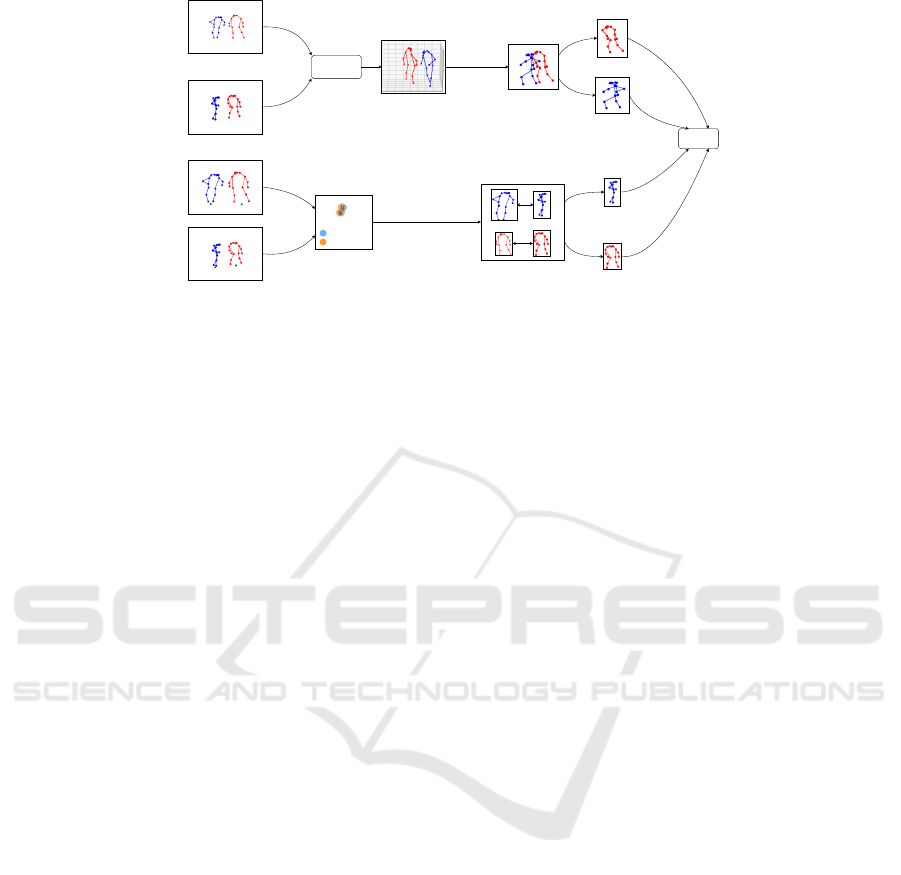
Target view

Reference view

3D pose

estimator

Loss

Target

Reference

Ground point

Target view

Reference view

Projection

Matching process

Ground points on

world coordinates

2D pose matched

2D projection

Figure 1: We have a well-deﬁned target and reference views. Using the 2D poses estimated in each view, we generate a 3D

pose estimation as in (Lin and Lee, 2021). Each 3D skeleton is projected onto the reference view, and we compare it with the

matched 2D poses. These matching 2D poses are obtained using ground points. For each 2D pose, we have ground points

associated and utilizing a homography matrix as in (Lima et al., 2021), we project these points onto world coordinates. Taking

the Euclidean distance, we build a cost matrix used on the Hungarian Algorithm to perform the matching. With the 2D poses

matched, we compare them with a smooth L

loss (Girshick, 2015).

simple neural structure, (Huang et al., 2020) outper-

formed the best geometric method - Mvpose (Dong

et al., 2019). The VoxelPose work (Tu et al., 2020)

uses 3D CNNs with an approach focusing on directly

generating a 3D space with the skeletons instead of

estimating 2D poses and, based on these 2D skeletons

estimating the 3D pose. VoxelPose improved com-

pared with (Huang et al., 2020); however, 3D CNNs

have a high computational cost. Lin & Lee (Lin and

Lee, 2021) brought the plane sweep approach and

achieved the state-of-the-art. Furthermore, the com-

putational cost was highly reduced compared with

VoxelPose.

Methods that obtain the best results use supervised

learning to train the network. However, the need for

annotated data creates several practical limitations be-

cause of the cost of getting these 3D annotations. Our

work aims for an unsupervised approach, which al-

leviates the need to use labeled data in the training

process. Instead of comparing the 3D pose with the

annotated ground truth, we compute a loss consider-

ing the projected 2D pose in a reference view and the

matched 2D pose related to that projected pose. This

process is generated along with the training, and to

perform this calculation, we only need the camera pa-

rameters and an off-the-shelf 2D pose detector. Com-

pared with geometric methods, we also do not need

to follow deﬁned steps such as (1) 2D pose estima-

tion, (2) matching between the 2D poses estimated

in each view, and (3) triangulation or the 3DPS ap-

proach to estimate the 3D pose based on the detected

2D poses. Our proposed method uses an end-to-end

solution (Lin and Lee, 2021) to obtain the 3D pose,

in which the input of our neural network is a matrix

score obtained using the plane sweep approach. To

calculate the reprojection error, we perform matching

to select the 2D poses that will be compared with the

2D projection of the estimated 3D pose. Our match-

ing process uses ground points as in (Lima et al.,

2021). We project these ground points onto world co-

ordinates and use Hungarian matching to obtain the

correspondences between the estimated target and ref-

erence 2D poses.

Using (Lin and Lee, 2021), we can estimate the

3D poses with an end-to-end solution. First, how-

ever, we need to perform some steps in parallel, such

as: taking the 2D poses in each view, calculating the

respective ground points, projecting them onto the

ground plane, using Hungarian matching, and com-

paring the 2D poses.

We propose an unsupervised approach to estimate

the 3D poses of multiple persons in a multi-view sce-

nario. The key points of our work are:

• We propose a new matching process using ground

points and a new loss function to optimize the

neural network using plane sweep pose.

• We do not need labeled data for 3D pose estima-

tion.

• We achieve state-of-the-art PCP measure when

compared with the best geometric methods as

(Belagiannis et al., 2014a), (Belagiannis et al.,

2015), (Belagiannis et al., 2014b), (Dong et al.,

2019). All these approaches do not need to use

labeled data, and we outperform them. Further-

more, the proposed method outperforms the exist-

ing unsupervised approach (UMVpose). We also

exceed some of the best-supervised techniques,

and our results are comparable to those from the

best-supervised process (Lin and Lee, 2021).

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

608

2 RELATED WORK

Ground point

Figure 2: We assign a ground point to each 2D pose. We

obtain this ground point as described in (Lima et al., 2021).

We estimate a bounding box for each 2D pose and build a

line between the ankles. So we take the middle point and

apply an offset in the direction of the ground. Our goal is to

represent each person by this point. Therefore the ground

points are our reference to match the 2D skeletons of the

target and reference views.

This section brieﬂy discusses multi-view multi-

person methods based on geometric, supervised, and

unsupervised approaches.

2.1 Multi-View Multi-Person Geometric

Methods

The ﬁrst works about 3D pose estimation of multi-

ple persons in a multi-view scenario were geometric-

based methods without using neural networks. The

technique in (Belagiannis et al., 2014a), for exam-

ple, detects 2D poses, obtains a reduced state space

using triangulation, and uses a 3DPS model in this

reduced state space to estimate the 3D pose. Simi-

larly, (Belagiannis et al., 2014b) also has a 3DPS ap-

proach, but now the 3DPS model is temporally con-

sistent, so they can track the individual and reduce the

state space, making the inference faster. The same au-

thors in (Belagiannis et al., 2015) make improvements

compared with (Belagiannis et al., 2014b). The ear-

lier work (Belagiannis et al., 2014b) deﬁned a body

part as a limb, considering its orientation and posi-

tion, while (Belagiannis et al., 2015) reduced the pa-

rameterization of the body part to consider only the

3D position. The translation and rotation information

is implicitly encoded in a factor graph, facilitating

the inference task. The Mvpose approach in (Dong

et al., 2019), similarly to (Belagiannis et al., 2015),

obtains a state-space using triangulation based on 2D

detections from a multi-view scenario. Mvpose has

a well-deﬁned pipeline, starting with 2D detections

and making a cluster of the 2D detections of each per-

son. After that, they reconstruct the 3D position. Be-

sides epipolar distance, Mvpose also uses a person-

reidentiﬁcation method to help the clustering process

using a multi-way matching with cycle consistency.

Mvpose has the best PCP compared with the others

and was outperformed only by supervised methods.

Our method uses deep learning. However, we do

not need 3D-labeled data. Instead, we can perform

a reprojection error loss using geometric techniques,

avoiding the 3D comparison between the inference

and annotated ground truth. Furthermore, we outper-

form these methods.

2.2 Multi-View Multi-Person

Supervised Methods

Among the state-of-the-art supervised methods, we

have the (Huang et al., 2020), (Lin and Lee, 2021),

and (Tu et al., 2020) approaches. The process by

(Huang et al., 2020) is the ﬁrst to achieve state-of-the-

art neural networks. It is also established with well-

deﬁned steps, starting with 2D detections, generating

a cluster of the detections obtained by each different

view. VoxelPose (Tu et al., 2020) needs a well-deﬁned

pipeline as (Huang et al., 2020). Instead, they work

directly on 3D space, avoiding problems generated

by noisy 2D detections. They use a Cuboid Proposal

Network (CPN) approach to localize all people and

a Pose Regression Network (PRN) to make the 3D

estimation. VoxelPose is robust to occlusions. How-

ever, it needs 3D CNNs, making this a highly costly

process. PlaneSweepPose (Lin and Lee, 2021) out-

performs VoxelPose (Tu et al., 2020), achieving state-

of-the-art, and it also inspired our work. Its approach

is faster than VoxelPose and is an end-to-end solution

based on the back-projection process. They build a

solution on a scenario captured by multiple cameras.

They generate a scoring matrix that is the input to the

neural network. In (Lin and Lee, 2021), we also have

a coarse-to-ﬁne process since they estimate the per-

son’s position and, after that, the joint position.

Compared with these methods, we do not use 3D

labeled data to perform 3D pose estimation. Using

reprojection error, we have a new loss. The loss com-

pares the 2D pose projected onto the reference view

with the matched 2D pose using a smooth L

norm

(Girshick, 2015). We also propose a matching pro-

cess using ground points (Lima et al., 2021) instead

of the back-projection approach as in (de Franc¸a Silva

et al., 2022).

UMVpose++: Unsupervised Multi-View Multi-Person 3D Pose Estimation Using Ground Point Matching

609

2.3 Multi-View Multi-Person

Unsupervised Methods

Besides works that are fully geometric or based

on deep learning, there is the UMVpose tech-

nique (de Franc¸a Silva et al., 2022). Using a deep

learning approach, (de Franc¸a Silva et al., 2022) uses

geometric methods to replace the loss, comparing 2D

poses instead of 3D labels.

In (de Franc¸a Silva et al., 2022), they use (Lin and

Lee, 2021) plane sweep stereo method. This method

establishes target and reference views and performs

2D pose estimations in each view. They use the

plane sweep stereo algorithm to generate a scoring

matrix related to the cross-view consistency among

the views. In this manner, they obtain the person-level

and joint-relative level depth; combining these values,

they can estimate the 3D pose.

As we have mentioned before, the

(de Franc¸a Silva et al., 2022) uses (Lin and Lee,

2021) plane sweep stereo method. This work deﬁnes

target and reference views related to the multi-view

scenario. They consider each view the target and

make the 3D estimation under that view. Finally, the

estimated 3D poses (related to each view) are fused

and taken to the same global coordinate space.

The (de Franc¸a Silva et al., 2022) uses reprojec-

tion error as a new loss, avoiding the comparison of

3D poses, as they compare 2D poses obtained along

with training. Using PlaneSweepPose (Lin and Lee,

2021), they get a 3D pose, so instead of comparing

this 3D pose with the ground truth, they project them

onto 2D poses and compare them with matched 2D

poses. Therefore, 3D ground truth is not used, and

they can perform training with an unsupervised ap-

proach. The advantages of our method are the use of

other losses when comparing the 2D poses and a more

robust matching algorithm, thus way outperforming

UMVpose. In (de Franc¸a Silva et al., 2022), they

use back projection in the matching process, gener-

ating 3D poses from the 2D poses in the target view,

while we compare only one point (the ground point)

to perform matching. Furthermore, using our ap-

proach with smooth L1 loss, we can outperform the

MSE loss used in (de Franc¸a Silva et al., 2022).

Considering unsupervised methods, we also have

unsupervised 3D pose estimation on multi-view sce-

narios as (Sun et al., 2021). These works exper-

iment on the Human3.6M (Ionescu et al., 2013)

dataset and are a one-person method, different from

(de Franc¸a Silva et al., 2022).

3 UMVpose++

Target

Reference

Target

Reference

Figure 3: The matching process occurs using ground points.

Each person has a ground point, and it is projected onto

world coordinates. Next, we measure the distance between

these points to obtain a cost matrix. Finally, we use the

Hungarian algorithm to perform matching between target

and reference views based on our cost matrix.

UMVpose++ is an improved version of UMVpose

(de Franc¸a Silva et al., 2022). Similar to UMVpose,

the goal of UMVpose++ is to learn to estimate the 3D

poses of multiple persons from multi-view images in

an unsupervised manner. As in UMVpose, we aim

to generate a 3D pose using the plane sweep stereo

approach as in (Lin and Lee, 2021). We then project

the 3D pose estimated onto one of the reference views

and compare the projection with the matched 2D pose

as described in Figure 1. However, differently from

UMVpose, we do the matching between the target and

reference views using a different approach based on

ground points attached to each person (Lima et al.,

2021). Instead of back-projection, we estimate the

2D ground points related to each person’s 2D pose,

project these points onto world points with a homog-

raphy matrix, and use the Hungarian algorithm to

match the poses based on the distances between the

ground points.

Our method also uses reprojection error as in

(de Franc¸a Silva et al., 2022), but now, besides a new

matching process, we also propose a new loss. Dif-

ferently from (de Franc¸a Silva et al., 2022), which

uses the MSE loss, we propose to use the smooth

loss to optimize the network. Although the MSE

loss is a typical approach when we have 2D poses,

as we can see in works such as (Li et al., 2021); for

our neural network smooth L

loss is a better option.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

610

Other works such as (Brynte and Kahl, 2020) also use

smooth L

loss to calculate the reprojection error. The

neural structure in (Lin and Lee, 2021) uses smooth

loss for comparing depths instead of 2D positions.

The smooth L

loss in our 2D comparisons signiﬁ-

cantly improved the results.

This matching process is used only during train-

ing. With the trained model, we can make 3D infer-

ences using the neural network provided by (Lin and

Lee, 2021).

3.1 Reprojection Error

In this section, we brieﬂy review the concept of re-

projection error (Hartley and Zisserman, 2003). We

use this error to compute our loss by comparing 2D

poses during the training process. The reprojection

error will allow us to train without using 3D anno-

tated ground truth.

Using (Lin and Lee, 2021), we estimate a 3D pose

for each 2D pose on the target view. Each estimated

3D pose is projected onto the reference views so that

the 3D pose becomes a 2D pose. Then, we compare

these projected poses with the related 2D pose of the

respective reference view obtained from the matching

process. We calculate the comparison using a smooth

norm deﬁned in our loss.

This way, we can claim that the reprojection error

is the process of projecting a 3D point onto an image

and comparing the position of the projected point with

the measured position of that point in the image.

3.2 Matching Process

This section describes how to perform the matching

process using ground points. We emphasize that this

matching process is used only in the training process.

We do not need to use matching in the inference.

We do unsupervised 3D pose estimation using re-

projection error as in (de Franc¸a Silva et al., 2022).

However, we perform the matching process using

ground points instead of back-projection matching.

The goal of the matching process is to identify the 2D

pose in a reference view related to the projected 2D

pose obtained from the 3D pose estimation. There-

fore, the matching process is crucial. Comparing the

correct 2D poses makes our loss coherent in the train-

ing process for estimating an accurate 3D pose.

The matching process is performed by using

ground points as deﬁned in (Lima et al., 2021) and

illustrated in Figure 2. The ground point is ﬁrst ob-

tained from the 2D pose. A line is built between

the right and left ankle joints, so we take the middle

point on this line, and, using an offset δ, we gener-

ate our ground point. This offset is obtained using the

2D skeleton. With the 2D pose, we take the highest

and lowest value of x and y coordinates; in this man-

ner, we have the dimensions of our bounding box as

in (Xiu et al., 2018). With the estimated bounding

box, we get the maximum y value of the bounding

box (bb

max

) and the highest y value between the right

(ra

) and left (la

) ankle joints, and ﬁnally compute δ

as follows:

δ = bb

max

− max(la

, ra

). (1)

The cameras on the Campus dataset are all cal-

ibrated. These 2D ground points are in the ground

plane; therefore, their Z world coordinate is zero, and

we project these points onto the world coordinate sys-

tem using a homography matrix H as in (Lima et al.,

2021):









= K[R













= K[R









= H

−1









(2)

where K is the intrinsic parameters matrix, and the

extrinsic parameters matrix is [R|t]. The coordinates

(X,Y) are related to the world ground points, and (x,y)

are image points. The R

is the i-th column of R.

We take a pair of views and project the 2D ground

points of each view onto world coordinates, as we see

in Figure 3. We take the Euclidean distance between

each ground point on world coordinates and build a

cost matrix. Each row on this cost matrix corresponds

to the Euclidean distance between the ground point

in the world coordinates of one person on the target

view and all the ground points of the people on a

given reference view. In this manner each element of

the cost matrix is given by d



target

person

,re f erence

person



where d is the distance between the ground points in

world coordinates of two persons in given views. Us-

ing the Hungarian algorithm (Kuhn, 1955), we can get

the matching positions. Instead of using back projec-

tion, we now have a new matching process. This new

method is more robust than back projection because

we only compare one point instead of all the joints of

a 2D pose. We also do not need to make several 3D

projections of all 2D points. We only need to project

UMVpose++: Unsupervised Multi-View Multi-Person 3D Pose Estimation Using Ground Point Matching

611

the ground point in world coordinates. Another rea-

son the new method is more robust than back projec-

tion is that back projection may generate false match-

ings when there is no match in the reference view for

a given pedestrian in the target view. The cost matrix

is as follows:

Cost matrix =







... d

. . . d







. (3)

Figure 4: Some examples of our 3D pose estimation on

Campus Dataset. We provide many results showing the 2D

skeleton estimated and the corresponding 3D pose. These

examples allow us to do a qualitative analysis of our results.

3.3 Loss Function

Considering the neural network structure in (Lin and

Lee, 2021), we keep the same structure and propose

a new loss. Our goal is to use reprojection errors to

avoid the need for 3D labeled data. With the matched

poses and the 2D projections obtained from the esti-

mated 3D pose, it is now possible to compare them

and deﬁne a loss without using ground truth infor-

mation. Differently from UMVpose (de Franc¸a Silva

et al., 2022), we propose to use the smooth L

loss

instead of the MSE loss.

Losses that consist in comparing 2D poses gener-

ally use MSE loss as in (Li et al., 2021). However,

works as (Brynte and Kahl, 2020) use smooth L

loss

to calculate the reprojection error, and besides that,

the neural network in (Lin and Lee, 2021) also use

smooth L

loss.

The deﬁnition of the smooth L

loss is

smooth

(x) =

(

0.5x

if |x| < 1

|x| − 0.5 otherwise.

Using the smooth L

loss in our scenario is similar

to applying an M-estimator function such as the Hu-

ber one when computing the reprojection error. This

contributes to making our approach more robust to

outliers. We also experimented with the Kullback-

Leibler loss regularizer and AdaBelief as an opti-

mizer.

Table 1: Comparing PCP on Campus Dataset of our method

with the one from UMVpose (de Franc¸a Silva et al., 2022).

Method Actor1 Actor2 Actor3 Average

Silva et al. with

Adam

(MSE loss) 78.0 85.1 83.0 82.0

Silva et al. with

Adabelief

(MSE loss) 96.9 87.8 88.9 91.2

Silva et al. with

Adabelief and

KL regularizer

(MSE loss) 93.3 86.8 89.4 89.8

Silva et al. with

Adam

(Smooth L

loss) 98.6 92.7 98.3 96.5

Silva et al. with

Adabelief

(Smooth L

loss) 98.2 92.9 98.2 96.4

Silva et al. with

Adabelief and

KL regularizer

(Smooth L

loss) 97.4 92.5 98.6 96.2

Ours with Adam

and ground

points matching 98.4 93.4 98.6 96.8

In (Lin and Lee, 2021), they have two losses, one

for the person position and the other for the joint posi-

tion. Person position is related to the center hip joint,

that is, a single point. However, joint loss is about

all person’s joints. We propose reprojection error to

compute these losses instead of comparing the esti-

mation with the 3D ground truth. This way, we have

a pose loss (person position) and a joint loss (joint

position). These losses are related to different neu-

ral networks: the person-level depth regression net-

work and the joint-level depth regression network, as

demonstrated in (Lin and Lee, 2021). The pose loss

is deﬁned as

pose

∑

r=0

∑

i=1

||position

(i)

pro j

− position

(i)

re f

(4)

In Equation 4, P is the number of individuals in our

target view, position

(i)

pro j

is our projected pose, and

position

(i)

re f

is the matched pose in the reference

view obtained using ground point matching. The R

value is the number of reference views. The s1 index

is related to the Smooth L

loss. The joint loss is given

joint

∑

r=0

∑

i=1

∑

j=1

|| joint

r, j

(i)

pro j

− joint

r, j

(i)

re f

(5)

where J is the total number of joints, joint

r, j

(i)

pro j

a joint projected onto the respective reference view,

and joint

r, j

(i)

re f

is a joint from the matched 2D pose

in the reference view. The s1 index designates that the

loss uses Smooth L

loss.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

612

4 EXPERIMENTS AND RESULTS

This section presents the 3D pose estimation exper-

iments as illustrated in Figure 4. First, we generate

the 3D pose of multiple persons in a multi-view sce-

nario. Then, we perform the training process using a

public dataset, and the metric evaluated is the Percent-

age of Correctly estimated Parts (PCP) (Wang et al.,

2021). Finally, we evaluate our method by comparing

its PCP with the ones from previous works (geometric

and neural network approaches).

4.1 Dataset

The dataset used was the Campus dataset

(Belagian-

nis et al., 2014a), and the 2D poses were estimated

using HR-Net (Sun et al., 2019), which is pre-trained

on the MS-COCO dataset (Lin et al., 2014), and the

2D pose has 17 joints. The Campus is one of the most

used datasets in works about the multi-view, multi-

person scenario. This dataset was used by the ge-

ometric and supervised methods to which we com-

pared our results. The Campus is an outdoor dataset

with mainly three actors. It was obtained with three

cameras capturing three persons interacting with each

other. The 3D ground truth annotations are incom-

plete, so we use synthesized 3D MoCap poses as in

(Lin and Lee, 2021) to perform our training. As in

previous works (Dong et al., 2019), (Huang et al.,

2020), (Tu et al., 2020), the evaluation is performed

on frames 350-470 and 650-750.

4.2 Metrics

The evaluation metric used is the PCP. This is the met-

ric that other works used, so to be fair in our compar-

ison we also use this metric. PCP (Wang et al., 2021)

is given by

||s

− ˆs

|| + ||e

− ˆe

≤ α||s

− e

||, (6)

where s

and e

are the start and end coordinates of

ground truth n-th body part, ˆs

and ˆe

are the corre-

sponding estimations, and α is a given threshold pa-

rameter, in our case α = 0.5.

4.3 Comparison with UMVpose

Considering the updates in our UMVpose++, we per-

form experiments comparing it with original UMV-

pose (de Franc¸a Silva et al., 2022). We also evaluate

UMVpose using a smooth L

loss.

https://campar.in.tum.de/Chair/MultiHumanPose

Table 2: Comparing PCP on Campus Dataset with the state-

of-the-art.

Method Actor1 Actor2 Actor3 Average

Belagiannis

et al., 2014a 82.0 72.4 73.7 75.8

Belagiannis

et al., 2014b 83.0 73.0 78.0 78.0

Belagiannis

et al., 2015 93.5 75.7 84.4 84.5

Ershadi-Nasab

et al., 2018 94.2 92.9 84.6 90.6

Dong

et al., 2019 97.6 93.3 98.0 96.3

de Franc¸a Silva

et al., 2022 96.9 87.8 88.9 91.2

Ours 98.4 93.4 98.6 96.8

Huang

et al., 2020 98.0 94.8 97.4 96.7

et al., 2020 97.6 93.8 98.8 96.7

Lin and Lee,

2021 98.4 93.7 99.0 97.0

Using ground point matching and smooth L

loss

instead of MSE loss, we obtain better results than

(de Franc¸a Silva et al., 2022) as we see in Table 1.

Keeping the back-projection matching and chang-

ing only the loss function, we got expressive improve-

ments in the PCP values. However, back-projection

is a complex manner of matching between target

and reference views and may also generate incor-

rect matches. Therefore, we change the matching for

using ground points. As a result, the ground point

matching with the Adam optimizer outperforms the

back-projection matching on average and in all actors.

4.4 Comparison with State-of-the-Art

We show Table 2 comparing UMVpose++ with all

other methods. We divided the table into two parts:

the ﬁrst part contains unsupervised/geometric meth-

ods, and the second part includes supervised methods.

We outperform all the unsupervised methods with our

approach using ground points in the matching process

and smooth L

reprojection error loss. We outperform

on average and also in all the actors.

Compared to the supervised methods, we outper-

form (Huang et al., 2020) and (Tu et al., 2020) on av-

erage, being below (Lin and Lee, 2021) only. More-

over, considering that (Huang et al., 2020) and (Tu

et al., 2020) need 3D annotations, our method has an

impressive advantage.

5 CONCLUSION

In this work, we build a solution with an unsupervised

approach using a simpler and more robust matching

UMVpose++: Unsupervised Multi-View Multi-Person 3D Pose Estimation Using Ground Point Matching

613

process. By using ground points, we do not need to

make 3D back-projections to perform the matching,

and by comparing only one point per person, we can

obtain the corresponding poses in two views. Besides

that, instead of comparing the 2D poses with MSE,

we use a smooth L

loss. The results show a huge po-

tential for using unsupervised losses instead of super-

vised ones based on 3D annotations. In future work,

we intend to do experiments on more datasets and to

reﬁne the loss using other regularizers such as Jensen-

Shanon (Fuglede and Topsoe, 2004).

REFERENCES

Belagiannis, V., Amin, S., Andriluka, M., Schiele, B.,

Navab, N., and Ilic, S. (2014a). 3d pictorial structures

for multiple human pose estimation. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 1669–1676.

Belagiannis, V., Amin, S., Andriluka, M., Schiele, B.,

Navab, N., and Ilic, S. (2015). 3d pictorial structures

revisited: Multiple human pose estimation. IEEE

transactions on pattern analysis and machine intelli-

gence, 38(10):1929–1942.

Belagiannis, V., Wang, X., Schiele, B., Fua, P., Ilic, S.,

and Navab, N. (2014b). Multiple human pose estima-

tion with temporally consistent 3d pictorial structures.

In European Conference on Computer Vision, pages

742–754. Springer.

Brynte, L. and Kahl, F. (2020). Pose proposal critic: Robust

pose reﬁnement by learning reprojection errors. arXiv

preprint arXiv:2005.06262.

de Franc¸a Silva, D. W., do Monte Lima, J. P. S., Mac

edo,

D., Zanchettin, C., Thomas, D. G. F., Uchiyama, H.,

and Teichrieb, V. (2022). Unsupervised multi-view

multi-person 3d pose estimation using reprojection er-

ror. In International Conference on Artiﬁcial Neural

Networks, pages 482–494. Springer.

Dong, J., Jiang, W., Huang, Q., Bao, H., and Zhou, X.

(2019). Fast and robust multi-person 3d pose esti-

mation from multiple views. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 7792–7801.

Fuglede, B. and Topsoe, F. (2004). Jensen-shannon diver-

gence and hilbert space embedding. In International

Symposium onInformation Theory, 2004. ISIT 2004.

Proceedings., page 31. IEEE.

Girshick, R. (2015). Fast r-cnn. In Proceedings of the IEEE

international conference on computer vision, pages

1440–1448.

Hartley, R. and Zisserman, A. (2003). Multiple view geom-

etry in computer vision. Cambridge university press.

Huang, C., Jiang, S., Li, Y., Zhang, Z., Traish, J., Deng,

C., Ferguson, S., and Xu, R. Y. D. (2020). End-to-

end dynamic matching network for multi-view multi-

person 3d pose estimation. In European Conference

on Computer Vision, pages 477–493. Springer.

Ionescu, C., Papava, D., Olaru, V., and Sminchisescu, C.

(2013). Human3. 6m: Large scale datasets and pre-

dictive methods for 3d human sensing in natural envi-

ronments. IEEE transactions on pattern analysis and

machine intelligence, 36(7):1325–1339.

Kuhn, H. W. (1955). The hungarian method for the as-

signment problem. Naval research logistics quarterly,

2(1-2):83–97.

Li, Z., Ye, J., Song, M., Huang, Y., and Pan, Z. (2021). On-

line knowledge distillation for efﬁcient pose estima-

tion. In Proceedings of the IEEE/CVF International

Conference on Computer Vision, pages 11740–11750.

Lima, J. P., Roberto, R., Figueiredo, L., Simoes, F., and

Teichrieb, V. (2021). Generalizable multi-camera 3d

pedestrian detection. In Proceedings of the IEEE/CVF

conference on computer vision and pattern recogni-

tion, pages 1232–1240.

Lin, J. and Lee, G. H. (2021). Multi-view multi-person 3d

pose estimation with plane sweep stereo. In Proceed-

ings of the IEEE/CVF Conference on Computer Vision

and Pattern Recognition, pages 11886–11895.

Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P.,

Ramanan, D., Doll

ar, P., and Zitnick, C. L. (2014).

Microsoft coco: Common objects in context. In Euro-

pean conference on computer vision, pages 740–755.

Springer.

Sun, C., Thomas, D., and Kawasaki, H. (2021). Unsuper-

vised 3d human pose estimation in multi-view-multi-

pose video. In 2020 25th International Conference on

Pattern Recognition (ICPR), pages 5959–5964. IEEE.

Sun, K., Xiao, B., Liu, D., and Wang, J. (2019). Deep high-

resolution representation learning for human pose es-

timation. In Proceedings of the IEEE/CVF conference

on computer vision and pattern recognition, pages

5693–5703.

Tu, H., Wang, C., and Zeng, W. (2020). Voxelpose: To-

wards multi-camera 3d human pose estimation in wild

environment. In European Conference on Computer

Vision, pages 197–212. Springer.

Wang, J., Tan, S., Zhen, X., Xu, S., Zheng, F., He, Z., and

Shao, L. (2021). Deep 3d human pose estimation: A

review. Computer Vision and Image Understanding,

210:103225.

Xiu, Y., Li, J., Wang, H., Fang, Y., and Lu, C. (2018). Pose

Flow: Efﬁcient online pose tracking. In BMVC.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

614