An Efﬁcient Uniﬁed Architecture for Polynomial Multiplications in

Lattice-Based Cryptoschemes

∗

Francesco Antognazza

1 a

, Alessandro Barenghi

1 b

, Gerardo Pelosi

1 c

and Ruggero Susella

Politecnico di Milano, Milano, Italy

STMicrolectronics S.r.l., Agrate Brianza (MB), Italy

Keywords:

Lattice-Based Cryptography, Hardware Accelerators, Polynomial Ring Multipliers.

Abstract:

The signiﬁcant effort in the research and design of large-scale quantum computers has spurred a transition to

post-quantum cryptographic primitives worldwide. The post-quantum cryptographic primitive standardization

effort led by the US NIST has recently selected the asymmetric encryption primitive Kyber as its candidate

for standardization. It has also indicated NTRU, another lattice-based primitive, as a valid alternative if in-

tellectual property issues are not solved. Finally, a more conservative alternative to NTRU, NTRUPrime was

also considered as an alternate candidate, due to its design choices which remove the possibility for a large

set of attacks preemptively. All the aforementioned asymmetric primitives provide good performances, and

are prime choices provide IoT devices with post-quantum conﬁdentiality services. In this work, we propose

a uniﬁed design for a hardware accelerator able to speed up the computation of polynomial multiplications,

the workhorse operation in all of the aforementioned cryptosystems, managing the differences in the polyno-

mial rings of the cryptosystems. Our design is also able to outperform the state of the art designs tailored

speciﬁcally for NTRU, and provide latencies similar to the symmetric cryptographic elements required by the

scheme for Kyber and NTRUPrime.

1 INTRODUCTION

Public-key cryptography (PKC) plays a fundamental

role in today’s technology providing the properties

of conﬁdentiality, data and origin authentication and

non-repudiability, and its diffusion is witnessed by the

number of widely-used protocols that rely on it, such

as TLS and PGP. PKC primitives are in wide use to

encrypt data between two parties without a pre-shared

secret over an insecure channel, or to build a Pub-

lic Key Infrastructure, and to guarantee the integrity

and authenticity of data in form of digital signatures.

Currently the most used algorithms, RSA and Ellip-

tic Curve cryptography, rely on the hardness of inte-

ger factoring, or the hardness of computing discrete

logarithm in ﬁnite cyclic groups. However, in 1994,

Peter Shor designed an algorithm for quantum com-

puters which solves both the prime factoring and dis-

crete logarithm problems with an exponential speedup

https://orcid.org/0000-0003-3480-486X

https://orcid.org/0000-0003-0840-6358

https://orcid.org/0000-0002-3812-5429

∗

This Research Was Made Possible Thanks to the Sup-

port of STMicroelectronics.

with respect to classical computers, effectively break-

ing the corresponding cryptosystems (Sklavos et al.,

2017).

Due to the long term conﬁdentiality and

data/origin authentication guarantees required from

asymmetric cryptographic primitives, and in sight of

the recent advancements in the implementation of

quantum computers, a signiﬁcant effort in standard-

izing quantum-resistant algorithms for public-key

cryptography is urgently required. For that reason,

the National Institute of Standards and Technology

(NIST) in 2016 started the Post-Quantum Cryptogra-

phy (PQC) standardization process to assess viable

candidates either for Public Key Encryption (PKE),

in form of a Key Encapsulation Mechanism (KEM),

and for digital signatures. The process reﬁned its 69

candidate algorithms, reducing them to to a single

KEM and three digital signatures for immediate

standardization at the end of the third round (NIST

PQC Team, 2022). Furthermore NIST provided a list

of candidates which are still under investigation as

alternate, as they rely on different computationally

hard problems. Arguably the the most successful

class of algorithms of this standardization process is

Antognazza, F., Barenghi, A., Pelosi, G. and Susella, R.

An Efﬁcient Uniﬁed Architecture for Polynomial Multiplications in Lattice-Based Cryptoschemes.

DOI: 10.5220/0011654200003405

In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 81-88

ISBN: 978-989-758-624-8; ISSN: 2184-4356

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

lattice-based algorithms, being attractive in terms of

computational latency and with acceptable key and

ciphertext sizes.

Besides the candidate selected for immediate stan-

dardization, Kyber, three other schemes were deemed

particularly interesting in the contest: NTRU, NTRU

Prime and Saber. NTRU was ofﬁcially recommended

as the fallback alternative in case patent issues cannot

be solved by the end of 2023 (Alagic et al., 2022);

NTRU Prime is an NTRU variant with conservative

choices in the underlying algebraic structure, which

prevent a number of attacks preemptively; Saber is

based on a slightly different algebraic problem with

respect to Kyber (Module Ring-learning with round-

ings instead of Module Ring-learning with errors)

which is at least as computationally hard as the one

of Kyber.

The four aforementioned lattice based cryptosys-

tems rely on the arithmetics of polynomials with in-

teger coefﬁcients modulo q, where q is either a power

of two, or a small prime; all considered modulo a

polynomial with a low number of terms. Depending

on the choices, the polynomial ring obtained may be

more or less friendly to sub-quadratic multiplication

techniques. Among such techniques, the Number-

Theoretic Transform (NTT) is the most efﬁcient way

to perform a multiplication, provided that the max-

imum degree of the polynomial generating the ring

is a power-of-two and the coefﬁcient ring is modulo

a prime: given an n degree polynomial, it runs in

O(nlog

(n))) sequential steps. By contrast, efﬁcient

versions of the schoolbook algorithm, which runs in

O(n

) such as the one by Comba, can always be ap-

plied, leading to extremely compact designs but also

reduced throughput. Software and hardware imple-

mentations of the multiplication algorithms also rely

on divide-et-impera techniques such as Karatsuba or

Toom-Cook decompositions: these techniques trade

off an increased design complexity and larger con-

stants hidden in the O notation for a constant decrease

in the complexity exponent. An emerging hardware

design approach is the one known in the literature

as x-net or LFSR-based multiplier. Its undelrying

idea is to perform n coefﬁcient-wise multiplications

per clock cycle, resulting in a total computation time

which is O(n).

Contributions. Our work aims to show that it is pos-

sible to have a uniﬁed design for an hardware accel-

erator computing the polynomial multiplication in all

the polynomial rings of the four lattice-based cryp-

tosystems: Kyber, NTRU, NTRU Prime and Saber.

The structure of such an accelerator stems from an

architecture able to achieve efﬁciency results beyond

the state of the art for NTRU-like cryptosystems. We

provide efﬁciency results of a synthesis-time special-

ized accelerator for the arithmetic used by NTRU

HPS and HRSS, NTRU Prime, Saber and Kyber cryp-

toschemes, namely every round-3 lattice-based KEM

proposals at NIST’s Post-Quantum standardization

contest. Subsequently, we provide a uniﬁed design

supporting all the polynomial rings, for all security

levels of the KEMs, allowing cryptographic agility

without the need of replacing the hardware compo-

nent. We validated the correctness of the results, gath-

ered the performance and resource ﬁgures for every

parameter set speciﬁed by the latest speciﬁcations, for

both an FPGA design ﬂow. We note that our design

uses a sequential memory layout to store polynomial

coefﬁcients in memory, and accesses them in a sin-

gle sweep: our design is thus eligible to be be used

in a pipelined fashion, a feature not achievable with

current NTT based multipliers.

2 BACKGROUND

In this section, we provide a summary of the polyno-

mial arithmetics for the polynomial rings employed

in Kyber, NTRU, NTRU Prime and Saber. Subse-

quently, we provide a summary of linear-time hard-

ware modular multipliers obtained with the x-net

technique. In the following, we will denote polyno-

mials of degree n with lowercase letters, highlighting

the variable, as a(x) =

∑

n−1

i=0

The aforementioned cryptosystems consider the

arithmetics over two quotient polynomial rings each,

and R

are Z

[x]/

p(x)

and Z

[x]/

p(x)

. The

differences in the ring structures arise from the choice

of the values of p,q and p(x), of which a summary is

reported in Table 2. In particular, p is always chosen

to be a small odd number between 3 and 11; q is ei-

ther a small power of two (between 2

and 2

) or a

prime number of the same order of magnitude. The

latter choice yields polynomials with coefﬁcient over

a ﬁeld, Z

, while the former choice allows a trivial

modular reduction mod q via truncation of the most

signiﬁcant bits.

The polynomial employed to obtain the quotient

ring, p(x) gives R

and R

a cyclic structure in Kyber

and Saber (x

+ 1), a nega-cyclic structure in NTRU

− 1). The cyclic structure name stems from the

fact that, given an element a(x ) ∈ R

, computing the

result of x · a(x) is equivalent to cyclically shifting its

coefﬁcients towards the higher degrees by one po-

sition. Similarly, the nega-cyclic structure implies

that the same cyclic shift takes place, but a sign ﬂip

of the constant term also takes place after the cyclic

shift. The authors of NTRU Prime chose x

−x −1 as

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

Table 1: Number of R

× R

multiplications in encapsu-

lation and decapsulation primitives of each analyzed cryp-

toschemes. One further R

× R

multiplication is used

during the decapsulation in NTRU, denoted by ? symbol.

Module-based cryptoschemes Saber and Kyber perform one

k ×k matrix-vector and either one or two vector-vector mul-

tiplications, where the elements are polynomials in R

, during encapsulation and decapsulation, respectively.

Cryptoscheme

Module Multiplications

rank k Encap. Decap.

NTRU / 1 2

NTRU Prime / 1 3

NTRU LPRime / 2 3

Saber 2,3,4 k

+ k k

+ 2k

Kyber 2,3,4 k

+ k k

+ 2k

Table 2: Summary of the features of the polynomial rings

= Z

[x]/

p(x)

and R

= Z

[x]/

p(x)

for each KEM.

Scheme q p n p(x)

Kyber

prime

5, 7

+ 1

valori 256

Saber

7, 9, 11

+ 1

valori 256

NTRU

prime

− 1

valori valori

NTRU Prime

prime

− x − 1

valori valori

the polynomial modulus, thus obtaining polynomial

ﬁelds for R

and R

: this removes constraints further

the ring structure which is present in Kyber and Saber,

preventing future attacks which may exploit it.

To align our notation with the one of the cipher

speciﬁcations, we will consider the representatives of

the coefﬁcient ring as the integers balanced around the

zero element, for example between −

(q − 1)/2

and

(q − 1)/2

Modular Polynomial Multiplication Algo-

rithms. Modular Polynomial multiplications with

large operands are extremely common in crypto-

graphic primitives, and have thus seen signiﬁcant

efforts in their optimization. A ﬁrst classiﬁcation

criterion is the strategy which is employed to perform

the modular polynomial reduction: indeed, depend-

ing on the algorithm being employed, it is sometimes

possible to interleave the reduction operation with the

intermediate steps of the multiplication algorithm,

saving on the memory elements required for the

computation. The second classiﬁcation criterion

is the asymptotic complexity of the multiplication

method, counted as the number of coefﬁcient-wise

multiplications, as a function of the number of

coefﬁcients of the operands, n.

The operand scanning, schoolbook method in-

volves O(n

) coefﬁcient-wise multiplications as it

adds together all the results of multiplying the ﬁrst

polynomial factor by each one of the monomials com-

posing the second factor. Sub-quadratic methods, pi-

oneered by Karatsuba (Karatsuba, 1963), provide an

algorithm to compute the polynomial multiplication

in O(n

log

(2a−1)

), where a ≥ 2, coefﬁcient-wise mul-

tiplications. In particular, Karatsuba proposed the al-

gorithmic variant for a = 2, while Toom and Cook

generalized the result for a > 2. The reason for avoid-

ing the ubiquitous application of such methods is that,

while the number of coefﬁcient-wise application de-

creases, they require an increasing number of poly-

nomial additions and subtractions to compute the re-

sult. While additions and subtractions have a lin-

ear cost in n, their overhead offsets the gains com-

ing from saving multiplications for small values of n.

Given that the ratio between the absolute values of

the computational costs of multiplications and addi-

tions/subtractions varies depending on the platform it

is commonplace to determine the break-even value for

a through exhaustive evaluation for a speciﬁc design.

In our context, Karatsuba was used in (Marotzke,

2020) instantiating three parallel schoolbook Comba

multipliers, and (Dang et al., 2021) design involved

a 3-way Toom-Cook computing ﬁve parallel multipli-

cations recursively with odd-even Karatsuba method.

Finally, it is possible to compute polynomial mul-

tiplications in O(n log

(n)) exploiting Fourier trans-

forms. The method relies on the fact that multi-

plying two polynomials can be seen as the convo-

lution of their coefﬁcients, interpreted as integer se-

quences. This allows to perform the multiplication

computing the discrete-time Fourier transform of the

sequences, performing the element-wise multiplica-

tion of the results and computing the inverse Fourier

transform. The total cost of the operation depends

on the cost of computing the Fourier transform, to

which a linear amount of coefﬁcient-wise multiplica-

tions must be added. For the special case where n is a

power of two, computing the Fourier transform takes

O(nlog

(n)), thus resulting in a O(2(n log

(n)) +

n) = O(n log

(n)) cost for the entire multiplication.

This technique is applied fruitfully to polynomials in

a ring Z

[x]/

p(x)

, provided that the degree of p(x )

is a power of two, and that Z

is a ﬁeld, thus providing

all the required roots of unity, and goes by the name

of Number Theoretic Transform (NTT) (Dang et al.,

2021). As it is the case for the sub-quadratic multipli-

cation techniques, also the NTT requires some linear-

time operations to be computed, and thus the break-

even point for the value of n is sought experimentally.

Of the four cryptosystems we are considering, only

Kyber has a parameter choice which allows the use of

An Efﬁcient Uniﬁed Architecture for Polynomial Multiplications in Lattice-Based Cryptoschemes

NTT based techniques.

Linear-Time Modular Multiplication Algorithms.

An orthogonal approach to the redesign of the multi-

plication algorithm is the one which exploits the in-

herent parallelism of the schoolbook approach. In-

deed, all the coefﬁcient-wise multiplications involved

in a factor-times-monomial product can be computed

independently. This observation leads to the design of

a linear-time multiplication algorithm which exploits

n computation units and n coefﬁcient-wide memories

to compute the entire product in O(n).

The ﬁrst proposal of a linear-time modular multi-

plication algorithm specialized for the NTRUEncrypt

polynomial ring comes from (Liu and Wu, 2015). The

work achieves the multiplication in n clock cycles us-

ing n parallel multiply-and-accumulate (MAC) units.

Furthermore, to reduce the area of each MAC unit, the

work replaces the multiplier with a multiplexer, which

selects one of the three possible coefﬁcient-wise mul-

tiplication outcomes, thanks to the small size of the

coefﬁcients of the R

operand.

This approach was then separately adapted for dif-

ferent polynomial rings of Saber, NTRU, and NTRU

Prime cryptoschemes in (Basso and Roy, 2021; Dang

et al., 2021; Farahmand et al., 2019). The authors of

(Basso and Roy, 2021) proposed a centralized way to

compute the few possible coefﬁcient-wise multiplica-

tion results, and distribute them to every MAC unit. In

(Peng et al., 2021) it is proposed to postpone the re-

duction mod q of the coefﬁcients of the multiplication

result to the end of the multiplication. This approach

entails larger accumulators to store them, while allow-

ing to save area as only a single modular reduction

unit is required.

3 PROPOSED ARCHITECTURE

Algorithm 1: x-Net polynomial multiplier.

Input: a(x) ∈ Z

[x]/hp(x)i, a(x) =

∑

n−1

i=0

b(x) ∈ Z

[x]/hp(x)i, b(x) =

∑

n−1

i=0

Output: r(x) = LIFT



a(x),Z

[x]/hp(x)i



b(x)

Data: p(x) ∈ Z

[x], monic, with degree n

1 r(x) ← 0

2 for i = 0 to (n − 1) do

3 r(x) ← r(x) + b

· a(x) // n parallel MACs

4 a(x) ← a(x) · x mod p(x) // via LFSR

5 return r(x)

In this section we ﬁrst provide a uniﬁed description of

the x-net approach to polynomial multiplication, for a

generic polynomial modulus p(x). Subsequently, we

employ our framework to describe the x-net multiplier

design for each one of the four polynomial rings re-

quired in Kyber, Saber, NTRU and NTRU Prime. Fi-

nally, we describe our uniﬁed multiplier architecture.

In the following, we consider the case of the mul-

tiplication of two polynomials where the ﬁrst has co-

efﬁcients in Z

, while the second has coefﬁcients in

and the product has coefﬁcients in Z

, which is the

polynomial multiplication taking place in all the four

cryptosystems at hand. The operation is intended to

be computed lifting the coefﬁcients of the ﬁrst poly-

nomial Z

simply reconsidering their values as being

in Z

. We note that NTRU also requires a multipli-

cation between two polynomials with coefﬁcients in

: the description in the following also covers this

case, simply substituting appropriately sized signals

and registers where needed.

The idea underpinning the x-net multiplication

is to rewrite the computation of the polynomial

ring multiplication a(x)·b(x) = r(x) mod p(x), where

each polynomial is in the form p(x) =

∑

n−1

i=0

, as

described in Algorithm 1. In the following, we will

assume that p(x) is monic, as it is always the case

in practice. The polynomial multiplication is de-

composed as a sequence of coefﬁcient-by-polynomial

multiplications and polynomial additions (line 3), and

multiplications by x and modular reductions (line 4).

The hardware structure of the x-net multipliers,

depicted in Figure 1 for the ring Z

[x]/

+ 1

tack-

les the two operations with two logical component

complexes.

The operation r(x) + b

· a(x ) is performed with

n independent Multiply and Accumulate (MAC) el-

ements which compute the product of the coefﬁcient

by each coefﬁcient of polynomial a(x), and add the

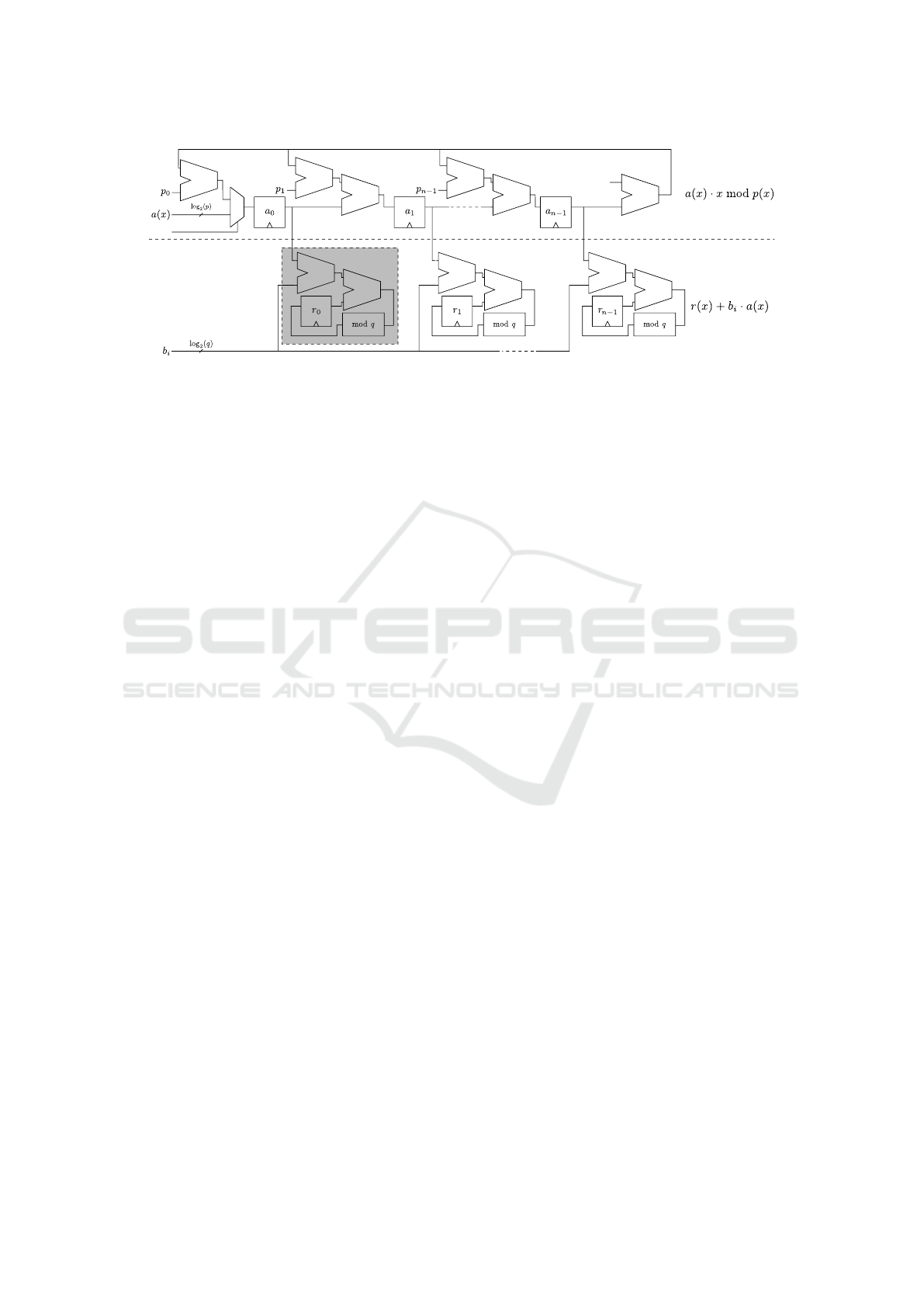
result to the corresponding coefﬁcient of r(x). One

MAC element is highlighted in grey in Figure 1, and

is composed by a multiplier, an adder, a register able

to contain a coefﬁcient of the result and a modular

reducer mod q.

The computation of a(x) ← a(x) · x is efﬁciently

done storing the coefﬁcients of a(x) in a shift regis-

ter, as the multiplication by x acts shifting the coef-

ﬁcients by one position towards higher degree mono-

mials (to the right, in Figure 1). The computation of

the modular reduction of a(x) ← a(x ) · x mod p(x) is

done efﬁciently, considering that a(x) · x has degree

at most n, and therefore a single polynomial subtrac-

tion is sufﬁcient to compute the mod p(x) operation.

To this end, the portion of the x-net multiplier man-

aging the operation (top portion of Figure 1) subtracts

n−1

p(x) from a(x) · x, materially adding the coefﬁ-

cients of (−a

n−1

)p(x) to the ones of a(x) · x by per-

forming the addition between any two elements of

the shift-register which contains a(x). This network

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

Multiply

and accumulate

MUL

ADD

MUL

ADD

MUL

ADD SUB

load

Computation

MUL

ADD

MUL

ADD

Figure 1: Structure of an x-net multiplier computing the product r(x) = (a(x)·b(x)) mod p(x). The top portion of the modular

multiplier takes care of computing x

· a(x) mod p(x) at the i-th clock cycle, while the bottom part performs the coefﬁcient-

by-polynomial multiplication.

structure will thus need as many multipliers and adder

as the number of non-null coefﬁcients in p(x), bene-

ﬁting from values of p(x) with a very small number

of coefﬁcients, as it is the case in the four considered

cryptosystems.

x-net Optimizations. The ﬁrst observation leading to

an optimization is that the topmost portion of the x net

multiplier may operate entirely with values mod p,

leading to a signiﬁcant saving in the resource con-

sumption. The lifting required to multiply coefﬁcient

in Z

by coefﬁcients in Z

is done within the mul-

tiplier units in the MAC elements simply by sign-

extending the two’s complement representation of the

element.

The second observation leading to an optimization

is that, in case p is very small, as it is the case in our

cryptosystems, the multiplier in the MAC can be sub-

stituted by a multiplexer which selects among a small

set of ﬁxed multiples of b

, which are computed by

a small number of additions. Taking as an example

p = 5, the multiplier is substituted by a multiplexer

selecting among the values {−2b

,−b

,0,b

,2b

} de-

pending on the value of the coefﬁcient of the a(x)

polynomial. The values can be either precomputed

only once, and distributed, or computed within the

MAC unit and selected in place. The former solution

trades off area savings for a higher wiring congestion.

A ﬁnal point concerning the optimization of the

x net multiplier is the tradeoff between performing

modular reductions in the multiply and accumulate

complex managing the coefﬁcients of the result, and

performing the reductions upon result readout. The

reductions-at-readout approach requires accumulator

registers for r(x ) of dlog

(2npq) + 1e bits, as n val-

ues mod q will be added by the x net multiplier dur-

ing its operation. This increase in area is however

compensated by the removal of the modq reducers

from each multiply and accumulate complex, which

typically take more area, unless the reduction by q is

trivial (e.g., q is a power of two). We explored both

strategies devising modular reducers as follows. In

the former case, each accumulator register has log

bits size, and we perform the mod q by conditionally

applying additions and subtractions. Since the dis-

tance between each integer multiplication result and a

valid Z

element is at most (q − 1)·

(p − 1)/2

, then

(p − 1)/2

additions and subtractions are carried out

in parallel with values multiple of q and the only valid

result in Z

is selected. In case of the coefﬁcient in-

teger ring reduction operation performed during the

readout a single Barrett reduction module is used.

Specialized and Uniﬁed x-net Designs. We now de-

scribe the specializations which have to be enacted

for the design of the x-net multiplier for all the four

cryptosystems at hand. For NTRU and Saber, q is a

power-of-two, therefore there is no advantage in per-

forming a delayed modular reduction of the coefﬁ-

cients, as it amounts to a simple bit truncation. The

feedback network of the computation is very small

for all the four cryptosystems. Both Kyber and Saber

only require a subtractor to ﬂip the sign of the a

n−1

coefﬁcient before being fed back to the multipliers

and adders; NTRU only requires that a

n−1

itself is

fed back (as p(x) = x

−1) and NTRU Prime requires

feeding back a

n−1

into two multiply and add elements

(as p(x) = x

− x − 1).

Providing a single uniﬁed design for all the four

cryptosystems was achieved considering the largest

among all the register sizes required by the four

designs, and inserting multiplexers regulating the

kind of coefﬁcient-wise modular reduction being per-

formed, which multiply-add elements are active on

the feedback network of the register containing a(x),

and whether or not the sign of a

n−1

should be ﬂipped.

Multiplying in Less than 3n Cycles. In our design,

we also explored the possibility of reducing the multi-

An Efﬁcient Uniﬁed Architecture for Polynomial Multiplications in Lattice-Based Cryptoschemes

Table 3: Results of the synthesis targeting an Xilinx UltraScale+ ZCU106 FPGA for every NTRU, NTRU Prime, Saber and

Kyber parameter. The results are reported for a design transferring 4 small coefﬁcients per clock cycle and either 1 or 2

large coefﬁcients per clock cycle. Results of each conﬁguration are grouped by security level (from top to bottom: AES-128,

AES-192, AES-256 equivalent security, plus three “above AES-256” parameter sets available in NTRU Prime).

Coefﬁcient

Parameter set

Loading 4 small and 1 large coefﬁcient per CC Loading 4 small and 2 large coefﬁcients per CC

Reduction

CLB CC

Freq. Latency (µs) AT product

CLB CC

Freq. Latency (µs) AT product

done at MHz Enc. Dec. Enc. Dec. MHz Enc. Dec. Enc. Dec.

readout kyber512 3186 585 328 10.70 14.27 34 45 5460 329 291 6.78 9.04 37 49

readout sntrup653 8138 1479 288 5.14 15.41 41 125 11867 827 238 3.48 10.43 41 123

readout ntrulpr653 8138 1479 288 10.27 15.41 83 125 11867 827 238 6.95 10.43 82 123

each CC kyber512 4226 583 312 11.21 14.95 47 63 6508 327 197 9.96 13.28 64 86

each CC ntruhps2048509 2150 1153 638 1.81 5.42 3

11 4455 645 438 1.47 4.42 6

each CC sntrup653 8411 1477 275 5.37 16.11 45 135 13992 825 200 4.12 12.38 57 173

each CC ntrulpr653 8411 1477 275 10.74 16.11 90 135 13992 825 200 8.25 12.38 115 173

each CC lightsaber 2468 583 581 6.02 8.03 14 19 4200 327 375 5.23 6.98 21 29

readout kyber768 2615 585 312 22.50 28.12 58 73 4733 329 291 13.57 16.96 64 80

readout sntrup761 9043 1722 312 5.52 16.56 49 149 13762 962 238 4.04 12.13 55 166

readout ntrulpr761 9043 1722 312 11.04 16.56 99 149 13762 962 238 8.08 12.13 111 166

each CC kyber768 3202 583 328 21.33 26.66 68 85 5579 327 206 19.05 23.81 106 132

each CC ntruhps2048677 2825 1531 625 2.45 7.35 6

20 6208 855 475 1.80 5.40 11

each CC ntruhrss701 3336 1585 600 2.64 7.93 8

26 7428 885 425 2.08 6.25 15

each CC sntrup761 9691 1720 325 5.29 15.88 51 153 16429 960 188 5.11 15.32 83 251

each CC ntrulpr761 9691 1720 325 10.58 15.88 102 153 16429 960 188 10.21 15.32 167 251

each CC saber 3019 583 553 12.65 15.81 38 47 4993 327 425 9.23 11.54 46 57

readout kyber1024 2615 585 312 37.50 45.00 98 117 4733 329 291 22.61 27.13 107 128

readout sntrup857 10141 1938 312 6.21 18.63 62 188 15404 1082 238 4.55 13.64 70 210

readout ntrulpr857 10141 1938 312 12.42 18.63 125 188 15404 1082 238 9.09 13.64 140 210

each CC kyber1024 3202 583 328 35.55 42.66 113 136 5579 327 206 31.75 38.09 177 212

each CC ntruhps4096821 3712 1855 562 3.30 9.90 12

36 8052 1035 438 2.36 7.09 19

each CC sntrup857 11142 1936 312 6.20 18.61 69 207 19034 1080 188 5.74 17.23 109 328

each CC ntrulpr857 11142 1936 312 12.41 18.61 138 207 19034 1080 188 11.49 17.23 218 328

each CC ﬁresaber 3245 583 497 23.46 28.15 76 91 5796 327 400 16.35 19.62 94 113

readout sntrup953 11073 2154 312 6.90 20.71 76 229 18111 1202 238 5.05 15.15 91 274

readout ntrulpr953 11073 2154 312 13.81 20.71 152 229 18111 1202 238 10.10 15.15 182 274

each CC sntrup953 12770 2152 312 6.90 20.69 88 264 21165 1200 188 6.38 19.15 135 405

each CC ntrulpr953 12770 2152 312 13.79 20.69 176 264 21165 1200 188 12.77 19.15 270 405

readout sntrup1013 12022 2289 312 7.34 22.01 88 264 19201 1277 238 5.37 16.10 103 309

readout ntrulpr1013 12022 2289 312 14.67 22.01 176 264 19201 1277 238 10.73 16.10 206 309

each CC sntrup1013 13017 2287 275 8.32 24.95 108 324 22219 1275 188 6.78 20.35 150 452

each CC ntrulpr1013 13017 2287 275 16.63 24.95 216 324 22219 1275 188 13.56 20.35 301 452

readout sntrup1277 14735 2883 325 8.87 26.61 130 392 23332 1607 238 6.75 20.26 157 472

readout ntrulpr1277 14735 2883 325 17.74 26.61 261 392 23332 1607 238 13.51 20.26 315 472

each CC sntrup1277 16686 2881 262 11.00 32.99 183 550 27283 1605 200 8.03 24.08 218 656

each CC ntrulpr1277 16686 2881 262 21.99 32.99 366 550 27283 1605 200 16.05 24.08 437 656

plication time under 3n cycles. Indeed, the described

architecture uses n clock cycles to load the a(x) from

memory, n cycles to compute the result of the mod-

ular multiplication (potentially without coefﬁcient-

wise modular reduction), and n cycles to read out the

ﬁnal polynomial multiplication result and store it into

the memory. This process can be sped up devising a

memory bus transferring multiple polynomial coefﬁ-

cients at once. Transferring α, β and γ coefﬁcients

for respectively the small, large and result polyno-

mials, the overall latency of a polynomial multipli-

cation is

n/α

n/β

n/γ

. Loading α coefﬁ-

cients of a(x) for each clock cycle is achieved trans-

ferring them in parallel from main memory, and hav-

ing the shift register containing a rotate by α posi-

tions at each clock cycle through appropriate connec-

tions. The same approach is applied for reading out γ

coefﬁcients of the result from the accumulator regis-

ters, possibly instantiating γ parallel Barrett modules

when performing the reductions-at-readout approach.

To compute the multiplication of β Z

coefﬁcients in

parallel, we need a total of β · n MACs. Indeed, to

compute the result of β multiplication steps, β mul-

tiplications and sums need to be computed at each

clock cycle, to obtain the result which is to be stored

β − 1 cells to the right of each MAC unit. Further-

more, it is to be noted that β steps of the update of

a(x) should be computed in a single step. This in turn

requires to perform β − 1 sign ﬂips of the Z

coefﬁ-

cient for speciﬁc MAC units of Kyber and Saber, and

additional 2(β −1) multiply and additions for speciﬁc

MAC units of NTRU Prime.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

Table 4: Comparing results of our x-net and x

-net with

(Farahmand et al., 2019) (a), and (Carter et al., 2022) (b)

with multiplier architectures adaptable to multiple cryp-

toschemes targeting a UltraScale+ target. The count of

clock cycles do not consider the time to transfer the

operands and the result. No DSP were used.

Work Par. set CLB Freq. CC LUT FF BRAM

x-net sntrup761 6757 312 762 38798 21768 2

(a) sntrup761 9699 255 762 65207 32929 6

x-net ntruhrss701 3088 588 702 18383 10898 2

(a) ntruhrss701 5476 300 702 33230 32327 6

-net ntruhps4096821 7766 412 413 46293 12029 2

(b) ntruhps4096821 8728 187 412 54478 9227 -

-net ﬁresaber 5602 338 129 30809 4654 2

(b) ﬁresaber 3427 310 128 22127 7841 -

4 EXPERIMENTAL RESULTS

In this section we present the results of our synthe-

sis campaign on specialized x-net multipliers for all

the four cryptosystems we considered, and compare

them with the current state of the art solutions. Fur-

thermore, we report the ﬁgures of merit of our uni-

ﬁed multiplier design. The correctness of the results

of our multipliers was tested through testbenches ob-

tained with a synthetic computation model written in

SageMath. We tested the correctness of the polyno-

mial multiplication for every ring deﬁned by the pa-

rameter sets of Kyber, Saber, NTRU and NTRU Prime

cryptoschemes.

We conducted our syntheses for the Xil-

inx UltraScale+ ZCU106 FPGA (target

xczu7ev-ffvc1156-3-e) using Vivado 2021.1

with FLOW ALTERNATEROUTABILITY and PERFOR-

MANCE NETDELAY HIGH strategies for synthesis and

implementation. We explored four different choices

of the amount of coefﬁcients being loaded namely

loading either one or four small coefﬁcients, and one

or two large coefﬁcients. As the conﬁgurations load-

ing four small coefﬁcients achieve better performance

ﬁgures (transferring two large coefﬁcients) and better

area-time product (transferring one large coefﬁcient)

than their alternatives, we report their results for the

sake of brevity. We thus have that the ﬁrst operand is

loaded into the registers 4 coefﬁcients at a time, with

a transfer of data from 8 to 16 bits per clock cycle

depending on the cryptoscheme and parameter set.

Finally, we report the results of our uniﬁed multi-

plier design, able to support all security levels pro-

posed for standardization to NIST, for all the four

ciphers in Table 5. We also report the potential ad-

vantage of leaving out Saber, as a means of com-

parison. Our uniﬁed design provides complete run-

time ﬂexibility at a cost of 36% more area resources,

than the largest tailored component required to run the

most demanding cipher it also runs. Furthermore, the

Table 5: Results of the synthesis targeting an Xilinx Ultra-

Scale+ ZCU106 FPGA compatible with parameter sets up

to security level 5. The uniﬁed design is conﬁgured to trans-

fer 4 small coefﬁcients and 1 large coefﬁcients per clock cy-

cle, and each parameter set can be selected at runtime. Two

DSPs and two BRAMs were used by both designs.

Supported Ciphers CLB Freq. LUT FF CARRY8

NTRU, NTRU Prime

15155 250 92575 27171 3452

Saber, Kyber

NTRU, NTRU Prime

11318 250 72089 25439 3442

Kyber

achieved running frequency is only 15% slower than

the slowest component it encompasses, while taking

no penalty on the number of clock cycles taken to

compute any of the multiplications with respect to a

dedicated design. Removing the support to Saber’s

polynomial rings, the area penalty drops to < 2%.

The results of our exploration are reported in Ta-

ble 3, in which we report the resource occupation

in Cell Logic Blocks (CLBs) of each multiplier, the

number of clock cycles taken for an entire modu-

lar multiplication, and the maximum target frequency

that the design was able to reach, obtained repeating

syntheses with a binary search strategy. Furthermore,

we also report the total latency taken by all R

× R

multiplications in the key encapsulation (encryption)

and key decapsulation (decryption) primitives of the

scheme, as some schemes require more than a sin-

gle multiplication (see Section 2). We evaluated both

coefﬁcient ring reduction strategies (at each clock cy-

cle, and upon readout) for NTRU Prime and Kyber

to determine which solution is to be preferred when

targeting an FPGA design.

By comparing the results among equivalent secu-

rity level, we can see that the time spent in polynomial

multiplications is larger in Kyber (a module RLWE

scheme) and Saber (a module RLWR) with respect to

NTRU-based schemes. Moreover, this difference in-

creases with the security level. This fact is balanced

by the ﬂexibility of Kyber and Saber schemes, which

have an almost identical polynomial multiplier usable

in every parameter set. As it can be clearly seen, given

the large amount of parameter sets for NTRU Prime,

the latency of the multiplication for our design and

this cryptoscheme is linear in the degree of the poly-

nomials. As a consequence the performance penalty

imposed by larger security levels grows more slowly

than for Kyber and Saber.

When comparing the coefﬁcient ring reduction

techniques, we note that delaying the reduction to the

readout yields a massive gain in logic resources uti-

lization and slight increase of working frequency, at

the cost of a moderate increase in Flip Flops. The

count of CLBs provides a joint indicator of the sil-

icon area employed since combines the number of

An Efﬁcient Uniﬁed Architecture for Polynomial Multiplications in Lattice-Based Cryptoschemes

used memory elements (Flip Flops) and boolean logic

implementation resources (Lookup Tables), and con-

ﬁrms that using this coefﬁcient reduction approach

decreases substantially the consumed FPGA area. We

report in tables the Area-Time (AT) product as an ef-

ﬁciency indicator to compare the designs, and com-

puted as the number of occupied CLBs times the

execution time in milliseconds. The gathered data

suggests that the x-net architecture is one order of

magnitude more efﬁcient when employed to compute

polynomial multiplications during encapsulations in

NTRU rings. During the decapsulation, this no longer

holds, as we recall that one of the three multiplica-

tions speciﬁed in round 3 submission of NTRU does

not have one operand with small coefﬁcients, thus re-

quiring an additional cost (indicated with a ? marker

in the table).

Table 4 reports the comparison of our

cryptosystem-specialized designs with the exist-

ing state of the art on NTRU and NTRU Prime linear

time multipliers. We note that our design achieves a

30% to 40% reduction in the required CLBs for both

cryptosystems, when comparing our solution which

loads a single large coefﬁcient (x-net) with the one

in (Farahmand et al., 2019). Furthermore, we also

obtain a 28% to 96% gain in working frequency with

respect to the same design, therefore achieving also a

higher area-time efﬁciency. We compare our solution

loading two large coefﬁcients at once, with the only

currently available datapoint in the public technical

report (Carter et al., 2022). The solution reported in

the technical report, where it is denoted as x

-net,

is 10% larger in area a 2.2× slower in the working

frequency for the design for NTRU. These results

show how the x-net design is a remarkable ﬁt for the

× R

multiplications in NTRU and NTRU Prime.

5 CONCLUSION

In this work, we analyzed a ﬂexible design for linear-

time polynomial multiplications, applicable to ac-

celerate four post-quantum cryptographic primitives:

Kyber, Saber, NTRU and NTRU Prime. We reported

quantitative results of the efﬁciency of primitive-

tailored designs, obtaining area savings (10%–40%)

and signiﬁcant frequency gains (96%–120%) with re-

spect to the state of the art of NTRU and NTRU Prime

multipliers. Our uniﬁed design provides the ﬁrst hard-

ware implementation of a polynomial multiplier able

to accelerate the computation of Kyber, Saber, NTRU

and NTRU Prime at all security levels in a single com-

ponent with a 15% frequency reduction, and only a

third of a dedicated multiplier in area increase.

REFERENCES

Alagic, G., Apon, D., Cooper, D., Dang, Q., Dang, T.,

Kelsey, J., Lichtinger, J., Miller, C., Moody, D., Per-

alta, R., Perlner, R., Robinson, A., Smith-Tone, D.,

and Liu, Y.-K. (2022). . https://doi.org/10.6028/NIST.

IR.8413-upd1.

Basso, A. and Roy, S. S. (2021). Optimized polynomial

multiplier architectures for post-quantum KEM saber.

In 58th ACM/IEEE Design Automation Conference,

DAC 2021, San Francisco, CA, USA, December 5-9,

2021, pages 1285–1290. IEEE.

Carter, E., He, P., and Xie, J. (2022). High-performance

polynomial multiplication hardware accelerators for

KEM saber and NTRU. IACR Cryptol. ePrint Arch.,

page 628.

Dang, V. B., Mohajerani, K., and Gaj, K. (2021). High-

Speed Hardware Architectures and FPGA Bench-

marking of CRYSTALS-Kyber, NTRU, and Saber.

IACR Cryptol. ePrint Arch., page 1508.

Farahmand, F., Dang, V. B., Nguyen, D. T., and Gaj, K.

(2019). Evaluating the potential for hardware accel-

eration of four ntru-based key encapsulation mech-

anisms using software/hardware codesign. In Ding,

J. and Steinwandt, R., editors, Post-Quantum Cryp-

tography - 10th International Conference, PQCrypto

2019, Chongqing, China, May 8-10, 2019 Revised

Selected Papers, volume 11505 of Lecture Notes in

Computer Science, pages 23–43. Springer.

Karatsuba, A. (1963). Multiplication of multidigit numbers

on automata. In Soviet physics doklady, volume 7,

pages 595–596.

Liu, B. and Wu, H. (2015). Efﬁcient architecture and im-

plementation for ntruencrypt system. In IEEE 58th In-

ternational Midwest Symposium on Circuits and Sys-

tems, MWSCAS 2015, Fort Collins, CO, USA, August

2-5, 2015, pages 1–4. IEEE.

Marotzke, A. (2020). A constant time full hardware imple-

mentation of streamlined NTRU prime. In Liardet, P.

and Mentens, N., editors, Smart Card Research and

Advanced Applications - 19th International Confer-

ence, CARDIS 2020, Virtual Event, November 18-19,

2020, Revised Selected Papers, volume 12609 of Lec-

ture Notes in Computer Science, pages 3–17. Springer.

NIST PQC Team (2022). PQC Standardization

Process: Announcing Four Candidates to

be Standardized, Plus Fourth Round Can-

didates. https://csrc.nist.gov/news/2022/

pqc-candidates-to-be-standardized-and-round-4.

Peng, B., Marotzke, A., Tsai, M., Yang, B., and Chen, H.

(2021). Streamlined NTRU prime on FPGA. IACR

Cryptol. ePrint Arch., page 1444.

Sklavos, N., Chaves, R., di Natale, G., and Regazzoni, F.

(2017). Hardware Security and Trust: Design and De-

ployment of Integrated Circuits in a Threatened En-

vironment. Springer Publishing Company, Incorpo-

rated, 1st edition.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy