Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for

Multi-Agent Cooperative Patrolling Problem

Kohei Matsumoto, Keisuke Yoneda and Toshiharu Sugawara

Department of Computer Science and Communications Engineering,

Waseda University, Tokyo 1698555, Japan

Keywords:

Multi-Agent Cooperative Patrolling, Coordination, Energy Saving, Self-Assessment.

Abstract:

In this study, we propose a method to autonomously reduce energy consumption in the multi-agent coop-

erative patrol problem (MACPP) while fulﬁlling quality requirements. While it is crucial for the system to

perform patrolling tasks as feasibly as possible, performing tasks beyond the required quality may consume

unnecessary energy. First, we propose a method to reduce energy consumption by having agents individually

estimate whether a given quality requirement is met through learning and consider energy-saving behaviors

when diligent patrolling behavior is determined to be unnecessary. Second, we propose a method to deactivate

redundant agents based on the values of parameters learned by each agent. Comparison experiments with the

existing methods show that the proposed method can effectively reduce energy consumption while fulﬁlling

the requirements. We also demonstrate that the proposed method can deactivate some agents for further energy

savings.

1 INTRODUCTION

Recently, robot technology has advanced and has ac-

celerated the use of multiple autonomous robots as a

replacement for tasks that humans repeat daily, such

as patrolling and cleaning, as well as for tasks in haz-

ardous locations, such as disaster-stricken areas, nu-

clear power plants, and outer space. One such prob-

lem in which multiple robots cooperate to perform a

common task is formulated as the multi-agent coop-

erative patrolling problem (MACPP), where robots

are modeled as agents capable of operating au-

tonomously. Studies of MACPP aim to ﬁnd meth-

ods/algorithms for efﬁcient and effective patrolling in

the given environments through the cooperation and

coordination of multiple agents.

Sophisticated actions and learning that aim to pur-

sue only efﬁciency may consume more energy than

necessary despite improving patrol efﬁciency, which

is a crucial issue for MACPP. The autonomous agents

envisioned in this study, in particular, have their

own batteries and will be forced to be frequently

recharged. Meanwhile, some applications have qual-

ity requirements for the patrolling tasks and are not

necessarily expected to exceed them. For example,

https://orcid.org/0000-0002-9271-4507

in a cleaning application, it is sufﬁcient if the envi-

ronment is clean to some extent, and excessive pa-

trolling will in fact reduce the effectiveness of the

work per unit of energy. Furthermore, if the environ-

ment is complex and large, it may not be possible to

determine in advance how many agents are needed;

fewer agents cannot fulﬁll the quality requirements,

whereas too many agents will result in a waste of en-

ergy.

A few studies focused on energy efﬁciency in the

context of collaborations in multi-agent systems (Kim

et al., 2016; Benkrid et al., 2019; Notomista et al.,

2022). For example, (Benkrid et al., 2019) proposed

a decentralized coordination method that shortens the

motion time to conserve the total motion energy of the

mobile robots in a multi-robot exploration problem.

However, these studies aimed at the methods to efﬁ-

ciently move and work for their tasks, consequently

reducing the total energy consumption. Meanwhile,

our method attempts to realize that some agents will

stop for a while or exit the system by their own deci-

sion if other agents can satisfy the required quality of

tasks. (Wu and Sugawara, 2019; Wu et al., 2019) also

proposed the method for MACPP, with which agents

autonomously pause for energy saving if they can ful-

ﬁll the requirement and return to recharge for future

exploration. However, we found that their method

Matsumoto, K., Yoneda, K. and Sugawara, T.

Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for Multi-Agent Cooperative Patrolling Problem.

DOI: 10.5220/0011645000003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 1, pages 37-47

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

was insufﬁcient, and agents still moved around the en-

vironment unnecessarily.

Therefore, we propose a method to both fulﬁll the

quality requirement and reduce energy consumption

more effectively by extending their method (Wu et al.,

2019), while autonomously foreseeing the possible

contributions by their subsequent actions and under-

standing the overall achievement of the required qual-

ity by estimating the current state of the environment.

The main difference is that because the progress of the

patrolling task while an agent pauses/recharges relies

on the behaviors of other agents and is not the same

for each agent, we introduce independent learning for

the energy-saving behavior from the viewpoint of in-

dividual agents.

We further found that as this learning progresses,

the agents split into two groups: the group of busy

agents that move with short pausing time and the

group of energy-saving agents that pause for rela-

tively long periods of time to not consume energy.

Therefore, the agents in the latter group can stop

their operations sequentially while still satisfying the

quality requirements. Our experiments show that our

method can signiﬁcantly reduce energy consumption

compared with the previous study. In addition, we

found that the number of busy agent groups varies

with environmental conditions. Subsequently, we

successfully reduced the number of operating agents

by sequentially deactivating agents in the energy-

saving group while fulﬁlling the quality requirements.

2 RELATED WORK

There have been many studies on MACPP and its ap-

plications (Hattori and Sugawara, 2021; Tevyashov

et al., 2022; Wiandt and Simon, 2018; Othmani-

Guibourg et al., 2017; Zhou et al., 2019). For ex-

ample, (Othmani-Guibourg et al., 2017) proposed a

model of dynamically changing environments based

on the edge Markov evolution graphs. (Zhou

et al., 2019) formulated the patrol problem as a

Bayesian adaptive transition-separating partially ob-

servable Markov decision process and proposed a dis-

tributed online learning and planning algorithm that

extends the Monte Carlo tree search method. In

(Othmani-Guibourg et al., 2018), the authors pro-

posed a method for predicting shared idleness from

individual idleness using artiﬁcial neural networks.

However, these studies only consider the efﬁciency

by ignoring the periodical pauses due to battery dis-

charge and energy consumption. (Yoneda et al., 2013)

proposed a method called adaptive meta-target deci-

sion strategy (AMTDS), in which multiple agents co-

operatively patrol the environment with periodic bat-

tery charge under a planning strategy determined by

Q-learning. However, this study also aimed at only

learning to improve patrolling efﬁciency without con-

sidering the reduction of energy consumption.

Meanwhile, (Kim et al., 2016; Benkrid et al.,

2019; Notomista et al., 2022; Kim et al., 2016;

Wu et al., 2019; Latif et al., 2021) in part fo-

cused on the energy saving. (Kim et al., 2016) in-

troduced several subrobots besides the ﬁreﬁghting

robots and attempted to extend the total operating

time in ﬁreﬁghting tasks. (Latif et al., 2021) proposed

an energy-conscious distributed task allocation algo-

rithm to solve continuous tasks, such as foraging, for

cooperative swarm robots to achieve highly effective

missions. However, unlike ours, these studies also

consider the extension of operating time. By con-

trast, (Wu et al., 2019) extended AMTDS to save en-

ergy subject to the quality requirements of patrolling.

However, their method is insufﬁcient for energy sav-

ing, and agents’ activities still contain unnecessary

actions. Therefore, we further reduced energy con-

sumption while fulﬁlling quality requirements by in-

troducing learning from individual viewpoints. More-

over, we also proposed a method to deactivate several

agents for patrolling in order to reduce energy con-

sumption.

3 BACKGROUND AND PROBLEM

FORMULATION

3.1 Environment

Because our method is an extension of the energy sav-

ing method for cleaning applications, adaptive meta-

target decision strategy for energy saving and cleanli-

ness (AMTDS/ESC) proposed by Wu et al. (Wu et al.,

2019), we follow their problem formulation and the

models of the environment and agents’ activities for

MACPP. The environment in which the agents move

around for patrolling is represented by the graph G =

(V, E), which can be embedded in a two-dimensional

Euclidean space, where V = {v

,...,v

} is the set of

nodes corresponding to the locations that agents visit,

and E is the set of edges e

i, j

connecting nodes v

and

corresponding to the paths along which the agents

move.

We denote the set of n agents by A = {1,...,n}

and introduce discrete time whose unit is step. For

simplicity, all edge lengths are assumed to be 1 by

adding dummy nodes if necessary. Hence, an agent

can move to one of the neighboring nodes with no

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

obstacle in a step. Let d(v

) be the shortest distance

(number of edges) between v

and v

An event occurs at node v ∈ V with its event oc-

currence probability (EOP), 0 ≤ p(v) ≤ 1, and accu-

mulates in v. Thus, the number of events accumulated

in v at time t, L

(v), is updated by

(v) =



t−1

(v) +1 (with EPO p(v))

t−1

(v) (otherwise)

However, the event in v is processed and L

(v) = 0

when an agent visits v at time t. The interpretation

of events differs depending on the applications; for

example, in a cleaning application, p(v) indicates the

tendency to be dirty at location v, and L

(v) expresses

the degree of accumulated dirt. In an application for

security surveillance patrol, p(v) indicates the degree

of required security for critical locations speciﬁed by

the application owner, and L

(v) can be interpreted as

the alert level. We assume that p(v) for all nodes is

speciﬁed in advance.

3.2 Agent Model

Agent i ∈ A has a battery whose capacity is described

by B

max

> 0 and can operate continuously by repeat-

edly recharging it at the charging base, B

; that is, after

leaving B

with a full battery, i patrols the environment

and returns to B

before it runs out. We assume that

the current battery capacity b

(t) at t is decremented,

i.e., b

(t) ← b

(t − 1) − 1 when i moves to a neigh-

boring node. b

≤ 0 signiﬁes the battery runout. By

introducing the charging speed constant k

charge

> 0, it

takes (B

max

− b

) · k

charge

steps to make its battery full

(so b

= B

max

Agent i knows p(v) of all nodes v but cannot know

the current number of the accumulated events L

(v) if

i is not on v. Therefore, the agents calculate the ex-

pected value E

(v)) from p(v) at time t. For this

calculation, we assumed that agents can know their

own and other agents’ locations. This can be achieved

easily by current technology; for example, using sen-

sors such as infrared rays or GPS, by direct commu-

nication between agents, or by cloud robotics, i.e., by

sharing information via a cloud. However, agents do

not share and infer their internal information and deci-

sions, such as strategies to set the destinations and the

planned routes to those destinations. We did not con-

sider collisions between agents because this study fo-

cuses on learning energy-saving actions while meet-

ing the required quality, and we believe that it is easy

to generate detour routes to avoid collisions in the

grid-like environment used in our experiments. In ad-

dition, several algorithms that generate collision-free

routes were proposed (e.g., (Yamauchi et al., 2022;

Ma et al., 2017)), and we can use one of these algo-

rithms for collision avoidance.

3.3 Target Decision Strategy

We describe the agents’ behaviors used in

AMTDS/ESC (Wu et al., 2019). When an agent

explores the environment further after reaching its

previous goal or after its battery is full, it determines

the next target node v

tar

∈ V and then moves along the

shortest path towards it.

Agent i selects the strategy

that i learned as the best for the target decision by

Q-learning from the following four strategies.

Random Selection (R): Agent i randomly selects

tar

∈ V from the environment.

Probabilistic Greedy Selection (PGS): Agent i ran-

domly selects v

tar

from the top N

nodes of

(v)).

Prioritizing Unvisited Interval (PI): Agent i ran-

domly selects v

tar

∈ V from the top N

nodes with

large intervals between the most recently visited

time and the current time.

Balanced Neighbor-Preferential Selection (BNPS):

Agent i examines E

(v)) in the neighbors and

prioritizes v

tar

if it is higher than the threshold;

otherwise it uses the PGS.

For more details, please refer to the original (Yoneda

et al., 2013; Wu et al., 2019).

3.4 Metrics for Task Quality from

Subjective Viewpoint

We introduce two evaluation measures: the time left

without checking events D

, and the total energy

consumption C

, as follows:

∑

v∈V

∑

t=t

(v), and (1)

∑

i∈A

∑

t=t

(i), (2)

where [t

] (t

< t

) denotes a time interval, and E

(i)

represents the energy consumed by agent i at t; there-

fore, E

(i) = 1 if i moved to a neighboring node and

(i) = 0 otherwise. For example, D

represents the

cumulative time of dust left without being vacuumed

in a cleaning application and the cumulative time and

More precisely, it will drop in at any node near the

shortest path that has a large value of E

(v)), using the

subgoal determination algorithm (Yoneda et al., 2013).

Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for Multi-Agent Cooperative Patrolling Problem

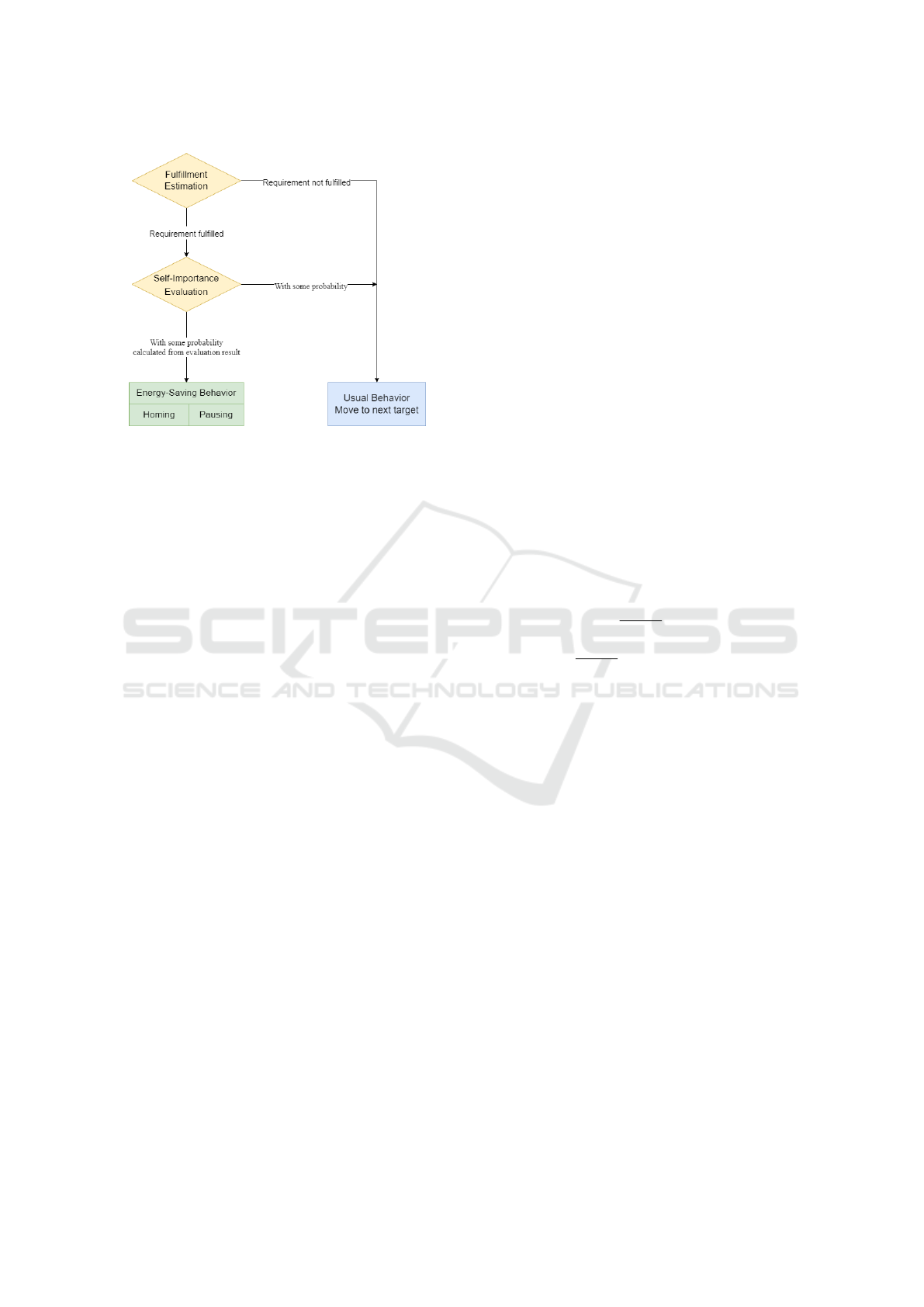
Figure 1: Flow for energy-saving behavior.

the number of secure locations left unchecked in secu-

rity patrols. Therefore, agents cooperatively maintain

less than the required value D

req

≥ 0 per step,

≤ D

req

× (t

−t

) (3)

Our aim is to keep C

as low as possible while satis-

fying the quality requirement Formula (3). Note that

D(s) and C(s) are used instead of D

and C

, by

omitting the subscripts unless confused.

4 PROPOSED METHOD

4.1 Estimating Quality Requirement

Fulﬁllment

We explain the proposed method by describing how it

differs from the energy-saving behavior in the previ-

ous study (Wu et al., 2019). Figure 1 shows the ﬂow

of the behaviors involved in the energy-saving behav-

ior of agents. Agents need to understand the cur-

rent state of the environment and compare it with the

required task quality to reduce energy consumption.

However, any agent cannot get the actual state and

must estimate it. In the fulﬁlling estimation, agents

regularly check if the required quality is accom-

plished while learning how they can predict the fu-

ture environmental state from individual viewpoints,

although in the previous method (Wu et al., 2019), all

agents estimate it in a uniformed viewpoint.

For this, agent i computes the expected value

(v)) for ∀v ∈ V at a future time t

+ T using

(v)) = p(v) × {(t

+ T ) −t

vis

} (4)

where t

denotes the current time, T > 0 represents

the parameter to specify how far into the future i esti-

mates, and t

vis

indicates the most recent time when an

agent visited v. Then, i should check if

∑

v∈V

(v)) ≤ D

req

(5)

is satisﬁed. Note that agent i estimates the future state

here to foresee the impact of its energy-saving behav-

ior, while i stops patrolling for some time.

However, this estimation by Formula (4) is an

ideal case based on the uniformed workload and ig-

nores the efforts of other agents. In particular, other

agents maintain the required quality D

req

even if the

agent stops for energy saving or charging. Such ef-

forts of other agents are obviously different depending

on the individual viewpoints because agents visit dif-

ferent locations with different characteristics. There-

fore, agents have to learn the possible efforts of other

agents during the energy-saving behavior.

We introduce the learning parameter K

for ∀i ∈ A

to adjust such differences. Then, agent i evaluates the

environment using the following Formula (6), instead

of Formula (5).

∑

v∈V

(v)) ÷K

≤ D

req

(6)

Moreover, K

is individually updated by











← (1 − α)K

+ α

req

)

(if E

) ≤ D

req

)

← K

−



)

req

− 1



(if E

) > D

req

)

(7)

where the estimated number of events at t is deﬁned

as E

) =

∑

v∈V

(v)), and α > 0 is the learning

rate. When K

is updated is explained in Section 4.3.2.

4.2 Self-Assessment for Energy-Saving

Behaviors

Agent i regularly checks Formula (6), and if it is

satisﬁed, i evaluates its contribution toward fulﬁlling

the quality requirement and foresees the impact of its

energy-saving behavior on the future state of the envi-

ronment (Fig. 1). For this purpose, we introduce the

self-assessment value of agent i at t, S

ass

(t), which

represents the degree of its recent contribution to de-

termine if i should continue to patrol for the cooper-

ative task or stop patrolling by adopting an energy-

saving behavior.

To calculate S

ass

), we deﬁne three parameters

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

for ∀i ∈ A, as follows:

) =

∑

−T

<t≤t

(t))

(8)

) =

∑

−T

<t≤t

(t))

(9)

) =

∑

<t≤t

(t)))

, (10)

where T

and T

(where 0 < T

< T

) denote the past

short- and long-term evaluation periods for the past,

(> 0) indicates the evaluation period for the future,

and v

(t) represents the node where i was or will be at

t. Intuitively, the short-term past contribution U

)

and the long-term past contribution U

represent the

numbers of events processed by i in the past, whereas

the estimated contribution U

) estimates the num-

ber of events that will be processed by i in the future

until t

. Note that the expected value E

(v)) is

used instead of L

(v) only in Formula (10).

Now, we deﬁne the self-assessment value S

ass

(t)

(0 ≤ S

ass

(t) ≤ 1) using

ass

(t) =











0 (if U

= 0)

(else if U

≤ U

)

1 (otherwise)

(11)

Then, i chooses an energy-saving behavior at the

probability of P

(t) computed using equation (12).

(t) = 1 − S

ass

(t) (12)

Therefore, a low self-assessment value facilitates the

agent’s energy-saving behavior.

4.3 Energy Saving Behaviors

Agents take one of two energy-saving behaviors:

Homing or Pausing, to eliminate movements that they

deem unnecessary.

Homing: Agent stops patrolling and returns to the

charging base regardless of the remaining battery

level.

Pausing: After charging is complete, the agent waits

for S

pause

steps without starting to move, where

pause

is a positive integer.

We will explain when the agents adopt these behav-

iors.

4.3.1 Homing Behavior

Agent i checks the requirement fulﬁllment (For-

mula (6)) every T

homing

steps after its battery level

becomes low, i.e., b

(t) < k

homing

· B

max

, where pos-

itive integer T

homing

is the parameter that avoids the

frequent return to charge by homing, and k

homing

(0 <

homing

< 1) is the parameter that decides low battery

level. If Formula (6) does not hold, i continues to

patrol; otherwise, with probability P

(t), i follows a

homing behavior in which i changes the current target

to its charging base B

. Note that agents patrolling far

from B

may return to base before this check.

Algorithm 1: PLength: To decide pausing time-length.

Require: S

pause

> 0, γ

= 0, T

> 0

1: while γ

≤ T

2: T ← (γ

+1)· S

pause

// T is used in Formula (6)

3: if Formula (6) holds then

4: γ

← γ

+ 1

5: else

6: break

7: end if

8: end while

9: // Agent takes a pausing behavior whose pausing

10: // time is γ

· S

pause

. If γ

= 0, agent immediately

11: // leaves for patrolling.

12: return γ

· S

pause

4.3.2 Variable-Length Pausing Behavior

In the previous method (Wu et al., 2019), when the

battery is fully charged at time t, agent i checks the

condition of the requirement (Formula (5)), and if the

condition is fulﬁlled, i takes the pausing behavior with

a constant pausing time S

pause

steps.

Meanwhile, in our proposed method, agents take

variable pausing time depending on the condition of

the estimated states. i takes the following variable-

length pausing behavior with probability P

(t) it com-

pletes charging at t. However, as an exception, i al-

ways takes the variable-length pausing behavior only

when it returns to the charging base B

by homing be-

havior.

First, in the variable-length pausing behavior, i de-

termines the pausing time as follows (see PLenght

in Algorithm 1). Initially, agent i set γ

= 0 and

T = S

pause

. When the battery is fully charged at time

t, agent i checks the requirement fulﬁllment (For-

mula (6)), and if it does not hold, i immediately leaves

the charging base for patrolling, i.e., the pausing time

is zero. If it holds, i increments γ

by 1 and sets

T ← (γ

+ 1) · S

pause

. Then, i checks the fulﬁllment

Formula (6) again; i repeats this process until i can

decide the length of the pausing time or γ

= T

where T

is the maximal value of this iteration. Sub-

sequently, i takes the pausing behavior whose length

Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for Multi-Agent Cooperative Patrolling Problem

is γ

·S

pause

. Agents always leave their charging bases

after the variable-length pausing behavior.

Unlike the previous method, agent i always takes

the variable-length pausing behavior after a full

charge if i returns to the charging base by a homing

behavior, as mentioned previously. This exception

can be explained by the fact that only homing behav-

ior has a marginal impact on energy saving because a

homing behavior shortens the current patrolling time

and reduces the time required for a full charge. Thus,

we believe that it is natural to always call a variable-

length pausing behavior to decrease energy consump-

tion. Certainly, it is possible that the pausing time is

zero by PLength, even in such a case. Hereafter, a

variable-length pausing behavior is simply referred to

as a pausing behavior.

Parameter K

for ∀i ∈ A is updated by Formula (7)

after i completes a pausing behavior even if the return

value of PLength is zero, because PLength carefully

estimates the current state to obtain the maximum du-

ration that each agent can wait up to while fulﬁlling

its quality requirements.

4.4 Deactivation of Unnecessary Agents

From the perspective of energy saving, if the num-

ber of agents needed for patrolling is sufﬁcient, even

excessive, it is effective not only to temporarily stop

agents but also to deactivate the patrolling of some

agents. Furthermore, these ceased agents can be used

elsewhere or as backups in case of agent failure. How-

ever, we cannot know in advance which agents should

be deactivated and determine how many agents are

needed to meet the required quality in the environ-

ment, which is complex and whose distribution of

POE is not uniform.

As we explain the data in detail in Section 5.3, we

found large variations in the value of K

among agents

and that they were divided into two main clusters. In

particular, because the agents belonging to the cluster

with relatively larger values of K

took pausing behav-

iors for a relatively longer duration to reduce energy

consumption, we propose to deactivate agent i

∈ A

that has the largest value of K

, i.e.,

= arg max

i∈A

(13)

Subsequently, if some agents still have a large value

of K

, the same deactivation process is repeated until

all agents have relatively smaller K

while the require-

ment is fulﬁlled.

Therefore, in every D

int

> 0 steps, the system

counts x

pause

, which is the number of times the func-

tion PLength has been called by all agents, and if

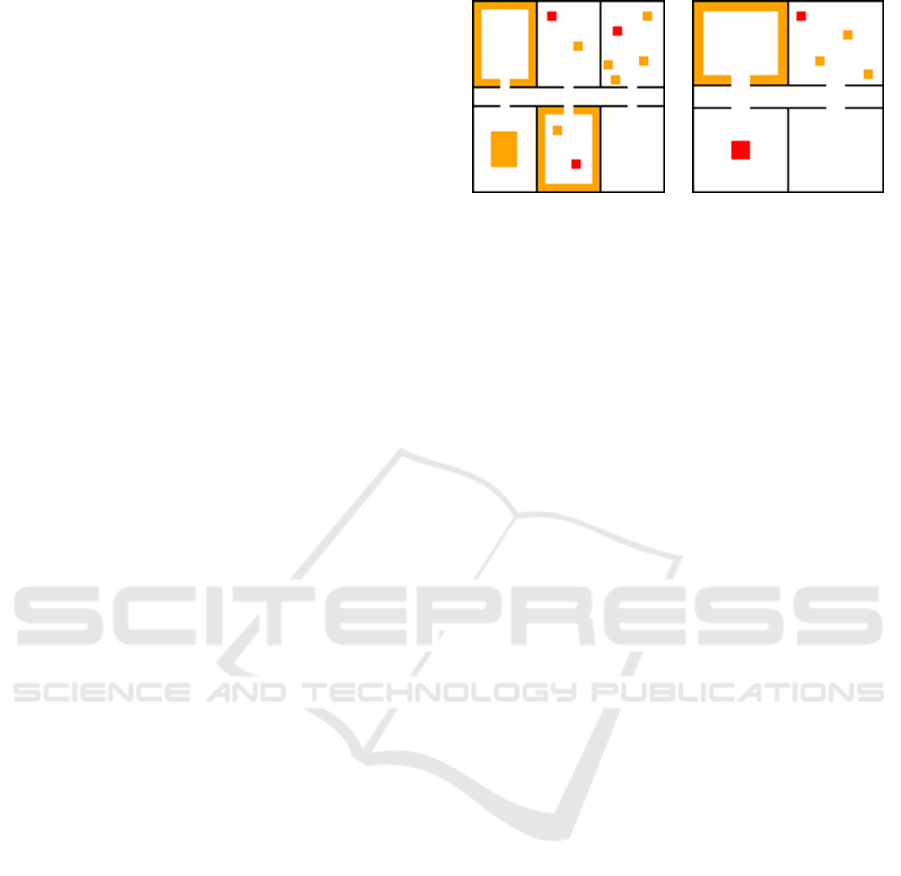
(a) Environment 1.

(b) Environment 2.

Figure 2: Experimental environments.

pause

and K

are large, i.e.,

pause

≥ N

deact

and max

i∈A

≥ K

deact

, (14)

then, i

is deactivated. Herein, K

deact

> 0 denotes the

threshold value for deactivation, and N

deact

indicates

the threshold to decide if several pausing behaviors

are attempted during the recent D

int

from the system’s

viewpoint.

5 EXPERIMENTS AND

DISCUSSION

5.1 Experimental Setting

We conducted experiments to compare the proposed

method AMTDS/ER with the conventional method

AMTDS(Yoneda et al., 2013) to verify the effec-

tiveness of the proposed method, in which agents

do not perform energy-saving behaviors, and that of

AMTDS/ESC(Wu et al., 2019), in which the agents

take homing and pausing behaviors but do not learn

the parameter that decides when agents should take

energy-saving behaviors. We demonstrate that the

proposed method is more effective than other meth-

ods in that the agents can reduce energy consumption

while fulﬁlling the quality requirement by investigat-

ing evaluation metrics D(s) and C(s). We analyzed

the distribution of the values of K

for ∀i ∈ A, and

agents were divided into two groups in accordance

with these values. Finally, we examined if our deacti-

vation method could reduce the number of patrolling

agents while fulﬁlling the quality requirement. We

list the parameter values used in our experiments in

Table 1. Note that the value of T in Formula (6) is

deﬁned in Algorithm 1.

We prepared two environments that have a two-

dimensional grid structure with a size of 101×101, as

shown in Fig. 2. The environment G

= (V

) for

the ﬁrst experiment (Exp. 1) is the same as the envi-

ronment used for the experiment in (Wu et al., 2019),

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

Table 1: List of parameter description.

Description Symbol Value

Maximal battery capacity B

max

900

Charging speed constant k

charge

Past short-term evaluation period T

Past long-term evaluation period T

Future evaluation period for self-assessment T

Learning rate for parameter K

α 0.1

Check point time for a homing behavior T

homing

100

Check point for remaining battery capacity for a homing behavior k

homing

1/3

Length of a pausing behavior S

pause

100

Interval to check deactivation D

int

250,000

Threshold for too many system-wide pause operations T

1,000

Parameter for deciding additional deactivation N

deact

100

Threshold for deactivation K

deact

1.0

for comparison (Fig. 2a). This environment has six

separate rooms and a corridor connecting these rooms

in the center. The black lines represent walls (obsta-

cles that agents cannot pass through). Each node v ∈

is represented by a coordinate of integers (x

where −50 ≤ x

≤ 50. The EOP p(v) for node

∀v ∈ V

was set according to colors in Fig. 2, as fol-

lows.

p(v) =











−3

(if v is in a red region)

−4

(if v is in an orange region)

−6

(if v is in a white region)

(15)

Therefore, the deeper the color, the higher the EOP.

In the second experiment (Exp. 2), the environ-

ment has four rooms, but the size of each room was

slightly wider (Fig. 2b). The EOPs are also speciﬁed

by Formula (15) using color as in Exp. 1. The sec-

ond environment looks simpler, and the total number

of events occurring there is smaller. However, this

necessitates more energy-saving behaviors by agents.

The number of agents |A| is 20, and the charg-

ing bases for all agents are placed at the center (0, 0).

Agents leave the charging bases with full batteries,

patrol the environment, return to the charging bases

before the batteries are dead, and repeat this cycle of

activities. We set the battery capacity to B

max

= 900,

and the charging speed constant k

charge

= 3. Thus, it

takes 2700 steps for the battery to fully charge from 0.

Therefore, the maximum activity cycle time is 3600

steps; hence, we set the data collection interval t

−t

for calculating D(s) and C(s) to 3600. We also set

the quality requirement value to D

req

= 600, and the

initial value of the parameter K

is 1.0. The values of

D(s) and C(s) shown below were the average values

of 50 independent trials.

Figure 3: C(S) over time in Exp. 1.

Figure 4: D(S) over time in Exp. 1.

5.2 Performance Evaluation

Figures 4 and 4 present a plot of the transition of

time left without checking events D(s), and total

energy consumption C(s) every 3600 steps, respec-

tively. Note that as D

req

= 600, agents are required

to keep D(s) ≤ 2160000 (= 3600D

req

) in Fig. 4. Fig-

ure 4 shows that all methods fulﬁlled the quality re-

quirement. In particular, the conventional methods,

AMTDS and AMTDS/ESC, maintained the D(s) to

considerably smaller values than the required value.

Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for Multi-Agent Cooperative Patrolling Problem

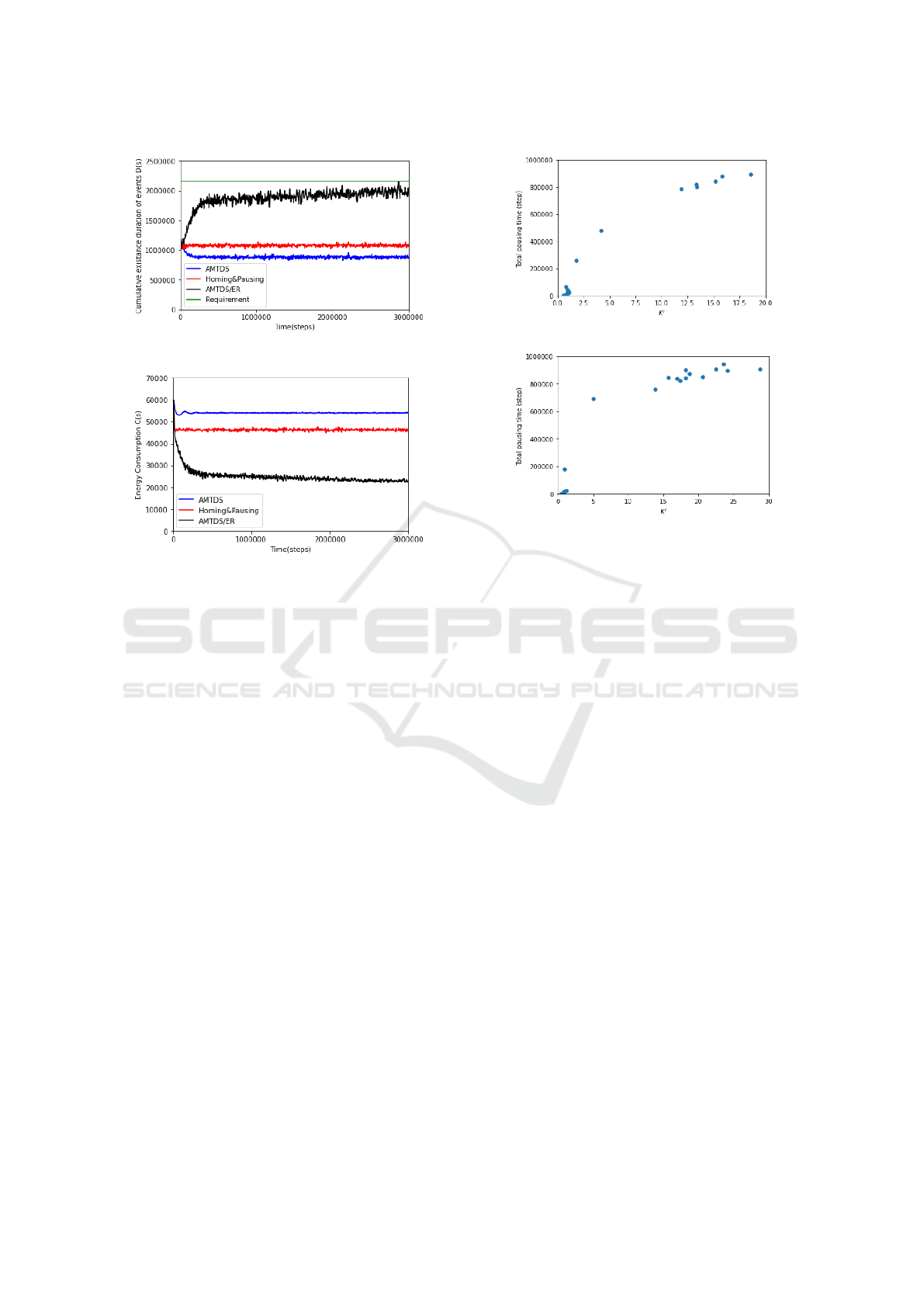
Figure 5: C(S) over time in Exp. 2.

Figure 6: D(S) over time in Exp. 2.

However, this suggested excessive energy con-

sumption by patrolling beyond the requirements, and

this situation is illustrated in Fig. 4. This ﬁgure indi-

cates that the proposed method AMTDS/ER could re-

duce total energy consumption C(s) by approximately

30.9% compared to AMTDS, although AMTDS/ER

increased the value of D(s) approximately by 40.3%,

where these data are the average values between

2,000,000 and 3,000,000. AMTDS/ESC could also

reduce energy consumption, but the reduction was

limited; AMTDS/ER could reduce C(s) approxi-

mately by 24.0% compared to AMTDS/ESC and in-

crease D(s) approximately by 26.2%. The increase

in effective reduction can be attributed to the intro-

duction of learning parameters K

because it enabled

each agent to predict the effect of other agents’ con-

tribution during its stops for energy-saving behaviors

to some extent.

Similar results can be observed in Exp. 2, as

shown in Figs. 6 and 6, which present plots of D(s)

and C(s) over time in Environment 2. In this envi-

ronment, the sum of the EOP values is much lower

than that in Environment 1, and we should conﬁrm if

agents could take more energy-saving behaviors to re-

duce more energy than that in Exp. 1. Agents could

achieve such expected behaviors; Fig. 6 shows that

agents gradually increased the energy-saving behav-

iors by fulﬁlling the requirement while they decreased

the consumed energy, as shown in Fig. 6. Thus, agents

Figure 7: Parameter K

and total pausing time (Exp. 1).

Figure 8: Parameter K

and total pausing time (Exp. 2).

with AMTDS/ER consumed energy that was almost

half of that consumed by agents with AMTDS/ESC.

5.3 Analysis of Behavior

We analyzed the characteristics of agents’ energy-

saving behaviors, particularly the sum of pausing

times, which is partly affected by the value of the

learning parameter K

in each agent. We calcu-

lated the sum of pausing times from 2,000,000 to

3,000,000 steps for ∀i ∈ A and plotted the relation-

ship between this sum and K

at 3,000,000 step in

Figs. 7 (Exp. 1) and 8 (Exp. 2). Note that these scat-

tered graphs were plotted using data obtained in one

experimental trial randomly selected from Exp. 1 and

Exp. 2, with no special intent.

Both of these graphs suggest that the agents can

be divided into roughly two clusters; one with rela-

tively large values of K

(e.g., K

≥ 10) and a large

sum of pausing times, and another one with small

values of K

(e.g., K

≤ 3) and a relatively small

sum of pausing times. We called the former cluster

the energy-saving group while the latter is called the

busy group. The ﬁndings of this analysis are as fol-

lows. First, because the length between 2,000, 000

and 3,000, 000 is 1,000,000, agents in the energy-

saving group that paused more than 800,000 times

rarely patrolled the environment. The non-pausing

time was less than 200,000, but the charging speed

constant k

charge

= 3. Thus, their actual patrolling time

was less than 50,000.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

Figure 9: C(S) over time in Exp. 3.

Figure 10: D(S) over time in Exp. 3.

Meanwhile, most agents in the busy group rarely

took the pausing behaviors. Note that homing behav-

ior is only returning to the charging base regardless of

the remaining capacity, shortening its time for charg-

ing. Therefore, the homing behaviors did not directly

contribute to the energy savings. The agents in the

busy group performed most of the required patrol to

fulﬁll the requirement, whereas the remaining agents

in the energy-saving group increased their pausing

time, and this type of differentiation occurred through

individual learning.

5.4 Evaluation of Deactivation

We have already described the deactivation method

in Section 4.4 based on the analysis in the previous

section. We conducted the third experiment (Exp. 3)

under the same setting as Exp. 1 to evaluate the pro-

posed deactivation method, i.e., to determine whether

the number of agents patrolling can be reduced to re-

duce the energy consumption while fulﬁlling the qual-

ity requirement. As listed in Table 1, we checked the

possibility of deactivation every D

int

= 250,000.

Figures 10 and 10 show the transition of D(s) and

C(s), respectively, until 5, 000, 000 steps, where label

“With deactivation” indicates the AMTDS/ER with

the proposed deactivation method. In this particular

experiment, the number of deactivated agents ranged

between six and eight, mostly seven. Note again that

Figure 11: Parameter K

and total pausing time (Exp. 3).

(a) D = 250, 000 steps. (b) D = 500, 000 steps.

Figure 12: Value of K

in agents not deactivated.

(a) Example 1.

(b) Example 2.

Figure 13: Value of K

in the agents deactivated at D steps.

smaller values of D(s) and C(s) are better.

Figure 10 indicates that the proposed AMTDS/ER

with the deactivation method could raise D(s) more

while fulﬁlling the quality requirement compared to

AMTDS/ER without deactivation, although their dif-

ference was small. This is because AMTDS/ER al-

ready maintained the value of D(s) near the required

quality level. The consumed energy was also slightly

reduced, as shown in Fig. 10. However, the main dif-

ference between with and without deactivation sce-

narios is that agents that were deactivated could com-

pletely transfer their patrolling tasks to other agents.

Furthermore, we would like to emphasize that even

though the performance differences in D(s) and C(s)

are not large, the advantages of deactivation are that

we can (1) use the deactivated agents in other envi-

ronments, (2) leave those agents on standby and use

them in case of failure, or (3) implement periodic in-

spections and alternating operations to extend the life

of the system.

Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for Multi-Agent Cooperative Patrolling Problem

5.5 Behaviors of Active and Deactivated

Agents

We analyzed the behaviors of active and deactivated

agents by investigating the transition of K

. We plot-

ted, in Fig. 11, the relationship between K

and the

total pausing time of i in one independent trial that

was randomly selected from Exp. 3, where K

is the

value at 5,000,000 steps, and the total pausing time is

the sum of the pause times during the last 1,000,000

steps of the experiment. Therefore, K

of a deacti-

vated agent i was the value when it was deactivated,

and the total pausing time of i must be zero. Seven red

plots correspond to deactivated agents. This ﬁgure in-

dicates that deactivated agents had relatively high val-

ues of K

and active agents continued patrolling with

a very short pausing time. This implies that thirteen

agents were sufﬁcient to maintain the required quality

set in this experiment.

Figures 13 and 13 present plots of the transition

of K

for agents that were deactivated at 250,000 and

500,000 steps (Fig. 13) and active agents (Fig. 13).

We can see from Fig. 13 that the K

values of these

agents rapidly increased and were then selected for

deactivation because the sum of its pausing time was

the largest at that time. Subsequently, their K

did

not change. Meanwhile, active agents temporally in-

creased their values of K

, but after that, the K

de-

creased and kept the relatively lower values because

some agents were deactivated. Thus, the active agents

must patrol more in their stead to fulﬁll the require-

ment.

Our experimental results show that the proposed

method can reduce energy consumption more than the

previous method (Wu et al., 2019) by introducing the

individual learning parameter K

. We further reduced

the number of operating agents based on the value of

while fulﬁlling the quality requirements.

6 CONCLUSIONS

Although conventional studies for MACPP usually

consider maximizing efﬁciency, it is often desirable

to reduce the energy used while fulﬁlling the qual-

ity requirement. Therefore, we proposed a method

that can save energy while meeting the requirement

in MACPP. The basic idea of our method is that each

agent individually foresees the state of the environ-

ment and assesses its own behavior from individual

viewpoints. Then, it returns to the charging base

or pauses for a while to save energy on determin-

ing that it is not necessary to start patrolling immedi-

ately. Moreover, we found that the proposed individ-

ual learning clusters the agents into two groups, and

by using these ﬁndings, we could successfully deacti-

vate redundant agents to reduce the number of work-

ing agents required for the current requirement.

This study assumed that the event probability

(EOP) p(v) in the environment is known, but this is

not always possible. Therefore, our future work is

to propose a method to reduce energy consumption

while agents learn the EOP in the environment.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Grant

Number 20H04245.

REFERENCES

Benkrid, A., Benallegue, A., and Achour, N. (2019). Multi-

robot coordination for energy-efﬁcient exploration.

Journal of Control, Automation and Electrical Sys-

tems, 30(6):911–920.

Hattori, K. and Sugawara, T. (2021). Effective Area Parti-

tioning in a Multi-Agent Patrolling Domain for Bet-

ter Efﬁciency. In Proceedings of the 13th Inter-

national Conference on Agents and Artiﬁcial Intel-

ligence - Volume 1: ICAART,, pages 281–288. IN-

STICC, SciTePress.

Kim, J., Dietz, J. E., and Matson, E. T. (2016). Modeling of

a multi-robot energy saving system to increase oper-

ating time of a ﬁreﬁghting robot. In 2016 IEEE Symp.

on Technologies for Homeland Security (HST), pages

1–6.

Latif, E., Gui, Y., Munir, A., and Parasuraman, R. (2021).

Energy-aware multi-robot task allocation in persistent

tasks.

Ma, H., Li, J., Kumar, T. S., and Koenig, S. (2017). Life-

long multi-agent path ﬁnding for online pickup and

delivery tasks. In Proc. of the 16th Conference on Au-

tonomous Agents and MultiAgent Systems, AAMAS

’17, pages 837–845, Richland, SC. IFAAMAS.

Notomista, G., Mayya, S., Emam, Y., Kroninger, C., Bo-

hannon, A., Hutchinson, S., and Egerstedt, M. (2022).

A resilient and energy-aware task allocation frame-

work for heterogeneous multirobot systems. IEEE

Transactions on Robotics, 38(1):159–179.

Othmani-Guibourg, M., El Fallah-Seghrouchni, A., Farges,

J.-L., and Potop-Butucaru, M. (2017). Multi-agent pa-

trolling in dynamic environments. In 2017 IEEE In-

ternational Conference on Agents (ICA), pages 72–77.

IEEE.

Othmani-Guibourg, M., Fallah-Seghrouchni, A. E., and

Farges, J.-L. (2018). Decentralized multi-agent pa-

trolling strategies using global idleness estimation. In

International Conference on Principles and Practice

of Multi-Agent Systems, pages 603–611. Springer.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

Tevyashov, G. K., Mamchenko, M. V., Migachev, A. N.,

Galin, R. R., Kulagin, K. A., Treﬁlov, P. M., Onisi-

mov, R. O., and Goloburdin, N. V. (2022). Algorithm

for multi-drone path planning and coverage of agricul-

tural ﬁelds. In Agriculture Digitalization and Organic

Production, pages 299–310. Springer.

Wiandt, B. and Simon, V. (2018). Autonomous graph par-

titioning for multi-agent patrolling problems. In 2018

Federated Conference on Computer Science and In-

formation Systems (FedCSIS), pages 261–268. IEEE.

Wu, L. and Sugawara, T. (2019). Strategies for Energy-

Aware Multi-agent Continuous Cooperative Patrolling

Problems Subject to Requirements. In PRIMA 2019:

Principles and Practice of Multi-Agent Systems, pages

585–593, Cham. Springer International Publishing.

Wu, L., Sugiyama, A., and Sugawara, T. (2019). Energy-

efﬁcient strategies for multi-agent continuous coop-

erative patrolling problems. Procedia Computer Sci-

ence, 159:465–474.

Yamauchi, T., Miyashita, Y., and Sugawara, T. (2022).

Standby-Based Deadlock Avoidance Method for

Multi-Agent Pickup and Delivery Tasks. In Pro-

ceedings of the 21st International Conference on

Autonomous Agents and Multiagent Systems, pages

1427–1435, Richland, SC. IFAAMAS.

Yoneda, K., Kato, C., and Sugawara, T. (2013). Au-

tonomous learning of target decision strategies

without communications for continuous coordinated

cleaning tasks. In 2013 IEEE/WIC/ACM International

Joint Conferences on Web Intelligence (WI) and In-

telligent Agent Technologies (IAT), volume 2, pages

216–223.

Zhou, X., Wang, W., Wang, T., Lei, Y., and Zhong, F.

(2019). Bayesian reinforcement learning for multi-

robot decentralized patrolling in uncertain environ-

ments. IEEE Transactions on Vehicular Technology,

68(12):11691–11703.

Autonomous Energy-Saving Behaviors with Fulﬁlling Requirements for Multi-Agent Cooperative Patrolling Problem