Logic of Awareness in Agent’s Reasoning
Yudai Kubono
a
, Teeradaj Racharak
b
and Satoshi Tojo
School of Information Science, Japan Advanced Institute of Science and Technology, Ishikawa, Japan
Keywords:
Awareness, Epistemic Logic, Multi-Agent Systems, Rational Agent, Axiomatization.
Abstract:
The aim of this study is to formally express awareness for modeling practical agent communication. The notion
of awareness has been proposed as a set of propositions for each agent, to which he/she pays attention, and
has contributed to avoiding logical omniscience. However, when an agent guesses another agent’s knowledge
states, what matters are not propositions but are accessible possible worlds. Therefore, we introduce a partition
of possible worlds connected to awareness, that is an equivalence relation, to denote indistinguishable worlds.
Our logic is called Awareness Logic with Partition (ALP ). In this paper, we first show a running example to
illustrate a practical social game. Thereafter, we introduce syntax and Kripke semantics of the logic and prove
its completeness. Finally, we outline an idea to incorporate some epistemic actions with dynamic operators
that change the state of awareness.
1 INTRODUCTION
In a society of rational agents, communication among
them can be defined by means of message’s ex-
changes in which each message is represented by a
logical formula. In this context, a recipient agent may
change or revise his/her belief according to the re-
ceived message to maintain the logical consistency of
knowledge.
First, we denote a unit of knowledge by ϕ, ψ, ···
and write K
a
ϕ for ‘agent a knows ϕ,’ or we may
write anonymously Kϕ. In such a formalization, log-
ical omniscience matters; in ordinary logic, we em-
ploy Modus Ponens (MP)
1
for logical inference, and
when one knows ϕ and ϕ → ψ, i.e., Kϕ and K(ϕ →
ψ), respectively, Kψ would necessarily be inferred in
his/her knowledge if we adopt the axiom K.
2
How-
ever, such exhaustive reasoning is unrealistic for hu-
man model. The logic of an agent’s knowledge/belief
is called epistemic logic, and its semantics is given
by a Kriple model that consists of a set of possible
worlds where each world has different valuation for
propositions, to which each agent may or may not be
accessible. When an agent can access two worlds of
different valuations, e.g., each of which includes ϕ or
¬ϕ, he/she does not know whether ϕ is true or not,
a
https://orcid.org/0000-0003-2617-8870
b
https://orcid.org/0000-0002-8823-2361
1
From ϕ and ϕ → ψ, we conclude ψ.
2
K: K(ϕ → ψ) → (Kϕ → Kψ).
that is, ¬Kϕ. On the contrary, when an agent can find
ϕ in all his/her accessible worlds, Kϕ holds. To avoid
logical omniscience, we need to restrict propositions
to be employed in reasoning, apart from those not to
be employed.
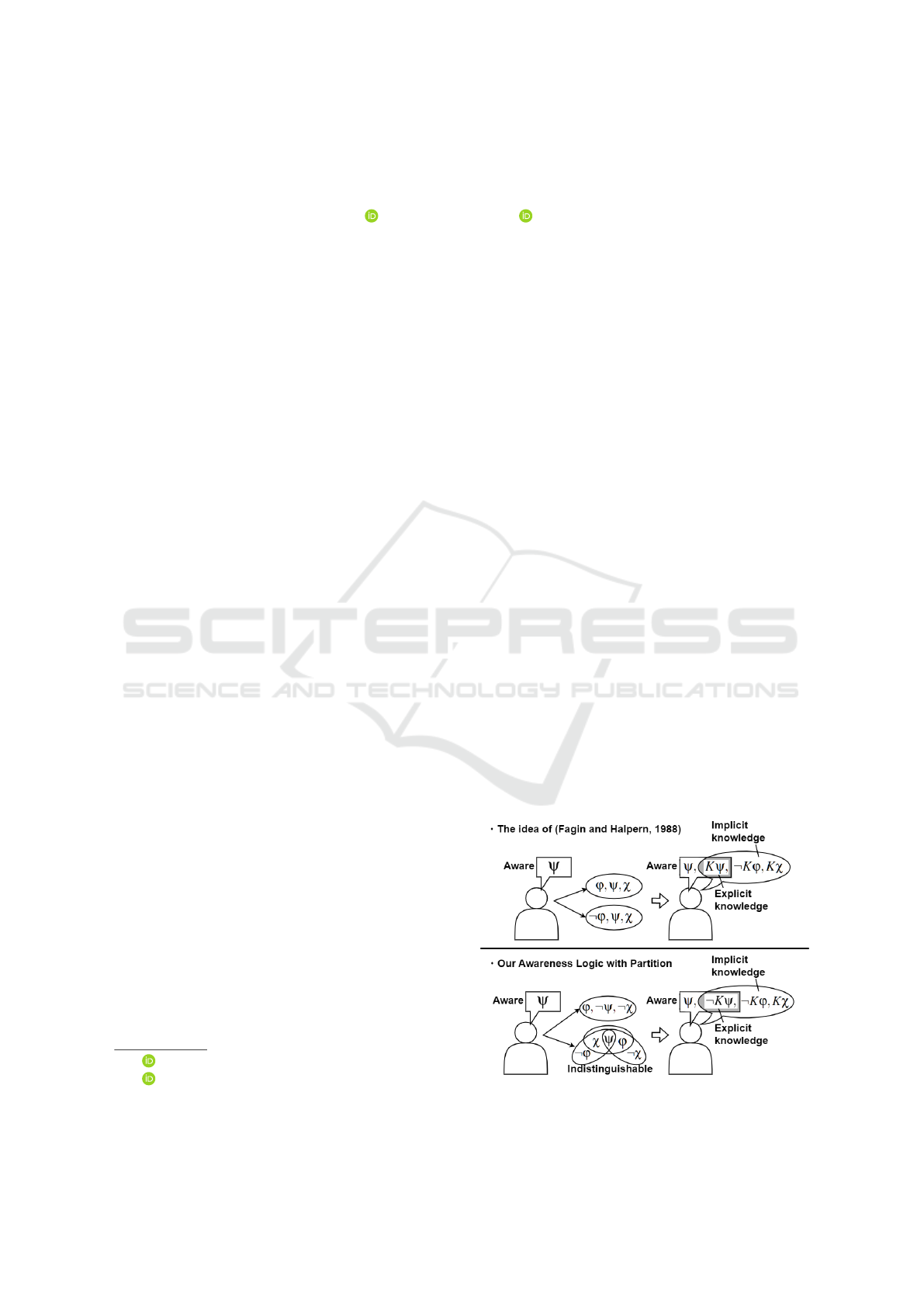
(Fagin and Halpern, 1988) proposed components
that represent agents’ state of awareness called an
awareness set and incorporated it into epistemic logic.
This logic distinguishes the knowledge that the agents
cannot use for their reasoning, called implicit knowl-
edge, from that they can, called explicit knowledge.
The former, implicit knowledge, represents unaware
information. The idea of (Fagin and Halpern, 1988) is
Figure 1: A comparison on the intuitions of the previous
study and this paper.
Kubono, Y., Racharak, T. and Tojo, S.
Logic of Awareness in Agent’s Reasoning.
DOI: 10.5220/0011630300003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 1, pages 207-216
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
207

w
1
w
2
w
3
w
4
w
5
w
6
w
7
w
8
p
a
, p
b
n
p
a
, p
b
¬n
p
a
, ¬p
b
n
p
a
, ¬p
b
¬n
¬p
a
, p
b
n
¬p
a
, p
b
¬n
¬p
a
, ¬p
b
n
¬p
a
, ¬p
b
¬n
a
a
b b
Figure 2: The left side: each agent’s knowledge and their reasoning, which affect their own decisions. The right side: the
Kripke model from a’s viewpoint.
to classify knowledge into implicit or explicit knowl-
edge according to whether an agent is aware of the
proposition (Figure 1). It is a simple, intuitive defini-
tion and the main approach in logic of awareness.
However, we argue that awareness should also af-
fect the distinction of possible worlds in addition to
propositions. In the previous study, awareness only
concerns the propositions. However, when an agent is
unaware of a certain proposition, he/she must not also
be aware of the distinction of two possible worlds. In
figure 1, the agent accesses only the possible worlds
where χ is true despite unawareness of χ. This in-
distinction plays an important role when agents make
inferences about other agents’ knowledge states, as
shown in our illustrative example in Section 2. There-
fore, in this paper, we propose a framework to men-
tion that two possible worlds are indistinguishable
from the viewpoint of an agent. Our logic can allow
us to handle reasoning correctly about what knowl-
edge other agents have and also enables to formalize
practical agent communications.
Besides, in game theory, players make their own
decisions by guessing other players’ reasoning. It is
based on specific decision criteria, such as the best
strategy to a dominant strategy. Whether player b is
aware of actions that player a can take affects b’s strat-
egy to find an equilibrium. In this sense, our logic is
supposed to be useful in its application to game the-
ory.
The paper is structured as follows. In Section
2, we introduce an example about inferences among
multi-agents that shows the necessity for introducing
our logic. In Section 3, we introduce Awareness Logic
with Partition (ALP ), which is based on Awareness
Logic (Fagin and Halpern, 1988). Its semantics was
given in the Kripke-style. We add a new equiva-
lence relation, which is connected to the states of an
agent’s awareness from another agent’s viewpoint, to
the standard Kripke model. Besides, we show how
our logic works using the example presented in Sec-
tion 2. In Section 4, we give a proof system ALP
of our logic ALP in Hilbert-style. As for proving
the completeness theorem, we use techniques of logic
of the modality for transitive closure (van Ditmarsch
et al., 2007). Section 5 discusses two epistemic ac-
tions: becoming aware of and becoming unaware of,
and gives an extension of ALP . In Section 6, we in-
troduce some related work. Section 7 concludes.
2 EXAMPLE: CONVENIENCE
STORE’S EXPANSION
This section gives an example at convenience stores.
It describes a situation where agents have different
states of awareness.
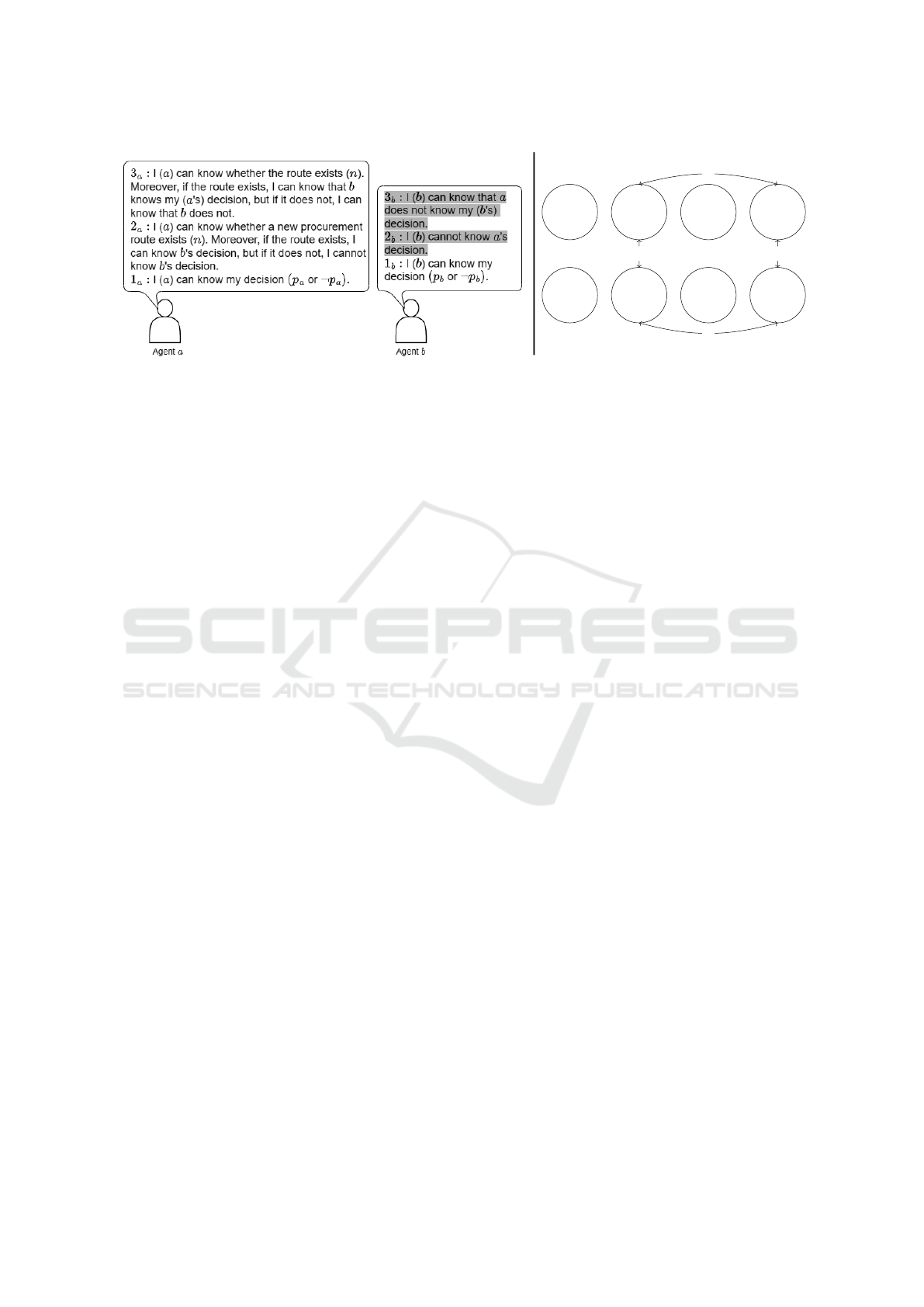
Example. Let agent a be the owner of the conve-
nience store A and agent b be the owner of the con-
venience store B considering to open his/her own new
store. The cost of products has risen due to poor har-
vests, and a reckless expansion leads to a significant
loss. Agent a is aware of a new procurement route
that allows the owners to purchase products at half
the current price. Moreover, a is unaware that b is
unaware of the existence of the new route.
In this example, if owner a can know b’s decision,
that decision can be a helpful factor in a’s decision.
For example, if owner b decides to open a new store,
owner a is also likely to decide to expand a new store
because otherwise, it may be disadvantageous.
We denote p
a
and p
b
for the propositions that a
and b expand their stores, respectively, and n for the
proposition that there is a new procurement route. As
for the agents’ knowledge, a can know p
a
and p
b
in the case that n is true. On the other hand, b can
know only p
b
in any case because he/she does not
have a clue about a’s knowledge state. Then, we give
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
208

the Kripke model in Figure 2 to see how each agent
guesses the opponent’s knowledge. Note that we omit
reflexivity on accessibility relations from a figure for
visibility. Basically, each agent does not know the
decision of the opponent, i.e., b’s decision for a and
a’s decision for b are unknown to each other. How-
ever, in possible worlds where n holds, a can know
p
b
, and b can know p
a
. Thus, there is no acces-
sibility relation between possible worlds such that it
has a different valuation for each p
b
and p
a
and n is
true. As for states of awareness, a is aware of p
a
, p
b
,
and n. However, b is unaware of n. We can summa-
rize it as awareness sets A
a
= {p
a
, p
b
, n} for a and
A
b
= {p
a
, p
b
} for b.
Note that 2
b
and 3
b
in Figure 2 cannot be cor-
rectly represented by the existing method. Let K
a
and K
b
be operators expressing each explicit knowl-
edge. We consider the truth value of K
b
K
a
p
b
at w
1
,
which means we assume w
1
as the actual world. In
the method of (Fagin and Halpern, 1988), a K
i
opera-
tor for each agent i is defined to be satisfied when the
proposition is included in an awareness set and holds
in all the accessible worlds (Figure 1). Thus, K
b
K
a
p
b
at w
1
implies that p
b
is contained in b’s awareness
set, and K
a
p
b
holds at w
1
that is accessible from w
1
on the edge labeled b. Also, K
a
p
b
implies that p
b
is
contained in a’s awareness set, and p
b
holds at w
1
that
is accessible from w
1
on the edge labeled a. Since p
b
holds in w
1
, the formula holds at w
1
.
However, K
b
K
a
p
b
contradicts 3
b
in Figure 2, and
our intuition considers that this formula should not
hold at w
1
. It is because b is unaware of n and can-
not think that a has a way of knowing p
b
at all. This
unawareness means that some worlds, such as w
1
and
w
2
, are indistinguishable from b’s viewpoint. There-
fore, the Kripke model from b’s viewpoint should be
the form of Figure 3, in which K
b
K
a
p
b
must be eval-
uated by whether p
b
holds in all possible worlds that
are w
0
1
, w
0
2
, w
0
3
and w
0
4
. Thus, K
b
K
a
p
b
does not hold.
Figure 2 is a Kripke model from a’s viewpoint who
is aware of all atomic propositions discussed, which
is different from that of b, because atomic proposi-
tions that a is aware of are different from of those b is
aware. Besides, a formula K
b
p
a
also holds at w
1
and
contradicts 2
b
for the same reason.
As we have seen, the existing method cannot treat
some information used in the decision-making. In
order to correctly represent inference of agents, it is
necessary not only to classify knowledge using states
of awareness about propositions, but also to consider
the distinction of possible worlds corresponding to
agents’ viewpoints.
Models that can distinguish between awareness of
and awareness that has been proposed in the field
w
0
1
w
0
2
w
0
3
w
0
4
p
a
, p
b
p
a
, ¬p
b
¬p
a
, p
b
¬p
a
, ¬p
b
a
a
b b
Figure 3: The Kripke model from b’s viewpoint.
of philosophy. The models allow us to represent a
more accurate description of situations (Grossi and
Vel
´
azquez-Quesada, 2015; Fern
´
andez-Fern
´
andez and
Vel
´
azquez-Quesada, 2021). The former is awareness
in the sense of being able to refer to the information.
The latter is awareness in the sense of acknowledg-
ing that the information is true through reasoning or
observation. Although both concepts are similar, they
have different properties. Previously proposed logic
defines explicit knowledge by combining these two
concepts. In this paper, we focus on ‘awareness of.’
This is because the concept is more relevant to the ex-
ample, and we do not need to consider the other one.
3 AWARENESS LOGIC WITH
PARTITION
3.1 Language
First of all, we define the syntax of ALP . Let P
be a countable set of atomic propositions and G be
a countable set of agents. The language L
P
is the set
of formulas generated by the following grammar:
L
P
3 ϕ ::= p | ¬ϕ | ϕ ∧ ϕ | A
i
j
ϕ |
L
j
ϕ | [≡]
i
j
ϕ | C
i
j
ϕ | K
i
j
ϕ,
where p ∈ P and i, j ∈ G. Other logical connectives
∨, →, and ↔ are defined in the usual manner.
We call A
i
j
, L
j
, and K
i
j
as an awareness opera-
tor, an implicit knowledge operator, and an explicit
knowledge operator, respectively. Notationally,
• A
i
j
ϕ means ϕ is information that j is aware of from
i’s viewpoint.
• L
j
ϕ means that ϕ is j’s implicit knowledge.
• K
i
j
ϕ means that ϕ is j’s explicit knowledge from
agent i’s viewpoint.
[≡]
i
j
and C
i
j
are special operators introduced to define
explicit knowledge and used as the basis for proofs
studied in this paper. The former operator means that
the information is true at j’s state of awareness from
Logic of Awareness in Agent’s Reasoning
209

i’s viewpoint. The latter means that ϕ is a kind of j’s
implicit knowledge from agent i’s viewpoint. Note
that implicit knowledge referred to by C
i
j
ϕ is stronger
than that referred to by L
j
ϕ. It might be interesting to
explore the relationship of these two operators; how-
ever, it is outside our scope and remains as our future
task.
3.2 Semantics
Now, we move on to the semantics of ALP .
Definition 1. An epistemic model with awareness M
is a tuple hW, {R
i
}
i∈G
, V, {A
i
j
}
i, j∈G
, {≡
i
j
}
i, j∈G
i con-
sists of a domain W , a set of accessibility relations R
i
,
a valuation function V , a set of awareness sets A
i
j
,
and a set of relations ≡
i
j
, where:
• W is a non-empty set of possible worlds;
• R
i
⊆ W ×W is an equivalence relation on W;
• V : P → 2
W
;
• A
i
j
is a non-empty set of atomic propositions
satisfying that A
i
j
⊆ A
i
i
;
• (w, v) ∈ ≡
i
j
iff (w ∈ V (p) iff v ∈ V (p)
for every p ∈ A
i
j
).
The pair (M, w) with M and w ∈ W in it is
called a pointed model. We can say that i’s view-
point is formally an epistemic model with awareness
where the superscript index is restricted to i, that is
hW, {R
j
}
j∈G
, V, {A
i
j
}
j∈G
, {≡
i
j
}
j∈G
i. We call the re-
stricted model i’s epistemic model with awareness.
The condition A
i
j
⊆ A
i
i
means that atomic propo-
sitions of which j is aware from i’s viewpoint do not
contain a proposition of which i himself/herself is un-
aware. We call ≡
i
j
indistinguishable relations for j
from i’s viewpoint. An indistinguishable relation ≡
i
j
is a relation between possible worlds with a different
valuation for atomic propositions that j is unaware
of from i’s viewpoint. This represents that, from i’s
viewpoint, j cannot distinguish such possible worlds.
By partitioning W using an indistinguishable relation,
we can formalize knowledge according to the propo-
sitions of which the agent is aware. Possible worlds
that are indistinguishable because of being unaware
are collapsed with an equivalence class.
Note that there are local and global definitions of
an awareness set. The former defines A
i
as a func-
tion that takes a possible world as an argument and
changes elements of an awareness set for each pos-
sible world. The latter defines an awareness set as
the same in all possible worlds. Generally, a state of
awareness is fixed within an agent’s scope, which is
a set of the agent’s accessible possible worlds. Thus,
a global definition is used in the logic that does not
consider the outside of a specific agent’s scope, such
as a single-agent case. On the other hand, a local def-
inition can represent a state of awareness in possible
worlds outside the agent’s scope. It is possible to ex-
press the possibility that there is a difference between
the state of an agent’s awareness in his/her scope and
that in other agents’ scope.
This logic adopts the global one, because even
with the global definition, it is possible to express the
possibility that the state of an agent’s awareness from
his/her viewpoint is different from that from other
agents’ viewpoints, which is an advantage of the lo-
cal definition. It follows easily from the definition that
every state of awareness is uniquely set for each agent.
We move on to the satisfaction relation. At first,
we introduce some notations for the definition: At(ϕ)
is denoted as the set of atomic propositions that ap-
pear in ϕ; R
j
◦ ≡
i
j
is denoted as a sequential com-
position of ≡
i
j
and R
j
; R
+
is denoted as the transi-
tive closure of R. This R
+
is the smallest set such
that R ⊆ R
+
, and for all x, y, z, if (x, y) ∈ R
+
and
(y, z) ∈ R
+
, then (x, z) ∈ R
+
.
Definition 2. For any epistemic models with aware-
ness M and possible worlds w ∈ W , the satisfaction
relation  is given as follows:
M, w  p iff w ∈ V (p);
M, w  ¬ϕ iff M, w 2 ϕ;
M, w  ϕ ∧ ψ iff M, w  ϕ, and M, w  ψ;
M, w  A
i
j
ϕ iff At(ϕ) ⊆ A
i
j
;
M, w  L
j
ϕ iff M, v  ϕ for all v
such that (w, v) ∈ R
j
;
M, w  [≡]
i
j
ϕ iff M, v  ϕ for all v
such that (w, v) ∈ ≡
i
j
;
M, w  C
i
j
ϕ iff M, v  ϕ for all v
such that (w, v) ∈ (R
j
◦ ≡
i
j
)
+
;
M, w  K
i
j
ϕ iff M, w  A
i
j
ϕ, and M, w  C
i
j
ϕ.
From Definition 1, it spells out that if both in-
distinguishable relations ≡
i
j
and accessibility rela-
tions R
j
is equivalent, then (R
j
◦ ≡
i
j
)
+
is equiva-
lent. Since both relations are equivalence relations,
the reverse direction on the composition is also reach-
able, although it consumes a few extra steps. Thus,
(R
j
◦ ≡
i
j
)
+
gives a new partition of possible worlds.
From the definitions, we can also find that [≡]
i
j
L
j
ϕ
corresponds to R
j
◦ ≡
i
j
. However, this relation is not
equivalent, unlike its transitive closure.
Next, we define the validity in the usual way.
Definition 3. A formula ϕ is valid at M, if ϕ holds at
every pointed model M, w in M, which is denoted by
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
210

≡
b
b
≡
b
b
≡
b
b
≡
b
b
w
1
w
2
w
3
w
4
w
5
w
6
w
7
w
8
p
a
, p
b
n
p
a
, p
b
¬n
p
a
, ¬p
b
n
p
a
, ¬p
b
¬n
¬p
a
, p
b
n
¬p
a
, p
b
¬n
¬p
a
, ¬p
b
n
¬p
a
, ¬p
b
¬n
a
a
b b
Figure 4: The Kripke model depicted by ALP .
M  ϕ. A formula ϕ is valid if ϕ holds at every pointed
model M, w, which is denoted by  ϕ.
3.3 Formalization of the Example
We formalize the running example using our logic
and consider the truth values of K
b
K
a
p
b
again. Agent
b is unaware of n. Then there are indistinguishable
relations between possible worlds where n holds
or not, such as w
1
and w
2
. Formally, we write
≡
a
a
and ≡
a
b
as
/
0. We also formalize ≡
b
a
and ≡
b
b
as
{(w
1
, w
2
), (w
3
, w
4
), (w
5
, w
6
), (w
7
, w
8
), (w
2
, w
1
),
(w
4
, w
3
), (w
6
, w
5
), (w
8
, w
7
), (w
1
, w
1
), ··· , (w
8
, w
8
)}.
In our logic, K
b
K
a
p
b
is rewritten as the form K
b
b
K
b
a
p
b
by introducing agents’ viewpoint. This formula is
evaluated by whether p
b
holds in all the reachable
worlds on ≡
b
b
, R
b
, ≡
b
a
, and R
a
. As seen in Figure 4,
since it is false in some worlds, the formula does not
hold at w
1
. On the other hand, K
b
b
¬K
b
a
p
b
, which is
consistent with 3
b
in Figure 2, is true.
As for other formulas, such as ¬K
b
b
p
a
, which is
consistent with 2
b
, and K
b
a
K
b
b
¬K
b
a
p
b
, these are also
consistent with our intuition. The latter means that
from b’s viewpoint, a knows that b knows that a does
not know p
b
. A formula K
a
a
K
a
b
¬K
a
a
p
b
, which has the
same meaning from a’s viewpoint, does not hold at
w
1
. Moreover, we can consider a situation where a is
aware that b is unaware of n and express the situation
by formalizing A
a
b
as {p
a
, p
b
}. K
a
a
K
a
b
¬K
a
a
p
b
is true
at w
1
, which is a knows b’s incorrect knowledge.
In Figure 4, the equivalence classes of the indistin-
guishable relation ≡
b
b
are represented by the light gray
background. By interpreting the equivalence class as
one possible world from b’s viewpoint, Figure 4 rep-
resents the same graph as the Kripke model from b’s
viewpoint in Figure 3 in terms of possible worlds and
accessibility relations. Thus, we can say that our logic
represents the distinction of possible worlds accord-
ing to states of awareness for each agent.
4 HILBERT-SYSTEM FOR ALP
We now move on to the proof theory for ALP . The
Hilbert-system of our logic is given in Table 1. AN,
AC, AA, AL, A[≡], and AK mean that if an agent is
aware of atomic propositions, he/she is aware of more
complex formulas produced by the atomic proposi-
tions and correspond to the meaning of ‘awareness
of.’ For K
L
, T
L
, 5
L
, K
[≡]
, T
[≡]
, and 5
[≡]
, we adopt K,T,
and 5 axioms in modal logic. 5
L
called negative in-
trospection in epistemic logic means that an agent al-
ways knows what he/she does not know. This axiom
also characterizes logical omniscience. In our logic,
as with most logics of awareness, this formula does
not hold for K
i
j
operators. Instead, ¬K
i
j
ϕ∧A
i
j
¬K
i
j
ϕ →
K
i
j
¬K
i
j
ϕ is valid. K
C
, IND, and MIX are based on ax-
ioms of logic with common knowledge (Fagin et al.,
1995), because the idea of transitive closure is the
same as that one. KAC corresponds to the definition
of satisfaction relation of K
i
j
. It means that explicit
knowledge is the things that meet implicit knowledge
referred to by C
i
j
and aware propositions.
Definition 4. A system ALP is a set of formulas that
contains the axioms in Table 1 and is closed under in-
ference rules in it. We write ` ϕ if ϕ ∈ ALP. Let Γ be
a set of formulas in ALP and
V
Γ be an abbreviation
of
V
ϕ∈Γ
ϕ. If there is a finite subset Γ
0
of Γ such that
`
V
Γ
0
→ ϕ, we write Γ ` ϕ and call ϕ derivation from
Γ.
4.1 Soundness
Theorem 1. If ` ϕ, then  ϕ.
Proof. By induction on the construction of ALP, we
prove it for any formulas. First, we prove that all ax-
ioms are valid. For logical connectives, L
j
, and [≡]
i
j
can be proven similarly to those used in S5. A
i
j
and K
i
j
are also straightforward. We show the proof of only
C
i
j
here.
• For K
C
, suppose that M, w  C
i
j
(ϕ → ψ), and
M, w  C
i
j
ϕ. Since M, v  ϕ → ψ, and M, v  ϕ
for all v such that (w, v) ∈ (R
j
◦ ≡
i
j
)
+
, M, v  ψ.
Thus M, w  C
i
j
ψ.
• For MIX, suppose that M, w  C
i
j
ϕ. Since
(R
j
◦ ≡
i
j
)
+
is equivalent and the transitive clo-
sure, M, w  ϕ ∧ [≡]
i
j
L
j
C
i
j
ϕ.
• For IND, suppose that M, w  C
i
j
(ϕ → [≡]
i
j
L
j
ϕ),
and M, w  ϕ, then for all v such that (w, v) ∈
(R
j
◦ ≡
i
j
)
+
, M, v  ϕ → [≡]
i
j
L
j
ϕ. Thus M, w 
[≡]
i
j
L
j
ϕ. It means ϕ holds at all possible worlds
Logic of Awareness in Agent’s Reasoning
211

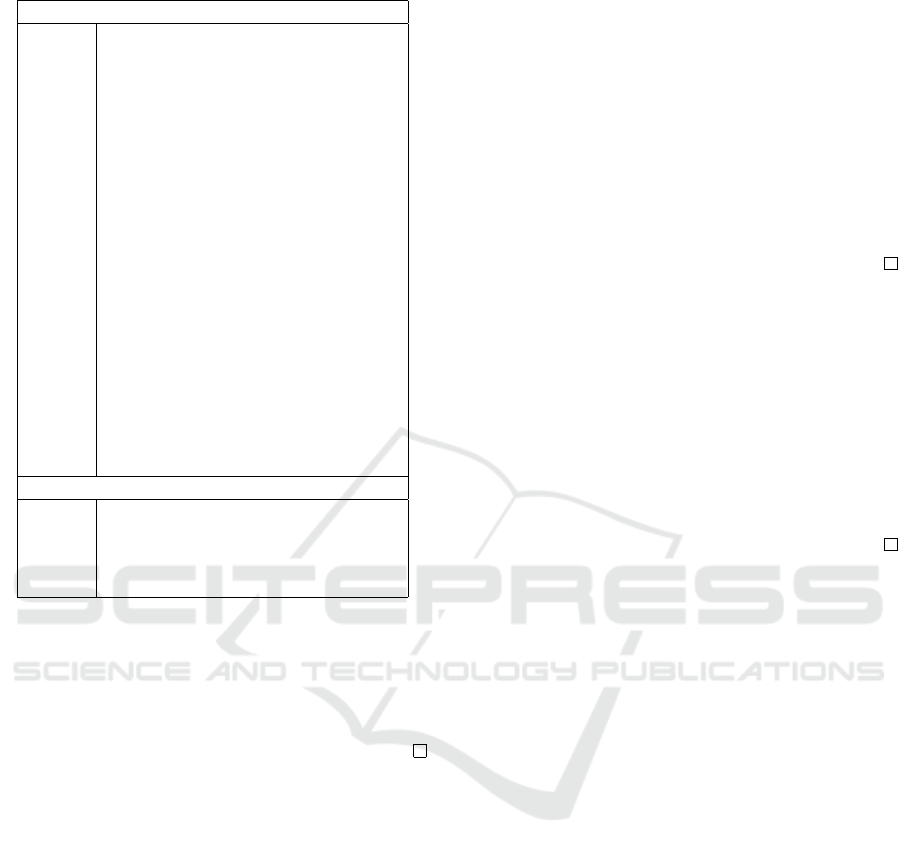
Table 1: Axiom schemas and inference rules of ALP.
Axioms
TAUT The set of propositional tautologies
AN ` A
i
j
ϕ ↔ A
i
j
¬ϕ
AC ` A
i
j
(ϕ ∧ ψ) ↔ A
i
j
ϕ ∧ A
i
j
ψ
AA ` A
i
j
ϕ ↔ A
i
j
A
k
l
ϕ
A[≡] ` A
i
j
ϕ ↔ A
i
j
[≡]
k
l
ϕ
AL ` A
i
j
ϕ ↔ A
i
j
L
k
ϕ
AK ` A
i
j
ϕ ↔ A
i
j
K
k
l
ϕ
AN[≡] ` A
i
j
ϕ ∧ ϕ → [≡]
i
j
ϕ
K
L
` L
j
(ϕ → ψ) → (L
j
ϕ → L
j
ψ)
T
L
` L
j
ϕ → ϕ
5
L
` ¬L
j
ϕ → L
j
¬L
j
ϕ
K
[≡]
` [≡]
i
j
(ϕ → ψ) → ([≡]
i
j
ϕ → [≡]
i
j
ψ)
T
[≡]
` [≡]
i
j
ϕ → ϕ
5
[≡]
` ¬[≡]
i
j
ϕ → [≡]
i
j
¬[≡]
i
j
ϕ
K
C
` C
i
j
(ϕ → ψ) → (C
i
j
ϕ → C
i
j
ψ)
MIX ` C
i
j
ϕ → ϕ ∧ [≡]
i
j
L
j
C
i
j
ϕ
IND ` C
i
j
(ϕ → [≡]
i
j
L
j
ϕ) → (ϕ → C
i
j
ϕ)
KAC ` K
i
j
ϕ ↔ A
i
j
ϕ ∧C
i
j
ϕ
Inference Rules
MP If ` ϕ and ` ϕ → ψ, then ` ψ
LG If ` ϕ then ` L
j
ϕ
[≡]G If ` ϕ then ` [≡]
i
j
ϕ
CG If ` ϕ then ` C
i
j
ϕ
from w on R
j
◦ ≡
i
j
, and [≡]
i
j
L
j
ϕ holds even at that
world. Therefore, M, w  ϕ → C
i
j
ϕ.
Then, it is enough to prove that if the assumptions are
valid, they are also valid for all inference rules. All of
them are straightforward.
4.2 Completeness
In proof of the completeness theorem, we use the
canonical model used in the proof on modal logic
(Chellas, 1980). However, in ALP, we can take a
set of formulas, such as Φ = {([≡]
i
j
L
j
)
n
ϕ | n ∈ N} ∪
{¬C
i
j
ϕ} for each i, j ∈ G, where ([≡]
i
j
L
j
)
n
is n iter-
ations of [≡]
i
j
L
j
. Therefore, our logic is no longer
compact. It is necessary to restrict canonical models
to a finite set of formulas. This technique is used in
proof on logic with common knowledge defined by
the reflexive-transitive closure of relations. We cus-
tomize the tools and techniques in (van Ditmarsch
et al., 2007) for our logic and use them.
First, we define closure as a restricted set of for-
mulas.
Definition 5. Let cl : L → 2
L
be the function such
that for every ϕ ∈ L and each i, j ∈ G, cl(ϕ) is the
smallest set satisfying that:
1. ϕ ∈ cl(ϕ);
2. If ψ ∈ cl(ϕ) then sub(ψ) ⊆ cl(ϕ) where sub(ψ) is
the set of subformulas of ψ;
3. If ψ ∈ cl(ϕ) and ψ is not a form of negation, then
¬ψ ∈ cl(ϕ);
4. If C
i
j
ψ ∈ cl(ϕ), then [≡]
i
j
L
j
C
i
j
ψ ∈ cl(ϕ).
We call it the closure of ϕ.
Lemma 1. For every ϕ, cl(ϕ) is finite.
Proof. We prove it by induction on the structure of ϕ.
This proof is straightforward.
Definition 6. Let Φ be the closure of a formula. Γ is
a maximal consistent set in Φ iff
1. Γ ⊆ Φ;
2. Γ 0 ⊥;
3. There is no Γ
0
such that Γ ⊂ Γ
0
and Γ
0
0 ⊥.
Lemma 2. Let Φ be the closure of a formula. If Γ
is a consistent set in Φ, then there exists a maximal
consistent set ∆ in Φ such that Γ ⊆ ∆.
Proof. It follows immediately from the property that
Φ is finite.
Then, a maximal consistent set can be generated
at any time from a consistent set.
Next, the canonical model for a restricted set of
formulas is defined as follows.
Definition 7. Let Φ be the closure of a for-
mula. The canonical model C(ALP) for Φ is a tu-
ple hC(W ), {C(R
j
)}
j∈G
, C(V ), {C(A
i
j
)}
i, j∈G
, {C(≡
i
j
)}
i, j∈G
i, where:
• C(W )
:
= {Γ | Γ is a maximal consistent set in Φ};
• (w, v) ∈ C(R
j
) iff {ϕ | L
j
ϕ ∈ w} ⊆ v;
• C(V )(p)
:
= {Γ | p ∈ Γ};
• C(A
i
j
)
:
= {p | for all w ∈ W, A
i
i
p ∧ A
i
j
p ∈ w};
• (w, v) ∈ C(≡
i
j
) iff {ϕ | [≡]
i
j
ϕ ∈ w} ⊆ v.
Lemma 3. For every ϕ, the canonical model for the
closure of ϕ is an epistemic model with awareness.
Proof. We prove that the canonical model for the clo-
sure of ϕ satisfies the definition of an epistemic model
with awareness.
• For C(R
i
), we can prove it in the same proof strat-
egy as S5.
• For C(A
i
j
), it is enough to prove that if p ∈ C(A
i
j
)
then p ∈ C(A
i
i
) for every p ∈ P . Suppose p ∈
C(A
i
j
), then for all w ∈ C(W ), A
i
i
p ∧ A
i
j
p ∈ w.
Thus, A
i
i
p ∧ A
i
i
p ∈ w for all w ∈ C(W ).
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
212

• For C(≡
i
j
), it is enough to prove that for all
(w, v) ∈ C(≡
i
j
), for every p ∈ C(A
i
j
), if w ∈
C(V )(p), then v ∈ C(V )(p), and vice versa. From
left to right, suppose that w ∈ C(V )(p) for every
p ∈ C(A
i
j
). Then, p ∈ w and A
i
j
p ∈ w. p ∈ v fol-
lows from AN[≡]. The reverse direction is proved
similarly.
We introduce C
i
j
-paths on the canonical models.
Definition 8. Let Φ be the closure of a formula. A C
i
j
-
path from Γ is a sequence Γ
0
, ··· , Γ
n
of maximal con-
sistent sets in Φ such that (Γ
k
, Γ
k+1
) ∈ C(R
j
) ◦C(≡
i
j
)
for all k, where 0 ≤ k ≤ n, and Γ
0
= Γ. The length of
Γ
0
, ··· , Γ
n
is n. A ϕ-path is a sequence Γ
0
, ··· , Γ
n
of
maximal consistent sets in Φ such that ϕ ∈ Γ
k
for all
k, where 0 ≤ k ≤ n.
Lemma 4. Let Φ be the closure of a formula and
Γ, ∆ be a maximal consistent set in Φ. If
V
Γ ∧ ¬[≡
]
i
j
L
j
¬
V
∆ is consistent, then (Γ, ∆) ∈ (C(R
j
) ◦C(≡
i
j
)).
Proof. Suppose that
V
Γ ∧ ¬[≡]
i
j
L
j
¬
V
∆ is consis-
tent, and [≡]
i
j
L
j
ϕ ∈ Γ for every ϕ. Then, [≡]
i
j
L
j
ϕ ∧
¬[≡]
i
j
L
j
¬
V
∆ is consistent. If ϕ 6∈ ∆, ¬ϕ ∈ ∆. It fol-
lows that [≡]
i
j
L
j
ϕ ∧ ¬[≡]
i
j
L
j
ϕ is consistent, but this
formula is a contradiction. Thus ϕ ∈ ∆.
Lemma 5. Let Φ be the closure of a formula and Γ, ∆
be maximal consistent sets in Φ. If C
i
j
ϕ ∈ Φ, then
C
i
j
ϕ ∈ Γ iff every C
i
j
-path from Γ is a ϕ-path.
Proof. (⇒) We prove it by induction on the length of
a C
i
j
-path.
• For the base case, suppose that the length of a C
i
j
-
path is 0, C
i
j
ϕ ∈ Φ, and C
i
j
ϕ ∈ Γ. Then Γ = Γ
0
=
Γ
n
. By MIX, ϕ ∈ Γ.
• For induction steps, suppose that the length of a
C
i
j
-path is k + 1, C
i
j
ϕ ∈ Φ, and C
i
j
ϕ ∈ Γ. By the
induction hypothesis, C
i
j
ϕ ∈ Γ
k
. Since MIX and
the definition of C(R
j
) and C(≡
i
j
), ϕ ∈ Γ
k+1
.
(⇐) Let S(C
i
j
, ϕ) be a set of maximal consistent
sets ∆ in Φ such that every C
i
j
-path from ∆ is a ϕ-path.
We introduce a special formula:
χ =
_
∆∈S(C
i
j
,ϕ)
^
∆.
Suppose that every C
i
j
-path from Γ is a ϕ-path.
First, we need to prove these three:
(1) `
^
Γ → χ; (2) ` χ → ϕ; (3) ` χ → [≡]
i
j
L
j
χ.
• For (1), Γ ∈ S(C
i
j
, ϕ) by the assumption. Thus,
`
V
Γ → χ.
• For (2), since every C
i
j
-path from ∆ is a ϕ-path,
ϕ ∈ ∆ for every ∆ ∈ S(C
i
j
, ϕ). Thus, ϕ is derived
from χ.
• For (3), we prove it by contradiction. Suppose χ∧
¬[≡]
i
j
L
j
χ is consistent. By the construction of χ,
there exists ∆ such that
V
∆ ∧ ¬[≡]
i
j
L
j
χ is consis-
tent. The set ¬
W
Θ∈C(W )\S(C
i
j
,ϕ)
V
Θ is equivalent
to χ because the disjunction of the complement
of the other combinations can express a particular
set of combinations represented by χ. Therefore,
V
∆∧¬[≡]
i
j
L
j
¬
W
Θ∈C(W )\S(C
i
j
,ϕ)
V
Θ is consistent.
There is Θ such that
V
∆ ∧ ¬[≡]
i
j
L
j
¬
V
Θ is con-
sistent. By Lemma 4, (∆, Θ) ∈ C(R
j
) ◦ C(≡
i
j
).
There exists a C
i
j
-path from ∆ that is not a ϕ-path.
This is a contradiction. Thus, ` χ → [≡]
i
j
L
j
χ.
By (3) and CG, ` C
i
j
(χ → [≡]
i
j
L
j
χ). It follows that
` χ → C
i
j
χ from IND. By (1) and (2), `
V
Γ → C
i
j
ϕ.
Thus, C
i
j
ϕ ∈ Γ.
Lemma 6. Let Φ be the closure of a formula and
C(ALP) be the canonical model for Φ. For all w ∈
C(W ) and every ϕ ∈ Φ, if C(ALP), w  ϕ then ϕ ∈ w.
Proof. We prove it by induction on the structure of
formulas. The cases other than A
i
j
, L
j
, and C
i
j
are triv-
ial, including the base case.
• For the case of A
i
j
ϕ, we prove A
i
j
ϕ ∈ w by in-
duction on the structure of ϕ. Suppose that
C(ALP), w  A
i
j
ϕ, then At(ϕ) ⊆ C(A
i
j
). It means
for every p ∈ P , and for all v ∈ C(W ), if p ∈ At(ϕ)
then A
i
i
p ∧ A
i
j
p ∈ v.
– For the base case, A
i
j
p ∈ v for all v ∈ C(W ),
since p = At(p). Thus, A
i
j
p ∈ w.
– For the other cases, we obtain it by induction
hypothesis and decomposing the formula with
corresponding axioms: AN, AC, AA, A[≡],
AL, and AK.
• For the case of L
j
ϕ, we prove it by contraposi-
tion. Suppose that L
j
ϕ 6∈ w. By the definition of
C(R
j
), ϕ 6∈ v for all v such that (w, v) ∈ C(R
j
).
Thus, C(ALP), w 2 L
j
ϕ.
• For the case of [≡]
i
j
, we prove it by contraposition.
Suppose that [≡]
i
j
ϕ 6∈ w. By the definition of C(≡
i
j
), ϕ 6∈ v for all v such that (w, v) ∈ C(≡
i
j
). Thus,
C(ALP), w 2 [≡]
i
j
ϕ.
• For the case of C
i
j
, suppose that C(ALP), w  C
i
j
ϕ.
Then, C(ALP), v  ϕ for all v such that (w, v) ∈
Logic of Awareness in Agent’s Reasoning
213

(C(R
j
) ◦C(≡
i
j
))
+
. It means every C
i
j
-path from
w is a ϕ-path. By Lemma 5, C
i
j
ϕ ∈ w.
Lemma 7. Let Φ be the closure of a formula and Γ
be a maximal consistent set in Φ. For every ϕ ∈ Φ
and every maximal consistent set Γ, if ϕ ∈ Γ then ` ϕ.
Proof. We prove it by contraposition. Suppose 0 ϕ.
It means any maximal consistent sets of ALP do not
contain ϕ. Thus, ϕ 6∈ Γ.
Theorem 2. For every ϕ ∈ L
P
, if  ϕ, then ` ϕ.
Proof. Suppose that  ϕ, then C(M), w  ϕ for the
closure of ϕ by Lemma 3. ϕ ∈ w by Lemma 6. Thus,
` ϕ by Lemma 7.
5 EPISTEMIC ACTIONS
In epistemic logic, including logic of awareness, we
formalize how the information held by agents changes
for applications and understanding of concepts. In
this paper, we introduce two actions that are ‘becom-
ing aware of’ and ‘becoming unaware of’ as prepa-
ration for incorporating agent communication. These
are the basic actions relevant to ‘awareness of’ (van
Benthem and Vel
´
azquez-Quesada, 2010).
First, we add two new operators to syntax, which
are [+ϕ]
i
j
and [−ϕ]
i
j
for each i, j ∈ G. [+ϕ]
i
j
ψ reads
‘ j become aware of ϕ in i’s viewpoint’. [−ϕ]
i
j
ψ reads
‘ j become unaware of ϕ in i’s viewpoint.’ We extend
the satisfaction relation of ALP as follows:
M, w  [+ϕ]
i
j
ϕ iff M[+ϕ]
i
j
, w  ϕ;
M, w  [−ϕ]
i
j
ϕ iff M[−ϕ]
i
j
, w  ϕ.
Formulas with dynamic operators are evaluated in the
updated models, which are M[+ϕ]
i
j
and M[−ϕ]
i
j
. We
define these as follows:
Definition 9. M[+ϕ]
i
j
is a tuple hW, {R
k
}
k∈G
, V,
{A [+ϕ]
k
l
}
k,l∈G
, {≡
k
l
}
k,l∈G
i, where:
A [+ϕ]
k
l
:
=
(
A
k
l
∪ {At(ϕ)} k = i and l = j,
A
k
l
otherwise.
M[−ϕ]
i
j
is a tuple hW, {R
k
}
k∈G
, V, {A [−ϕ]
k
l
}
k,l∈G
,
{≡
k
l
}
k,l∈G
i, where:
A [−ϕ]
k
l
:
=
(
A
k
l
\ {At(ϕ)} k = i and l = j,
A
k
l
otherwise.
For example, [+n]
b
b
K
b
b
K
b
a
p
b
is true at w
1
in the ex-
ample in Section 3.
In order to provide the corresponding Hilbert-
system, there is a technique to prove the complete-
ness theorem of logic with dynamic operators, such
as PAL (Public Announcement Logic) (Plaza, 1989).
The technique replaces a formula with a dynamic op-
erator of a simple formula that is logically equivalent.
For example, [+ϕ]L
j
ψ ↔ L
j
[+ϕ]ψ holds for L
j
op-
erator. For [≡]
i
j
and C
i
j
operators, we refer to (Grossi
et al., 2015) for identifying possible worlds with the
same valuation for atomic propositions in the changed
awareness set. The logic in (Grossi et al., 2015) has
the operator that represents a proposition holds at the
possible world whose the same valuation for all the el-
ements of a particular set of atomic propositions. We
leave this part as our future work.
6 RELATED WORK
We introduce some logic or ideas relevant to our logic.
(van Ditmarsch and French, 2009; van Ditmarsch and
French, 2011) is based on a similar idea as this paper,
which is to connect agents’ state of awareness with
the distinctions of possible worlds. The main differ-
ence is that our logic can represent not only the dis-
tinctions of possible worlds but also possible worlds
searched according to the distinction. Unlike our
logic, these logics can search even for worlds with a
different valuation for propositions of which an agent
is unaware but do not adjust accessibility.
Team semantics used in dependence logic (Sano
and Virtema, 2015) also has a similar idea that for-
mulas are true in a specific group of possible worlds.
This semantics has a structure that a subset of possible
worlds called a term supports a formula.
As for epistemic actions for awareness, several pa-
pers are using the idea of PAL (Plaza, 1989), includ-
ing this paper. In particular, (Grossi and Vel
´
azquez-
Quesada, 2015; Fern
´
andez-Fern
´
andez and Vel
´
azquez-
Quesada, 2021) proposed a realistic formalization of
epistemic actions, such as updating awareness by in-
ference. The idea of an action model (Baltag et al.,
1998) might help formalize agent communication in
our logic. Action models control communicative ac-
tions separately from a Kripke model that decides
knowledge. It allows us to formalize complex actions,
such as a misleading private announcement.
Semantic approaches to awareness are active in
the field of economics. It is also called the event-
based approach, in which the concept of events that
are a set of possible worlds is introduced, and knowl-
edge is expressed as an operator on events. The logic
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
214

system proposed in (Modica and Rustichini, 1994) is
the early work of the approach. (Halpern, 2001) found
it to be equivalent to a part of the logic in (Fagin and
Halpern, 1988). Since the work of (Modica and Rus-
tichini, 1999), the focus has been on a formalization
of the concept of unawareness (Heifetz et al., 2006;
Heifetz et al., 2008).
7 CONCLUSION
In this paper, we have introduced Awareness Logic
with Partition (ALP ), where we incorporated the no-
tion of partition among possible worlds and have ex-
tended the distinction of aware/unaware propositions
to indistinguishable possible worlds. With this, we
have properly reflected the agent’s awareness to other
agents’ knowledge. Employing this framework, we
have shown an example where the behavior of each
agent could be logically explained.
Our contributions of this logic are two-fold. From
the logical viewpoint, we introduced the syntax and
the semantics of ALP and have shown its complete-
ness. From the viewpoint of applicability to real
world, we have shown the architecture to explain the
strategic behavior of rational agents in a society or
game theory. We expect that the logic offers a founda-
tion for formal expressions of human minds and prac-
tical agent communication.
There are several directions in the future. On the
conceptual side, we consider incorporating more epis-
temic actions and concepts, such as common knowl-
edge, to represent practical agent communication. On
the technical side, the axiomatic system of the dy-
namic extension, discussed in Section 5, remains. In
addition, our logic is applicable to the studies deal-
ing with multiple agents’ reasoning, such as descrip-
tion and analysis of games that take into account play-
ers’ awareness of possible strategies (Feinberg, 2005;
Kaneko and Suzuki, 2002). Specifically, we plan to
use the logic to analyze rationality to reach an equi-
librium in games with awareness.
ACKNOWLEDGMENTS
The authors thank Professor Thomas
˚
Agotnes and
the anonymous reviewers for their many insightful
comments. This work was supported by JSPS kaken
22H00597.
REFERENCES
Baltag, A., Moss, L. S., and Solecki, S. (1998). The logic of
public announcements, common knowledge, and pri-
vate suspicions. In Proceedings of the 7th Conference
on Theoretical Aspects of Rationality and Knowledge
(TARK VII), pages 43–56. Morgan Kaufmann Publish-
ers.
Chellas, B. F. (1980). Modal logic: an introduction. Cam-
bridge University Press.
Fagin, R. and Halpern, J. Y. (1988). Belief, awareness, and
limited reasoning. Artificial Intelligence, 34:39–76.
Fagin, R., Halpern, J. Y., Moses, Y., and Vardi, M. (1995).
Reasoning About Knowledge. MIT Press.
Feinberg, Y. (2005). Games with incomplete awareness.
Technical report, Technical Report Resarch Paper Se-
ries# 1894, Stanford Graduate School of Business.
Fern
´
andez-Fern
´
andez, C. and Vel
´
azquez-Quesada, F. R.
(2021). Awareness of and awareness that: their com-
bination and dynamics. Logic Journal of the IGPL,
29(4):601–626.
Grossi, D., Lorini, E., and Schwarzentruber, F. (2015).
The ceteris paribus structure of logics of game forms.
Journal of Artificial Intelligence Research, 53:91–
126.
Grossi, D. and Vel
´
azquez-Quesada, F. R. (2015). Syn-
tactic awareness in logical dynamics. Synthese,
192(12):4071–4105.
Halpern, J. Y. (2001). Alternative semantics for unaware-
ness. Games and Economic Behavior, 37(2):321–339.
Heifetz, A., Meier, M., and Schipper, B. C. (2006). In-
teractive unawareness. Journal of Economic Theory,
130(1):78–94.
Heifetz, A., Meier, M., and Schipper, B. C. (2008). A
canonical model for interactive unawareness. Games
and Economic Behavior, 62:304–324.
Kaneko, M. and Suzuki, N.-Y. (2002). Bounded interper-
sonal inferences and decision making. Economic The-
ory, 19(1):63–103.
Modica, S. and Rustichini, A. (1994). Awareness and par-
titional information structures. Theory and Decision,
37(1):107–124.
Modica, S. and Rustichini, A. (1999). Unawareness and
partitional information structures. Games and Eco-
nomic Behavior, 27(2):265–298.
Plaza, J. (1989). Logics of public communications. In
Proceedings of the fourth international symposium on
methodologies for intelligent systems: Poster session
program, volume 158, pages 201–216. Oak Ridge Na-
tional Laboratory.
Sano, K. and Virtema, J. (2015). Axiomatizing proposi-
tional dependence logics. In 24th EACSL Annual Con-
ference on Computer Science Logic (CSL 2015), vol-
ume 41, pages 292–307. Schloss Dagstuhl–Leibniz-
Zentrum fuer Informatik.
van Benthem, J. and Vel
´
azquez-Quesada, F. R. (2010). The
dynamics of awareness. Synthese, 177(1):5–27.
van Ditmarsch, H. and French, T. (2009). Aware-
ness and forgetting of facts and agents. In 2009
Logic of Awareness in Agent’s Reasoning
215

IEEE/WIC/ACM International Joint Conference on
Web Intelligence and Intelligent Agent Technology,
pages 478–483. IEEE.
van Ditmarsch, H. and French, T. (2011). Becoming aware
of propositional variables. In Banerjee, M. and Seth,
A., editors, Logic and Its Applications, pages 204–
218. Springer.
van Ditmarsch, H., van Der Hoek, W., and Kooi, B. (2007).
Dynamic Epistemic Logic. Springer Science & Busi-
ness Media.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
216