
Concrete Quantum Circuits to Prepare Generalized Dicke States on a
Quantum Machine
Shintaro Narisada
a
, Shohei Beppu
b
, Kazuhide Fukushima
c
and Shinsaku Kiyomoto
d
KDDI Research, Inc., Fujimino, Japan
Keywords:
Dicke State, Hamming Weight, Noisy Computation, Quantum Circuit, Quantum Computing, Generalization.
Abstract:
A Dicke state is a superposition of n-qubit with Hamming weight k, denoted by |D
n
k
i. Dicke states are fre-
quently employed to prepare input superpositions for quantum search algorithms (e.g., Grover search and
quantum walks) that solve combinatorial problems with a certain number
n
k
of candidate solutions. B
¨
artschi
and Eidenbenz propose a concrete quantum circuit to construct the Dicke state |D
n
k
i with polynomial quantum
gates, and they generalize the circuit in terms of Hamming weight k to prepare a superposition of Dicke states.
Subsequently, Esser et al. present another quantum circuit to generate the Dicke state |D
n
k
i with polynomial
gates and a few auxiliary quantum bits. In this paper, we generalize Esser’s state preparation circuit to con-
struct a superposition of Dicke states. We conduct a concrete comparison with two generalized Dicke state
preparation circuits. We perform noisy simulations and experiments using real quantum machines from the
IBM quantum experience service (IBMQ). Both circuits successfully construct the generalized Dicke state
superposition using a noisy intermediate-scale quantum (NISQ) device, albeit somewhat affected by noise.
1 INTRODUCTION
The exponential hardness of combinatorial problems
is one of the foundations of the security of modern so-
ciety. With the advent of quantum computers, quan-
tum search algorithms to solve combinatorial prob-
lems such as the Grover algorithm (Grover, 1996),
quantum amplitude amplification (QAA) (Brassard
et al., 2002) and quantum walks (Ambainis, 2004)
are being realized (Mandviwalla et al., 2018; Acasi-
ete et al., 2020). The input to these algorithms is nor-
mally a quantum state superposition associated with
the candidate solutions to a specific problem to be
solved. While uniform superposition of all 2
n
n-qubit
states can be prepared with n Hadamard gates, it is
known that constructing an arbitrary superposition re-
quires Θ(2
n
) quantum gates (Shende et al., 2006).
There are several studies of quantum circuits that ef-
ficiently prepare superpositions of a certain class of
states, including circuits to generate linear-size su-
perpositions called the |GHZ
n
i and |W
n
i states (Cruz
et al., 2019), and circuits to generate exponential-size
a
https://orcid.org/0000-0002-9399-9778
b
https://orcid.org/0000-0002-8220-9515
c
https://orcid.org/0000-0003-2571-0116
d
https://orcid.org/0000-0003-0268-0532
superpositions called the Dicke state |D
n
k
i probabilis-
tically (Childs et al., 2000; Chakraborty et al., 2014)
or deterministically (Kaye and Mosca, 2001; B
¨
artschi
and Eidenbenz, 2019; Mukherjee et al., 2020; Esser
et al., 2021; B
¨
artschi and Eidenbenz, 2022) in poly-
nomial time.
|D
n
k
i is the superposition of all n-qubit states with
Hamming weight k of size
n
k
, which has a close re-
lationship to combinatorial problems such as the k-
vertex cover problem (Cook et al., 2020), extractive
summarization (Niroula et al., 2022) and syndrome
decoding (SD) problem (Esser et al., 2022; Perriello
et al., 2021; Chailloux et al., 2021), which is the
security basis of code-based cryptosystems. A gen-
eralized Dicke state preparation circuit to construct
a superposition of Dicke states |D
n
k
i for any k ≤ n
with polynomial gates is also proposed in (Kaye and
Mosca, 2001; B
¨
artschi and Eidenbenz, 2019). For
certain combinatorial problems, the number of com-
binations for candidate solutions may be a sum of
n
i
for any 0 ≤ i ≤ n rather than
n
k
. For example, the
SD problem can be easier to solve if it is extended to
choose binary vectors with weight ≤ k than vectors
with weight k from n vectors.
In this paper, we generalize the Dicke state prepa-
ration circuit shown in (Esser et al., 2021) and pro-
pose another circuit to construct an equal superposi-
Narisada, S., Beppu, S., Fukushima, K. and Kiyomoto, S.
Concrete Quantum Circuits to Prepare Generalized Dicke States on a Quantum Machine.
DOI: 10.5220/0011618000003405
In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 329-338
ISBN: 978-989-758-624-8; ISSN: 2184-4356
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
329

tion of |D
n
k
i for any 0 ≤ i ≤ k with polynomial size
quantum gates. We implement the generalized cir-
cuit and B
¨
artschi’s circuit using the Qiskit library and
give a comparison between two generalized Dicke
state preparation circuits. Quantum simulations of our
implementations in both noise-free models and noisy
circuit models are also conducted. We run our imple-
mentations on the quantum device from IBMQ and
achieved superposition for some generalized Dicke
states.
2 PRELIMINARIES
We write a qubit as |xi,x ∈{0,1}. A tensor product of
two qubits |xi and |yi is |xi⊗|yi or simply |xi|yi. A
tensor product of two identical qubits |xi is shortened
by |xi
⊗2
= |xi⊗|xi. Let |x
1
x
2
...x
n
i,x
i
∈ {0, 1},1 ≤
i ≤ n be an n-qubit quantum state. |x
i
x
i+1
...i
i
de-
notes the sequence of qubits starting at i. We may
treat a quantum state |x
1
x
2
...x
n
i as a binary string
b
n
= x
1
x
2
...x
n
for simplicity of explanation. The
Hamming weight of a binary string b
n
is wt(b
n
) =
|{i | x
i
= 1}|. A binary string of length n and Ham-
ming weight k is written by b
n,k
. The empty string is
denoted by ε. |ψ
n
i = c
00...0
|00...0i+ c
00...1
|00...1i+
... + c
11...1
|11...1i denotes the n-qubit superposition,
where
∑
i
1
,...,i
n
|c
i
1
...i
n
|
2
= 1. Each |c
i
1
...i
n
|
2
can be con-
sidered as the existence probability p
i
1
...i
n
of the cor-
responding quantum state |i
1
...i
n
i. Measuring the n-
qubit superposition yields one n-qubit state |i
1
...i
n
i
with probability p
i
1
...i
n
. A Dicke state is defined as
follows:
Definition 1. A Dicke state |D
n
k
i is the equal super-
position of all n-qubit states |xi with Hamming weight
wt(x) = k,
|D
n
k
i =
s
1
n
k
∑
x∈{0,1}
n
,wt(x)=k
|xi. (1)
For example, |D
3
1
i =
1
√
3
(|100i+ |010i+ |001i).
A superposition of Dicke states is written by
∑
0≤i≤n
α
i
|D
n
i
i, (2)
where α
i
∈ C, α
2
0
+ . .. + α
2
n
= 1 (Kaye and Mosca,
2001; Bastin et al., 2009). Hereafter, we consider
an equal superposition of Dicke states for arbitrary
weights. For an integer set K ⊆ [0, n], we will refer to
equal superpositions of Dicke states with Hamming
weights i ∈ K as a generalized Dicke state:
Definition 2. Generalized Dicke state |D
n
K
i for an in-
teger set K ⊆ [0,n] is the equal superposition of all
n-qubit states |xi with Hamming weight wt(x) ∈ K,
|D
n
K
i =
s
1
|C
n
K
|
∑
x∈{0,1}
n
,wt(x)∈K
|xi, (3)
where |C
n
K
| =
∑
n
i∈K
n
i
. For example, |D
3
K
i =
1
√
5
(|000i+ |100i+ |010i+ |001i + |111i) for K =
{0,1,3}. Using Equation 2, the generalized Dicke
state is a case when α
i
=
q
n
i
/|C
n
K
| for all i ∈K and
α
i
= 0 otherwise.
Any unitary operation on the quantum state |xi is
denoted by U|xi, where U is a unitary matrix. We will
introduce certain basic unitary operations on quantum
states.
• I: identity operator I =
1 0
0 1
, I|0i = |0i and
I|1i = |1i.
• X: single qubit gate defined as X =
0 1
1 0
.
X|0i = |1i and X|1i = |0i as with the classical
NOT gate.
• CNOT (controlled-X): 2-qubits gate that applies
X to the target qubit when the control qubit is |1i
and does nothing when the control qubit is |0i.
• C
n
X (multi-controlled-X): (n+1)-qubits gate that
applies X to the target qubit when the control n-
qubit satisfy some quantum state |b
n
i and does
nothing when the control is not |b
n
i. When n = 2
and b
2
= 11, C
n
X is called a Toffoli gate.
• R
y
(θ): single qubit gate defined by R
y
(θ) =
cos(θ/2) −sin(θ/2)
sin(θ/2) cos(θ/2)
. Note that since
R
y
(2cos
−1
(
√
p))|0i =
√
p|0i+
√
1 − p|1i, it is
helpful when we want to partition the prob-
ability of |0i into p and 1 − p. We also
use CR
y
(θ) (controlled-R
y
(θ)) gates and C
n
R
y
(θ)
(multi-controlled-R
y
(θ)) gates.
Thereafter, these basic gates are combined to achieve
our desired unitary operation. A tensor product of two
unitary operators U
1
and U
2
is U
1
⊗U
2
. A tensor prod-
uct of two identical unitary operators U is shortened
by U
⊗2
= U ⊗U. A quantum circuit is a sequence of
unitary operations starting from |00...0i. The purpose
of a quantum circuit is to obtain the desired quantum
state |ψi(e.g., corresponding to the solution of a com-
binatorial problem) with high probability when mea-
suring the qubits at the endpoint of the circuit.
The computational complexity of a quantum cir-
cuit (circuit complexity) is evaluated by its width and
depth. The width of a quantum circuit is the total
number of qubits required for the circuit. Depth is
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
330

the longest path in the circuit. Auxiliary qubits (an-
cilla) are extra qubits that are often employed to sim-
plify gating operations. For example, ancilla qubits
are employed to store the carry of the quantum full
adder circuit.
3 DETERMINISTIC DICKE
STATE PREPARATION
We will explain previous deterministic Dicke state
preparation circuits proposed by B
¨
artschi (B
¨
artschi
and Eidenbenz, 2019) and Esser (Esser et al., 2021)
et al. The former uses no ancilla qubits, but its circuit
is somewhat complicated. The latter is intuitive con-
struction by using some ancilla qubits as a counter.
3.1 Dicke State Preparation Without
Ancilla Qubits
The central part of their circuit is the construction of
a unitary operator U
n,k
such that |00..00
|{z}
n−`
1..1
|{z}
`
i is an
input and |D
n
`
i is an output for any 0 ≤ ` ≤ k.
Definition 3 (U
n,k
). n-qubit unitary gate satisfying
U
n,k
|0i
⊗n−`
|1i
⊗`
= |D
n
`
i for all 0 ≤ ` ≤ k.
By setting ` ≤ k instead of ` = k, we can induc-
tively construct U
n,k
by using the following property
for the Dicke state.
Lemma 1. (Lamata et al., 2013; Moreno and Parisio,
2018) |D
n
`
i has the following inductive sum form:
|D
n
`
i=
r
`
n
|D
n−1
`−1
i⊗|1i+
r
n −`
n
|D
n−1
`
i⊗|0i. (4)
Intuitively, |D
n−1
`−1
i contains
n−1
`−1
strings, and
|D
n−1
`
i contains
n−1
`
strings with equal existence
probabilities
n−1
`−1
−1
and
n−1
`
−1
, respectively. The
sum of |D
n−1
`−1
i⊗|1i and |D
n−1
`
i⊗|0i then contains
n−1
`−1
+
n−1
`
=
n
`
distinct strings. The coefficients
of each term are intended to equalize the probability.
Both Dicke states |D
n−1
`−1
i and |D
n−1
`
i can be gen-
erated by the same unitary U
n−1,k
given the inputs
|0i
⊗n−`
|1i
⊗`−1
and |0i
⊗n−1−`
|1i
⊗`
, respectively. To
inductively construct U
n,k
, we need a unitary gate that
corresponds to the following operation that changes
(actually left shift) the last qubit |1i to |0i with prob-
ability
n−`
n
for inputs |0i
⊗n−`
|1i
⊗`
for all ` ≤ k
|0i
⊗n−`
|1i
⊗`
7→
r
`
n
|0i
⊗n−`
|1i
⊗`−1
|1i+
r
n −`
n
|0i
⊗n−`−1
|1i
⊗`−1
|0i. (5)
Note that we can disregard the first n −k −1 qubits
since they are always 0. Next, we can consider a uni-
tary S
n,k
(referred to as split and cyclic shift in the
original paper) such that for the last k + 1 qubits it
performs a left shift operation with probability
n−`
n
for all ` ≤ k.
Definition 4 (S
n,k
). (k + 1)-qubits unitary gate for all
1 ≤ ` ≤ k satisfying
S
n,k
|0i
⊗k+1
=|0i
⊗k+1
S
n,k
|0i
⊗k+1−`
|1i
⊗`
=
r
`
n
|0i
⊗k+1−`
|1i
⊗`−1
|1i+
r
n −`
n
|0i
⊗k−`
|1i
⊗`−1
|0i
S
n,k
|1i
⊗k+1
=|1i
⊗k+1
.
One can construct the S
n,k
gate concretely by com-
bining the CNOT, CR
y
(θ) gate and C
n
R
y
(θ) gate:
Definition 5 (Building blocks of S
n,k
). S
n,k
is the con-
nection of k basic gates B
n,1
to B
n,k
B
n,1
:|00i
n−1
→|00i
n−1
|11i
n−1
→|11i
n−1
|01i
n−1
→
r
1
n
|01i
n−1
+
r
n −1
n
|10i
n−1
B
n,`
:|00i
n−`
|0i
n
→|00i
n−`
|0i
n
|01i
n−`
|0i
n
→|01i
n−`
|0i
n
|00i
n−`
|1i
n
→|00i
n−`
|1i
n
|11i
n−`
|0i
n
→|11i
n−`
|0i
n
|01i
n−`
|1i
n
→
r
`
n
|01i
n−`
|1i
n
+
r
n −`
n
|11i
n−`
|0i
n
where 2 ≤` ≤k. Namely, S
n,k
= B
n,k
B
n,k−1
...B
n,2
B
n,1
| {z }
k basic gates
.
Figure 1 shows the basic gate components of B
n,1
and
B
n,`
.
Using the inductive property U
i,i
= (U
i−1,i−1
⊗
I
⊗k−i
)·S
i,i−1
for 2 ≤i ≤k and U
i,k
= (U
i−1,k
⊗I
⊗n−i
)·
(I
⊗i−k−1
⊗S
i,k
) for k + 1 ≤i ≤n, U
n,k
is decomposed
by S
n,k
gates as follows:
Lemma 2. (B
¨
artschi and Eidenbenz, 2019) The fol-
lowing inductive construction of U
n,k
is consistent
with Definition 3.
Concrete Quantum Circuits to Prepare Generalized Dicke States on a Quantum Machine
331

𝑛 − 1
𝑛
𝑅
!
(2 cos
"#
1/𝑛)
𝑛 − ℓ 𝑅
!
(2 cos
"#
ℓ/𝑛)
𝑛
⋯
𝑛 − ℓ + 1
Figure 1: B
n,1
gate (left) and B
n,`
gate for 2 ≤ ` ≤ k (right).
U
n,k
:
=
k
∏
i=2
(S
i,i−1
⊗I
⊗n−i
) ·
n
∏
i=k+1
(I
⊗i−k−1
⊗S
i,k
⊗I
⊗n−i
).
For instance, U
5,3
|00111i = (S
2,1
⊗I
⊗3
) ·(S
3,2
⊗
I
⊗2
) · (S
4,3
⊗ I) · (I ⊗ S
5,3
)|00111i = |D
5
3
i. Since
|0i
⊗n−k
|1i
k
can be constructed from |00...0i by ap-
plying X gates, Dicke state |D
n
k
i can be prepared from
the initial state |00...0i. The circuit complexity is
shown as follows:
Theorem 1. (B
¨
artschi and Eidenbenz, 2019) Dicke
states |D
n
k
i can be prepared with a circuit of width n
and depth O(n) using k X gates and one U
n,k
gate.
We can further reduce the number of
gates (Mukherjee et al., 2020) or the circuit depth to
O(k log
n
k
) for constant k (B
¨
artschi and Eidenbenz,
2022). However, for the sake of circuit simplicity,
only the circuit from (B
¨
artschi and Eidenbenz, 2019)
is considered in this paper.
3.2 Dicke State Preparation with
Ancilla Qubits
Esser’s circuit is also based on the inductive prop-
erty of the Dicke state (Lemma 1). However, un-
like B
¨
artschi’s circuit, which determines the qubit se-
quence from right to left, Esser’s circuit determines
the quantum bit string in left-to-right order by consid-
ering Lemma 1 as follows:
|D
n
k
i =
r
n −k
n
|0i|D
n−1
k
i+
r
k
n
|1i|D
n−1
k−1
i,
|D
n
0
i = |0i
⊗n
,|D
n
n
i = |1i
⊗n
.
The lemma can be written like a Markov chain.
For example, |D
4
2
i =
q
1
2
|0i|D
3
2
i +
q
1
2
|1i|D
3
1
i =
q
1
6
|00i|D
2
2
i +
q
1
3
|01i|D
2
1
i +
q
1
3
|10i|D
2
1
i +
q
1
6
|11i|D
2
0
i =
q
1
6
(|0011i + |0101i + |0110i +
|1001i + |1010i + |1100i). Recall that the
R
y
(θ) gate can divide the existence prob-
ability of qubits to α
2
and 1 − α
2
by
R
y
(2cos
−1
(α))|0i = α|0i+
√
1 −α
2
|1i. In particu-
lar, when the i-th qubit is rotated, |b
i−1, j
i|D
n−(i−1)
k−j
i=
α
i, j
|b
i−1, j
i|0i|D
n−i
k−j
i +
q
1 −α
2
i, j
|b
i−1, j
i|1i|D
n−i
k−j−1
i
is satisfied for probability α
i, j
=
q
n−i
k−j
/
n−i+1
k−j
=
p
(n −i + 1 −k + j)/(n −i + 1) and any binary pre-
fix b
i−1, j
of length i −1 with weight j for 1 ≤ i ≤ n
and 0 ≤ j ≤ k −1. The probability distribution is
independent of the pattern of bit subsequence b
i−1, j
but depends on the length and weight of b
i−1, j
, and
thus, the number of required R
y
(θ) gates to divide the
probability is estimated to be O(nk).
To achieve such a Markov chain for |D
n
k
i on
a quantum circuit, we just need to keep track of
the Hamming weight j of the b
i−1, j
. We prepare
ancilla dlog(k + 1)e-qubits c to store the weight
as binary digits. When i = 1, c is initialized to
0 and b
0,0
= ε. Applying the R
y
(2cos
−1
(α
i, j
))
gate yields |b
i−1, j
iR
y
(2cos
−1
(α
i, j
))|0i
i
→
√
α
i, j
|b
i−1, j
i|0i
i
+
q
1 −α
2
i, j
|b
i−1, j
i|1i
i
. Next,
c is incremented by 1 for the quantum state
|b
i−1, j
i|1i
i
→ |b
i, j+1
i. We show a pseudocode
for constructing |D
n
k
i with auxiliary variable c in
Algorithm 1.
Algorithm 1: Preparation of |D
n
k
i with auxiliary variable c.
Input: integer k ≤ n, n-qubit
|x
1
x
2
...x
n
i = |0i
⊗n
and dlog(k + 1)e
ancilla qubits to store c
Output: |D
n
k
i
1 c ← 0
2 for i ← 1, ... , n do
3 for j ← 0, ..., k −1 do
4 if c = j then
5 |0i
i
→ α
i, j
|0i
i
+
q
1 −α
2
i, j
|1i
i
6 if x
i
= 1 then
7 c ← c + 1
8 return |x
1
x
2
...x
n
i
Quantum Gates for Algorithm 1
Similar to U
n,k
, we construct a unitary opera-
tor A
n,k
such that |0i
⊗n+dlog(k+1)e
is an input and
|D
n
k
i|0i
⊗dlog(k+1)e
is an output.
Definition 6 (A
n,k
). n-qubit unitary gate satisfying
A
n,k
|0i
⊗n+dlog(k+1)e
= |D
n
k
i|0i
⊗dlog(k+1)e
.
The building blocks of A
n,k
are C
n
X and C
n
R
y
(θ)
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
332

𝑖
𝛼
! ,#
𝑛 + 1
⋯
|0 ⟩
⋯
⋯
⋯
|𝑘 − 1⟩
𝑛 + 2
⋯
𝑛 + log(𝑘 + 1)
⋯
⋯
⋯
⋯
⋯
⋯
⋯
𝛼
!,$ %&
Figure 2: R
i
gate (left) and N
i
gate (right) for 1 ≤ i ≤n. The R
y
(2cos
−1
(α
i, j
)) gate is abbreviated by α
i, j
.
gates. We prepare two quantum registers |x
1
...x
n
i and
|c
1
...c
dlog(k+1)e
ito store the Dicke state and weight for
bit strings. For these two registers, the rotation unitary
R
i
and increment unitary N
i
are applied in alternating
order from 1 to n.
Definition 7 (Building blocks of R
i
). R
i
rotates the i-
th qubit |0i
i
according to the value of the ancilla qubit
for 1 ≤ i ≤ n and 0 ≤ j ≤k −1
R
i
:|0i
i
|ji
n+1
→
α
i, j
|0i
i
+
q
1 −α
2
i, j
|1i
i
|ji
n+1
,
where α
i, j
=
q
n−i+1−k+ j
n−i+1
. |ji
n+1
is the ancilla qubits
|c
1
...c
dlog(k+1)e
i corresponding to the binary repre-
sentation of an integer j for 0 ≤ j ≤ k −1. R
i
is con-
structed by k C
n
R
y
(θ) gates shown in Figure 2 (left).
Definition 8 (Building blocks N
i
). N
i
increments the
ancilla qubit if |xi
i
= |1i
i
for 1 ≤ i ≤ n
N
i
:|0i
i
|ji
n+1
→|0i
i
|ji
n+1
|1i
i
|ji
n+1
→|1i
i
|j + 1i
n+1
N
i
can be constructed by k C
n
X gates in Figure 2
(right).
|D
n
k
i can be generated using a circuit with ancilla
qubits, whose circuit complexity is computed as in the
next theorem.
Theorem 2. (Esser et al., 2021; da Silva and Park,
2022) Dicke states |D
n
k
ican be prepared with a circuit
of width n + dlog(k + 1)e and depth O(nk log k) using
one A
n,k
gate.
Note that the original circuit depth in (Esser
et al., 2021) is O(nk log k log log k) using 2dlog(k +
1)e ancilla qubits since the C
n
R
y
(θ) gate with
log(k + 1) control can be decomposed into a depth
O(logk log log k) elementary circuit with additional
dlog(k + 1)e ancilla. However, due to (da Silva and
Park, 2022), one can implement any n-controlled
single-qubit unitary gate C
n
U with O(n) depth and
O(n
2
) elementary gates without ancilla qubits. There-
fore, we removed the log log k term and dlog(k + 1)e
additional ancilla from the original theorem.
The circuit can also be a concrete instantiation of
the circuit in (Kaye and Mosca, 2001) with a smaller
number of ancilla qubits of size dlog(k + 1)e than
log(n/ε) of the original circuit, where ε 1 is a pre-
cision parameter.
4 GENERALIZED DICKE STATE
PREPARATION
In this section, we review the generalized Dicke
state preparation circuit proposed in (B
¨
artschi and Ei-
denbenz, 2019). Based on the circuit, we general-
ize another Dicke state preparation circuit proposed
in (Esser et al., 2021) with the same circuit complex-
ity.
4.1 Dicke State Generalization Without
Ancilla Qubits
Algorithm 2: Prepare-|D
n
K
i without ancilla.
Input: n,k, empty quantum circuit qc
Output: qc constructs |D
n
K
i
1 qc.ry(2cos
−1
(β
0
,n)
2 for i ← 1, ... , k −1 do
3 qc.cry(2cos
−1
(β
i
),n −i + 1,n −i)
4 qc.U
n,k
// concat U
n,k
gate
5 return qc
First, we review the concrete construction of |D
n
K
i
for any integer set i ∈ K (B
¨
artschi and Eidenbenz,
2019). To construct |D
n
K
i in polynomial gates, the
authors use the property of the U
n,k
gate such that
U
n,k
|0i
⊗n−`
|1i
⊗`
= |D
n
`
i for all 0 ≤ ` ≤ k. Recall
that the input of U
n,k
for the original algorithm is
|0i
⊗n−k
|1i
⊗k
. However, because U
n,k
accepts weights
` ≤k, U
n,k
also returns |D
n
`
ifor the input |0i
⊗n−`
|1i
⊗`
for all ` < k. Thus, to achieve a superposition of
Dicke states, one can set k ← maxK and input the
superposition of |00..00i, |00..01i, ..., |00..11..11
|{z}
k
i
to the U
n,k
gate. Since we want the equal superposi-
tion of Dicke states, the input superposition for U
n,k
is given by
∑
0≤i≤n
α
i
|D
n
i
i, where α
i
=
q
n
i
/|C
n
K
|
Concrete Quantum Circuits to Prepare Generalized Dicke States on a Quantum Machine
333

p
1
11
|0i
|0i
|0i
|0i
p
4
10
⊕ ⊕
p
1
4
⊕ ⊕
p
2
4
⊕ ⊕
p
1
3
⊕ ⊕
p
2
3
⊕ ⊕
p
1
2
|D
≤
4
2
i
U
4,2
Figure 3: Quantum circuit to prepare |D
≤
4
2
i =
q
1
11
∑
x∈{0,1}
4
,wt(x)≤2
|xi generated from Algorithm 2.
for all i ∈ K and α
i
= 0 otherwise. Such a super-
position can be constructed with one R
y
(θ) gate and
k −1 CR
y
(θ) gates. Algorithm 2 is a Qiskit-like pseu-
docode to generate a quantum circuit to prepare |D
n
K
i,
where β
i
= (
q
α
2
i
/(1 −
∑
i−1
j=0
α
2
j
). qc.a represents the
append of gate a to circuit qc. The R
y
(θ) gate is de-
noted by ry(θ,i), where i is the target qubit to which
the gate is applied. The CR
y
(θ) gate is denoted by
cry(θ,i, j), where i is the control and j is the target
qubit. We show an example of the circuit for |D
4
K
i
with K = {0, 1,2} in Figure 3.
Theorem 3. (B
¨
artschi and Eidenbenz, 2019) Gener-
alized Dicke states |D
n
K
i can be prepared with a cir-
cuit of width n and depth O(n) using one R
y
(θ) gate,
k −1 CR
y
(θ) gates and one U
n,k
gate with k ←max K.
4.2 Dicke State Generalization with
Ancilla Qubits
We show that Esser’s quantum circuit can also be gen-
eralized by considering the Markov chain for the sum
of combinations
∑
i∈K
n
i
by using the same building
blocks R
i
and N
i
. To do so, we set k ←maxK to store
the weight w in the ancilla qubits for all 0 ≤ w ≤ i,
i ∈ K. The angle value α
i, j
in block R
i
is replaced by
α
i, j
= β
i, j
/β
i−1, j
, (6)
where β
i, j
=
q
∑
`∈K,`≥j
n−i
`−j
. The entire algorithm
to construct |D
n
K
i is described in Algorithm 3. The
C
n
R
y
(θ) gate is denoted by mcry(θ, j,i), where j is
the control state and i is the target. Increment(i, qc)
in Line 7 appends N
i
unitary to qc. The correctness of
the Algorithm 3 is shown as follows.
Theorem 4. Algorithm 3 outputs a circuit to pre-
pare |D
n
K
i from |0i
⊗n+dlog(k+1)e
with a circuit of width
n + dlog(k + 1)e and depth O(nk log k) , where k ←
maxK.
Proof. In Line 3, Algorithm 3 rotates the 1st qubits
by R
y
(2cos
−1
(α
1,0
)):
|0i
⊗n
α
1,0
−−→α
1,0
|0i
⊗n
+
q
1 −α
2
1,0
|1i|0i
⊗n−1
=
β
1,0
β
0,0
|0i
⊗n
+
β
1,1
β
0,0
|1i|0i
⊗n−1
Algorithm 3: Prepare-|D
n
K
i with ancilla.
Input: n,k ← max K, qc with registers
|bi ← |0i
⊗n
,|ci ← |0i
⊗dlog(k+1)e
Output: qc constructs |D
n
K
i
1 for i ← 1, ... , n do
2 if i = 1 then
3 qc.ry(2cos
−1
(α
1,0
),1)
4 else
5 for j ← 0, ..., k −1 do
6 qc.mcry(2cos
−1
(α
i, j
),|ci = j, i)
7 qc ← Increment(i,qc)
8 return qc
⊕
p
7
11
|0i
|0i
|0i
|0i
|0i
|0i
⊕
p
4
7
p
3
4
⊕
⊕
p
2
4
p
2
3
⊕
⊕
p
1
2
p
1
2
⊕
⊕
|D
≤
4
2
i
Figure 4: Quantum circuit to prepare |D
≤
4
2
i generated from
Algorithm 3.
since
q
1 −α
2
i, j
= β
i, j+1
/β
i−1, j
from
i
j
=
i−1
j
+
i−1
j−1
. After n rotations, we obtain
∑
b
n,w
n
n
∏
i=1
β
i,w
i
β
i−1,w
i−1
!
|b
n,w
n
i =
∑
b
n,w
n
β
n,w
n
β
0,w
0
|b
n,w
n
i,
(7)
where w
0
= 0 and w
i−1
≤ w
i
≤ w
i−1
+ 1. If w
n
∈ K,
β
n,w
n
=
q
0
0
= 1 and 0 otherwise. Since β
0,0
=
p
|C
n
K
|, we obtain the equal superposition for all states
|b
n,w
n
i, w
n
∈K with probability
1
|C
n
K
|
. The circuit com-
plexity is the same as in (Esser et al., 2021) since
we only change the angle of the R
y
(θ) gate and C
n
X
gates.
The whole quantum circuit for |D
4
K
i with K =
{0,1,2} is presented in Figure 4.
5 EXPERIMENTS
To verify the performance of the generalized Dicke
state preparation circuits, we conduct several exper-
iments on both the quantum simulator and the ac-
tual quantum machine from IBM Quantum. All al-
gorithms are implemented in Qiskit.
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
334
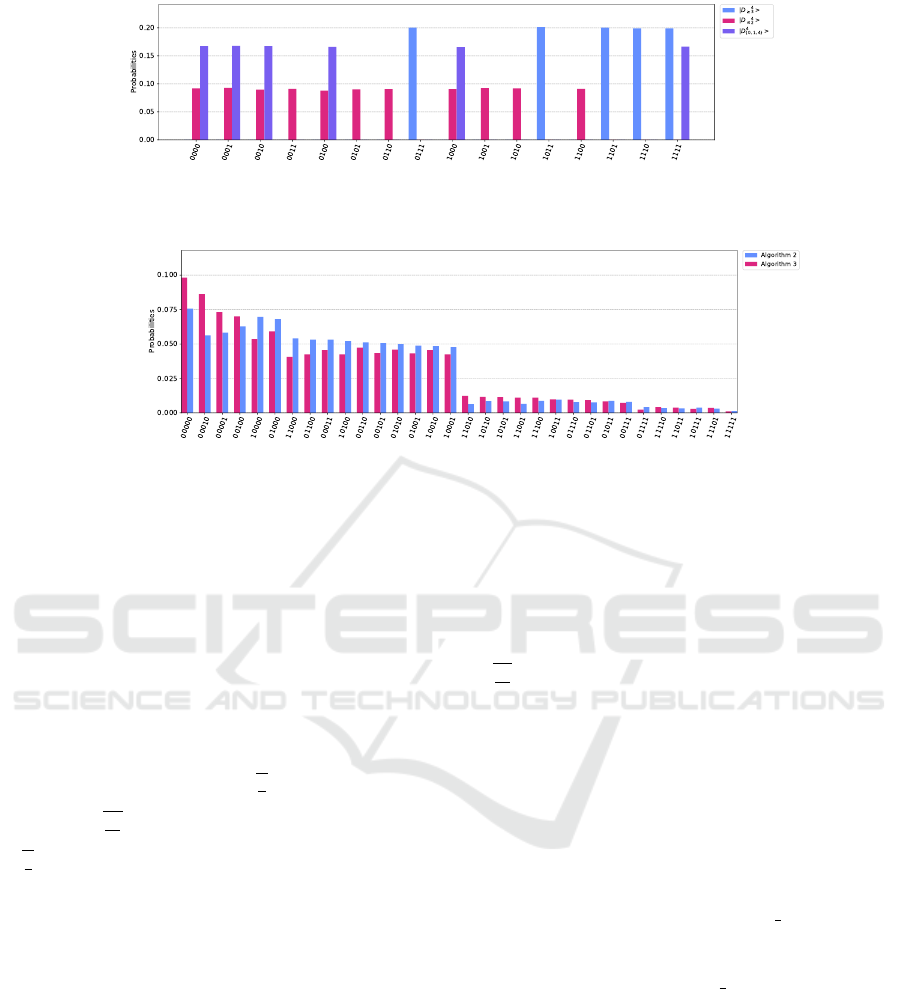
Figure 5: Probability distribution obtained from the noise-free simulated quantum circuit for 10
5
shots corresponding to
|D
≥
4
3
i, |D
≤
4
2
i, and |D
4
{0,1,4}
i.
Figure 6: Comparison of the noisy probability distribution obtained from Algorithm 2 and Algorithm 3 corresponding to
|D
≤
5
2
i.
5.1 Noise Free Simulation
First, we verify that Algorithm 2 and Algorithm 3
indeed construct generalized Dicke states using
the QASM quantum simulator under the condi-
tion that the circuit is noise-free. Circuit runs
and measurements were repeated numerous times
specified by shots. We observe whether the de-
sired probability distribution (superposition) is con-
structed by aggregating the quantum state measured
at each run. In our experiments, we built cir-
cuits that prepare |D
≥
4
3
i =
q
1
5
∑
x∈{0,1}
4
,wt(x)≥3
|xi,
|D
≤
4
2
i =
q
1
11
∑
x∈{0,1}
4
,wt(x)≤2
|xi and |D
4
{0,1,4}
i =
q
1
6
∑
x∈{0,1}
4
,wt(x)∈{0,1,4}
|xi. The results of Algo-
rithm 3 for 10
5
shots are shown in Figure 5. The
figure shows that our algorithms indeed generate uni-
form superpositions |D
≥
4
3
i, |D
≤
4
2
i, and |D
4
{0,1,4}
i by
observing the distribution aggregated from the mea-
sured quantum state for each shot. For Algorithm 2,
we confirm that the uniform distributions are correctly
constructed. Note that since Algorithm 2 and Algo-
rithm 3 are deterministic, no quantum state with un-
desired Hamming weights can be obtained as long as
the quantum circuit is noise-free.
5.2 Noisy Simulation
Next, we compared the probability distribution gath-
ered from Algorithm 2 and Algorithm 3 in the noisy
simulation model. In the experiment, the error rate
of a 1-qubit gate such as X is set to 10
−3
and that
of CNOT is set to 10
−2
. These values are plausible
and are derived from the error rates of IBM’s quan-
tum computers, such as Falcon (IBM, 2022). Fig-
ure 6 shows the results of running the circuit gen-
erated from each algorithm that obtains |D
≤
5
2
i =
q
1
16
∑
x∈{0,1}
5
,wt(x)≤2
|xi for 10
5
shots. Unlike the
noiseless case, quantum states with incorrect weights
≥ k were observed with a small probability. For the
desired states, Algorithm 3 generated |00000i and
states near |00000i with a higher probability than
other states. Therefore, the result is somewhat dif-
ferent from the uniform superposition. Algorithm 2
seems to generate correct weight states more uni-
formly than Algorithm 3. We transpile two cir-
cuits generated from Algorithm 2 and Algorithm 3.
The backend of the transpiler is ibm nairobi from
IBMQ, which is a 7-qubits quantum machine we will
use in our experiments in the next subsection. Ba-
sic gates implemented in ibm nairobi are [’id’,
’rz’, ’sx’, ’x’, ’cx’, ’reset’]. The depth of
the transpiled circuit of Algorithm 3 is 382, which is
twice as large as 189 of Algorithm 2. The result is
reasonable given that the depth complexity of Algo-
rithm 3 is O(k log k) larger than that of Algorithm 2.
5.3 Real Quantum Machine
We deployed Algorithm 2 and Algorithm 3 on a
real quantum machine produced by IBM Quan-
tum for toy examples. The 7-qubits quantum
Concrete Quantum Circuits to Prepare Generalized Dicke States on a Quantum Machine
335
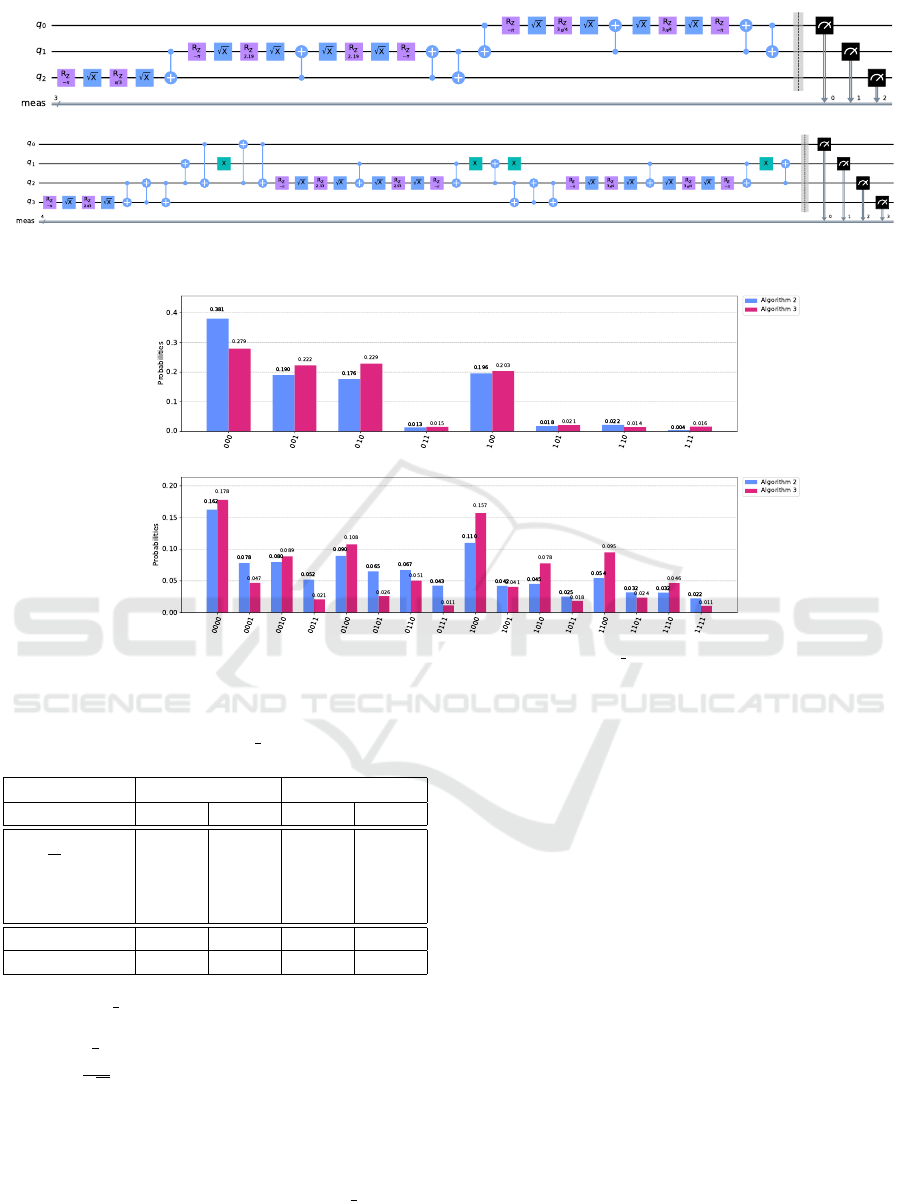
Figure 7: Transpiled quantum circuits for |D
≤
3
1
i generated from Algorithm 2 (top) and Algorithm 3 (bottom).
Figure 8: Probability distribution obtained from Algorithm 2 and Algorithm 3 on ibm nairobi quantum machine for |D
≤
3
1
i
(top) and |D
≤
4
2
i (bottom).
Table 1: Gate summary of quantum circuits for Algorithm 2
and Algorithm 3 transpiled in ibm nairobi quantum ma-
chine.
Target State |D
≤
3
1
i |D
≤
4
2
i
Algorithm Alg. 2 Alg. 3 Alg. 2 Alg. 3
X gates 0 4 0 6
√
X gates 10 10 28 37
Rz gates 10 10 52 141
CNOT gates 8 16 79 234
Circuit Width 3 4 4 6
Circuit Depth 29 39 133 298
machine ibm nairobi was utilized in the exper-
iment. Our target generalized Dicke states are
|D
≤
3
1
i =
1
2
(|000i + |001i + |010i + |100i) and
|D
≤
4
2
i =
1
√
11
(|0000i + |0001i + |0010i + |0100i +
|1000i + |0011i + |0110i + |1100i + |0101i +
|1010i + |1001i). Again, we compared the prob-
ability distribution achieved by Algorithm 2 and
Algorithm 3. Table 1 summarizes the number of
gates for each circuit transpiled in the ibm nairobi
quantum machine. Figure 7 displays the transpiled
circuits to construct |D
≤
3
1
i for both algorithms. You
can also see the circuits for |D
≤
4
2
i in Appendix 6.
The average CNOT error during the experiment was
0.01225. The number of shots is 20000. To eliminate
coincidence, 100 batch executions for the same
circuit were performed and we calculated the average
value. The result is displayed in Figure 8. For |D
≤
3
1
i,
both algorithms can generate correct weight states
with high probability (94.2% for Algorithm 2 and
93.4% for Algorithm 3). For the standard deviation
in the correct states, Algorithm 3 achieves 0.118,
which is smaller than 0.145 for Algorithm 2. Thus,
Algorithm 3 obtained better uniformity than Algo-
rithm 2 for |D
≤
3
1
i. The success probability for |D
≤
4
2
i
is 84.6% for Algorithm 2 and
88.9% for Algorithm 3. The standard deviation
in the correct states is 0.0516 for Algorithm 2 and
0.0631 for Algorithm 3. In particular, it is surpris-
ing that the success probability of Algorithm 3, which
uses more than 200 CNOT gates, is higher than that
of Algorithm 2 even though the CNOT error rate ex-
ceeds 0.01. The presumed reason for this is that Al-
gorithm 3 has a circuit structure with no dependencies
among the qubits except for the ancilla. Since errors
are assumed to accumulate in the ancilla, quantum er-
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
336

ror correction should be performed preferentially on
the ancilla qubits. To construct generalized Dicke
states for larger n,k precisely, a quantum computer
with error correction capability is essentially needed.
6 CONCLUSION
We generalized a quantum circuit to prepare a su-
perposition of Dicke states proposed by (Esser et al.,
2021) with the same circuit complexity. We imple-
mented and compared two generalized Dicke state
preparation circuits using the Qiskit library. In our
experiments, we validated that both circuits can con-
struct the generalized Dicke state in a noisy quantum
simulator and a real quantum device. Future work
includes developing end-to-end quantum circuits to
solve a combinatorial problem employing the super-
position constructed from a generalized Dicke state
preparation circuit.
REFERENCES
Acasiete, F., Agostini, F. P., Moqadam, J. K., and Portugal,
R. (2020). Implementation of quantum walks on IBM
quantum computers. Quantum Information Process-
ing, 19(12):1–20.
Ambainis, A. (2004). Quantum walk algorithm for ele-
ment distinctness. In 45th Annual IEEE Symposium
on Foundations of Computer Science, pages 22–31.
B
¨
artschi, A. and Eidenbenz, S. (2019). Deterministic prepa-
ration of Dicke states. In International Symposium
on Fundamentals of Computation Theory, pages 126–
139. Springer.
B
¨
artschi, A. and Eidenbenz, S. (2022). Short-depth circuits
for Dicke state preparation. In 2022 IEEE Interna-
tional Conference on Quantum Computing and Engi-
neering (QCE). IEEE. To appear.
Bastin, T., Thiel, C., von Zanthier, J., Lamata, L., Solano,
E., and Agarwal, G. S. (2009). Operational determi-
nation of multiqubit entanglement classes via tuning
of local operations. Phys. Rev. Lett., 102:053601.
Brassard, G., Hoyer, P., Mosca, M., and Tapp, A. (2002).
Quantum amplitude amplification and estimation.
Contemporary Mathematics, 305:53–74.
Chailloux, A., Debris-Alazard, T., and Etinski, S. (2021).
Classical and quantum algorithms for generic syn-
drome decoding problems and applications to the lee
metric. In International Conference on Post-Quantum
Cryptography, pages 44–62. Springer.
Chakraborty, K., Choi, B.-S., Maitra, A., and Maitra, S.
(2014). Efficient quantum algorithms to construct ar-
bitrary Dicke states. Quantum information processing,
13(9):2049–2069.
Childs, A. M., Farhi, E., Goldstone, J., and Gutmann, S.
(2000). Finding cliques by quantum adiabatic evolu-
tion. arXiv preprint quant-ph/0012104.
Cook, J., Eidenbenz, S., and B
¨
artschi, A. (2020). The quan-
tum alternating operator ansatz on maximum k-vertex
cover. In 2020 IEEE International Conference on
Quantum Computing and Engineering (QCE), pages
83–92. IEEE.
Cruz, D., Fournier, R., Gremion, F., Jeannerot, A., Koma-
gata, K., Tosic, T., Thiesbrummel, J., Chan, C. L.,
Macris, N., Dupertuis, M.-A., et al. (2019). Efficient
quantum algorithms for ghz and w states, and imple-
mentation on the IBM quantum computer. Advanced
Quantum Technologies, 2(5-6):1900015.
da Silva, A. J. and Park, D. K. (2022). Linear-depth quan-
tum circuits for multiqubit controlled gates. Phys. Rev.
A, 106:042602.
Esser, A., Ramos-Calderer, S., Bellini, E., Latorre, J. I.,
and Manzano, M. (2021). An optimized quantum im-
plementation of ISD on scalable quantum resources.
arXiv preprint arXiv:2112.06157.
Esser, A., Ramos-Calderer, S., Bellini, E., Latorre, J. I., and
Manzano, M. (2022). Hybrid decoding – classical-
quantum trade-offs for information set decoding. In
International Conference on Post-Quantum Cryptog-
raphy. Springer. To appear.
Grover, L. K. (1996). A fast quantum mechanical algorithm
for database search. In Proceedings of the twenty-
eighth annual ACM symposium on Theory of comput-
ing, pages 212–219.
IBM (2022). IBM quantum. https://quantum-computing.
ibm.com/.
Kaye, P. and Mosca, M. (2001). Quantum networks for
generating arbitrary quantum states. In Optical Fiber
Communication Conference and International Con-
ference on Quantum Information, page PB28. Optica
Publishing Group.
Lamata, L., Lopez, C. E., Lanyon, B., Bastin, T., Retamal,
J. C., and Solano, E. (2013). Deterministic genera-
tion of arbitrary symmetric states and entanglement
classes. Physical Review A, 87(3):032325.
Mandviwalla, A., Ohshiro, K., and Ji, B. (2018). Imple-
menting grover’s algorithm on the IBM quantum com-
puters. In 2018 IEEE International Conference on Big
Data (Big Data), pages 2531–2537. IEEE.
Moreno, M. and Parisio, F. (2018). All bipartitions of arbi-
trary Dicke states. arXiv preprint arXiv:1801.00762.
Mukherjee, C. S., Maitra, S., Gaurav, V., and Roy, D.
(2020). Preparing Dicke states on a quantum com-
puter. IEEE Transactions on Quantum Engineering,
1:1–17.
Niroula, P., Shaydulin, R., Yalovetzky, R., Minssen, P.,
Herman, D., Hu, S., and Pistoia, M. (2022). Con-
strained quantum optimization for extractive summa-
rization on a trapped-ion quantum computer.
Perriello, S., Barenghi, A., and Pelosi, G. (2021). A
complete quantum circuit to solve the information
set decoding problem. In 2021 IEEE International
Conference on Quantum Computing and Engineering
(QCE), pages 366–377. IEEE.
Concrete Quantum Circuits to Prepare Generalized Dicke States on a Quantum Machine
337

Shende, V. V., Bullock, S. S., and Markov, I. L. (2006). Syn-
thesis of quantum-logic circuits. IEEE Transactions
on Computer-Aided Design of Integrated Circuits and
Systems, 25(6):1000–1010.
APPENDIX
We show the quantum circuits for |D
≤
4
2
iwith elemen-
tary gates transpiled by the ibm nairobi backend in
the IBM quantum experience service in Figure 9 and
Figure 10.
Figure 9: Transpiled quantum circuit for |D
≤
4
2
i generated
from Algorithm 2.
Figure 10: Transpiled quantum circuit for |D
≤
4
2
i generated
from Algorithm 3.
ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy
338
