A Multi-Class Probabilistic Optimum-Path Forest
Silas E. Nachif Fernandes
1 a
, Leandro A. Passos
2 b
, Danilo Jodas
1 c
, Marco Akio
3 d
,
Andr
´
e N. Souza
3 e
and Jo
˜
ao Paulo Papa
1 f
1
Department of Computing, S
˜
ao Paulo State University, Bauru, Brazil
2
School of Engineering and Informatics, University Wolverhampton, Wolverhampton, England, U.K.
3
Department of Electrical Engineering, S
˜
ao Paulo State University, Bauru, Brazil
Keywords:
Optimum-Path Forest, Probabilistic Classification, Multi-Class.
Abstract:
The advent of machine learning provided numerous benefits to humankind, impacting fields such as medicine,
military, and entertainment, to cite a few. In most cases, given some instances from a previously known
domain, the intelligent algorithm is encharged of predicting a label that categorizes such samples in some
learned context. Among several techniques capable of accomplishing such classification tasks, one may refer
to Support Vector Machines, Neural Networks, or graph-based classifiers, such as the Optimum-Path Forest
(OPF). Even though such a paradigm satisfies a wide sort of problems, others require the predicted class
label and the classifier’s confidence, i.e., how sure the model is while attributing labels. Recently, an OPF-
based variant was proposed to tackle this problem, i.e., the Probabilistic Optimum-Path Forest. Despite its
satisfactory results over a considerable number of datasets, it was conceived to deal with binary classification
only, thus lacking in the context of multi-class problems. Therefore, this paper proposes the Multi-Class
Probabilistic Optimum-Path Forest, an extension designed to outdraw limitations observed in the standard
Probabilistic OPF.
1 INTRODUCTION
Machine learning-based approaches became essential
in the twenty-first century’s daily life, impacting in
trivial tasks such as movie recommendations, as well
as complex ones, such as safety and health condition
predictions, among others. In general, most of these
techniques learn patterns from data and assign each
compounding sample a label, thus classifying them
as a member of a specific group.
Despite the aforementioned paradigm, several
problems demand a different approach concerning the
classification procedure. Consider, for instance, an
automotive insurance company computing the risks
associated with each customer profile (Apte et al.,
1999). In this scenario, a specialist usually consid-
ers the driver’s age, gender, vehicle price, vehicle
a
https://orcid.org/0000-0001-7228-1364
b
https://orcid.org/0000-0003-3529-3109
c
https://orcid.org/0000-0002-0370-1211
d
https://orcid.org/0000-0002-8288-1758
e
https://orcid.org/0000-0001-9783-6311
f
https://orcid.org/0000-0002-6494-7514
age, among others (Huang and Meng, 2019), to es-
timate the probabilities of theft and accidents, thus
implying in the final price charged by the company.
A common alternative to undertaking such problems
engages probabilistic models, which returns a real-
valued number denoting the degree of confidence or
probability of an event.
Different solutions may include Bayesian ap-
proaches, whose inference mechanism is based on a
stream of probabilities, and watershed-based models,
such as the Probabilistic Watershed (Sanmartin et al.,
2019), which considers all possible spanning forests
in a graph to compute the probability of connecting a
particular seed to a node. Besides, one can consider
extending traditional classifiers to create probabilistic
models, e.g., the probabilistic Nearest Neighbor (Ma
et al., 2020) and the probabilistic Support Vector Ma-
chines (SVM) (Platt, 1999).
Considering traditional classification techniques,
a graph-based approach called Optimum-Path For-
est (OPF) (Papa et al., 2009; Papa et al., 2012) ob-
tained notorious relevance in the last years due to its
outstanding results in a wide range of applications,
Fernandes, S., Passos, L., Jodas, D., Akio, M., Souza, A. and Papa, J.
A Multi-Class Probabilistic Optimum-Path Forest.
DOI: 10.5220/0011597700003417
In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 5: VISAPP, pages
361-368
ISBN: 978-989-758-634-7; ISSN: 2184-4321
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
361

such as anomaly detection, data oversampling, and
medical issues, to cite a few. In short, the OPF is
a graph-based framework developed to tackle super-
vised (Papa et al., 2009; Papa et al., 2017) and unsu-
pervised (Rocha et al., 2009) classification problems,
among others. Contextualizing with pertinency-based
methods, Souza et. al (Souza et al., 2019) proposed
the Fuzzy OPF, a variant that considers each sam-
ple’s membership while computing its predicted la-
bel. Besides, Fernandes et. al (Fernandes et al., 2018)
proposed an OPF extension to deal with probabilis-
tic classification problems, the so-called Probabilistic
Optimum-Path Forest.
The Probabilistic OPF extends the “Platt Scaling”
concept (Platt, 1999) to the context of the Optimum-
Path Forest classifier. In a nutshell, the variant consid-
ers the cost assigned to each sample during OPF train-
ing and classification steps to approximate the poste-
rior class probability distribution. Even though ex-
periments conducted over distinct scenarios demon-
strated that the algorithm is suitable to attack several
problems, they regard to binary classification tasks
only.
Therefore, this paper proposes two main contri-
butions to address such a drawback: (i) to propose
the Multi-Class Probabilistic Optimum-Path (MCP-
OPF), an extension of the Probabilistic OPF to carry
out probabilistic classification issues in multi-class
environments; and (ii) to promote the literature re-
garding graph-based learning architectures, proba-
bilistic classification, and multi-class handling meth-
ods.
The remainder of this paper is presented as fol-
lows. Section 2 describes the supervised Optimum-
Path Forest, as well as the Probabilistic OPF, while
Section 3 introduces the proposed approach to tackle
multi-class problems through the Probabilistic OPF.
Further, Sections 4 and 5 present the methodology
and experiments conducted in work, respectively. Fi-
nally, Section 6 states the conclusions and future
work.
2 THEORETICAL BACKGROUND
In this section, we present a brief introduction to the
Optimum-Path Forest classifier, as well as its exten-
sion for probabilistic classification.
2.1 Optimum-Path Forest Classifier
Let D = {(x
x
x
1
, y
1
), (x
x
x
2
, y
2
), . . . , (x
x
x
m
, y
m
)} be a dataset
of samples such that x
x
x
i
∈ R
n
and y
i
∈ {−1, +1}. Be-
sides, we have that D = D
1
∪D
2
∪D
3
, where D
1
, D
2
,
and D
3
denote the training, validation, and testing
sets, respectively. The Optimum-path Forest classi-
fier (Papa et al., 2009; Papa et al., 2017) is a graph-
based algorithm where the nodes denote data samples,
and edges represent connections between each pair of
instances. Besides, the most representative samples
are selected as prototypes, i.e., the nodes that com-
pete among themselves in a conquering-like process
whose objective is offering optimum-path costs to the
remaining samples in the graph. Consequently, the
training process is succeeded by minimizing a path-
cost function f
max
, described as follows:
f
max
(⟨v
v
v⟩) =

0 if v
v
v ∈ P ,
+∞ otherwise
f
max
(φ
v
v
v
· ⟨v
v
v,t
t
t⟩) = max{ f
max
(φ
v
v
v
), d(v
v
v,t
t
t)}, (1)
where φ
v
v
v
represents a path starting from a root in P
and ending at sample v
v
v, d(v
v
v,t
t
t) denotes the distance
between samples v
v
v and t
t
t, and P stands for the set
prototypes. Moreover, φ
v
v
v
· ⟨v
v
v,t
t
t⟩ represents the con-
catenation between the path φ
v
v
v
and the edge ⟨v
v
v,t
t
t⟩.
In short, f
max
(φ
v
v
v
) computes the maximum distance
among adjacent samples in the path φ
v
v
v
.
Let P
∗
⊆ P be the set of optimum prototypes
1
,
i.e., a set of adjacent samples with different labels dis-
covered after computing the Minimum Spanning Tree
over D
1
. Such a step is accomplished by assigning an
optimum cost C
t
t
t
to each sample t
t
t ∈ D
1
, i.e.:
C
t
t
t
= min
∀v
v
v∈D
1
{max{C
v
v
v
, d(v
v
v,t
t
t)}}, (2)
where v
v
v represents the training instance that con-
quered t
t
t. The classification step is achieved by
discovering the training sample that confers the
optimum-path cost to each test instance, computed
through Equation 2.
2.2 Probabilistic Optimum-Path Forest
The first change imposed to OPF in order to ac-
complish probabilistic classification concerns approx-
imating the posterior class probability based on the
f
max
path-cost function (Fernandes et al., 2018), per-
formed as follows:
P( ˆy
i
= y
i
|x
x
x
i
) ≈ P
A,B
(C
x
x
x
i
) =
1
1 + exp(Ay
i
C
x
x
x
i
+ B)
,
(3)
where A and B are parameters to be learned, C
x
x
x
i
stands
for the cost assigned to sample x
x
x
i
during OPF train-
ing or classification steps, and ˆy
i
denotes the label
1
P
∗
denotes the set of optimum prototypes, i.e., the set
of prototypes that minimizes the training error over D
1
.
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
362

predicted by the classifier. The rationale behind the
proposed approach is to assume the lower the cost as-
signed to sample x
x
x
i
, the higher the probability of that
sample be correctly classified. Therefore, the training
process considers minimizing the classification error,
determined as follows:
F(θ) =
|D
2
|
∑
i=1
(t
i
q
i
+ log(1 + exp(−Ay
i
C
x
x
x
i
− B))), (4)
where θ = (A
∗
, B
∗
) denotes the set of parameters that
optimizes the equation, and q
i
= C
x
x
x
i
+ B. Since prob-
abilistic OPF deals with binary values only, t
i
is for-
mulated as follows:
t
i
=
(
N
+
+1
N
+
+2
if y
i
= +1
1
N
−
+2
if y
i
= −1,
(5)
where N
+
and N
−
stand for the number of positive
and negative samples, respectively. Such an approach
is considered to handle unbalanced datasets.
Finally, one can attribute a label +1 to a sample
whose probablitily P(ˆy
x
x
x
= 1|x) > P( ˆy
x
x
x
= −1|x). Oth-
erwise, the sample is labeled with −1.
3 Multi-Class Probabilistic
Optimum-Path Forest Algorithm
Even though the Probabilistic OPF was designed to
tackle binary classification problems in its original
formulation (Fernandes et al., 2018), several tech-
niques have been developed to decompose multi-class
problems into a variety of simple multi-class prob-
lems (Madzarov et al., 2009). Among them, the one-
against-all (OvA) (Vapnik, 1999) approach obtained
notorious popularity due to its simplicity and effec-
tive results. Therefore, such a method was adopted to
extend the binary version of the Probabilistic OPF.
To deal with problems composed of K-classes,
where K > 2, the Multi-Class Probabilistic OPF in-
stantiates K versions of the binary Probabilistic OPF,
such that the k-th model is trained to classify k labeled
samples as positive, and the remaining as negative,
such that k ∈ {1, 2, . . . , K}. Further, the testing pro-
cedure considers presenting each testing sample to all
K binary Probabilistic OPFs and attributing the sam-
ple to a label whose respective classifier provided the
maximum output among all others.
Algorithm 1 implements the proposed approach.
Lines 2−8 construct a new k-class set for training and
validation purposes. Lines 9 and 10 execute the OPF
training and classification algorithm according to sec-
tion 2.1. Line 11 is in charge of optimizing parame-
ters A and B, i.e., they aim at computing the best set of
parameters using Newton’s method with backtracking
line search proposed by Platt et al. (Platt, 1999) and
further improved by Lin et al. (Lin et al., 2007). Lines
12−13 repeats the OPF training and testing algorithm
using the original training set. Parameters A and B for
the k-th model are then used to compute the probabil-
ity of each test sample in Lines 14 − 20. The steps
mentioned above are repeated during K times to ob-
tain an array of probabilities for each sample in D
3
.
Finally, the loop presented in Lines 21 − 22 assigns
each test sample the label whose score obtained the
highest probability.
The additional training step (Line 11) provides the
parameters A and B by solving the regularized max-
imum likelihood problem, according to Equation 4.
Even though any optimization algorithm could be em-
ployed for the task, the optimization approach pro-
posed by Platt et al. (Platt, 1999) and further improved
by Lin et al. (Lin et al., 2007), has been proved to be a
simple and robust solution, and it has been integrated
into LibSVM
2
source code. Consider the works pro-
posed by Platt et al. (Platt, 1999) and Lin et al. (Lin
et al., 2007)
3
for more details about the optimization
method.
The main drawback related to the OvA approach
regards its increasingly training complexity when the
number of training samples is large. Such behavior
is expected since each of the K classifiers is trained
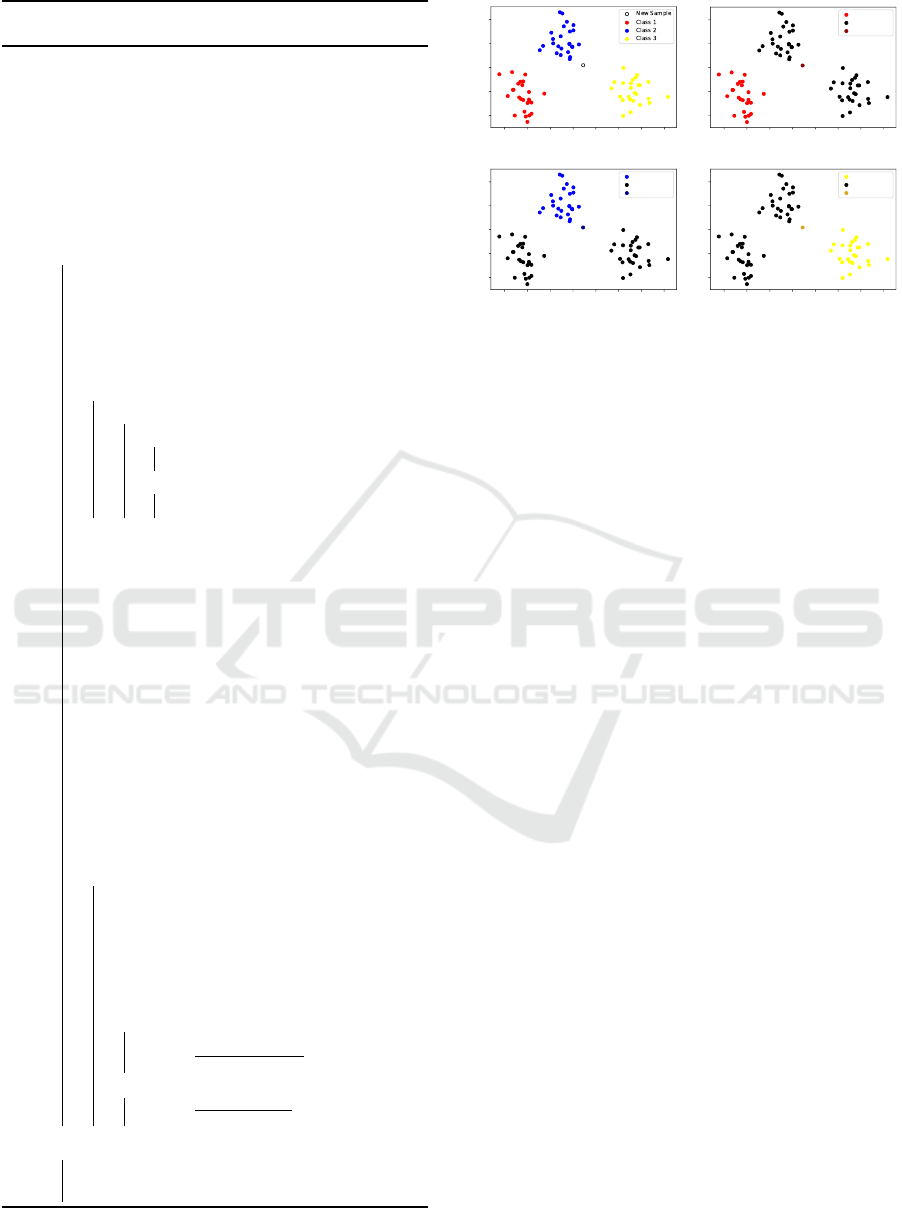
considering the whole training set. Figure 1 illustrates
the OvA probabilistic classification idea. Notice the
probability of the class pertinence presented in each
image denote the values obtained by the Probabilistic
OPF after normalizing the outputs obtained through
OvA.
4 METHODOLOGY
This section describes the datasets employed in the
work. Further, it also presents the setup considered in
the experiments.
4.1 Datasets
The experiments performed in this paper were con-
ducted over seven datasets, described as follows:
• Gases05 (Lupi Filho, 2012): it comprises 1, 201
2
https://www.csie.ntu.edu.tw/
∼
cjlin/libsvm/
3
https://www.csie.ntu.edu.tw/
∼
cjlin/papers/plattprob.
pdf
A Multi-Class Probabilistic Optimum-Path Forest
363

Algorithm 1: Probabilistic Optimum-Path Forest Algo-
rithm.
Input: A λ-labeled training G
tr
= (D
1
, A) and
validating G
vl
= (D
2
, A) sets, unlabeled
test G
ts
= (D
3
, A) set, and the number
of classes K.
Auxiliary: Optimum-path forest P, cost map C,
and label map L.
Output: Probability output p for each sample in
D
3
.
1 for each k ∈ {1, . . . , K} do
// Build a new λ-labeled
training and validation
sets
2 D
k
1
←
/
0 and D
k
2
←
/
0;
3 for each d ∈ {D
1
, D
2
} do
4 for each v ∈ D
d
do
5 if λ(v) = k then
6 D
k
d
← (v, +1);
7 else
8 D
k
d
← (v, −1);
9 P
1
← OPF Training(D
k
1
);
10 [C
2
, L
2
] ← OPF Testing(P
1
, D
k
2
);
// Newton’s method with a
backtracking line search, a
Platt’s Probabilistic
Output with an improvement
from Lin et al. (Lin
et al., 2007).
11 [A
k
, B
k
] ←
Sigmoid Training (D
k
1
,C
2
, L
2
)
12 P
1
← OPF Training(D
k
1
∪ D
k
2
);
13 [C
3
, L
3
] ← OPF Testing(P
1
, D
3
);
14 for each i ∈ D
3
do
15 f ACpB ← A
k
L
i
3
C
i
3
+ B
k
;
16 f ACmB ← A
k
L
i
3
C
i
3
− B
k
;
// Compute sigmoid
probability
17 if ( f ACpB) ≥ 0 then
18 p
k
i
←
exp(− f ACmB)
1+exp(− f ACmB)
;
19 else
20 p
k
i
←
1
1+exp( f AC pB)
;
21 for each i ∈ D
3
do
22 [k, p
i
] ← argmax
k∈{1,...,K}
(p
k
i
)
Class 1
Not Class 1
New Sample
p=4.46%
(a) (b)
Class 2
Not Class 2
New Sample
p=95.11%
Class 3
Not Class 3
New Sample
p=0.43%
(c) (d)
Figure 1: Illustration of the OvA procedure. (a) the 2-D plot
considers three distinct classes and a new sample to be clas-
sified. Further, frames (b), (c), and (d) depict the normalized
probability of this sample belonging to classes 1 (4.46%), 2
(95.11%), and 3 (0.43%), respectively, compared against all
other classes.
instances with 5 features each describing dis-
solved gas analysis in oil-filled power transform-
ers. The dataset is composed of 3 classes, repre-
senting normal behavior, thermal faults, and elec-
trical faults.
• Gases07 (Lupi Filho, 2012): similar to the
Gases05 dataset. The difference lies in the num-
ber of samples, i.e., 1, 144 instances, and the num-
ber of features, comprising 7 distinct gasses, in-
stead of 5.
• Scene (Boutell et al., 2004): it is composed of
2, 407 semantic scene classication samples repre-
sented by 294 extracted features each, divided into
6 classes, i.e., Beach, Sunset, Fall foliage, Field,
Mountain, and Urban.
• Sonar (Gorman and Sejnowski, 1988): it is com-
posed of 208 instances with 60 features each, this
dataset is employed to discriminate sonar signals
bounced off a metal cylinder or cylindrical rocks.
• Synthetic: dataset generatad by sampling over a
Gaussian distribution. Comprises 1, 000 samples
with 6 features each. The dataset is divided into 3
classes.
• Synthetic01 and Synthetic02: similar to Syn-
thetic dataset, Synthetic01 and Synthetic02 were
generatade by sampling over Gaussian distribu-
tions. Both of them comprise 1, 000 samples with
2 features each. Both are also divided into 2
classes.
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
364

4.2 Experimental Setup
The experiments conducted in this paper compare the
Multi-Class Probabilistic OPF against six baselines:
the standard OPF (Papa et al., 2009), as well as five
other probabilistic classifiers adopted, i.e., the prob-
abilistic SVM (Platt, 1999), Naive Bayes (Kuncheva,
2006), Decision Tree (Nagabhushan and Pai, 1999),
Linear Discriminant Analysis (LDA) (Al-Dulaimi
et al., 2019), and Logistic Regression (Yang and
Loog, 2018). The methodology considered for the
evaluation employs a data pre-processing procedure
using the z-score normalization, described as follows:
t
′
=
t − µ
ρ
, (6)
where µ denotes the mean and ρ stands for the stan-
dard deviation. Besides, t and t
′
correspond to the
original and normalized features, respectively.
Further, a cross-validation process with 30 runs
is performed for statistical analysis based on the
Wilcoxon signed-rank test (Wilcoxon, 1945) with a
significance of 0.05. In this scenario, the best method
over each dataset (i.e., the one that obtained the high-
est F1 score) is compared against all other algorithms
individually. Furthermore, a post hoc analysis is con-
ducted using the Nemenyi test (Nemenyi, 1963) with
α = 0.05, which exposes the critical difference (CD)
among all techniques. Finally, the runs mentioned
above are divided into three groups of 10 runs each,
such that the datasets are randomly split as follows:
1. 10 runs using 70% of the samples for training and
30% for testing;
2. 10 runs using 80% of the samples for training and
20% for testing; and
3. 10 runs using 90% of the samples for training and
10% for testing.
The evaluation procedure focuses on finding the
set of hyperparameters that maximizes the models’
accuracy. In this context, both MCP-OPF and Proba-
bilistic SVM were optimized using Newton’s method
with a backtracking line search comprising a minimal
step of 1e
−7
, Hessian’s partial derivatives σ = 1e
−7
,
stopping criteria η = 1e
−3
, and the maximal num-
ber of iterations equal to t
max
= 100. At the same
time, the probabilistic SVM hyperparameters C and γ,
and the remaining techniques were optimized using a
grid search. The optimization process was performed
through a 5-fold cross-validation procedure, i.e., for
each fold, 80% of the training set was used to train the
model, while the remaining 20% was used for valida-
tion purposes. Finally, Table 1 presents the parame-
ter configuration. Notice the probabilistic SVM em-
ploys a Radial Basis Function kernel. Additionally,
the standard OPF and Naive Bayes have no hyperpa-
rameters to be tuned.
Table 1: Parameter configuration.
Algorithm Parameters
Decision Tree
criterion ∈ {‘gini’, ‘entropy’}
max depth ∈ [2, 15]
LDA
Solver ∈ {‘svd’, ‘lsqr’, ‘eigen’}
tol ∈ [1.0e
−5
, 1.0e
−1
]
Logistic Regression
Solver ∈ {‘newton-cg’,‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}
C ∈ {0.01, 0.1, 1.0, 10.0, 100.0}
Probabilistic SVM
C ∈ {1, 10, 100, 1, 000}
γ ∈ {0.001, 0.01, 0.1, 1}
Finally, the experiments were conducted over the
C-based library LibOPF
4
for both OPF and MCP-
OPF, as well as the well-known Python library Scikit-
learn (Pedregosa et al., 2011) considering other tech-
niques. Besides, the computational environment com-
prises a 3.9 GHz Intel i7 processor with 16 GB of
RAM, running over an Ubuntu 16.04 Linux machine.
5 EXPERIMENTS
This section discusses the experimental results con-
sidering the proposed Multi-Class Probabilistic OPF
classification effectiveness and computational burden.
Results presented in bold denote the best values ac-
cording to the Wilcoxon signed-rank test.
5.1 Effectiveness
Table 2 presents the F1 score and the accuracy
5
val-
ues obtained over the aforementioned datasets
6
. Even
though MCP-OPF did not obtain the best results in
some cases, it is worth noting some interesting partic-
ularities. Regarding the standard OPF, even though
its absolute value outperformed the ones obtained
by the proposed approach in four-out-seven datasets,
i.e., SCENE, SONAR, SYNTHETIC01, and SYN-
THETIC02, the accuracy difference is minimal (ap-
proximately 0.5%). On the other hand, MCP-OPF
is capable of producing results considerably higher
than the ones obtained by OPF in some cases, as ob-
served over the GASES05 dataset, where MCP-OPF
performed 36% better.
Concerning the remaining techniques, one can ob-
serve that MCP-OPF obtained the best results in two-
out-of-seven datasets, i.e., SYNTHETIC01 and SYN-
4
https://github.com/jppbsi/LibOPF
5
By accuracy, this work considers the number of cor-
rected classified instances over the total number of testing
samples.
6
Results presented in bold denote the best values ac-
cording to the Wilcoxon signed-rank test.
A Multi-Class Probabilistic Optimum-Path Forest
365

THETIC02, as well as similar statistical results over
SONAR datasets and a relatively small accuracy dif-
ference over GASES05 and GASES07 (≈ 2%). In
fact, SVM presents a considerable upper hand over
two datasets, i.e., SCENE and SYNTHETIC. How-
ever, such an advantage comes at a price of 9 to 49
times the computational burden cost demanded in the
learning process, as presented in the next section.
Notice the purpose of the present work is not to
outperforming the standard OPF classifier, but to pro-
vide a suitable alternative considering the context of
multi-class probabilistic classification. Nevertheless,
the Probabilistic OPF obtained results comparable to
the standard OPF in the worst case and much better
ones in others, e.g., Gases05. Further, together with
the standard OPF, the model also outperformed the
baselines considering different cases, such as Syn-
thetic01 and Synthetic02, confirming the contribu-
tion’s relevance.
5.2 Computational Burden
Table 3 exhibits the execution time for the learning
(i.e., training + evaluating), expressed in seconds.
Since both standard OPF and Naive Bayes do no
perform an evaluation step, i.e., they do not present
any hyperparameter to be tuned, they present the
lowest computational costs. Moreover, the standard
Optimum-Path Florest is incorporated as a procedural
step executed multiple times in the Multi-Class Prob-
abilistic OPF, as described in Algorithm 1. Therefore,
it is convenient to accept a considerable difference in
their computational burden. Even though this differ-
ence is proportionally significant, the algorithm can
provide a substantial gain in some cases, such as the
36% over the GASES05 dataset (Table 2), in an ef-
ficient manner if compared to SVM or Logistic Re-
gression, for instance. Indeed, the probabilistic SVM
is the most onerous technique in terms of computa-
tional resources since its learning time demanded, on
average, 256 and 24 times slower than OPF and MCP-
OPF, respectively.
Such an in-depth analysis of the results consider-
ing both the accuracy and the computational burden
shows that MCP-OPF poses itself as an efficient al-
ternative for the task of multi-class probabilistic clas-
sification, providing a balance between reasonable ac-
curacies at the cost of an acceptable execution time.
5.3 Statistical Analysis
Despite the statistical analysis performed in Sec-
tion 5.1, which compares all techniques against the
one that obtained the highest F1 score value consid-
ering the Wilcoxon signed-rank test, this section pro-
vides an alternative statistical analysis considering the
Nemenyi test. Such an approach verifies the presence
of critical difference among all techniques and depicts
the results in a diagram representing each method’s
average rank in a horizontal bar (Dem
ˇ
sar, 2006), pre-
sented in Figure 2. Notice lower ranks denote the bet-
ter techniques, and methods connected do not signifi-
cantly differ between themselves.
One can notice that MCP-OPF obtained the best
results in four-out-of-seven datasets, i.e., Gases07,
Sonar, Synthetic01, and Synthetic02, performing bet-
ter than most of the techniques. Considering a solo
comparison against the standard OPF classifier, MCP-
OPF obtained statistically similar or better results.
Regarding the other techniques, the Nemenyi test
could not provide explicitly correlated patterns among
themselves, with exception to Logistic regression and
the LDA, which were considered similar in all situa-
tions. Such results confirm the suitability of the MCP-
OPF for multi-class probabilistic classification tasks,
once it provided a satisfactory classification perfor-
mance in a reasonably efficient fashion.
6 CONCLUSION
This paper proposes the Multi-Class Probabilistic
Optimum-Path Forest, a variant of the OPF classi-
fier designed to deal with probabilistic classification
problems over datasets composed of more than two
classes. Experiments conducted over seven datasets
showed the method is capable of outperforming the
standard OPF with considerable difference in some
cases or obtaining pretty approximate results in oth-
ers. Concerning the other techniques, the proposed
MCP-OPF obtained the best results over four datasets
considering the Nemenyi test, i.e., Gases07, Sonar,
Synthetic01, and Synthetic02, as well as comparative
effectiveness considering Gases05 dataset. Moreover,
the proposed approach showed itself computationally
efficient, performing way faster than traditional tech-
niques, such as the Probabilistic SVM and Logistic
Regression, for instance.
ACKNOWLEDGEMENTS
The authors are grateful to FAPESP grants
#2013/07375-0, #2014/12236-1, #2017/02286-0,
#2018/21934-5, #2019/07665-4, #2019/18287-0, and
#2020/12101-0, CNPq grants #307066/2017-7, and
#427968/2018-6, as well as the UK Engineering and
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
366

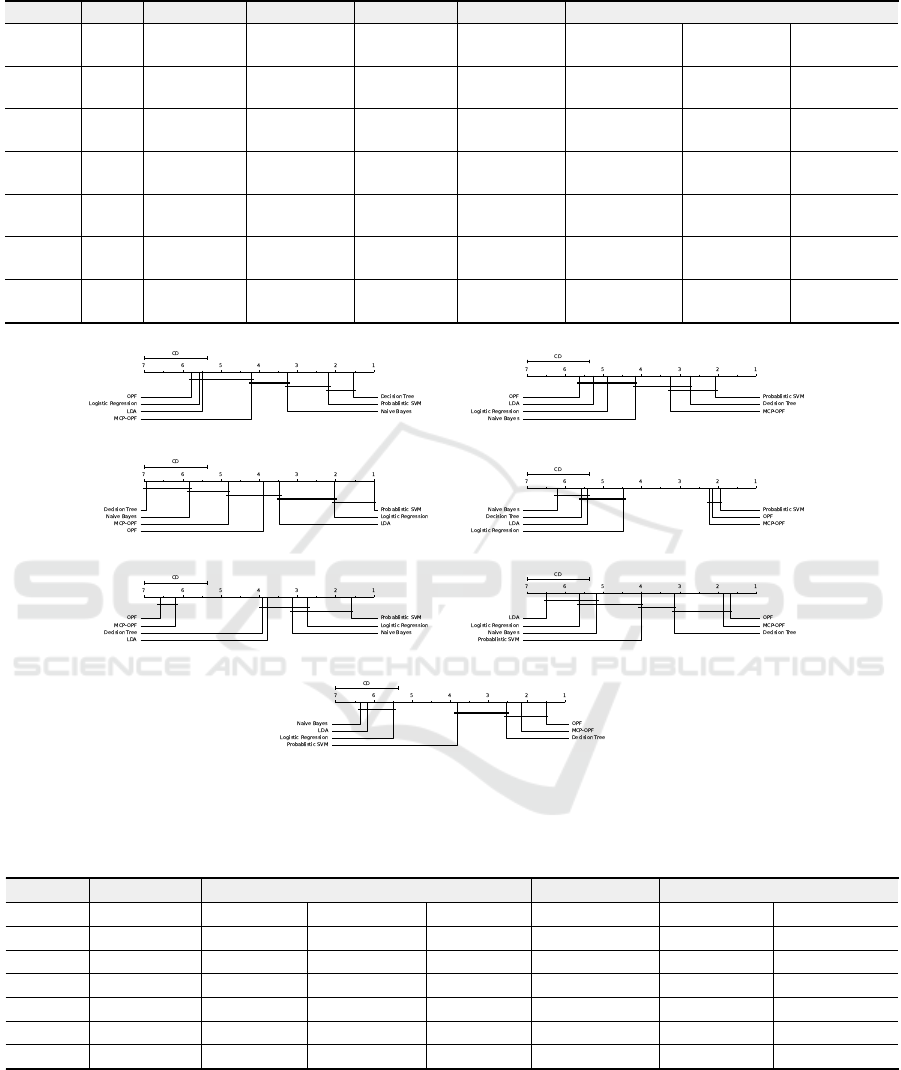
Table 2: F1 scores and accuracies of the techniques considered in the work.
Algorithm Metric MCP-OPF OPF Decision Tree LDA Logistic Regression Naive Bayes Probablistic SVM
Gases05
F1 0.9207 ± 0.0107 0.6771 ± 0.3113 0
0
0.
.
.9
9
94
4
46
6
62
2
2 ±
±
± 0
0
0.
.
.0
0
01
1
16
6
62
2
2 0.9117 ± 0.0016 0.9121 ± 0.0024 0.9315 ± 0.0112 0.9392 ± 0.0090
Accuracy 89.5210 ±2.5432 68.8818 ± 30.0493 94.5281 ±1.5203 86.1681 ± 1.0248 87.2736 ± 1.0018 91.7969 ± 1.2873 93.1041 ± 1.2255
Gases07
F1 0.9424 ± 0.0092 0.9256 ± 0.0222 0
0
0.
.
.9
9
94
4
49
9
91
1
1 ±
±
± 0
0
0.
.
.0
0
01
1
14
4
41
1
1 0.9338 ± 0.0050 0.9349 ± 0.0024 0.9390 ± 0.0129 0
0
0.
.
.9
9
95
5
51
1
15
5
5 ±
±
± 0
0
0.
.
.0
0
00
0
07
7
75
5
5
Accuracy 92.5401 ±1.8654 92.3230 ± 1.9651 94.7790 ± 1.3552 89.6237 ± 1.2499 90.2258 ± 0.9331 92.8461 ± 1.1565 94.2133 ±1.0482
Scene
F1 0.6809 ± 0.0224 0.6861 ± 0.0223 0.6045 ± 0.0247 0.6990 ± 0.0228 0.7559 ± 0.0178 0.6526 ±0.0295 0
0
0.
.
.8
8
80
0
06
6
69
9
9 ±
±
± 0
0
0.
.
.0
0
01
1
16
6
64
4
4
Accuracy 68.3735 ±2.2019 68.8663 ± 2.1772 60.7388 ± 2.4528 70.1881 ± 2.2343 75.6337 ± 1.7203 65.3087 ± 2.7866 80.6974 ±1.5899
Sonar
F1 0
0
0.
.
.8
8
84
4
44
4
44
4
4 ±
±
± 0
0
0.
.
.0
0
04
4
45
5
58
8
8 0
0
0.
.
.8
8
84
4
45
5
54
4
4 ±
±
± 0
0
0.
.
.0
0
04
4
45
5
56
6
6 0.7155 ± 0.0613 0.7159 ± 0.0657 0.7525 ± 0.0542 0.6572 ± 0.0577 0
0
0.
.
.8
8
85
5
59
9
97
7
7 ±
±
± 0
0
0.
.
.0
0
05
5
50
0
01
1
1
Accuracy 84.3362 ±4.5961 84.4404 ± 4.5781 71.2518 ± 6.2225 71.3648 ± 6.5491 75.0477 ± 5.4414 65.1180 ± 6.3343 85.9040 ±5.0213
Synthetic
F1 0.8376 ± 0.0217 0.8360 ± 0.0228 0.8793 ± 0.0199 0.8808 ± 0.0213 0.8896 ± 0.0206 0.8873 ±0.0190 0
0
0.
.
.8
8
89
9
96
6
66
6
6 ±
±
± 0
0
0.
.
.0
0
01
1
18
8
82
2
2
Accuracy 83.7388 ±2.2380 83.6064 ± 2.3354 87.9310 ± 1.9876 87.9698 ± 2.2083 88.8961 ± 2.0998 88.6087 ± 1.9734 89.5588 ±1.8843
Synthetic01
F1 0
0
0.
.
.6
6
61
1
18
8
80
0
0 ±
±
± 0
0
0.
.
.0
0
02
2
26
6
63
3
3 0
0
0.
.
.6
6
62
2
21
1
11
1
1 ±
±
± 0
0
0.
.
.0
0
02
2
28
8
80
0
0 0.5892 ± 0.0215 0.4749 ± 0.0401 0.5184 ± 0.0601 0.5260 ± 0.0350 0.5657 ± 0.0268
Accuracy 61.7222 ±2.6775 62.0444 ± 2.8281 58.3556 ± 2.2055 47.3667 ± 3.9752 48.7444 ± 2.9331 51.5833 ± 3.5535 56.3778 ±3.0218
Synthetic02
F1 0.9029 ± 0.0212 0
0
0.
.
.9
9
90
0
08
8
89
9
9 ±
±
± 0
0
0.
.
.0
0
01
1
18
8
82
2
2 0.8917 ± 0.0207 0.4768 ± 0.1017 0.5510 ± 0.0712 0.4649 ± 0.0989 0.8448 ± 0.0308
Accuracy 90.2833 ±2.1201 90.8889 ± 1.8188 89.1556 ± 2.0794 47.5944 ± 10.1727 52.8389 ± 6.7255 45.9389 ± 10.1153 84.4667 ± 3.0817
(a) Gases05 (b) Gases07
(c) Scene (d) Sonar
(e) Synthetic (f) Synthetic01
(g) Synthetic02
Figure 2: Comparison of Nemenyi test concerning all techniques over (a) Gases05, (b) Gases07, (c) Scene, (d) Sonar, (e)
Synthetic, (f) Synthetic01, and (g) Synthetic02 datasets. Groups connected does not present a critical difference.
Table 3: Learning (training + evaluating) time, in seconds.
Algorithm MCP-OPF OPF Decision Tree LDA Logistic Regression Naive Bayes Probablistic SVM
Gases05
0.3228 ±0.0965 0.0257 ± 0.0071 0.1148 ± 0.0135 0.0285± 0.0053 1.2868 ± 0.1762 0
0
0.
.
.0
0
00
0
01
1
12
2
2 ±
±
± 0
0
0.
.
.0
0
00
0
00
0
04
4
4 4.4331 ±1.0348
Gases07
0.4669 ±0.1281 0.0426 ± 0.0143 0.1491 ± 0.0120 0.0344± 0.0088 1.4851 ± 0.2446 0
0
0.
.
.0
0
00
0
01
1
12
2
2 ±
±
± 0
0
0.
.
.0
0
00
0
00
0
03
3
3 4.2941 ±1.0569
Scene
32.4470 ±6.5194 1.0816 ±0.2626 49.1499 ±15.2594 4.7377 ±1.3074 133.1621 ± 13.4707 0
0
0.
.
.0
0
00
0
08
8
84
4
4 ±
±
± 0
0
0.
.
.0
0
00
0
01
1
12
2
2 291.4601 ± 51.9725
Sonar
0.0273 ±0.0060 0.0029 ± 0.0007 0.2563 ± 0.0314 0.0962± 0.0497 0.8907 ± 0.2161 0
0
0.
.
.0
0
00
0
01
1
10
0
0 ±
±
± 0
0
0.
.
.0
0
00
0
00
0
02
2
2 1.3286 ±0.3268
Synthetic
0.3734 ±0.0708 0.0344 ± 0.0126 0.2427 ± 0.0419 0.0326± 0.0081 1.6555 ± 0.2443 0
0
0.
.
.0
0
00
0
01
1
12
2
2 ±
±
± 0
0
0.
.
.0
0
00
0
00
0
02
2
2 6.2055 ±1.0522
Synthetic01
0.2278 ±0.0611 0.0261 ± 0.0105 0.1426 ± 0.0176 0.0252± 0.0057 0.3356 ± 0.0609 0
0
0.
.
.0
0
00
0
01
1
11
1
1 ±
±
± 0
0
0.
.
.0
0
00
0
00
0
02
2
2 8.9314 ±1.8717
Synthetic02
0.2679 ±0.0672 0.0321 ± 0.0098 0.1269 ± 0.0166 0.0264± 0.0057 0.3369 ± 0.0589 0
0
0.
.
.0
0
00
0
01
1
10
0
0 ±
±
± 0
0
0.
.
.0
0
00
0
00
0
02
2
2 8.5503 ±1.8026
Physical Sciences Research Council (EPSRC) Grant
Ref. EP/T021063/1.
REFERENCES
Al-Dulaimi, K., Chandran, V., Nguyen, K., Banks, J., and
Tomeo-Reyes, I. (2019). Benchmarking hep-2 speci-
A Multi-Class Probabilistic Optimum-Path Forest
367

men cells classification using linear discriminant anal-
ysis on higher order spectra features of cell shape. Pat-
tern Recognition Letters, 125:534–541.
Apte, C., Grossman, E., Pednault, E. P., Rosen, B. K.,
Tipu, F. A., and White, B. (1999). Probabilistic
estimation-based data mining for discovering insur-
ance risks. IEEE Intelligent Systems and their Appli-
cations, 14(6):49–58.
Boutell, M. R., Luo, J., Shen, X., and Brown, C. M.
(2004). Learning multi-label scene classification. Pat-
tern recognition, 37(9):1757–1771.
Dem
ˇ
sar, J. (2006). Statistical comparisons of classifiers
over multiple data sets. The Journal of Machine
Learning Research, 7:1–30.
Fernandes, S. E., Pereira, D. R., Ramos, C. C., Souza,
A. N., Gastaldello, D. S., and Papa, J. P. (2018). A
probabilistic optimum-path forest classifier for non-
technical losses detection. IEEE Transactions on
Smart Grid, 10(3):3226–3235.
Gorman, R. P. and Sejnowski, T. J. (1988). Analysis of
hidden units in a layered network trained to classify
sonar targets. Neural networks, 1(1):75–89.
Huang, Y. and Meng, S. (2019). Automobile insurance clas-
sification ratemaking based on telematics driving data.
Decision Support Systems, 127:113156.
Kuncheva, L. I. (2006). On the optimality of na
¨
ıve bayes
with dependent binary features. Pattern Recognition
Letters, 27(7):830–837.
Lin, H.-T., Lin, C.-J., and Weng, R. C. (2007). A note
on platt’s probabilistic outputs for support vector ma-
chines. Machine Learning, 68(3):267–276.
Lupi Filho, G. (2012). Comparac¸
˜
ao entre os crit
´
erios
de diagn
´
osticos por an
´
alise cromatogr
´
afica de gases
dissolvidos em
´
oleo isolante de transformador de
pot
ˆ
encia. PhD thesis, Universidade de S
˜
ao Paulo.
Ma, J., Xiao, B., and Deng, C. (2020). Graph based
semi-supervised classification with probabilistic near-
est neighbors. Pattern Recognition Letters, 133:94–
101.
Madzarov, G., Gjorgjevikj, D., and Chorbev, I. (2009).
A multi-class svm classifier utilizing binary decision
tree. Informatica, 33(2).
Nagabhushan, P. and Pai, R. M. (1999). Modified region de-
composition method and optimal depth decision tree
in the recognition of non-uniform sized characters–
an experimentation with kannada characters. Pattern
Recognition Letters, 20(14):1467–1475.
Nemenyi, P. (1963). Distribution-free Multiple Compar-
isons. Princeton University.
Papa, J. P., Falc
˜
ao, A. X., Albuquerque, V. H. C., and
Tavares, J. M. R. S. (2012). Efficient supervised
optimum-path forest classification for large datasets.
Pattern Recognition, 45(1):512–520.
Papa, J. P., Falc
˜
ao, A. X., and Suzuki, C. T. N. (2009). Su-
pervised pattern classification based on optimum-path
forest. International Journal of Imaging Systems and
Technology, 19(2):120–131.
Papa, J. P., Fernandes, S. E. N., and Falc
˜
ao, A. X. (2017).
Optimum-Path Forest based on k-connectivity: The-
ory and Applications. Pattern Recognition Letters,
87:117–126.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Platt, J. C. (1999). Probabilistic outputs for support vector
machines and comparisons to regularized likelihood
methods. In Advances in Large Margin Classifiers,
pages 61–74. MIT Press.
Rocha, L. M., Cappabianco, F. A. M., and Falc
˜
ao, A. X.
(2009). Data clustering as an optimum-path forest
problem with applications in image analysis. Inter-
national Journal of Imaging Systems and Technology,
19(2):50–68.
Sanmartin, E. F., Damrich, S., and Hamprecht, F. A.
(2019). Probabilistic watershed: Sampling all
spanning forests for seeded segmentation and semi-
supervised learning. In Advances in Neural Informa-
tion Processing Systems, pages 2776–2787.
Souza, R. W. R., Oliveira, J. V. C., Passos, L. A., Ding, W.,
Papa, J. P., and Albuquerque, V. H. (2019). A novel
approach for optimum-path forest classification using
fuzzy logic. IEEE Transactions on Fuzzy Systems.
Vapnik, V. N. (1999). An overview of statistical learn-
ing theory. IEEE transactions on neural networks,
10(5):988–999.
Wilcoxon, F. (1945). Individual comparisons by ranking
methods. Biometrics Bulletin, 1(6):80–83.
Yang, Y. and Loog, M. (2018). A benchmark and compar-
ison of active learning for logistic regression. Pattern
Recognition, 83:401–415.
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
368