A Novel Dual-Role Two Pursuers and Two Evaders Simple Motion Game

Pengfei Zhang, Peifeng Chen, Hao Zhang, Yiqun Zhang

∗

, Feng Song and Hongwei Lan

Beijing Institute of Electronic System Engineering, Beijing, 100854, China

Keywords:

Dual-Role, Two Pursuers Two Evaders, Simple Motion, Differential Games.

Abstract:

Multiple players pursuit evasion differential games are signiﬁcant for the development of unmanned aircraft.

In this study, a two pursuers and two evaders game is to be investigated, of which the payoff function is the

instant when both the evaders are ﬁrst time captured by the pursuers. The pursuers wish to minimize the

capture instant while the evaders have the opposite purpose. In this game, the positional coincidence of any

two players implies that the two players are destroyed. Different from previous literature, the players are

considered to have two roles, that is the evader has the role of escaping from the pursuer as well as the role

of pursuing the pursuer. To solve the problem, we ﬁrst present the state feedback strategies of the pursuers.

Secondly, the payoff function and the best strategies of the evaders are deduced under the condition that the

evader does not intercept the pursuers. Thirdly, by contradiction, it is proved that the capture instant will be

decreased when the evaders try to intercept one of the pursuers. As a result, the underlying strategies are

equilibrium strategies.

1 INTRODUCTION

The topic of multi-player pursuit evasion games be-

comes popular due to the development of unmanned

artiﬁcial vehicles (Exarchos et al., 2015; Zhang et al.,

2022). In a multi-player pursuit evasion differential

game, the pursuers try to capture all the evaders while

the evaders act against being captured. Compared

with the one-one, multi-one and one-multi differen-

tial games, the underlying problem is more compli-

cated. The major reason is that the players should

be allocated so as to make it clear that which pursuer

pursuit which evader. Moreover, the allocation might

not be ﬁxed in the whole game interval, for instance,

one pursuer might change the pursuing target. In real

combats, the evader can also act as the ”pursuer” to at-

tack the pursuers, thus forming a more intricate prob-

lem, which is of concern to this paper.

In regard to the simple motion differential games,

there have been extensive studies (Yan et al., 2019;

Garcia et al., 2017; Makkapati et al., 2018; Pachter

et al., 2020; Pachter et al., 2019; Sun et al., 2017;

Ibragimov et al., 2018). Issacs’ two cutters and fugi-

tive ship differential game where two faster pursuers

cooperate to capture a slower evader in minimum time

is a typical simple motion differential game (Isaacs,

1965). The Appolonius circle is often adopted to an-

alyze the simple motion differential games. In the

simple motion games, most of the optimal strategies

are moving straight. Garcia et.al (Garcia et al., 2017)

proposed a geometric approach for the Issacs’ two

cutters and fugitive ship game to obtain the solution.

In another publication (Garcia et al., 2019), Garcia

et.al studied the goal line two pursuers one evader

game, in which the evader aims at reaching a goal line

which is protected by the pursuers, showing that the

optimal strategies of the players are moving straight.

Pachter et.al (Pachter et al., 2019) also studied the is-

sue of two pursuers and one evader game. Moll et.al

(Von Moll et al., 2020) studied the mutiple-pursuer

and one evader border defense differential game, with

a geometric property-based approach. Pachter et.al

(Pachter et al., 2020) studied the multiple-pursuer and

one evader differential game. Sun et.al (Sun et al.,

2017) studied the multiple pursuers and one evader

game in dynamic ﬂowﬁelds. Chen et.al (Chen et al.,

2016) studied the multi-player game with one supe-

rior evader, providing a cooperative scheme for the

pursuers to shrink the encirclement. Alias et.al (Alias

et al., 2017) studied the simple motion pursuit eva-

sion game with many evaders and many pursuers sub-

ject to integral constraints, obtaining the conclusion

that the evasion is possible when the total resource

of the evaders is greater than that of the pursuers.

Ibragimov et.al (Ibragimov et al., 2018) studied the

simple motion differential game with many pursuers

674

Zhang, P., Chen, P., Zhang, H., Zhang, Y., Song, F. and Lan, H.

A Novel Dual-Role Two Pursuers and Two Evaders Simple Motion Game.

DOI: 10.5220/0012016100003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 674-680

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

and many evaders with integral constraints and ex-

plicitly constructed the evasion strategies. Makkap-

ati et.al (Makkapati and Tsiotras, 2019) studied the

multi-player pursuit evasion problem with a dynamic

divide and conquer approach. In regard to the active

target defense games, Garcia et.al (Garc

ıa et al., 2015)

studied the simple motion game with a fast defender,

and the result showed that the optimal trajectories are

straight lines. For the same problem, Garcia et.al

(Garcia et al., 2018) developed the state-feedback op-

timal strategies. It has been proved that it is possi-

ble for several pursuers capture one evader with zero

miss, in which the control bounds of the players are

identical (Kumkov et al., 2017).

The aforementioned studies have investigated dif-

ferent kinds of simple motion games, including the

life line game, multiple pursuers one evader game,

multiple pursuers multiple evaders game and integral

constraint game. Rare works have considered the

many pursuers and many evaders game in which the

evader could attack the pursuer. For this sake, this

paper focuses on studying the underlying problem.

The approach is by providing the best strategies in ad-

vance, and checking whether intercepting the pursuer

by the evader could bring in beneﬁt or not.

2 MATHEMATICAL

FORMULATION

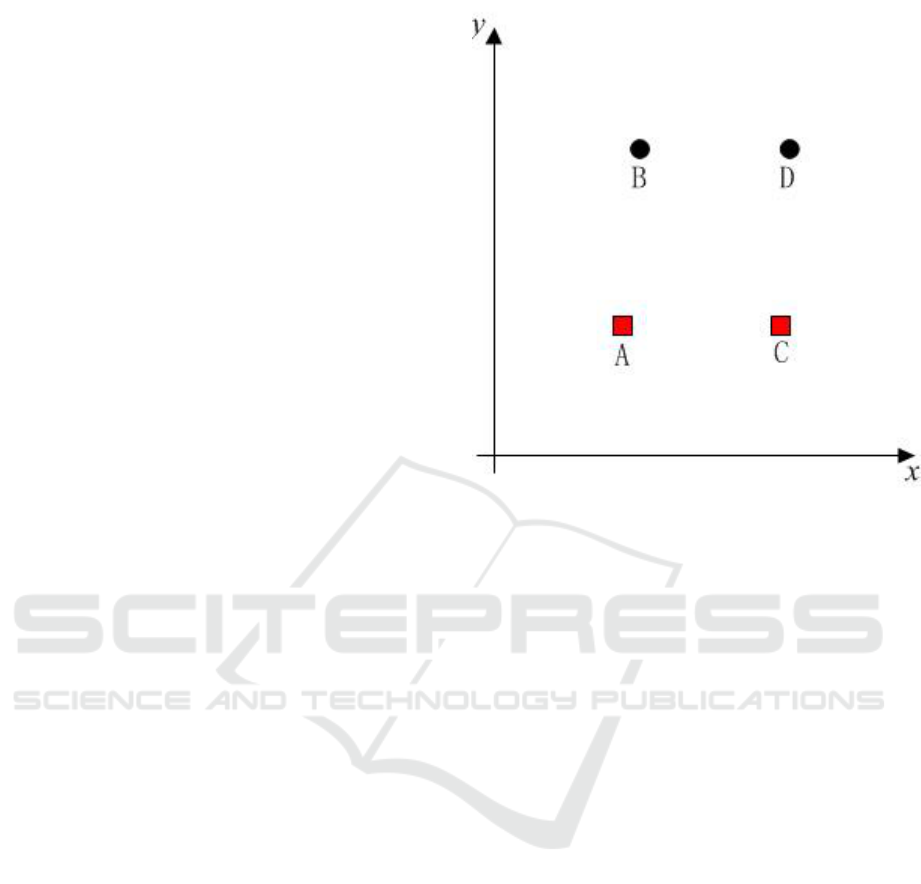
Four players move on a plane, marked by A, B, C and

D. Player A and C are the pursuers, player B and D

are the evaders, As depicted in Fig. 1.

The initial positions of the four players are de-

noted by r

, respectively. The four

players have simple motion dynamics, the state equa-

tion are written as:

˙x

= v

cosθ

˙y

= v

sinθ

˙x

= v

cosθ

˙y

= v

sinθ

˙x

= v

cosθ

˙y

= v

sinθ

˙x

= v

cosθ

˙y

= v

sinθ

. (1)

where θ

, θ

, and θ

are the control variables

belong to the interval [0,2π).

For simpliﬁcation, some new variables are intro-

Figure 1: Sketch of the two pursuers and the two evaders.

duced:







cosθ

sinθ









cosθ

sinθ









cosθ

sinθ









cosθ

sinθ



(2)

Based on Eq. (1) and Eq. (2), the state equation is

rewritten as:

= v

(3)

In this problem, any two players are destroyed

when their positional coordinates coincides. Different

from the previous pursuit evasion games, the evaders

B and D in this game can also pursuit the pursuers

A and C. In other words, the pursuers and the evaders

have two roles. The evader is called captured when its

positional coordinate coincides with a pursuer. The

game ends when all the evaders are captured by the

pursuers. The purpose of the players A and C is to

capture the players B and D as soon as possible, while

the purpose of B and D is the opposite. We assume

that the magnitudes of the velocity vectors v

, v

and v

satisfy v

> v

. By now, the game

is established and to be analyzed.

A Novel Dual-Role Two Pursuers and Two Evaders Simple Motion Game

675

3 GAME ANALYSIS WHEN THE

EVADERS DO NOT INTERCEPT

THE PURSUERS

In this section, the evaders do not intercept the pur-

suers, only playing the role of escaping from the pur-

suers. Since v

> v

, A has to capture B

while C has to capture D. The one-one game of A and

B is called sub-game 1; the one-one game of C and

D is called sub-game 2. Evidently, the equilibrium

strategies in the sub-game 1 and sub-game 2 are writ-

ten as:

(

∗

= v

−r

∥

−r

∥

∗

= v

−r

∥

−r

∥

(

∗

= v

−r

∥

−r

∥

∗

= v

−r

∥

−r

∥

(4)

The payoff functions, the capture instants, of sub-

game 1 and sub-game 2 are denoted as J

and J

respectively. Under the the equilibrium strategies

listed in Eq. (4), the capture instants of B and D are

∗

) and J

∗

), respectively. The payoff

function of the two-two game is denoted as J. Ob-

viously, J = max(J

) when the evaders do not in-

tercept the pursuers.

Lemma 1: If the payoff function J of

the underlying two-two game is bigger than

max(J

∗

),J

∗

)), then player B must inter-

cept player C.

Proof: Based on the law of contrapositive, the

proposition is equivalent with ”Suppose that the

player B does not intercept the player C in the under-

lying two-two game, then the equilibrium strategies

are the same with sub-game 1 and sub-game 2, while

the J = max(J

∗

),J

∗

)).”

Since v

> v

, C cannot capture B for

B has a bigger velocity. Thereby, C has to capture D

and A has to capture B. In the case A and C take the

best strategy of sub-game 1 and-sub game 2, B and D

will make the payoff functions of sub-game 1 and sub-

game 2 decrease when taking non-optimal strategies,

implying that:

J (v

∗

) ≤ J (v

∗

) (5)

In the case B and D take the best strategies of sub-

game 1 and sub-game 2, A and C will make the the

payoff functions of sub-game 1 and sub-game 2 in-

crease when taking non-optimal strategies, implying

that:

J (v

∗

) ≤ J (v

∗

) (6)

From Eq. (5) and Eq. (6), it is concluded that

the best strategies of sub-game 1 and sub-game 2

are the equilibrium strategies while the game value

J = max(J

∗

),J

∗

)). This completes the

proof. ■

Another lemma about the time moment when B

intercepts C is given below.

Lemma 2: Under the best strategies of A and C

in sub-game 1 and sub-game 2, if the payoff function

J is bigger than max(J

∗

),J

∗

)), then the

player B must intercept the player C before C captures

D and A captures B.

Proof : The proposition can be proved by con-

tradiction. Suppose the player B intercepts C af-

ter C captures D, the capture time of B by A must

be less than or equal to J

∗

), indicating that

J ≤ max(J

∗

),J

∗

)); Suppose the player

B intercepts C after A captures B, B is destroyed and

can not intercept C. Therefore, the player B must in-

tercept the player C before C captures D and A cap-

tures B, from which the proof is completed. ■

In summary, it is concluded that when A and C

adopt the best sub-game strategies, there is no possi-

bility for B and D to obtain a better result except that

B intercepts C earlier than C captures D and A cap-

tures B.

4 GAME ANALYSIS WHEN THE

EVADER INTERCEPT THE

PURSUER AT A TIME

The time moment when B captures C is denoted

as t

, as depicted in Fig. 2. The positions

of the four players at time t

are denoted as

),r

Lemma 3: If A and C adopt the best strategies of

the two sub-games, the following inequalities hold:

≤

∥

−r

∥

−v

−

∥

)−r

)

∥

−v

≤

∥

−r

∥

−v

−

∥

)−r

)

∥

−v

(7)

Proof : We only prove the inequality in the ﬁrst

row, the second row can be proved by a similar argu-

ment.

Let:

= ⟨r

− r

⟩ (8)

Taking derivative of the two sides in Eq. (8):

ρ = ⟨

− r

⟩ − ⟨

− r

⟩ (9)

By integrating Eq. (9):

ρ(t) − ρ (0) =

⟨

−r

⟩dt −

⟨

−r

⟩d t

↔

ρ(t) = ρ(0) +

⟨

−r

⟩dt −

⟨

−r

⟩d t

(10)

ISAIC 2022 - International Symposium on Automation, Information and Computing

676

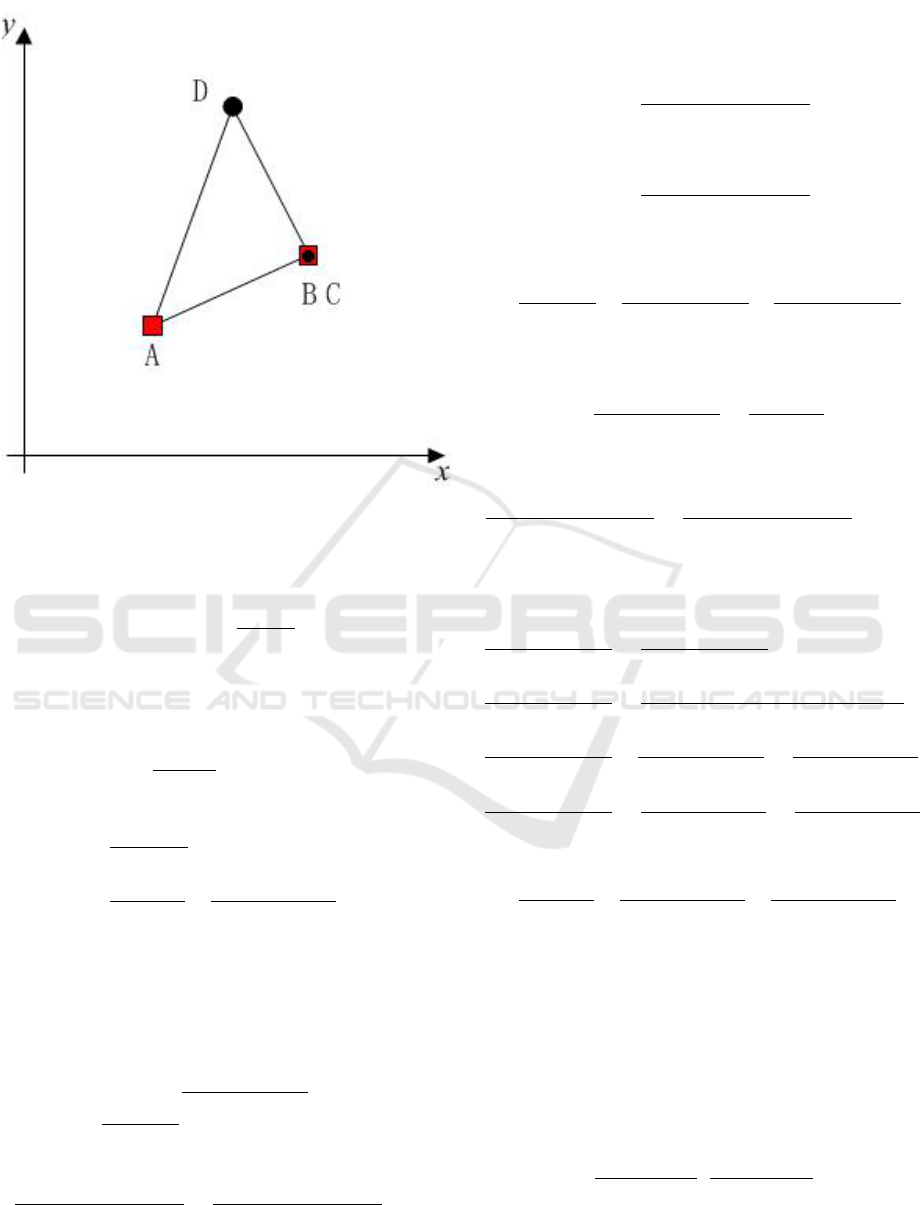
Figure 2: The player B captures player C at t

The purpose of A in sub-game 1 is to reduce ρ as

quick as possible with a strategy of A:

ρ(t) = ρ (0) − v

−

⟨

− r

⟩dt (11)

Based on Eq. (11):

ρ(t) ≤ ρ (0) − v

t +v

↔

t ≤

ρ(0)−ρ(t)

−v

(12)

Substituting t = t

into Eq. (12):

≤

ρ(0)−ρ(t

)

−v

↔

≤

∥

−r

∥

−v

−

∥

)−r

)

∥

−v

(13)

The second row can be proved by a similar argu-

ment. The proof is completed. ■

The relations between the payoff function J and

∗

), J

∗

) are presented in lemma 4 and

lemma 5.

Lemma 4: The inequality

J = t

∥

)−r

)

∥

−v

≤

∥

−r

∥

−v

= J

∗

)

(14)

holds if

∥

) − r

)

∥

− v

≤

∥

) − r

)

∥

− v

(15)

holds at time t

Proof : After time t

, only A and D participates

in the game. The total time B and D captured by C

and A is derived as:

J = t

∥

) − r

)

∥

− v

(16)

Based on Eq. (15) and Eq. (16):

J ≤ t

∥

) − r

)

∥

− v

(17)

The inequality of the second row of Eq. (7) in

lemma 3 and Eq. (17) yield:

J ≤

∥

−r

∥

−v

−

∥

)−r

)

∥

−v

∥

)−r

)

∥

−v

= J

∗

)

(18)

Lemma 5: The inequality

J = t

∥

)−r

)

∥

−v

≤

∥

−r

∥

−v

= J

∗

)

(19)

holds if

∥

) − r

)

∥

− v

∥

) − r

)

∥

− v

(20)

holds at time t

Proof : Based on Eq. (20) and the sum of two sides

of a triangle is greater than the third side:

∥

)−r

)

∥

−v

∥

)−r

)

∥

−v

→

∥

)−r

)

∥

−v

∥

)−r

)

∥

−

∥

)−r

)

∥

−v

↔

∥

)−r

)

∥

−v

−

∥

)−r

)

∥

−v

∥

)−r

)

∥

−v

↔

∥

)−r

)

∥

−v

∥

)−r

)

∥

−v

∥

)−r

)

∥

−v

(21)

Based on lemma 3 and Eq. (16):

J ≤

∥

−r

∥

−v

−

∥

)−r

)

∥

−v

∥

)−r

)

∥

−v

= J

∗

)

(22)

This completes the proof. ■

We end this section with a theorem to show that

the equilibrium strategies of the two-two game is con-

sistent with the equilibrium strategies of the sub-game

1 and sub-game 2.

Thereom 1: The value of the dual-role game of

two pursuers and two evaders with simple motion,

where v

> v

, is written as:

J = max



∥

− r

∥

− v

∥

− r

∥

− v



(23)

The corresponding equilibrium strategies are

listed in Eq. (4).

A Novel Dual-Role Two Pursuers and Two Evaders Simple Motion Game

677

Proof : For the evaders B and D, they have two

choices. One is escaping from A and B without in-

tercepting them; the other one is escaping as well as

intercepting the pursuers.

In the ﬁrst choice, the game is decomposed of sub-

game 1 and sub-game 2. The game value and equilib-

rium strategies are the same with the sub-game 1 and

sub-game 2, which completes the proof in this case.

In the second choice, B and D will not

use the strategies v

∗

and v

∗

. From lemma 4

and lemma 5, it can be inferred that the J ≤

∗

) or J ≤ J

∗

), yielding that J ≤

max(J

∗

),J

∗

). It turns out that the cap-

ture time is less than or equal to Eq. (23) no matter

what the evaders act. Since the evaders wish to max-

imize the capture time, there’s no need for them to

intercept the pursuers, which completes the proof in

this case. ■

5 SIMULATION

Two simulation cases are developed. One is that the

players adopt the equilibrium strategies of the sub-

game 1 and sub-game 2; the other one is that the

players A and C still adopt the best strategies in sub-

game 1 and sub-game 2, while the player B tries his

best to intercept the player C and the player D tries

his best to escape from the player A. In both cases,

= 5(m/s), v

= 4(m/s), v

= 3(m/s), v

= 2(m/s).

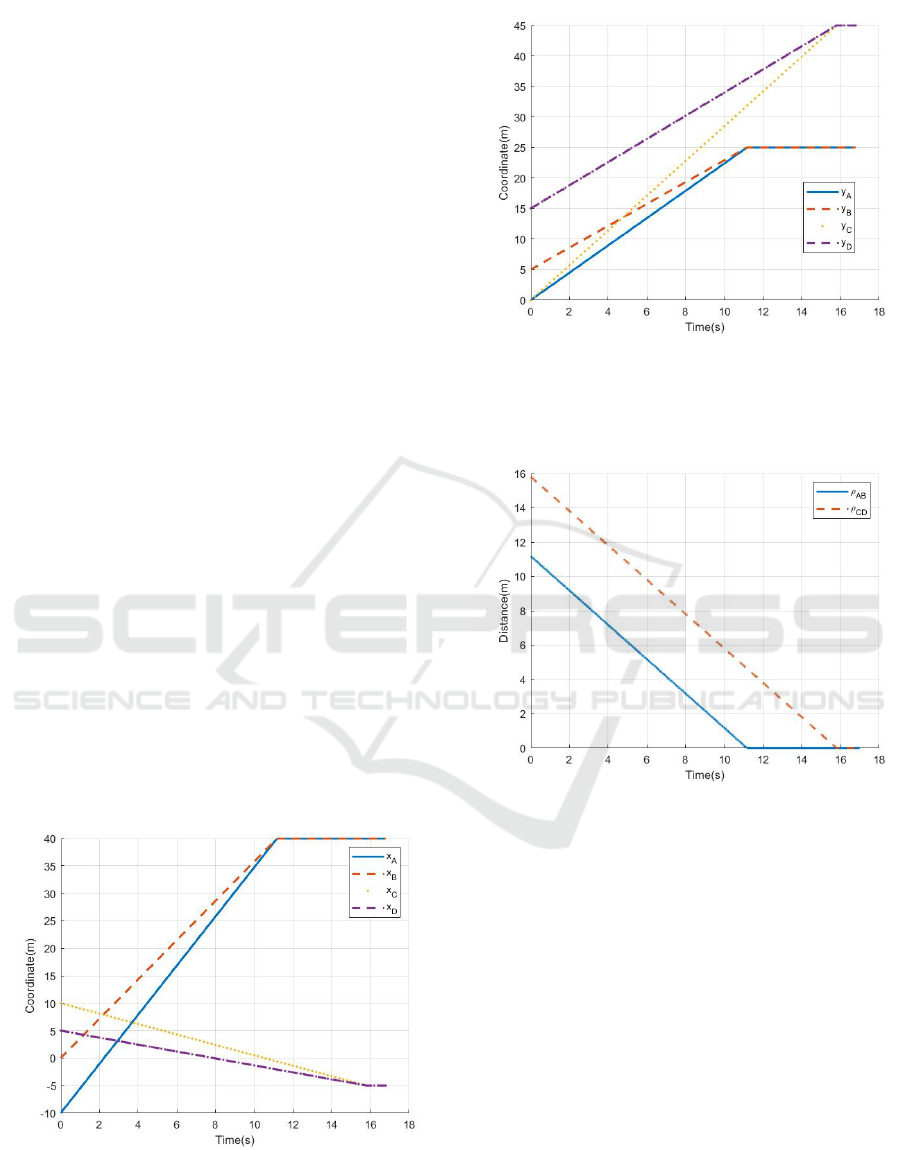
a) Case 1

Under the given strategies, the coordinates of the

four players with respect to time are shown in Fig. 3

and Fig. 4.

Figure 3: x coordinate of the four players.

The distances of (A, B) and (C, D) with respect

to time are shown in Fig. 5. The captures of B and

Figure 4: y coordinate of the four players.

D occur at time 11.171 s and 15.802 s, respectively.

Thus, the capture time is 15.802 s.

Figure 5: The distances of (A, B) and (C, D) with respect to

time.

The trajectories of the four players is shown in

Fig. 6.

b) Case 2

Under the given strategies, the coordinates of the

four players with respect to time are shown in Fig. 7

and Fig. 8.

The distances of (A, D) and (C, B) with respect to

time are shown in Fig. 9. The captures of B and D

occur at time 3.472 s and 8.381 s, respectively. Thus,

the capture time is 8.381 s.

The trajectories of the four players is shown in

Fig. 10.

The capture time in case 1 is greater than case 2,

which is consistent with the theoretical results in the

previous section.

ISAIC 2022 - International Symposium on Automation, Information and Computing

678

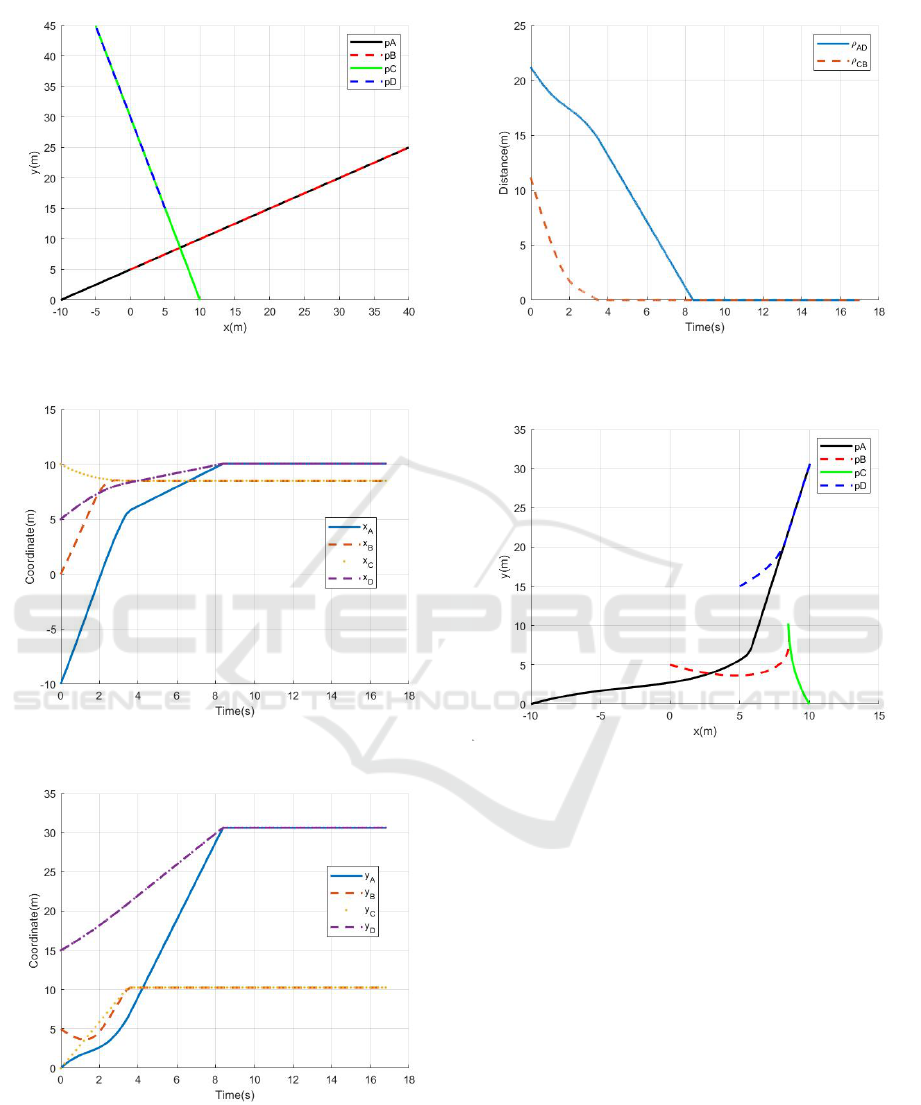
Figure 6: The trajectories of the four players.

Figure 7: x coordinate of the four players.

Figure 8: y coordinate of the four players.

6 CONCLUSIONS

This paper has investigated a novel two pursuers and

two evaders game, considering the dual-role of the

Figure 9: The distances of (A, D) and (C, B) with respect to

time.

Figure 10: The trajectories of the four players.

players. The evaders act as the evader as well as

the pursuer, that is the evader can choose to hit the

pursuer to protect his teammate. Accordingly, the

pursuers also have two roles, for they might be cap-

tured and destroyed by the evader. The state feedback

strategies of all the players are presented and proved.

In particular, it is rigorously demonstrated that the in-

terception by the evader will not increase the capture

time. Therefore, the evaders’ best strategies are con-

sistent with the two one-one games. For validation,

two simulation cases have been developed and com-

pared. The results have a good agreement with the

theoretical analysis.

ACKNOWLEDGMENTS

The authors would like to thank associate editor and

anonymous reviewers for their valuable and construc-

tive comments that improved the paper.

A Novel Dual-Role Two Pursuers and Two Evaders Simple Motion Game

679

REFERENCES

Alias, I. A., Ibragimov, G., and Rakhmanov, A. (2017).

Evasion differential game of inﬁnitely many evaders

from inﬁnitely many pursuers in hilbert space. Dy-

namic Games and Applications, 7(3):347–359.

Chen, J., Zha, W., Peng, Z., and Gu, D. (2016). Multi-player

pursuit–evasion games with one superior evader. Au-

tomatica, 71:24–32.

Exarchos, I., Tsiotras, P., and Pachter, M. (2015). On the

suicidal pedestrian differential game. Dynamic Games

and Applications, 5(3):297–317.

Garcia, E., Casbeer, D. W., and Pachter, M. (2018). Design

and analysis of state-feedback optimal strategies for

the differential game of active defense. IEEE Trans-

actions on Automatic Control, 64(2):553–568.

Garcia, E., Casbeer, D. W., Von Moll, A., and Pachter, M.

(2019). Cooperative two-pursuer one-evader blocking

differential game. In 2019 American Control Confer-

ence (ACC), pages 2702–2709. IEEE.

Garcia, E., Fuchs, Z. E., Milutinovic, D., Casbeer, D. W.,

and Pachter, M. (2017). A geometric approach for the

cooperative two-pursuer one-evader differential game.

Ifac Papersonline, 50(1):15209–15214.

Garc

ıa, E., Casbeer, D., and Pachter, M. (2015). Ac-

tive target defense differential game with a fast de-

fender. Proceedings of the American Control Confer-

ence, 2015.

Ibragimov, G., Ferrara, M., Kuchkarov, A., and Pansera,

B. A. (2018). Simple motion evasion differential

game of many pursuers and evaders with integral con-

straints. Dynamic Games and Applications, 8(2):352–

378.

Isaacs, R. (1965). Differential games: a mathematical the-

ory with applications to warfare and pursuit, control

and optimization. Wiley.

Kumkov, S. S., Le M

enec, S., and Patsko, V. S. (2017).

Zero-sum pursuit-evasion differential games with

many objects: survey of publications. Dynamic games

and applications, 7(4):609–633.

Makkapati, V. R., Sun, W., and Tsiotras, P. (2018). Pursuit-

evasion problems involving two pursuers and one

evader. In 2018 AIAA Guidance, Navigation, and

Control Conference, page 2107.

Makkapati, V. R. and Tsiotras, P. (2019). Optimal evading

strategies and task allocation in multi-player pursuit–

evasion problems. Dynamic Games and Applications,

9(4):1168–1187.

Pachter, M., Moll, A. V., Garcia, E., Casbeer, D., and Mi-

lutinovi, D. (2020). Cooperative pursuit by multiple

pursuers of a single evader. Journal of Aerospace In-

formation Systems, (2):1–19.

Pachter, M., Von Moll, A., Garcia, E., Casbeer, D. W., and

Milutinovi

c, D. (2019). Two-on-one pursuit. Journal

of Guidance Control & Dynamics, pages 1–7.

Sun, W., Tsiotras, P., Lolla, T., Subramani, D. N., and Ler-

musiaux, P. F. (2017). Multiple-pursuer/one-evader

pursuit–evasion game in dynamic ﬂowﬁelds. Journal

of guidance, control, and dynamics, 40(7):1627–1637.

Von Moll, A., Garcia, E., Casbeer, D., Suresh, M.,

and Swar, S. C. (2020). Multiple-pursuer, single-

evader border defense differential game. Journal of

Aerospace Information Systems, 17(8):407–416.

Yan, R., Shi, Z., and Zhong, Y. (2019). Optimal strategies

for the lifeline differential game with limited lifetime.

International Journal of Control, pages 1–14.

Zhang, Y., Zhang, P., Wang, X., Song, F., and Li, C. (2022).

A payoff augmentation approach to two pursuers and

one evader inertial model differential game. IEEE

Transactions on Aerospace and Electronic Systems.

ISAIC 2022 - International Symposium on Automation, Information and Computing

680