Adaptive Combination of a Genetic Algorithm and Novelty Search for
Deep Neuroevolution
Eyal Segal and Moshe Sipper
a
Department of Computer Science, Ben-Gurion University, Beer Sheva 84105, Israel
Keywords:
Reinforcement Learning, Evolutionary Computation, Novelty Search, Genetic Algorithm.
Abstract:
Evolutionary Computation (EC) has been shown to be able to quickly train Deep Artificial Neural Networks
(DNNs) to solve Reinforcement Learning (RL) problems. While a Genetic Algorithm (GA) is well-suited
for exploiting reward functions that are neither deceptive nor sparse, it struggles when the reward function is
either of those. To that end, Novelty Search (NS) has been shown to be able to outperform gradient-following
optimizers in some cases, while under-performing in others. We propose a new algorithm: Explore-Exploit γ-
Adaptive Learner (E
2
γAL, or EyAL). By preserving a dynamically-sized niche of novelty-seeking agents, the
algorithm manages to maintain population diversity, exploiting the reward signal when possible and exploring
otherwise. The algorithm combines both the exploitation power of a GA and the exploration power of NS,
while maintaining their simplicity and elegance. Our experiments show that EyAL outperforms NS in most
scenarios, while being on par with a GA—and in some scenarios it can outperform both. EyAL also allows
the substitution of the exploiting component (GA) and the exploring component (NS) with other algorithms,
e.g., Evolution Strategy and Surprise Search, thus opening the door for future research.
1 INTRODUCTION
As the field of Reinforcement Learning (RL) (Sut-
ton and Barto, 2018) is being applied to harder tasks,
two unfortunate trends emerge: larger policies that re-
quire more computing time to train, and “deceptive”
optima. While gradient-based methods do not scale
well to large clusters, evolutionary computation (EC)
techniques have been shown to greatly reduce training
time by using modern distributed infrastructure (Sali-
mans et al., 2017; Such et al., 2017).
The problem of deceptive optima has long since
been known in the EC community: Exploiting the ob-
jective function too early might lead to a sub-optimal
solution, and attempting to escape it incurs an initial
loss in the objective function. Novelty Search (NS)
mitigates this issue by ignoring the objective function
while searching for new behaviors (Lehman and Stan-
ley, 2008). This method had been shown to work for
RL (Such et al., 2017).
While both genetic algorithms (GAs) and NS have
been shown to work in different environments (Such
et al., 2017), we attempt herein to combine the two
to produce a new algorithm that does not fall behind
a
https://orcid.org/0000-0003-1811-472X
either, and in some scenarios surpasses both.
Section 2 presents previous work. In Section 3 we
describe the methods used herein: GA, NS, and our
new algorithm. The experimental setup is delineated
in Section 4, followed by results in Section 5. We
end with a discussion in Section 6 and future work in
Section 7.
2 PREVIOUS WORK
2.1 Reinforcement Learning
In Reinforcement Learning (RL) problems the goal is
to find a behavior that accomplishes a specific task,
without explicitly telling the learner what to do; in-
stead, a given reward function judges the behavior of
the learner. The learning algorithm’s purpose is to de-
vise a behavior that will maximize the cumulative re-
turns of the given reward function (Sutton and Barto,
2018).
Segal, E. and Sipper, M.
Adaptive Combination of a Genetic Algorithm and Novelty Search for Deep Neuroevolution.
DOI: 10.5220/0011550200003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 143-150
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
143

2.2 Evolutionary Computation in
Reinforcement Learning
While most traditional RL research attempts to as-
sign credit to previous actions and diffuse the re-
wards throughout the run (Sutton and Barto, 2018),
EC attempts to holistically judge the agent as a black
box: The cumulative sum of episodic rewards is used
as a fitness metric, without assigning credit to intra-
episode actions. While these methods can sometimes
be less sample-efficient, they scale well with the num-
ber of CPUs available, and thus save wall-clock time
overall (Salimans et al., 2017; Such et al., 2017).
Evolution Strategies (ES) (Rechenberg, 1989;
Beyer and Schwefel, 2002) work by empirically esti-
mating the gradient. By sampling enough points near
the current solution, one can estimate the impact of
“nudging” the solution to any direction. When ap-
plied to RL, ES can be used to adjust the weights of a
DNN-based policy to maximize rewards, as shown in
(Salimans et al., 2017).
The Genetic Algorithm (GA) is a gradient-free al-
gorithm that works by allowing higher-fitness agents
to reproduce and accrue random mutations. Nov-
elty Search (NS) works similarly, but instead of be-
ing driven by fitness, it disregards the reward function
and searches for novel behaviours. GA and NS were
shown to be able to solve RL problems in (Such et al.,
2017).
2.3 Exploration-exploitation in
Evolutionary Computation
While a GA and Novelty Search both optimize either
fitness or novelty (but not both), previous attempts
have tried to optimize both simultaneously.
Multi-Oobjective Optimization. Several algo-
rithms have previously managed to simultaneously
optimize more than one objective, by looking for
solutions on the Pareto front. The basic idea is to
hold a number of such solutions, where each one
represents some trade-off between the objectives
(Coello Coello, 2006). These methods do not apply
to the domain of RL: though the exploitation (sum of
rewards) can be a dimension in the Pareto front, the
exploration (novelty) cannot. The latter is because the
goal of exploration is dynamic—once a solution is
found to be dominating, it is no longer novel and thus
by definition not on the Pareto front. Additionally,
the objective is not to find a novel solution that
is also well-adjusted (and vice versa)—novelty is
just a mechanism to explore the search space more
effectively.
SAFE. In the SAFE algorithm (Solution And Fit-
ness Evolution) a population of problem solutions co-
evolves along with a population of objective func-
tions, wherein each objective function unifies all ob-
jectives into a single objective (Sipper et al., 2019b;
Sipper et al., 2019a). The objective functions’ evo-
lution is driven by genotypic novelty, which does not
suit our purpose—we would like to increase or de-
crease the importance of novelty as the population be-
comes less or more diverse, respectively—and not try
new ratios independently.
Method II. A previous attempt to hybridize a GA
and NS was done in (Jackson and Daley, 2019). In
their so-called Method II, whenever the GA’s popu-
lation grew stale—i.e., no improvement in cumula-
tive rewards—the population was resampled from the
NS’s archive instead, looking for agents with behav-
ior as different from the current, stale population as
possible. In some simulations, Method II managed
to avoid local optima, which the GA did not manage
to escape, thus continuing to learn and achieve better
results.
Quality-diversity. In Quality-Diversity methods
such as Novelty Search with Local Competition
(Lehman and Stanley, 2011) and MAP-elites (Mouret
and Clune, 2015; Colas et al., 2020), diversity is en-
sured by dividing the population into cells (niches),
and quality is ensured by allowing local competition
within each cell.
3 METHODS
In this section we present an outline of the neuroevo-
lution policy representation, and the pseudo-code of
the GA used (Algorithm 1) and of NS (Algorithm 2).
Then, we present our technique for hybridizing them
in Algorithm 3.
3.1 Policy Representation
In order to find a policy through neuroevolution,
a representation scheme for the policy is needed.
One such representation is a pre-configured, fixed-
architecture DNN whose weights are encoded as a
fixed-length vector. The architecture can also be en-
coded and evolved using NEAT (Stanley and Miikku-
lainen, 2002) or one of its later variants. Decision
Trees can be encoded through Genetic Programming
(Koza et al., 1992).
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
144

3.2 Genetic Algorithm
The GA (Algorithm 1) (Holland, 1992) is a
population-based algorithm, in which the population
is measured against a fitness function. At each iter-
ation, the better-fitted individuals survive while the
lesser-fitted ones die off. The survivors then repro-
duce, and their descendants mutate to accrue random
mutations—which explore the search space. In the
domain of RL the fitness function is usually the sum
of returns of the reward function.
Algorithm 1: Genetic Algorithm.
input: max training steps, popsize
while training step < max training steps do
if first generation then
population ← initialize(popsize)
else
survivors ← select
survivors(population, fitnesses)
parents ← select parents(survivors,
popsize - 1)
children ← mutate(parents)
population ← children + {generation
elite}
end
trajectories ← rollouts(population)
fitnesses ← sum rewards(trajectories)
generation elite ← extract elite(population,
fitnesses)
report elite(generation elite)
end
3.3 Novelty Search
In some cases, the reward signal can be deceptive. For
example, in the short run, waiting for an elevator will
get you no closer to the 100th floor and will yield no
rewards, while climbing the stairs will grant immedi-
ate rewards. Thus, the reward function deceives you
into taking the stairs, while waiting a few minutes for
the elevator will get you closer to the objective in the
long run. To that end, Lehman and Stanley (Lehman
and Stanley, 2008) presented Novelty Search (Algo-
rithm 2), which essentially ignores the objective and
searches for behavioral novelty (using a novelty met-
ric that requires careful consideration).
Novelty Search is an exploratory algorithm, but
when it gets “close” to an optimum it does not always
optimize towards it before exhausting the rest of the
search space.
Algorithm 2: Novelty Search.
input: max training steps, popsize
while training step < max training steps do
if first generation then
population ← initialize(popsize)
else
survivors ← select
survivors(population, novelty scores)
parents ← select parents(survivors,
popsize - 1)
children ← mutate(parents)
population ← children + {generation
elite}
end
trajectories ← rollouts(population)
fitnesses ← sum rewards(trajectories)
generation elite ← extract elite(population,
fitnesses)
report elite(generation elite)
bcs ← behavior characterstic(trajectories)
novelty scores ← novelty measure(bcs,
archive)
update archive(bcs)
end
3.4 Adaptive Explore-exploit
EyAL (Algorithm 3) combines the two algorithms—
one mainly exploratory, the other mainly
exploitative—and introduces a control variable γ
to control the size of the exploratory niche. We have
chosen the Genetic Algorithm to be the exploitative
algorithm, and Novelty Search to be the exploratory
algorithm. It should be noted, however, that these can
be easily swapped with other algorithms, which we
leave for future research.
At every generation, both the fitness (sum of re-
wards) and novelty score of each specimen in the
population is calculated. Then, (population size) × γ
children are created using the novelty scores, and
(population size) × (1 − γ) are created using the fit-
ness. This ensures the survival of two niches: one
that tries to optimize the rewards, and one that tries to
search for new, unexplored behaviours.
The main principle in this approach is that γ is dy-
namic, and auto-adjusts during the run. If the pop-
ulation grows stale (no improvement in fitness with
relation to the previous generation), γ increases to
promote exploration and increase the size of the ex-
ploring niche. Otherwise, γ decreases to promote ex-
ploitation, increasing the size of the exploiting niche.
Adaptive Combination of a Genetic Algorithm and Novelty Search for Deep Neuroevolution
145

Algorithm 3: Explore-Exploit γ-Adaptive
Learner.
input: max training steps, population size,
initial exploration rate γ, exploration
growth rate α, exploration decay rate β
while training step < max training steps do
if first generation then
population ← initialize(popsize)
else
exploring survivors ← select
survivors(population, novelty scores)
exploiting survivors ← select
survivors(population, fitnesses)
exploring parents ← select
parents(exploring survivors, γ ×
(popsize - 1))
exploiting parents ← select
parents(exploiting survivors, (1 - γ) ×
(popsize - 1) )
children ← mutate(exploring parents) +
mutate(exploiting parents)
population ← children + {generation
elite}
end
trajectories ← rollouts(population)
fitnesses ← sum rewards(trajectories)
generation elite ← extract elite(population,
fitnesses)
report elite(generation elite) if generation
elite > previous generation elite then
γ ← γ − β
else
γ ← γ + α
end
γ ← clamp(0, 1, γ)
bcs ← behavior characteristic(trajectories)
novelty scores ← novelty measure(bcs,
archive)
update archive(bcs)
end
3.5 Operators and Terminology
While the pseudo-code describes the general scheme,
the details have been left out. This design allows
modularity—one can easily swap the implementation
of any of these operators with ease. We believe that
this design both promotes the elegance and clarity of
the algorithm itself and allows easy experimentation
with different operator implementations. In this sec-
tion we present the operators used in the algorithm
and provide information about our implementation
for said operators.
Policy. A policy is a strategy that allows an agent to
make decisions; at each state, the policy determines
which action should be taken. We have used a fixed-
architecture deep neural network (DNN) to represent
our policy; additional possibilities for such encodings
are discussed in 3.1.
In discrete environments, the (DNN) represents a
state-value function, taking an observation from the
environment and returning a vector of possible actions
and their respective (internal) values. The agent then
chooses the action with the highest value (i.e., in a
deterministic manner—probabilistic selection is also
possible, although not in the scope of this work).
In continuous environments the output represents
a single action. For example, if the task is controlling
the k joints of a robot, the output is a k-dimensional
vector.
Trajectory. A trajectory represents a single, com-
plete run of an agent in the environment, consisting
of a chain of <state, action, reward> tuples.
Rollout. A rollout takes an agent, performs a single
run in the environment, and returns the trajectory of
the run.
Initializer. The initializer method creates initial
agents for the evolutionary algorithm. In our context,
this method generated the parameter vectors for the
agent policy DNNs. We used the default initialization
in PyTorch (Paszke et al., 2019).
Survivor Selection. This operation receives the
population and the fitness of each individual in the
population, and returns the subset of the population
that survived this generation. We used truncated se-
lection, which selects only the truncation size speci-
mens with the highest fitness.
Other methods that were not used in this paper in-
clude the selection of only the newest solutions, the
selection of only the elite, and more.
Parent Selection. An operation that receives sur-
vivors and the number of parents to output, and se-
lects this number of parents from the survivors. We
used random selection with repetition. Since we did
not perform crossover, we selected a single parent per
specimen in the population.
Mutation. This method receives an agent, and re-
turns a slightly mutated agent. We added a random
Gaussian noise vector
−→
v ∼ N (0, σ
2
) to the DNN’s
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
146

parameter vector, where σ
2
(Mutation Power) is a hy-
perparameter.
Extract Elite. This method receives the population
and the matching fitness of each individual in the
population, and returns the generation’s elite. Be-
cause the environments are stochastic, we took the
elite candidates individuals with the highest fitness
and tested them against elite robustness more rollouts
(these were counted towards the algorithm’s training
steps). The agent with the highest average score in
these rollouts was chosen as the elite. Both elite can-
didates and elite robustness are hyperparameters.
Behavior Characteristic. This method receives a
trajectory and returns a vector (preferably shorter than
that of the trajectory) that represents an aspect of the
trajectory. Novelty is measured with respect to that
characteristic. The behavior characteristic is domain-
specific; we used the following in our experiments:
use the last observation vector of the trajectory, and
concatenate the last time-step (the length of the tra-
jectory chain) normalized by the maximal timestep al-
lowed in the environment.
Novelty Measure. This method receives the current
population—represented by their respective behavior
characteristics—and an archive of previous genera-
tions, and measures how novel each specimen of the
population is (with respect to the behavior charac-
teristics). We used the average distance from the k-
nearest-neighbors as a novelty measure, where k is a
hyperparameter.
Update Archive. This method updates the archive
to contain some representation of the current popula-
tion. Since we do not wish to store the entirety of the
evolution, we only store each individual of the popu-
lation with pr probability, where pr is a hyperparam-
eter.
The Code. is available at github.com/EyalSeg/ecrl.
4 EXPERIMENTS
4.1 Trials
A trial is an independent, complete run of the algo-
rithm in a specific environment.
When a generation finishes, the elite reported by
the algorithm is evaluated for another 100 validation
episodes. This evaluation is used for reporting pur-
poses only, and the algorithm does not get to use these
results; as such, they do not count towards the time-
step limit. The score of a trial is the highest validation
score of an elite (from any generation).
We created our own maze environment in Mujoco
(Todorov et al., 2012), in which we ran 40 trials of the
tested algorithms.
4.2 Hyperparameters
As with many optimization algorithms, evolutionary
algorithms require hyperparameters, and ours is no
exception. We used the same hyperparameters in all
algorithms (where applicable). Due to a shortage of
computational resources available to us, the values
for the hyperparameters were derived through limited
trial-and-error experimentation (in the future we plan
to perform a more thorough hyperparameter sweep,
resources permitting). Table 1 lists the full set of hy-
perparameters.
The network architecture—comprising two 256-
units linear layers and tanh activation—is that used
by (Such et al., 2017).
4.3 Mujoco Maze
We hypothesized that EyAL will perform better in
environments in which the reward itself can deceive
the agent vis-a-vis the objective; thus, greedily opti-
mizing the reward will lead to poor episodic rewards
overall. To test this we created a simple maze (Fig-
ure 1) in which going straight toward the exit will lead
to an obstacle. To circumvent this, the agent must
go back—away from the destination—which incurs a
penalty.
We tested the algorithms in this environment with
respect to two reward functions. In PointMazeDe-
ceptive, at every time step the agent receives a neg-
ative reward equal to the Euclidean distance from the
agent’s position to the destination. When the agent
gets to the exit it receives a positive reward of 10,000
points; thus, if the agent gets to the destination it will
have a positive episodic reward. In PointMazeSparse,
at every time step the agent receives a negative reward
of −1, and thus the episodic score will be the negative
of the number of time steps it took the agent to reach
the exit, or −500 if it did not escape.
The behavior characteristic for this environment is
defined as the last position the agent had been in.
Adaptive Combination of a Genetic Algorithm and Novelty Search for Deep Neuroevolution
147

Figure 1: Maze environment. The agent is the orange dot,
the destination is the red dot. Observe the obstacle creating
a pocket in between the initial position of the agent and the
destination.
Table 1: General hyperparameters. Some are represented
by a symbol, shown in parentheses.
Designation Value
DNN Hidden Layer Dimensions 256, 256
DNN Activation tanh
Mutation Power (σ
2
) 0.005
Population Size (M) 50 + 1
Truncation Size (T) 20
Elite Candidates 5
Elite Fitness Robustness 5
Novelty Archive Probability (pr) 0.01
Novelty K-Nearest Neighbors (K) 25
Exploration Growth Rate (α) See Table 2
Exploration Decay Rate (β) See Table 2
(Initial) Exploration Rate (γ) See Table 2
Training Steps See Table 2
Validation Episodes 100
Table 2: Environment-specific hyperparameters: α, β, γ,
and training steps.
Environment α β γ Steps
PointMazeSparse 0.1 0.1 0.75 5e
7
PointMazeDeceptive 0.1 0.1 0.75 5e
7
5 RESULTS
Comparing different evolutionary algorithms is often
not straightforward, and care must be taken to com-
pare in a fair manner (e.g., account for differences
in resources expended). Since our score reporting
is done at the end of each generation, the fitness-vs-
timestep curve is sparse—which makes aggregating
multiple runs complicated, as not all fitness reports
share the same timestep. To allow such an aggrega-
tion, we split the x-axis (time steps) into intervals,
and used “forward-fill” to populate the figure at these
interval points: by propagating results forward from
previous time steps, we ensure that at these inter-
val points the algorithm accounts for the previously
known best result. This method allows the compari-
son of all runs at the same points, enabling the plotting
of a fair mean and confidence bounds.
Figure 2 presents the results of our experiments in
our custom Mujoco environment.
6 DISCUSSION
While our computational resources were rather lim-
ited, allowing much smaller populations and far less
time than (Such et al., 2017), EyAL managed to
achieve good results.
In PointMazeSparse, the reward signal is very
sparse: for every time step the robot did not exit the
valley the agent gets a negative reward of -1. Thus,
until it finds a viable solution, the learner does not
receive any signal it can exploit. In this regard, a
specimen that is just one mutation away from find-
ing the exit is just as unfit as an agent that does not
even try to exit. This fact makes this problem hard
for eager-exploiters such as a GA. On the other hand,
when an agent gets to the exit once, any other solution
that finds the exit is no longer novel, which makes
it harder for NS to obtain a solution that gets to the
exit slightly faster. When the novelty-seeking niche of
EyAL finds the exit, the episodic reward increases—
and the exploiting niche increases in size. Thus, while
NS seeks new positions it has never been to (which
are not viable solutions), EyAL optimizes the solu-
tion it found—which explains why EyAL improves a
bit even after NS starts to plateau .
In PointMazeDeceptive, the reward signal de-
ceives the learner to run into the obstacle. For a GA,
any specimen that goes back from the obstacle and
then does not proceed straight down, will incur a neg-
ative penalty, and will not survive to the next gener-
ation. To escape the obstacle, a single random muta-
tion has to make the agent both go around the obstacle
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
148

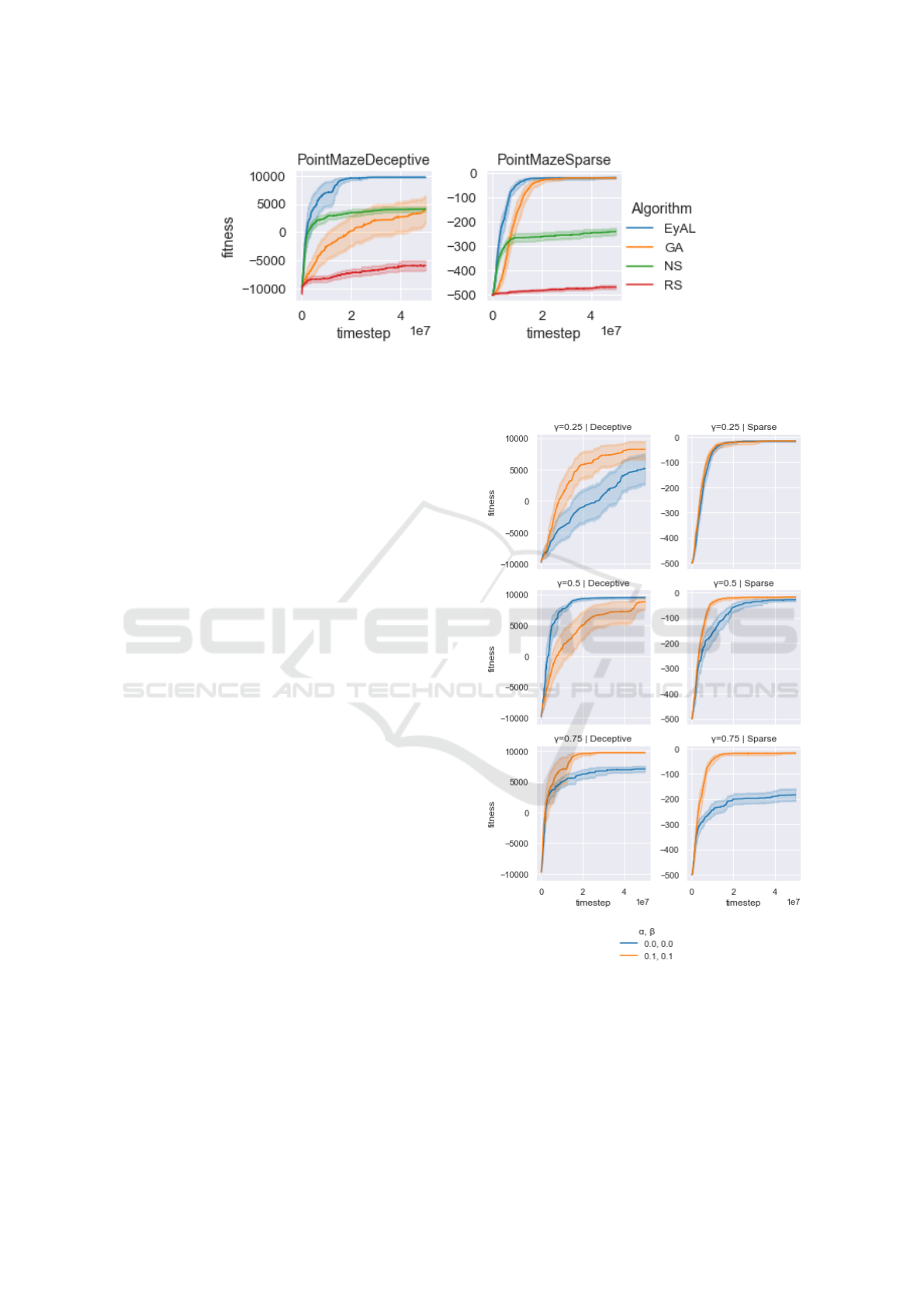
Figure 2: Comparison of EyAL, GA, NS, and Random Search (RS) in our custom Mujoco environment. Plots include
the mean of 40 trials, along with 95% confidence intervals. Since every generation takes a different number of time steps,
comparisons were made every 10,000 time steps, using forward-fill from previous generations.
and then go downwards. For NS, however, just go-
ing around the corner yields an immediate improve-
ment. But, when the destination is reached, NS has
a hard time improving it, because novelty lies in ex-
hausting other destinations. While it does take EyAL
slightly longer to find the destination (with respect to
NS), it optimizes much better when the destination is
found—which explains why EyAL keeps improving
after NS plateaus.
In Figure 3, the benefit of an adaptive γ can be
seen. In the deceptive case, the adaptive version is
best at most initial γ values tested, with the excep-
tion of one. In the sparse setting, the adaptive version
consistently improves the results—or at least does not
harm them.
One interesting finding is the difference between
the algorithms in the two PointMaze environments
tested. Unsurprisingly, NS is not affected by the
choice of reward function, as it does not try to op-
timize for it. On the other hand, GA suffers greatly
from the deceptive function. While EyAL does suf-
fer from deception, the effect of it is not as adverse as
it is for GA. In the sparse environment, EyAL learns
faster than GA but does not provide a better solution
overall. In the deceptive environment, EyAL—which
hybridizes GA and NS—provides a better solution
than either. We find this fact interesting, as adding
the under-performing GA to NS improves NS.
7 FUTURE WORK
Optimizing EyAL. The modular design of EyAL
allows for the replacement of many genetic opera-
tors, as mentioned in 3.5. Likewise, the underly-
ing exploring and exploiting algorithms can also be
modified with different flavours of GA (such as intro-
ducing fitness sharing (McKay, 2000), self-adaptive
mutation (Schwefel, 1981), or replaced altogether by
Figure 3: Comparison of an adaptive (α 6= 0, β 6= 0) and
an un-adaptive (α = 0 = β) Explore-Exploit learners. Plots
include the mean of 20 trials, along with 95% confidence
intervals.
algorithms such as Evolution Strategies or Surprise
Search. As the core idea of this paper was to explore
whether the dynamic hybridization of two algorithms
can result in a third, better algorithm—these ideas are
Adaptive Combination of a Genetic Algorithm and Novelty Search for Deep Neuroevolution
149

left for future work.
It should be mentioned that our implementation of
behaviour characteristic was naive, yet even with this
basic BC our technique yielded improvement over
both the standard GA and NS.
EyAL and Quality-diversity. Since we did not op-
timize EyAL, we left direct comparison to state-of-
the-art QD methods for future work.
It should be mentioned that the principles of QD
and of EyAL are not mutually exclusive. While QD
methods use a fixed number of niches, the adaptive-
ness of EyAL can be introduced to increase and de-
crease the number of cells, or to allocate additional
computational resources to more promising niches
at the expense of less promising niches. Likewise,
the local-competition principles of QD can be intro-
duced to EyAL by various methods of fitness sharing
(McKay, 2000).
While the global competition of EyAL has been
shown to be inferior to local competition in (Colas
et al., 2020), the adaptiveness of EyAL is yet to be
explored in this context. An algorithm that exploits
both of these traits would be interesting to see.
REFERENCES
Beyer, H.-G. and Schwefel, H.-P. (2002). Evolution strate-
gies – a comprehensive introduction. Natural comput-
ing, 1(1):3–52.
Coello Coello, C. (2006). Evolutionary multi-objective op-
timization: a historical view of the field. IEEE Com-
putational Intelligence Magazine, 1(1):28–36.
Colas, C., Madhavan, V., Huizinga, J., and Clune, J. (2020).
Scaling map-elites to deep neuroevolution. In Pro-
ceedings of the 2020 Genetic and Evolutionary Com-
putation Conference, pages 67–75.
Holland, J. H. (1992). Genetic algorithms. Scientific Amer-
ican, 267(1):66–73.
Jackson, E. C. and Daley, M. (2019). Novelty search for
deep reinforcement learning policy network weights
by action sequence edit metric distance. In Proceed-
ings of the Genetic and Evolutionary Computation
Conference Companion, pages 173–174.
Koza, J. R. et al. (1992). Evolution of subsumption using
genetic programming. In Proceedings of the first Eu-
ropean conference on artificial life, pages 110–119.
MIT Press Cambridge, MA, USA.
Lehman, J. and Stanley, K. O. (2008). Exploiting open-
endedness to solve problems through the search for
novelty. In Proceedings of the Eleventh International
Conference on Artificial Life (ALIFE), Cambridge,
MA. MIT Press.
Lehman, J. and Stanley, K. O. (2011). Evolving a diver-
sity of virtual creatures through novelty search and lo-
cal competition. In Proceedings of the 13th annual
conference on Genetic and evolutionary computation,
pages 211–218.
McKay, R. I. (2000). Fitness sharing in genetic program-
ming. In GECCO, pages 435–442.
Mouret, J.-B. and Clune, J. (2015). Illuminating
search spaces by mapping elites. arXiv preprint
arXiv:1504.04909.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,
Antiga, L., et al. (2019). PyTorch: An imperative
style, high-performance deep learning library. arXiv
preprint arXiv:1912.01703.
Rechenberg, I. (1989). Evolution strategy: Natures way of
optimization. In Optimization: Methods and appli-
cations, possibilities and limitations, pages 106–126.
Springer.
Salimans, T., Ho, J., Chen, X., Sidor, S., and Sutskever, I.
(2017). Evolution strategies as a scalable alternative
to reinforcement learning. arXiv:1703.03864.
Schwefel, H.-P. (1981). Numerical optimization of com-
puter models. John Wiley & Sons, Inc.
Sipper, M., Moore, J. H., and Urbanowicz, R. J. (2019a).
Solution and fitness evolution (SAFE): A study of
multiobjective problems. In 2019 IEEE Congress on
Evolutionary Computation (CEC), pages 1868–1874.
IEEE.
Sipper, M., Moore, J. H., and Urbanowicz, R. J. (2019b).
Solution and fitness evolution (SAFE): Coevolving
solutions and their objective functions. In European
Conference on Genetic Programming, pages 146–161.
Springer.
Stanley, K. O. and Miikkulainen, R. (2002). Evolving neu-
ral networks through augmenting topologies. Evolu-
tionary computation, 10(2):99–127.
Such, F. P., Madhavan, V., Conti, E., Lehman, J., Stanley,
K. O., and Clune, J. (2017). Deep neuroevolution: Ge-
netic algorithms are a competitive alternative for train-
ing deep neural networks for reinforcement learning.
arxiv.1712.06567.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-
ing: An Introduction. MIT press, 2nd edition.
Todorov, E., Erez, T., and Tassa, Y. (2012). Mujoco:
A physics engine for model-based control. In 2012
IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 5026–5033. IEEE.
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
150