SENN: Self-evolving Neural Network to Recognize Motor Imagery
Thought Patterns
Stuti Chug
a
and Vandana Agarwal
b
Department of Computer Science and Information Systems, BITS Pilani, Pilani Campus, India
Keywords:
Brain Computer Interface, Clustering, Radial Basis Function Neural Network, Particle Swarm Optimization.
Abstract:
The EEG-based motor imagery task classification has been a challenge for researchers due to the complex
nature of EEG data. Human thoughts are a complex combination of different body limb activations and it
is difficult to capture only one thought at a time. The data belonging to different motor imagery thought
classes are also not separable linearly. In this paper, a novel technique for efficient and improved motor
imagery task classification is proposed. Two major issues in motor imagery task classification of EEG data
are addressed - channel selection and radial basis function neural network centers. The channel selection
is posed as a combinatorial problem and an evolutionary nature-inspired algorithm PSOCS is proposed to
select the most informative and discriminative channels using the Particle Swarm Optimization algorithm.
The features are extracted using the selected channels and are subjected to classification. In this paper, a self-
evolving radial basis functions neural network (SENN) is proposed based on sub-clusters within each motor
imagery task class. The number, centers, and spread of hidden neurons are obtained by the k-means clustering
algorithm. The proposed algorithm is validated using the benchmarked datasets BCI Competition IV 2a and
BCI Competition IV 2b data set. The proposed technique outperforms some of the existing techniques and
classifies the motor imagery tasks efficiently.
1 INTRODUCTION
The thought patterns are captured using a vari-
ety of sensors electroencephalogram (EEG), func-
tional magnetic resonance imaging (fMRI), magne-
toencephalography (MEG), and electrocorticography
(ECoG). These signals are non-stationary and suffer
due to multiple overlapping thoughts. A human with
a neuromuscular disorder is provided assistance using
a Brain-Computer Interface (BCI), in which the com-
putational model recognizes the thought of imagina-
tion of movement of the body limb and translates the
output to the control command such as movement of
the prosthetic limb and robotic arms. The signals are
captured using multiple receiving units, called chan-
nels of one or more types. Multiple units of these
sensors are placed in different regions of the skull to
capture the signals in the nearest portions of the brain.
It becomes very difficult for a BCI to identify the best
channels. Using a channel selection algorithm aims to
enhance the classification accuracy by reducing over-
a
https://orcid.org/0000-0002-9380-3923
b
https://orcid.org/0000-0002-8942-5114
fitting issues and reducing computational complexity
while using EEG data. Channel selection is consid-
ered part of the feature extraction process.
The channels are required to be selected in the
most appropriate way so as to discriminate between
thoughts resulting in the most correct recognition of
the motor imagery thought patterns. Therefore, chan-
nel selection is viewed as a combinatorial problem
that is solved using an optimization technique. Re-
searchers have shown an interest in exploring the po-
tential of Particle Swarm Optimization (PSO) in solv-
ing the channel selection problem. Binary quantum
behaved particle swarm optimization (QBPSO) us-
ing Common Spatial Pattern (CSP), Fractional Order
Darwinian Particle Swarm Optimization (FODPSO)
algorithm and Binary Particle Swarm Optimization
(BPSO) have been proposed in the literature. (Zhang
and Wei, 2019; Sheoran and Saini, 2022; Kim et al.,
2012). Other works include the Sequential Floating
Forward Selection (SFFS) algorithm and Cohen’s d
effect size CSP (E-CSP) algorithm using z-score for
channel selection (Baig et al., 2020; Qiu et al., 2016;
Das and Suresh, 2015; Zhou et al., 2019).
Once the channels are selected, the most appro-
Chug, S. and Agarwal, V.
SENN: Self-evolving Neural Network to Recognize Motor Imagery Thought Patterns.
DOI: 10.5220/0011526800003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 349-358
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
349

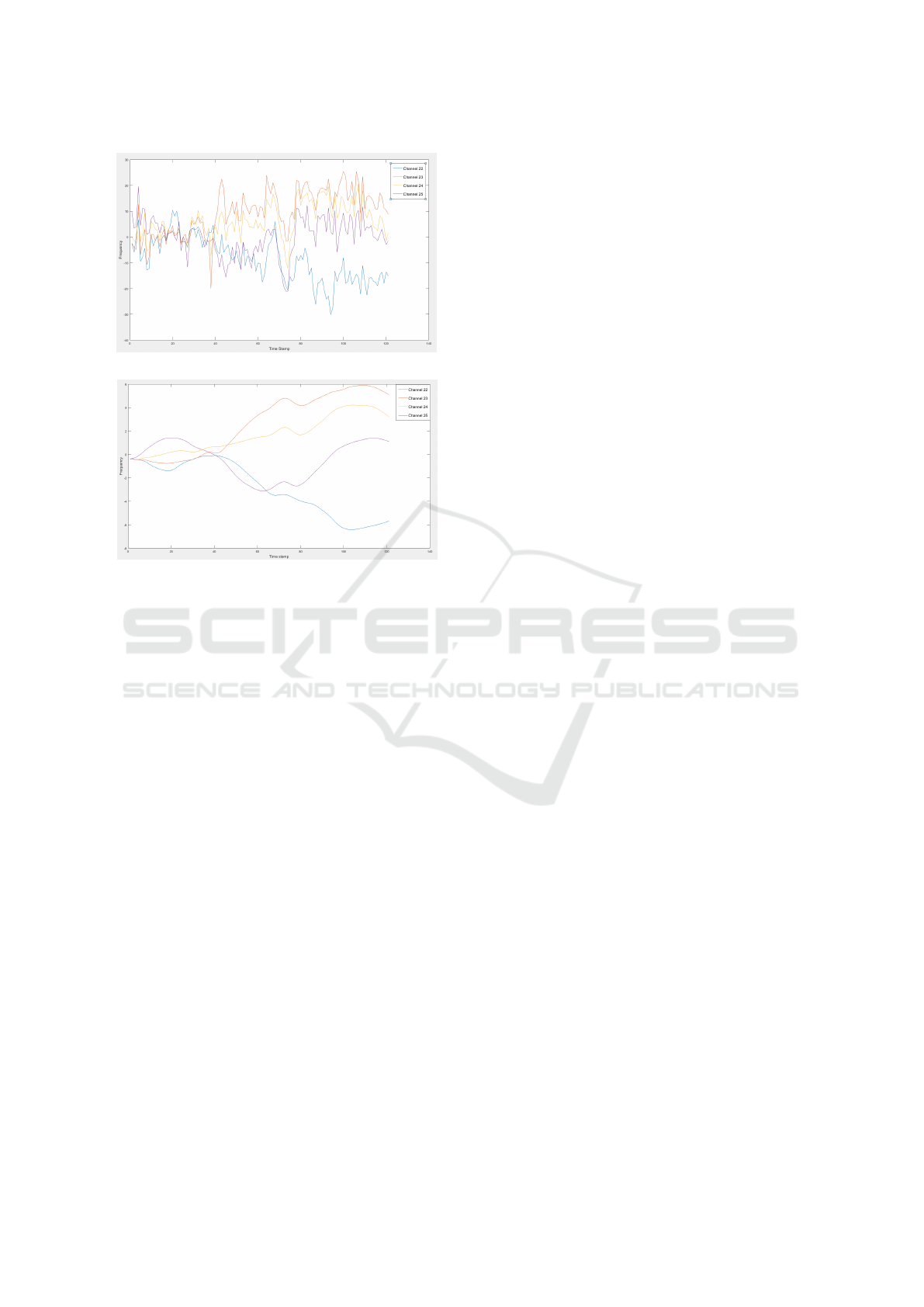
(a) Raw EEG signals.
(b) After preprocessing and standardization.
Figure 1: Raw, Preprocessed and standardized signals rep-
resentation of Subject 5 of class 2 on BCI competition IV
2a dataset.
priate features are also extracted and subjected to the
classification model. The classification model repre-
sents the decision hyperplane and needs to have the
best parameters defining that. The selected features
from each training data pair (x, y) form d-dimensional
feature vectors x =< x
1
,x
2
,x
3
,...,x
d
>. The raw EEG
data from selected channels are subjected to stan-
dardization to overcome the non-stationary behav-
ior of the signals (Ang et al., 2012). The effect of
preprocessing using standardization is depicted for a
few channels in Figure 1. The preprocessed data is
then used for feature extraction using various meth-
ods such as Fourier transform, Discrete Wavelet trans-
forms (DWT), and Haar wavelet (Nicolas-Alonso and
Gomez-Gil, 2012).
Various classification algorithms are used for mo-
tor imagery task classification, such as linear clas-
sifier, nonlinear Bayesian classifier, nearest neigh-
bor classifier, support vector machines (SVM), ra-
dial basis function neural network (RBFNN), deep
neural network, and combination of classifiers (Baig
et al., 2020; Nicolas-Alonso and Gomez-Gil, 2012;
Davoudi et al., 2017; Agarwal, 2019; Alam et al.,
2021; Bhatti et al., 2019; Zhao et al., 2020). Common
spatial pattern (CSP) algorithm was also used in EEG
classification (Zhang and Eskandarian, 2020; Miao
et al., 2017; Ang et al., 2012). A pre-processing filter
approach Subject Specific Multivariate EMD Filter
(SS-MEMDBF) has been proposed where the filters
based on MEMD reduce the non-stationaries caused
by inter and intra-subject differences, thus obtaining
enhanced EEG signals (Xie et al., 2016). For classifi-
cation, Riemannian mean computation for all classes
was used by the authors (Ko et al., 2018).
Of various classification models such as a k-
nearest neighbor, support vector machines, and neu-
ral networks, the neural network has been used ef-
fectively in a variety of recognition tasks due to their
capability to handle nonlinearity in training data ef-
fectively. The radial basis function neural network
(RBFNN) is said to have the best approximation abil-
ity and is simple in its architecture with only one hid-
den layer (Haykin, 2005). The EEG data is highly
complex and poses challenges in identifying the num-
ber of neurons in the hidden layer. Particle Swarm
Optimization (PSO) has been used in different recog-
nition tasks and is said to converge to the optimal so-
lution provided the algorithm parameters are carefully
chosen.
In this paper, the two main problems are ad-
dressed, channel selection and RBFNN design. A
population of particles is initially randomly generated
and moved in the search space using a guided heuris-
tic, where each particle not only remembers its own
best solution found (known as the cognitive part), also
each particle knows the position in the search space
which is the best among all particles (this is known
as social intelligence). While many existing tech-
niques tend to display a greedy approach of optimiza-
tion leading to suboptimal solutions, PSO provides a
mechanism to explore the search space effectively and
to exploit the neighborhood. We are motivated by the
computational efficiency of particle swarm optimiza-
tion (PSO) and use it to address the issues appropri-
ately.
Our Contribution in this Paper: In this paper,
we propose a novel approach to classify the complex
EEG signals for four motor imagery classes. The ap-
proach uses PSO to select the most informative EEG
channels. The selected channels are used to extract
Haar features. The proposed classifier design has self-
evolving hidden layer where the number and centers
of neurons are computed using K-Means and PSO al-
gorithm. This algorithm finds sub-clusters with sub-
jective similarities within each class. Based on the
number of natural clusters the centers are computed.
This paper is organized as follows: Section 2
presents the basic framework and the proposed algo-
rithm, section 3 describes the experimental part, sec-
tion 4 discusses the results and section 5 presents the
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
350

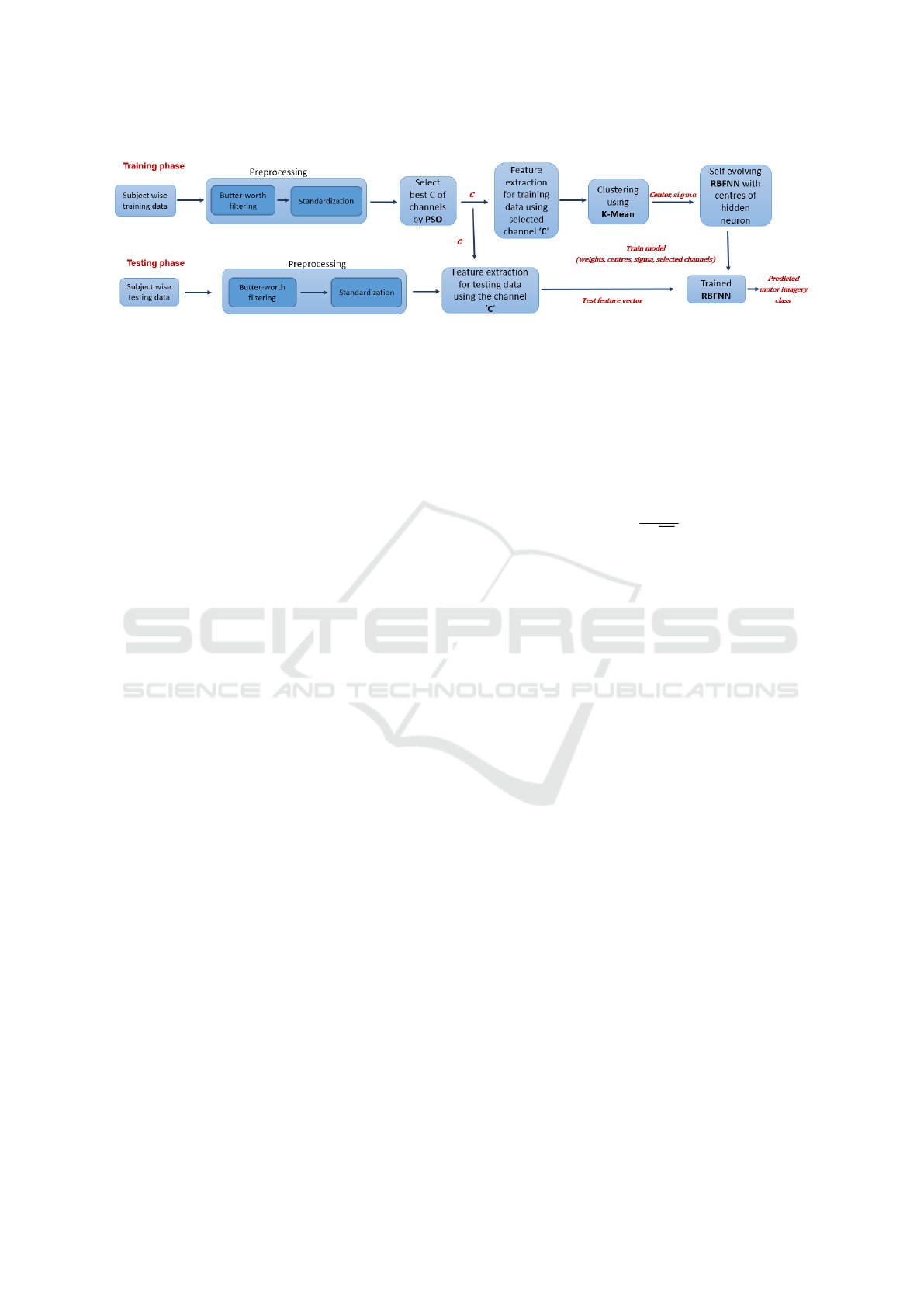
Figure 2: Flow diagram of proposed model.
conclusion and future work.
2 PROPOSED ALGORITHM
In this study, we propose a technique that uses PSO
algorithm to capture the most informative channels
from a large channel set. In this technique, the clas-
sification is done by self-evolving radial basis neural
network. A self-evolving radial basis functions neu-
ral network is proposed based on sub-clusters within
each motor imagery task class. The k-means and PSO
clustering algorithms obtains the number, centers, and
spread of hidden neurons.
In the proposed algorithm, first, we filter out ar-
tifacts from raw EEG signals with the help of But-
ter worth filter with a frequency cutoff between 4-
38HZ after extracting appropriate features from pre-
possessing data. Then class-wise K-Means clustering
is applied on selected features that provide center and
spread (sigma) value for each neuron. The RBFNN
model is generated, and each hidden layer neuron has
its center and sigma value. Finally, the RBFNN model
is used for classification based on selected features.
Figure 2 represents the block diagram of the proposed
approach.
2.1 Prepossessing
EEG Brain signals are sensitive to noise, and remov-
ing artifacts from original signals is essential. Band-
pass filtering and standardization are required before
feeding the raw data into our model (Ang et al., 2012).
As shown in Figure 1(a), the raw signal has high
distortion, but after filtering out the artifacts using
the Butterworth filter, signals are relatively smooth in
[Figure 1(b)]. Based on(Ang et al., 2012), the Butter-
worth filter is engaged to filter out disentangle senso-
rimotor rhythms. Our model used a Butterworth filter
ranging from (4-38 Hz) because it contains the most
relevant information in motor imagery applications.
2.2 Standardization
Exponential moving standardization is employed to
reduce non-stationary fluctuations (Ang et al., 2012).
Electrodes standardization was used to standardize
the band-pass filter data. The mathematical formu-
lation is defined below:
s
′
t
=
s
t
− µ
t
p
σ
t
2
(1)
µ
t
= (1 − α)s
t
+ αµ
t−1
(2)
σ
2
t
= (1 − α)(s
t
− µ
t
)
2
+ ασ
2
t−1
(3)
where s
′
t
and s
t
are standardized signal and input sig-
nal at time t. µ
t
and σ
2
t
denote mean and variance
value of each electrode in a trial. The α is a parameter
known as the decay factor. Standardization removes
the occasional movements of the signals and protects
each trial’s trend from the past signal.
2.3 Channel Selection based on Particle
Swarm Optimization
Particle swarm optimization (PSO) is an optimiza-
tion algorithm based on animals/birds’ behavior.
In the PSO algorithm, swarm particles search for
food in a cooperative way, and each particle in
the swarm learns from its experience and another
particle experience for updating the search pattern
to find the food. PSO is a popular and effective
global search technique. It is an appropriate al-
gorithm for addressing feature selection problems
for the following reasons: easy feature encoding,
global search capability, reasonable computation-
ally, fewer parameters, and easier implementation.
PSO algorithm finds optimal solution from a multi
dimensional search space. There are 25 (q say)
channels in BCI competition IV 2a dataset of which
only a few are significant in our application. The
problem of finding p (say) best channels from q chan-
nels is an exponentially high combinatorial problem
SENN: Self-evolving Neural Network to Recognize Motor Imagery Thought Patterns
351

Algorithm 1: PSOCS.
Input: feature matrix
Output: Optimal channel set
Initalize:
P
i
,velo
i
,max iteration,Gbest, Pbest, c
1
c
2
Generate random particles (p) and each
particle range between [1 25]
for i=1 to no of particles do
calculate f itness f unction f it
i
updatePbest,Gbest
for K=1 to max iteration do
for each particle i do
r
1
= Generaterandom(0,1)
r
2
= Generaterandom(0,1)
// Random number uniformly
distributed between 0 and
1
w =

w
max
−
w
max
−w
min
I
max
∗ i

for each particle’s dimension j do
velocity part = w ∗ velo
k
i j
cognitive part =
c
1
r
1
(Pbest
k
i j
− P
k
i j
)
social part = c
2
r
2
(Gbest
k
j
− P
k
i j
)
velo
k+1
i j
= velocity part +
cognitive part + sociaL part
temp = P
k
i j
+ velo
k+1
i j
// Rounded values
if (temp <= 25&&temp >= 1)
then
P
k+1
i j
= P
k
i j
+ velo
k+1
i j
Calculate f itness f unction f it
J
U pdatePbest,Gbest
Optimal channel set = Gbest channels
and requires exponential time. In this paper, we use
PSO for selecting an optimal number of channels for
classification as described in Algorithm 1. In poly-
nomial time the PSO algorithm starts with initializa-
tion of a population of particles randomly in channel
search space. Every particle Particle
i
{i = 1, 2, ...K}
has properties such as P
i
, velo
i
and Pbest, where P
i
is the position with velocity velo
i
and a memory of
personal best position Pbest. The global best (Gbest)
value defines the best particle found from all the parti-
cles. The population is a collection of particles where
each particle represents the selected channel set, and
each particle ranges between 1 and 25. The particle
velocity (velo) is updated by eqn(4), which is a com-
bination of three part namely: momentum (w∗ velo
t
i j
)
where w is weight inertia, velo
t
i j
is memory of previ-
ous t direction, (2) term is the cognitive part where it
quantifies the performance relative to its past experi-
ence and (3) term is the social part where it quantifies
the performance relative to its neighbour.
velo
k+1
i j
= w ∗ velo
k
i j
+ c
1
r
1
(Pbest
k
i j
− P
k
i j
) + c
2
r
2
(Gbest
k
− P
k
i j
)
(4)
Where k represents the previous iteration and k+1 is
the current iteration. The right hand side of eqn(4)
uses the values computed in the k
th
iteration and the
left hand side uses all to modify velocity of the parti-
cle in k + 1
th
iteration. Position of particle P
i j
is up-
dated at k + 1
th
iteration as given below
P
k+1
i j
= P
k
i j
+ velo
k+1
i j
(5)
where w is weight inertia that is calculated by eqn(6).
The acceleration coefficient c
1
and c
2
are set to range
between 0 and 1. The parameters r
1
, r
2
are random
numbers uniformly distributed between 0 and 1. I
max
and I are the maximum and the current iteration, and
w
max
=0.9 and w
min
=0.4 are the initial and final value
of weight inertia.
w = w
max
−

w
max
− w
min
I
max
∗ i

(6)
Each particle is designed to represent a vector of num-
bers from 1 to 25. They are randomly generated initial
and later it moves to a position representative another
set of channels. The particle can change the number
of unique channels while it moves in the 25 dimen-
sional space. The fitness function for channel selec-
tion problem is taken as the accuracy of classification.
2.4 Clustering
Clustering is the process of dividing a set of data
points into groups so that data points in the same
group are more similar than data points in other
groups. In other words, the goal is to separate groups
with similar characteristics and assign them to clus-
ters. K-means clustering is simpler and has a lin-
ear time complexity with data size (less expensive).
The class-wise K-Means Clustering Algorithm starts
by initializing the k number of centers randomly and
assign the data point x to one of the K subsets in p
th
class. It then uses a procedure to end up with a par-
tition of the data points into K disjoint clusters clust
in p
th
class. Then we combine all class cluster data
points T and check that the sum of the distance of
each cluster member to its cluster center should be
minimized.
J = min
k
∑
i=1
∑
dεclust
j



X
d
−C
j



(7)
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
352

Algorithm 2: SENN.
Input: Feature matrix[features extracted
using channels selected by PSOCS
(Algorithm 1)], class label
Class cluster no = n;
// Create Class cluster no random
center class wise
for i=1 to no. of classes do
class cluster= class i
th
training data;
for j=1 to Class cluster no do
Pos= random position in class cluster
center = class cluster(Pos)
center= Concatenate all class cluster’s
center
cluster info=class information of all
cluster
while True do
for i=1 to no. of training sample do
class i cluster = all center whose
class is same as class label i
for j=1 to no. of class i cluster do
Dist
j
=
distance(x data
i
,class i cluster
j
)
Min dist = min(Dist)
cluster index=cluster index whose
distance is minimum
count(cluster index) = count + 1
sum(cluster index) =
sum(cluster index)+ x data(i)
cluster no = cluster index
// find new center
for i=1 to center do
// only consider those
cluster whose count is not
equal to zero
if count ̸= 0 then
mean(i) = sum(i)/count(i)
center new = mean
// Sigma value
for i=1 to center do
for j=1 to i
th
cluster do
σ
i
=
1
p
∑



cluster
i
j
−Center
i



2
// stopping condition
if center new==center then
break;
center = center new
for i=1 to no of training sample do
for j=1 to no of center do
φ
j
(x) = e
−
∥
x data
i
−center
j
∥
2
2σ
2
j
Output: φ
where C
j
is the mean of the data points in set clust
j
given by
C
j
=
1
T
j
∑
dεclust
j
X
d
(8)
Iteratively searching the closest mean C
j
to each data
point x
p
reallocating and the data points to the associ-
ated clusters clust
j
, and then recomputing the cluster
means C
j
. The K-means clustering terminates when
no data points change their cluster from one to an-
other. Multiple runs can be carried out to find the lo-
cal minimum with the lowest J.
2.5 Self Evolving Radial Basis
Functions Neural Network Design
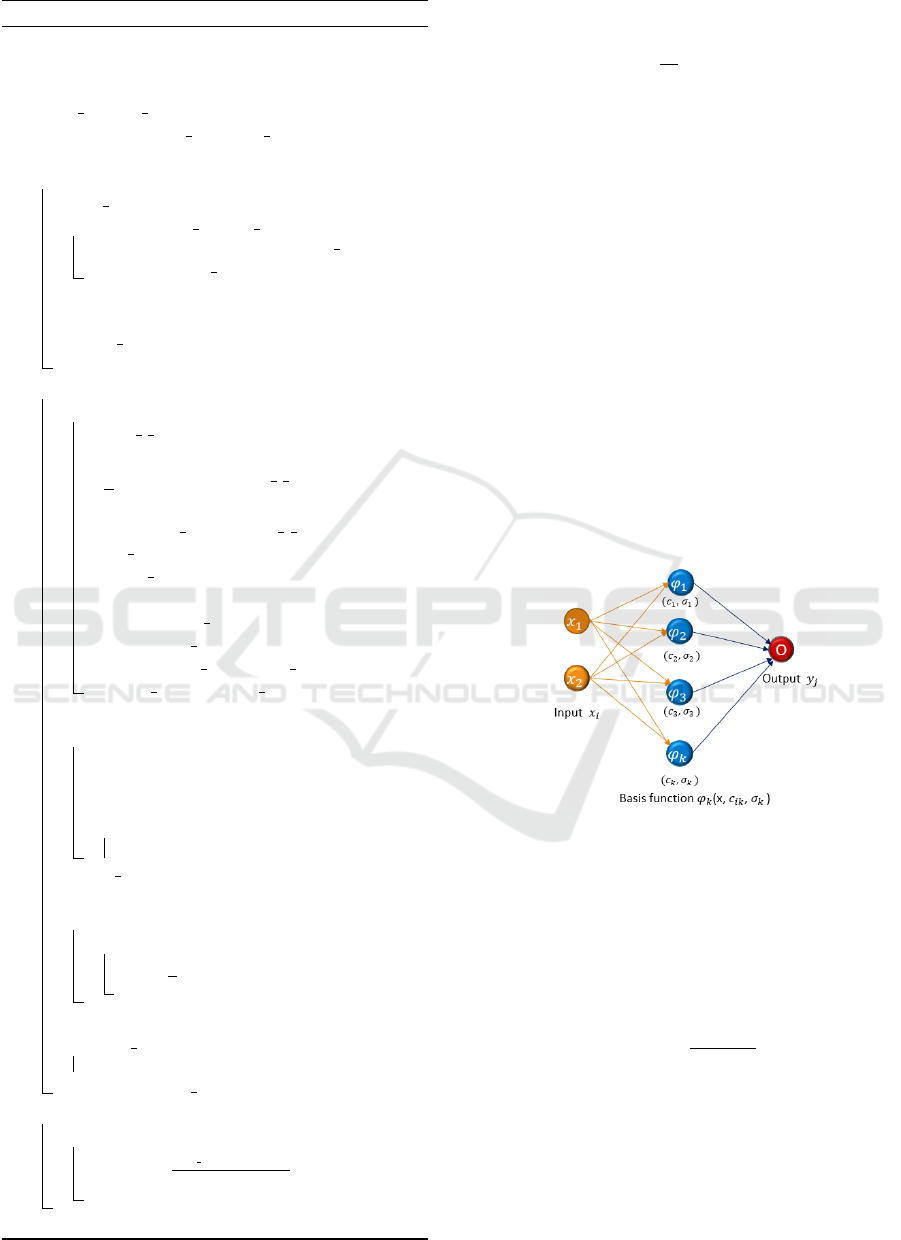
RBFNN is a single hidden layer network with an in-
put layer fully connected to a hidden layer. Then, the
output of the hidden layer performs a weighted sum
of input features to get the output. Unlike the Multi
Layer Perceptron (MLP), calculating weights for lay-
ers in RBFNN is very different; even the interpreta-
tion role of hidden layer nodes is easy. The RBFNN
topological diagram is explained in Figure 3. The hid-
Figure 3: RBFNN structure.
den layer to the output layer works in the same way
as feed-forward MLP, with the sum of the weighted
hidden unit activation given the output unit activa-
tion by eqn(10). The hidden unit activation functions
are given by the basis function φ(x, c
j
,σ
j
), which de-
pends on the center, sigma and the input data. The
mathematical form of RBF Gaussian function
φ
j
(x) = e
−
∥
x
i
−c
j
∥
2
2σ
2
(9)
y
j
(x) =
k
∑
i=1
w
ji
φ
i
(x)) (10)
The sigma σ values are defined, usually with the p-
closest neighbor method which alters the values to
achieve overlapping of the response of every hidden
SENN: Self-evolving Neural Network to Recognize Motor Imagery Thought Patterns
353

and its neighboring unit. The function used is:
σ
j
=
1
p
∑


X
i
−C
j


2
(11)
where c
j
the p-closest neighbor of X
i
To explain the working flow of RBFNN, Suppose
we have X data set with N samples and D dimen-
sion (x data
i
,y
i
) where x data
i
is input data, and y
i
is its class label. The output of the hidden unit ac-
tivation function φ
j
computed by eqn(9) is based on
the distance between x data
i
and center
j
. The spread
of cluster is also used in the formation of φ
j
. The
weights between the hidden and output layers are
calculated using Moore-Penrose generalized pseudo-
inverse. Then, the output of the network is calculated
using eqn(10).
2.5.1 Center Generation
Algorithm 2 discusses the implementation of self-
evolving neural network (SENN) which finds cen-
ters of hidden neurons for RBFNN. These centers are
based on the underlying structure of EEG data which
uses K-Means clustering. Also, we experimented the
evolution of RBFNN using the PSO algorithm to pro-
duce classwise centres. At first, random centres were
chosen, and each center’s dimensions were within a
dimension-wise range. Then the particles move us-
ing eqn(4). The center dimension search space is c ∗d
where c is the number of centers and d is the number
of dimensions. A particle P
i
is moved by its velocity
Velo
i
in the search space at time t is represented as P
t
i
.
Figure 4: PSO convergence with respect to very small value
of c1 on Subject 5 BCI competition IV datasetIIa.
The position of centers is updated according to
the global and local best in c ∗ d search space where
Figure 5: PSO convergence with respect to very small value
of c2 on Subject 5 BCI competition IV datasetIIa.
each row represents positions of sub-cluster centers.
Let there be a population P of particles that search
exploring and exploiting through their interactions.
The mathamatical formation of velocity movement
towards minima shown in eqn(4). The step size taken
by particles is 0.0001 for C
1
and C
2
. Both algorithms
employ the same goal function for convergence as il-
lustrated in eqn(7). We already covered K-Means cen-
tres generation part in section 2.4.
3 DATASET AND
EXPERIMENTAL DETAILS
3.1 Dataset Description
BCI Competition IV dataset IIa has four classes of
motor imagery tasks. The EEG signals were collected
from nine volunteers for four classes: left hand, right
hand, tongue, and feet movement. Two sessions for
motor imagery tasks were recorded from each sub-
ject, one for training and the other for testing. Each
session contains 288 trials recorded with 25 channels
(22 EEG Channels and 3 EOG channels). These chan-
nels are associated with right and left-hand motor im-
agery areas.
BCI Competition IV dataset IIb has two classes
of motor imagery tasks. The EEG signals were col-
lected from nine volunteers for two classes: left-hand
and right-hand movements. Two sessions of motor
imagery tasks were recorded from each subject, one
for training and the other for testing. Each session
contains 120 trials of data recorded with 3 channels
(http://www.bbci.de /competition/iv/).
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
354

We categorized the BCI competition data set into
two phases: the subject dependent dataset and the
subject independent dataset. In the dependent dataset,
data is used subject-wise, where each subject has
training and testing data separately for each motor im-
agery class. There are nine subjects in the BCI com-
petition IV IIa dataset, so we train the model subject
wise and test its performance accordingly on the test-
ing dataset.
For validating our algorithm on the subject-
independent dataset, we merge all subject’s training
data into one set and train the model. The testing
is done on combined testing data. We do not know
about the subject specification during training and
testing in the independent phase. In the dependent
dataset phase, the model’s training is subject wise, but
model training is subject-independent in the indepen-
dent dataset phase.
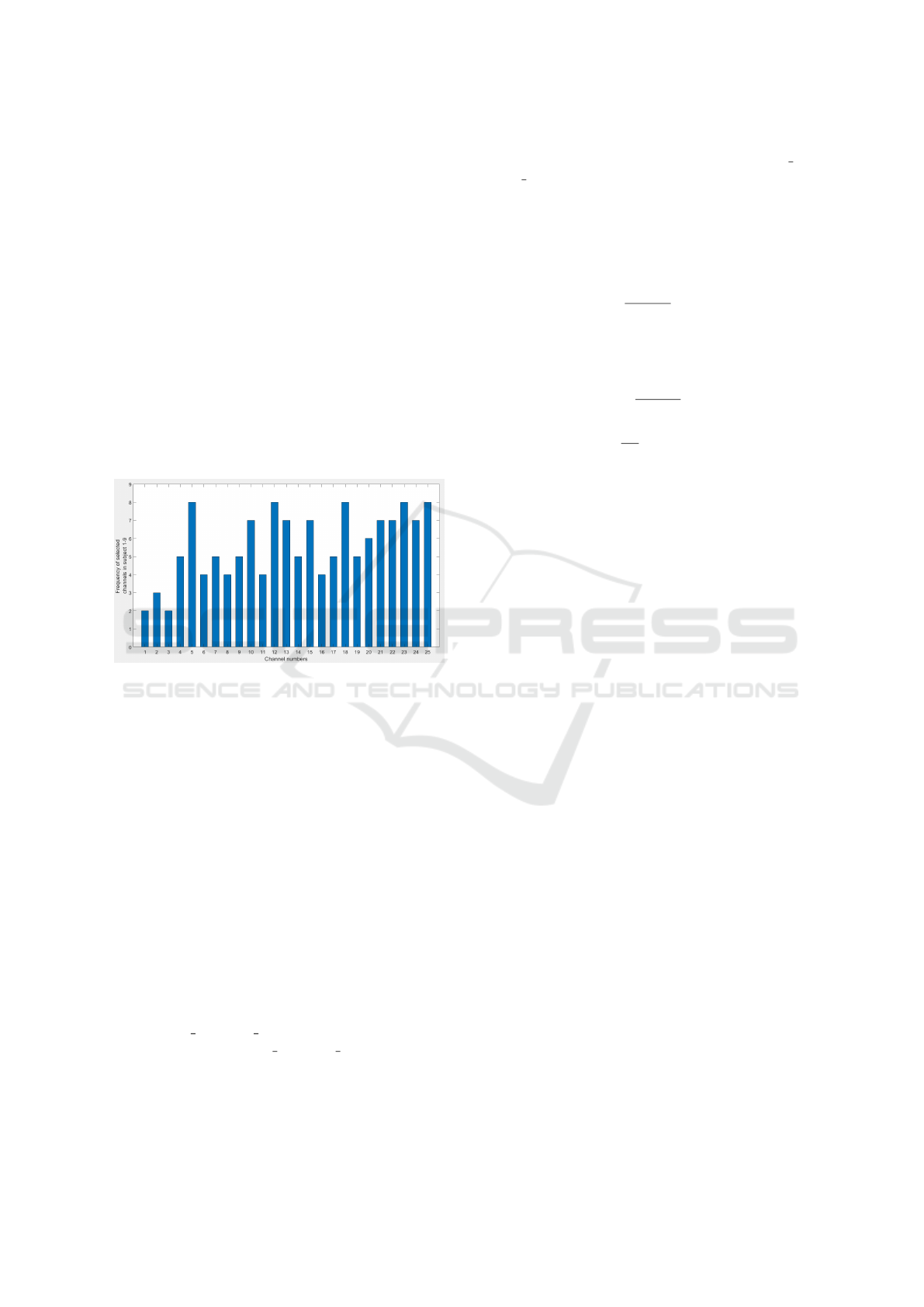
Figure 6: Number of times channel comes in selected chan-
nels set from subject 1-9 in BCI competition IV IIa dataset
[Channels 6,12,18,23 and 25 are significant for 8 out of 9
subjects].
3.2 Experiment Evaluation
The performance of the proposed algorithm is eval-
uated on BCI Competition IV datasets IIa and IIb,
as discussed above. The BCI Competition IV IIa
dataset has nine subjects, as is mentioned above, and
each subject data partitioned into training and testing.
We train the model on the training dataset and vali-
date the accuracy of the testing dataset. We find the
best channels by using PSOCS; the population size of
PSOCS is 20, and parameters c1 c2 are shown in Ta-
ble I; for all subjects. Features were extracted using
Haar wavelet with parameters n=5 and m=4 (where n
and m are decomposition levels) from selected chan-
nels on the training dataset. We pass the data to
the RBFNN K-Means classwise classifier for classi-
fication. In the RBFNN K-Means classwise classi-
fier, first, we grouped similar thought patterns into
sub-clusters and generated their center and spread
values. We pass center and spread parameter to
RBFNN model for classification. In the RBFNN K-
Means classwise model, we start with k equal to the
number of samples in the class, and at each iteration,
we remove clusters with no single point. Two perfor-
mance measures were used to evaluate the proposed
algorithm; cohen’s kappa coefficient(k) and accuracy
(Acc). The accuracy (Acc) was computed as the ratio.
Acc =
∑
n
t=1
n
t
1
∑
n
t=1
n
t
2
∗ 100 (12)
Cohen’s kappa coefficient given below is used for
evaluating the performance of the proposed algo-
rithm.
κ =
P
o
− P
a
1 − P
a
(13)
P
a
=
1
N
2
n
∑
t=1
n
t
1
∗ n
t
2
(14)
where, P
o
and P
a
represent observed agreement and
chance agreement on test samples respectively. N is
the total number of test samples, n is the total number
of classes, n
t
1
is the total number of samples predicted
to be belonging to class t and n
t
2
is the total number of
samples from actual class t.The proposed algorithm
was implemented using MATLAB R2020b and all ex-
periments were performed on Intel(R) Core(TM) i5-
4590 CPU Processor(3.30GHz).
4 RESULTS AND DISCUSSION
In this section, we discuss the results of the proposed
algorithm validates on datasets IIa and IIb from the
BCI Competitions IV. (i) Analysis of PSOCS() algo-
rithm: The PSOCS method was used to choose the
best channels out of 25 channels, with the parame-
ters c
1
and c
2
tuned between 0.0001 and 10. To ex-
plore the search space, the values of c
1
is varied from
0.0001 to 10 in multiples of 10 [Figure 4]. The con-
vergence of the proposed PSOCS was investigated for
subject 5 for 20 iterations. In algorithm this experi-
ment, a population size of 20 particles was used. It
is observed that the best accuracy of 85.5% is ob-
tained with c
1
= 0.0001. Figure 5 depicts the same
experiment for dataset IV IIa and gives an accuracy
of 79.8% with c
1
= 0.001.
Subject-wise parameters and channel details are
present in Table 1. For each subject, the best channels
were obtained. In order to understand the significance
of each channel across all 9 subjects, we computed
the total number of subjects where a channel was se-
lected. This number is plotted on y-axis in Figure 6.
Channels such as 5,12,18,24 and 25 were selected by
our algorithm for 8 (out of 9 subjects) emphasizing
SENN: Self-evolving Neural Network to Recognize Motor Imagery Thought Patterns
355

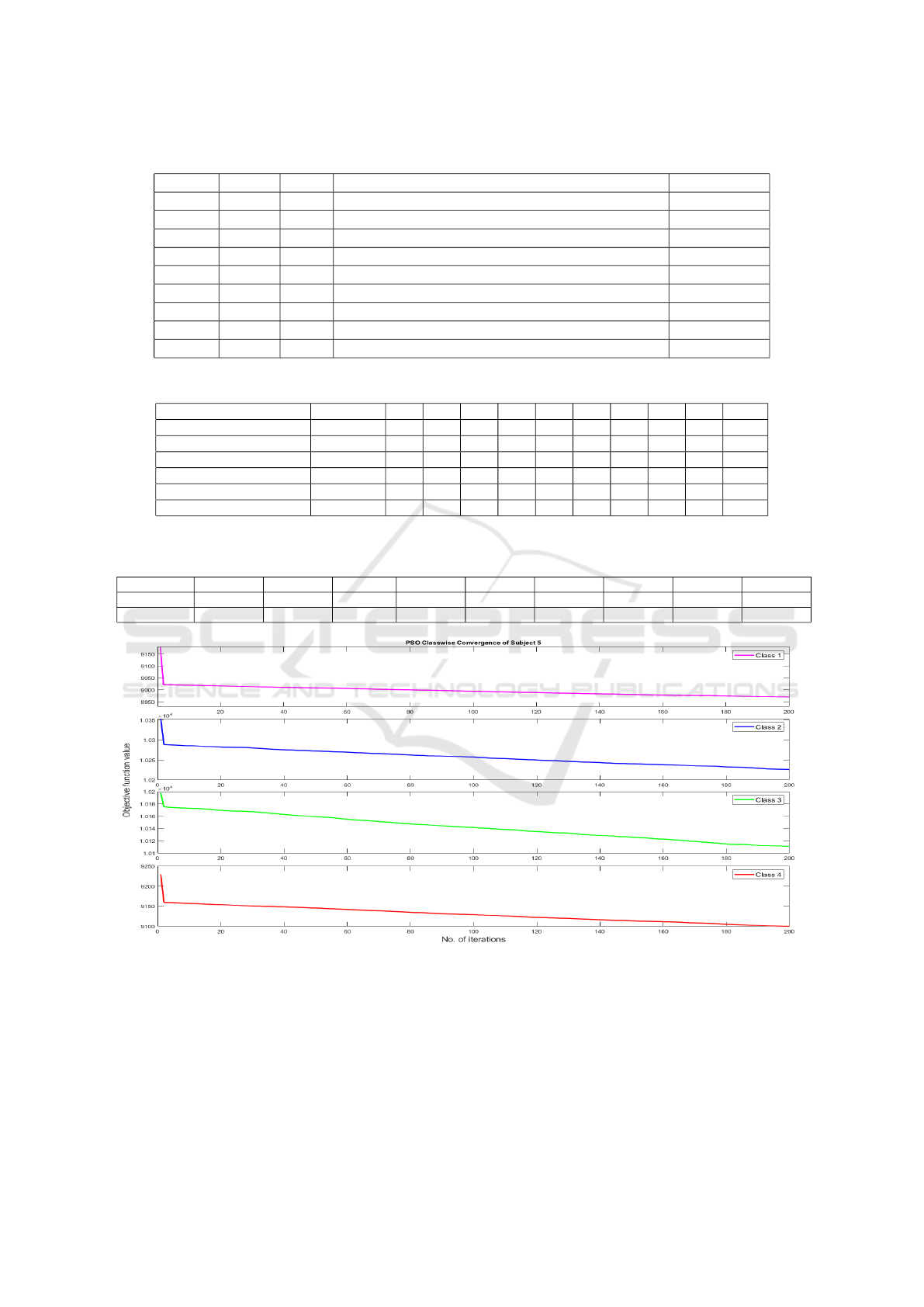
Table 1: Parameters and channel details of every subject of BCI competition IV IIa dataset using PSOCS().
Subject C1 C2 Channels Accuracy(%)
Sub 1 0.0001 0.01 3 5 7 13 14 15 16 17 20 21 22 24 25 54.51±4.06
Sub 2 0.0001 0.001 4 5 6 8 10 11 12 13 14 15 18 21 23 24 25 49.65±3.12
Sub 3 0.01 0.1 5 7 8 9 10 11 12 14 16 18 19 21 22 23 25 59.13±2.51
Sub 4 0.001 0.1 4 5 9 10 12 13 15 17 18 19 20 22 23 24 25 53.48±3.96
Sub 5 0.0001 0.001 1 4 5 6 7 11 12 13 18 19 20 21 23 24 25 72.86±2.96
Sub 6 0.01 0.1 3 4 5 6 8 9 10 12 13 14 15 16 18 19 20 22 23 24 25 50.45±4.23
Sub 7 1 0.01 2 5 9 10 12 13 15 17 18 21 22 23 25 73.00±3.22
Sub 8 0.01 0.01 4 5 6 7 8 10 12 13 15 17 18 19 20 21 22 23 24 25 67.40±2.86
Sub 9 0.001 0.1 2 7 9 10 11 12 14 15 16 17 18 20 21 22 23 24 55.25±4.02
Table 2: Kappa values of the proposed PSOCS() algorithm and existing approaches for BCI competition IV IIa dataset.
Study Approach 1 2 3 4 5 6 7 8 9 Mean
(Xie et al., 2016) TSSM+LDA 0.77 0.33 0.77 0.51 0.35 0.36 0.71 0.72 0.83 0.59
(Miao et al., 2017) DSFTP 0.63 0.43 0.74 0.54 0.19 0.26 0.63 0.62 0.69 0.53
(Zhang and Eskandarian, 2020) TFCSP 0.62 0.36 0.76 0.40 0.29 0.34 0.59 0.57 0.62 0.51
(Ko et al., 2018) RSTNN 0.69 0.29 0.68 0.34 0.09 0.30 0.57 0.49 0.56 0.45
(Ang et al., 2012) FBCSP 0.68 0.42 0.75 0.48 0.40 0.27 0.77 0.75 0.61 0.57
Proposed Algorithm 0.58 0.49 0.57 0.52 0.72 0.48 0.74 0.67 0.54 0.59
Table 3: Accuracy and Kappa values for all subject on BCI competition IV IIb dataset using selected channels obtained by
PSOCS().
Subject Sub1 Sub2 Sub3 Sub4 Sub5 Sub6 Sub7 Sub8 Sub9
Accuracy (%) 52.12±2.16 58.37±3.56 58.7±5.86 52.13±4.77 73.63±2.34 53.78±4.35 49.14±3.06 59.13±4.06 58.37±2.98
Kappa 0.44±0.02 0.45±0.03 0.49±0.04 0.39±0.04 0.64±0.02 0.44±0.05 0.35±0.03 0.49±0.04 0.46±0.03
Figure 7: Convergence of PSOCS() algorithm on subject 5.
their importance in thought classification. The com-
parative analysis with previous studies of BCI compe-
tition IV dataset IIa shows that the proposed algorithm
outperforms some of the existing techniques [Table
2]. Table 3 summarises the performance of our algo-
rithm in terms of accuracy and kappa value of all sub-
jects with all channels of BCI competition IV dataset
IIb. Table 4 shows the confusion matrix for subject 1
of BCI competition IV dataset IIa.
(ii) Analysis of SENN: In Table 5 we can analyze
the self-evolving property of the model by using K-
means and PSO algorithm. Each class has, on an aver-
age, 60 samples per subject. In the beginning, we pass
60 clusters for each class, and after that clusters self-
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
356

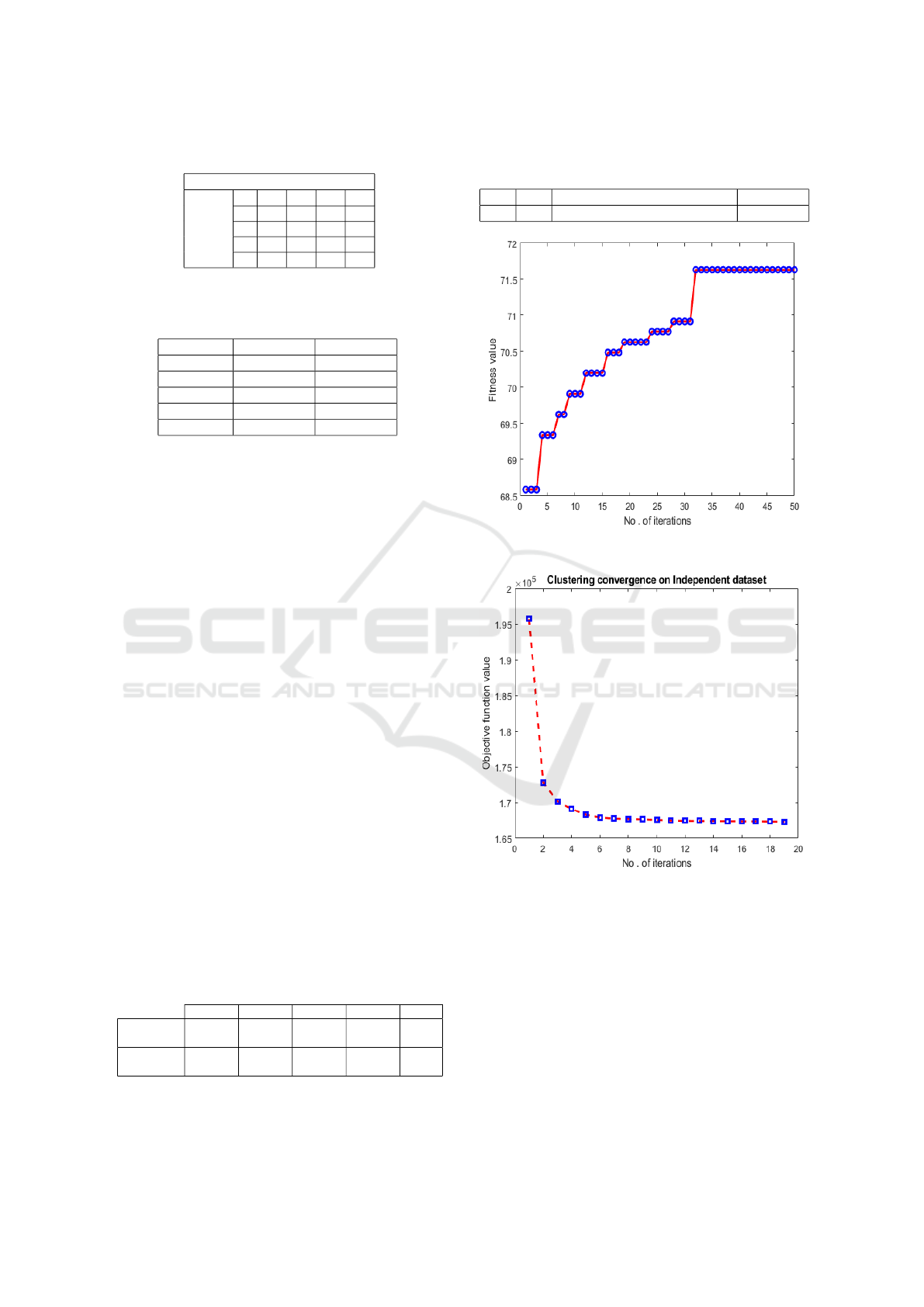
Table 4: Confusion matrix for subject 1.
Predicted class
1 2 3 4
1 35 16 13 8
2 14 44 9 5
3 8 8 50 6
Actual
class
4 7 6 7 52
Table 5: Number of hidden neurons produced by SENN()
evolved by Kmean and PSO algorithm in each class of sub-
ject 5 BCI competition IV dataset IIa.
Kmean PSO
Class 1 40 ±1.58 17.4 ±2.61
Class 2 39.2 ±2.95 17.8±1.48
Class 3 38 ±2.83 17.6±4.16
Class 4 37.8 ±2.49 19.4±0.89
Accuracy 73.0 ±3.22 65.8±2.59
evolve by using the K-means and PSO algorithms. A
characteristic of each neuron in the RBFNN model is
the center and spread information of those clusters. It
is evident that the total number of evolved neurons is
the sum total of clusters of all four classes.
(iii) Subject independent Analysis: Figure 7
demonstrates the convergence of the classwise clus-
ters of subject 5 BCI competition IV dataset IIa using
the PSO algorithm, with the parameters c1 and c2 set
to 0.0001. In 200 iterations, the objective function’s
value decreases. If the c1 and c2 values are more than
0.0001, there is a high risk of local minima due to the
cluster’s rapid convergence.
In subject independent BCI com-
petition IV dataset IIa, 11 channels
[3,6,7,11,12,15,18,22,23,24,25] were selected
with parameters c
1
=0.1 c
1
=0.6 and population size
is taken as 20 on 50 iteration. Figure 8 shows
the convergence of PSOCS on independent BCI
competition IV dataset IIa.
Table 6 summarizes the cluster information for
each class. Initially, we pass 100 clusters in each
class and get the converged cluster 352 clusters out of
500. The convergence of Kmean clustering is shown
in Figure 9, wherein the value of the objective func-
tion is minimized in each iteration. Table 7 summa-
rizes all the parameters and accuracy of the indepen-
dent dataset.
Table 6: Number of hidden neurons evolved in each class
of subject independent BCI competition IV dataset IIa.
Class 1 Class 2 Class 3 Class 4 Total
Initial no
of Cluster
100 100 100 100 500
Obtained
Cluster
81 89 88 90 352
Table 7: Accuracy of PSOCS() on independent BCI com-
petition IV dataset IIa.
C
1
C
2
Channels Accuracy
0.1 0.6 3,6,7,11,12,15,18,22,23,24,25 71.45%
Figure 8: PSOCS() convergence on independent BCI com-
petition IV IIa dataset.
Figure 9: Clustering convergence on independent BCI com-
petition IV dataset IIa [eqn 7 used for objective function
value].
5 CONCLUSION AND FUTURE
WORK
The proposed model learns from the underlying data
and evolves the RBFNN hidden neuron in terms of
numbers and locations of the centers. Therefore, the
proposed work can easily be used in other applica-
tions independent of the domain-specific knowledge,
SENN: Self-evolving Neural Network to Recognize Motor Imagery Thought Patterns
357

given the feature vectors representing samples. The
centers of the hidden neurons capture similar clusters
of the training data from a given class. The com-
plex phenomenon of thought patterns is handled ef-
ficiently using the proposed algorithm. Our algorithm
outperforms those with an accuracy of 71.45% for
subject-independent motor imagery task classification
for the dataset IIa. The mean kappa value for subject-
dependent task classification is obtained as 0.59 for
the same dataset. The algorithm also performed well
for dataset IIb. In the future, we will explore the
potential of this algorithm to work with more com-
plex thought classes such as music and mathematic
problem solving. We plan to use the transfer learning
methods for other mental activity recognition.
REFERENCES
Agarwal, V. (2019). Adaptive radial basis functions neu-
ral network for motor imagery task classification. In
2019 Twelfth International Conference on Contempo-
rary Computing (IC3), pages 1–6. IEEE.
Alam, M. N., Ibrahimy, M. I., and Motakabber, S. (2021).
Feature extraction of eeg signal by power spectral den-
sity for motor imagery based bci. In 2021 8th Interna-
tional Conference on Computer and Communication
Engineering (ICCCE), pages 234–237. IEEE.
Ang, K. K., Chin, Z. Y., Wang, C., Guan, C., and Zhang, H.
(2012). Filter bank common spatial pattern algorithm
on bci competition iv datasets 2a and 2b. Frontiers in
neuroscience, 6:39.
Baig, M. Z., Aslam, N., and Shum, H. P. (2020). Filtering
techniques for channel selection in motor imagery eeg
applications: a survey. Artificial intelligence review,
53(2):1207–1232.
Bhatti, M. H., Khan, J., Khan, M. U. G., Iqbal, R., Alo-
qaily, M., Jararweh, Y., and Gupta, B. (2019). Soft
computing-based eeg classification by optimal feature
selection and neural networks. IEEE Transactions on
Industrial Informatics, 15(10):5747–5754.
Das, A. and Suresh, S. (2015). An effect-size based chan-
nel selection algorithm for mental task classification
in brain computer interface. In 2015 IEEE Interna-
tional Conference on Systems, Man, and Cybernetics,
pages 3140–3145. IEEE.
Davoudi, A., Ghidary, S. S., and Sadatnejad, K. (2017). Di-
mensionality reduction based on distance preservation
to local mean for symmetric positive definite matrices
and its application in brain–computer interfaces. Jour-
nal of neural engineering, 14(3):036019.
Haykin, S. (2005). Neural Networks. PEARSON.
Kim, J.-Y., Park, S.-M., Ko, K.-E., and Sim, K.-B. (2012).
A binary pso-based optimal eeg channel selection
method for a motor imagery based bci system. In In-
ternational Conference on Hybrid Information Tech-
nology, pages 245–252. Springer.
Ko, W., Yoon, J., Kang, E., Jun, E., Choi, J.-S., and Suk,
H.-I. (2018). Deep recurrent spatio-temporal neural
network for motor imagery based bci. In 2018 6th In-
ternational Conference on Brain-Computer Interface
(BCI), pages 1–3. IEEE.
Miao, M., Zeng, H., Wang, A., Zhao, C., and Liu, F.
(2017). Discriminative spatial-frequency-temporal
feature extraction and classification of motor im-
agery eeg: An sparse regression and weighted na
¨
ıve
bayesian classifier-based approach. Journal of neuro-
science methods, 278:13–24.
Nicolas-Alonso, L. F. and Gomez-Gil, J. (2012). Brain
computer interfaces, a review. sensors, 12(2):1211–
1279.
Qiu, Z., Jin, J., Lam, H.-K., Zhang, Y., Wang, X., and Ci-
chocki, A. (2016). Improved sffs method for channel
selection in motor imagery based bci. Neurocomput-
ing, 207:519–527.
Sheoran, P. and Saini, J. (2022). Optimizing channel selec-
tion using multi-objective fodpso for bci applications.
Brain-Computer Interfaces, 9(1):7–22.
Xie, X., Yu, Z. L., Lu, H., Gu, Z., and Li, Y. (2016).
Motor imagery classification based on bilinear sub-
manifold learning of symmetric positive-definite ma-
trices. IEEE Transactions on Neural Systems and Re-
habilitation Engineering, 25(6):504–516.
Zhang, C. and Eskandarian, A. (2020). A computation-
ally efficient multiclass time-frequency common spa-
tial pattern analysis on eeg motor imagery. In 2020
42nd Annual International Conference of the IEEE
Engineering in Medicine & Biology Society (EMBC),
pages 514–518. IEEE.
Zhang, L. and Wei, Q. (2019). Channel selection in motor
imaginary-based brain-computer interfaces: a particle
swarm optimization algorithm. Journal of integrative
neuroscience, 18(2):141–152.
Zhao, H., Zheng, Q., Ma, K., Li, H., and Zheng, Y.
(2020). Deep representation-based domain adapta-
tion for nonstationary eeg classification. IEEE Trans-
actions on Neural Networks and Learning Systems,
32(2):535–545.
Zhou, B., Wu, X., Ruan, J., Zhao, L., and Zhang, L. (2019).
How many channels are suitable for independent com-
ponent analysis in motor imagery brain-computer in-
terface. Biomedical Signal Processing and Control,
50:103–120.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
358