Explaining Reject Options of Learning Vector Quantization Classifiers
Andr
´
e Artelt
1,2 a
, Johannes Brinkrolf
1 b
, Roel Visser
1
and Barbara Hammer
1 c
1
Faculty of Technology, Bielefeld University, Bielefeld, Germany
2
KIOS – Research and Innovation Center of Excellence, University of Cyprus, Nicosia, Cyprus
Keywords:
XAI, Contrasting Explanations, Learning Vector Quantization, Reject Options.
Abstract:
While machine learning models are usually assumed to always output a prediction, there also exist exten-
sions in the form of reject options which allow the model to reject inputs where only a prediction with an
unacceptably low certainty would be possible. With the ongoing rise of eXplainable AI, a lot of methods for
explaining model predictions have been developed. However, understanding why a given input was rejected,
instead of being classified by the model, is also of interest. Surprisingly, explanations of rejects have not been
considered so far. We propose to use counterfactual explanations for explaining rejects and investigate how
to efficiently compute counterfactual explanations of different reject options for an important class of models,
namely prototype-based classifiers such as learning vector quantization models.
1 INTRODUCTION
Nowadays, machine learning (ML) based decision
making systems are increasingly used in safety-
critical or high-impact applications like autonomous
driving (Sallab et al., 2017), credit (risk) assess-
ment (Khandani et al., 2010) and predictive polic-
ing (Stalidis et al., 2018). Because of this, there is an
increasing demand for transparency which was also
recognized by the policy makers and emphasized in
legal regulations like the EU’s GDPR (European par-
liament and council, 2016). It is a common approach
to realize transparency by explanations – i.e. provid-
ing an explanation of why the system behaved in the
way it did – which gave rise to the field of explainable
artificial intelligence (XAI or eXplainable AI) (Tjoa
and Guan, 2019; Samek et al., 2017). Although it
is still unclear what exactly makes up a “good” ex-
planation (Doshi-Velez and Kim, 2017; Offert, 2017),
a lot of different explanation methods have been de-
veloped (Guidotti et al., 2019; Molnar, 2019). Pop-
ular explanations methods (Molnar, 2019; Tjoa and
Guan, 2019) are feature relevance/importance meth-
ods (Fisher et al., 2019) and examples based meth-
ods (Aamodt and Plaza., 1994). Instances of example
based methods are contrasting explanations like coun-
a
https://orcid.org/0000-0002-2426-3126
b
https://orcid.org/0000-0002-0032-7623
c
https://orcid.org/0000-0002-0935-5591
terfactual explanations (Wachter et al., 2017; Verma
et al., 2020) and prototypes & criticisms (Kim et al.,
2016) – these methods use a set or a single example
for explaining the behavior of the system.
Another important aspect, in particular in safety-
critical and high-risk applications, is reliability: if
the system is not “absolutely” certain about its de-
cision/prediction it might be better to refuse making
a prediction and, for instance, pass the input back
to human – if making mistakes is “expensive” or
critical, the system should reject inputs where it is
not certain enough in its prediction. As a conse-
quence, a mechanism called reject options has been
pioneered (Chow, 1970), where optimal reject rates
are determined based on costs assigned to misclas-
sifications (e.g. false positives and false negatives)
and rejects. Many realizations of reject options are
based on probabilities, like class probabilities in clas-
sification (Chow, 1970). However, not all models
output probabilities along with their predictions or if
they do, their computed probabilities might be of “bad
quality” (e.g. just a score in [0,1] without any prob-
abilistic/statistical foundation). One possible rem-
edy is to use a general (i.e. model agnostic) post-
processing method or wrapper on top of the model
for computing reliable certainty scores, as is done
in (Herbei and Wegkamp, 2006), or use a method
like conformal prediction (Shafer and Vovk, 2008)
in which a non-conformity measure together with
a hold-out data set is used for computing certain-
Artelt, A., Brinkrolf, J., Visser, R. and Hammer, B.
Explaining Reject Options of Learning Vector Quantization Classifiers.
DOI: 10.5220/0011389600003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 249-261
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
249

ties and confidences of predictions. Another option
is to develop model specific certainty measures and
consequently reject options, which for instance was
done for prototype-based methods like learning vector
quantization (LVQ) models. These are a class of mod-
els that maintain simplicity (and thus interpretability),
while still being powerful predictive models, and have
also excelled in settings like life-long learning and
biomedical applications (Nova and Est
´
evez, 2014;
Kirstein et al., 2012; Xu et al., 2009; Owomugisha
et al., 2020; Brinkrolf and Hammer, 2020a; Fischer
et al., 2015b; Fischer et al., 2015a).
We think that while explaining the prediction of
the model is important, similarly explaining why a
given input was rejected is also important – i.e. ex-
plaining why the model “thinks” that it does not
know enough for making a proper and reliable pre-
diction. For instance, consider a biomedical appli-
cation where a model is supposed to assist in some
kind of early cancer detection – such a scenario could
be considered a high-risk application where the addi-
tion of a reject option to the model would be neces-
sary. In such a scenario, it would be very useful if
a reject is accompanied with an explanation of why
this sample was rejected, because by this we could
learn more about the model and the domain itself –
e.g. an explanation could state that some combination
of serum values is very unusual compared to what the
model has seen before. Surprisingly, (to the best of
our knowledge) explaining rejects have not been con-
sidered so far.
Contributions. In this work, we focus on
prototype-based models such as learning vector
quantization (LVQ) models and propose to explain
LVQ reject options by means of counterfactual expla-
nations – i.e. explaining why a particular sample was
rejected by the LVQ model. Whereby we consider
different reject options separately and study how to
efficiently compute counterfactual explanations in
each of these cases.
The remainder of this work is structured as fol-
lows: after reviewing the foundations of learning vec-
tor quantization (Section 2.1), popular reject options
for LVQ (Section 2.2), and counterfactual explana-
tions (Section 2.3), we propose a modeling and algo-
rithms for efficiently computing counterfactual expla-
nations of different LVQ reject options (Section 3). In
Section 4, we empirically evaluate our proposed mod-
elings and algorithms on several different data sets
with respect to different aspects. Finally, this work
closes with a summary and conclusion in Section 5.
Note that for the purpose of readability, all proofs and
derivations are given in Appendix 5.
2 FOUNDATIONS
2.1 Learning Vector Quantization
In this work, we focus on learning vector quantiza-
tion (LVQ) models. In modern variants, these models
constitute state-of-the-art classifiers which can also
be used for incremental, online, and federated learn-
ing (Gepperth and Hammer, 2016; Losing et al., 2018;
Brinkrolf and Hammer, 2021). Modern versions area
based on cost functions which have the benefit that
they can be easily extended to a more flexible met-
ric learning scheme (Schneider et al., 2009). First,
we introduce generalized LVQ (GLVQ) (Sato and Ya-
mada, 1995) and then take a look at extensions for
metric learning. In the following, we assume that
X = R
d
and {1, . . .,k} = Y . An LVQ model is
characterized by m labeled prototypes (

p
j
,c(

p
j
)) ∈
R
d
× Y , j ∈ {1, ...,m}, whereby the labels c(

p
j
) of
the prototypes are fixed. Classification of a sample
x ∈ R
d
takes place by a winner takes all scheme:
x 7→ c(

p
j
) with j = argmin
j ∈{1,...,m}
d(x,

p
j
) where
the squared Euclidean distance is used:
d(x,

p
j
) = (x −

p
j
)
>
(x −

p
j
) (1)
Note that the prototypes’ positions not only allow an
interpretable classification but also act as a represen-
tation of the data and its underlying classes. Training
of LVQ models is done in a supervised fashion – i.e.
based on given labeled samples (x
i
,y
i
) ∈ R
d
×Y with
i ∈ {1,... , N}. For GLVQ (Sato and Yamada, 1995),
the learning rule originates from minimizing the fol-
lowing cost function:
E =
N
∑
i=1
sgd

d(x
i
,

p
+
) − d(x
i
,

p
−
)
d(x
i
,

p
+
) + d(x
i
,

p
−
)

(2)
where sgd(·) is a monotonously increasing function –
e.g. the logistic function or the identity. Furthermore,

p
+
denotes the closest prototype with the same label
– i.e. c(x) = c(

p
+
) – and

p
−
denotes the closest pro-
totype which belongs to a different class. Note that
the models’ performance heavily depends on the suit-
ability of the Euclidean metric for the given classifi-
cation problem – this is often not the case, in partic-
ular in case of different feature relevances. Because
of this, a powerful metric learning scheme has been
proposed in (Schneider et al., 2009) which substitutes
the squared Euclidean metric in Eq. (1) by a weighted
alternative:
d(x,

p) = (x −

p)
>
Ω(x −

p) (3)
where Ω ∈ S
d
+
refers to a positive semidefinite matrix
encoding the relevance of each feature. This matrix is
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
250

treated as an additional parameter which is, together
with the prototypes’ positions, chosen such that the
cost function Eq. (2) is minimized – usually, a gra-
dient based method like LBFGS is used. Due to the
parameterization of the metric, this LVQ variant is of-
ten named generalized matrix LVQ (GMLVQ). Fur-
ther details can be found in (Schneider et al., 2009).
2.2 Reject Options
LVQ schemes provide a classification rule which as-
signs a label to every possible input no matter how
reliable & reasonable such classifications might be.
Reject options allow the classifier to reject a sample
if a certain prediction is not possible – i.e. the sam-
ple is too close to the decision boundary, or it is very
different from the observed training data and there-
fore a classification based on the learned prototypes
would not be reasonable. In order to realize such a re-
ject option, we extend the set of possible predictions
by a new class which represents a reject – i.e. for a
classifier h : X → Y , we construct h : X → Y ∪ {R}.
Several methods for doing so have been proposed and
evaluated in (Fischer et al., 2015a). Those methods
use a function r : X → R for computing the certainty
of a prediction by the classifier (Chow, 1970). If the
certainty is below some threshold θ, the sample is re-
jected, more formally if r(x) < θ then h(x) = R. As
demonstrated in the work (Chow, 1970), this strat-
egy is optimum if the certainty reliably estimates the
class posterior probability. In the following, we con-
sider three popular realizations of the certainty func-
tion r(·) for LVQ models.
Relative Similarity. In (Fischer et al., 2015a), a
very natural realization of r(·) called relative similar-
ity (RelSim) yields excellent results for LVQ models:
r
RelSim
(x) =
d(x,

p
−
) − d(x,

p
+
)
d(x,

p
−
) + d(x,

p
+
)
(4)
where

p
+
denotes the closest prototype and

p
−
de-
notes the closest prototype belonging to a different
class than

p
+
. Note that this fraction is always non-
negative and smaller than 1. Obviously, it is 0 if the
distance between the sample and the closest prototype

p
+
equals the distance to

p
−
. At the same time, Rel-
Sim gets close to 0 if the sample is far away – i.e. both
distances are large (Brinkrolf and Hammer, 2018).
Decision Boundary Distance. Another, similar, re-
alization of a certainty measure is the distance to the
decision boundary (Dist). In case of LVQ, this can be
formalized as follows (Fischer et al., 2015a):
r
Dist
(x) =
|d(x,

p
+
) − d(x,

p
−
)|
2k

p
+
−

p
−
k
2
2
(5)
where

p
+
and

p
−
are defined in the same way as in
RelSim Eq. (4). Note that Eq. (5) is not normalized
and depends on the prototypes and their distances to
the samplex. It is worthwhile mentioning that Eq. (5)
is closely related to the reject option of an SVM (Platt,
1999) – in case of binary classification problem and a
single prototype per class in a LVQ model, both mod-
els determine a separating hyperplane.
Probabilistic Certainty. The third certainty mea-
sure is a probabilistic one. The idea is to obtain proper
class probabilities p(y |x) for each class y ∈ Y and re-
ject a samplex if the probability for the most probable
class is lower than a given threshold θ. We denote the
probabilistic certainty measure as follows:
r
Proba
(x) = max
y∈Y
p(y |x). (6)
In the following, we use the fastest method
from (Brinkrolf and Hammer, 2020b) for computing
class probabilities given a trained LVQ models. The
method (Price et al., 1994) combines estimates from
binary classifiers in order to obtain class probabilities
for the final prediction. First, to obtain estimates of
class-wise binary classifiers, we train a single LVQ
model for each pair of classes using only the sam-
ples belonging to those two classes. This yields a
set of |Y |(|Y | − 1)/2 binary classifiers. Next, a data-
dependent scaling of the predictions follows to yield
pairwise probabilities. Here, we use RelSim Eq. (4)
and fit a sigmoid function to the real-valued scores.
This mimics the approach by Platt (Platt, 1999) which
is very popular in the context of SVMs. This post-
processing yields estimates r
i, j
(x) of pairwise proba-
bilities for every sample x and pairs of classes i and
j: r
i, j
≡ p(y = i | y = i ∨ j,x). Given those pairwise
probabilities and assuming a symmetric completion
of the pairs r
i, j
+ r
j,i
= 1, the posterior probabilities
are obtained as follows:
p(y = i |x) =
1
∑
j6=i
1
r
i, j
− (|Y |− 2)
(7)
where i, j ∈ Y (Price et al., 1994). After computing
all probabilities, a normalization step is required such
that
∑
k
i=1
p(y = i | x) = 1. We refer to (Brinkrolf and
Hammer, 2020b) for further details on all these steps.
2.3 Counterfactual Explanations
Counterfactual explanations (often just called coun-
terfactuals) are a prominent instance of contrasting
Explaining Reject Options of Learning Vector Quantization Classifiers
251

explanations, which state a change to some features
of a given input such that the resulting data point,
called the counterfactual, causes a different behavior
of the system than the original input does. Thus, one
can think of a counterfactual explanation as a sugges-
tion of actions that change the model’s behavior/pre-
diction. One reason why counterfactual explanations
are so popular is that there exists evidence that expla-
nations used by humans are often contrasting in na-
ture (Byrne, 2019) – i.e. people often ask questions
like “What would have to be different in order to ob-
serve a different outcome?”. For illustrative purposes,
consider the example of loan application: imagine you
applied for a credit at a bank, but your application
is rejected. Now, you would like to know why and
what you could have done to get accepted. A possible
counterfactual explanation might be that you would
have been accepted if you had earned 500$ more per
month and if you had not had a second credit card.
Despite their popularity, the missing uniqueness of
counterfactuals could pose a problem: often there ex-
ist more than one possible & valid counterfactual –
this is called the Rashomon effect (Molnar, 2019) –
and in such cases, it is not clear which or how many
of them should be presented to the user. One com-
mon modeling approach is to enforce uniqueness by a
suitable formalization or regularization.
In order to keep the explanation (suggested
changes) simple – i.e. easy to understand – an obvi-
ous strategy is to look for a small number of changes
so that the resulting sample (counterfactual) is simi-
lar/close to the original sample, which is aimed to be
captured by Definition 1.
Definition 1 ((Closest) Counterfactual Explana-
tion (Wachter et al., 2017)). Assume a prediction
function h : R
d
→ Y is given. Computing a counter-
factualx
cf
∈ R
d
for a given inputx
orig
∈ R
d
is phrased
as an optimization problem:
argmin
x
cf
∈R
d


h(x
cf
),y
0

+C ·φ(x
cf
,x
orig
) (8)
where (·) denotes a loss function, y
0
the target pre-
diction, φ(·) a penalty for dissimilarity ofx
cf
andx
orig
,
and C > 0 denotes the regularization strength.
The counterfactuals from Definition 1 are also
called closest counterfactuals because the optimiza-
tion problem Eq. (8) tries to find an explanation x
cf
that is as close as possible to the original sample x
orig
.
However, other aspects like plausibility and action-
ability are ignored in Definition 1, but are covered in
other work (Looveren and Klaise, 2021; Artelt and
Hammer, 2020; Artelt and Hammer, 2021).
3 COUNTERFACTUAL
EXPLANATIONS OF REJECT
In this section, we elaborate our proposal of using
counterfactual explanations for explaining LVQ reject
options. First, we introduce the general modeling in
Section 3.1, and then study the computational aspects
of each reject option in Section 3.2.
3.1 Modeling
Because counterfactual explanations (see Section 2.3)
proved to be an effective and useful explanation,
we propose to use counterfactual explanations for
explaining reject options of LVQ models (see Sec-
tion 2.1). Therefore, a counterfactual of a reject
provides the user with actionable feedback of what
to change in order to be able to classify. Further-
more, such an explanation also communicates why
the model is too uncertain for making a prediction in
this particular case.
Since there exist evidence that people prefer low
complexity (i.e. “simple”) explanations, we are look-
ing for sparse counterfactuals. Similar to Definition 1,
we phrase a counterfactual explanation x
cf
of a given
input x
orig
as the following optimization problem:
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. r(x
cf
) ≥ θ
(9)
where r(·) denotes the specific reject option and the
l
1
-norm objective is supposed to yield a sparse and
hence a “low complexity explanation”.
3.2 Computational Aspects of LVQ
Reject Options
In the following, we propose modeling and algo-
rithms which phrase problem (9) as convex optimiza-
tions problems, for efficiently computing counterfac-
tual explanations of LVQ rejects – whereby we con-
sider each of the three reject options from Section 2.2
separately. For the purpose of readability, we moved
all proofs and derivations to Appendix 5.
3.2.1 Relative Similarity
In case of the relative similarity reject option Eq. (4),
the optimization problem Eq. (9) can be solved by us-
ing a divide & conquer approach, where we need to
solve a number of convex quadratic programs of the
following form:
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. x
>
cf
Ωx
cf
+q
>
j
x
cf
+ c
j
≤ 0 ∀

p
j
∈ P (o
+
)
(10)
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
252

where P (o
+
) denotes a set of prototypes, q
j
and c
j
are defined in Eq. (20) and Eq. (21) (see Appendix 5
for details). Note that convex quadratic programs can
be solved efficiently (Boyd and Vandenberghe, 2014).
The complete algorithm for computing a counter-
factual explanation is given in Algorithm 1.
Algorithm 1: Counterfactual under RelSim/DistanceToDe-
cisionBoundary reject option.
Input: Original input x
orig
, reject threshold θ, the
LVQ model
Output: Counterfactual x
cf
1: x
cf
=

0  Initialize dummy solution
2: z = ∞  Sparsity of the best solution so far
3: for

p
+
∈ P do  Loop over every possible
prototype
4: Solving Eq. (10)/Eq. (19) yields a counterfac-
tual x
cf
∗
5: if kx
orig
−x
cf
∗
k
1
< z then 
Keep this counterfactual if it is sparser than the
currently “best” counterfactual
6: z = kx
orig
−x
cf
∗
k
1
7: x
cf
=x
cf
∗
8: end if
9: end for
3.2.2 Distance to Decision Boundary
Similar to the relative similarity reject option, we
again use a divide & conquer approach for solv-
ing Eq. (9). But in contrast to the relative similar-
ity reject option, we have to solve a number of linear
programs only, which can be solved even faster than
convex quadratic programs (Boyd and Vandenberghe,
2014):
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. q
>
j
x
cf
+ c
j
≥ 0 ∀

p
j
∈ P (o
+
)
(11)
where P (o
+
) denotes a set of prototypes, q
j
and c
j
are defined in Eq. (27) (see Appendix 5 for details).
The final algorithm for computing a counterfac-
tual explanation is equivalent to Algorithm 1 for the
relative similarity reject option, except that instead of
solving Eq. (10) in line 4, we have to solve Eq. (19).
3.2.3 Probabilistic Certainty Measure
In case of the probabilistic certainty measure as a re-
ject option Eq. (6), it holds:
r
Proba
(x) ≥ θ ⇔ max
y∈Y
p(y |x) ≥ θ
⇔ ∃ i ∈ Y : p(y = i |x) ≥ θ
(12)
Applying the divide & conquer paradigm over i ∈ Y
for solving Eq. (9), yields optimization problems of
the following form:
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t.
∑
j6=i
exp α
d
i, j
(x
cf
,

p
−
) − d
i, j
(x
cf
,

p
+
)
d
i, j
(x
cf
,

p
−
) + d
i, j
(x
cf
,

p
+
)
+ β
!
+
1 −
1
θ
≤ 0
(13)
While we could solve Eq. (13) directly – yield-
ing Algorithm 2 –, it is a rather difficult optimization
problem because of its lack of any structure like con-
vexity – e.g. general (black-box) solvers might be the
only applicable choice. We therefore, additionally,
propose a convex approximation where we can still
guarantee feasibility (i.e. validity of the final counter-
factual) at the price of losing closeness – i.e. we might
not find the sparsest possible counterfactual, although
finding a global optimum of Eq. (13) might be diffi-
cult as well. Approximating the constraint in Eq. (13)
Algorithm 2: Counterfactual under the probabilistic cer-
tainty reject option.
Input: Original input x
orig
, reject threshold θ, the
LVQ model
Output: Counterfactual x
cf
1: x
cf
=

0  Initialize dummy solution
2: z = ∞  Sparsity of the best solution so far
3: for i ∈ Y do  Loop over every possible class
4: Solving Eq. (13) yields a counterfactualx
cf
∗
5: if kx
orig
−x
cf
∗
k
1
< z then 
Keep this counterfactual if it is sparser than the
currently “best” counterfactual
6: z = kx
orig
−x
cf
∗
k
1
7: x
cf
=x
cf
∗
8: end if
9: end for
yields a convex quadratic constraint, which then re-
sults in a convex quadratic program as a final approx-
imation of Eq. (13) – for details see Appendix 5:
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. x
>
Ωx +q
>
j
x + c
j
≤ 0 ∀

p
j
∈ P (o
i
)
(14)
Using the approximation Eq. (14) requires us to iter-
ate over every possible prototype, every possible class
different from the i-th class, and finally over every
possible class – i.e. finally yielding Algorithm 3. Al-
though our proposed approximation Eq. (14) can be
computed quite fast (because it is a convex quadratic
program), it comes at the price of “drastically” in-
creasing the complexity of the final divide & conquer
algorithm. While we have to solve |Y | optimization
problems Eq. (13) in Algorithm 2, we get a quadratic
Explaining Reject Options of Learning Vector Quantization Classifiers
253

Algorithm 3: Counterfactual under the probabilistic cer-
tainty reject option – Approximation.
Input: Original input x
orig
, reject threshold θ, the
LVQ model
Output: Counterfactual x
cf
1: x
cf
=

0  Initialize dummy solution
2: z = ∞  Sparsity of the best solution so far
3: for i ∈ Y do  Loop over every possible class
4: for j ∈ Y \ {i} do  Loop over all other
classes
5: for

p
i
∈ P do  Loop over every possible
prototype
6: Solving Eq. (14) yields a counterfac-
tual x
cf
∗
7: if kx
orig
−x
cf
∗
k
1
< z then 
Keep this counterfactual if it is sparser than the
currently “best” counterfactual
8: z = kx
orig
−x
cf
∗
k
1
9: x
cf
=x
cf
∗
10: end if
11: end for
12: end for
13: end for
complexity (quadratic in the number of classes) for
our proposed convex approximation (Algorithm 3):
|Y |
2
· P
N
− |Y |· P
N
(15)
where P
N
denotes the number of prototypes per class
used in the pair-wise classifiers. This quadratic com-
plexity could become a problem in case of a large
number of classes and a large number of prototypes
per class.
To summarize, we propose two divide & conquer
algorithms for computing counterfactual explanations
of the probabilistic certainty reject option Eq. (6). In
Algorithm 2, we have to solve a rather complicated
(i.e. unstructured) optimization problem, but we have
to do this only a few times, whereas in Algorithm 3
we have to solve many convex quadratic programs.
Although we have to solve more optimization prob-
lems in Algorithm 3 than in Algorithm 2, solving the
optimization problems in Algorithm 3 is much easier
and it is also possible to easily extend the optimization
problems with additional constraints, such as plausi-
bility constraints (Artelt and Hammer, 2020). Hence
both algorithms have their areas of application and
it is worthwhile to enable practitioners to choose be-
tween them depending on their needs and the specific
scenario.
4 EXPERIMENTS
We empirically evaluate all proposed algorithms for
computing counterfactual explanations of different re-
ject options (see Sections 2.1, 2.2) for GMLVQ on
several different data sets. We evaluate two different
properties:
• Algorithmic properties like sparsity, validity (in
case of black-box solvers).
• Goodness of the explanations – i.e. whether our
proposed counterfactual explanations of reject are
able to find and explain known ground truth rea-
sons for rejects.
All experiments are implemented in Python and the
source code is available on GitHub
1
.
4.1 Data Sets
We consider the following data sets for our empirical
evaluation:
4.1.1 Wine
The “Wine data set” (S. Aeberhard and de Vel, 1992)
is used for predicting the cultivator of given wine sam-
ples based on their chemical properties. The data set
contains 178 samples and 13 numerical features such
as alcohol, hue and color intensity.
4.1.2 Breast Cancer
The “Breast Cancer Wisconsin (Diagnostic) Data
Set” (William H. Wolberg, 1995) is used for classify-
ing breast cancer samples into benign and malignant.
The data set contains 569 samples and 30 numerical
features such as area and smoothness.
4.1.3 Flip
This data set (Sowa et al., 2013) is used for the pre-
diction of fibrosis. The set consists of samples of
118 patients and 12 numerical features such as blood
glucose, BMI and total cholesterol. As the data set
contains some rows with missing values, we chose to
replace these missing values with the corresponding
feature mean.
4.1.4 T21
This data set (Nicolaides et al., 2005) is used for early
diagnosis of chromosomal abnormalities, such as tri-
somy 21, in pregnant women. The data set consists of
18 numerical features such as heart rate and weight,
1
https://github.com/andreArtelt/explaining lvq reject
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
254

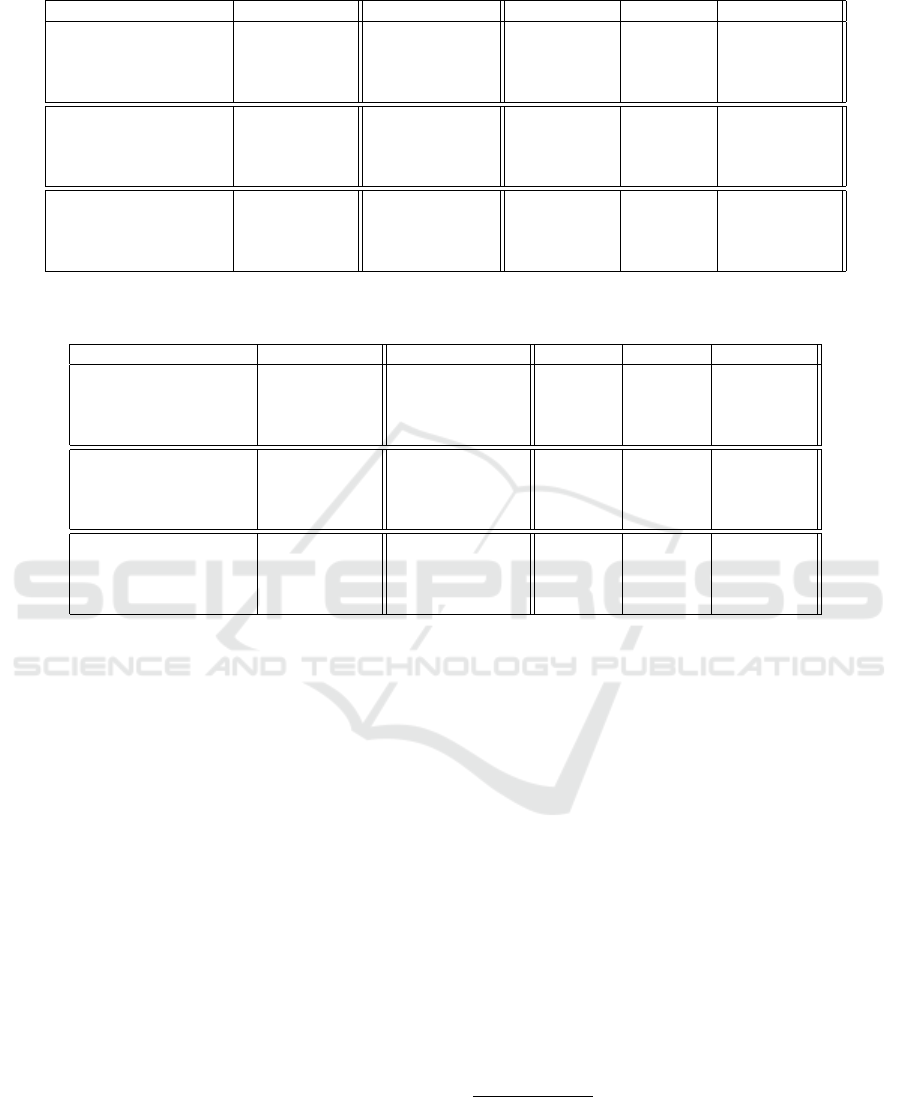
Table 1: Algorithmic properties – Mean sparsity (incl. variance) of different counterfactuals, smaller values are better.
DataSet BbCfFeasibility BbCf TrainCf ClosestCf
Relative
Similarity
Eq. (4)
Wine 1.0 ± 0.0 11.14 ± 1.41 13.0 ± 0.0 5.68 ± 11.36
Breast Cancer 0.99 ± 0.0 27.64 ± 4.38 30.0 ± 0.0 12.69 ± 52.31
t21 0.99 ± 0.0 16.14 ± 1.91 11.0 ± 1.0 4.39 ± 12.79
Flip 1.0 ± 0.0 10.52 ± 1.38 12.0 ± 0.0 4.07 ± 8.02
Distance
DecisionBoundary
Eq. (5)
Wine 1.0 ± 0.0 10.98 ± 1.12 13.0 ± 0.0 2.8 ± 9.13
Breast Cancer 1.0± 0.0 27.5 ± 2.78 30.0 ± 0.0 4.16±48.19
t21 1.0 ± 0.0 16.02 ± 1.43 11.0 ± 1.0 2.12 ± 5.19
Flip 1.0 ± 0.0 10.31 ± 1.2 12.0 ± 0.0 1.88 ± 3.11
Probabilistic
Certainty
Eq. (6)
Wine 0.45 ± 0.21 13.0 ± 0.0 13.0 ± 0.0 12.67 ± 0.22
Breast Cancer 0.94 ± 0.02 30.0 ± 0.0 30.0 ± 0.0 26.04 ± 60.5
t21 0.4 ± 0.24 17.39 ± 0.64 11.0 ± 0.0 12.55 ± 7.41
Flip 0.4 ± 0.24 11.75 ± 0.23 12.0 ±0.0 11.5 ± 1.47
Table 2: Goodness of counterfactual explanations – Mean and variance recall of identified relevant features (larger numbers
are better).
DataSet BbCfFeasiblility BbCf TrainCf Cf
Relative
Similarity
Eq. (4)
Wine 1.0 ± 0.0 1.0 ± 0.0 1.0 ± 0.0 1.0 ± 0.0
Breast Cancer 1.0± 0.0 1.0± 0.0 1.0 ± 0.0 0.99 ± 0.01
t21 1.0 ± 0.0 1.0 ± 0.0 1.0 ± 0.0 0.98 ± 0.0
Flip 1.0± 0.0 1.0± 0.0 1.0 ± 0.0 0.96 ± 0.02
Distance
DecisionBoundary
Eq. (5)
Wine 0.8 ± 0.16 1.0 ± 0.0 1.0 ± 0.0 0.72 ± 0.15
Breast Cancer 1.0± 0.0 1.0± 0.0 1.0 ± 0.0 0.45 ± 0.18
t21 0.6 ± 0.24 1.0 ± 0.0 1.0 ± 0.0 0.63 ± 0.15
Flip 1.0± 0.0 1.0± 0.0 1.0 ± 0.0 0.62 ± 0.22
Probabilistic
Certainty
Eq. (6)
Wine 0.8 ± 0.16 1.0 ± 0.0 1.0 ± 0.0 1.0 ± 0.0
Breast Cancer 0.8± 0.16 1.0± 0.0 1.0 ± 0.0 1.0 ± 0.0
t21 0.85 ± 0.02 1.0 ± 0.0 1.0 ± 0.0 0.94 ± 0.01
Flip 0.73 ± 0.06 1.0 ± 0.0 1.0 ± 0.0 0.75 ± 0.19
and contains over 50000 samples but only 0.8 percent
abnormal samples (e.g. cases of trisomy 21).
4.2 Setup
For finding the best model parameters, we perform a
grid search on the GMLVQ hyperparameters and re-
jection thresholds. In order to reduce the risk of over-
fitting, we cross validate the GMLVQ models’ accu-
racy and rejection rates on the different reject thresh-
olds using a 5-fold cross validation.
For each GMLVQ model hyperparameterization,
the rejection rates for each of the thresholds is com-
puted as well as the impact of this on the accuracy of
the model. Based on these rejection rates and accu-
racies, the accuracy-rejection curve (ARC) (Nadeem
et al., 2010) can be computed. The area under the
ARC measure (AU-ARC) gives an indication of how
well the reject model performs given the GMLVQ
model type and its hyperparameterization. For each
combination of data set, GMLVQ model type, and re-
ject option method, we can then determine the best
GMLVQ model parameters and rejection threshold.
We do this by selecting the GMLVQ hyperparameters
with the highest accuracy.
Following the selection of the best GMLVQ hy-
perparameters, the best rejection threshold is found
by determining the “optimal” threshold in the ARC
by finding the so-called knee-point using the Kneedle
algorithm (Satopaa et al., 2011). By finding the opti-
mal hyperparameters for each model, our evaluation
of the different model types will be less dependent on
potentially poor hyperparamerization.
We run all experiments (5-fold cross validation)
for each data set, each reject option and each method
for computing the counterfactuals – i.e black-box
solver for solving Eq. (9)
2
, our proposed algorithms
from Section 3) and the closest sample from the train-
ing data set which is not rejected (this “naive” way of
computing a counterfactual serves as a baseline).
4.2.1 Algorithmic Properties
We evaluate the sparsity of the counterfactual expla-
nations by using the l
0
-norm
3
. Since our methods
2
We use the penalty method (with equal weighting) to
turn Eq. (9) into an unconstrained problem, solve it by using
the Nelder-Mead black-box method.
3
For numerical reasons, we use a threshold at which we
consider a floating point number to be equal to zero – see
provided source code for details.
Explaining Reject Options of Learning Vector Quantization Classifiers
255

and algorithms are guaranteed to output feasible (i.e.
valid) counterfactuals, we only evaluate validity (re-
ported as percentage) of the counterfactuals computed
by the black-box solver.
4.2.2 Goodness of Counterfactual Explanations
For evaluating the ground truth recovery rate (good-
ness) of the counterfactuals, we create scenarios with
ground truth as follows: for each data set, we select a
random subset of features (30%) and perturb these in
the test set by adding Gaussian noise – we then check
which of these samples are rejected due to the noise
(i.e. applying the reject option before and after ap-
plying the perturbation), and compute counterfactual
explanations of these samples only. We then evaluate
for each counterfactual how many of the relevant fea-
tures (from the known ground truth) are detected and
included in the counterfactual explanation.
4.3 Results & Discussion
When reporting the results, we use the following ab-
breviations: BbCfFeasibility – Feasibility of the coun-
terfactuals computed by the black-box solver, in case
of the probabilistic reject option Eq. (6), we report
the results of using Algorithm 2 (the results for the
“true” black-box solver can be found in Appendix 5);
BbCf – Counterfactuals computed by the black-box
solver, TrainCf – Counterfactuals by selecting the
closest sample from the training set which is not re-
jected; ClosestCf – Counterfactuals computed by our
proposed algorithms.
Note that we round all values to two decimal
points.
4.3.1 Algorithmic Properties
In Table 1, we report the mean sparsity (along with
the variance) of the counterfactuals for different reject
options and different data sets. We observe that our
proposed methods for computing counterfactual ex-
planation of reject options is consistently able to com-
pute very sparse (i.e. low complexity) counterfactu-
als – however, the variance is often quite large which
suggests that there exist a few outliers in the data set
for which it is not possible to compute a sparse coun-
terfactuals. As it is to be expected, we observe the
worst performance when choosing a sample from the
training set as a counterfactual. The counterfactuals
computed by a black-box solver are often a bit better
than those from the training set but still far away from
the counterfactuals computed by our proposed algo-
rithms. While the black-box solver works quite well
in case of the relative similarity and distance to deci-
sion boundary reject options, the performance drops
significantly (for many but not all data sets) in case
of the probabilistic certainty reject option. We think
this might be due to the increased complexity of the
reject option, compared to the other two reject op-
tions which have much simpler mathematical form.
For this reject option, our proposed algorithm is still
able to consistently yield the sparsest counterfactuals
but the difference to other counterfactuals is not that
significant like it is the case for the other two reject
options.
4.3.2 Goodness of Counterfactual Explanations
The mean recall (along with the variance) of re-
covered (ground truth) relevant features for different
counterfactuals, data sets and reject options, is given
in Table 2. We observe that all methods are able to
identify the relevant features that caused the reject.
There exist few instances where counterfactuals com-
puted by our proposed algorithms miss a few relevant
features – this is most likely due to the fact that fea-
ture correlations might exist and the objective to find
a sparse counterfactual can yield to different resolu-
tions of such redundancies. Here, other regularization
terms (such as L2) might yield better stability possi-
bly at the cost of decreased interpretability.
5 SUMMARY & CONCLUSION
In this work we proposed to explain reject options
of LVQ models by means of counterfactual explana-
tions. We considered three popular reject options and
for each, proposed (extendable) modelings and algo-
rithms for efficiently computing counterfactual expla-
nations under the particular reject option. We empiri-
cally evaluated all our proposed methods under differ-
ent aspects – in particular, we demonstrated that our
algorithms delivers sparse (i.e. “low-complexity”)
explanations, and that counterfactual explanations in
general seem to be able to detect and highlight rele-
vant features in scenarios where the ground truth is
known.
Although our proposed idea of using counterfac-
tual explanations for explaining rejects is rather gen-
eral, our proposed methods and algorithms are tai-
lored towards LVQ models and thus not applicable
to other ML models. Therefore, it would be of in-
terest to see other, either model specific or even more
general (e.g. model agnostic) methods for computing
counterfactual explanations of reject under other ML
models.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
256

Our evaluation focused on algorithmic properties
such as sparsity and feature relevances for assessing
the ground truth recovery rate (goodness) of the com-
puted counterfactuals. However, it is still unclear how
and if these kinds of explanations of reject are use-
ful and helpful to humans – since it is difficult to im-
plement “human usefulness” as a scoring function, a
proper user study for evaluating the usefulness is nec-
essary.
We leave these aspects as future work.
ACKNOWLEDGEMENT
We gratefully acknowledge funding from the
Deutsche Forschungsgemeinschaft (DFG, German
Research Foundation) for grant TRR 318/1 2021 –
438445824, from the BMWi for grant 01MK20007E,
and the VW-Foundation for the project IMPACT
funded in the frame of the funding line AI and its
Implications for Future Society.
REFERENCES
Aamodt, A. and Plaza., E. (1994). Case-based reasoning:
Foundational issues, methodological variations, and
systemapproaches. AI communications.
Artelt, A. and Hammer, B. (2020). Convex density con-
straints for computing plausible counterfactual expla-
nations. In Farkas, I., Masulli, P., and Wermter, S., ed-
itors, Artificial Neural Networks and Machine Learn-
ing - ICANN 2020 - 29th International Conference
on Artificial Neural Networks, Bratislava, Slovakia,
September 15-18, 2020, Proceedings, Part I, volume
12396 of Lecture Notes in Computer Science, pages
353–365. Springer.
Artelt, A. and Hammer, B. (2021). Convex optimization for
actionable \& plausible counterfactual explanations.
CoRR, abs/2105.07630.
Boyd, S. P. and Vandenberghe, L. (2014). Convex Optimiza-
tion. Cambridge University Press.
Brinkrolf, J. and Hammer, B. (2018). Interpretable machine
learning with reject option. Autom., 66(4):283–290.
Brinkrolf, J. and Hammer, B. (2020a). Time integration
and reject options for probabilistic output of pairwise
LVQ. Neural Comput. Appl., 32(24):18009–18022.
Brinkrolf, J. and Hammer, B. (2020b). Time integration
and reject options for probabilistic output of pairwise
LVQ. Neural Comput. Appl., 32(24):18009–18022.
Brinkrolf, J. and Hammer, B. (2021). Federated learning
vector quantization. In 29th European Symposium
on Artificial Neural Networks, Computational Intel-
ligence and Machine Learning, ESANN 2021, Online
event (Bruges, Belgium), October 6-8, 2021.
Byrne, R. M. J. (2019). Counterfactuals in explainable arti-
ficial intelligence (XAI): evidence from human rea-
soning. In Kraus, S., editor, Proceedings of the
Twenty-Eighth International Joint Conference on Arti-
ficial Intelligence, IJCAI 2019, Macao, China, August
10-16, 2019, pages 6276–6282. ijcai.org.
Chow, C. K. (1970). On optimum recognition error and
reject tradeoff. IEEE Trans. Inf. Theory, 16(1):41–46.
Doshi-Velez, F. and Kim, B. (2017). Towards a rigorous
science of interpretable machine learning.
European parliament and council (2016). General data pro-
tection regulation: Regulation (eu) 2016/679 of the
european parliament.
Fischer, L., Hammer, B., and Wersing, H. (2015a). Efficient
rejection strategies for prototype-based classification.
Neurocomputing, 169:334–342.
Fischer, L., Hammer, B., and Wersing, H. (2015b). Opti-
mum reject options for prototype-based classification.
CoRR, abs/1503.06549.
Fisher, A., Rudin, C., and Dominici, F. (2019). All mod-
els are wrong, but many are useful: Learning a vari-
able’s importance by studying an entire class of pre-
diction models simultaneously. J. Mach. Learn. Res.,
20:177:1–177:81.
Gepperth, A. and Hammer, B. (2016). Incremental learning
algorithms and applications. In 24th European Sym-
posium on Artificial Neural Networks, ESANN 2016,
Bruges, Belgium, April 27-29, 2016.
Guidotti, R., Monreale, A., Ruggieri, S., Turini, F., Gian-
notti, F., and Pedreschi, D. (2019). A survey of meth-
ods for explaining black box models. ACM Comput.
Surv., 51(5):93:1–93:42.
Herbei, R. and Wegkamp, M. H. (2006). Classification
with reject option. Canadian Journal of Statistics,
34(4):709–721.
Khandani, A. E., Kim, A. J., and Lo, A. (2010). Con-
sumer credit-risk models via machine-learning algo-
rithms. Journal of Banking & Finance, 34(11).
Kim, B., Koyejo, O., and Khanna, R. (2016). Examples
are not enough, learn to criticize! criticism for inter-
pretability. In Lee, D. D., Sugiyama, M., von Luxburg,
U., Guyon, I., and Garnett, R., editors, Advances in
Neural Information Processing Systems 29: Annual
Conference on Neural Information Processing Sys-
tems 2016, December 5-10, 2016, Barcelona, Spain,
pages 2280–2288.
Kirstein, S., Wersing, H., Gross, H.-M., and K
¨
orner, E.
(2012). A life-long learning vector quantization ap-
proach for interactive learning of multiple categories.
Neural networks : the official journal of the Interna-
tional Neural Network Society, 28:90–105.
Looveren, A. V. and Klaise, J. (2021). Interpretable
counterfactual explanations guided by prototypes.
12976:650–665.
Losing, V., Hammer, B., and Wersing, H. (2018). Incremen-
tal on-line learning: A review and comparison of state
of the art algorithms. Neurocomputing, 275:1261–
1274.
Molnar, C. (2019). Interpretable Machine Learning.
Nadeem, M. S. A., Zucker, J., and Hanczar, B. (2010).
Accuracy-rejection curves (arcs) for comparing clas-
sification methods with a reject option. In Dzeroski,
Explaining Reject Options of Learning Vector Quantization Classifiers
257

S., Geurts, P., and Rousu, J., editors, Proceedings of
the third International Workshop on Machine Learn-
ing in Systems Biology, MLSB 2009, Ljubljana, Slove-
nia, September 5-6, 2009, volume 8 of JMLR Pro-
ceedings, pages 65–81. JMLR.org.
Nicolaides, K. H., Spencer, K., Avgidou, K., Faiola, S., and
Falcon, O. (2005). Multicenter study of first-trimester
screening for trisomy 21 in 75 821 pregnancies: re-
sults and estimation of the potential impact of individ-
ual risk-orientated two-stage first-trimester screening.
Ultrasound in Obstetrics & Gynecology, 25(3):221–
226.
Nova, D. and Est
´
evez, P. A. (2014). A review of learning
vector quantization classifiers. Neural Comput. Appl.,
25(3-4):511–524.
Offert, F. (2017). ”i know it when i see it”. visualization and
intuitive interpretability.
Owomugisha, G., Nuwamanya, E., Quinn, J. A., Biehl, M.,
and Mwebaze, E. (2020). Early detection of plant
diseases using spectral data. In Petkov, N., Strisci-
uglio, N., and Travieso-Gonz
´
alez, C. M., editors, AP-
PIS 2020: 3rd International Conference on Applica-
tions of Intelligent Systems, APPIS 2020, Las Palmas
de Gran Canaria Spain, 7-9 January 2020. ACM.
Platt, J. C. (1999). Probabilistic Outputs for Support Vec-
tor Machines and Comparisons to Regularized Likeli-
hood Methods. In Advances in Large Margin Classi-
fiers, pages 61–74. MIT Press.
Price, D., Knerr, S., Personnaz, L., and Dreyfus, G. (1994).
Pairwise neural network classifiers with probabilistic
outputs. In Tesauro, G., Touretzky, D. S., and Leen,
T. K., editors, Advances in Neural Information Pro-
cessing Systems 7, [NIPS Conference, Denver, Col-
orado, USA, 1994], pages 1109–1116. MIT Press.
S. Aeberhard, D. C. and de Vel, O. (1992). Comparison of
classifiers in high dimensional settings. Tech. Rep. no.
92-02.
Sallab, A. E., Abdou, M., Perot, E., and Yogamani,
S. (2017). Deep reinforcement learning frame-
work for autonomous driving. Electronic Imaging,
2017(19):70–76.
Samek, W., Wiegand, T., and M
¨
uller, K. (2017). Explain-
able artificial intelligence: Understanding, visualiz-
ing and interpreting deep learning models. CoRR,
abs/1708.08296.
Sato, A. and Yamada, K. (1995). Generalized learning
vector quantization. In Touretzky, D. S., Mozer, M.,
and Hasselmo, M. E., editors, Advances in Neural In-
formation Processing Systems 8, NIPS, Denver, CO,
USA, November 27-30, 1995, pages 423–429. MIT
Press.
Satopaa, V., Albrecht, J. R., Irwin, D. E., and Raghavan,
B. (2011). Finding a ”kneedle” in a haystack: De-
tecting knee points in system behavior. In 31st IEEE
International Conference on Distributed Computing
Systems Workshops (ICDCS 2011 Workshops), 20-24
June 2011, Minneapolis, Minnesota, USA, pages 166–
171. IEEE Computer Society.
Schneider, P., Biehl, M., and Hammer, B. (2009). Adaptive
Relevance Matrices in Learning Vector Quantization.
Neural Computation, 21(12):3532–3561.
Shafer, G. and Vovk, V. (2008). A tutorial on conformal
prediction. J. Mach. Learn. Res., 9:371–421.
Sowa, J.-P., Heider, D., Bechmann, L. P., Gerken, G., Hoff-
mann, D., and Canbay, A. (2013). Novel algorithm
for non-invasive assessment of fibrosis in nafld. PLOS
ONE, 8(4):1–6.
Stalidis, P., Semertzidis, T., and Daras, P. (2018). Examin-
ing deep learning architectures for crime classification
and prediction. abs/1812.00602.
Tjoa, E. and Guan, C. (2019). A survey on explainable
artificial intelligence (XAI): towards medical XAI.
CoRR, abs/1907.07374.
Verma, S., Dickerson, J., and Hines, K. (2020). Counterfac-
tual explanations for machine learning: A review.
Wachter, S., Mittelstadt, B., and Russell, C. (2017). Coun-
terfactual explanations without opening the black box:
Automated decisions and the gdpr. Harv. JL & Tech.,
31:841.
William H. Wolberg, W. Nick Street, O. L. M.
(1995). Breast cancer wisconsin (diagnostic) data
set. https://archive.ics.uci.edu/ml/datasets/Breast+
Cancer+Wisconsin+(Diagnostic).
Xu, Y., Furao, S., Hasegawa, O., and Zhao, J. (2009).
An online incremental learning vector quantization.
In Advances in Knowledge Discovery and Data Min-
ing, 13th Pacific-Asia Conference, PAKDD 2009,
Bangkok, Thailand, April 27-30, 2009, Proceedings,
pages 1046–1053.
APPENDIX
Proofs & Derivations
Counterfactual Explanations
Relative Similarity. In order for a samplex ∈ R
d
to
be classified, it must hold that:
r
RelSim
(x) ≥ θ (16)
Using the shorter notation d
+
(x) = d(x,

p
+
) and
d
−
(x) = d(x,

p
−
), respectively, where

p
+
refers to the
closest prototype and

p
−
revers to the closest one be-
longs to a different class, this further translates into:
r
RelSim
(x) ≥ θ
⇔
d
−
(x) − d
+
(x)
d
−
(x) + d
+
(x)
≥ θ
⇔ (1 − θ)d
−
(x) − (1 + θ)d
+
(x) ≥ 0
(17)
Assuming that the closest prototype

p
+
is fixed, we
can rewrite Eq. (17) as follows:
(1 − θ)d(x,

p
j
) − (1 + θ)d(x,

p
+
) ≥ 0 ∀

p
j
∈ P (o
+
)
(18)
where P (o
+
) denotes the set of all prototypes that are
not labeled as o
+
. The intuition behind the translation
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
258

of Eq. (17) into Eq. (18) is that, if Eq. (17) holds for
all possible

p
−
, then also for the particular choice of

p
−
in Eq. (16).
These constraints can be rewritten as the following
convex quadratic constraints – for a given

p
j
:
(1 − θ)d(x,

p
j
) − (1 + θ)d(x,

p
+
) ≥ 0
⇔ d(x,

p
j
) − d(x,

p
+
) − θ

d(x,

p
j
) + d(x,

p
+
)

≥ 0
⇔ −2(

p
>
+
Ω−

p
>
j
Ω)x −

p
>
j
Ω

p
j
+

p
>
+
Ω

p
+
+
θ

2x
>
Ωx − 2(

p
>
j
Ω+

p
>
+
Ω)x +

p
>
j
Ω

p
j
+

p
>
+
Ω

p
+

≤ 0
⇔x
>
Ωx +q
>
j
x + c
j
≤ 0
(19)
where
q
>
j
=

−
1
θ
− 1


p
>
+
Ω+

1
θ
− 1


p
>
j
Ω (20)
c
j
=
1
2

1 −
1
θ


p
>
j
Ω

p
j
+

1 +
1
θ


p
>
+
Ω

p
+
!
(21)
We therefore get the following convex quadratic op-
timization problem – note that convex quadratic pro-
grams can be solved efficiently (Boyd and Vanden-
berghe, 2014):
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. x
>
cf
Ωx
cf
+q
>
j
x
cf
+ c
j
≤ 0 ∀

p
j
∈ P (o
+
)
(22)
We simply solve this optimization problem Eq. (22)
for all possible target prototypes and select the coun-
terfactual which is the closest to the original sample
– since every possible prototype could be a poten-
tial closest prototype

p
+
, we have to solve as many
optimization problems as we have prototypes. How-
ever, one could introduce some kind of early stopping
by adding an additional constraint on the distance of
the counterfactual to the original sample – i.e. use
the currently best known solution as a upper bound
on the objective, which might result in an infeasible
program and hence will be aborted quickly. Alter-
natively, one could solve the different optimization
problems in parallel because they are independent.
Distance to Decision Boundary. In order for a
samplex ∈ R
d
to be accepted (i.e. not being rejected),
it must hold that:
r
Dist
(x) ≥ θ (23)
This further translates into:
r
Dist
(x) ≥ θ
⇔
|d
+
(x) − d
−
(x)|
2k

p
+
−

p
−
k
2
2
≥ θ
⇔ d
−
(x) − d
+
(x) − 2θk

p
+
−

p
−
k
2
2
≥ 0
(24)
Assuming that the closest prototype

p
+
is fixed, we
get:
d(x,

p
j
)−d(x,

p
+
)−2θk

p
+
−

p
j
k
2
2
≥ 0 ∀

p
j
∈ P (o
+
)
(25)
where P (o
+
) denotes the set of prototypes that are
not labeled as o
+
. Again, the intuition behind this
translation is that, if Eq. (24) holds for all possible

p
−
,
then also for the particular choice of

p
−
in Eq. (23).
These constraints can be rewritten as the following
linear constraints – for a given

p
j
:
d(x,

p
j
) − d(x,

p
+
) − 2θk

p
+
−

p
j
k
2
2
≥ 0
⇔ (x −

p
j
)
>
Ω(x −

p
j
) − (x −

p
+
)
>
Ω(x −

p
+
)−
2θ(

p
+
−

p
j
)
>
Ω(

p
+
−

p
j
) ≥ 0
⇔

2

p
>
+
Ω−2

p
>
j
Ω

x +

p
>
j
Ω

p
j
−

p
>
+
Ω

p
+
−
2θ(

p
+
−

p
j
)
>
Ω(

p
+
−

p
j
) ≥ 0
⇔q
>
j
x + c
j
≥ 0
(26)
where
q
>
j
= 2

p
>
+
Ω−2

p
>
j
Ω
c
j
=

p
>
j
Ω

p
j
−

p
>
+
Ω

p
+
− 2θ(

p
+
−

p
j
)
>
Ω(

p
+
−

p
j
)
(27)
Finally, we get the following linear optimization prob-
lem – note that linear programs can be solved even
faster than convex quadratic programs (Boyd and
Vandenberghe, 2014):
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. q
>
j
x
cf
+ c
j
≥ 0 ∀

p
j
∈ P (o
+
)
(28)
Again, we try all possible target prototypes

p
+
and
select the best counterfactual – everything from the
relative similarity case applies (see Section 5).
Probabilistic Certainty Measure. In order for a
samplex ∈ R
d
to be classified (i.e. not being rejected),
it must hold that:
r
Proba
(x) ≥ θ (29)
This further translates into:
r
Proba
(x) ≥ θ ⇔ max
y∈ Y
p(y |x) ≥ θ
⇔ ∃ i ∈ Y : p(y = i |x) ≥ θ
(30)
Explaining Reject Options of Learning Vector Quantization Classifiers
259

Table 3: Algorithmic properties – Mean sparsity (incl. variance) of different counterfactuals, smaller values are better, for
feasibility, larger values are better for feasibility.
DataSet Bb Eq. (9) Feasibility Algo. 2 Feasibility BlackBox Eq. (9) Algo. 2 Algo. 3
Wine 0.45 ± 0.15 0.45 ± 0.21 11.1 ± 2.09 13.0 ± 0.0 12.67 ± 0.22
Breast Cancer 0.69 ± 0.12 0.49 ± 0.02 26.43 ± 3.45 30.0 ± 0.0 26.04 ± 60.5
t21 0.82 ± 0.03 0.4 ± 0.24 15.94 ± 2.34 17.39 ± 0.64 12.55 ± 7.41
Flip 0.5 ± 0.2 0.4 ±0.24 9.5 ± 2.25 11.75 ± 0.23 11.5 ± 1.47
For the moment, we assume that i is fixed – i.e. using
a divide & conquer approach. It follows that:
p(y = i |x) ≥ θ
⇔
1
∑
j6=i
1
p(y=i|(i, j),x)
− (|Y |− 2)
≥ θ
⇔ 1 ≥ θ
∑
j6=i
1
p(y = i | (i, j),x)
− (|Y |− 2)
!
⇔
∑
j6=i
1
p(y = i | (i, j),x)
− c ≤ 0
(31)
where
c = |Y | − 2 +
1
θ
(32)
Further simplifications of Eq. (31) yield:
∑
j6=i
1
p(y = i | (i, j),x)
− c ≤ 0
⇔
∑
j6=i
1 + exp(α · r
i, j
(x) + β) − c ≤ 0
⇔
∑
j6=i
exp α
d
−
i, j
(x
cf
) − d
+
i, j
(x
cf
)
d
−
i, j
(x
cf
) + d
+
i, j
(x
cf
)
+ β
!
+ c
0
≤ 0
(33)
where
c
0
= |Y | − 1 − c = 1 −
1
θ
(34)
We therefore get the following optimization problem:
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t.
∑
j6=i
exp α
d
−
i, j
(x) − d
+
i, j
(x)
d
−
i, j
(x) + d
+
i, j
(x)
+ β
!
+ c
0
≤ 0
(35)
Because of the divide & conquer paradigm, we would
have to try all possible target classes i ∈ Y and finally
select the one yielding the lowest objective – i.e. the
closest counterfactual. While one could do this using
constraint Eq. (33), the optimization would be rather
complicated because the constraint is not convex and
rather “ugly” – although it could be tackled by an evo-
lutionary optimization method. However, the number
of optimization problems we have to solve is rather
small – it is equal to the number of classes.
We therefore, additionally, propose a surrogate
constraint which captures the same “meaning/intu-
ition” as Eq. (33) does, but is easier to optimize over
– however, note that by using a surrogate instead of
the original constraint Eq. (33) we give up closeness
which, in our opinion, would be acceptable if the so-
lutions stay somewhat close to each other
4
. We try
out and compare both approaches in the experiments
(see Section 4).
First, we apply the natural logarithm to Eq. (33)
and then bound it by using the maximum:
log
∑
j6=i
exp α
d
−
i, j
(x) − d
+
i, j
(x)
d
−
i, j
(x) + d
+
i, j
(x)
+ β
!!
≤ max
j6=i
α
d
−
i, j
(x) − d
+
i, j
(x)
d
−
i, j
(x) + d
+
i, j
(x)
+ β
!
+ log(|Y | − 1)
(36)
We therefore approximate the constraint Eq. (33) by
using Eq. (36), which yields the following constraint:
max
j6=i
α
d
−
i, j
(x) − d
+
i, j
(x)
d
−
i, j
(x) + d
+
i, j
(x)
+ β
!
≤ log(−c
0
)
− log(|Y |− 1)
(37)
Note that, in theory it could happen that −c
0
≤ 0 – we
fix this by simply taking max(−c
0
,ε), which results
in a feasible solution but the approximation gets a bit
worse.
Assuming that the maximum j is fixed, we get the
following constraint:
d
−
i, j
(x) − d
+
i, j
(x)
d
−
i, j
(x) + d
+
i, j
(x)
≤ γ (38)
where
γ =
log(−c
0
) − log(|Y | − 1) − β
α
(39)
Further simplifications reveal that:
d
−
i, j
(x) − d
+
i, j
(x)
d
−
i, j
(x) + d
+
i, j
(x)
≤ γ
⇔ (1 − γ)d
−
i, j
(x) − (1 + γ)d
+
i, j
(x) ≤ 0
⇔ (γ − 1)d
−
i, j
(x) + (1 + γ)d
+
i, j
(x) ≥ 0
(40)
4
Furthermore, in case of additional plausibility & ac-
tionability constraints, closeness becomes even less impor-
tant.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
260

Next, we assume that the closest prototype with the
correct label is fixed and denote it by

p
i
– we de-
note prototypes from the other class as

p
j
. In the
end, we iterate over all possible closest prototypes

p
i
and select the one that minimizes the objective
(i.e. closeness to the original sample) – note that
this approximation drastically increases the number
of optimization problems that must be solved and thus
the overall complexity of the final algorithm. We
then can rewrite Eq. (40) as follows – we make sure
that Eq. (40) is satisfied for every possible

p
−
:
(γ − 1)d
−
i, j
(x) + (1 + γ)d
+
i, j
(x) ≥ 0
⇔ (γ − 1)d(x,

p
j
) + (1 + γ)d(x,

p
i
) ≥ 0 ∀

p
j
∈ P (o
i
)
(41)
Applying even more simplifications yield:
(γ − 1)d(x,

p
j
) + (1 + γ)d(x,

p
i
) ≥ 0
⇔ (γ − 1)

x
>
Ωx − 2

p
>
j
Ωx +

p
>
j
Ω

p
j

+
(1 + γ)

x
>
Ωx − 2

p
>
i
Ωx +

p
>
i
Ω

p
i

≥ 0
⇔ 2γx
>
Ωx − 2(γ − 1)

p
>
j
Ωx − 2(1 + γ)

p
>
i
Ωx+
(γ − 1)

p
>
j
Ω

p
j
+ (1 + γ)

p
>
i
Ω

p
i
≥ 0
⇔x
>
Ωx +q
>
j
x + c
j
≤ 0
(42)
where
q
>
j
=
1
−2γ

−2(γ − 1)

p
>
j
Ω−2(1 + γ)

p
>
i
Ω

c
j
=
1
−2γ

(γ − 1)

p
>
j
Ω

p
j
+ (1 + γ)

p
>
i
Ω

p
i

(43)
Finally, we get the following convex quadratic opti-
mization program:
min
x
cf
∈R
d
kx
orig
−x
cf
k
1
s.t. x
>
Ωx +q
>
j
x + c
j
≤ 0 ∀

p
j
∈ P (o
i
)
(44)
Note that we have to solve Eq. (44) for every pos-
sible closest prototype, every possible class different
from the i-th class and finally for every possible class.
Thus, we get the following number of optimization
problems (quadratic in the number of classes):
|Y | · (|Y | − 1) · P
N
= |Y |
2
· P
N
− |Y |· P
N
(45)
where P
N
denotes the number of prototypes per class
used in the pair-wise classifiers.
Note that this number is much larger than |Y |
which we got without introducing any surrogate or
approximation. However, in contrast to Eq. (35), the
surrogate Eq. (44) is much easier to solve because it
is a convex quadratic program which are known to be
solved very fast (Boyd and Vandenberghe, 2014).
Additional Empirical Results
Probabilistic Reject Option
The results for the different methods for computing
counterfactual explanations of the probabilistic reject
option Eq. (6) are given in Table 3.
Explaining Reject Options of Learning Vector Quantization Classifiers
261