
MLP-Supported Mathematical Optimization of Simulation Models:
Investigation into the Approximation of Black Box Functions of Any
Simulation Model with MLPs with the Aim of Functional Analysis
Bastian Stollfuss
1,2
and Michael Bacher
2
1
University Stuttgart, Stuttgart, Germany
2
University of Applied Science, Kempten, Germany
Keywords: Machine Learning, Supervised Learning by Regression, Mathematical Analysis, Approximation, Material
Flow Simulation, Process Optimization, Artificial Neuronal Network, Newton’s Method.
Abstract: This paper contains results from a feasibility study. The optimization of manufacturing processes is an
elementary part of economic thinking and acting. In many cases, complex processes have unknown analytical
and mathematical methods. If mathematical functions for the behaviour of a process are missing, one often
tries to optimize the process according to the trial-and-error principle in combination with expertise. However,
this method requires a lot of time, computational resources, and trained personnel to validate the results. The
method developed below can significantly reduce these cost factors by mathematically optimizing the
unknown functions of a complex system in an automatic process. This is accomplished with discrete
performance and behaviour measurements. For this purpose, an approximate prediction function is modelled
using a multi-layer perceptron (MLP). The resulting continuous function can now be analysed with
mathematical optimization methods. After formulating the learned prediction function, it is examined for
minima using Newton’s method. It is not necessary to know the exact mathematical and physical context of
the system that needs improving. Calculating a precise interpolation also results in further optimization and
visualization options for the production plant.
1 INTRODUCTION
The modern-day possibilities of digitization mean
that given processes are not simply adopted, but also
optimized. Especially in information technology and
business informatics, process or data mining, data
science, process management, artificial intelligence
(AI) are implemented as a matter of course (Laue et
al. 2021), (Li Zheng, Chunqiu Zeng, Lei Li, Yexi
Jiang, Wei Xue, Jingxuan Li, Chao Shen, Wubai
Zhou, Hongtai Li, Liang Tang, Tao Li, Bing Duan,
Ming Lei, Pengnian Wang 2014). Data-driven
process optimization is a huge topic of industry 4.0
(Paasche und Groppe 2022). This paper concerns the
feasibility of a new method of data-driven process
optimization.
If mathematical functions for the description of a
process are missing, one often tries to optimize the
process according to the archaic trial and error
principle (Bei et al. 2013).
When optimizing the simulation models, which
involved expert knowledge, empirical values and trial
and error in combination with expertise were mainly
used. The methodology is inefficient because of the
missing explanation component, which is replaced by
manual documentation and the associated high time
duration and human resources. This approach offers
opportunities for optimization by approximating the
discrete black box function of the simulation model
through a continuous function. Plant simulations do
not generate a continuous function, which would be
necessary for further mathematical processing (Rubin
et al. 1993).
We have to find a continuous approximation
function with an effective optimization and
subsequent return of the found results to the
simulation model.
The state of the art and the theory building of this
paper are summered in chapter 1. Chapter 2 covers
the system developed including plant simulation,
designing an MLP, definition of validation
parameters, training of the MLP, mathematical
Stollfuss, B. and Bacher, M.
MLP-Supported Mathematical Optimization of Simulation Models: Investigation into the Approximation of Black Box Functions of Any Simulation Model with MLPs with the Aim of Functional
Analysis.
DOI: 10.5220/0011379800003329
In Proceedings of the 3rd International Conference on Innovative Intelligent Industrial Production and Logistics (IN4PL 2022), pages 107-114
ISBN: 978-989-758-612-5; ISSN: 2184-9285
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
107

optimization. Chapter 3 contains the evaluation of the
developed system. Chapter 4 is discussing the
research results. The following chapter 5 gives a
Summary of our results. Finally, chapter 6 gives an
insight into the future research perspectives.
1.1 State of the Art
The topics of the optimization methods, which are
presented in the publications discussed, are artificial
neural network (ANN), Support Vector Regression
(SVR), Immune Particle Swarm Optimization
(IPSO), multi-layer perceptron (MLP), mathematical
optimization (MO), autoregressive integrated moving
average (ARIMA), evolutionary algorithm (EA).
The Paper (Yan Wang, Juexin Wang, Wei Du,
Chen Zhang, Yu Zhang, Chunguang Zhou 2009) is
about the downstream optimization of the SVR
learning method with the help of IPSO. It's about
improving hyperparameters of the SVR. In this work
the hyperparameter setting of the SVR is optimized
via IPSO.
The authors in (Andrei Solomon 2011) use
different prediction models, including ARIMA and
linear regression on time series, to improve the
simulation process parameters.
In (Ankur Sinha, Pekka Malo, Peng Xu,
Kalyanmoy Deb 2014), like SVR, hyperparameters
should be optimized. It's not about optimizing the
result, but about optimizing the hyperparameters for
a machine learning process. Bilevel optimization is a
special kind of programming in which an
optimization problem is embedded in an outer and
inner optimization problem, with an upper and lower
bound on the boundary conditions.
Generic algorithms are special optimization
methods in the field of evolutionary algorithms. The
publication (Nadir Mahammed, Souad Bennabi,
Mahmoud Fahsi 2020) deals with the optimization of
a business model design by Genetic Algorithm based
on multiple populations. Based on the business model
design, a mathematical representation is created and
fed into the optimization process. Starting with an
initial population, descendants are selected with the
help of an evaluation function and subsequent
selection. The selected offspring are modified and
entered into the original population. A new
population is obtained as the return value of the
evaluation function, which is processed in the same
way. The result is optimally parameterized business
process. Business process parameters have been
improved and greater diversity has been achieved.
Basically, the trial-and-error process is developed
further here because the random factor is preserved.
(B. Cavallo, M. D. Penta, and G. Canfora 2010) is
about an empirical study to reliably predict Quality of
Service (QoS). Various prediction models are used
for this, as Andrei Solomon in (Andrei Solomon
2011) ARIMA was also used here. For further
information see (Box 2015).
From the data generated in an industrial process,
the parameters are analysed with the help of data
mining (Li Zheng, Chunqiu Zeng, Lei Li, Yexi Jiang,
Wei Xue, Jingxuan Li, Chao Shen, Wubai Zhou,
Hongtai Li, Liang Tang, Tao Li, Bing Duan, Ming
Lei, Pengnian Wang 2014). The results are analysed
and processed, and the process parameters are
optimized using possibility theory and linear
regression.
In the publication (Zhaoxia Chen, Bailin He, and
Xianfeng Xu 2011), an ANN with backpropagation
(BP) is used directly to optimize processes. The data
is generated by a measuring stand. The structure of
the ANN is not analysed in detail, but the ANN
outputs the control parameters for the machine
directly. So direct error minimization takes place via
the ANN and BP.
Mathematical optimization is also a discipline of
applied mathematics. Like analytics, it is about
finding optimal parameters in a system so that a target
function can be minimized or maximized. An
analytical solution of optimization problems is often
not possible or too time-consuming and could be
replaced or supplemented by numerical methods.
However, the mathematical function to be analysed is
often unknown. Optimization is therefore also a
problem of approximation, which involves
minimizing the distance between two functions in
order to then process the function further (Alpaydın
2019).
In the method developed by the mining engineer
D. G. Kriging, a solution to the specific problem is
described, which determines promising locations for
further drilling sites with increased ore deposits based
on previous drilling sites. To achieve this, he
designed a method that became known as the Kriging
method or Gaussian Process Regression and thus
developed one of the first machine learning methods.
It is still used today when a function is to be
maximized for which an evaluation of the function
parameters is very complex and whose mathematical
derivations are not available (JARRE und Stoer
2019).
Because process optimization is a ‘black box
problem’, the use of ANN is suitable. The process
optimization creates large amounts of data from
which information is to be extracted, taking the black
box system into account. By training the ANN with
IN4PL 2022 - 3rd International Conference on Innovative Intelligent Industrial Production and Logistics
108
the discrete output values, we get a prediction
function. The weights are adjusted by the
backpropagation algorithm. We use the method
similar to the Gaussian process to solve a regression
problem. In our case, we use MLP for the following
task. The production times or cycle times represent
the output values depending on the input parameters
of the prediction function.
1.2 Hypothesis
The hypothesis of this study concerned whether an
MLP is able to approximate an unknown function
with sufficient accuracy in order to be able to draw
conclusions as to where the minima or maxima of this
unknown function are located.
1.3 Objective
The aim was to test an optimization method that uses
MLP to approximate functions in order to then
examine the prediction function for optima. The
optima found should be validated by returning them
to the simulation model. Furthermore, it should be
examined whether this method is better suited than
trial and error methods.
2 METHODS
2.1 Summary
Production plants can be simulated as a Blackbox
function with the input parameters A and B and the
output C, as cited below. C needs to be optimized
with the input parameters A and B. MLPs are able to
carry out universal approximations of Blackbox
functions (Alpaydın 2019). In our case the MLP
should now approximate the unknown function of the
simulation of a production plant. The resulting
prediction function is known in its entirety and can be
MO. Specifically, the goal is that after the learning
process, the MLP should behave exactly like the
simulation. The MLP used is extended by a special
activation function. Based on Fourier, the sine
function is used instead of the frequently used
sigmoid function (Egger 2006). The backpropagation
algorithm and Newton’s method can be easily
implemented through the simple symbolic derivation
of the sine function.
After successful training of the MLP, the
determined weights of the connections are saved.
With the known structure and the stored weights of
the MLP, the prediction function is formulated by a
self-implemented program. The prediction function
built in this way results in C´ depending on A and B.
C´ approximates C. C´ is now to be mathematically
optimized depending on A and B using the Newton
method. The parameters A and B can be determined
by the found minima of C´. The quality of the
prediction function can be verified by directly
comparing the Blackbox function output C with the
prediction function output C´. The MO works
automatically, apart from the hyperparameter
settings.
2.2 Simulation
The feasibility of the process described above is to be
proven and analysed using a material flow simulation.
A production plant should be optimized regarding its
cycle time. For this purpose, concrete data sets of this
production plant were first generated with a material
flow simulation.
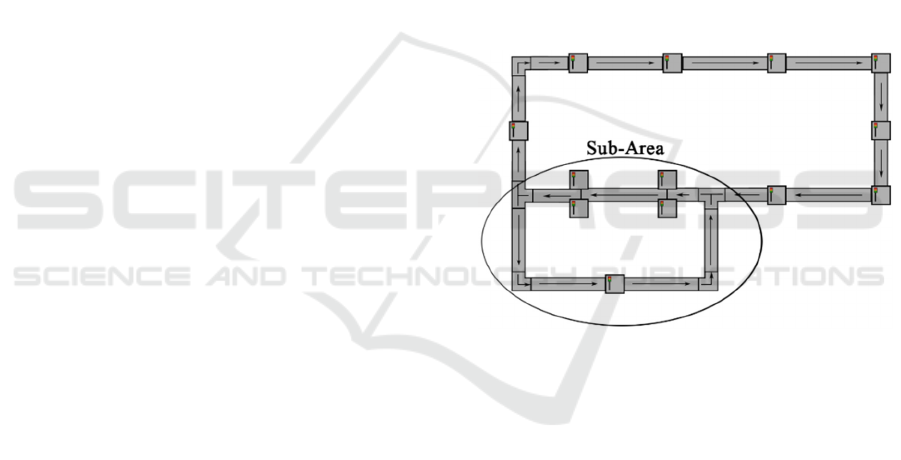
Figure 1: Production plant.
The data records created contained the variable
parameters: workpiece carriers in the system and
permitted simultaneous number of workpiece carriers
in a part of the system (Sub Area), shown in Figure 1.
The training data generated by the simulation model
were discrete data pairs, which were then used for the
supervised learning of the MLP. The data were
automatically generated and mapped a combinatorial
grid over the area of interest.
The area of definition of the black box function to
be examined is the area in which a minimum is
assumed or an area that is determined by external
specifications and limitations. The simulation
calculated an output data structure containing the
cycle times with which the finished workpieces left
the system (Table 1).
MLP-Supported Mathematical Optimization of Simulation Models: Investigation into the Approximation of Black Box Functions of Any
Simulation Model with MLPs with the Aim of Functional Analysis
109
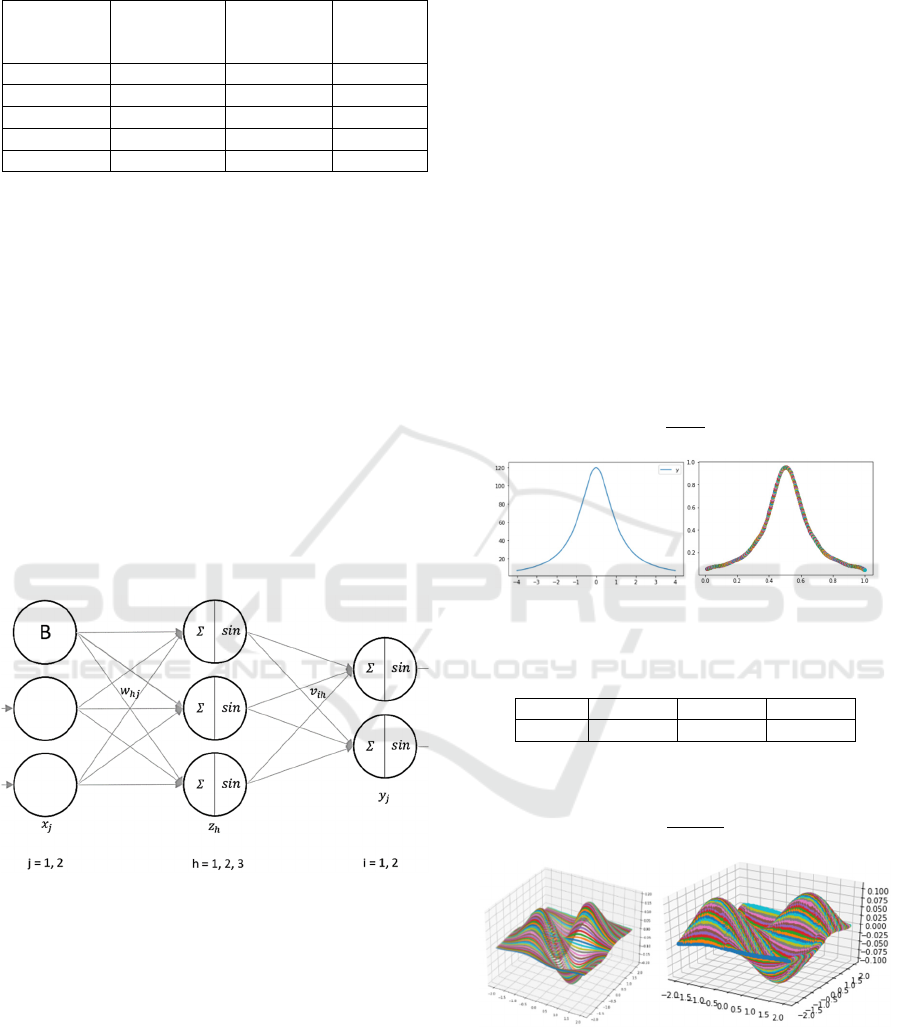
Table 1: Output data.
Workpiece
carriers
Produced
Workpieces
Workpiece
carriers in
sub-area
Average
cycle
time [s]
94 1000 5 707.4768
94 1000 6 688.9963
94 1000 7 682.2486
94 1000 8 671.8879
94 1000 9 670.1345
The structure of the output data is formed as a grid
area. The cycle time must be minimized by correctly
setting the variable parameters to improve the overall
productivity of the system. A prediction function is
now formulated from the MLP so that it can be
mathematically optimized.
2.3 Modified MLP
For this purpose, an MLP was created to train the data
sets, in this case the cycle time depending on the
variable system parameters. The MLP used was
expanded to include the sine function as an activation
function as shown in Figure 2, with amplitude a,
angular frequency ω and phase ϕ. Since the cosine
function is only phase-shifted, it is also described
(Papula 2014).
Figure 2: Illustration of the network structure with modified
activation function.
The property of a simple derivation of the sine or
cosine function forms the basis for the idea of using
this as an activation function. Since the weights
should not diverge or convert to zero during the
learning process, the input and output values were
normalized beforehand. The backpropagation
algorithm was used to adjust the weights in the
learning process. Depending on the previous weights,
this propagates the error back and adjusts the current
weights according to their influence.
2.4 Validation
Various error parameters were calculated to evaluate
the quality of the prediction function, including
RMSE, MAE and
R
(Alpaydın 2019).
Since this is a new activation function that cannot
be set in the usual libraries, the MLP was self-
implemented. Known functions for determining the
quality of the MLP were used to test the created
program code for correct functionality. The first test
runs took place with random well-known (Eq. 1., Eq.
2), two-dimensional functions. Once these could be
approximated very well after setting the
hyperparameters, the test was extended to three-
dimensional functions, which also has been
successfully approximated.
2.4.1 2D-Function
f
x
=
120
x
2
+1
(1)
Figure 3: Original function (left) and funtion approximation
(right).
Table 2: Results of test run with 2d function.
E
p
och RMSE MAE R2
198 0.287285 0.215675 0.999898
2.4.2 3D-Function
f
x
=
x⋅y
ⅇ
x
2
+y
2
(2)
Figure 4: Original function (left) and function
approximation (right).
The pairwise-compared functions, original function
and approximation agree in a self-defined quality
criterion up to 2% MAE. (Figure. 3,4) and Table 2,
Table 3.
IN4PL 2022 - 3rd International Conference on Innovative Intelligent Industrial Production and Logistics
110

Table 3: Results of test run with 3d function.
Epoch RMSE MAE R2
19 1.192364 0.780794 0.998744
2.5 Training
The data set generated by the simulation contains
about 650 labelled data (Fig. 5). After successful
online learning, the MLP can predict the cycle time
with a corresponding level of accuracy, which can be
found in Table 4.
Figure 5: Plot of the data set calculated by the simulation
model.
Figure 6: Approximation of the data set by ANN4.
The prediction function of the fully trained MLP,
which is shown in Fig. 6, was now used to find the
minima of the cycle time. The prediction function was
extracted using a program designed for this purpose.
The number of summed and nested sine functions is
defined by the structure of the MLP. The learned
weights were each inserted as a factor in front of the
individual sine functions. Since the nesting and the
summation always follow the same pattern, this
surrogate function was created in different “for-
loops”. At the end of the algorithm, the finished
prediction function was outputted.
Table 4: Results of the MLP training.
MLP: Epoch RMSE MAE
𝑅
MLP1 904 0.069216 0.054091 0.834757
MLP2 312 0.055734 0.047214 0.883755
MLP3 21815 0.053844 0.044480 0.830314
MLP4 7803 0.041716 0.034093 0.941049
For the purpose of mathematically optimizing the
prediction function, minima were now sought in the
area shown in Table 5. The definition area of the
prediction function (Fig. 6) consists of the limited
ranges of the input parameters. The range of
parameters to be examined was between 20 100
workpiece carriers in the entire system and 5 20
workpiece carriers in the limited sub-area of the
system (Fig. 1).
Table 5: Limits of the generated data set.
Workpiece
carriers [n]
Workpiece
carriers in
sub-area[n]
Average
cycle
time [s]
Lower limit 20 5 640.64
Upper limit 100 20 862.65
Increment 2 1
2.6 Mathematical Optimization
The Newton method as an iteration method is very
well suited to finding extreme points. For this
purpose, the first and second partial derivatives of the
prediction function were formed first. Since the
prediction function only consists of nested and
weighted sine functions, it can be derived simply
symbolically, and a numerical derivation is not
necessary. This avoids rounding errors and
discretization errors. The second partial derivatives
MLP-Supported Mathematical Optimization of Simulation Models: Investigation into the Approximation of Black Box Functions of Any
Simulation Model with MLPs with the Aim of Functional Analysis
111
were assembled into the Jacobian matrix, which is
used in the so-called Newton step to determine the
local gradient of the prediction function. Since there
are multidimensional extreme points, it must be
checked whether each extremum is a minimum in all
dimensions by using the Jacobian matrix.
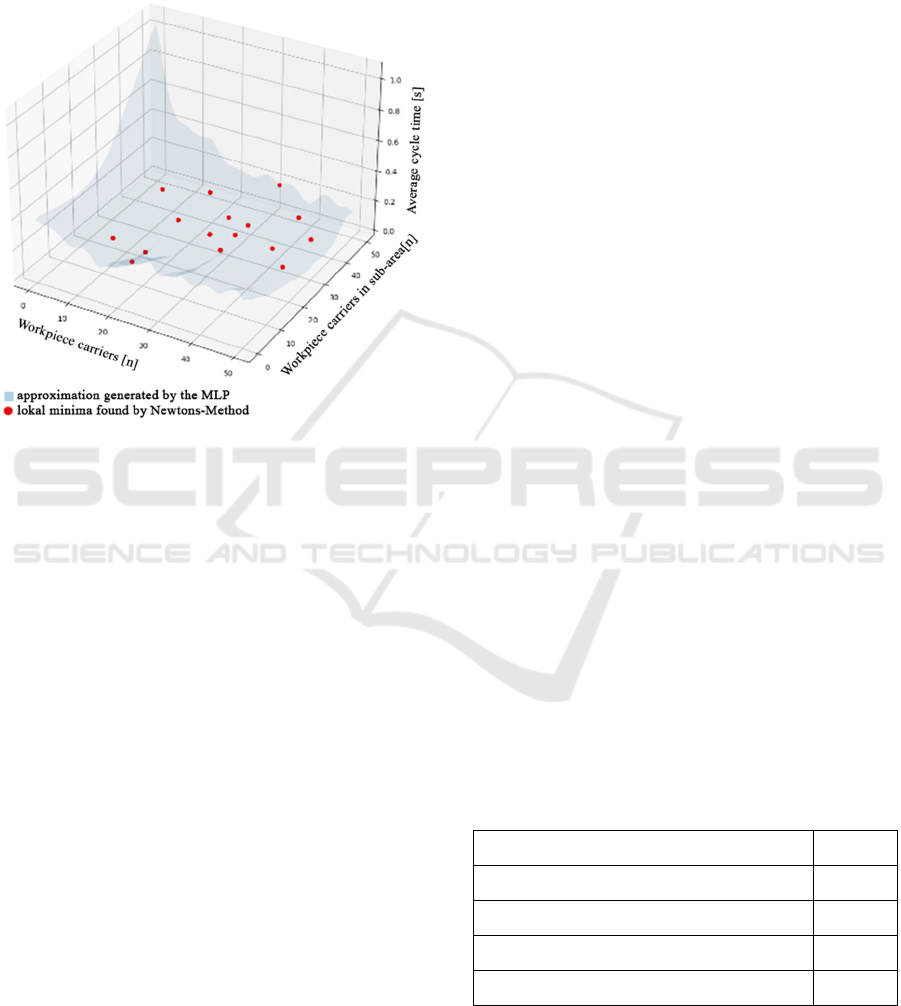
Figure 7: Approximation by MLP3P4 and identified
minima.
A starting point in the definition area is first
defined in the Newton´s method, after which several
Newton steps are carried out from this starting point.
The starting point can converge to a local minimum.
If the starting point diverges, the program aborts after
a certain number of Newton steps. In order to find as
many local minima as possible in the target area, a
combinatorial grid out of the definition area with the
required resolution of starting points was created.
Now local minima of the cycle time and their
responsible parameters in the prediction function
could be determined using the Newton method
(Figure 7).
The parameters of the calculated local minima
were converted to inverse the normalization that was
initially introduced. Then, the parameters found,
which lead to a minimum of the cycle time were
entered into the simulation for evaluation. Finally, it
was checked whether a shorter cycle time was
achieved with the calculated parameters.
3 EVALUATION
As a result, it was possible to train the MLP in such a
way that the cycle time of the plant could be predicted
with a high degree of certainty (Table 4). The
function of the best MLP approximates the behaviour
of the simulation model regarding the cycle time with
a coefficient of determination R
2
up to 0.94. The mean
absolute error corresponded to about 7.56 seconds out
of an average of 686.63 seconds for the cycle time
(1.1%). The result is better than the deviation of 2%
determined with the test functions in section 2.4.
After successfully training and extracting the
prediction function, it could be visualized as a
continuum. Checking the found minima provides
certainty, and the procedure does not require human
assistance, but works automatically.
If the predicted minima were greater than the
values calculated by the simulation, they were
classified as incorrect. The incorrectly predicted
minima could be traced back to interpolation
inaccuracies. The global minimum was determined
by paired comparison of all local minima. In four of
the 16 MLPs examined, an improvement in the cycle
time was achieved due to mathematical optimization.
The data set for all 16 MLPs examined includes
around 10,000 label data. In order to compare the
mathematically optimized procedure with the trial-
and-error method, randomly selected parameter
combinations were entered manually, and the results
collated to a test suite.
Collecting the data from the trial-and-error
method should take about as long as the procedure of
the developed algorithm.
For this purpose, the time required for training the
MLP and mathematical optimization was calculated,
as shown in Table 6.
For the benchmark of the MLP and MO versus
trial and error, both processes are given 6 hours to
find the global minimum of the cycle time. The trial-
and-error test suite mentioned above was generated in
6 hours by hand. In contrast to the trial-and-error
procedure, training the MLP by hand only takes 2
hours, thus saving 4 man-hours.
Table 6: Duration time.
650 data generated automatically 1.5 h
Training 2 h
Determining minima and global minimum 2 h
Other steps of procedure 0.5 h
Sum 6 h
The data set comprised 500 data pairs (Fig. 8).
Due to the manual input of the parameters and the
aimless generation of data, the data record is shorter
IN4PL 2022 - 3rd International Conference on Innovative Intelligent Industrial Production and Logistics
112
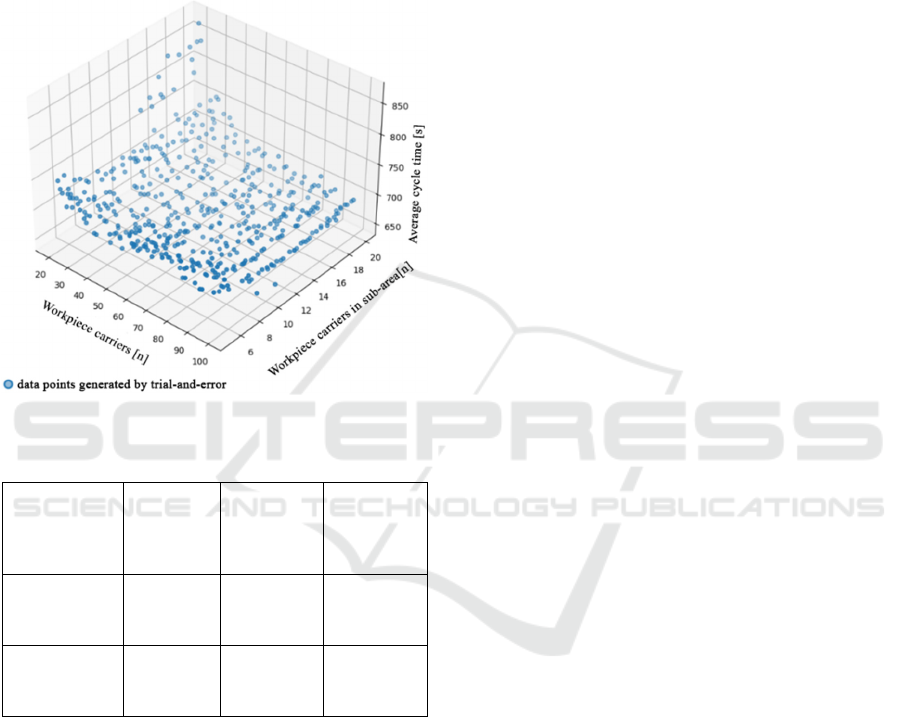
than the automatically generated data record. In
addition, it is not as evenly distributed over the
definition area, while the MLP dataset is discrete.
The global minimum in this dataset is 646,78s.
The global minimum determined by trial and error is
5.12s worse than the minimum time determined by
the MLP and the mathematical optimization, shown
in Table 7.
Figure 8: Test suite.
Table 7: Results.
Process Global
Minimum
[s]
Workpiece
carrier
[n]
Workpiece
carrier in
sub-area
[n]
MLP and
mathematical
optimization
641.66 100 17
Trial and
error in Plant
Simulation
646.78 92 15
4 DISCUSSION
Process optimization of complex manufacturing
systems, which is used in many production plants, is
often difficult and confusing in practice, since the
mathematical and physical relationships of the factors
influencing the system are not known, resulting in a
black box function.
Finding suitable hyperparameters for the
respective learning task is sometimes very time-
consuming. However, once hyperparameters were
found, they could be used again and again for the
application. The time required to train the MLP was
2 hours, on average, requiring no further work steps
by hand. However, the calculation time was
dependent on external factors, such as the number of
input data, size of the MLP, number of epochs,
performance of the source code, and the performance
of the computing components. Overall, however, very
good automation of the process was possible.
Furthermore, only short, wide MLPs could be
evaluated, as the gradient calculation for long, narrow
MLPs is significantly more complex. The reason for
this lies in the partial derivatives for the gradient
method, which are calculated symbolically. The
extracted function is a nesting of the transfer and
activation function. Thus, the need for post-
differentiation increases exponentially with each
additional layer.
5 SUMMARY
Training an MLP with a complex black box function
has proven to be feasible. In some cases, a cycle time
advantage of the MLP and MO procedure compared
to the trial-and-error method could also be shown.
This benefit is tied to its definition area. This means
that the global minimum is outside of our definition
area. In this case it is only a local minimum inside the
definition area. However, the definition range was
realistic from a technical point of view. For example,
it is not possible to feed any number of workpiece
carriers into a limited conveyor belt section, even if
this would result in infinitely short cycle times.
The process can be automated in the main and, in
the case of complex problems, is faster than the trial-
and-error method due to the reduction in manual
work. This results in a productivity advantage
through the saving of human resources. With the
method using MLPs and MO, it is not necessary to
know the exact mathematical and physical
relationships of the Blackbox system to be improved.
6 PERSPECTIVE
The MLP and MO procedure can also be applied to
other functions. In this way, functions could be
predicted for which there are no simulation models.
In this case, a test stand forms the basis from which
empirically discrete data can be obtained, but the
exact mathematical function behind the system is
unknown. With the help of base values, a prediction
function is interpolated with MLPs. The subject of a
MLP-Supported Mathematical Optimization of Simulation Models: Investigation into the Approximation of Black Box Functions of Any
Simulation Model with MLPs with the Aim of Functional Analysis
113

further publication could be a performance evaluation
and comparison between the MLP and MO procedure
and the trial-and-error procedure on a simulation
model.
REFERENCES
Alpaydın, Ethem (2019): Maschinelles Lernen. 2. Auflage.
Berlin, Boston: De Gruyter (De Gruyter Studium).
Andrei Solomon, Marin Litoiu (2011): Business Process
Performance Prediction on a Tracked Simulation
Model. In: Manuel Carro (Hg.): Proceedings of the 3rd
International Workshop on Principles of Engineering
Service-Oriented Systems. New York, NY: ACM
(ACM Conferences), S. 50–56.
Ankur Sinha, Pekka Malo, Peng Xu, Kalyanmoy Deb
(2014): A Bilevel Optimization Approach to
Automated Parameter Tuning. In: Proceedings and
companion publication of the 2014 Genetic and
Evolutionary Computation Conference, July 12 - 16,
2014, Vancouver, BC, Canada ; a recombination of the
23rd International Conference on Genetic Algorithms
(ICGA) and the 19th Annual Genetic Programming
Conference (GP) ; one conference - many mini-
conferences ; [and co-located workshops proceedings].
New York, NY: ACM, S. 847–854.
B. Cavallo, M. D. Penta, and G. Canfora (2010): An
empirical comparison of methods to support QoS-
aware service selection. In: Grace A. Lewis (Hg.):
Proceedings of the 2nd International Workshop on
Principles of Engineering Service-Oriented Systems.
New York, NY: ACM (ACM Conferences), S. 64–70.
Bei, Xiaohui; Chen, Ning; Zhang, Shengyu (2013): On the
complexity of trial and error. In: Dan Boneh, Tim
Roughgarden und Joan Feigenbaum (Hg.): Proceedings
of the 45th annual ACM symposium on Symposium on
theory of computing - STOC '13. the 45th annual ACM
symposium. Palo Alto, California, USA, 01.06.2013 -
04.06.2013. New York, New York, USA: ACM Press,
S. 31.
Box, George E. P. (2015): Time Series Analysis.
Forecasting and Control. 5th ed. Hoboken: Wiley
(Wiley Series in Probability and Statistics).
Egger, Dieter (2006): Sinus-Netzwerk. In: TU München:
Schriftenreihe des Instituts für Astronomische und
Physikalische Geodäsie und der Forschungseinrichtung
Satellitengeodäsie 22.
Jarre, Florian; Stoer, Josef (2019): Optimierung.
Einführung in mathematische Theorie und Methoden.
2. Auflage. Berlin, Heidelberg: Springer Spektrum
(Masterclass).
Laue, Ralf; Koschmider, Agnes; Fahland, Dirk (Hg.)
(2021): Prozessmanagement und Process-Mining.
Grundlagen. Berlin/München/Boston: Walter de
Gruyter GmbH (De Gruyter Studium Ser). Online
verfügbar unter https://ebookcentral.proquest.com/lib/
kxp/detail.action?docID=5156279.
Li Zheng, Chunqiu Zeng, Lei Li, Yexi Jiang, Wei Xue,
Jingxuan Li, Chao Shen, Wubai Zhou, Hongtai Li,
Liang Tang, Tao Li, Bing Duan, Ming Lei, Pengnian
Wang (2014): Applying Data Mining Techniques to
Address Critical Process Optimization Needs in
Advanced Manufacturing. In: Proceedings of the 20th
ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining, August 24 -
27, 2014, New York, NY, USA. New York, NY: ACM,
S. 1739–1748.
Nadir Mahammed, Souad Bennabi, Mahmoud Fahsi
(2020): Optimizing Business Process Designs with a
Multiple Population Genetic Algorithm. In: Richard
Chbeir (Hg.): Proceedings of the 10th International
Conference on Web Intelligence, Mining and
Semantics. New York, NY,United States: Association
for Computing Machinery (ACM Digital Library), S.
252–254.
Paasche, Simon; Groppe, Sven (2022): Enhancing data
quality and process optimization for smart
manufacturing lines in industry 4.0 scenarios. In: Sven
Groppe, Le Gruenwald und Ching-Hsien Hsu (Hg.):
Proceedings of The International Workshop on Big
Data in Emergent Distributed Environments.
SIGMOD/PODS '22: International Conference on
Management of Data. Philadelphia Pennsylvania, 12 06
2022 12 06 2022. New York, NY, USA: ACM, S. 1–7.
Papula, Lothar (2014): Mathematik für Ingenieure und
Naturwissenschaftler. 14., überarb. und erw. Aufl.
Erscheinungsort nicht ermittelbar (Mathematik für
Ingenieure und Naturwissenschaftler).
Rubin, Stuart H.; Fogel, David; Hanson, John C.; Kick,
Russell; Malki, Heidar A.; Sigwart, Charles et al.
(1993): The impact of machine learning on expert
systems. In: Stan C. Kwasny und John F. Buck (Hg.):
Proceedings of the 1993 ACM conference on Computer
science - CSC '93. the 1993 ACM conference.
Indianapolis, Indiana, United States, 16.02.1993 -
18.02.1993. New York, New York, USA: ACM Press,
S. 522–527.
Yan Wang, Juexin Wang, Wei Du, Chen Zhang, Yu Zhang,
Chunguang Zhou (2009): Parameters Optimization of
Support Vector Regression Based on Immune Particle
Swarm Optimization Algorithm. In: 2009 World
Summit on Genetic and Evolutionary Computation.
2009 GEC Summit; June 12 - 14, 2009, Shanghai,
China. New York, NY: ACM Press, S. 997–1000.
Zhaoxia Chen, Bailin He, and Xianfeng Xu (2011):
Application of Improved BP Neural Network in
Controlling the Constant-Force Grinding Feed. In:
Computer and computing technologies in agriculture
IV. 4th IFIP TC 12 conference, CCTA 2010, Nanchang,
China, October 22-25, 2010; selected papers.
Heidelberg: SPRINGER (IFIP advances in information
and communication technology, 347), S. 63–70.
IN4PL 2022 - 3rd International Conference on Innovative Intelligent Industrial Production and Logistics
114
