The Impact of Marketing Mix’s Efficacy on the Sales Quantity based

on Multivariate Regression

Yisheng Chen

1,† a

, Xiankang Liu

2,† b

and Peikun Xu

3,† c

Letter and Science, University of California Davis, Davis, U.S.A.

Tianjin Yinghua International School, Tianjin, China

3411267425@qq.com

Kunming NO.8 High School Kunming, China

15368002979@163.com

†

These authors contributed equally

Keywords: Multivariate Regression, Sales Prediction, P-Value Test.

Abstract: In this paper, we aim at investigating the effect of marketing mix on the demand of a new low-carbohydrate

food product, K-Pack. The key variables of marketing mix with respect to the total sales, 24 datasets in total,

are price, advertising, location and cities. To figure out which variables strongly affects the total sales, the test

will comprise two parts: Model selection and Model inference. Under the first part, the dataset will be

resampled to reduce the bias while assuming the assumptions of linear regression are met. When constructing

the model, a Hypothesis validation will be carried out to ensure the variables are statistically significant.

Considering the Inference section, several statistics metrics and features (coefficient, R squared and AIC) will

be presented in table formats for Data Analysis. Instead of focusing on all the marketing mix to determine the

demand, the company should only consider Price, Advertising, City index, Store Volume and interaction

between Price and Store Volume as efficacious. These results offer a guideline and new insight for sales

predictions based on multivariate linear regression.

1 INTRODUCTION

Generally, the sales prediction plays a vital role

especially when a smart food company decides to

produce a new kind of healthy snack (Zliobaite,

Bakker, Pechenizkiy, 2012, Zliobaite, Bakker,

Pechenizkiy, 2009, Tsoumakas, 2019, Xin, Ichise,

2017, Bakker, Pechenizkiy, 2014). However, as for

the short life cycle products, one is unable to know the

demand of customers on the market. The reason can

be attributed to that the company did not sell this kind

of new product in the past (Meeran, Dyussekeneva,

Goodwin, 2013). Besides, sales prediction is the

process of estimating future revenue by analyzing the

available data.

The research will utilize data from a specific case

to illustrate the predict sales number in the future.

Specifically, we decide to observe whether sales will

meet the expectation number of 750,000 cases or not.

https://orcid.org/ 0000-0002-0674-759X

https://orcid.org/ 0000-0002-2040-2272

https://orcid.org/ 0000-0002-6209-8862

In the previous research, we find that there are three

main objects, the first one is about to develop a

structure to calculate the current state of research

conducted within marketing strategy; the second one

is about to describe the “description of knowledge” in

development and execution of marketing strategy; the

last one is about to develop a research topic which can

identify different kinds of better marketing strategy.

Based on previous literature, it is found that

multifactorial linear model is an outperformance

approach (Blech, et al, 2011, Sarukhanyan, et al, 2014,

Braga, et al, 2019, Ye, Yang, 2020, Reinsel, 1984).

The whole process starts with the goals of the forecast.

Then, one ought to understand the average sales cycle.

Afterwards, it is crucial to get buy-in to the model

construction. Then, sales process can be formalized

accordingly. Subsequently, the historical data is

utilized for training to establish seasonality, which

determines sales forecast maturity eventually.

Chen, Y., Liu, X. and Xu, P.

The Impact of Marketing Mix’s Efﬁcacy on the Sales Quantity based on Multivariate Regression.

DOI: 10.5220/0011349500003440

In Proceedings of the International Conference on Big Data Economy and Digital Management (BDEDM 2022), pages 795-800

ISBN: 978-989-758-593-7

795

Overall, we will investigate K-Pack’s 4-month

marketing performance based on data, and 2

marketing strategies (both reach the expectation) are

proposed according to the analysis. The rest part of the

paper is organized as follows. The Sec. 2 will

introduce the data analysis methods. Afterwards, the

regression results will be displayed and explained.

Eventually, a brief summary is given in Sec. 5.

Besides, the linear regression is applied at the field of

the measurement of the median particle size of drugs

and pharmaceutical excipients by near-infrared

spectroscopy.

2 DATA & METHOD

The data was aimed to test out which variables affects

the sales of K-packs includes 24 objects with different

conditions: Price [50,60,70], Advertisement

[advertising, non-advertising], Location [bakery,

breakfast section] and Cities [A, B, C, D]. Before

carrying out statistically analysis, the data needs to be

re-arranged with corresponding dummy variables so

that we could test multiple groups within only one

regression model: Price expanded to P

, P

and P

;

is the reference level, which is a baseline for the

model only containing given items. Advertisement

expanded to Advertising at 3 million and advertising

at 3.5 million; advertising at 3.5 million is the

reference level. Location expanded to Bakery and

Breakfast Section; Breakfast Section is the reference

level. Cities expanded to city1, city2, city3 and city4,

where city4 is the reference level. Since the CEO of

the SMART FOOD cares about the demand from

customers, accordingly, we set the total sales as

dependent variable and the rest variables as predictors

based on R language.

Before checking with the multicollinearity,

normality, homoscedasticity, and independence, we

first need to construct a model for the Residual

Analysis. Based on the linear regression model in

terms of ordinary least square procedure, we create our

first model. Here the total sale is the dependent

variable with Price at 50, Price at 60, advertising at

3million, focusing on the Bakery section, Volume and

City1 through 4 becoming predictors.

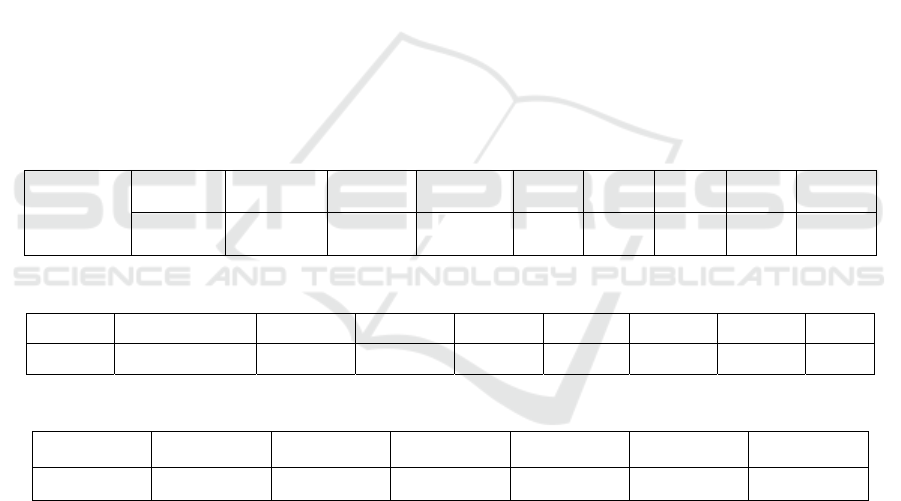
Table 1: The corresponding coefficients for each variable in the first model.

The

Coefficients

intercept P

V C

312.189 196.237 69.269 -194.058

49.719

14.457 -33.587 NA 10.048

Table 2: The output from ‘alias function’.

intercept P

0 0 0 1 0 -1 0 0

Table 3: The results of VLF.

1.638199 1.547341 2.028505 1.001002 1.548102 2.368834 1.934640

To make sure there’s no multicollinearity in the

first model, utilizing the ‘alias’ function to test the

dependency among variables could be necessary. From

the output, it’s clear that C

and C

is strongly

correlated since the coefficient under C

is -1. To

eliminate the effect of the multicollinearity, we decide

to remove the C

column and made a new model.

By checking the Variance inflation factor, which

can be seen as the measurement of multicollinearity,

one sees all the VIF numbers for existing variables are

all smaller than 7. This indicates the overly

dependency disappear.

In order to check the three other regression

assumption, we decided to draw a set of diagnostic

plots According to the Normal QQ plot, we could see

only a few of the points fall long the dashed line. We

cannot conclude it’s almost normally distributed.

According to the Scale-Location plot, the residuals

spread without any specific patterns around

the red line,

but the red line is not as straight as expected, hence we

cannot assume for the constant variance. According to

the Residuals and Fitted plot, we found a decreasing

pattern for the distributed data, so the test for non-

linearity is not met. The residuals weren’t distributed

independently.

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

796

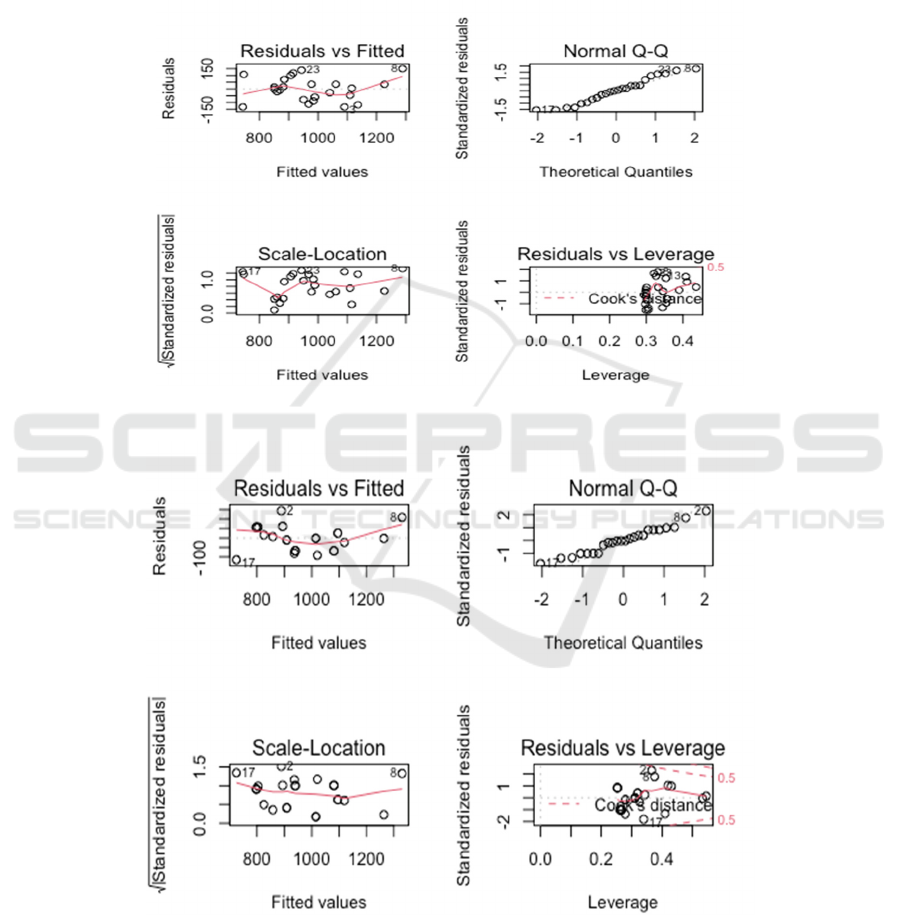
Since none of the regression assumptions are met,

there must be something wrong with the data. By

reviewing the data, the sample size is too small to

either construct unbiased analysis or maintain statistic

powers. Bootstrap, a technique for re-sampling might

help us to reduce these biases brought by small sample

sizes. Here we repeated 1000 times to construct a new

model.

Here, we draw four diagnostic plots again in Fig. 2

and found that even thought these plots are not

perfectly matched with regression assumption, they are

much better than the model we generated by only 24

data. Since the assumptions are almost met, the

Hypothesis test and Variable selection could be applied

in the following part.

Figure 1: The first 4-diagnostic plots.

Figure 2: The second 4-diagnostic plots.

The Impact of Marketing Mix’s Efﬁcacy on the Sales Quantity based on Multivariate Regression

797

Table 4: Regression Results.

The

coefficients

intercept P

438.096 232.905 107.824 -268.098 -62.656 19.770 -5.270 12.204

Table 5: The First P-values for parameters.

P-Value

intercept P

0.073879 0.000254 0.033911 6.63e-05 0.092959 0.660419 0.932532 0.008625

Table 6: The Second P-values for parameters.

P-Value

intercept P

V P

:V P

0.42790 0.29707 0.04658 0.00541 0.88797 0.35840 0.90640 0.01366 0.13293 0.07565

Table 7: Regression Results for new model.

The

coefficients

intercept P_50 P_60 A_0 C_1 V P_50:V P_60:V

207.891 -591.513 792.621 -175.677 -46.527 15.202 18.037 -14.042

3 RESULTS & DISCUSSION

The full Model is obtained based on regression, where

the coefficients values are listed in Table. IV. Here,

means that setting price at 50 could induce

232.905 more sales than setting price at 70, P

indicates that setting price at 60 could induce 107.824

more sales than setting price at 70, the A

denotes for

the 3 million advertising policy would bring 268.098

less sales than 3.5 million advertising policy, L

means that focusing on the Bakery section would

bring 62.656 less sales than that of Breakfast section,

is operating in city1 sell 19.770 more than

operating in city4, C

is operating in city3 sell 5.270

less than operating in city4 and V represents for each

unit increase in Store Volume is associated with an

increase of 12.204 in total sales.

To test whether these coefficients are statistically

significant, a Hypothesis test with significance level

is 0.1 will be used. H0: the coefficient is 0 and H1:

the coefficient is not 0

all the variable with corresponding p-value will be

compared with 0.1; if their p-value is less than 0.1, we

conclude that these variables are statistically

significant.

Based on the output summary, only C1 and C3

have extremely big P-value, which means these two

variables might be useless for the following analysis.

In order to figure out if the effect exsits, which

provided by different price, to the total sales depends

on the volumes, two interaction terms are added in

full model. The p-values results are given in Tables V

and VI.

The p-value for interaction between price at 60

and volumes is 0.07565, which is less than the

significance level (0.1), i.e., interaction term is

statistically significant. Even though one can tell

which variables affect the total sales by these full

model, it’s not good enough. In this case, a model

with less complexity is needed with more explained

variance. Less complexity means less terms in the

model, we want to make sure if there are any variables

we could remove. Here, we’ll refer to the notion of

Akaike information criterion, which compares the

quality for each model, with Stepwise Selection. The

model with the smallest AIC will be chosen.

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

798

The reduced model coefficients are given in

Table. VII. Another way to test the quality of two

models is to compare their coefficient of

determination (R squared), which measures the

proportion of total variation explained by the

regression model. With regard to deal with Multiple

Linear regression, the R squared is not accurate

enough since it would always increase when a new

variable is added to the model. We’ll focus on the

modified version (Adjusted R squared), which works

the as R squared. The larger the adjusted R squared

is, the better the model fit.

Table 8: Metics for the model.

Reduced Model (with

interaction)

Full Model (with

interaction)

AIC 206.41 210.34

R squared 0.8473 0.826

While viewing the variables of the model, we

could make another interpretation with interaction.

: If the company consider setting price at 50, they

will induce 519.513 less sales than setting price at 70.

: If the company consider setting price at 60, they

will induce 792.621 more sales than setting price at

70. A

: the 3 million advertising policy would bring

175.677 less sales than 3.5 million advertising policy.

stores in city1 will bring 46.527 less sales than that

of city4. V: if the company considered setting price at

50, each unit increase in Store Volume is associated

with an increase of (15.202+18.037) in total sales. If

the company considered setting price at 60, each unit

increase in Store Volume is associated with an

increase of (15.202-14.042) in total sales. If the

company considered setting price at 70, each unit

increase in Store Volume is associated with an

increase of 15.202 in total sales.

According to the multiple linear regression, the

variables Price, Advertising, City Index, Store

Volume and interaction between Price and Store

Volume can determine the total sales of the Product–

K-pack. As a matter of fact, this regression model is

not perfect even though we did the bootstrap re-

sampling technique to reduce the bias. In the future,

if one could collect more data from the

SMARTFOOD company, a better regression analysis

can be formed, e.g., split data to carry out cross

validation and construct complex nonlinear model

(neural networks). The training data set would be

used to construct models and the test data set would

be used to evaluate the quality of linear models. Then,

the over-fitting problems might be eliminated and the

precision of regression analysis would be improved.

In addition, we need to reveal more variables which

might also affect the total sales of product. The more

variables the model includes, the better performance

one can obtain.

4 CONCLUSION

In summary, we investigate K-Pack’s 4-month

marketing performance based on multivariate linear

regression. According to the analysis, the feasibility to

sales prediction is verified and the impacts of efficacy

of marketing mix on the sales are demonstrated. In the

future, to construct a more robust and improve the

performance, we can consider more variables as well

as enlarging the sample quantities. Besides, it is

necessary to pay attention to the marketing strategy of

competitors, detect market changes timely as well as

given questionnaires to customers regularly Market is

full of change. we have to pay attention to everything

about it, i.e., the prediction will be more reliable and

closer to the fact. Overall, these results offer a

guideline for sales prediction for a specific case.

REFERENCES

Bakker, J., and M. Pechenizkiy. "2009 IEEE International

Conference on Data Mining Workshops Towards

Context Aware Food Sales Prediction." (2014).

Blech, et al. "Predicting Diabetic Nephropathy Using a

Multifactorial Genetic Model. " Plos One (2011).

Braga, J. P. , et al. "Prediction of the electrical response of

solution-processed thin-film transistors using

multifactorial analysis." Journal of Materials Science:

Materials in Electronics 30.11(2019).

Meeran, S. , K. Dyussekeneva , and P. Goodwin . "Sales

Forecasting Using Combination of Diffusion Model

and Forecast Market an Adaption of

Prediction/preference Markets." IFAC Proceedings

Volumes 46.9(2013): 87-92.

Meeran, S., K. Dyussekeneva, and P. Goodwin. sales

forecasting using combination of diffusion model and

forecast market -an adaption of prediction/preference

markets. 2013.

The Impact of Marketing Mix’s Efﬁcacy on the Sales Quantity based on Multivariate Regression

799

Reinsel, G. . "Estimation and Prediction in a Multivariate

Random Effects Generalized Linear Model." Journal of

the American Statal Association 79.386(1984):406-

414.

Sarukhanyan, A. , et al. "Multifactorial Linear Regression

Method For Prediction Of Mountain Rivers Flow."

(2014).

Tsoumakas, G. . "A survey of machine learning techniques

for food sales prediction." Artificial Intelligence

Review 52.1(2019):441-447.

Xin, L., and R. Ichise. "Food Sales Prediction with

Meteorological Data — A Case Study of a Japanese

Chain Supermarket." Springer, Cham (2017).

Ye, J., Y. Dang, and Y. Yang . "Forecasting the

multifactorial interval grey number sequences using

grey relational model and GM (1, N) model based on

effective information transformation." Soft Computing

24.7(2020):5255-5269.

Zliobaite, I., J. Bakker, and M. Pechenizkiy . "Beating the

baseline prediction in food sales: How intelligent an

intelligent predictor is?." Expert systems with

applications 39.1(2012):p.806-815.

Zliobaite, I., J. Bakker , and M. Pechenizkiy. "Towards

Context Aware Food Sales Prediction." IEEE

International Conference on Data Mining Workshops

IEEE, 2009.

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

800