The Forecast of the Fish Consumption in China based on

Experimental Analysis

Jiaqi Qin

1,a

Shansong Huang

1,b

, Boying Yang

2,c

, Shuqi Chen

2,d

and Zheng Tao

3,e

Department of Mathematics, Wenzhou-Kean University, Wenzhou, China

College of Business & Public Management, Wenzhou-Kean University, Wenzhou, China

Department of Statistics, National University of Singapore, Singapore

Keywords: Fish Consumption, Simultaneous Equation Model, Supply Equation, Demand Equation, Endogenous

Relationship.

Abstract: Fish is one of the critical sources for people to obtain animal protein. About 3.1 billion people worldwide rely

on fish for 20% of their daily protein intake, and even more, than 70% of some coastal communities rely on

fish (Sustainable Seafood 101 - Sustainable Fisheries UW, 2021). Therefore, the fish consumption is an

important indicator to judge people's health. Fish consumption is the intersection of the fish supply equation

and the fish demand equation. However, the quantity and price variables in equations affect each other which

are not independent. Therefore, this article adopts simultaneous equation model to deal with the correlation

between the price and quantity of endogenous variables. And this article chooses four exogenous variables:

the ex-factory price index of industrial producers, sea surface temperature, the price of eggs and per capita

GDP to construct the supply equation and the demand equation. After using 𝐬𝐲𝐬𝐭𝐞𝐦𝐟𝐢𝐭() function in R to

estimate supply equation and demand equation based on the data from 2003 to 2017, the data from 2018 is

used to verify the accuracy of the model.

1 INTRODUCTION

1.1 Why Is It Important?

The consumed fish intersects market demand and

supply (Ye, 1999). According to OECD-FAO

Agricultural Outlook 2015-2024, the protein intake by

fish increases over time in the least developed

countries, developed countries, and developing

countries. The proportion of protein consumed by fish

in developing countries has increased rapidly (OECD-

FAO, 2015), which means that with the economic

growth of some developing countries such as China,

people are paying more attention to a healthy diet,

which has also contributed to the increase in the

consumption of global fishery products in the past few

decades. The body needs 20 kinds of amino acids to

maintain body health and normal functions, of which

the body can produce about 11 types. The other nine

amino acids, the so-called "essential" amino acids,

must enter the human body through our diet. And, fish

meat can provide these nine essential amino acids, in

addition to its omega-3 fatty acids, minerals, and

vitamins through its protein (Heffernan, 2021).

"According to the Dietary Reference Intake report for

macronutrients, a sedentary adult should consume 0.8

grams of protein per kilogram of body weight, or 0.36

grams per pound. That means that the average

sedentary man should eat about 56 grams of protein

per day, and the average woman should eat 46 grams"

(https://www.sclhealth.org/blog/2019/07/how-much-

protein-is-simply-too-much/, 2021). Combined with

the protein content of fish, 100 grams of cooked food

for most types of fish and shellfish can provide

approximately 15-25 grams of protein (Heffernan,

2021). The protein content of fish means that fish is

rich in amino acids and high in protein. At the same

time, compared with other meats, fish has less fat

content, which shows that fish is a healthier source of

protein. It is precise because fish has so many nutrients

that it serves as an essential source of animal protein,

accounting for 17% of the world's meat consumption.

At the same time, about 3.1 billion people rely on fish

for 20% of their daily protein intake, and more than

70% of some coastal communities rely on fish

(Sustainable Seafood 101 - Sustainable Fisheries UW,

2021).

Qin, J., Huang, S., Yang, B., Chen, S. and Tao, Z.

The Forecast of the Fish Consumption in China based on Experimental Analysis.

DOI: 10.5220/0011285800003440

In Proceedings of the International Conference on Big Data Economy and Digital Management (BDEDM 2022), pages 737-741

ISBN: 978-989-758-593-7

737

1.2 How Is It Changing?

According to FAO's HISTORICAL

CONSUMPTION AND FUTURE DEMAND FOR

FISH AND FISHERY PRODUCTS, the world

average per capita fish consumption has shown an

upward trend from 1965 to 1995. Especially in Asia,

fish consumption and consumption growth rate are

higher than in other continents (Ye, 1999). Many

factors affect fish consumption, but they can be

classified based on the relationship between supply

and demand. For example, factors affecting supply

include price, weather, production costs, government

policies, etc. (Hu, Pan, Zhang, Tao, 2020). Factors

affecting the market include income, substitutes and

complementary products, and product quality (Hu,

Pan, Han, Lin, Tao, 2020).

1.3 Objectives

Since fish meat is essential for human protein intake,

fish consumption is a crucial indicator of people's

protein intake or health. The main goal of this article

is to find appropriate exogenous variables to establish

a supply equation model that conforms to the laws of

the market based on the relevant data from 2003 to

2017 in China to predict the future consumption of fish

in China to provide essential data for people's protein

intake.

2 METHODOLOGY

2.1 Data Source

The data in this article comes from Chinese national

data, our world data, and statist. Among them, the ex-

factory price index of industrial producers

(1985=100), the current value of the market price of

eggs (ordinary fresh eggs) (yuan/kg), hairtail (0.5-1)

(Kg), the current value of the market price (yuan/kg)

and the per capita GDP (yuan) come from Chinese

national data. Fish and Seafood supply quantity

(kg/capita/yr) comes from our world data. Annual

anomalies in global ocean surface temperature from

1880 to 2020, based on temperature departure (in

degrees Celsius), comes from Statista.

2.2 Supply and Demand Function

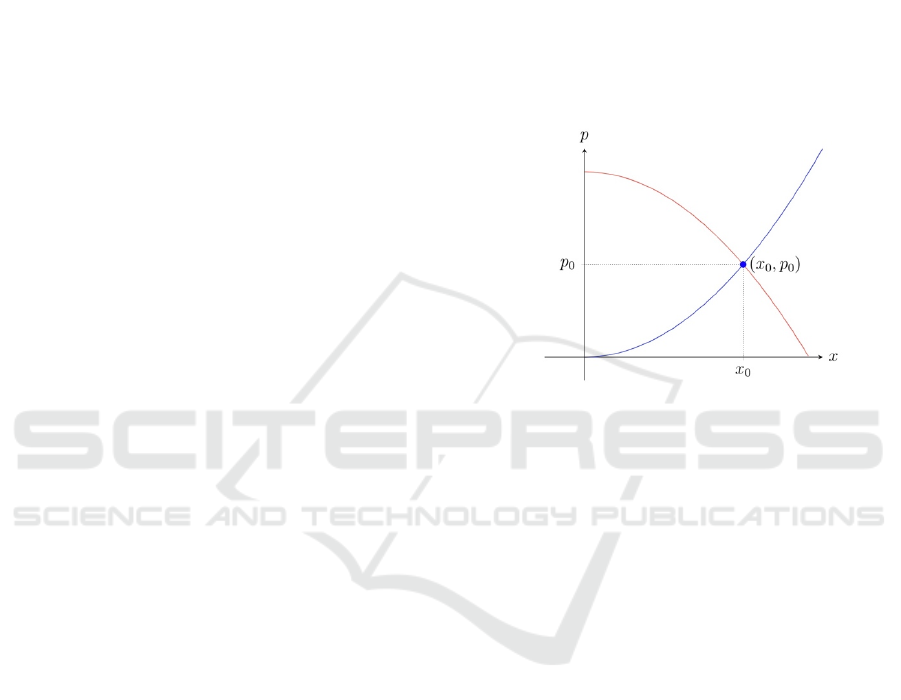
1) Demand Function: A demand function is

defined by 𝑝 = 𝑓(𝑥)where 𝑝 measures the unit price

and 𝑥 measures the number of units of the commodity

in question and is generally characterized as a

decreasing function of 𝑥; that is, 𝑝=𝑓(𝑥) decreases

as x increases. Since both 𝑥 and 𝑝 assume only

nonnegative values, the demand curve is that part of

the graph of 𝑓(𝑥) that lies in the first quadrant

(figure.1) (Pettinger, 2021).

2) Supply Function: A supply function defined

by 𝑝=𝑓(𝑥)with 𝑝 and 𝑥 as before is generally

characterized as an increasing function of 𝑥; that is,

𝑝=𝑓(𝑥) increases as 𝑥 increases. Since both 𝑥 and

𝑝 assume only nonnegative values, the supply curve

is that part of the graph of 𝑓(𝑥) that lies in the first

quadrant (figure.1) (Economic Models, 2021)..

Figure 1: Example of a supply curve (in blue) and a demand

curve (in red). The point of intersection corresponds to

market equilibrium.

2.3 Simultaneous Equations Models

1) Introduction to Simultaneous Equations Models:

A simultaneous equation model is a statistical model

in a set of simultaneous linear equations. They differ

from regular regression models because there are two

or more dependent variables (Pettinger, 2021).

Because the concurrent equation model can solve the

endogenous relationship between variables. For

example, the variable price is both an explained

variable and an explanatory variable to express

quantity. The same is true for the number of variables.

So, I choose the simultaneous equation model to solve

the supply and demand equation.

2) Variable Selection of Price of Fish: This

article uses the price of hairtail to replace the price of

fish because data on fish prices in China has not been

found. The production of hairtail is relatively large,

and it is distributed in China's Yellow Sea, East China

Sea, Bohai Sea, and even the South China Sea.

3) Variable Selection of Supply Function:

Supply refers to the quantity of a good that the

producer plans to sell in the market. The pool will be

determined by price, the number of suppliers, the

state of technology, government subsidies, weather

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

738

conditions, and the availability of workers to produce

the good (Hu, Pan, Zhang, Tao, 2020). Based on this

reminder of factors affecting supply, first, I chose the

ex-factory price index of industrial producers to

estimate the cost of raw materials. The increase in the

ex-factory price index of industrial producers means

an increase in the cost of the enterprise, so this will

lead to a decrease in the production of the enterprise,

which will naturally lead to a reduction in supply.

Secondly, I chose sea level temperature as the second

variable that affects supply because the problem

which I am exploring is to predict the consumption of

fish in China. The response of fish to changes in water

temperature is enormous. If the temperature exceeds

or falls below the optimum temperature for the fish, it

will cause the death of the fish and thus reduce the

yield. Therefore, the supply function can be expressed

as follows:

𝑆𝑢𝑝𝑝𝑙𝑦: 𝑄 = 𝛼



+𝛼



𝑃+𝛼



𝑃𝐹 + 𝛼



𝑆𝑇 + 𝜖



Table 1: The explanation of variables in supply function.

Variables Explanation

Q Per capita fish consumption

P The price of hairtail

The ex-factory price index of industrial

producers

ST Sea surface temperatur

4) Variable Selection of Demand function:

The demand for a good depends on several factors,

such as the price of the sound, perceived quality,

advertising, income, the confidence of consumers,

and changes in taste and fashion (Yobero, 2016).

Based on such a reminder of factors that affect

demand, I plan to choose residents' per capita

disposable income as the first variable of the demand

equation, but because China only began to investigate

residents' per capita disposable income in 2013. So, I

chose GDP per capita as the variable that affects

demand. Secondly, I chose eggs as a substitute for

fish. Because eggs and fish are both important sources

of protein for humans. Therefore, the price of eggs is

used as the second variable that affects demand. Thus,

the demand function can be expressed as follows:

𝐷𝑒𝑚𝑎𝑛𝑑: 𝑄 = 𝛽



+𝛽



𝑃+𝛽



𝑃𝑆 + 𝛽



𝐷𝐼 + 𝜖



Table 2: The explanation of variables in demand function.

Variables Explanation

Q Per capita fish consumption

P The price of hairtail

PS The price of eggs

DI Per capita GDP

5) The Reduced-Form Equation: The

reduced-form equations express the endogenous

variables as a function of the exogenous variables,

where 𝑃 and 𝑄 are exogenous variables and 𝑃𝑆,

𝐷𝐼, 𝑆𝑇, 𝑎𝑛𝑑 𝑃𝐹 are exogenous variables.

𝑃=𝜋



+𝜋



𝑃𝑆 + 𝜋



𝐷𝐼 + 𝜋



𝑃𝐹 + 𝜋



𝑆𝑇 + 𝑣



𝑄=𝜋



+𝜋



𝑃𝑆 + 𝜋



𝐷𝐼 + 𝜋



𝑃𝐹 + 𝜋



𝑆𝑇

+𝑣



2.4 Identification

Because the reduced-form equation has 8 parameters

equal to the structural equation's parameters, this

simultaneous equation system is just recognized.

2.5 Two-stage Least Squares

Estimation

1) The Process of Two-Stage Least Squares

Estimation: Because the endogenous variable is

related to the error term in the supply and demand

equation, the least square method cannot estimate the

parameters here. Instead, choose to use Two-Stage

Least Squares Estimation. The first step is to apply

the least-squares method to the reduced-form

equation of the endogenous variable 𝑌



as the

explanatory variable to obtain its estimated value 𝑌





The second step is to substitute the estimated value

𝑌





. into the right side of the estimated structural

equation to replace the endogenous variable 𝑌



as the

explanatory variable, and then apply the least square

method again to obtain the estimated value of the

structural parameter.

2) Correlation of Exogenous Variable: The

use condition of Two-Stage Least Squares Estimation

is that there is no serious multicollinearity between

exogenous variables. So, the correlation between

exogenous variables needs to be tested.

3 ASSUMPTION

1. Assume that people all over China do not have

serious prejudice against hairtail.

The Forecast of the Fish Consumption in China based on Experimental Analysis

739

2.Assume that per capita GDP is even people’s

disposable income.

3. Assume that there is no large-scale outbreak of

infectious diseases (such as the outbreak of Covid19).

4 RESULT

4.1 The Result of Correlation of

Exogenous Variable

Test the correlation between exogenous variables

using the c𝑜𝑟() function in R, as shown in figure 2

below. As a result, it can be found that there is a certain

correlation between exogenous variables, but the

severity of multiple gong xian x cannot be clearly

defined. Therefore, it cannot be judged whether there

is serious multicollinearity between them.

Figure 2: The result of the correlation of exogenous variable

by using 𝑐𝑜𝑟() in r.

4.2 Estimated Supply and Demand

Function

According to the result of the 𝑠𝑦𝑠𝑡𝑒𝑚𝑓𝑖𝑡() function

in r (Figure 3). The estimated parameters of structural

equations of supply and demand function can be

determined. The estimated supply function is

𝑄 = 24.748772945 + 0.648236619𝑃

− 0.000467179𝑃𝐹

+ −6.362028375𝑆𝑇

and the estimated demand function is

𝑄 = 22.304304122 + −0.310007465𝑃

+ 0.365297703𝑃𝑆

+ 0.000363223𝐷𝐼

Figure 3: The estimated parameters of structural equations

of supply and demand function.

4.3 Verification

Bring the values of the four variables of PT, PS, DI,

and ST in 2018 into the estimated supply equation and

demand equation, and get the estimated supply

equation:

𝑄 = 20.2406741474 + 0.648236619𝑃

and the estimated demand equation

𝑄 = 49.79757141783484099 − 0.310007465𝑃

The graph of the two equations can be shown in

figure 4.

Figure 4: The estimated supply equation and demand

equation for 2018.

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

740

Combining these two equations can then get the

predicted value of the price 𝑃



，

49.79757141783484099 − 0.310007465𝑃

= 20.2406741474

+ 0.648236619𝑃

𝑃



= 30.8449

Then substitute the predicted value into the

estimated supply equation to get the predicted value of

the fish consumption 𝑄



，

𝑄



= 20.2406741474 + 0.648236619 ∗ 30.8449

= 40.2354678367931

Compared with the actual value of the price 𝑃=

27.3467,

𝐸𝑅𝑅 =

|𝑃 − 𝑃



𝑃

≈ 0.1134136707

Therefore, the relative error of the model is about

11.3%.

5 CONCLUSION

In general, the simultaneous equation model used in

this article can get a rougher supply equation and

demand equation. I think three reasons affect the

accuracy of the model: The first reason is that the

Pearson correlation coefficient obtained in the

previous correlation test of exogenous variables is

significant, which shows that the correlation between

exogenous variables is very high. It may affect the

accuracy of the model. The second reason is that I used

per capita GDP instead of the more real per capita

disposable income. This approach has significantly

improved the judgment of the people's economic level,

which will shift the demand equation. The third is that

I used the price of hairtail to replace the price of fish,

but hairtail is not a very accurate replacement for the

cost of fish. Because hairtail is not so popular in every

part of China, people in the mainland may reduce their

consumption of hairtail because of its fishy smell.

In addition, the more severe problem is that the

method in this article can only get the estimated supply

equation and demand equation. But if you want to use

this estimated equation to predict fish consumption in

China, you need to predict the values of four

exogenous variables (ST, DI, SF, and PS). This is

more difficult than getting the estimated supply and

demand equation.

ACKNOWLEDGMENT

We would like to thank Professor Sangeet Kumar

Srivastava who provided useful comments on this

research. In addition, I also need to thank other

students who helped us in this research.

REFERENCES

Economic Models. Retrieved 5 December 2021, from

https://www.sfu.ca/math-

coursenotes/Math%20157%20Course%20Notes/sec_e

conomic_models.html.

Heffernan, S. (2021). How much protein can fish provide

us with?. Retrieved 5 December 2021, from

https://www.rte.ie/brainstorm/2021/1027/1256148-

fish-protein-health/.

How Much Protein Is Simply Too Much?. Retrieved 5

December 2021, from

https://www.sclhealth.org/blog/2019/07/how-much-

protein-is-simply-too-much/.

Hu, Y., Pan, Z., Han, Z., Lin, Z., & Tao, Z. (2020,

November). Forecasts for the fish Migration and

Fishing time under Marine Environment Changes based

on the ARIMA model. In 2020 2nd International

Conference on Economic Management and Model

Engineering (ICEMME) (pp. 352-355). IEEE.

Hu, Y., Pan, Z., Zhang, C., & Tao, Z. (2020, November).

Risk Assessment and Investment Strategy of Fishery

Company under Marine Environment Changes. In 2020

2nd International Conference on Economic

Management and Model Engineering (ICEMME) (pp.

692-695). IEEE.

OECD-FAO Agricultural Outlook 2015-2024. (2015).

Retrieved 5 December 2021, from

https://www.fao.org/3/i4738e/i4738e.pdf.

Pettinger, T. (2021). Factors affecting demand - Economics

Help. Retrieved 5 December 2021, from

https://www.economicshelp.org/microessays/equilibri

um/demand/.

Sustainable Seafood 101 - Sustainable Fisheries UW.

Retrieved 5 December 2021, from

https://sustainablefisheries-uw.org/seafood-101/.

Ye, Y. (1999). Retrieved 5 December 2021, from

https://www.fao.org/3/X3216e/X3216E00.pdf.

Yobero, C. (2016). Simultaneous Equation Models:

Estimating Supply and Demand Functions. Retrieved 5

December 2021, from https://rstudio-pubs-

static.s3.amazonaws.com/195495_d47be7c818424a3c

9bfa5452dd17c6c6.html.

The Forecast of the Fish Consumption in China based on Experimental Analysis

741