Aggregating Statistically Correlated Metabolic Pathways Into Groups to

Improve Prediction Performance

Abdur Rahman M. A. Basher

1 a

and Steven J. Hallam

1,2 b

Graduate Program in Bioinformatics, University of British Columbia, Vancouver, BC V5Z 4S6, Canada

Department of Microbiology & Immunology, University of British Columbia, Vancouver, BC V6T 1Z3, Canada

Keywords:

Pathway Group, Relabeling, Data Augmentation, Correlated Models, Metabolic Pathway Prediction,

MetaCyc.

Abstract:

Metabolic pathway prediction from genomic sequence information is an essential step in determining the ca-

pacity of living things to transform matter and energy at different levels of biological organization. A detailed

and accurate pathway map enables researchers to interpret and engineer the ﬂow of biological information

from genotype to phenotype in both organismal and multi-organismal contexts. In this paper, we propose

two novel hierarchical mixture models, SOAP (sparse correlated pathway group) and SPREAT (distributed

sparse correlated pathway group), to improve pathway prediction outcomes. Both models leverage pathway

abundance to represent an organismal genome as a mixed distribution of groups, and each group, in turn, is

a mixture of pathways. Moreover, both models deal with missing potential pathways in the training set by

provisioning supplementary pathways into the learning framework as part of noise reduction efforts. Because

the introduction of supplementary pathways may lead to overestimation of some pathways, dual sparseness is

applied. The resulting pathway group dataset is then used to train multi-label learning algorithms. Model ef-

fectiveness was evaluated on metabolic pathway prediction where correlated models, in particular, SOAP was

able to equal or exceed the performance of previous pathway prediction algorithms on organismal genomes.

1 INTRODUCTION

Rapid advances in high-throughput sequencing and

mass spectrometry over the past two decades have

produced a veritable tidal wave of multi-omic infor-

mation spanning the central dogma of biology (DNA,

RNA, protein and metabolites) at the individual, pop-

ulation and community levels of organization (Wang

et al., 2015) (Hassa et al., 2018) (Aguiar-Pulido et al.,

2016) (Loh et al., 2012). As the ubiquity and abun-

dance of these datasets increases there is a concomi-

tant need to develop bioinformatics applications that

scale with data volume and complexity. In particu-

lar, methods for predicting metabolic pathways have

become essential to interpret and engineer the ﬂow

of biological information from genotype to phenotype

(Lawson et al., 2019) (Hahn et al., 2016).

A metabolic pathway can be deﬁned as a series

of linked chemical reactions occurring within or be-

tween cells, often catalyzed and coordinated by a

https://orcid.org/0000-0002-3407-1187

https://orcid.org/0000-0002-4889-6876

group of enzymes, resulting in metabolic ﬂux from

substrate to product and so on to completion. A va-

riety of rule-based and machine learning prediction

methods have been developed to model these path-

ways in both organismal and multi-organismal con-

texts (Mascher et al., 2019) (Baranwal et al., 2020)

(Yamanishi et al., 2015) (Tabei et al., 2016) (Ye

and Doak, 2009) (Dale et al., 2010) (Karp et al.,

2016) (M. A. Basher et al., 2020) (M. A. Basher

et al., 2021b). While these methods rely on reference

metabolic pathway databases (e.g., MetaCyc (Caspi

et al., 2019) and KEGG (Kanehisa et al., 2017)) to re-

construct pathways, other computational methods ig-

nore the use of reference database or follow an agnos-

tic approach pathway boundaries in the reconstruction

process (Zhao et al., 2012) (Qi et al., 2014) (Shaﬁei

et al., 2014) (Jiao et al., 2013).

Among recently developed pathway prediction

methods is triUMPF (M. A. Basher et al., 2021b)

which uses several layers of interactions among path-

ways and enzymes within a network to improve the

precision of pathway predictions in terms of com-

munities represented by a cluster of nodes (pathways

M. A. Basher, A. and Hallam, S.

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance.

DOI: 10.5220/0010910100003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 3: BIOINFORMATICS, pages 49-61

ISBN: 978-989-758-552-4; ISSN: 2184-4305

Figure 1: Group-based pathway prediction workﬂow. The

training phase (a) takes pathway abundance data to discover

groups using any correlated models in the CHAP pack-

age. Then, groups are used to map examples in the path-

way abundance data to groups using reMap (Hallam Lab,

2021b). Then, the results of this mapping are used in leADS

(Hallam Lab, 2021a), along with pathway data, to learn

the model. After training, pathways can be predicted for

a newly sequenced genome (b), by ﬁrst inferring groups us-

ing reMap, and then apply the pretrained leADS to predict

pathways from groups.

and enzymes). Despite triUMPF’s predictive gains,

its performance remained error prone because its pre-

diction process depends on the quality of commu-

nities detected from both pathway and enzyme net-

works that are learned from pathway datasets which

contain missing pathway information (M. A. Basher

et al., 2020).

Previously, Shaﬁei and colleagues developed

BiomeNet (Shaﬁei et al., 2014), an extension of

MetaNetSim (Jiao et al., 2013), which is a hierarchi-

cal Bayesian network to reconstruct metabolic net-

works in a purely data-driven manner by leverag-

ing enzyme abundances present in multi-organismal

datasets. Instead of relying on deﬁned pathway

boundaries (Khatri et al., 2012), BiomeNet discovers

functions that are referred to as subnetworks, where

a subnetwork constitutes a group of connected reac-

tions. Applications of BiomeNet to the human gut

microbiome revealed subnetworks that are common

among healthy and inﬂammatory bowel disease (IBD)

microbiome patients as well as distinct subnetworks

associated with IBD patients.

Inspired by BiomeNet, we developed CHAP

(correlated pathway-group) a software package com-

prised of three correlated mixed-membership hier-

archical Bayesian models, CTM (Blei and Lafferty,

2006), SOAP, and SPREAT, to capture mixed compo-

nents given pathway abundance data. The component

is referred to as a “pathway group”, which is com-

prised of a set of correlated pathways, while path-

ways are permitted to be inter-mixed across groups

with different proportions, resulting in overlapping

pathways on groups. Modeling explicitly correlations

among pathways, using a Gaussian covariance matrix,

is fundamental as functions of similar organisms or

communities are shared. Moreover, due to noise or

missing pathways information, the two novel models:

SOAP and SPREAT provision supplementary path-

ways into the learning framework as part of noise

reduction efforts. Because the introduction of sup-

plementary pathways may lead to overestimation of

some pathways, dual sparseness is applied where each

example in the pathway abundance data is represented

by a few focused mixing groups and each pathway

group consists of a few relevant pathways. These last

two properties were not included in CTM. By model-

ing examples as mixing groups, one may use results

from correlated models for downstream group-based

pathway prediction (Fig. 1).

Using CTM, SOAP, and SPREAT, we evaluated

groups on metabolic pathway prediction. Resulting

pathway group datasets were used to train reMap

(Hallam Lab, 2021b) to map examples to groups.

For pathway prediction using groups, we applied

leADS software (Hallam Lab, 2021a) using the rec-

ommended settings discussed in (M. A. Basher and

Hallam, 2021). The results were then compared to

two heuristic or rule-based pathway prediction algo-

rithms: MinPath (Ye and Doak, 2009) and Patho-

Logic (Karp et al., 2016), and to two machine

learning algorithms: mlLGPR (M. A. Basher et al.,

2020) and triUMPF (M. A. Basher et al., 2021a)

on a set of Tier 1 (T1) pathway genome databases

(PGDBs) and genomes used in the Critical Assess-

ment of Metagenome Interpretation (CAMI) initiative

(Sczyrba et al., 2017) following established bench-

marks (M. A. Basher et al., 2020).

2 CORRELATED MODELS

In this section, we present three correlated path-

way models: i)-CTM (correlated topic model) (Blei

and Lafferty, 2006), ii)- SOAP (sparse correlated

pathway group) and iii)- SPREAT (distributed sparse

correlated pathway group). These models incorporate

pathway abundance information to encode each ex-

ample as a mixture distribution of groups, and each

pathway group, in turn, is a mixture of pathways

with different mixing proportions. The pathway abun-

dance information can be obtained by mapping en-

zyme –with abundances– onto a reference pathway

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

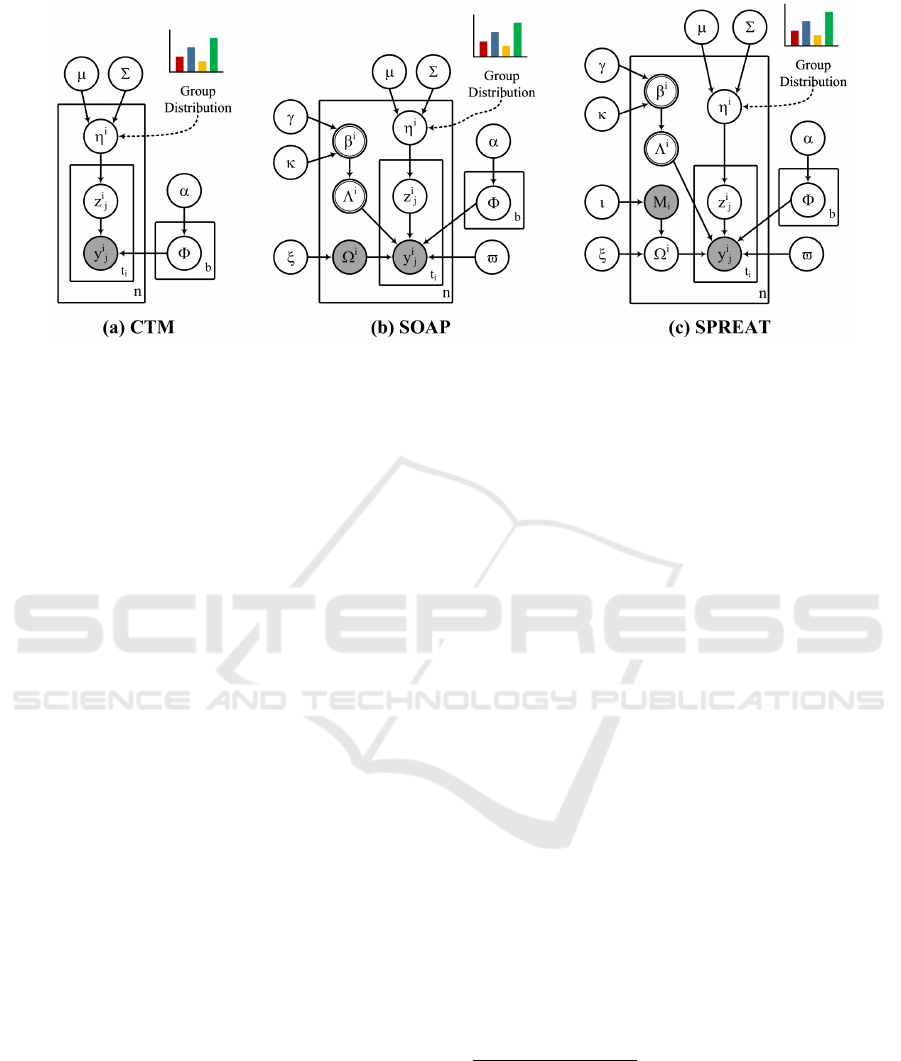
Figure 2: Graphical model representation of the correlated group models. The boxes are “plates” representing replicates. The

outer plate represents examples, while the inner plate represents the repeated choice of pathways for an example. The logistic

normal distribution, used to model the latent group proportions for an example, captures correlations among groups that are

impossible to capture using a single Dirichlet. The observed data for each example i are a set of annotated pathways y

(i)

and a set of hypothetical pathways M

. The hidden variables are: per-example group proportions η

(i)

, per-example group

selection parameters Λ

(i)

, per-example hypothetical pathway distributions Ω

(i)

, per-pathway group assignment parameter z

(i)

and per-group distribution over pathways Φ

database (e.g. MetaCyc (Caspi et al., 2019)). Be-

fore we discuss these three models, let us ﬁrst provide

some deﬁnitions and notations.

Pathway Abundance Data. Let P = {y

(i)

: 1 <

i 6 n} be a collection of n examples correspond-

ing organismal or multi-organismal genomes (e.g.

Escherichia coli K-12), where each example y

(i)

,...,y

(i)

) is a vector encoding the unnormal-

ized abundance information of pathways and t is the

pathway size. Let Y = {h

,...,h

} be a set of

all known metabolic pathways obtained from a ref-

erence database (e.g., MetaCyc (Caspi et al., 2019)),

and Y

⊆ Y corresponds to a subset of true pathways

associated with the ith example.

Group Modeling. Given P , a pathway group dis-

tribution for the ith example is a multinomial distri-

bution vector, denoted by η

(i)

of size b groups, i.e.,

{p(Φ

|η

(i)

)}

a=b

a=1

, where Φ

in a multinomial pathway

distribution over the group j, i.e., {p(y

|Φ

)}

k=t

k=1

. The

overall goal of group modeling is to discover b hidden

groups for each example.

The deﬁnition states that a pathway is distributed

over groups, implying group correlation, i.e., if l ∈

≥ 0 and l ∈ Φ

> 0 then Σ

j,k

6= 0, where Σ ∈ R

b×b

is a group-correlation matrix.

Group Correlation. Given P , the pairwise group-

correlation is deﬁned by a Gaussian covariance ma-

trix, denoted by Σ ∈ R

b×b

. Each entry s

i, j

in Σ char-

acterizes the magnitude of correlation between i and

j pathway groups, where a larger score indicates both

pathway groups are highly correlated.

Missing pathway information in P is common in

both organismal and multi-organismal contexts due

to errors in open reading frame prediction or anno-

tation as well as unknown protein function. Previ-

ously, Hanson and colleagues (Hanson et al., 2014)

reported missing a set of potential pathways for the

Hawaii Ocean Time-series data (Stewart et al., 2011),

such as tricarboxylic acid cycle (TCA). These missing

pathways have negative implications in group mod-

eling as P , in this case, would be exposed to ex-

treme noise. Although manually incorporating miss-

ing pathways to P may provide a solution to model

groups, this solution has the potential to increase false

discovery pending experimental validation. A good

compromise would be to record missing pathways in a

separate list while keeping the original pathway abun-

dance data intact. Lets us denote M ∈ Z

n×t

≥0

a matrix

holding a set of missing pathways where each entry is

an integer value indicating the abundance of a path-

way for an example. This matrix is called the back-

ground or the supplementary matrix. Now, with these

deﬁnitions, let us describe the research problem.

Problem Statement. Given P and M, the objective

is to recover the group distribution η for each exam-

ple such that applying group based metabolic pathway

prediction would recover more accurate pathways for

an organismal or multi-organismal genome.

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance

1 for a ∈ {1,.. .,b} do

2 Sample a distribution over pathways

∼ Dir(.|α);

3 for i ∈ {1,.. .,n} do

4 Draw per example group weight

(i)

∼ N (.|µ, Σ);

5 Draw group proportions θ

(i)

= softmax(η

(i)

);

6 for j ∈ {1,.. .,t

(i)

} do

7 Sample a group assignment

(i)

∼ Mult(.|θ

(i)

);

8 Sample a pathway y

(i)

∼ Mult(.|Φ

(i)

);

Algorithm 1: The generative process for CTM given a col-

lection of examples.

2.1 Correlated Topic Model

The correlated topic model (CTM) is a probabilistic

graphical model that extends the generative story of

latent Dirichlet allocation (LDA) (Blei et al., 2003) to

incorporate correlation among groups (or topics in the

original paper). Fig. 2a shows the Bayesian graphi-

cal model for CTM using plate notation. Like LDA,

CTM is composed of a hierarchical Bayesian mixture

model, where features (words in the original paper)

are mixed to constitute groups that are assumed to be

correlated, modeled by a Gaussian covariance matrix.

Note that in this paper, we use the terms feature and

pathway interchangeably.

Formally, let n be the total number of examples in

P , where each example i consists of features, i.e., y

(i)

Then, the generative process for CTM is described

as follows. First, we draw a multinomial feature

distribution Φ

from a Dirichlet prior α > R

for

each group a ∈ {1, . . . , b}. Then, for each example i,

a Gaussian random variable is drawn η

(i)

∼ N (µ,Σ),

where µ is a b dimensional mean and Σ ∈ R

b×b

the covariance matrix. The random variable η

(i)

projected onto the probability simplex to obtain the

group distributions θ

(i)

= softmax(η

(i)

), correspond-

ing the logistic-normal distribution, from which a

group indicator z

(i)

∈ {1,...,b} is sampled. Finally,

each observed feature j ∈ {1,...,t

} is drawn from

the associated feature distribution, indicated by it’s

group assignment z

, i.e., y

(i)

∼ Φ

(i)

. This generative

process (Algorithm 1) is identical to LDA except that

the group distributions is sampled from the logistic

normal instead from a Dirichlet prior as in LDA.

2.2 Correlated Pathway-group Model

Correlated pathway group models are extensions to

CTM: i)- SOAP (Fig. 2b) and ii)- SPREAT (Fig. 2c).

Both models incorporate dual sparseness and supple-

mentary pathways in modeling group proportions.

The two properties were not implemented in CTM.

Let us discuss these two models.

Analogous to CTM, given n number of examples

in P and a matrix encoding missing pathways M, the

generative process for SOAP and SPREAT can be

described as follows. First, we draw a multinomial

pathway distribution Φ

from asymmetric Dirichlet

prior α ∈ R

for each group a ∈ {1,...,b}, where b

is assumed to be known and ﬁxed in advance. The

symmetric assumption is appropriate, in such a sce-

nario, because our prior knowledge, associated with

these pathways, is inaccessible. For each example

i, a group proportion is drawn θ

(i)

= softmax(η

(i)

where η

(i)

is a Gaussian random variable with mean

and covariance are denoted by µ and Σ, respectability.

To sample a group, it is reasonable to expect

that: i)- each example is usually explained with a

handful set of a mixed proportion of groups and ii)- a

group should consist only of a few related pathways.

Therefore, we apply dual sparsity (Lin et al., 2014)

(Airoldi et al., 2008) (Bien and Tibshirani, 2011)

(He et al., 2017) to retain those relevant focused

groups and pathways by: i)- introducing an auxiliary

Bernoulli variable Λ

(i)

of size b to determine whether

a group is selected for the ith example or ignored

and ii)- applying a cutoff threshold to keep top

k  t pathways, based on their probabilities, for

each group. Instead of sampling each entry in Λ

(i)

directly from a Bernoulli coin toss, we assume that

each entry is sampled from a Beta distribution β

(i)

parameterized by two hyperparameters γ ∈ R

and

κ ∈ R

. Applying this dual sparsity, we aim to

enhance the interpretability of the learned pathway

groups while reducing the negative correlation among

groups on Σ.

Next, a group indicator z

(i)

∈ {1,...,b} is drawn

according to the example-speciﬁc mixture proportion

(i)

 θ

(i)

, where  represents the Hadamard prod-

uct. Now each pathway y

(i)

for the ith example is

generated from a weighted distribution Ω

(i)

 Φ

(i)

using a smoothing prior ϖ ∈ R

. The parameter

Ω

(i)

∈ R

, derived from M

, represents a normal-

ized supplementary pathway of size t, which is as-

sumed to be drawn from a symmetric Dirichlet prior

ξ ∈ R

. For SPREAT, this parameter encodes distri-

bution, where each element of Ω

(i)

corresponds to the

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

pathway probability y

(i)

∈ M

for ith example. Here,

the background pathway is assumed to be drawn from

a sparse binary vector prior ι ∈ R

that is included

for completeness because pathways in M for each ex-

ample are known.

1 for a ∈ {1,.. .,b} do

2 Sample a distribution over pathways

∼ Dir(.|α);

3 for i ∈ {1,.. .,n} do

4 Draw per example group weight

(i)

∼ N (.|µ, Σ);

5 Draw group proportions θ

(i)

= softmax(η

(i)

);

6 Draw beta distribution β

(i)

∼ Beta(.|γ,κ);

7 Draw a sparsity indicator vector

(i)

∼ Bernoulli(.|β

(i)

);

8 if SPREAT then

9 Sample a vector M

∼ Prior(.|ι);

10 Sample background distribution

Ω

(i)

∼ Dir(.|ξ);

11 else

12 Draw background feature proportions

Ω

(i)

∼ Dir(.|ξ);

13 for j ∈ {1,.. .,t

(i)

} do

14 Sample a group assignment

(i)

∼ Mult(.|Λ

(i)

 θ

(i)

);

15 Sample a pathway

(i)

∼ Mult(.|(1 − Ω

(i)

)  Φ

(i)

);

Algorithm 2: The generative process for SOAP and

SPREAT.

Representing SOAP and SPREAT as layer-wise

mixing components supports the hierarchical mod-

ularity of metabolic pathway generation, where the

components of one level (e.g., pathways) permit to

contribute to groups with different degrees of granu-

larity. The generative process of SOAP and SPREAT

models is summarized in Algorithm 2. Notice that

by setting all entries in Ω, Λ, and ϖ to 1, SOAP

and SPREAT are reduced to CTM (“collapse2ctm” or

c2m), reﬂecting the ﬂexibility of these models.

3 INFERENCE AND PARAMETER

ESTIMATION FOR SPREAT

Here, we discuss the inference for the SPREAT

model. A similar expression is derived for SOAP.

Given P , the goal of inference is to compute the

posterior distribution of per-example group propor-

tions (η), per-example group selection parameters (Λ)

Table 1: Correspondence between variational and original

parameters.

Original parameter Φ µ Σ Λ Ω z

Variational parameter φ ν ζ

λ ω ς

and the associated beta distributions (β), per-example

background pathway distributions (Ω), per-pathway

group assignment (z), and per-group distribution over

pathways (Φ). By denoting all parameters as Θ and

variables as V while omitting hyperparameters, we

apply the Jensen’s inequality on a variational distri-

bution over hidden variables q(Θ,V) to obtain the ev-

idence lower bound (ELBO) as:

L(q) = E

[log p(Y,M, Θ, V)] + H(q)

(3.1)

where p(Y, M, Θ, V) represents the joint distri-

bution of all observed and latent variables of the

model. The ELBO contains two terms. The ﬁrst term,

[log p(Y,M, Θ, V)], captures how well q(Θ,V) de-

scribes a distribution of the model. The second

term is the entropy of the variational distribution,

[−logq(Θ,V)], which protects the variational dis-

tribution from “overﬁtting”. The two terms depends

on q(Θ,V) which is deﬁned as:

q(Θ,V) =

∏

a=1

q(Φ

|φ

)

∏

i=1

q(η

(i)

|ν,ζ

)

× q(Λ

(i)

|λ

(i)

)q(Ω

(i)

|ω

(i)

)

j=t

∏

j=1

q(z

(i)

|ς

(i)

)

(3.2)

where φ,ν,ζ

,λ,ω and ς are variational free pa-

rameters. Table 1 shows the correspondence between

variational and the original parameters. Now, the ﬁrst

term in Eq. 3.1 is decomposed into:

[log p(Y, M,Θ,V )] =

a=b

∑

a=1

[log p(Φ

|α)]

i=n

∑

i=1

[log p(η|µ, Σ)] + E

[log p(Λ

(i)

|β

)]

+ E

[log p(β

|γ,κ)] + E

[log p(Ω

(i)

,ξ)]

j=t

∑

j=1



[log p(y

(i)

,Ω

(i)

,Λ

(i)

,Φ, ϖ)]

+ E

[p(z

(i)

|η)]



(3.3)

where,

[log p(Φ

|α)] = log Γ



j=t

∑

j=1



−

j=t

∑

j=1

logΓ(α

)

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance

j=t

∑

j=1

(α

− 1)E

[logΦ

a, j

]

[log p(η|µ, Σ)] =

log|Σ

−1

| −

log2π

−



tr(diag(ζ

)Σ

−1

)

+ (ν −µ)

−1

(ν − µ)



[log p(Λ

(i)

|β

(i)

)] =

a=b

∑

a=1



(i)

logβ

(i)

+ (1 −λ

(i)

)

× log(1 −β

(i)

)



[log p(β

(i)

|γ,κ))] =

a=b

∑

a=1



(γ − 1)log(β

(i)

)

+ (κ −1)log(1 − β

(i)

) − log(B(γ,κ)



[log p(Ω

(i)

,ξ)] = log Γ



j=t

∑

j=1

+ M

(i)



−

j=t

∑

j=1

logΓ(ξ

+ M

(i)

)

j=t

∑

j=1

(ξ

+ M

(i)

− 1)E

[logΩ

(i)

]

[log p(y

(i)

,Ω

(i)

,Λ

(i)

,Φ, ϖ)] = log ϖ

c=t

∑

c=1

a=b

∑

a=1



(i)

j,c

(i)

a, j

(i)

[(1 − Ω

(i)

)]E

[logΦ

a, j

]



[log p(z

(i)

|η)] ≈ 1 − logρ +

a=b

∑

a=1

(i)

a, j

−



k=b

∑

k=1

[exp(η

)]



−1

The second term H(q) in Eq. 3.1 has the following

parametric forms (see Eq. 3.2):

H(q) = −

a=b

∑

a=1

[logq(Φ

|φ

)] −

i=n

∑

i=1

[logq(η

(i)

|ν,ζ

)]

+ E

[logq(Λ

(i)

|λ

(i)

)] + E

[logq(Ω

(i)

|ω

(i)

)]

j=t

∑

j=1

[logq(z

(i)

|ς

(i)

)]

(3.4)

where,

[logq(Φ

|φ

)] = log Γ



j=t

∑

j=1

a, j



−

j=t

∑

j=1

logΓ(φ

a, j

)

j=t

∑

j=1

(φ

a, j

− 1)E

[logΦ

a, j

]

[logq(η

(i)

|ν,ζ

)] = −

a=b

∑

a=1



logζ

+ log(2π) +1



[logq(Λ

(i)

|λ

(i)

)] =

a=b

∑

a=1



(i)

logλ

(i)

+ (1 −λ

(i)

)log(1 − λ

(i)

)



[logq(Ω

(i)

|ω

(i)

)] = log Γ



j=t

∑

j=1

(i)



−

j=t

∑

j=1

logΓ(ω

(i)

)

j=t

∑

j=1

(ω

(i)

− 1)E

[logΩ

(i)

]

[logq(z

(i)

|ς

(i)

)] = E

log

a=b

∏

a=1

(ς

(i)

a, j

)

(i)

a, j

a=b

∑

a=1

(i)

a, j

logς

(i)

a, j

The exceptions that correspond to the above equations

are:

[logΦ

a, j

] =



Ψ(φ

a, j

) − Ψ(

k=t

∑

k=1

a,k

)



[logΩ

(i)

] =



Ψ(ω

(i)

) − Ψ(

k=t

∑

k=1

(i)

)



[(1 − Ω

(i)

)] =

1 − ω

(i)

∑

k=t

k=1

(1 − ω

(i)

)

[exp(η

)] = exp(ν

)

B(γ,κ) =

Γ(γ)Γ(κ)

Γ(γ + κ)

where Γ denotes the Gamma function while Ψ is the

logarithmic derivative of the Gamma function.

After expanding both terms in Eq. 3.1, we can

now maximize the bound in Eq. 3.1 with respect to

each variational parameters using mini-batch coordi-

nate ascent updates (Hoffman et al., 2013) as:

Optimize ς. The analytical expression of the varia-

tional group assignment q(ς) for each pathway j and

group a for the ith example is not amenable due to

the non-conjugacy of logistic-normal with latent vari-

ables. Instead, we approximate the solution as:

(i)

a, j

∝ exp

c=t

∑

c=1

(i)

j,c

(i)

1 − ω

(i)

∑

k=t

k=1

(1 − ω

(i)

)



Ψ(φ

a, j

)

− Ψ(

k=t

∑

k=1

a,k

)



+ ν

− 1

(3.5)

where Ψ(.) is the digamma function. Notice that

the variational parameter ω

(i)

∗

acts as an smoothing pa-

rameter to selecting groups for each pathways, either

from M

or from P .

Optimize ν. Collecting terms in the ELBO bound

that contain only ν and taking derivatives w.r.t. ν

for

each group a, we obtain:

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

∂L(q)

[ν]

∂ν

= − Σ

−1

(ν − µ)+

j=t

∑

j=1

(i)

a, j

−



exp(ν

)



−1

(3.6)

where ρ is another variational parameter, as in

CTM (Blei and Lafferty, 2006). The above equation

in hard to optimize, instead, we use a conjugate gra-

dient algorithm.

Optimize ζ

. By symmetry, we gather all the terms

that has ζ

from Eq. 3.1, and take derivatives w.r.t. ζ

for each group a to obtain:

∂L(q)

[ζ

]

∂ζ

= −



−1

a,a

−1

exp





−



(3.7)

Again, there is no analytical solution to the above

formula. Instead, we use Newton’s method for each

coordinate such that ζ

∈ R

Optimize ρ. We extract terms involved with the vari-

ational parameter ρ, and equating it’s derivative to

zero, we get:

ρ =

k=b

∑

k=1

exp(ν

)

(3.8)

1 Initialize φ, ν, ζ

, λ, ω, ς, γ, κ, ξ, α, ϖ, ι, s = 0,

l ≥ 0, g ∈ (0.5,1]

2 repeat

3 s = s + 1;

4 example a minibatch randomly B ⊂ P ;

5 for i ∈ B do

6 repeat

7 Update ς

(i)

with Eq. 3.5;

8 Update ν

(i)

with Eq. 3.6 using

conjugate gradient algorithm;

9 Update ζ

2,(i)

with Eq. 3.7 using

Newton’s method;

10 Update ρ

(i)

with Eq. 3.8;

11 Update ω

(i)

with Eq. 3.9;

12 Update λ

(i)

with Eq. 3.10;

13 until local variational parameters

converge;

14 Compute optimal values µ =

|B|

Σ = diag(

|B|

) + µµ

;

15 Compute global optimal values φ with Eq.

3.11;

16 Update the current estimate of the global

variational paramters,

x = (1 − τ)x +τx, where x ∈ {φ,µ,Σ};

17 Update the learning rate τ = (s + l)

−g

;

18 until global convergence criterion is satisﬁed;

Algorithm 3: Minibatch variational inference for SPREAT.

Optimize ω. We next isolate only the terms in the

bound that contain variational background pathway

distributions q(ω). However, setting it’s derivatives to

zero does not lead to a closed-form solution, instead,

we approximate ω

(i)

for each example i according to:

(i)

∝ξ

+ M

(i)

−



1 − ω

(i)

−

∑

k=t

k=1

(1 − ω

(i)

)

(

∑

k=t

k=1

(1 − ω

(i)

))



j=t

∑

j=1

a=b

∑

a=1

(i)

j,c

(i)

a, j

(i)



Ψ(φ

a, j

) − Ψ(

k=t

∑

k=1

a,k

)



(3.9)

Optimize λ. To optimize λ, we use the canonical pa-

rameterisation of the Bernoulli distribution to get the

following updates for each group a for each example:

(i)

1 + exp

−(log(β

(i)

)−log(1−β

(i)

))

(3.10)

Optimize φ. Finally, the optimal solution of the vari-

ational pathway distribution q(Φ

|φ

) for each group

a is obtained by isolating terms involved in the ELBO

bound in Eq. 3.1 and setting it’s gradient to zero:

a,c

=α

i=n

∑

i=1

j=t

∑

j=1

(i)

j,c

(i)

a, j

(i)

1 − ω

(i)

∑

k=t

k=1

(1 − ω

(i)

)

(3.11)

The variational inference algorithm samples a

mini-batch from a collection, and uses it to compute

the local latent parameters in Eqs 3.5, 3.6, 3.7, 3.8,

3.9, and 3.10 until the evidence lower bound in Eq.

3.1 converges. Then, the global variational parame-

ter φ is updated in Eq. 3.11 using the posteriors (β,

Λ, η, z, Ω) collected from the previous step after be-

ing scaled according to the learning rate τ = (s+l)

−g

where s is the current step, l ≥ 0 is the delay factor,

and g ∈ (0.5, 1] is the forgetting rate. This process for

SPREAT is summarized in Algorithm 3.

3.1 Posterior Predictive Distribution

The posterior predictive distribution estimates the dis-

tribution of an unobserved value (

y) given the ob-

served values (Y

obs

) and parameters (Θ and V) that

are trained on a held-out training set (Hoffman et al.,

2013). The predictive distribution for SPREAT is:

y|Y

obs

M,M

obs

) =

y|Θ,

M)p(Θ|Y

obs

)dΘ

≈

a=b

∑

a=1



(i)

j=t

∑

j=1



a, j

(i)





× q(Θ,V)

(3.12)

where

M is

y’s background pathways and q(Θ,V)

corresponds to Eq. 3.2, trained on Y

obs

and M

obs

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance

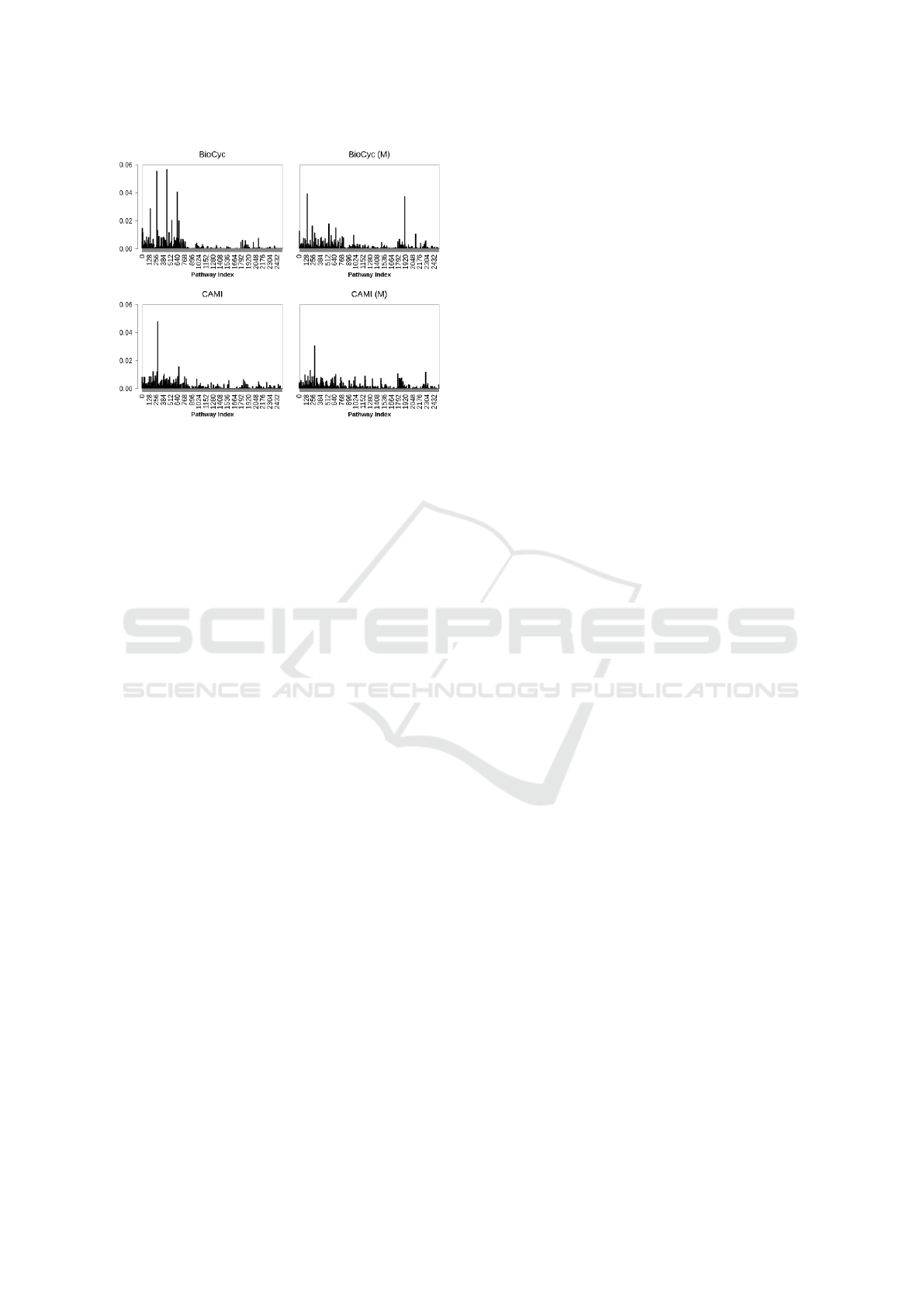
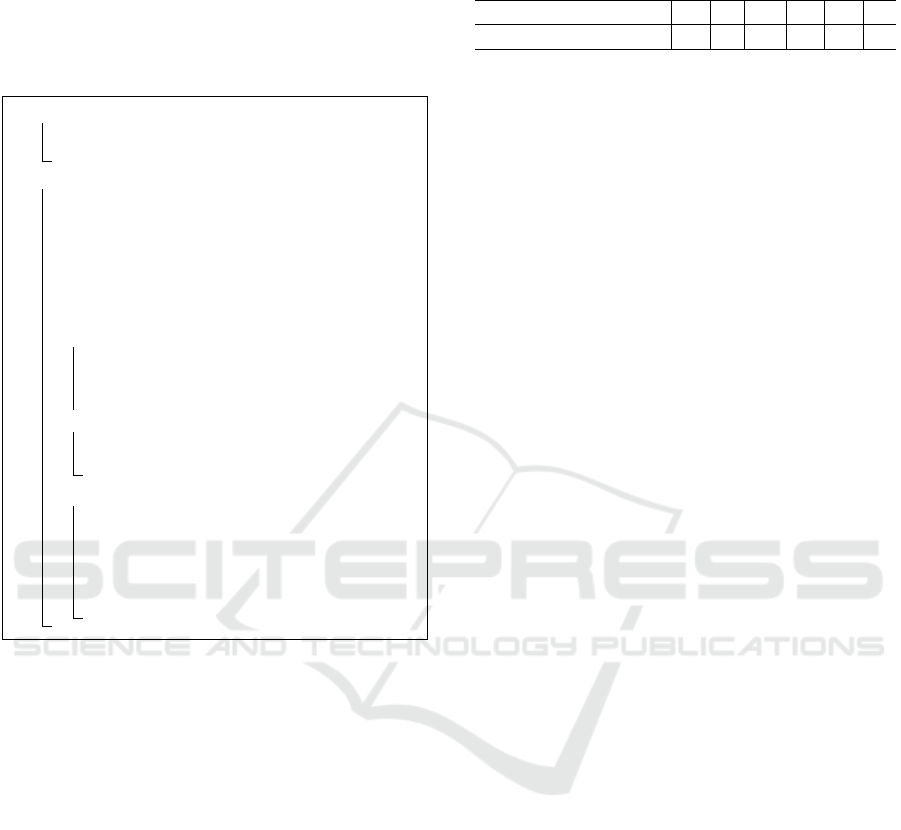
Figure 3: Pathway frequency (averaged on all examples)

in BioCyc (v20.5 T2 &3) and CAMI data, and their back-

ground pathways, indicated by M.

4 EXPERIMENTAL SETTINGS

In this section, we describe the experimental datasets

and settings used to validate the performance of the

three correlated models. The CHAP package was

written in Python v3 and is available under the GNU

license at github.com/hallamlab/chap. All tests were

conducted on a Linux server using 10 cores of Intel

Xeon CPU E5-2650.

4.1 Description of Datasets

The three models were evaluated on diverse path-

way datasets traversing the genomic information hi-

erarchy (M. A. Basher et al., 2020): i)- T1 golden

consisting of EcoCyc, HumanCyc, AraCyc, Yeast-

Cyc, LeishCyc, and TrypanoCyc; ii)- BioCyc (v20.5

T2 & 3) (Caspi et al., 2016); iii)- Critical Assess-

ment of Metagenome Interpretation (CAMI) dataset

composed of 40 genomes (Sczyrba et al., 2017);

and iv)- Synset-2, a noisy training dataset, intro-

duced in (M. A. Basher et al., 2020). For train-

ing, we applied BioCyc (v20.5 T2 & 3) data, while

for evaluating and testing we used T1 golden and

CAMI data. The Synset-2 data was used to ob-

tain supplementary pathways (see Section 4.2). The

preprocessed experimental datasets can be obtained

from zenodo.org/record/5630322#.YYXur2DMK3B

while information about these data is provided in

(M. A. Basher et al., 2020).

4.2 Parameter Settings

Three experiments were conducted: i)- parameter

sensitivity analysis, ii)- groups visualization, and

iii)- metabolic pathway prediction. Unless otherwise

mentioned, we applied the following default conﬁgu-

rations: the pathway distribution over groups Φ were

initialized using gamma distribution (with shape and

scale parameters were ﬁxed to 100 and 1/100, re-

spectively), the forgetting rate was g = 0.9, the delay

rate was l = 1, the batch size was 100, the number of

epochs was 3, the number of groups was b = 200, top

k pathways was 100 (only for SOAP and SPREAT),

the Dirichlet hyperparameters α and ξ were 0.0001,

and the beta hyperparameters γ and κ were 2 and 3,

respectively. The supplementary pathways M for Bio-

Cyc, CAMI, and golden T1 datasets were obtained us-

ing mlLGPR (elastic-net with enzymatic reaction and

pathway evidence features)(M. A. Basher et al., 2020)

trained on Synset-2. A schematic view of pathway

frequency for BioCyc T2 &3 and CAMI data with

their background pathways is depicted in Fig. 3.

After obtaining groups, we followed the pathway

prediction pipeline in Fig. 1 by ﬁrst mapping ex-

amples to groups using reMap software (Hallam Lab,

2021b) and, then, the pathway prediction is achieved

using leADS software (Hallam Lab, 2021a). All hy-

perparameters in reMap, leADS, and mlLGPR, were

ﬁxed to their default values.

5 EXPERIMENTAL RESULTS

This section analyzes the three models using the set-

tings explained in the previous section.

5.1 Sensitivity Analysis

Experimental Setup. Following the common prac-

tice, here we study the effect of hyperparameters on

the performance of correlated models. First, we com-

pare the sensitivity of SOAP and SPREAT against

CTM by incorporating the background pathways M

while varying the number of groups according to

b ∈ {50, 100, 150, 200, 300}. Next, we examine the

SOAP and SPREAT with collapsed option (or c2m)

to compare their performances to CTM, where the

former models should exhibit similar performances

as CTM. Finally, we conduct sparsity analysis of

group distribution by varying the cutoff threshold

value according to k ∈ {50,100,150,200,300,500}

(Section 2.2). For comparative analysis, we apply

CAMI as test data to report the log predictive dis-

tribution (Section 3.1), where a lower score entails

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

50 100 150 200 300

−0.9

−0.8

−0.7

−0.6

Log Pred ic tive Probability

CTM SOAP SPREAT

(a) Effect of b

50 100 150 200 300

−0.9

−0.8

−0.7

−0.6

Log Pred ic tive Probability

CTM SOAP+c2m SPREAT+c2m

(b) Effect of b by collapsing

50 100 150 200 300 500

−1.0

−0.8

−0.6

Log Pred ic tive Probability

SOAP SPREAT

Figure 4: Log predictive distribution on CAMI data. Figs 4a and 4b show the effect of group size b to the performance of

CTM, SOAP, and SPREAT and the collapsed models, respectively. Fig. 4c demonstrates the effect of retaining top k pathways

to the performance SOAP and SPREAT. The performance is measures according to the log predictive probability where higher

values indicate better performances.

higher generalization capability for the corresponding

model.

Experimental Results. While the log predictive

scores for SOAP and SPREAT in Fig. 4a appear to

be ﬂat across various group sizes, the CTM model

projects a more realistic view where its performances

are seen to be gaining by including more groups. Both

SOAP and SPREAT incorporate supplementary path-

ways in modeling the pathway distribution. There-

fore, it is expected to learn additional pathways from

M that has an average of ∼ 500 pathways in relation

to BioCyc v20.5 T2 & 3 which has ∼ 195 pathways

on average. By excluding M (“c2m” in Section 2.2)

in the SOAP and SPREAT training, the log predic-

tive distribution of these models exhibit similar per-

formance as CTM (Fig. 4b). From Figs 4a and 4b, it

is evident that b = 200 represents an optimum group

size. To ﬁnd an optimum k value, we ﬁxed b = 200

and retrained all models. From Fig. 4c, the perfor-

mances for SOAP and SPREAT are seen to decline

(< −0.6) when k > 100.

Results from this experiment suggest that the set-

tings b ∈ Z

[150,300]

and k ∈ Z

[50,100]

are optimum for

discovering pathway groups in P .

5.2 Groups Visualization

Experimental Setup. Recall that groups constitute

overlapping pathways. In this experiment, we visu-

ally explore the recovered groups from the three cor-

related models trained on BioCyc (v20.5 T2 &3) data

using conﬁgurations discussed in Section 4.2. We in-

vestigate group correlations, reﬂected in Σ, for SOAP,

SPREAT, CTM, SOAP+c2m, and SPREAT+c2m

models, to analyze the inﬂuence of dual sparseness

(Section 2.2) and background pathways on Σ.

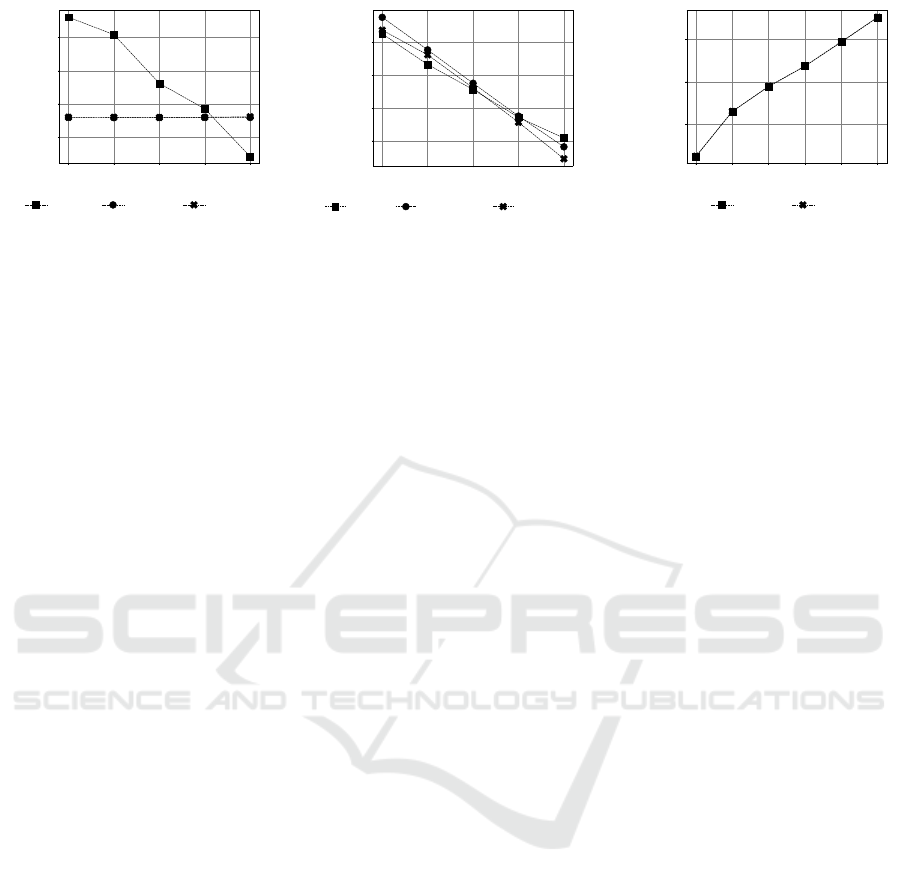
Experimental Results. Fig. 5 demonstrates 50 ran-

domly picked groups and their correlations as rep-

resented by Σ for all models. The width of edges

indicates the strength of correlations. Essentially

for every group in these models, there are approxi-

mately 12 to 19 closely related groups. This indicates

that metabolic pathways are distributed over multi-

ple groups, therefore, forming overlapping pathways.

With regard to M, as explained in Section 5.1, back-

ground pathways in M consist of ∼ 500 pathways for

organismal or multi-organismal genomes in compari-

son to BioCyc (v20.5 T2 &3) data that has an average

of ∼ 195 pathways. These additive pathways inﬂu-

ence the construction of group correlation for both

SOAP and SPREAT. Pathway groups in SOAP con-

sist of more associated groups (∼ 19 groups) than the

remaining models. This has an important implication

for pathway prediction outcomes, discussed in Sec-

tion 5.3. Sparse models share a similar group struc-

ture as CTM (also they have similar log predictive

scores in Section 5.1), therefore, they may exhibit

similar effects on pathway prediction performance.

Results from this experiment show that SOAP and

SPREAT are better contenders than CTM. Speciﬁ-

cally, both models incorporate supplementary path-

ways and apply dual sparseness to reduce both the

group size and the statistically irrelevant pathways.

5.3 Metabolic Pathway Prediction

Experimental Setup. Pathway groups obtained from

correlated models are used for pathway prediction.

We consider ﬁve models: CTM, two models with

background pathways (SOAP and SPREAT), and two

collapsed models (SOAP+c2m and SPREAT+c2m).

After obtaining groups, we trained reMap using the

conﬁguration discussed in Section 4.2. The results

are reported on golden T1 data using four evaluation

metrics: Hamming loss, average precision, average

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance

(a) SOAP (#groups:

∼ 19)

(b) SPREAT

(#groups: ∼ 13)

∼ 12)

(d) SOAP+c2m

(#groups: ∼ 12)

(e) SPREAT+c2m

(#groups: ∼ 12)

Figure 5: 50 randomly picked pathway groups, represented by blue circles, and their correlations, indicated by black links,

for each model. The average number of related groups to each pathway group is indicated by #groups. CTM, SOAP+c2m,

and SPREAT+c2m form two distinct clusters of groups, indicating pathways are less shared among groups while SOAP and

SPREAT have more shared pathways in their groups.

recall, and average F1 score. For comparative

analysis, four pathway prediction algorithms are

used: i)- MinPath v1.2 (Ye and Doak, 2009), ii)-

PathoLogic v21 (Karp et al., 2016), iii)- mlLGPR

(elastic net with enzymatic reaction and pathway

evidence features) (M. A. Basher et al., 2020), and

iv)- triUMPF (M. A. Basher et al., 2021a).

Experimental Results. Table 2 shows that groups

from SOAP result in competitive performance against

the other methods in terms of average F1 score with

optimal performance on EcoCyc (0.8336). However,

it seems to be underperforming on AraCyc, YeastCyc,

and LeishCyc, yielding average F1 scores of 0.4764,

0.4914, and 0.4144, respectively. This is attributed

to incorrect background pathways in M (see Section

5.1), hence, impacting the training process. Inter-

estingly, SPREAT’s performance appears to be infe-

rior to SOAP. As alluded in Section 5.2, the average

number of correlated groups for SOAP is signiﬁcantly

larger than SPREAT (Section 5.2), enforcing to revisit

a true positive pathway for an organism multiple times

across groups in SOAP to signal its presence in con-

trast to groups from SPREAT. With respect to the sen-

sitivity score, correlated models, in general, resulted

in higher scores than triUMPF reinforcing the beneﬁt

of modeling groups to improve predictions.

Results from this experiment demonstrate that the

group-based approach, in particular SOAP, improves

metabolic pathway prediction outcomes. We suggest

applying SOAP for pathway predictions using the de-

fault conﬁgurations discussed in Section 4.2.

6 CONCLUSIONS

In this paper, we presented two novel statistical hier-

archical mixture models, SOAP and SPREAT, to un-

cover correlated pathway groups given pathway abun-

dance data. The work is motivated by the prob-

lem of missing pathways, which is very common

in pathway prediction from organismal and multi-

organismal datasets. We empirically evaluated corre-

lated models for pathway prediction using golden T1

data and compared results to other prediction meth-

ods including PathoLogic, MinPath, mlLGPR, and

triUMPF. Overall, correlated models showed promis-

ing results in boosting prediction performance over

ML-based algorithms, such as triUMPF. There are

several directions for future study. Foremost, we in-

tend to build a model that combines both graph-based

(M. A. Basher et al., 2021a) and group-based meth-

ods to improve metabolic pathway prediction with

emphasis on multi-organismal genomes. Additional

attention should be paid to sparseness induction in

the covariance matrix for better interpretability (Fan

et al., 2016).

ACKNOWLEDGEMENTS

This work was performed under the auspices of

Genome Canada, Genome British Columbia, the

Natural Sciences and Engineering Research Council

(NSERC) of Canada, and Compute/Calcul Canada).

ARMAB was supported by a UBC four-year doc-

toral fellowship (4YF) administered through the UBC

Graduate Program in Bioinformatics.

REFERENCES

Aguiar-Pulido, V., Huang, W., Suarez-Ulloa, V., Cickovski,

T., Mathee, K., and Narasimhan, G. (2016). Metage-

nomics, metatranscriptomics, and metabolomics ap-

proaches for microbiome analysis: supplementary is-

sue: bioinformatics methods and applications for big

metagenomics data. Evolutionary Bioinformatics,

12:EBO–S36436.

Airoldi, E. M., Blei, D. M., Fienberg, S. E., and Xing, E. P.

(2008). Mixed membership stochastic blockmodels.

Journal of machine learning research, 9(Sep):1981–

2014.

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

Table 2: Predictive performance of each comparing algorithm on 6 benchmark datasets. For each performance metric, ‘↓’

indicates the smaller score is better while ‘↑’ indicates the higher score is better. Bold text suggests the best performance in

each column.

Methods

Hamming Loss ↓

EcoCyc HumanCyc AraCyc YeastCyc LeishCyc TrypanoCyc

PathoLogic 0.0610 0.0633 0.1188 0.0424 0.0368 0.0424

MinPath 0.2257 0.2530 0.3266 0.2482 0.1615 0.2561

mlLGPR 0.0804 0.0633 0.1069 0.0550 0.0380 0.0590

triUMPF 0.0435 0.0954 0.1560 0.0649 0.0443 0.0776

SOAP 0.0392 0.0400 0.1714 0.0934 0.0772 0.0479

SPREAT 0.0519 0.0827 0.1489 0.0748 0.0629 0.0503

CTM 0.0558 0.0835 0.1425 0.0804 0.0622 0.0503

SOAP+c2m 0.0590 0.0780 0.1457 0.0772 0.0614 0.0534

SPREAT+c2m 0.0542 0.0796 0.1520 0.0772 0.0598 0.0558

Methods

Average Precision Score ↑

EcoCyc HumanCyc AraCyc YeastCyc LeishCyc TrypanoCyc

PathoLogic 0.7230 0.6695 0.7011 0.7194 0.4803 0.5480

MinPath 0.3490 0.3004 0.3806 0.2675 0.1758 0.2129

mlLGPR 0.6187 0.6686 0.7372 0.6480 0.4731 0.5455

triUMPF 0.8662 0.6080 0.7377 0.7273 0.4161 0.4561

SOAP 0.8611 0.7871 0.6215 0.4851 0.2805 0.5985

SPREAT 0.9400 0.6750 0.8350 0.6000 0.3200 0.6200

CTM 0.9150 0.6700 0.8750 0.5650 0.3250 0.6200

SOAP+c2m 0.8950 0.7050 0.8550 0.5850 0.3300 0.6000

SPREAT+c2m 0.9250 0.6950 0.8150 0.5850 0.3400 0.5850

Methods

Average Recall Score ↑

EcoCyc HumanCyc AraCyc YeastCyc LeishCyc TrypanoCyc

PathoLogic 0.8078 0.8423 0.7176 0.8734 0.8391 0.7829

MinPath 0.9902 0.9713 0.9843 1.0000 1.0000 1.0000

mlLGPR 0.8827 0.8459 0.7314 0.8603 0.9080 0.8914

triUMPF 0.7590 0.3835 0.3529 0.3319 0.7126 0.6229

SOAP 0.8078 0.8746 0.3863 0.4978 0.7931 0.9371

SPREAT 0.6124 0.4839 0.3275 0.5240 0.7356 0.7086

CTM 0.5961 0.4803 0.3431 0.4934 0.7471 0.7086

SOAP+c2m 0.5831 0.5054 0.3353 0.5109 0.7586 0.6857

SPREAT+c2m 0.6026 0.4982 0.3196 0.5109 0.7816 0.6686

Methods

Average F1 Score ↑

EcoCyc HumanCyc AraCyc YeastCyc LeishCyc TrypanoCyc

PathoLogic 0.7631 0.7460 0.7093 0.7890 0.6109 0.6447

MinPath 0.5161 0.4589 0.5489 0.4221 0.2990 0.3511

mlLGPR 0.7275 0.7468 0.7343 0.7392 0.6220 0.6768

triUMPF 0.8090 0.4703 0.4775 0.4735 0.5254 0.5266

SOAP 0.8336 0.8285 0.4764 0.4914 0.4144 0.7305

SPREAT 0.7416 0.5637 0.4704 0.5594 0.4460 0.6613

CTM 0.7219 0.5595 0.4930 0.5268 0.4530 0.6613

SOAP+c2m 0.7061 0.5887 0.4817 0.5455 0.4599 0.6400

SPREAT+c2m 0.7298 0.5804 0.4592 0.5455 0.4739 0.6240

Baranwal, M., Magner, A., Elvati, P., Saldinger, J., Violi,

A., and Hero, A. O. (2020). A deep learning architec-

ture for metabolic pathway prediction. Bioinformat-

ics, 36(8):2547–2553.

Bien, J. and Tibshirani, R. J. (2011). Sparse estimation of a

covariance matrix. Biometrika, 98(4):807–820.

Blei, D. and Lafferty, J. (2006). Correlated topic models.

Advances in neural information processing systems,

18:147.

Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance

dirichlet allocation. Journal of machine Learning re-

search, 3(Jan):993–1022.

Caspi, R., Billington, R., Foerster, H., and et al.

(2016). Biocyc: Online resource for genome and

metabolic pathway analysis. The FASEB Journal, 30(1

Supplement):lb192–lb192.

Caspi, R., Billington, R., Keseler, I. M., Kothari, A., Krum-

menacker, M., Midford, P. E., Ong, W. K., Paley, S.,

Subhraveti, P., and Karp, P. D. (2019). The metacyc

database of metabolic pathways and enzymes-a 2019

update. Nucleic acids research.

Dale, J. M., Popescu, L., and Karp, P. D. (2010). Machine

learning methods for metabolic pathway prediction.

BMC bioinformatics, 11(1):1.

Fan, J., Liao, Y., and Liu, H. (2016). An overview of the

estimation of large covariance and precision matrices.

The Econometrics Journal, 19(1):C1–C32.

Hahn, A. S., Konwar, K. M., Louca, S., and et al. (2016).

The information science of microbial ecology. Cur-

rent opinion in microbiology, 31:209–216.

Hanson, N. W., Konwar, K. M., Hawley, A. K., and

et al.(2014). Metabolic pathways for the whole com-

munity. BMC genomics, 15(1):1.

Hassa, J., Maus, I., Off, S., P

uhler, A., Scherer, P., Klocke,

M., and Schl

uter, A. (2018). Metagenome, metatran-

scriptome, and metaproteome approaches unraveled

compositions and functional relationships of micro-

bial communities residing in biogas plants. Applied

microbiology and biotechnology, 102(12):5045–5063.

He, J., Hu, Z., Berg-Kirkpatrick, T., and et al. (2017). Efﬁ-

cient correlated topic modeling with topic embedding.

In Proceedings of the 23rd ACM SIGKDD Interna-

tional Conference on Knowledge Discovery and Data

Mining, pages 225–233. ACM.

Hoffman, M. D., Blei, D. M., Wang, C., and Paisley,

J. W.(2013). Stochastic variational inference. Jour-

nal of Machine Learning Research, 14(1):1303–1347.

Jiao, D., Ye, Y., and Tang, H. (2013). Probabilistic infer-

ence of biochemical reactions in microbial communi-

ties from metagenomic sequences. PLoS Comput Biol,

9(3):e1002981.

Kanehisa, M., Furumichi, M., Tanabe, M., and et al.

(2017). Kegg: new perspectives on genomes, path-

ways, diseases and drugs. Nucleic Acids Research,

45(D1):D353–D361.

Karp, P. D., Latendresse, M., Paley, S. M., and et al. (2016).

Pathway tools version 19.0 update: software for path-

way/genome informatics and systems biology. Brief-

ings in bioinformatics, 17(5):877–890.

Khatri, P., Sirota, M., and Butte, A. J. (2012). Ten years

of pathway analysis: current approaches and out-

standing challenges. PLoS computational biology,

8(2):e1002375.

Lawson, C. E., Harcombe, W. R., Hatzenpichler, R., and

et al. (2019). Common principles and best practices

for engineering microbiomes. Nature Reviews Micro-

biology, pages 1–17.

Lin, T., Tian, W., Mei, Q., and Cheng, H.(2014). The

dual-sparse topic model: mining focused topics and

focused terms in short text. In Proceedings of the 23rd

international conference on World wide web, pages

539–550. ACM.

Loh, P.-R., Baym, M., and Berger, B. (2012). Compressive

genomics. Nature biotechnology, 30(7):627.

M. A. Basher, A. R. and Hallam, S. J. (2021). Relabeling

metabolic pathway data with groups to improve pre-

diction outcomes. BioRxiv.

M. A. Basher, A. R., McLaughlin, R. J., and Hallam, S. J.

(2020). Metabolic pathway inference using multi-

label classiﬁcation with rich pathway features. PLOS

Computational Biology, 16(10):1–22.

M. A. Basher, A. R., McLaughlin, R. J., and Hallam, S. J.

(2021a). Metabolic pathway prediction using non-

negative matrix factorization with improved precision.

Journal of Computational Biology.

M. A. Basher, A. R., McLaughlin, R. J., and Hallam,

S. J. (2021b). Metabolic pathway prediction using

non-negative matrix factorization with improved pre-

cision. In Computational Advances in Bio and Med-

ical Sciences, pages 33–44, Cham. Springer Interna-

tional Publishing.

Mascher, M., Schreiber, M., Scholz, U., Graner, A.,

Reif, J. C., and Stein, N. (2019). Genebank ge-

nomics bridges the gap between the conservation of

crop diversity and plant breeding. Nature genetics,

51(7):1076–1081.

Qi, Q., Li, J., and Cheng, J. (2014). Reconstruction

of metabolic pathways by combining probabilistic

graphical model-based and knowledge-based meth-

ods. In BMC proceedings, volume 8, pages 1–10.

Springer.

Sczyrba, A., Hofmann, P., Belmann, P., and et al. (2017).

Critical assessment of metagenome interpretation—a

benchmark of metagenomics software. Nature meth-

ods, 14(11):1063.

Shaﬁei, M., Dunn, K. A., Chipman, H., Gu, H.,

and Bielawski, J. P. (2014). Biomenet: A

bayesian model for inference of metabolic divergence

among microbial communities. PLoS Comput Biol,

10(11):e1003918.

Stewart, F. J., Sharma, A. K., Bryant, J. A., and et al. (2011).

Community transcriptomics reveals universal patterns

of protein sequence conservation in natural microbial

communities. Genome biology, 12(3):R26.

Tabei, Y., Yamanishi, Y., and Kotera, M. (2016). Simul-

taneous prediction of enzyme orthologs from chem-

ical transformation patterns for de novo metabolic

pathway reconstruction. Bioinformatics, 32(12):i278–

i287.

Hallam Lab(2021a). leADS: https://github.com/ hallam-

lab/leADS.

Hallam Lab(2021b). reMap: https://github.com/ hallam-

lab/reMap.

Wang, W.-L., Xu, S.-Y., Ren, Z.-G., Tao, L., Jiang, J.-W.,

and Zheng, S.-S.(2015). Application of metagenomics

in the human gut microbiome. World journal of gas-

troenterology: WJG, 21(3):803.

Yamanishi, Y., Tabei, Y., and Kotera, M. (2015).

Metabolome-scale de novo pathway reconstruction

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

using regioisomer-sensitive graph alignments. Bioin-

formatics, 31(12):i161–i170.

Ye, Y. and Doak, T. G. (2009). A parsimony approach

to biological pathway reconstruction/inference for

genomes and metagenomes. PLoS Comput Biol,

5(8):e1000465.

Zhao, Y., Chen, M.-H., Pei, B., Rowe, D., Shin, D.-G.,

Xie, W., Yu, F., and Kuo, L. (2012). A bayesian ap-

proach to pathway analysis by integrating gene–gene

functional directions and microarray data. Statistics in

biosciences, 4(1):105–131.

Aggregating Statistically Correlated Metabolic Pathways Into Groups to Improve Prediction Performance