Separation of Concerns in Extended Epidemiological

Compartmental Models

A Yvan Guifo Fodjo

1,6,7 a

, Mikal Ziane

2,1 b

, Serge Stinckwich

3 c

, Bui Thi Mai Anh

and Samuel Bowong

5,6

CNRS, UMR 7606, LIP6, Sorbonne Universit

e, Paris, France

Universit

e de Paris, Paris, France

United Nations University Institute in Macau, Macau SAR, China

School of Information and Communication Technology, Laboratory of Intelligent Software Engineering,

Hanoi University of Science and Technology, Hanoi, Vietnam

epartement de Math

ematiques, Universit

e de Douala, Douala, Cameroon

IRD, UMI 209, UMMISCO, Bondy, France

URIFIA, Universit

e de Dschang, Dschang, Cameroon

Keywords:

Separation of Concerns, Compartmental Models, Contact Network, Epidemiology Modeling Tool.

Abstract:

Epidemiological models become more and more complex as new concerns are taken into account (age, sex,

spatial heterogeneity, containment or vaccination policies, etc.). This is problematic because these aspects are

typically intertwined which makes models difﬁcult to extend, change or reuse. The Kendrick approach has

shown promising results to separate epidemiological concerns but is restricted to homogeneous compartmental

models. In this paper, we report on an attempt to generalize the Kendrick approach to support some aspects

of contact networks, thereby improving the predictive quality of models with signiﬁcant heterogeneity in the

structure of contacts, while keeping the simplicity of compartmental models. This approach has been validated

on two different techniques to generalize compartmental models.

1 INTRODUCTION

Modeling and simulation have been heavily used in

epidemiology, for instance to inform control strate-

gies (Levin and Durrett, 1996). Epidemiological

models largely rely on the compartmental framework

where the individuals of a population are grouped

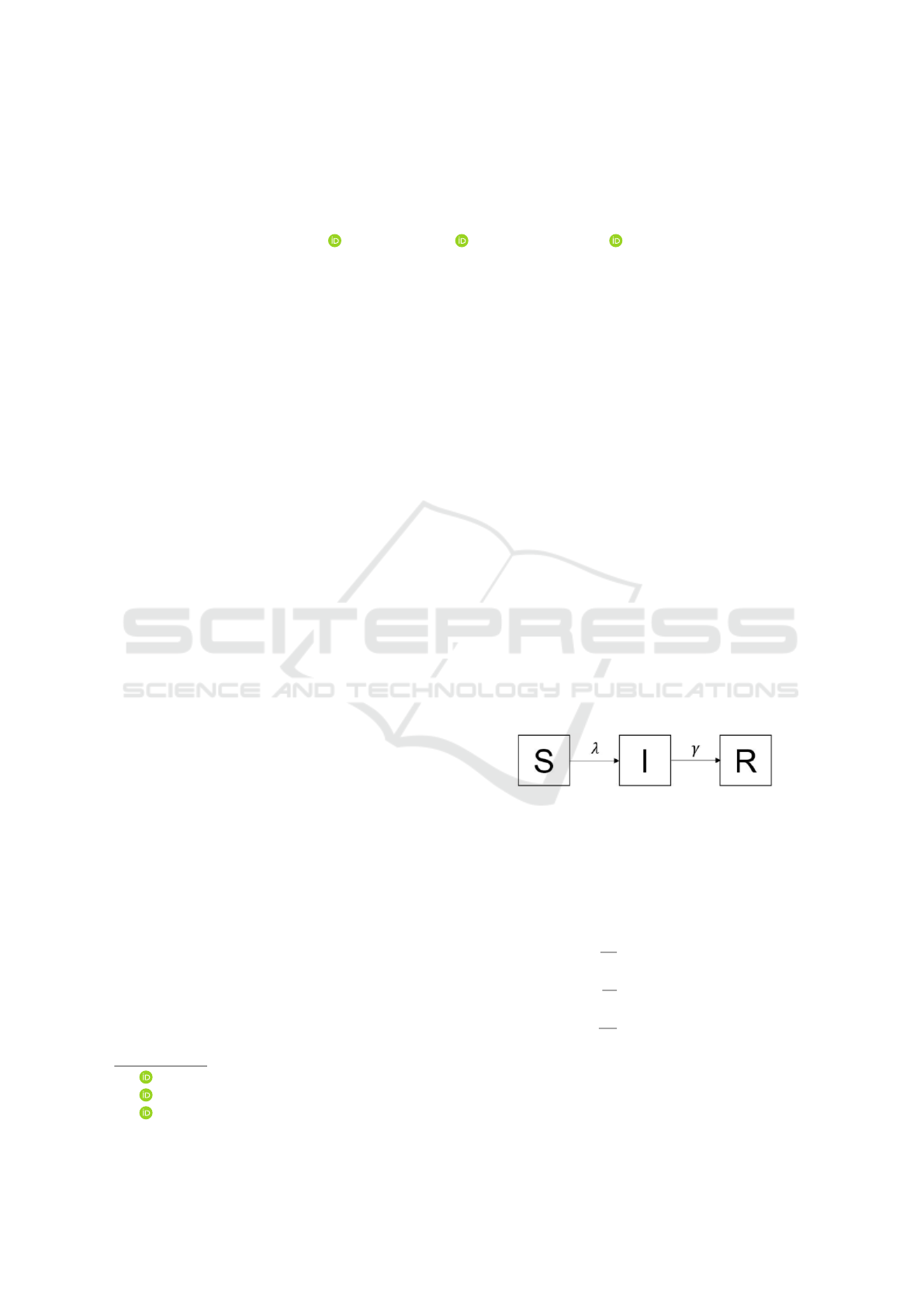
by their epidemiological status (Keeling and Rohani,

2011). Those Susceptible to the pathogen (state S)

can be infected with rate λ, the Infectious ones (state

I) can transmit the disease or become immune a.k.a

Recovered (state R) with rate γ (See Figure 1).

Compartmental models are typically ﬁrst deﬁned

as ordinary differential equations (ODEs), such as

Equation 1 below, which can be studied analytically

and/or simulated using algorithms such as Runge-

Kutta. It is however considered more realistic to adopt

https://orcid.org/0000-0002-0714-6737

https://orcid.org/0000-0003-1860-485X

https://orcid.org/0000-0002-8755-9848

Figure 1: Flow diagram of the SIR (Susceptible, Infected,

Recovered) mathematical model.

a stochastic viewpoint on these models, typically con-

sidering them as Continuous-Time Markov Chains

(CTMCs), that can be derived from the ODEs modulo

some widely-accepted, albeit simplifying, probabilis-

tic assumptions.











= −λS

= λS −γI

= γI

N = S +I + R

(1)

Aside from this core epidemiological concern,

other concerns may have to be taken into account

such as the age structure, the social or sexual mix-

152

Guifo Fodjo, A., Ziane, M., Stinckwich, S., Anh, B. and Bowong, S.

Separation of Concerns in Extended Epidemiological Compartmental Models.

DOI: 10.5220/0010881900003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 3: BIOINFORMATICS, pages 152-159

ISBN: 978-989-758-552-4; ISSN: 2184-4305

ing and the spatial heterogeneity of the transmission

that may be caused by various considerations. Each of

these additional aspects may lead to further partition-

ing the population. Unfortunately, concerns are typ-

ically intertwined in epidemiological models in both

executable code and mathematical equations.

At ﬁrst sight at least, it seems difﬁcult to sepa-

rate these concerns since, when a concern is added

to a model, it is precisely because it interferes with

the core epidemiological concern to introduce some

kind of heterogeneity. For example, in a spatial SIR

model, the spatial concern impacts the epidemic con-

cern at each region which assigns a speciﬁc value to

an epidemic parameter. If the epidemic parameters

had the same value on the whole space, there would

be little point in introducing a spatial concern in the

ﬁrst place.

The Kendrick approach(Bui et al., 2016) consists

in deﬁning concerns (age, sex, spatial heterogene-

ity, ...) as independent, possibly incomplete, mod-

els that are then combined into Stochastic Automata

Networks (SANs) (Plateau and Stewart, 2000) using a

tensor-sum operator. The stochastic dependencies be-

tween concerns are then introduced in a second phase

so that the independent concerns can be reused and

combined in other models much more easily.

A typical assumption of compartmental models is

that individuals mix (meet others individual with po-

tential disease transmission) uniformly, at least in the

same compartments, i.e. with the same probability.

This assumption is getting more and more criticized

as unrealistic as it has been observed that, in many

outbreaks, a few super-spreaders initially infect other

individuals more quickly than homogeneous models

predict. Later in an epidemic, on the contrary, when

a lot of individuals are infected, the reverse has been

observed: homogeneous models predict more infec-

tions than what happens, because the remaining sus-

ceptible individuals are typically the most isolated

ones.

It has thus been proposed to deﬁne, study or simu-

late contact-network models in which nodes denote

individuals or groups of individuals and edges de-

note potential contacts. These models, however, are

more involved to deﬁne and study than compartmen-

tal models. It is thus natural to try and extend com-

partmental models to include some contact hetero-

geneity.

Several adaptations have been published to im-

prove the homogeneous compartmental approach for

at least some classes of contact networks. Bansal et

al. (Bansal et al., 2007) have then proposed a general

framework to capture such adaptations as changes to

the parameters that deﬁne the force of infection, and

have redeﬁned two of these adaptations, that they

deemed typical enough, using their proposal: the

Stroud (Stroud et al., 2006) and the Aparicio (Apari-

cio and Pascual, 2007) adaptations.

In this paper, we report on our attempt to integrate

Bansal’s framework in the Kendrick approach to sep-

aration of concerns(Bui et al., 2016). The challenge

consists in expressing Bansal’s framework as well as

any specialization of it such as Stroud’s or Aparicio’s

adaptation as separate Kendrick concerns. The bene-

ﬁt of our proposal is that adaptations to the homoge-

neous compartmental model may now take advantage

of separation of concerns and be combined with other

kind of concerns that are not directly related to the

contact network.

2 INTEGRATING BANSAL’S

FRAMEWORK IN THE

KENDRICK APPROACH

Seen from a software engineer’s viewpoint, our idea

is somehow similar to applying the Template Method

design pattern (Gamma et al., 1995) to epidemic

model equations

: it consists in expressing λ as a

function of 3 parameters, α, i

and τ.

α is the average number of individuals with which

a susceptible individual has contact or the average de-

gree of nodes in a contact network, i

is the proportion

of contacts that are infectious

and τ is the per-contact

rate at which the disease is transmitted between an in-

fectious and a susceptible individual.

Following Bansal et al. we have renamed these

3 usual parameters to α

gen

, it

gen

and τ

gen

to insist

on their special meaning when applied to a model

based on a contact-network and to signal that they are

generic hot-spots, i.e. varying points. The generic

deﬁnition for the force of infection λ is given by

Equation 2. We have, however, for the sake of sim-

plicity and of readability, often kept the original sim-

ple names without the ”gen” subscript, especially

when they have their usual homogeneous meaning,

typically before a model is made generic using the

Kendrick approach. We have used names with ”gen”

in ﬁnal generic deﬁnitions of models and in Kendrick

code.

λ = α

gen

(2)

The most obvious difference with the Template pattern

is that there is no object-oriented inheritance involved here

but there was of course no such inheritance either in the

original patterns from Alexander.

Caveat: this means the proportion of infectious individ-

uals among the individuals a susceptible individual meets.

Separation of Concerns in Extended Epidemiological Compartmental Models

153

In traditional (homogeneous-compartmental)

models i

is typically deﬁned this way:

(3)

(Bansal et al., 2007) reports on two proposals,

Stroud et al. (Stroud et al., 2006) and Aparicio et

al. (Aparicio and Pascual, 2007), to generalize com-

partmental models to capture some aspects of contact-

network models. Both proposals were captured by

giving (α

gen

, it

gen

and τ

gen

) speciﬁc values. In order to

explain these approaches in the limited allowed space

for this paper, we have chosen to simplify the rational

and hypotheses behind them and more generally the

epidemiological questions in this paper. The inter-

ested reader will need to refer to the original papers

to get the full explanations of these models.

Consider Figures 5, 6 and 7. The curves are the

daily incidence

predicted by different models assum-

ing a Poisson, exponential and scale-free contact net-

work respectively . The red line denotes a traditional

(homogeneous) compartmental model. By deﬁnition,

it does not depend on the network but then, in some

cases, it suffers from two problems: the height of the

peak is wrong and it happens too late.

The blue and green curves are run using our

Kendrick compartmental tool but using the approach

from Stroud et al. and from Aparicio et al., respec-

tively, to approximate some aspects of contact net-

works. The former approach improves (lowers) the

height of the peak on some classes of networks. The

latter approach improves the timing of the peak on

some classes of networks although sometimes exag-

gerating its height. Ideally, it should be easy to try

one or several of these approaches to decide which

approach best matches the observed data.

In this paper, we thus want to check if both these

approaches can be captured as Kendrick concerns to

keep the beneﬁts of separation of concerns. This way

these approaches can be changed more easily than in

monolithic models where all concerns are mixed to-

gether (Bui et al., 2016).

In case of success, our middle-term objective, out-

side of the scope of this paper, would be to investigate

what class of extensions can be deﬁned as Kendrick

concerns so that compartmental models can more eas-

ily be enriched with some of the properties of contact

networks.

Incidence is the number of new infections per day,

sometimes normalized by dividing by some value. (Bansal

et al., 2007) do not give which value they chose for the de-

nominator we thus did not normalize incidence.

2.1 Stroud et al.’s Extension

In traditional homogeneous-mixing compartmental

modeling, the expected number of new infections per

day per infectious person is assumed to be propor-

tional to the fraction of the population that is suscep-

tible. In real social structures, however, some suscep-

tible individuals have a greater chance to receive and

transmit the disease than others. (Stroud et al., 2006)

claim that ”epidemic models can practically incorpo-

rate inhomogeneous mixing by taking the number of

new infections per day per infectious person to scale

as a power (greater than one) of the fraction of the

population that is susceptible”.

Introducing this power law can be done in two

steps. First, combining Equations 1, 2 and 3 leads

to:

= −ατI

(4)

Then, this equation is generalized by introducing a

constant, ν, greater than 1, that is postulated to be a

power of S/N. This constant must be ”ﬁtted” from real

data i.e. estimated to minimize errors. Intuitively,

a higher value for ν represents a higher degree of

heterogeneity, especially (although not necessarily) in

the number of contacts among individuals or similarly

in the degree of nodes in a contact network.

The generalized equation becomes:

= −α

gen

)

(5)

which leads to:

gen

(

)

(6)

The parameters α

gen

and τ

gen

are constants whose val-

ues are best set outside of models themselves, in so-

called simulation scenarios. Capturing this idea in

Kendrick is quite simple and merely consists in as-

signing the above value to it

gen

which will implicitly

declare an additional parameter ν to be assigned in

simulation scenarios. The Kendrick code of this con-

cern is given in Section 3. Remember that the point

was to try and keep the implementation of this idea

separate from the rest of the model, here from the SIR

concern.

2.2 Aparicio et al.’s Extension

Homogeneous models often fail to predict when the

peek of an epidemic will occur. Early in epidemics,

the most likely individuals to be infected are typically

”hubs” that have a lot contacts and thus are also likely

to secondary infect more individuals than an average

individual would. Late in epidemics, on the contrary,

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

154

the new infected individuals are typically more iso-

lated and induce less secondary infections. On Fig-

ures 5, 6 and 7, the peek of the red curve comes too

late.

In (Aparicio and Pascual, 2007), the authors pro-

pose an SIYR model to better account for secondary

infections. Their idea is to split the usual I compart-

ment into I and Y, where their I is individuals that

are infected and infectious and Y individuals that are

infected but not infectious, meaning that they do not

produce secondary infections.

Their model is given by 7 where γ

= τ + γ, is the

constant rate at which infectious nodes become in-

active while γ is the constant rate at which infected

nodes become recovered, g is the constant rate at

which inactive nodes recover, and R

, the basic re-

production rate, depends on the network.











= −γ

= γ

I − γ

= γ

I − gY

= gY

N = S +I +Y + R

(7)

Note that there is here a potential confusion be-

tween the usual τ parameter and the generic τ

gen

which in this speciﬁc model is not equal to τ. From

the above formulas we deduce: α

gen

= γ

; it

gen

and τ

gen

= R

. (Bansal et al., 2007) (supplementary

material) gives R

= T

i−hki

hki

where hki is the mean

degree of the network (set to 10 in our examples),

while hk

i is the mean square degree and T =

the probability of transmission of the pathogen.

For a Poisson random network hk

i = hki(hki +1)

(Barab

asi et al., 2016) but for more general networks

it is an issue to estimate hk

i without an actual net-

work. (Bansal et al., 2007) relies on computations on

the random networks they used.

For the exponential network, we have generated a

sequence of degrees with an exponential distribution

and have computed hk

For the scale-free network, in order to calculate

the mean square degree, we proceed in a similar way

as in the exponential case, but we use the (Barab

asi

and Albert, 1999) algorithm to generate the graph.

3 VALIDATION AND

DISCUSSION

To validate our approach, we have replicated the ex-

periments of (Bansal et al., 2007) comparing the

simulation results from homogeneous compartmental

models with the models of Stroud et al. and of Apari-

cio et al. with those obtained by (Bansal et al., 2007)

for Poisson, exponential and scale-free networks.

The homogeneous model is a special case of Stroud

et al.’s model with ν = 1.

All models were deﬁned using the Kendrick

tool(Bui et al., 2019) even though we used the

low-level Kendrick language rather than its domain-

speciﬁc language which is currently under revision.

The parameters α

gen

, it

gen

and τ

gen

are noted in

Kendrick as alpha gen, it gen and tau gen.

Our implementation of Stroud et al. is shown Fig-

ure 2. The code is divided into three parts: deﬁning

the concerns (SIR and Stroud), initializing the param-

eters, running the simulation. The code for the Apari-

cio et al. case is divided in a similar way (See Figure

4).

The results of the simulations can be seen on Fig-

ures 5, 6 and 7 are similar to those of Figures 6 (b),

6 (d) and 6 (f) in (Bansal et al., 2007), taking into

account that used random networks and that differ-

ent scale-free or exponential networks may have dif-

ferent values for hk

i. This suggests that integrating

Bansal’s idea was successful.

Both adaptations alter the homogeneous case in

very different ways. As heterogeneity in the degree

of nodes grows from the Poisson to the exponential

to the scale-free case the Stroud adaptation further

shrinks the peek of daily incidence but does not ﬁx its

dynamics: it still comes too late. On the contrary, the

Aparicio adaptation shifts this peak to the left (earlier

in the outbreak) but outside of the case of their pub-

lication (Poisson networks) the height of the peek is

deemed exaggerated by (Bansal et al., 2007).

The challenge was to check if the Kendrick ap-

proach to separation of concerns could capture ap-

proaches such as those from Stroud et al. or Apari-

cio et al. while keeping the familiar compartmental

framework.

We ﬁrst deﬁned a classical SIR model (line 1-14)

in a usual way except for the deﬁnition of lambda

(lines 9-10). Note however that this deﬁnition of

lambda is general and not, by any means, restricted

to trying and capture some aspects of contact net-

works. The SIR model deﬁned this way can thus be

Python and Kendrick code of our experiments are

available online: https://github.com/KendrickOrg/

BIOINFORMATICS22-code

Separation of Concerns in Extended Epidemiological Compartmental Models

155

Figure 2: Deﬁnition of SIR and Stroud concerns.

Figure 3: Deﬁnition of the scenario’s parameters.

used quite generally.

The Stroud concern is then quite simple: it merely

gives a value to the it

gen

parameter (lines 16-18). This

concern is separate from the SIR in the sense that it is

a distinct syntactic structure. The SIR concern can be

reused without the Stroud concern.

One issue is the fact that the SIR concern was not

reused in the SIYR one for the implementation of

Aparicio et al’s approach. Factoring out commonal-

ities between the core epidemic concerns (SIR, SEIR,

SIYR...) that deﬁne the epidemic status is a bit in-

volved and does not always simplify models.

It might be tempting to introduce some kind of in-

heritance between models (using the Kendrick DSL)

but the beneﬁts are not impressive as far as core con-

cerns are considered. In low-level Kendrick it is pos-

sible to copy SIR into SIYR, add a Y status, redeﬁne

the transitions and so on, but this is not clearly simpler

than redeﬁning SYIR from scratch as we did. There

are only a few kinds of core concerns so that redeﬁn-

Figure 4: Deﬁnition of an Aparicio concern.

Figure 5: Daily incidence for the homogeneous, Stroud and

Aparicio approaches on a Poisson network of 10000 nodes

with a mean degree of 10.

ing them from scratch is not a heavy burden.

Other concerns, on the contrary, are quite varied

and are the focus of the Kendrick approach. Because

it relies on a speciﬁc core concern (SIYR), imple-

menting the Aparicio et al. extension is more involved

than with the Stroud et al. one. It is however still pos-

sible to beneﬁt from the Kendrick approach and com-

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

156

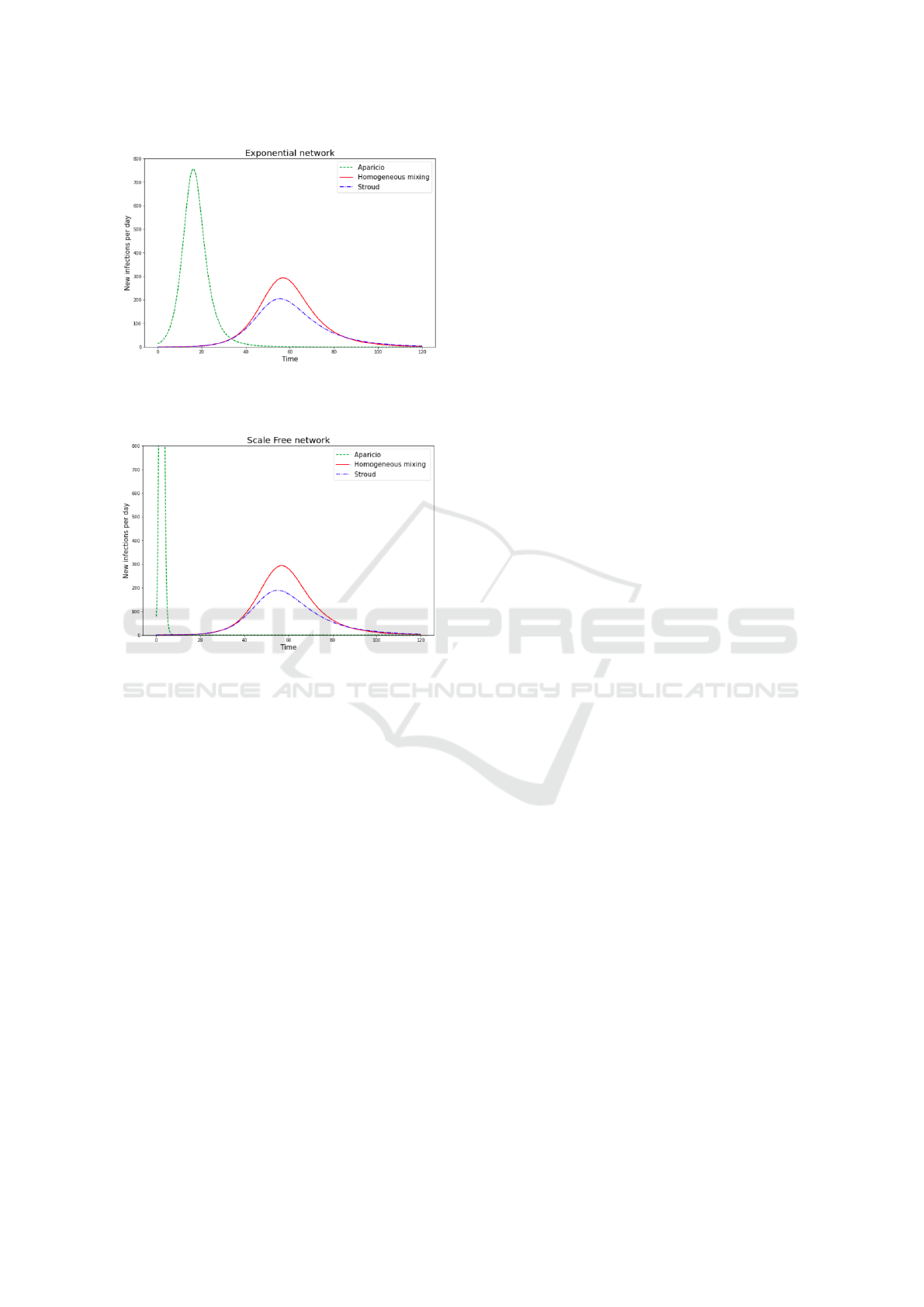
Figure 6: Daily incidence for the homogeneous, Stroud and

Aparicio approaches on an exponential network of 10000

nodes with a mean degree of 10.

Figure 7: Daily incidence for the homogeneous, Stroud

and Aparicio approaches on an scale-free network of 10000

nodes with a mean degree of 10.

bine the SIYR and the Aparicio concerns with other

concerns such as the age or sex structure. For this

reason we consider that this was also a success.

Another issue is the relationship between the

Stroud concern and SIR and more generally of non-

core concerns with the core concern of the model.

Non-core concerns are expected not to structurally

depend (use names introduced in other concerns) on

each other even though this may possibly happen in

huge models (e.g. a global pandemic model) that

are quite beyond the scope of this paper. Non-core

concerns may however depend on the core one. In-

deed, the Stroud concern gives value to a parameter

introduced in SIR and uses names that are deﬁned

in SIR. In low-level Kendrick there is little support,

aside from the host system complaining at run time,

to avoid pitfalls such as misspelling a name or avoid-

ing name conﬂicts across concerns. This is obviously

something the Kendrick DSL must address e.g. by

preﬁxing names by that of their concern, importing

the names of concern, ...

The reader may wonder if it would be possible to

combine the approaches of Stroud et al. and from

Aparicio et al. The Kendrick approach would support

it but the respective domains of validity, or at least of

reasonable quality of prediction, of both approaches

do not necessarily intersect so that neither (Bansal

et al., 2007) nor we, have considered this possibility.

Finally, in (Bansal et al., 2007) the idea to

adapt compartmental models, that was transposed to

Kendrick in this paper, was further developed to dis-

tinguish the edges of Susceptible individuals from

those of Infected individuals. Including other param-

eters to concerns is not difﬁcult but Bansal et al. con-

sider that obtaining values (by ﬁtting on simulations

run on a contact network) or formulas (by analyti-

cal methods) for these parameters may become more

cumbersome than using network models. We think

this suggests that it may be worth in future work to try

and capture more aspects of contact networks in con-

cerns and check if this helps combining or switching

between the compartmental approach and the contact-

network one in models.

4 RELATED WORK

Separation of concerns (H

ursch and Lopes, 1995) is a

major goal of software engineering and more gener-

ally of any discipline where models or artifacts may

be too complex to grasp, change or reuse easily when

they are not decomposed into separate parts whose de-

pendencies on each other are kept minimal.

The Kendrick approach, language and tool (Bui

et al., 2016; Bui et al., 2019) achieve separation

of concerns in compartmental epidemic models by

deﬁning each concern (age, sex, spatial heterogene-

ity, containment or vaccination policies, etc.), i.e.

each potential source of heterogeneity, as a sepa-

rate stochastic automaton and by deferring combining

concerns until a composition phase where they are put

together into a SAN using a tensor sum operator.

Process algebras and SANs have similar objec-

tives and have both been used to deﬁne compartmen-

tal epidemic models, although not, as far as we know,

to support a general approach to separation of con-

cerns that introduce heterogeneity in epidemic models

(Mccaig et al., 2009). Moreover, process algebras are

not initially meant to model epidemic models which

makes them awkward.

Bio-PEPA, for instance, is an extension of PEPA

(Performance Evaluation Progress Algebra) (Gilmore

and Hillston, 1994) with some features for biologi-

cal system modeling. Some PEPA models however

cannot be translated into ODEs which requires check-

ing some conditions to do it (Benkirane, 2011). Also,

Separation of Concerns in Extended Epidemiological Compartmental Models

157

deﬁning compartments is tedious and PEPA’s syntax

”might look daunting” (Benkirane, 2011). A subse-

quent adaptation of Bio-PEPA was thus introduced to

better support compartmental epidemic models (Cioc-

chetta and Hillston, 2010). We are not aware of any

extensions to Bio-PEPA to support contact networks.

Generally, traditional mathematical models (com-

partmental models) used in epidemiology, make sim-

plifying assumptions about the interaction between

hosts. This is because they implicitly deﬁne host-

to-host contact and assume that hosts have identical

contact rates, which does not always agree with real-

world models. However, these models have the par-

ticularity of being manageable, easily implementable,

robust and predictive (Anderson and May, 1992; Mol-

lison et al., 1994). However, faced with their difﬁ-

culties in reﬂecting certain real-world models, in re-

cent years epidemiologists have largely focused on

so-called contact network models, which have the

characteristic of explicitly capturing the various mod-

els of interactions that underlie transmission of dis-

ease (Watts and Strogatz, 1998; Pastor-Satorras and

Vespignani, 2001; Shirley and Rushton, 2005). These

models also have the advantage of providing very

good prediction but have the disadvantage of requir-

ing more programming skills. In order to ﬁnd an

ideal compromise between compartment-based mod-

els and contact network models, at least from the

point of view of implementation, the Kendrick (Bui

et al., 2016; Bui et al., 2016; Bui et al., 2019) ap-

proach was thus generalized in order to take into ac-

count aspects of contact network models from models

based on compartments that are known to be easily

manipulated.

Many epidemiology modeling and simulation

platforms take into account deterministic/stochastic

models based on compartments or/and contact net-

works (Muellner et al., 2018; Bui et al., 2016; Bui

et al., 2019; Picault et al., 2019; Miller and Ting,

2020; Hladish et al., 2012). Hladish et al. introduce

EpiFire (Hladish et al., 2012) - an API

implemented

in C++ for generating network models of epidemi-

ology. EpiFire also provides a graphical user inter-

face (GUI) which allows to fast conﬁgure the struc-

ture of different networks (i.e., random, small-world,

scale-free etc.) for SIR models. Although the au-

thors have achieved the separation between the net-

work construction and the simulation of the disease

spreading through networks, they have ignored other

epidemiological concerns, only considered the SIR

structure. The most recent work on the ﬁeld of con-

tact network modeling for epidemiology is EoN of

Miller et al. (Miller and Ting, 2020). EoN provides

Application Programming Interface

the same features as EpiFire with the aim of model-

ing the spread of SIR and SIS models over different

networks. It is arguable that most of these tools do not

formalize the principle of separations of concerns in

epidemiology as the Kendrick (Bui et al., 2016; Bui

et al., 2019) and Emulsion (Picault et al., 2019) tools

do. Indeed, Emulsion is a platform that was built with

the aim of helping modelers to focus on the design of

models rather than on the programming aspect. It is

a domain speciﬁc language which makes it possible

to make explicit all the components of an epidemio-

logical model (structure, process, parameters, ...) in

the form of a structured text ﬁle. Even if the authors

of Emulsion do not speciﬁcally specify how this prin-

ciple of separation of concerns was formalized, they

highlight the fact that it allows modelers to design

processes (infection, demography, detection, control,

etc.) and different scales (individuals, populations,

meta-populations) independently, which would allow

the management of multiple hosts, the diversity of

pathogens, as well as realistic detection methods and

control measures.

5 CONCLUSION

In this paper, we have proposed to generalize the

Kendrick approach to separation of concerns in com-

partmental epidemic models (Bui et al., 2016) to eas-

ily capture some aspects of contact network models.

To do this we have applied an idea from (Bansal et al.,

2007) which consists in deﬁning the usual λ parame-

ter of epidemic models as a kind of template method

with three extension points.

We have then applied this approach to 2 exten-

sions of compartmental models, Stroud et al. (Apari-

cio and Pascual, 2007) and Aparicio et al. (Stroud

et al., 2006) and we have been able to get results close

to those of (Bansal et al., 2007). Stroud et al.’s ex-

tension was deﬁned as a very simple concern that was

separate from the core SIR model. Aparicio et al.’s ex-

tension was a bit more complex to implement because

it relies on a speciﬁc core concern, namely SIYR,

but the resulting concerns can still be combined with

other epidemic concerns in Kendrick.

Building on these promising results we aim at

generalizing our approach to express more general

aspects of contact networks as separate concerns.

(Bansal et al., 2007) pointed out that the approach we

have reported on was probably not enough to cope

with heavy heterogeneity in the contact network un-

less much more signiﬁcant efforts are made to adapt

compartmental models and suggested to abandon

them in this case for a full-ﬂedged contact-network

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

158

approach. It is thus interesting to see whether sepa-

ration of concerns can be even further generalized to

alleviate these additional efforts. This will probably

lead to developing concerns that capture more infor-

mation of contact networks to the point that the orig-

inal compartmental framework may become a mere

speciﬁc concern itself. Finally, we also plan to in-

clude this generalized approach in the Kendrick DSL

to offer better support to avoid some caveats, espe-

cially those involving name clashes or ambiguities in

the global model.

ACKNOWLEDGEMENTS

The authors would like to thank the anonymous refer-

ees for their help in improving this paper.

REFERENCES

Anderson, R. M. and May, R. M. (1992). Infectious diseases

of humans: dynamics and control. Oxford university

press.

Aparicio, J. P. and Pascual, M. (2007). Building epidemi-

ological models from R0: an implicit treatment of

transmission in networks. Proceedings of the Royal

Society B: Biological Sciences, 274(1609):505–512.

Bansal, S., Grenfell, B. T., and Meyers, L. A. (2007). When

individual behaviour matters: homogeneous and net-

work models in epidemiology. Journal of the Royal

Society Interface, 4(16):879–891.

Barab

asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. science, 286(5439):509–512.

Barab

asi, A.-L. et al. (2016). Network Science. Cambridge

University Press.

Benkirane, S. (2011). Process algebra for epidemiology:

evaluating and enhancing the ability of PEPA to de-

scribe biological systems. PhD thesis, University of

Stirling.

Bui, T., Papoulias, N., Stinckwich, S., Ziane, M., and

Roche, B. (2019). The Kendrick modelling platform:

language abstractions and tools for epidemiology [+

correction art. no 439, 1 p.]. BMC Bioinformatics, 20.

Bui, T. M. A., Ziane, M., Stinckwich, S., Ho, T. V., Roche,

B., and Papoulias, N. (2016). Separation of concerns

in epidemiological modelling. In Companion pro-

ceedings of the 15th international conference on mod-

ularity, pages 196–200.

Ciocchetta, F. and Hillston, J. (2010). Bio-PEPA for epi-

demiological models. Electronic Notes in Theoretical

Computer Science, 261:43–69.

Gamma, E., Helm, R., Johnson, R., Vlissides, J., and Pat-

terns, D. (1995). Elements of reusable object-oriented

software, volume 99. Addison-Wesley Reading, Mas-

sachusetts.

Gilmore, S. and Hillston, J. (1994). The PEPA workbench:

A tool to support a process algebra-based approach to

performance modelling. In Haring, G. and Kotsis, G.,

editors, Computer Performance Evaluation Modelling

Techniques and Tools, pages 353–368, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Hladish, T., Melamud, E., Barrera, L. A., Galvani, A., and

Meyers, L. A. (2012). EpiFire: An open source C++

library and application for contact network epidemiol-

ogy. BMC bioinformatics, 13(1):1–12.

ursch, W. L. and Lopes, C. V. (1995). Separation of con-

cerns. Technical Report NU-CCC-95-03, Northeast-

ern University, Boston, USA.

Keeling, M. J. and Rohani, P. (2011). Modeling infectious

diseases in humans and animals. Princeton university

press.

Levin, S. A. and Durrett, R. (1996). From individu-

als to epidemics. Philosophical Transactions of the

Royal Society of London. Series B: Biological Sci-

ences, 351(1347):1615–1621.

Mccaig, C., Norman, R., and Shankland, C. (2009). From

individuals to populations: A symbolic process alge-

bra approach to epidemiology. Mathematics in Com-

puter Science, 2:535–556.

Miller, J. C. and Ting, T. (2020). EoN (Epidemics on Net-

works): a fast, ﬂexible python package for simulation,

analytic approximation, and analysis of epidemics on

networks. arXiv preprint arXiv:2001.02436.

Mollison, D., Isham, V., and Grenfell, B. (1994). Epi-

demics: models and data. Journal of the Royal

Statistical Society: Series A (Statistics in Society),

157(1):115–129.

Muellner, U., Fourni

e, G., Muellner, P., Ahlstrom, C.,

and Pfeiffer, D. U. (2018). epidemix—an interactive

multi-model application for teaching and visualizing

infectious disease transmission. Epidemics, 23:49–54.

Pastor-Satorras, R. and Vespignani, A. (2001). Epidemic

spreading in scale-free networks. Physical review let-

ters, 86(14):3200.

Picault, S., Huang, Y.-L., Sicard, V., Arnoux, S., Beaun

ee,

G., and Ezanno, P. (2019). Emulsion: Transparent

and ﬂexible multiscale stochastic models in human,

animal and plant epidemiology. PLoS computational

biology, 15(9):e1007342.

Plateau, B. and Stewart, W. J. (2000). Stochastic automata

networks. In Computational Probability, pages 113–

151. Springer.

Shirley, M. D. and Rushton, S. P. (2005). The impacts of

network topology on disease spread. Ecological Com-

plexity, 2(3):287–299.

Stroud, P. D., Sydoriak, S. J., Riese, J. M., Smith, J. P.,

Mniszewski, S. M., and Romero, P. R. (2006). Semi-

empirical power-law scaling of new infection rate to

model epidemic dynamics with inhomogeneous mix-

ing. Mathematical biosciences, 203(2):301–318.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ‘small-world’ networks. Nature, 393(6684):440–

442.

Separation of Concerns in Extended Epidemiological Compartmental Models

159