Towards Deep Learning-based 6D Bin Pose Estimation in 3D Scans

Luk

s Gajdo

sech

1,2 a

, Viktor Kocur

2,4 b

, Martin Stuchl

ık

1 c

, Luk

s Hudec

3 d

and Martin Madaras

1,2 e

Skeletex Research, Slovakia

Faculty of Mathematics, Physics and Informatics, Comenius University Bratislava, Slovakia

Faculty of Informatics and Information Technologies, Slovak Technical University Bratislava, Slovakia

Faculty of Information Technology, Brno University of Technology, Czech Republic

Keywords:

Computer Vision, Bin Pose Estimation, 6D Pose Estimation, Deep Learning, Point Clouds.

Abstract:

An automated robotic system needs to be as robust as possible and fail-safe in general while having relatively

high precision and repeatability. Although deep learning-based methods are becoming research standard on

how to approach 3D scan and image processing tasks, the industry standard for processing this data is still

analytically-based. Our paper claims that analytical methods are less robust and harder for testing, updating,

and maintaining. This paper focuses on a speciﬁc task of 6D pose estimation of a bin in 3D scans. Therefore,

we present a high-quality dataset composed of synthetic data and real scans captured by a structured-light

scanner with precise annotations. Additionally, we propose two different methods for 6D bin pose estimation,

an analytical method as the industrial standard and a baseline data-driven method. Both approaches are cross-

evaluated, and our experiments show that augmenting the training on real scans with synthetic data improves

our proposed data-driven neural model. This position paper is preliminary, as proposed methods are trained

and evaluated on a relatively small initial dataset which we plan to extend in the future.

1 INTRODUCTION

Capturing a scene with 3D scanners is a standard for

automatized systems analyzing a scene. To pick me-

chanical parts from a bin by a robotic arm equipped

with a gripper, the parts need to be localized. First,

the localization of bin is essential to restrain the robot

from collisions. Then, the kinematics of the robot is

optimized for path planning. The problem of bin lo-

calization can be deﬁned as a 6 DoF pose estimation

of a template 3D model of the bin in the 3D scan.

Nowadays, analytical methods are still the indus-

trial standard for the processing of 3D scans. On the

contrary, the academic and research standards have

evolved to data-driven or hybrid approaches. Ana-

lytical computation of bin transformation in captured

point clouds might be vulnerable to missing critical

information in the captured scans, like corners and

https://orcid.org/0000-0002-8646-2147

https://orcid.org/0000-0001-8752-2685

https://orcid.org/0000-0001-8556-8364

https://orcid.org/0000-0002-1659-0362

https://orcid.org/0000-0003-3917-4510

edges, yielding lower robustness than expected. The

computation precision of a hard-deﬁned analytical al-

gorithm might be higher but at the cost of lower ro-

bustness if a key content is missing. In applications

of automated intelligent systems, it may be interest-

ing to lower its precision to increase the robustness

in some scenarios. The other possible approach is

to split the pipeline into two steps - the ﬁrst part of

the pipeline orients on the robustness and raw data-

driven localization. The second part focuses on the

precision-based analytical solution starting from the

predicted pose estimations, thus having the robustness

properties inherited from the data-driven approach.

In this paper, we present a novel dataset contain-

ing high-quality real and synthetic 3D scans of dif-

ferent bins in various poses containing a variety of

items captured by structured light scanners. We pub-

lish the dataset

for further research. We propose

an analytical method and a conceptually simple deep

convolutional neural network for 6D bin pose estima-

tion. We experimentally evaluate it and show that our

network is more robust than the analytical method.

http://skeletex.xyz/portfolio/datasets

Gajdošech, L., Kocur, V., Stuchlík, M., Hudec, L. and Madaras, M.

Towards Deep Learning-based 6D Bin Pose Estimation in 3D Scan.

DOI: 10.5220/0010878200003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

545-552

ISBN: 978-989-758-555-5; ISSN: 2184-4321

545

Our method achieves better accuracy than existing

6D pose estimation methods. We also show the in-

clusion of synthetic data into the training process is

beneﬁcial. We experimentally verify that cases of

successful pose approximations done by our network

can be further reﬁned in post-processing with iterative

closest point (ICP), substantially increasing the por-

tion of data with close-to-zero ﬁnal error. We present

this work as a position paper. We nevertheless feel

that the preliminary results presented in this paper

show promise, and we intend to continue this research

by collecting a larger dataset and performing a more

thorough evaluation.

2 RELATED WORK

Finding the 6D pose of an object is one of the clas-

sical computer vision problems tackled using vari-

ous methods over the years. Existing algorithms for

images and point clouds categorize into two main

groups, analytical algorithms (Stein and Medioni,

1992; Katsoulas, 2003b), and data-driven algo-

rithms. Data-driven algorithms can be further split

into feature-based methods (Vidal et al., 2018; Drost

et al., 2010) and Deep Neural Networks (DNN)-based

methods (Park et al., 2019; Bukschat and Vetter,

2020).

On the one hand, the feature-based methods are

optimized using only the 3D object model, as they

match pairs of points between the model and the cap-

tured scene. DNN-based methods, on the other hand,

are trained on large sets of actual 3D scenes to gener-

alize the solution. Moreover, a hybrid method can be

composed of a sequence of data-driven steps and the

ﬁnal analytical step, with the ICP-like methods being

the widely-used analytical post-processing step (Besl

and McKay, 1992; Xiang et al., 2017). BOP chal-

lenge is trying to capture the state-of-the-art in this

area, comparing traditional and data-driven methods

on benchmark datasets (Hoda

n et al., 2020).

Even though the problem of ﬁnding 3D translation

and 3D rotation of rigid objects is very general, it is

nevertheless dependant on the input data. Most of the

widely adopted datasets consist of RGBD images of

textured objects with complex geometries from a sin-

gle device with known internal camera parameters.

2.1 Analytical and Feature-based

Methods

A traditional approach of registering objects has been

detecting the local descriptors combined into shape-

based primitives and searching for their correspond-

ing pairs on 3D CAD models. The simplest case is

Hough transform applied to detect lines (Katsoulas,

2003b). The efforts to enhance the algorithm to re-

duce the number of possible detections resulted in

specifying that lines have to be orthogonal to repre-

sent the shape borders (Katsoulas, 2003a).

Similar to Hough transform, the RANSAC algo-

rithm extracts the geometric description of the object

by ﬁtting the corresponding shape primitives into the

3D data. The non-deterministic algorithm is used in

a sequence of standard steps. (Guo et al., 2020) en-

hance the algorithm by using shape primitives to ap-

proximate the objects. (Vock et al., 2019) propose to

reduce 3D points into point pair features (PPF). How-

ever, RANSAC usually ends with many false pos-

itives (e.g., ﬂoor points); therefore, an ICP is usu-

ally required for ﬁne-tuning. PPFs are widely used

in literature to estimate object points in point cloud

or RGBD data (Drost et al., 2010; Vidal et al., 2018;

Guo et al., 2021).

2.2 Deep Neural Network-based

Methods

Some methods estimate 6D poses from a single RGB

image either directly by modifying an existing 2D ob-

ject detection framework (Bukschat and Vetter, 2020)

or by using a neural network to obtain 2D-3D corre-

spondences further used in a PnP solver to obtain the

ﬁnal pose (Park et al., 2019; Zakharov et al., 2019).

In contrast to RGB data, the scanners utilized in our

work output only texture from a grayscale camera -

not color, limiting the application of related papers

even further.

RGB with depth information is also commonly

used as input for deep learning base pose estimation.

Several methods (Mitash et al., 2018; Hosseini Ja-

fari et al., 2019) use deep learning models to output

hypotheses which are then processed in a hypothesis

validation pipeline to obtain the ﬁnal poses. Other

indirect methods use deep learning networks to out-

put keypoints (He et al., 2020) or object fragments

(Hoda

n et al., 2020) which are then used in a PnP

solver to obtain the ﬁnal poses.

Other deep learning approaches apply neural net-

works directly to compute the 6D pose. DenseFu-

sion (Wang et al., 2020) uses RGB information to ob-

tain segmentation masks of objects. These are used

to combine depth and RGB data to generate per-

pixel embeddings, which are then used to estimate

object poses in a voting scheme. An improved ver-

sion of the algorithm called MaskedFusion (Pereira

and Alexandre, 2020) improves accuracy by masking

non-relevant data.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

546

Figure 1: In this work we present a novel dataset contain-

ing 520 real and 370 synthetic 3D scans of bins. (Left)

Synthetic sample. (Right) Real scan annotated by hand.

The ground truth transformations of bin 3D model into the

scanner-space is demonstrated by purple mesh.

These approaches are trained for speciﬁc objects

and require their 3D models to be available during

training. We aim to be able to estimate 6D poses of

arbitrary bin-shaped objects. The mentioned meth-

ods are thus not easily transferable to our scenario.

Moreover, the methods are usually trained for cam-

eras with speciﬁc internal parameters, a constraint we

aim to avoid in our work.

2.3 Pose Parameterization

The pose of a rigid object can be described with a pair

of a rotation matrix R ∈ SO(3) and a translation vec-

tor

t ∈ R

. The translation vector can usually be rep-

resented directly as an output of a neural network and

used in a loss function since the space R

has a direct

continuous representation. On the other hand, there

are no continuous representations of SO(3), making

it difﬁcult for neural networks to learn such represen-

tations (Zhou et al., 2019).

Rotational matrices only have 3 degrees of free-

dom while having 9 elements. Constraining the ele-

ments directly during the training process is imprac-

tical, so an orthogonalization procedure must be uti-

lized (Zhou et al., 2019). Rotation can also be rep-

resented using different equivalent parameterizations

such as quaternions (Xiang et al., 2017; Wang et al.,

2020; Pereira and Alexandre, 2020) or axis-angle vec-

tors (Bukschat and Vetter, 2020).

Symmetric objects pose a speciﬁc problem for ro-

tation representation. Depending on the type of sym-

metry, multiple different rotation parameterizations

can be valid for the same pose. This might introduce

problems as some loss functions can then have un-

desirable multiple global minima. Some approaches

mitigate these issues for some types of symmetries by

using losses based on distances of sampled points on

object models (Xiang et al., 2017; Wang et al., 2020;

Pereira and Alexandre, 2020) A different approach

(Pitteri et al., 2019) proposes mapping all represen-

tations onto a single canonical representation used

during training. Some methods avoid these issues

altogether by not directly outputting the object pose

but calculating it indirectly from keypoints (He et al.,

2020) or object fragments (Hoda

n et al., 2020).

3 DATASET

We have collected a new dataset consisting of both

real captures (scans) from Photoneo PhoXi structured

light scanner devices (Photoneo, 2017) annotated by

hand and synthetic samples produced by our gener-

ator. See Figure 1 for an example of both real and

synthetic 3D scanner captures of scenes composed of

mechanical parts in a bin from our dataset.

In comparison with existing datasets, some no-

table differences include:

• most of the captured bins are texture-less, made

from uniform, single-colored materials,

• all bins are of cuboid shape with different propor-

tions. Compared to objects with complex geom-

etry, bins consist of ﬂat faces with edges, which

are not guaranteed to be seen in the capture due

to occlusion. Surface models of these bins are not

provided, just their approximate bounding boxes,

• PhoXi scanner provides high-resolution 3D ge-

ometry data, but no RGB data, with a rough and

noisy gray-scale intensity image being the closest

equivalent,

• captures come from different devices with various

intrinsic camera parameters. We aim to work di-

rectly on 3D point clouds, which contain these pa-

rameters implicitly as opposed to RGBD images.

The original scans contain various parameters,

such as gray-scale intensities and normals. We rely

only on 2D single-view maps of 3D coordinates in

2064 × 1544 resolution in our proposed approaches.

We use 80% as the training data, and the remaining

20% (every ﬁfth sample) plus a unique set of indepen-

dently captured 49 samples (including 10 synthetic

samples) as a test set. Due to its currently limited size,

we recommend cross-validation instead of an explicit

train-validation split. We plan to add more samples

into the dataset, as we will further enhance our meth-

ods in the future.

4 BIN POSE ESTIMATION IN 3D

POINT CLOUD

The bin pose estimation is a computation process of

estimating a transformation matrix that maps coordi-

nates of a bin-space into a scanner-space. As outlined

Towards Deep Learning-based 6D Bin Pose Estimation in 3D Scan

547

in the previous sections, the speciﬁc task of bin pose

estimation differs in many key aspects from the gen-

eral task of 6D pose estimation. Therefore, we have

decided to propose also two methods for this task.

The ﬁrst method is an analytical heuristic we have

developed, and the second is a CNN-based pose es-

timation method. We deliberately designed the meth-

ods to be conceptually simple to provide solid base-

lines without bells and whistles. The following sub-

sections describe the proposed methods. Evaluation

and comparison of results for a set of experiments are

in Section 5.

4.1 Analytical Edge-based Fitting

An analytical algorithm for pose estimation is com-

posed of a set of steps performed sequentially in the

pipeline. This four-step method assumes that the top

edges of the bin are closer to the camera than back-

ground objects, and at least a part of every top edge

can be seen.

Figure 2: (From left to right) the camera space is row-wise

and column-wise segmented into similar depth intervals,

from which horizontal and vertical bin-cuts are constructed.

A plane is ﬁtted into the bin-cuts, and wall-cuts not corre-

sponding to this plane are discarded as outliers. The re-

maining wall-cuts are assigned to four bin walls according

to corners ﬁtted into horizontal and vertical bin-cuts. Fi-

nally, the lines are ﬁtted into categorized wall-cuts, which

deﬁne the bin basis.

Initially, the horizontal and vertical scan-lines are

deﬁned in scan-space. Each scan-line is divided into

intervals, where scan-line interval going through the

whole bin is called bin-cut. Speciﬁcally, each bin-cut

is composed of two wall-cuts and one interval for the

ﬂoor (representing the ground of the bin).

Next, minimum depth values in camera-space in

the intervals are detected, and vectors describing

edge-to-edge direction are computed. The set of such

vectors is computed in both directions, horizontally

and vertically (see Figure 2, left).

Moreover, a mode vector direction is computed in

both horizontal and vertical directions. Those mode

directions are used to compute the cross product of

these directions to compute the normal deﬁning the

top of the bin. At the end of the step, the wall-cuts are

ﬁltered according to the calculated plane.

Consequently, a corner detection is performed on

the ﬁltered data. Each corner is detected as a bin-

cut endpoint, where the change of direction between

neighboring bin-cut endpoints is the highest; such de-

tection is performed in every direction, and all four

corners are detected (see Figure 2, right).

Finally, the set of detected corners categorizes

wall-cuts into four categories of the bin walls. Lines

are ﬁtted into ﬁltered wall-cuts, and the bin-space is

deﬁned using the computed plane normal and ﬁtted

lines, which can be used for the bin-space deﬁnition

and calculation of the ﬁnal bin-space to camera-space

transformation.

4.2 CNN-based Pose Estimation

The analytical method may fail when bin edges or

corners are occluded or outside of the scanner view.

Such instances may frequently occur in industrial ap-

plications when human or robotic operators manipu-

late bins or contain items that cover the bin edges.

To overcome these issues, we propose a data-

driven approach using a convolutional neural net-

work. We propose a simple network that can reliably

estimate the pose up to a reasonable level of accuracy.

This estimate provided by the network is then reﬁned

using an ICP algorithm to obtain the ﬁnal bin pose.

4.2.1 Parameterization of the Bin Pose

The pose of the bin can be parameterized using a rota-

tion matrix R ∈ SO(3) and a translation vector

t ∈ R

We represent the translation vector directly. To repre-

sent rotation, we opt to use a strategy similar to (Zhou

et al., 2019) and represent the rotation by using two

vectors from R

which can be used to determine the

rotation matrix uniquely except for degenerate cases

discussed later. The two vectors represent the orien-

tation of the z and y axes of the bin in the camera

coordinates. We denote these vectors as ~v

and ~v

, re-

spectively.

To obtain the rotation matrix R from the vectors

and ~v

, we employ the Gram–Schmidt orthogonal-

ization process to calculate the columns of the actual

rotation matrix they represent. During the procedure,

we perform the following calculations:

k~v

, (1)

=~v

−

|~u

, (2)

k~w

, (3)

=~u

×~u

. (4)

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

548

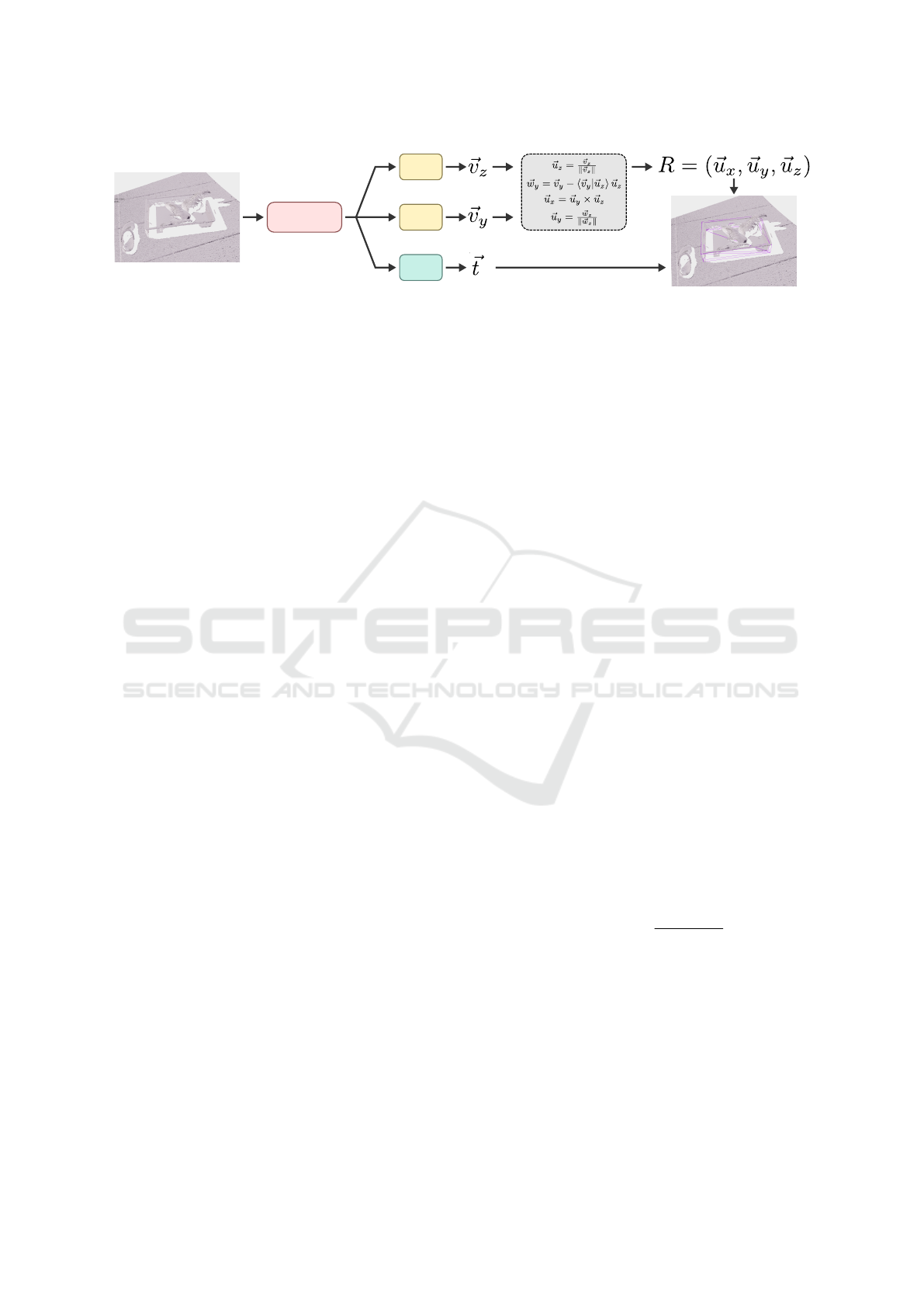
MLP

MLPMLP

ResNet

Figure 3: The architecture of the bin-pose estimation network. The structured point cloud is fed into a ResNet backbone. The

resulting features are fed into three separate heads. Each head is composed of a few fully-connected layers. One of the heads

outputs the resulting translation vector

t. The other two heads output intermediate vectors ~v

and ~u

. Equations (1-4) are then

used to obtain the columns of the resulting rotation matrix R.

The vectors ~u

,~u

form an orthonormal basis of

. We can then construct a matrix (~u

,~u

) which

is a valid rotation matrix. The fact that the matrix rep-

resents a proper rotation (e.g. det(R) = 1) is enforced

by equation (4).

Using this procedure, any two vectors ~u

and ~u

can yield a valid rotation matrix provided that they

are linearly independent. We found this limitation to

not be of concern in practice.

Under this parameterization, any rotation matrix

can be parameterized by many pairs of such vectors,

and it is thus not unique in this regard. However,

this is not an issue as we use a loss function which

only depends on orientations of ~u

and ~u

, which are

unique. To obtain a single pair of valid vectors ~u

and

, which would yield a given matrix R, we can use

the third and second columns of the matrix.

4.2.2 Bin Symmetry

We aim to detect bins of rectangular shapes. Rect-

angular bins are symmetric in a 180-degree rotation

around an axis parallel to the bin-base normal going

through the center of the base. Therefore, there are

always two valid rotation matrices for each possible

bin pose, which introduces issues during training as

the network is forced to learn only one correct output

of two possible outputs for a similar input, resulting

in the network’s inability to converge.

To remedy this issue we employ a simple strategy.

The two possible rotations R

and R

are related by a

symmetry rotation (5) such that R

= R

, where





−1 0 0

0 −1 0

0 0 1





. (5)

Therefore, the only differences between the matrices

are the signs in the ﬁrst two columns, which allows us

always to choose one of the matrices based on the sign

of the matrix elements. We always select the matrix

which has a positive element in the ﬁrst row and sec-

ond column. If this element is zero, we use the sign of

the next element below. If the value is zero again, we

use the sign of the last row and second column, which

has to be 1 or -1.

4.2.3 Network Architecture

In our experiments we use a standard ResNet back-

bone (He et al., 2016) for feature extraction. We apply

global average pooling on the feature maps and feed

the resulting features into three separate branch-heads

to output the three vectors ~v

,~v

and

t. Each head

comprises two fully-connected layers, with ReLU ac-

tivations used in rotational heads and Leaky ReLU

activations used in the translational branch. The

whole network architecture, along with output post-

processing, is shown in Figure 3.

4.2.4 Loss Function

For a given ground truth pose deﬁned by R and

t we

ﬁrst check whether to transform the rotation matrix

using R

as described in subsection 4.2.2. We extract

the vectors ~u

and ~u

as the third and second columns

of the rotation matrix. We then train the network,

which outputs three vectors ~u

,~u

t using a joint loss

function:

L = L

(~u

,~v

) + L

(~u

,~v

) + λL

(

t), (6)

where L

is the standard L1 loss, λ is a weight hy-

perparameter and L

is the angle between two vectors

in radians:

(~u,~v) = acos



~u|~v

k~ukk~vk + ε



, (7)

with ε added to prevent undeﬁned loss for output vec-

tors with small norm.

5 EVALUATION AND FINAL

EXPERIMENTS

We evaluate the analytical method proposed in Sec-

tion 4.1 and the neural network described in Section

Towards Deep Learning-based 6D Bin Pose Estimation in 3D Scan

549

4.2 using the dataset described in Section 3. We also

show the results after reﬁnement of the network out-

put with ICP and provide an experimental comparison

of our method to existing approaches.

5.1 Evaluation Metrics

Since we do not have 3D surface reconstruction of ev-

ery bin in our dataset, we rely on model-independent

pose error functions, i.e. comparing just the ground

truth

P = (

t ) and estimated P = (R,

t ) transforma-

tion matrices. All our ground-truth rotation matrices

consider the same orientation of the cuboid bin with

the longer dimension along the x-axis, therefore we

can use the strategy from subsection 4.2.2 to obtain

symmetries

and minimize the metrics. We plan

to complete the dataset with model reconstructions in

the future. This will allow the calculation of metrics

like e

ADI

VSD

MSSD

allowing for evaluation of the

actual surface alignment (Hinterstoißer et al., 2012).

Evaluating the translation

t is straight-forward us-

ing the euclidean distance e

(

t ) = k

t −

t k

. For

comparison of rotation, we use the angular distance

(

R,R), which is the angle between rotational axis

in angle-axis representation and can be directly com-

puted from the rotation matrices as:

(

R,R) = min

∈{

}

arcos

Tr(

−1

) − 1

, (8)

where Tr is the matrix trace operator.

5.2 Baseline Network Results

We have experimented with different conﬁgurations

of the proposed baseline network

, see Table 1 for re-

sults. Apart from the backbone, we tried two differ-

ent input resolutions, half and quarter of the raw scan,

which resulted in resolutions 1032 × 772 and 516 ×

386, respectively. ResNet18 with half-resolution of

the input scan has the worst performance, proba-

bly due to the small receptive ﬁeld of the network.

Interestingly, ResNet34 with quarter-resolution out-

performed half-resolution. Additional sub-sampling

probably acted as a noise-suppression.

Additionally, we have trained the best performing

conﬁguration on a subset of the dataset without the

synthetic samples. Naturally, it achieved the worst

test error since this set also contains synthetic scans,

which were not encountered during training. Surpris-

ingly, it also has higher errors e

= 7.656, e

0.559 on a subset of the test data with real samples

only. Conﬁguration trained on both real and synthetic

https://github.com/gajdosech2/bin-detect

Table 1: Comparison of test errors of different conﬁgura-

tions. Column R denotes the fraction of raw scan resolution

used as network input. Column S denotes whether synthetic

samples were used during training.

Backbone R S L

ResNet18 1/4 3 0.058 0.198 3.808 0.256

ResNet34 1/4 3 0.057 0.145 3.469 0.197

ResNet18 1/2 3 0.070 0.249 5.791 0.234

ResNet34 1/2 3 0.063 0.222 3.979 0.266

ResNet34 1/4 7 0.042 0.281 5.379 0.323

samples achieves e

= 6.108 and e

= 0.529 on

such subset. This would suggest that the synthetic

data helps the model generalize on real scans, despite

the evident gap between real and synthetic samples.

Figure 4: (Left) ﬁnal improvement of data-driven method

using ICP algorithm, (right) a fail-case of the ICP, where the

bin was snapped to ground points of the bin, worsening the

ﬁt. Points of raw scan are in blue, prediction of the network

in pink and ICP reﬁnement in green.

Apart from average values of metrics e

, the

Table 1 also shows average losses L

= L

(~u

,~v

) and

= L

(~u

,~v

) over the validation set. The loss func-

tion has, in this case, useful interpretation even as an

evaluation metric. L

represents the error in the pre-

dicted normal of the bin’s bottom face, with L

denot-

ing the rotation around this axis.

A qualitative sample of the hybrid two-step ap-

proach, where the data-driven method is reﬁned with

post-alignment using ICP, can be seen in Figure 4.

This reﬁnement improved the results (both

and

) in 91 samples out of the 218 in validation + test

set. In general, it improves the pose estimation if the

bin model has exact size and walls are visible. How-

ever, as mentioned in Section 3, the dataset currently

does not contain complete surface reconstructions of

the bins, just their approximate bounding boxes.

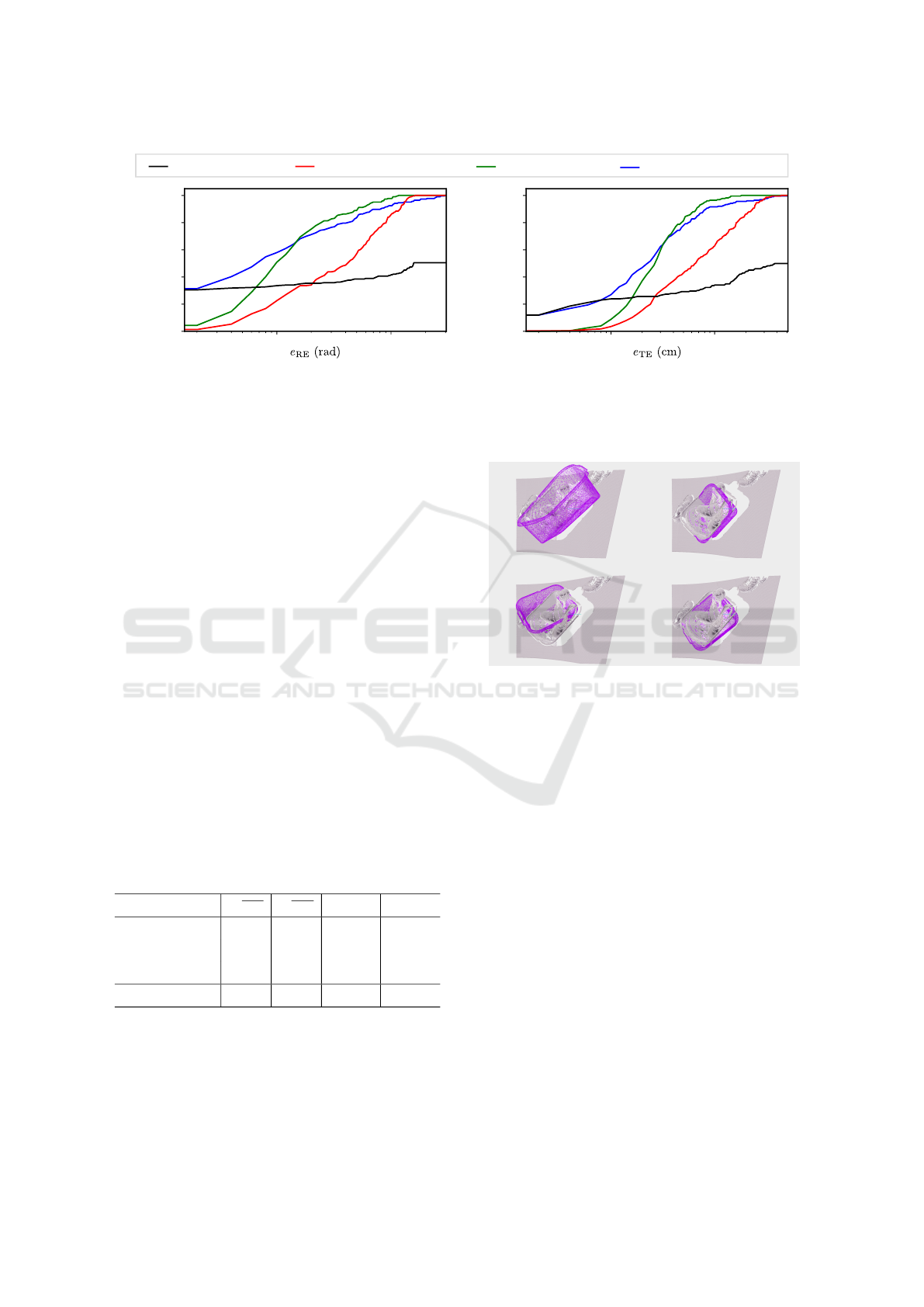
Figure 5 shows the comparison between the base-

line network, its results after ICP reﬁnement, the

same version trained over real data only, and our

analytical method. As can be seen, the analytical

method achieves reasonable error for approximately

40% samples. The remaining samples had either high

errors or the method failed to estimate in 47% cases,

which was treated as an inﬁnite error. The ICP reﬁne-

ment achieved almost zero error in a few cases. How-

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

550

ResNet34 1/2 full + ICP

ResNet34 1/2 full

ResNet34 1/2 w/o synthAnalytical method

0.0

0.2

0.4

0.6

0.8

1.0

portion of samples

0.0

0.2

0.4

0.6

0.8

1.0

portion of samples

0.1 1.0 1.0 3.00.30.30.03 10.0 30.0

Figure 5: Vertical axes show the fraction of the test samples with the error below the value of the metrics e

on the

horizontal axes. The analytical method achieves low error on a few samples but fails to predict pose for approximately half of

the cases. Using synthetic data in training improves the overall performance of the neural network. The hybrid method with

ICP reﬁnement lowers the minimum error of the network, matching the analytical approach while also retaining robustness.

However, in some cases, the ICP fails to improve the bin pose, resulting in slightly increased overall maximum error.

ever, samples with non-corresponding points aligned

produced higher errors which can be improved by

limiting the usage of ICP only for conﬁdent cases,

where the number of paired-points is higher than

some threshold. This would mitigate the negative ef-

fect in a few cases, lowering the average error.

5.3 Comparison with Existing Methods

Despite the uniqueness of our data, we have trained

and qualitatively evaluated existing state of the art

models: DPOD (Zakharov et al., 2019), DenseFu-

sion (Wang et al., 2020), MaskedFusion (Pereira and

Alexandre, 2020) and EfﬁcientPose (Bukschat and

Vetter, 2020). We performed the evaluation only on

a subset of our dataset (120 samples) with a single

bin model, for which we have made the required sur-

face reconstruction as the compared methods require

such data. See Figure 6 for qualitative comparison

and Table 2 for quantitative results over test set of 14

samples. We also show the performance of our pro-

posed baseline model.

Table 2: Results over small test set of 14 samples.

Model e

std e

DenseFusion 7.544 0.493 2.473 0.364

MaskedFusion 6.583 0.494 2.145 0.361

EfﬁcientPose 4.148 0.454 2.256 0.308

Ours 4.024 0.418 2.124 0.368

The scope of this experiment is limited, and

further evaluation is necessary to draw any strong

conclusions. However, this preliminary experiment

shows that our method can outperform the existing

ones while being conceptually simpler and not requir-

ing a model of the detected bin during training.

Figure 6: Qualitative comparison on single sample: Top

Left: DPOD, Top Right: EfﬁcientPose, Bottom Left: Dense

Fusion, Bottom Right: Masked Fusion.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we have introduced a task of bin pose

estimation, which we identiﬁed as an essential com-

ponent in many vision-based automation systems in

the industry. We have collected a dataset of high-

quality 3D scans of various bins in different environ-

ments using scanners with various parameters. In our

future work, we aim to improve the dataset by collect-

ing more data to enable a more thorough evaluation of

bin pose estimation methods. We hope that such data

will be useful for further research in this area.

We also propose two baseline methods for 6D bin

pose estimation. The evaluation results suggest that

the bin poses can be estimated reliably with a sim-

ple convolutional neural network. In many cases, the

resulting poses can be further reﬁned using ICP to im-

prove the accuracy of poses. We see the potential for

further research in this area, especially regarding the

Towards Deep Learning-based 6D Bin Pose Estimation in 3D Scan

551

effects of different types of bin pose parametrization

on the network performance.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the support of

NVIDIA Corporation with the donation of GPUs.

REFERENCES

Besl, P. and McKay, N. D. (1992). A method for registration

of 3-d shapes. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 14(2):239–256.

Bukschat, Y. and Vetter, M. (2020). Efﬁcientpose: An efﬁ-

cient, accurate and scalable end-to-end 6d multi object

pose estimation approach.

Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model

globally, match locally: Efﬁcient and robust 3d object

recognition. In Proceedings of the IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition, pages 998–1005.

Guo, J., Xing, X., Quan, W., Yan, D.-M., Gu, Q., Liu,

Y., and Zhang, X. (2021). Efﬁcient center voting

for object detection and 6d pose estimation in 3d

point cloud. IEEE Transactions on Image Processing,

30:5072–5084.

Guo, N., Zhang, B., Zhou, J., Zhan, K., and Lai, S.

(2020). Pose estimation and adaptable grasp conﬁgu-

ration with point cloud registration and geometry un-

derstanding for fruit grasp planning. Computers and

Electronics in Agriculture, 179:105818.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. 2016 IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 770–778.

He, Y., Sun, W., Huang, H., Liu, J., Fan, H., and Sun, J.

(2020). Pvn3d: A deep point-wise 3d keypoints voting

network for 6dof pose estimation.

Hinterstoißer, S., Lepetit, V., Ilic, S., Holzer, S., Brad-

ski, G. R., Konolige, K., and Navab, N. (2012).

Model based training, detection and pose estimation

of texture-less 3d objects in heavily cluttered scenes.

In ACCV.

Hoda

n, T., Sundermeyer, M., Drost, B., Labb

e, Y., Brach-

mann, E., Michel, F., Rother, C., and Matas, J. (2020).

BOP challenge 2020 on 6D object localization. Euro-

pean Conference on Computer Vision Workshops (EC-

CVW).

Hoda

n, T., Barath, D., and Matas, J. (2020). Epos: Estimat-

ing 6d pose of objects with symmetries. In Proceed-

ings of the IEEE/CVF Conference on Computer Vi-

sion and Pattern Recognition (CVPR), pages 11703–

11712.

Hosseini Jafari, O., Mustikovela, S. K., Pertsch, K., Brach-

mann, E., and Rother, C. (2019). ipose: Instance-

aware 6d pose estimation of partly occluded objects.

In Jawahar, C. V., Li, H., Mori, G., and Schindler, K.,

editors, Computer Vision – ACCV 2018, pages 477–

492, Cham. Springer International Publishing.

Katsoulas, D. (2003a). Localization of piled boxes by

means of the hough transform. In Joint Pattern Recog-

nition Symposium, pages 44–51. Springer.

Katsoulas, D. (2003b). Robust extraction of vertices in

range images by constraining the hough transform. In

IbPRIA, pages 360–369.

Mitash, C., Boularias, A., and Bekris, K. E. (2018). Im-

proving 6d pose estimation of objects in clutter via

physics-aware monte carlo tree search. In 2018 IEEE

International Conference on Robotics and Automation

(ICRA), pages 3331–3338.

Park, K., Patten, T., and Vincze, M. (2019). Pix2pose:

Pixel-wise coordinate regression of objects for 6d

pose estimation. 2019 IEEE/CVF International Con-

ference on Computer Vision (ICCV), pages 7667–

7676.

Pereira, N. and Alexandre, L. A. (2020). Maskedfusion:

Mask-based 6d object pose estimation.

Photoneo (2017). Phoxi 3d scanner. https://www.photoneo.

com/products/phoxi-scan-m/.

Pitteri, G., Ramamonjisoa, M., Ilic, S., and Lepetit, V.

(2019). On object symmetries and 6d pose estima-

tion from images. In 2019 International Conference

on 3D Vision (3DV), pages 614–622. IEEE.

Stein, F. and Medioni, G. (1992). Structural index-

ing: efﬁcient 3-d object recognition. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

14(2):125–145.

Vidal, J., Lin, C.-Y., Llado, X., and Mart

ı, R. (2018). A

method for 6d pose estimation of free-form rigid ob-

jects using point pair features on range data. Sensors,

18:2678.

Vock, R., Dieckmann, A., Ochmann, S., and Klein, R.

(2019). Fast template matching and pose estimation

in 3d point clouds. Computers & Graphics, 79:36–45.

Wang, C., Xu, D., Zhu, Y., Mart

ın-Mart

ın, R., Lu, C., Fei-

Fei, L., and Savarese, S. (2020). Densefusion: 6d ob-

ject pose estimation by iterative dense fusion.

Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2017).

Posecnn: A convolutional neural network for 6d ob-

ject pose estimation in cluttered scenes. arXiv preprint

arXiv:1711.00199.

Zakharov, S., Shugurov, I., and Ilic, S. (2019). Dpod: 6d

pose object detector and reﬁner. In International Con-

ference on Computer Vision (ICCV).

Zhou, Y., Barnes, C., Lu, J., Yang, J., and Li, H. (2019). On

the continuity of rotation representations in neural net-

works. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

5745–5753.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

552