
Classification Performance of RanSaC Algorithms
with Automatic Threshold Estimation
Cl
´
ement Riu
1
, Vincent Nozick
1
, Pascal Monasse
1
and Joachim Dehais
2
1
Universit
´
e Paris-Est, LIGM (UMR CNRS 8049), UGE, ENPC, F-77455 Marne-la-Vall
´
ee, France
2
Arcondis AG 4153 Basel, Switzerland
Keywords:
Multi-View Stereo, Structue-from-Motion, RanSaC, Semi-synthetic Dataset, Benchmark.
Abstract:
The RANdom SAmpling Consensus method (RanSaC) is a staple of computer vision systems and offers a
simple way of fitting parameterized models to data corrupted by outliers. It builds many models from small
sets of randomly selected data points, and then scores them to keep the best. The original scoring function is
the number of inliers, points that fit the model up to some tolerance. The threshold that separates inliers from
outliers is data- and model-dependent, and estimating the quality of a RanSaC method is difficult as ground
truth data is scarce or not quite reliable. To remedy that, we propose a data generation method to create at will
ground truths both realistic and perfectly reliable. We then compare the RanSaC methods that simultaneously
fit a model and estimate an appropriate threshold. We measure their classification performance on those semi-
synthetic feature correspondence pairs for homography, fundamental, and essential matrices. Whereas the
reviewed methods perform on par with the RanSaC baseline for standard cases, they do better in difficult
cases, maintaining over 80 % precision and recall. The performance increase comes at the cost of running
time and analytical complexity, and unexpected failures for some algorithms.
1 INTRODUCTION
Over fourty years have passed since the publication of
the RANdom SAmple Consensus algorithm (Fischler
and Bolles, 1981). The algorithm approximates a so-
lution to the NP-hard consensus maximization prob-
lem (Chin et al., 2018): fitting a parameterized model
to data corrupted by noise and outliers. RanSaC gen-
erates tentative models using random, minimal sub-
sets of data and validates them with the distance of
data points to each model. Data points whose model
distance are below a given threshold are inliers, and
the retained model maximizes the inlier count, or
consensus. Defining this threshold however requires
knowing the noise level in the data. Some methods lift
this constraint by estimating jointly a threshold and a
model. For them, the inlier count is replaced by new
measures involving both threshold and inlier count for
optimization. We call these methods adaptive or au-
tomatic.
We review these methods and examine their per-
formance on a benchmark of three computer vi-
sion problems central to Multi-View Stereo (MVS)
and Structure-From-Motion (SfM) pipelines (Schon-
berger and Frahm, 2016; Moulon et al., 2016): ho-
mography, fundamental and essential matrix fitting.
Data for these problems consists of feature point pair
correspondences, leading the algorithm to classify
them as inlier or outlier.
Firstly, automatic threshold estimation does ben-
efit MVS pipelines (Moulon et al., 2012), although
its performance should be measured on ground-truth
data independently. Secondly, incremental MVS
pipelines also benefit from good inlier classification,
as inliers are triangulated to from 3D points, there-
after used as anchors for following views to estimate
their pose through Perspective from n Points (PnP).
Thirdly, since RanSaC methods are the basis of SfM
and MVS software, robust analysis will improve the
state of the art. Fourthly and finally, deep-learning 3D
pipelines use the output of MVS pipelines, most often
(Schonberger and Frahm, 2016), for training database
generation (Li and Snavely, 2018).
We first contribute a method to create semi-
synthetic data with ground truth labels to assess clas-
sification power of RanSaC algorithms. Previous
artificial datasets are unrealistic; e.g. (Cohen and
Zach, 2015) performs the evaluation on plane es-
timation in random 3D point clouds, and (Barath
et al., 2019) generates random homographies and cor-
Riu, C., Nozick, V., Monasse, P. and Dehais, J.
Classification Performance of RanSaC Algorithms with Automatic Threshold Estimation.
DOI: 10.5220/0010873300003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
723-733
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
723

Table 1: Notations.
Definition Description
k ∈ N
>0
dimension of data points
S = R
k
space of data points
P ⊂ S set of input data points
d ∈ N
>0
degrees of freedom of a model
Θ ⊂ R
d
space of model parameters
θ ∈ Θ parameter vector of a model
s ∈ N
>0
data sample size
Sa : 2
S
→ S
s
sampling function
F : S
s
→ Θ fitting function
p : [0,1] → [0,1] proba. of sampling inliers only
D : S × Θ → R point-model residual function
σ ∈ R inlier threshold
I : Θ × R → 2
P
inlier selector function
I = I(θ,σ) ⊂ P
set of model inliers
Q : 2
P
× Θ → R model quality function
respondences. Real datasets on the opposite end can-
not offer a control over the noise and outliers: they
often rely on an algorithm to calibrate an active sen-
sor to the data which introduces error like the KITTI
dataset (Geiger et al., 2012) and the 7 scenes dataset
(Shotton et al., 2013) or do not correct inlier noise as
in (Cordts et al., 2016). Our method offers the pos-
sibility to create, from any image dataset, a realistic
semi-synthetic dataset.
Note that there have already been comparative
studies of RanSaC, such as (Choi et al., 2009).
These studies however focus on threshold-controlled
RanSaC derivatives on a small real-world dataset
without ground truth. We contribute an analysis
of the classification and retrieval power of adaptive
RanSaC algorithms. We thus pit threshold-free meth-
ods against each other, rather than against baseline
RanSaC as was done before.
Section 2 reviews the automatic RanSaC meth-
ods, Section 3 the benchmark data and methods. Sec-
tions 4 and 5 cover the results and their analysis, and
Section 6 concludes.
2 AUTOMATIC RanSaC
METHODS
2.1 Notation
We reuse and simplify the notation of (Barath et al.,
2019), standardized in Table 1. Input points exist in
S = R
k
,k > 0, with the input point set noted as P ⊂ S.
For image coordinates, the point dimension k = 2; for
pair correspondences, k = 4.
A model of d degrees of freedom exists in Θ ⊂ R
d
,
and can be obtained via the fitting function F, applied
to a set of data points sampled by the sampling func-
tion Sa. d = 8 for homographies, 7 for fundamental
matrices, and 5 for essential matrices.
The probability of Sa drawing an uncontaminated
sample (including only correct data) is p(ε), with ε ∈
[0,1] the true (hence generally unknown) inlier ratio.
Sa typically samples s points uniformly in P , hence
p(ε) = ε
s
, an increasing function of ε.
Given a model θ, we can calculate the residual
error between that model and a data point P using
D(P,θ). I selects the points that are inliers to a model
based on the residuals. Finally, Q defines the quality
of the fit θ on P .
While D is model-dependent, the standard selec-
tor I keeps points with residuals below a threshold σ:
I = I(θ,σ) = {P ∈ P : D(P,θ) < σ}. Q(I , θ) = |I |
is then the number of inliers. Since inlier count in-
creases with σ, standard Q definitions are unreliable
quality measures for RanSaC variants. Algorithm 1 is
the pseudo-code for a generic RanSaC. A type II error
corresponds to missing the true model due to insuffi-
cient search.
Input: P , Sa, F, p, Q, σ
Input: confidence against type II error β,
it
max
(or min. inlier rate ε)
Output: Best model parameters and set of
inliers
I
max
=
/
0, q
max
= 0
it = 0 (and it
max
=
ln(1−β)
ln(1−p(ε))
if ε is input)
while it ≤ it
max
do
sample = Sa(P ), θ = F(sample)
I = I(θ,σ), q = Q(I ,θ)
if q > q
max
then
q
max
= q,θ
max
= θ,I
max
= I
ε = |I |/|P |,it
max
=
ln(1−β)
ln(1−p(ε))
it = it + 1
return θ
max
,I
max
Algorithm 1: RanSaC algorithm.
2.2 Existing Algorithms
The methods gathered in Table 2 generate new in-
lier and model quality definitions to behave adap-
tively. They rely on three types of consistency mod-
els: inlier, outlier, and cross-model. An inlier- (resp.
outlier-)consistent method enforces a parameterized
distribution on the inlier (resp. outlier) residuals, and
searches for a model and parameter set that fit the
data. A cross-model-consistent method looks for re-
peated patterns in residuals of different models us-
ing cross correlations or clustering. The original
RanSaC (Fischler and Bolles, 1981) algorithm uses
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
724
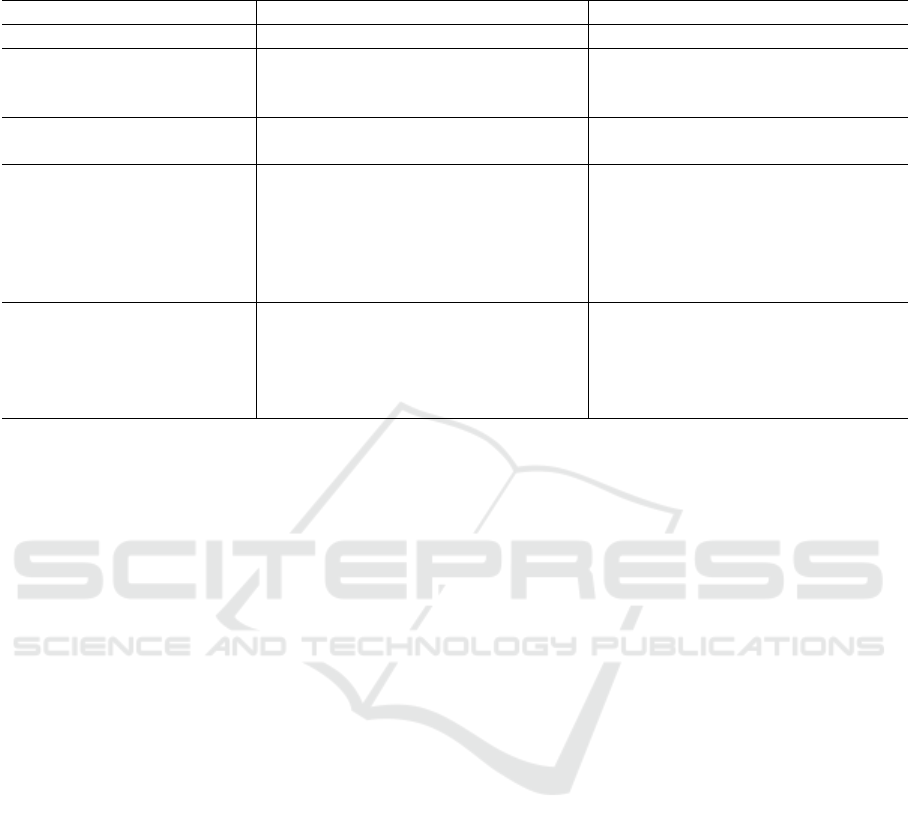
Table 2: Overview of robust fitting methods with adaptive inlier criteria. Bracketed terms in the “Consistency assumption”
column specify where the assumption is made.
Ref. Consistency assumption Optimized function
(Fischler and Bolles, 1981) Bounded residuals (inliers) Inlier set size
(Miller and Stewart, 1996) Gaussian residual distribution (inliers) Scale estimate
(Wang and Suter, 2004) Gaussian (inliers) Inlier/threshold
Minimal residual density (transition)
(Fan and Pylv
¨
an
¨
ainen, 2008) Gaussian (inliers) Scale estimate
Residuals correlate (cross-model)
(Choi and Medioni, 2009) Low parameter variance (cross-model) Variance
(Moisan et al., 2012) Problem specific (outlier) Number of false alarms
(Cohen and Zach, 2015) Uniform (outliers) Likelihood
(Moisan et al., 2016) Problem specific (outliers) Number of false alarms
(Dehais et al., 2017) Data-driven (outliers) False discovery rate
(Barath et al., 2019) Uniform (inliers) - Uniform (outliers) Deviation
(Rabin et al., 2010) Problem specific (outliers) Greedy number of false alarms
(Isack and Boykov, 2012) Graph cuts energy
(Toldo and Fusiello, 2013) Residuals correlate (cross-model) Inlier cluster merging cost
(Magri and Fusiello, 2014) Residuals correlate (cross-model) Residual cluster merging cost
(Magri and Fusiello, 2015) Residuals correlate (cross-model) Factorization error of residual matrix
inlier consistency: all inliers have residuals below a
certain threshold.
The first automatic threshold method was
MUSE (Miller and Stewart, 1996). MUSE assumes
that inlier residuals follow a Gaussian distribution,
and estimates the noise level for all inlier sets of all
tested models. The smallest noise for each model
becomes its quality measure, and the model with the
smallest noise level is selected overall.
(Wang and Suter, 2004) relies on inliers follow-
ing a unimodal distribution (specifically Gaussian in
experiments). For single models, this method puts a
threshold on residual distribution density. The quality
measure is the ratio of inliers to inlier threshold value.
The method in (Fan and Pylv
¨
an
¨
ainen, 2008)
merges inlier and cross-model consistency. This
method uses the weighted median absolute deviation
of all residuals as both scale estimate and quality
function. Each time a data point has a small resid-
ual for a sampled model, its weight and probability to
be sampled increase. This way, the weight biases the
quality function towards the median absolute devia-
tion of inliers to stable models.
StarSaC (Choi and Medioni, 2009) uses cross-
model consistency as well, namely that variance of
model parameters is minimal for the optimal thresh-
old. The method calls RanSaC with multiple thresh-
olds, multiple times per threshold. The quality mea-
sure is the variance of resulting model parameters for
a given threshold.
A Contrario RanSaC (Moisan et al., 2012;
Moisan et al., 2016) (AC-RanSaC, originally named
ORSA (Moisan and Stival, 2004)) was the first
outlier-consistent method. AC-RanSaC approximates
for each problem the probability distribution of resid-
uals for random input: the background distribution.
It then minimizes a combinatorial prediction of false
inliers by comparing the cumulative distributions of
data and background residuals.
An extension of AC-RanSaC (Dehais et al., 2017)
adapts the method in two ways: by generating out-
lier data from inlier data, and simplifying the signifi-
cance measure. This method scrambles input matches
to generate background distributions, and seeks the
model with the most inliers subject to a maximal rate
of inliers in the background data.
The likelihood-ratio method (Cohen and Zach,
2015) relies on a uniform distribution of outlier resid-
uals. The quality function approximates the likeli-
hood of each model against this uniform distribution,
using substantial statistical derivations.
MAGSAC (Barath et al., 2019) is the most recent
publication on this work’s subject. It combines in-
lier and outlier consistency assumptions, where both
follow uniform distributions on different intervals.
MAGSAC then estimates the model’s deviation from
the background noise, without explicitly classifying
inputs into inliers and outliers.
Other methods exist to detect multiple models in
data; though they are out of scope, we list some here.
(Rabin et al., 2010) uses the principle of A Contrario
RanSac (Moisan et al., 2012) in a greedy optimization
to extract multiple models. (Isack and Boykov, 2012)
generates multiple models, before attaching data to
those models to minimize total residuals and number
of models. J-Linkage (Toldo and Fusiello, 2013), its
Classification Performance of RanSaC Algorithms with Automatic Threshold Estimation
725

extension T-Linkage (Magri and Fusiello, 2014), and
Low-Rank Preference Analysis (Magri and Fusiello,
2015) rely on cross-model consistency, while using
different methods to cluster inlier sets and models
jointly.
3 BENCHMARK
3.1 Data Generator
The distributions of inliers and ouliers in the image
space have a major impact on the effectiveness of
model fitting. Benchmarks on data extracted from
photographs are invaluable, but lack the power to gen-
eralize observations because of their small size and
the lack of control over noise and outliers. Synthetic
data on the other hand are flexible and customizable
but unrealistic as the chosen model generation and in-
lier sampling methods impact the results.
We propose a simple procedure to generate real-
istic, semi-synthetic data with ground truth classifica-
tion. It gives access to real models and inliers, with
outliers whose distance to the model is controlled.
The data generator takes an image pair with point
matches and evaluates its underlying model using
AC-RanSaC (Moisan et al., 2012; Moisan et al.,
2016) at arbitrary precision and up to 10 000 itera-
tions. The returned model is then used as “ground
truth”, and the estimated inliers as the basis for data-
driven yet perfect inliers.
To generate perfect inliers, the matches are mod-
ified with respect to the ground truth model. For
homographies, inlier points in the first image are
mapped into the second using the ground truth ho-
mography (figure 1). For fundamental and essential
matrices, the point on the second image of each inlier
match is projected on the true epipolar line of the first
point (figure 2).
The artificial inlier matches and outlier matches
can then be derived from those “ground truth” inlier
matches. Inlier matches are created by adding noise
uniformly drawn in [−σ
noise
,σ
noise
]
2
to the second im-
age point of each match to generate a controled pixel
error. Uniform noise gives here better control and
testability for the inlier/outlier threshold than Gaus-
sian noise, which is unbounded.
Once inlier matches are generated, outliers are in-
serted by generating random matches in the two im-
ages, uniformly sampled in error space ensuring a dis-
tance to the model greater than the maximum inlier
error σ
noise
. Sampling in error space is explained for
homography estimation in figure 3 and for fundamen-
tal and essential matrix estimation in figure 4. This
choice of distribution in error space returns a realis-
tic outlier distribution and truly challenges the algo-
rithms. A simple uniform distribution of outliers in
match space on the contrary has too little structure
to disturb the RanSaC algorithm. For each dataset
and inlier ratio, we generate enough outliers to ob-
tain the desired ratio, and downsample uniformly to
have 4000 data points or fewer.
3.2 Tested Algorithms
We benchmark seven algorithms with varied ap-
proaches to inlier classification: the baseline RanSaC
(Fischler and Bolles, 1981), MUSE (Miller and Stew-
art, 1996), StaRSaC (Choi and Medioni, 2009),
A-Contrario RanSaC (AC-RanSaC) (Moisan et al.,
2016), Likelihood Ratio Test (LRT) (Cohen and Zach,
2015), Marginalizing Sample Consensus (MAGSAC)
(Barath et al., 2019) and Fast-AC-RanSaC—an adap-
tation of AC-RanSaC. (Isack and Boykov, 2012;
Toldo and Fusiello, 2013; Magri and Fusiello, 2014),
though relatively recent, have been excluded as they
tackle the multi-model settup which we do not con-
sider in this study.
RanSaC acts as baseline, with fixed inlier/outlier
thresholds σ(px) to show non-adaptive results. To
avoid degenerate cases in the worst case we
strengthen its stopping criterion to ensure it draws
5 outlier-free samples instead of just 1 with confi-
dence β. This requires a modification in the formula
for it
max
in Algorithm 1.
MUSE proposes an improvement over Least Me-
dian of Squares (Leroy and Rousseeuw, 1987) with
a new objective function based on a scale estimate
to increase robustness wrt outliers. The algorithm
works similarly to RanSaC, with multiple iterations
of a minimal sampler estimating a model and then
ranking based on their scale estimate. We adapted the
algorithm by adding the classic termination criterion
of RanSaC to speed up the execution.
StaRSaC removes the need for a user set threshold
of RanSaC by launching multiple RanSaCs for differ-
ent thresholds. It then estimates at each threshold the
variance over the parameters and the threshold yield-
ing the lowest variance is selected. Our implemen-
tation uses the same thresholds as (Cohen and Zach,
2015) to speed up the process by only considering
thresholds that make sense in pixel-scale problems.
AC-RanSaC seeks the model with the lowest risk
of type I error. This is measured as the Number of
False Alarms (NFA), which estimates the expected
number of false positive models generated by an in-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
726

Figure 1: From an imperfect match (p
1
, p
2
) considered inlier by AC-RanSaC, the “perfect match” (p
1
, p
0
2
) is constructed
such that p
0
2
= H p
1
using a realistic homography H given by AC-RanSaC.
Figure 2: From an imperfect match (p
1
, p
2
) considered inlier by AC-RanSaC, the “perfect match” (p
1
, p
0
2
) is constructed
using p
0
2
the orthogonal projection of p
2
on the epipolar line L
1
= F p
1
where F is a realistic fundamental matrix given by
AC-RanSac. This does not guarantee that p
0
2
represents the same physical point as p
1
, but that some 3D point at possibly
different depth projects exactly at p
1
and p
0
2
.
Figure 3: A random point q
1
is drawn from the left image.
Using the ground truth model H, its perfect match q
0
2
= Hq
1
is computed. Then a direction and a distance to q
0
2
are drawn
uniformly in order to create q
2
so that it remains in the im-
age and out of the inlier zone (marked in red) defined by the
inlier noise level.
Figure 4: A random point q
1
is drawn from the left image.
Using the ground truth model F, the epipolar line L
1
= Fq
1
is computed. Then position on this line and a distance to
L
1
are drawn uniformly in order to create q
2
so that it re-
mains in the image and out of the inlier zone (marked in
red) defined by the inlier noise level.
lier set:
NFA(θ,σ) ∼
|P |
k(σ)
k(σ)
s
p
k(σ)−s
σ
, (1)
with k(σ) = |I(θ,σ)| the number of inliers at thresh-
old σ and p
σ
the relative area of the image zone
definining inliers at σ. This function is computed
for all σ ≤ σ
max
such that k(σ) ∈ {s + 1,..., n}. The
method is virtually parameter-free, with σ
max
= +∞
and the NFA upper bound NFA
max
= 1.
The Likelihood Ratio Test (LRT) proposes a fast
method to control type I and type II errors. Its qual-
ity function is the likelihood that the dataset is non-
random for a given model:
L(ε,σ) = 2|P |
εlog
ε
p
σ
+ (1 − ε)log
1 − ε
1 − p
σ
, (2)
with inlier ratio ε = k(σ)/|P | and σ spanning a prede-
fined list {σ
min
,. . . , σ
max
}. The adjustment of it
max
is
the same as RanSaC, with an early bailout system to
sift through models faster, controlled by a new param-
eter γ for the type II error (rejection of a good model).
MAGSAC introduces a new quality function,
based on the likelihood of a model given uniform in-
liers and outliers, a speedup method using computing
blocks, and a post processing method, σ-consensus,
that refits the final model on a weighted set of pseudo-
inliers. It uses four parameters: the threshold for
pseudo-inliers σ
max
, a reference threshold σ
re f
, a
lower bound on model likelihood, and the number of
data blocks.
Fast-AC-RanSaC is a speed up of AC-RanSaC by
exploiting ideas from LRT. The idea to create this
method comes from our observations, see Section 5.
It uses the same objective function as AC-RanSaC but
instead of testing all thresholds it considers the same
quantified thresholds as LRT. Using this selection of
Classification Performance of RanSaC Algorithms with Automatic Threshold Estimation
727

thresholds removes the need for a sorting of the resid-
uals and thus speeds up the method.
3.3 Performance Measures
To compare the classification power of the various al-
gorithms, we use precision—the ratio of correctly de-
tected inliers among all detected inliers—and recall—
the ratio of correctly detected inliers among true in-
liers. To represent results more easily, we use the har-
monic mean of precision and recall, the F1-Score. We
quantify the impact of noise and outliers on these met-
rics using the semi-synthetic data of Section 3.1. For
efficiency evaluation, we measure execution time.
As MAGSAC does not separate data points into
inliers and outliers but weighs them, we evaluate
its performance through three metrics: highest re-
call at the precision of AC-RanSaC, which will be
called Magsac-P, highest precision at the recall of
AC-RanSaC, Magsac-R, and weighted equivalents of
precision and recall, Magsac-W.
3.4 Parameters
We experimented the data generator on the
SIFT (Lowe, 2004) point matches from the USAC
dataset as well as SIFT points computed on Multi-H,
kusvod2 and the homogr datasets. A SIFT ratio of
0.6 was used. USAC (Raguram et al., 2012) proposes
SIFT matches for 10 homography image pairs, 11
fundamental matrix image pairs, and 6 essential
matrix image pairs with calibration matrices. Multi-
H (Barath et al., 2016) proposes 24 fundamental
matrix image pairs, kusvod2 16 fundamental matrix
image pairs, and homogr 16 homography image
pairs.
1
The inlier noise σ
noise
varied between 0 and 3 pix-
els by steps of 0.1. The outlier ratio 1 − ε varied be-
tween 0 and 0.9 by steps of 0.1. For each image pair
and setting, we generate N
gen
= 5 different datasets,
and run each algorithm N
run
= 5 times on each for
a total of 25 experiments. We average the precision
and recall over each dataset and run, excluding cases
where an algorithm failed to find a good model.
As minimal solvers F, we use the standard 4-point
algorithm for homography and 7-point algorithm for
fundamental matrix (Hartley and Zisserman, 2004),
and the 5-point algorithm for essential matrix (Nist
´
er,
2004).
We take the standard RanSaC algorithm as base-
line and benchmark MUSE, StarSAC, LRT, AC-
RanSaC, Fast-AC-RanSaC, and MAGSAC algo-
rithms. RanSaC and AC-RanSaC implementations
1
http://cmp.felk.cvut.cz/data/geometry2view/
came from (Moulon, 2012), MAGSAC from (Barath,
2019), MUSE from VXL
2
whereas LRT, Fast-
AC-RanSaC and StarSAC were implemented from
scratch.
The parameters defined in section 3.2 are set as
follows (from the relevant publicaion when avail-
able). β, the standard success confidence, is set to
0.99. σ
max
, the inlier search cutoff threshold for AC-
RanSaC, Fast-AC-RanSaC, StarSaC and LRT, is set to
16 pixels to improve speed. NFA
max
, the NFA thresh-
old for AC-RanSaC and Fast-AC-RanSaC, is set to 1
false alarm. The other parameters of LRT, were set to
α = 0.01, γ = 0.05.
The other parameters of MAGSAC were set to p =
10 data partitions, σ
max
= 10 pixels, and σ
re f
= 1.
4 RESULTS
Before presenting results for the different methods,
StarSAC has been excluded from this benchmark. In-
deed, after initial tests, it runs very slowly, even with
modification to the initial algorithm to reduce run-
time. A usual run will take 3 to 5 minutes with preci-
sion and recall only slightly above baseline.
Figure 5 gives an overview of each algorithm’s
execution time. LRT, MUSE, Fast-AC-RanSaC and
RanSaC are usually the fastest, with LRT faster than
the others on easy cases. Both LRT and RanSaC how-
ever are quite sensitive to the task complexity: when
facing high inlier noise or outlier ratio, their runtime
increases significantly, sometimes up to four or five
seconds per run. MUSE and Fast-AC-RanSaC keep
relatively low runtimes in all settings, always below
1s. AC-RanSaC’s runtime is not impacted by inlier
noise, only by the number of matches in the dataset.
Its runtime remains almost always under one second
per run, though it is often the slowest algorithm on
easy settings. However, it can be faster than Fast-AC-
RanSac on easy settings with not many points where
the sorting time of residuals is fast compared to the
computation of the residuals themselves. MAGSAC
is the most efficient algorithm on complex tasks with
runtimes up to ten times lower than AC-RanSaC.
However, because of instabilities in MAGSAC’s exe-
cution, a 1-second cap was used: for inlier noise level
above 1 pixel or outlier ratio below 0.4, MAGSAC
can find a good model but still fail to terminate.
Except for RanSaC, no algorithm presented a
compromise between precision and recall (one in-
creasing while the other decreases). This justifies the
use of F1-Score over either precision or recall.
2
https://github.com/vxl/vxl
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
728
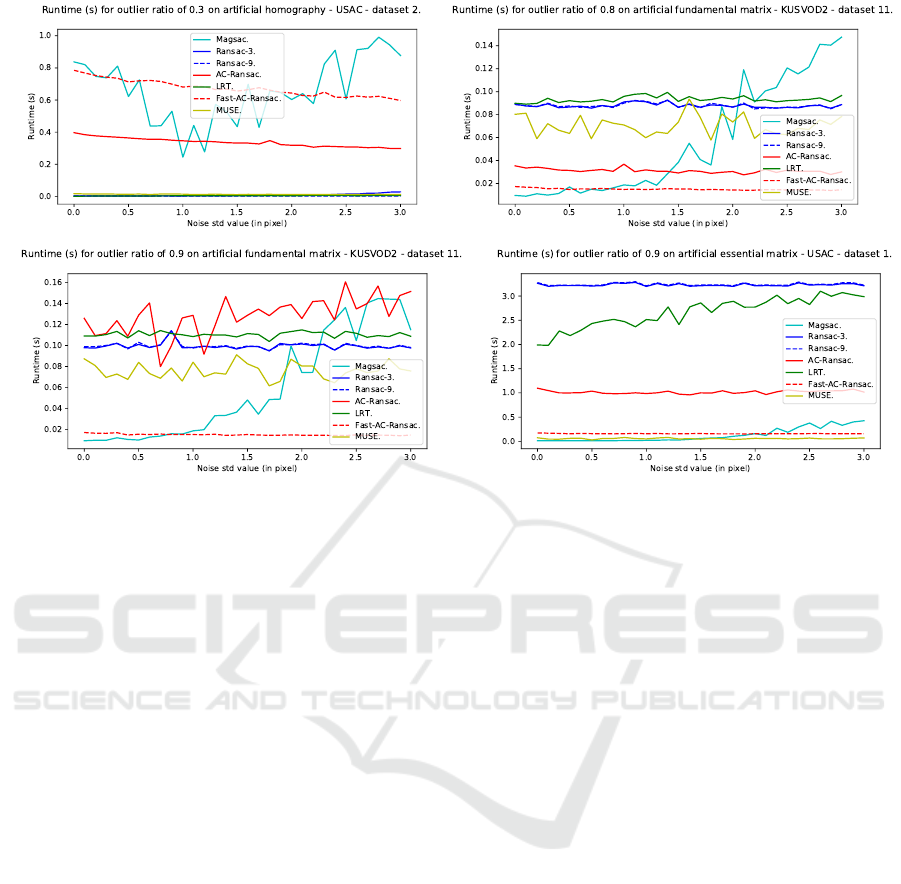
Figure 5: Runtimes over different inlier noise levels and outlier ratios. The fitting problem, dataset name, and image pair
number are in each graph title. Ransac-σ corresponds to RanSaC with threshold σ.
Trends in behavior were impacted by the noise
level and outlier ratio for all algorithms, but were nei-
ther by task, be it homography, fundamental matrix
or essential matrix estimation, nor by dataset. While
performance differed between image pairs or different
tasks, performance always decreased consistently rel-
ative to the data generator parameters. Figures 6 and
7 illustrate the typical behaviors with low and high
outlier ratios on a variety of estimation problems and
datasets. An intermediate setting, for example an out-
lier ratio around 0.5, is not included as the behavior
was observed to be intermediate between the two ex-
tremes.
The two fixed-threshold RanSaC have opposite
behaviors.The “tight” RanSaC with a threshold of
3 pixels has high precision on easy situations, but poor
recall, and both drop as noise and outliers increase.
The “loose” RanSaC with a threshold of 9 pixels has
stable recall, but precision drops as noise and out-
lier ratio increase. Both eventually perform poorly in
complex cases as too many outliers are wrongly clas-
sified.
MUSE’s performance is not impacted much by
the semi-artificial generation parameters but does not
show consistently good behavior. On the one hand, it
can have poor performance on easy settings, with be-
low baseline precision and recall. On the other hand,
it can show very good precision, above 95% on very
complex settings. However, its recall is always low as
the thresholds selected are usually smaller than other
methods.
AC-RanSaC shows a very good performance on
low outlier ratios. It maintains good precision as the
outlier ratio increases, but its recall drops, impacting
the F1-score.
LRT returns slightly lower precision and recall
than AC-RanSaC, for low outlier ratios or cases where
all algorithms perform well. The gap increases signif-
icantly for the highest inlier noise levels or outlier ra-
tios data become more challenging, the performance
dropping to baseline.
Fast-AC-RanSaC has medium performance. It has
usually good recall but average precision as it selects
a threshold twice as big as the real inlier noise level.
It can however, in some cases perform relatively well
or even to the same level as normal AC-RanSac but it
is not a consistent behavior.
MAGSAC displays two interesting behaviors. For
outlier ratios below 0.4, MAGSAC alternates between
great fits and nearly random models, instead of con-
sistently returning a satisfactory model. This explains
the F1-scores around 0.75 on figure 6, the result of
averaging models with precision and recall below 0.5
and models with precision and recall above 0.95. For
outlier ratios above 0.4, MAGSAC shows equal or
greater performances than AC-RanSaC and far less
sensitivity to inlier noise. MAGSAC is also the only
method to maintain precision and recall scores above
0.9 (resp. 0.8) in challenging cases. The 1-second cap
on MAGSAC runtime does not impact performance
in simple cases, where bad models are estimated irre-
spectively of runtime. On challenging cases, this cap
Classification Performance of RanSaC Algorithms with Automatic Threshold Estimation
729
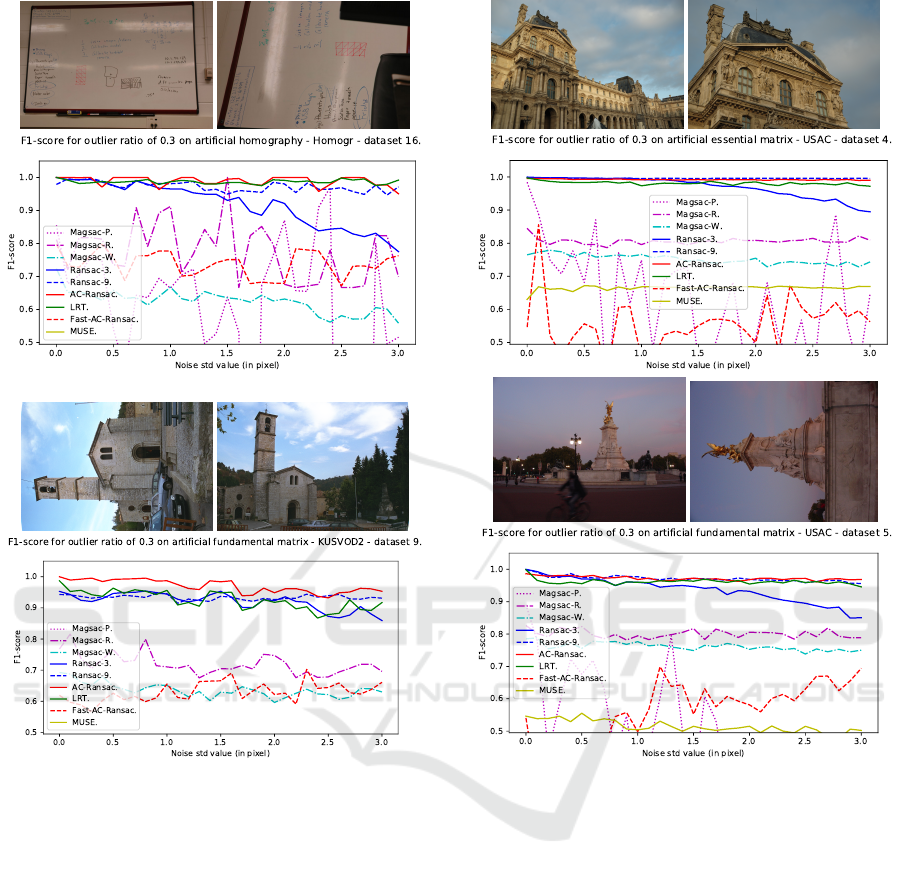
Figure 6: Typical F1-score evolution over inlier noise for a low outlier ratio (0.3). Estimation problem, dataset name and image
pair number can be found in each graph’s title. Magsac-P, Magsac-R and Magsac-W correspond to the metrics presented in
Section 3.3.
is sometimes reached but performance remains over-
all better than other algorithms.
5 DISCUSSION
Differences in runtime can be explained by the num-
ber of iterations in each algorithm as much as their
design. Indeed, each algorithm has to compute
models—which is fast—and compute residuals for all
points—slow. LRT’s high and low speeds likely stem
from its early bailout strategy, skipping residuals en-
tirely. This is a benefit in easy settings, where correct
models are plentiful, but hurts complexity in the op-
posite case, where some rare correct models are not
fully evaluated. AC-RanSaC’s high runtime for large
datasets comes from its sorting step, which takes then
as much time as computing residuals. However, this
may be amended by bucket sorting and discretization
of σ as with LRT to remove sorting entirely. This
is what led to the development of Fast-AC-RanSaC
which shows promising results but could be improved
as its performance is usually worst than that of LRT
that was developped directly in this settings.
StarSAC offers poor performance compared to
other methods except RanSaC. Except in some rare
cases, MUSE’s performance is below that of newer
methods. As explained below, in all settings one of
the newest methods will offer better performance.
Though it is usually the slowest method, AC-
RanSaC shows consistently good precision and re-
call. The algorithm does adapt well to change, and
performs far above baseline in difficult cases. It is a
robust but slower algorithm and except in our most
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
730

Figure 7: Typical F1-score evolution over inlier noise for a high outlier ratio (0.8). Estimation problem, dataset name and
image pair number can be found in each graph’s title. Magsac-P, Magsac-R and Magsac-W correspond to the metrics presented
in Section 3.3.
complex settings, it produces a good result so it is a
good pick when high classification performance is re-
quired.
LRT performed slightly worse than AC-RanSaC,
with selected inlier threshold usually larger, yet much
faster. LRT thus offers a valuable trade-off between
quality and speed. It is however fairly sensitive to the
complexity of the task: a decrease in performance to
baseline level in complex settings and a steep increase
in runtime.
Fast-AC-RanSaC was developped to improve over
AC-RanSaC by reducing runtime but it fails to outper-
form LRT in most cases.
MAGSAC has the potential to perform similarly
or better than AC-RanSaC, at comparable or bet-
ter speeds with impressive performance on the most
complex tasks. It has a very strong resilience to out-
lier and inlier noise and should be used when other al-
gorithms fail to produce a satisfying result. The lack
of robustness of its current implementation makes it
more risky to use first hand.
Finally, our semi-artificial datasets help reveal be-
havior independent of the dataset chosen as initial in-
put, and thus offers new insight in automatic RanSaC
algorithm analysis.
6 CONCLUSION
RanSaC is a robust and efficient algorithm for a wide
range of situations, whose major weaknesses appear
in case of high outlier ratios and unknown inlier noise.
Thanks to a new method to generate semi-synthetic
ground truth data we have made a quantitative evalu-
ation of three major algorithms for noise- and outlier-
robust fitting based on RanSaC. For most standard us-
ages, all algorithms perform well, with only execution
speed varying. When outliers outnumber inliers and
noise is large, adaptive methods justify their existence
by outperforming standard RanSaC by a large mar-
gin, at the cost of speed. Overall, the algorithms offer
a choice for those who seek to trade robustness, ac-
curacy, and execution speed. For example, LRT is a
good algorithm to use on simple cases, offering bet-
ter performance than traditional RanSaC in compara-
ble runtime. MAGSAC has a very strong resilience
to outlier and inlier noise and should be used when
other algorithms fail to produce a satisfying result.
The lack of robustness of its current implementation
makes it more risky to use first hand. AC-RanSaC
would then be a more robust but slower algorithm.
Except in our most complex settings, it produces a
good result so it is a good pick when high accuracy
is required. The variety of tests show the strength of
the data generation procedure in exhibiting the sensi-
tivity of the methods to each problem, to noise, and to
outliers.
Thanks to such observations, we plan to im-
prove these methods using the optimizations proposed
above as we did with Fast-AC-RanSaC that proved a
potential improvement if a more stable implementa-
tion can be developped. It is also possible now to per-
form an ablation study of each proposed ingredient
like the σ-consensus post-processing of MAGSAC to
determine precisly their impact on the robustness and
Classification Performance of RanSaC Algorithms with Automatic Threshold Estimation
731

retrieval power of each method. Finally, we plan to
extend the study on the remaining model-fitting prob-
lem involved in MVS pipelines: Perspective from n
points (PnP). This problem recovers the camera pose
of a view inserted in the pipeline from 2D-3D cor-
respondences, and model quality measures should be
adapted to that specific case.
REFERENCES
Barath, D. (2019). MAGSAC implementation. https:
//github.com/danini/magsac. [Online; accessed 22-
January-2021].
Barath, D., Matas, J., and Hajder, L. (2016). Multi-H: Ef-
ficient recovery of tangent planes in stereo images. In
Richard C. Wilson, E. R. H. and Smith, W. A. P., ed-
itors, Proceedings of the British Machine Vision Con-
ference (BMVC), pages 13.1–13.13. BMVA Press.
Barath, D., Matas, J., and Noskova, J. (2019). MAGSAC:
marginalizing sample consensus. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 10197–10205.
Chin, T.-J., Cai, Z., and Neumann, F. (2018). Robust fitting
in computer vision: Easy or hard? In Proceedings
of the IEEE European Conference of Computer Vision
(ECCV), pages 701–716.
Choi, J. and Medioni, G. (2009). StaRSaC: Stable ran-
dom sample consensus for parameter estimation. In
2009 IEEE Conference on Computer Vision and Pat-
tern Recognition (CVPR), pages 675–682.
Choi, S., Kim, T., and Yu, W. (2009). Performance evalua-
tion of RANSAC family. In Proceedings of the British
Machine Vision Conference (BMVC).
Cohen, A. and Zach, C. (2015). The likelihood-ratio test
and efficient robust estimation. In Proceedings of the
IEEE International Conference on Computer Vision
(ICCV), pages 2282–2290.
Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler,
M., Benenson, R., Franke, U., Roth, S., and Schiele,
B. (2016). The cityscapes dataset for semantic urban
scene understanding. In Proc. of the IEEE Conference
on Computer Vision and Pattern Recognition (CVPR).
Dehais, J., Anthimopoulos, M., Shevchik, S., and
Mougiakakou, S. (2017). Two-view 3D reconstruc-
tion for food volume estimation. IEEE Transactions
on Multimedia, 19(5):1090–1099.
Fan, L. and Pylv
¨
an
¨
ainen, T. (2008). Robust scale estimation
from ensemble inlier sets for random sample consen-
sus methods. In Proceedings of the IEEE European
Conference of Computer Vision (ECCV), pages 182–
195. Springer Berlin Heidelberg.
Fischler, M. and Bolles, R. (1981). Random sample consen-
sus: A paradigm for model fitting with applications to
image analysis and automated cartography. Commu-
nications of the ACM, 24(6):381–395.
Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready
for autonomous driving? the kitti vision benchmark
suite. In Conference on Computer Vision and Pattern
Recognition (CVPR).
Hartley, R. and Zisserman, A. (2004). Multiple view geom-
etry in computer vision. Cambridge University Press,
2nd edition. ISBN 978-0521540513.
Isack, H. and Boykov, Y. (2012). Energy-based geomet-
ric multi-model fitting. International Journal of Com-
puter Vision (IJCV), 97(2):123–147.
Leroy, A. M. and Rousseeuw, P. J. (1987). Robust regres-
sion and outlier detection. Wiley series in probability
and mathematical statistics.
Li, Z. and Snavely, N. (2018). MegaDepth: Learning single-
view depth prediction from internet photos. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 2041–2050.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision (IJCV), 60(2):91–110.
Magri, L. and Fusiello, A. (2014). T-linkage: A continuous
relaxation of J-linkage for multi-model fitting. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 3954–3961.
Magri, L. and Fusiello, A. (2015). Robust multiple model
fitting with preference analysis and low-rank approxi-
mation. In Proceedings of the British Machine Vision
Conference (BMVC), pages 20.1–20.12.
Miller, J. V. and Stewart, C. V. (1996). MUSE: Robust sur-
face fitting using unbiased scale estimates. Proceed-
ings of the IEEE Conference on Computer Vision and
Pattern Recognition (CVPR), pages 300–306.
Moisan, L., Moulon, P., and Monasse, P. (2012). Automatic
homographic registration of a pair of images, with a
contrario elimination of outliers. Image Processing
On Line (IPOL), 2:56–73.
Moisan, L., Moulon, P., and Monasse, P. (2016). Funda-
mental matrix of a stereo pair, with a contrario elimi-
nation of outliers. Image Processing On Line (IPOL),
6:89–113.
Moisan, L. and Stival, B. (2004). A probabilistic criterion
to detect rigid point matches between two images and
estimate the fundamental matrix. International Jour-
nal of Computer Vision (IJCV), 57(3):201–218.
Moulon, P. (2012). AC-RanSaC implementation. https:
//github.com/pmoulon/IPOL AC RANSAC. [Online;
accessed 22-January-2021].
Moulon, P., Monasse, P., and Marlet, R. (2012). Adaptive
structure from motion with a contrario model estima-
tion. In Proceedings ot the Asian Conference of Com-
puter Vision (ACCV), pages 257–270. Springer.
Moulon, P., Monasse, P., Perrot, R., and Marlet, R. (2016).
OpenMVG: Open multiple view geometry. In Interna-
tional Workshop on Reproducible Research in Pattern
Recognition, pages 60–74. Springer.
Nist
´
er, D. (2004). An efficient solution to the five-
point relative pose problem. IEEE Transactions on
Pattern Analysis and Machine Intelligence (PAMI),
26(6):756–770.
Rabin, J., Delon, J., Gousseau, Y., and Moisan, L. (2010).
MAC-RANSAC: a robust algorithm for the recogni-
tion of multiple objects. Proceedings of the Fifth In-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
732

ternational Symposium on 3D Data Processing, Visu-
alization and Transmission (3DPVT), pages 51–58.
Raguram, R., Chum, O., Pollefeys, M., Matas, J., and
Frahm, J.-M. (2012). USAC: a universal framework
for random sample consensus. IEEE Transactions
on Pattern Analysis and Machine Intelligence (PAMI),
35(8):2022–2038.
Schonberger, J. L. and Frahm, J.-M. (2016). Structure-
from-motion revisited. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 4104–4113.
Shotton, J., Glocker, B., Zach, C., Izadi, S., Criminisi, A.,
and Fitzgibbon, A. (2013). Scene coordinate regres-
sion forests for camera relocalization in rgb-d images.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 2930–2937.
Toldo, R. and Fusiello, A. (2013). Image-consistent patches
from unstructured points with J-linkage. Image and
Vision Computing, 31:756–770.
Wang, H. and Suter, D. (2004). Robust adaptive-scale para-
metric model estimation for computer vision. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence (PAMI), 26(11):1459–1474.
Classification Performance of RanSaC Algorithms with Automatic Threshold Estimation
733
