Buildings Extraction from Historical Topographic Maps via a Deep

Convolution Neural Network

Christos Xydas

, Anastasios L. Kesidis

, Kleomenis Kalogeropoulos

and Andreas Tsatsaris

Department of Surveying and Geoinformatics Engineering, University of West Attica, Athens, Greece

Department of Geography, Harokopio University, Athens, Greece

Keywords: Building Detection, Historical Maps, Deep Learning.

Abstract: The cartographic representation is static by definition. Therefore, reading a map of the past can provide

information, which corresponds to the accuracy, technology, as well as scientific knowledge of the time of

their creation. Digital technology enables the current researcher to "copy" a historical map and "transcribe" it

to today. In this way, a cartographic reduction from the past to the present is possible, with parallel

visualization of new information (historical geodata), which the researcher has at his disposal, in addition to

the background. In this work a deep learning approach is presented for the extraction of buildings within

historical topographic maps. A deep convolution neural network based on the U-Net architecture is trained

by a large number of images patches in a deep image-to-image regression mode in order to effectively isolate

the buildings from the topographic map while ignoring other surrounding or overlapping information like

texts or other irrelevant geospatial features. Several experimental scenarios on a historical census topographic

map investigate the applicability of the method under various patch sizes as well as patch sampling methods.

The so far results show that the proposed method delivers promising outcomes in terms of building detection

accuracy.

1 INTRODUCTION

Automated retrieval of information from many

different images is a very important task. Historical

maps provide valuable information about the site,

with a chronological reference to the time they were

built. Thus, they may contain information on

topography, toponyms, and in relation to urban space,

streets, blocks, buildings, etc. It is therefore important

that this information can be extracted and be available

for analysis and identification of the urban landscape

of the past.

There are plenty of such maps (topographic,

urban) in public services and which can be a useful

source of information if one can take advantage of

them. These maps can be studied by many scientists

from a wide range of disciplines. This current study

uses as object the digitized maps of the Hellenic

Statistical Authority (ELSTAT) and was used for

inventory purposes (pre-enumeration, enumeration,

and post-enumeration). Such a sample map is

presented in Figure 1 and depicts the Settlement of

Petroupoli, which is a suburb of Athens, Greece, in

the 1971 Housing and Population Census. Its initial

size is 70 × 50 cm and its scale is 1:5000.

There are many GIS software and not only, which

provide the ability to vectorize an image. This process

can be performed either (semi) manually under the

supervision of a special user, or automatically. The

product resulting from this process, however, does

not differentiate the objects displayed on a map. That

is, linear elements are not separated from polygonal,

texts (letters, numbers) or point data.

Figure 1: Sample historical topographic map.

Xydas, C., Kesidis, A., Kalogeropoulos, K. and Tsatsaris, A.

Buildings Extraction from Historical Topographic Maps via a Deep Convolution Neural Network.

DOI: 10.5220/0010839700003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages

485-492

ISBN: 978-989-758-555-5; ISSN: 2184-4321

485

Therefore, in order to achieve a distinct rendering

of the objects, another approach must be implemented

that aims at the specific recognition of the desired

objects. The aim of this study is to extract the

geometry of the buildings from the above-mentioned

historical topographic maps that are initially in the

form of an image. Figure 2 shows an example of this

kind of conversion. Specifically, Figure 2(a) shows

the original binarized form of the image, while Figure

2(b) shows the footprints of the buildings, which is

the desired result. Indeed, textual information as well

as other irrelevant graphic information is effectively

isolated.

(

)

(

)

Figure 2: (a) Original binarized map subarea (b) Buildings

footprints detection.

Detecting a building footprint often becomes

difficult, as various specific challenges arise that are

usually related to the removal of background map

noise (which is common), irrelevant graphics or

textual information, etc. For example, building

geometry is often overlapped with block’s number, as

shown in Figure 3(a). In addition, there may be a

dense display of text information on the map, e.g.

street names adjacent to the lines of the building

block, free text in the map space, or either in a variety

of characters’ size, as shown in Figures 3(b) and 3(c),

respectively. In addition, there may be an overlap of

one edge of the building with the boundaries of the

building block or even two edges of the building

footprint overlapping with the block boundaries as

shown in Figure 3(d).

(a)

(b)

(

)

(d)

Figure 3: Building footprints detection challenges (a) Dense

textual overlapping content (b) Free text over the map (c)

Buildings footprints with varying shape, size and

orientation (d) Overlapping issues between building block

and building footprints.

In terms of buildings extraction from high resolution

aerial images, there is a variety of previous studies in

the literature (Fischer et al., 1998; Peng et al., 2005;

Dornaika and Hammoudi, 2009; Hecht et al., 2015).

However, these methodologies have limited results

on historical maps since they are considered as

significantly lower quality. In this context, (Suzuki

and Chikatsu, 2003) propose a technique for

automatic building extraction that detects rectangular

building footprints that are described by their four

corner coordinates. In another work, (Laycock et al.,

2011) represent the extracted buildings as non-

intersecting closed polygons. Recently, deep learning

approaches have attracted significant attention since

they provide state-of-the-art results (Liu et al., 2017).

Specifically, Convolutional Neural Networks

(CNNs) are deep architectures that are able to find

complicated inherent structures by transferring

features through multiple hidden layers in a non-

linear fashion (Voulodimos et al., 2018). Uhl et al.

designed an automatic sampling system, guided by

geographic contextual data, for generating training

images (Uhl et al., 2017). Using these automatically

collected graphical examples, they trained a variant of

the classical LeNet architecture (LeCun et al., 1998),

for extracting building footprints and urban areas

from historical sheets of the United States Geological

Survey topographic map series. In another recent

work, they present an improved framework for

automatically collect training data, deploying

locational information given in ancillary spatial data

and sampling patches containing building symbols,

from map images, by cropping them at those locations

(Uhl et al., 2019). Consequently, they use these data

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

486

to train CNNs, which they use for subsequent semantic

segmentation in a weakly supervised manner. Heitzler

et al. presented a framework for extracting polygon

representations of building footprints, that consists of

training an ensemble of 10 U-Nets, for segmentation,

using data from the Siegfried map series, and

vectorizing using methods based on contour tracing

and density-based clustering on transformed wall

orientations (Heitzler et al., 2020).

In this work we propose a Deep Convolutional

Neural Network (DCNN) approach based on the U-

Net architecture (Ronneberger et al., 2015) that

addresses the problem of extracting building

footprints from historical digital maps represented as

raster images. The DCNN is trained by a large

number of images patches in a deep image-to-image

regression mode in order to effectively isolate the

buildings from the map while ignoring other

surrounding or overlapping information like texts and

other irrelevant geospatial features. The proposed

method is tested on a historical topographic map

dataset which is partially annotated by human

experts. This annotation provides the ground truth

which serves as the desired target response of the

network. Several scenarios are considered that

investigate the applicability of the method under

various patch sizes as well as patch sampling

methods. The efficiency of the method is

quantitatively assessed by a set of metrics that

compare the systems’ output to the annotated ground

truth. The experimental results show that the

proposed method provides promising results under

several setup scenarios. The rest of this paper is

organized as follows: Section 2 describes the

proposed approach and provides details regarding the

DCNN architecture and the overall training process.

Section 3 describes the evaluation protocol and

presents experimental results under various setups.

Indicative examples are also provided and discussed

that highlight the performance of the proposed

method. Finally, section 4 draws the conclusions.

2 PROPOSED METHOD

In this work the problem of extracting building

footprints from historical maps is addressed in a deep

learning framework, where a DCNN is trained using

as inputs patches extracted from the original

topographic map image, as well as, patches extracted

from the ground-truth image, as desired outputs. The

network’s model is based on the U-Net architecture

that implements a deep, pixel-wise regression. The

network’s architecture consists of two basic parts.

The first part is the encoder, which processes the

input image through a contraction path, where down-

sampling is being done by sequential convolutions,

ReLUs and max poolings. The second part is the

decoder, which processes the encoder’s result through

an expansion path, where up-sampling is performed

through sequential convolutions, ReLUs and

transposed convolutions. A main feature of this

architecture is its ability to find the right balance

between locality and context. Indeed, for better

localization accuracy, in every decoder’s step, skip

connections are being used, joining the outputs of the

transposed convolutions, with the feature maps from

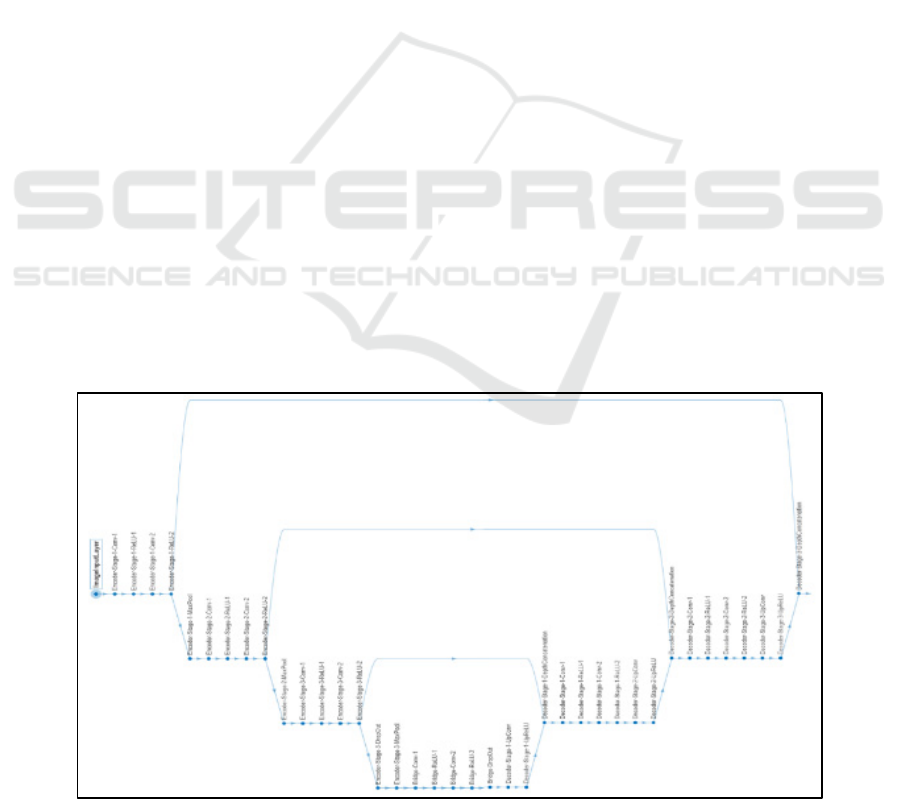
the corresponding layer of the encoder part. Figure 4

visualizes the proposed network’s architecture.

Figure 4: U-net architecture of the proposed DCNN.

Buildings Extraction from Historical Topographic Maps via a Deep Convolution Neural Network

487

In the proposed DCNN, the goal is to predict, for

each pixel of the input patch, a value that is as close

as possible to the corresponding pixel value in the

ground truth patch. Regarding the objective function

employed to optimize the model the half-mean-

squared-error is applied, however not normalized by

the number of patch pixels, that is,

𝐶

𝑦



𝑦











(1)

where 𝐻,𝑊 denote the height and width of the

ground truth patch, 𝑦



is its binary pixel value and

𝑦



is the predicted response, given as output from the

DCNN. The above cost is backpropagated to all the

hidden layers of the DCNN and the network’s

parameters are updated iteratively using the Adam

optimizer (Kingma and Ba, 2014). Considering that

the output of the DCNN is a set of dense predictions,

where each pixel corresponds to a continuous

numerical value between 0 and 1, the output of the

network is converted to a binary one in order to be

compared to the corresponding ground-truth patch.

Training the U-Net is based on a large number of

images patches pairs extracted from the original and

the ground truth image, respectively. The original

image is a colored image map that depicts the

topographic area under consideration while the

ground truth is a binary image denoting only the

building footprints. A patch from the original image

is used as input to the network while the

corresponding binary ground truth image patch is

used as the desired network’s output. The patches are

created using three different approaches named

“Random”, “Grid-Random” and “Grid-Grid”,

respectively. They differ in the way the patches cover

the entire area of the original and ground truth

images.

In the “Random” case, patches from the original

and ground truth images are extracted in a fully

random fashion. The patch size is defined by the user

and is a system’s parameter. In order to avoid patch

overlapping the process keeps track of the patch

coordinates already created and allows new patches

whose coordinates differ from the previous ones by at

least a minimum number of pixels. Moreover, a cover

percentage parameter discards patches for which the

ground truth counterpart contains insufficient number

of active (black) pixels. This check ensures that the

ground truth generated patches contain an acceptable

minimum of valuable information, that is, pixels

indicating building footprints. Figure 5 depicts an

instance of the “Random” patches’ creation process.

Figure 5: Snapshot of the “Random” patches process

implementation. The overall number of requested patches

is given by the user.

Identical patches coordinates apply to the original

color image and the ground truth image, respectively.

Figure 6 shows a pair of training patches. The patch

on the top is extracted from the original image and

serves as input for the DCNN network. The patch on

the bottom depicts the corresponding part of the

ground truth image which is used as the training target

of the network.

(

)

(

)

Figure 6: Example pair of training patches of size 224×224

pixels. (a) Patch in the original image (b) Corresponding

patch in the ground truth image.

In the “Grid-Random” case, the patches from the

original and the ground truth images, are created in a

sequential sliding-window approach based on a user

defined grid step. Figure 7 depicts an example of the

process for patches of size 128×128 pixels. Again, a

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

488

cover percentage parameter prevents blank patches or

those with extremely few active pixels to be included.

While the patches are created in a sequential manner,

they are shuffled by re-indexing in a random order.

This sampling approach allows the DCNN to be

trained with patches that systematically cover, in a

grid fashion, the whole spatial range of the original

input and ground truth images while assuring a

certain percentage of patches diversity.

Finally, in case of the “Grid-Grid” sampling, the

patches are being extracted similarly to the “Grid-

Random” case, however the original sequential

indexing is preserved.

Figure 7: Snapshot of the “Grid-Random” and “Grid-Grid”

patches process implementation. The sequential patches

generation continues until the whole are is covered.

The last sampling approach affects the training

process since it does not allow the DCNN to be

trained with patches from the whole spatial range of

the original and ground truth images. Indeed, the

patches datasets are divided during the training of the

network into three parts: 50% of the dataset for

training, 25% for validation and 25% for testing. It is

important to notice that the splitting process is

sequentially performed based on the patches index.

Therefore, in the first two sampling scenarios

“Random” and “Grid-Random”, the patches

eventually cover the whole spatial range of the

original and ground truth images. In contrast, in the

third sampling case, “Grid-Grid”, only the first 50%

of the patches are used for training, leaving the next

25% and 25% for validation and testing, respectively.

Clearly, the minimum pixel difference parameter

for the “Random” sampling, the grid step parameter

for both the “Grid-Random” and “Grid-Grid”

sampling and the cover percentage parameter, for all

three cases, affect the total number of the extracted

patches pairs. Indeed, the lower the grid step or the

cover percentage value, the higher the number of

patches pairs that can be extracted. On the contrary,

increasing the minimum pixel difference between the

patches, decreases the number of extracted patches

pairs in the “Random” case.

After the patches are created, data augmentation

techniques are also involved in order to enhance the

size and quality of the training datasets facilitating the

network to build better models. Specifically, every

input and ground truth patch pair images are further

augmented by rotation by 90, 180, 270 degrees

in accordance with a horizontally flip leading to

an augmented set of 8 patches pairs, as shown in

Figure 8.

(a)

(

)

Figure 8: Data augmentation example for (a) an original

patch and (b) its corresponding ground truth instance. In

both rows, the first image is the original patch while the

following 7 patches are produced by the data augmentation

process.

3 EXPERIMENTAL RESULTS

The proposed method for extracting building

footprints from topographic map images is tested

under several experiment scenarios. The experiments

can be grouped into three different cases, according

to the sampling approach that has been followed. In

addition, for each sampling scenario three sub-

experiments were performed, using different patch

sizes.

Buildings Extraction from Historical Topographic Maps via a Deep Convolution Neural Network

489

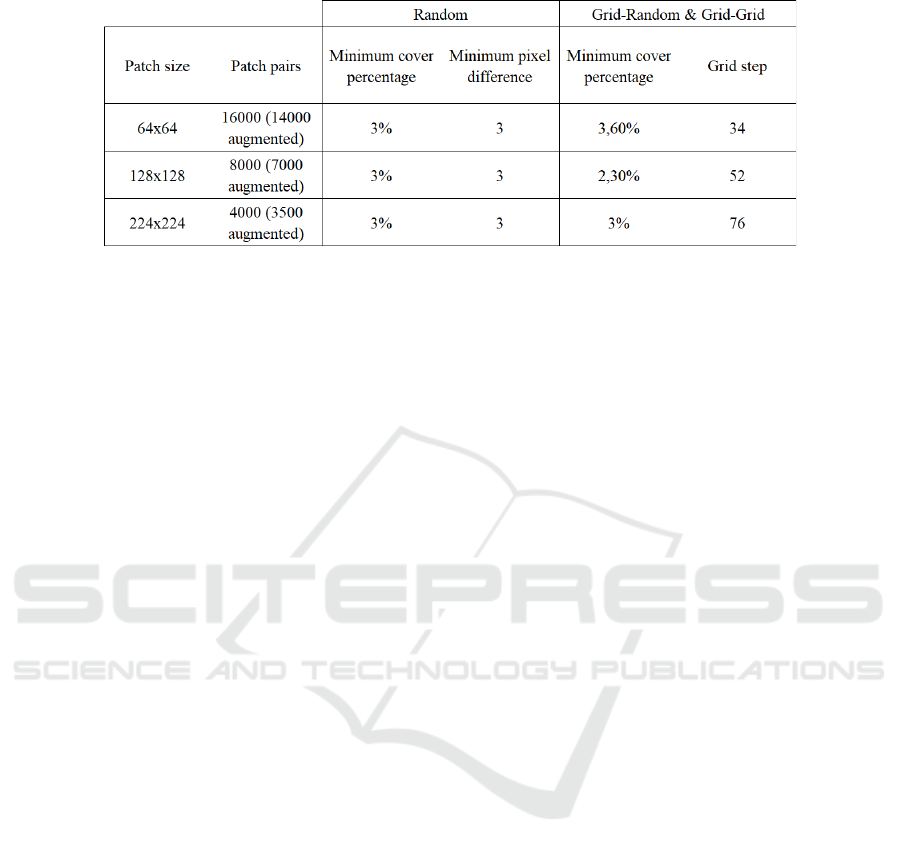
Table 1: Setup parameters used in the experiments.

Specifically, the first dataset contains 16000 input

and 16000 ground-truth patches of size 64×64 pixels

(the 2000 of them extracted from the original input

and ground-truth images, while the rest 14000 pairs

as a result of data augmentation), the second dataset

contains 8000 patches pairs of size 128×128 pixels

(accordingly, 1000 original and 7000 augmented) and

the third contains 4000 patches pairs of size 224×224

pixels (accordingly, 500 originally extracted and

3500 augmented). Table 1 summarizes the number of

patches as well as the parameter values for each

experiment dataset. Considering the DCNN, a

stochastic gradient descent approach is followed,

using Adam optimizer. The number of epochs is set

to 100, using a mini-batch of 8, with an initial learning

rate of 0.001, without learning rate scheduling.

Regarding the other network parameters, the default

values are applied as given in (Kingma and Ba, 2014).

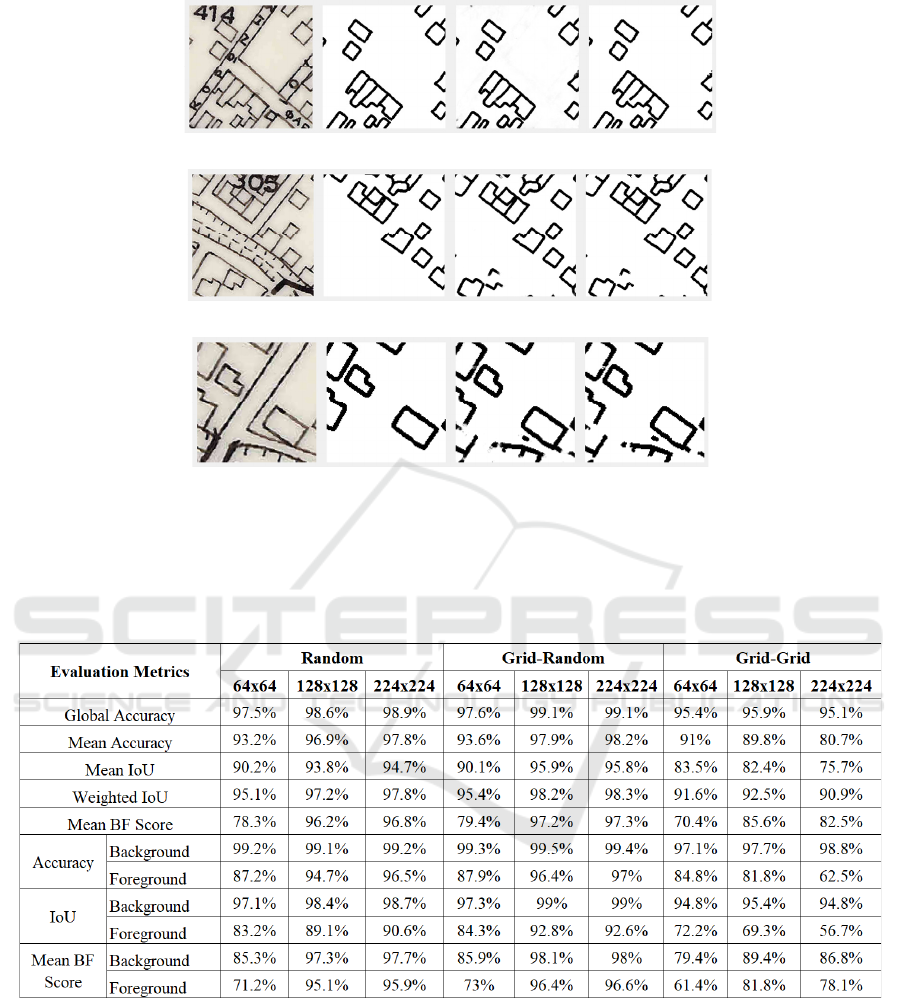
In Figure 9 three examples of networks predictions

are given. In each case, the first image is the input

patch from test data, the second image is the

corresponding ground-truth patch, the third image is

the network’s prediction and the fourth image is the

corresponding binarized predicted patch. Figure 9(a)

depicts a 224×224 “Grid-Random” sampling

example. It can be seen that the network efficiently

removed the building block number, the street lines

as well as the street names. Figure 9(b) demonstrates

a 224×224 “Random” sampling example where the

building block number is correctly removed even if it

overlaps several buildings. The graphical

representation of the riverbed is also ignored as object

of no interest. More interestingly, the buildings in the

lower left part are correctly detected by the network

even that they are missing from the ground truth.

Figure 9(c) refers to a 128×128 “Grid-Grid” sampling

example. The road lines are correctly ignored

however the network does not fully remove the river

graphics in the bottom left corner since similar

graphical content was not part of the training set.

The metrics used to evaluate the performance of

the DCNNs in the various experiments are based on a

pixel-by-pixel comparison between the ground truth

patch and the predicted binarized patch, counting the

true positives (TP), false positives (FP) and false

negatives (FN), respectively. For the ground truth

patches, as well as the predicted binarized images, the

white pixels are considered as the background class

while the black pixels denote the foreground class.

The metrics analytically are:

• Global Accuracy: The ratio of correctly

predicted pixels, regardless of class, to the

total pixels number of pixels.

• Mean Accuracy: The average accuracy of all

classes in all images, where for each class,

accuracy is the ratio of correctly classified

pixels to the total number of pixels in that

class, according to the ground truth, i.e.,

accuracy score = TP / (TP + FN).

• Mean Intersection over Union: The average IoU

score of all classes in all images, where for

each class, IoU is the ratio of correctly

classified pixels to the total number of ground

truth and predicted pixels in that class, i.e.,

IoU score = TP / (TP + FP + FN).

• Weighted Intersection over Union: The weighted

average IoU score of all classes in all images,

where for each class, weighted IoU is the

average IoU, weighted by the number of pixels

in that class.

• Mean Boundary F1 (BF) Score: The contour

matching score that indicates how well the

predicted boundary of each class aligns with

the true boundary. For the aggregate data set,

Mean BF Score is the average BF score of all

classes in all images and for each class, Mean

BF Score is the average BF score of that class

over all images.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

490

(a)

(b)

(

)

Figure 9: Visual results of the proposed method. In each row the first image is the input patch from test data, the second image

depicts the corresponding ground-truth, the third image is the network’s prediction while the fourth image corresponds to the

binarized predicted patch (a) 224×224 “Grid-Random” example (b) 224×224 “Random” example (c) 128×128 “Grid-Grid”

example.

Table 2: Evaluation metrics results for the various experiments.

The results of the above metrics for all the

experimental scenarios are summarized in Table 2.

Regarding the class metrics, namely, Accuracy, IOU

and Mean BF Score, the most representative are the

ones that refer to the foreground class (black pixels)

since it contains the geographical features of interest,

i.e. the building footprints. It can be noticed that both

“Random” and “Grid-Random” sampling cases

increase their performance according to the patch size

which however is not the case in most of the “Grid-

Grid” cases. Moreover, the “Random” and “Grid-

Random” sampling cases provide high detection

accuracy, especially in the cases of 128×128 and

224×224 patches sizes. The sampling method

adopted in these two cases feeds the DCNN with

patches from multiple areas of the original image,

therefore providing the network with multiple

representations of desired input-output pairs. In the

Buildings Extraction from Historical Topographic Maps via a Deep Convolution Neural Network

491

case of “Grid-Grid” sampling, the DCNN is not that

high since it is trained with patches that do not cover

the whole spatial range of the original image. The best

global accuracy 99.1% is achieved for the “Grid-

Random” case for both patch sizes 128×128 and

224×224.

4 CONCLUSIONS

In this work a deep learning approach is presented

that tackles the problem of extracting buildings from

historical topographic maps. For this purpose, a

DCNN based on the U-Net architecture is trained in a

deep image-to-image regression mode. Experiments

on a historical topographic map demonstrate that the

proposed method efficiently extracts the buildings

from the map even when they are densely surrounded

or even overlapped by text or other geospatial

features. Evaluation under several sampling and patch

size scenarios gives promising results in terms of

building detection accuracy, especially when large

patch sizes are involved and when training the

network is based on randomly generated patches.

ACKNOWLEDGMENTS

Article processing charges are covered by the

University of West Attica.

REFERENCES

Dornaika, F., & Hammoudi, K. (2009, May). Extracting 3D

Polyhedral Building Models from Aerial Images Using

a Featureless and Direct Approach. In MVA (pp. 378-

381).

Fischer, A., Kolbe, T. H., Lang, F., Cremers, A. B.,

Förstner, W., Plümer, L., & Steinhage, V. (1998).

Extracting buildings from aerial images using

hierarchical aggregation in 2D and 3D. Computer

Vision and Image Understanding, 72(2), 185-203.

Hecht, R., Meinel, G., & Buchroithner, M. (2015).

Automatic identification of building types based on

topographic databases–a comparison of different data

sources. International Journal of Cartography, 1(1),

18-31.

Heitzler, M., & Hurni, L. (2020). Cartographic

reconstruction of building footprints from historical

maps: A study on the Swiss Siegfried map.

Transactions in GIS, 24(2), 442-461.

Kingma, D. P., & Ba, J. (2014). Adam: A method for

stochastic optimization. arXiv preprint

arXiv:1412.6980.

Laycock, S. D., Brown, P. G., Laycock, R. G., & Day, A.

M. (2011). Aligning archive maps and extracting

footprints for analysis of historic urban environments.

Computers & Graphics, 35(2), 242-249.

LeCun, Y., Bottou, L., Bengio, Y. & Haffner, P. (1998).

Gradient-based learning applied to document

recognition. Proceedings of the IEEE. 86(11): 2278 –

2324.

Li, B. H., Hou, B. C., Yu, W. T., Lu, X. B., & Yang, C. W.

(2017). Applications of artificial intelligence in

intelligent manufacturing: a review. Frontiers of

Information Technology & Electronic Engineering,

18(1), 86-96.

Peng, J., Zhang, D., & Liu, Y. (2005). An improved snake

model for building detection from urban aerial images.

Pattern Recognition Letters, 26(5), 587-595.

Ronneberger, O., Fischer, P., & Brox, T. (2015, October).

U-net: Convolutional networks for biomedical image

segmentation. In International Conference on Medical

image computing and computer-assisted intervention

(pp. 234-241). Springer, Cham.

Suzuki, S., & Chikatsu, H. (2003). Recreating the past city

model of historical town Kawagoe from antique map.

International Archives of Photogrammetry and Remote

Sensing, 34, 5.

Uhl, J. H., Leyk, S., Chiang, Y. Y., Duan, W., & Knoblock,

C. A. (2017, July). Extracting human settlement

footprint from historical topographic map series using

context-based machine learning. In 8th International

Conference of Pattern Recognition Systems (ICPRS

2017) (pp. 1-6).

Uhl, J. H., Leyk, S., Chiang, Y. Y., Duan, W., & Knoblock,

C. A. (2019). Automated extraction of human

settlement patterns from historical topographic map

series using weakly supervised convolutional neural

networks. IEEE Access, 8, 6978-6996.

Voulodimos, A., Doulamis, N., Doulamis, A., &

Protopapadakis, E. (2018). Deep learning for computer

vision: A brief review. Computational intelligence and

neuroscience, 2018.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

492