
Monocular Estimation of Translation, Pose and 3D Shape on Detected
Objects using a Convolutional Autoencoder
Ivar Persson
a
, Martin Ahrnbom
b
and Mikael Nilsson
c
Centre for Mathematical Sciences, Lund University, Sweden
{first name.second name}@math.lth.se
Keywords:
Autoencoder, 6DoF-positioning, Traffic Surveillance, Autonomous Vehicles, 6DoF Pose Estimation.
Abstract:
This paper present a 6DoF-positioning method and shape estimation method for cars from monocular images.
We pre-learn principal components, using Principal Component Analysis (PCA), from the shape of cars and
use a learnt encoder-decoder structure in order to position the cars and create binary masks of each cam-
era instance. The proposed method is tailored towards usefulness for autonomous driving and traffic safety
surveillance. The work introduces a novel encoder-decoder framework for this purpose, thus expanding and
extending state-of-the-art models for the task. Quantitative and qualitative analysis is performed on the Apol-
loscape dataset, showing promising results, in particular regarding rotations and segmentation masks.
1 INTRODUCTION
In order to safely and reliably run autonomous cars,
or to have an automatic traffic surveillance system, it
is necessary to detect and estimate position and rota-
tion of cars, just as a human driver or operator does
on a daily basis. The functionality and superiority of
using deep neural networks rather than traditional fea-
ture based methods to detect and classify objects, such
as cars, has been shown multiple times (Krizhevsky
et al., 2012; Fang et al., 2015). Traditionally you
would need two or more cameras to gain proper depth
information through triangulation, however, in recent
times this requirement has been avoided, for example
by using depth sensors (Li et al., 2020) or by using
neural networks (Chen et al., 2016; Liu et al., 2020;
Tatarchenko et al., 2016).
In this paper we present a method to estimate posi-
tion and rotation of cars in an urban environment. We
will, from a single image create a binary mask for the
car and an estimation of the true world coordinates,
both 3D position and 3D rotation. This method will be
based on the Skinned Multi-Animal Linear (SMAL)
method, formulated and used by Zuffi et al. (Zuffi
et al., 2017).
Our contribution is to build on the work by
Liu et al. (Liu et al., 2020), where 3D bounding boxes
a
https://orcid.org/0000-0003-4958-3043
b
https://orcid.org/0000-0001-9010-7175
c
https://orcid.org/0000-0003-1712-8345
Figure 1: Intended result, of the Encoder-Decoder solution
presented in this paper. All masks are sorted by z-distance
to show the correct mask, formed from pose and shape vec-
tors, where different cars overlap.
are calculated for cars. We will in the same man-
ner detect cars, however, we will instead calculate
a per-pixel binary mask segmentation of the car, by
using keypoints and a learnt decoder. The segmen-
tation mask will be based on the SMAL method by
Zuffi et al. (Zuffi et al., 2017), where a shape model
is fitted to a pre-learnt space of principal components,
using Principal Component Analysis (PCA), from the
keypoints. These results are of interest as a camera
mounted on a car can then detect and position cars
from a single image, rather than two. Apart from an
Automated Driving context this can also be used in
Traffic Monitoring to e.g. monitor busy intersections.
The idea is that this method can be relatively easily
expanded, given training data, to cover not only cars
but also other road users, such as lorries, bicycles and
390
Persson, I., Ahrnbom, M. and Nilsson, M.
Monocular Estimation of Translation, Pose and 3D Shape on Detected Objects using a Convolutional Autoencoder.
DOI: 10.5220/0010826600003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
390-396
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

possibly pedestrians, but then maybe with some mod-
elling modifications to better cope with more non-
rigidity.
The training and validation is done with the Apol-
loscape dataset, by Song et al. (Song et al., 2019).
This dataset is an extensive dataset spanning multi-
ple problems in autonomous driving, where the car
instance part will be used in this paper. Over 4000
images for training, containing 47573 annotated cars,
and 200 images for validation, containing 2403 anno-
tated cars. Each annotated car have been annotated
with semantic keypoints, along real-world spatial co-
ordinates relative to the camera and relative euler an-
gle rotation are provided.
2 RELATED WORK
Many previous advances in the field of 3D reconstruc-
tion have been made. One of the key points of this
paper is to predict 3D translation of cars from a sin-
gle image. Earlier you would have needed specialised
sensors to get depth information or by using a stereo
camera pair, as Chen et al. (Chen et al., 2015) uses.
This technique is still useful and relevant, especially
in robotics (Grenzd
¨
orffer et al., 2020). However, with
the introduction of Deep Neural Netowks (DNNs),
single image 3D detection and fitting of 3D boxes on
the cars have been made possible (Mousavian et al.,
2017; Liu et al., 2020). Here (Mousavian et al., 2017)
uses the 2D bounding boxes from an object detec-
tor as input and creates a 3D box from this, with one
side of the bounding box denoting the front of the car.
Chabot et al. (Chabot et al., 2017) takes this idea one
step further by taking a 3D box and, with the help of
semantic keypoints, make a finer segmentation mask.
One distinction between different 6DoF-
estimation systems is whether the implementation
is end-to-end (Zou et al., 2021; Kundu et al., 2018)
or if you use high-performance object detectors to
get bounding boxes and cropped images as input
to the system (Mousavian et al., 2017). We will
use the latter and generate results similar to the
work by Mousavian et al. (Mousavian et al., 2017)
and Chabot et al. (Chabot et al., 2017), but with a
closer fit to the shape of cars. In order to achieve
this we will use robust shape models, pre-learnt
and calculated similarly to the SMAL method pre-
sented by Zuffi et al. (Zuffi et al., 2017). A similar
approach to what we do can be found in the work
by Kundu et al. (Kundu et al., 2018). The main
difference is that they use a differentiable render-and-
compare operation, while we reduce the complexity
of the solution by using a learnt decoder network.
3 METHOD
The idea behind the method is to create an average car
that can be modified to better fit different car models.
We use the detailed car models in the Apolloscape
dataset, by Song et al. (Song et al., 2019), as a basis
together with the semantically useful keypoints also
provided in the dataset. The keypoints are mapped
to each car model. With this mapping we have 66
semantic keypoints from 34 different car models.
Further on we make use of the results presented by
Zuffi et al. (Zuffi et al., 2017) who use average shape
of four-legged animals. Here, we do not need to think
about bending of joints as the cars are rigid bodies.
3.1 SMAL
Zuffi et al. presents the SMAL model in (Zuffi et al.,
2017) where they describe a function to estimate
shapes and poses of animals. Animals’ flexibility is
also addressed in this model, however, since cars are
inflexible we can simplify the equations to
C
i,p
= m + Dθ
i
. (1)
Here m is the template, or mean, of a car, θ
i
is the
vector of parameters describing car i and D is a learnt
PCA-space for all available car models. This equals
C
i,p
, which is car i parameterized. Both the mean, m
and the PCA-space D will be discussed further in 3.2.
Zuffi et al. presented their model as:
p
i
= t
i
+ m
p,i
+ B
s,i
s
i
+ B
p,i
d
i
, (2)
where p
i
is part i of the animal. t
i
is a template, m
p,i
is
the average pose displacements, B
s,i
is a matrix with
columns containing basis of shape displacements and
B
p,i
is a matrix with the basis of pose displacements.
This equation is formulated for dividing the ani-
mal in several pieces where each piece can be bent
and moved independently (but still being connected
with each other). We, however, have rigid cars and
we do not divide the car into several pieces, but keep
it as one.
Therefore, we can ignore the terms B
p,i
and m
p,i
,
as they will be zero for rigid objects. By simplifying
notation as t
i
= m, B
s,i
= D and also renaming s
i
to θ
i
,
we have then simplified Equation 2 into 1.
The PCA-space, D, in Equation 1, allows us to es-
timate shapes of cars robustly while only having to es-
timate the elements of θ
i
in the Encoder. The SMAL
method is then a matter of minimising the error
E(θ
i
) = (C
i
−C
i,p
)
2
, (3)
Monocular Estimation of Translation, Pose and 3D Shape on Detected Objects using a Convolutional Autoencoder
391
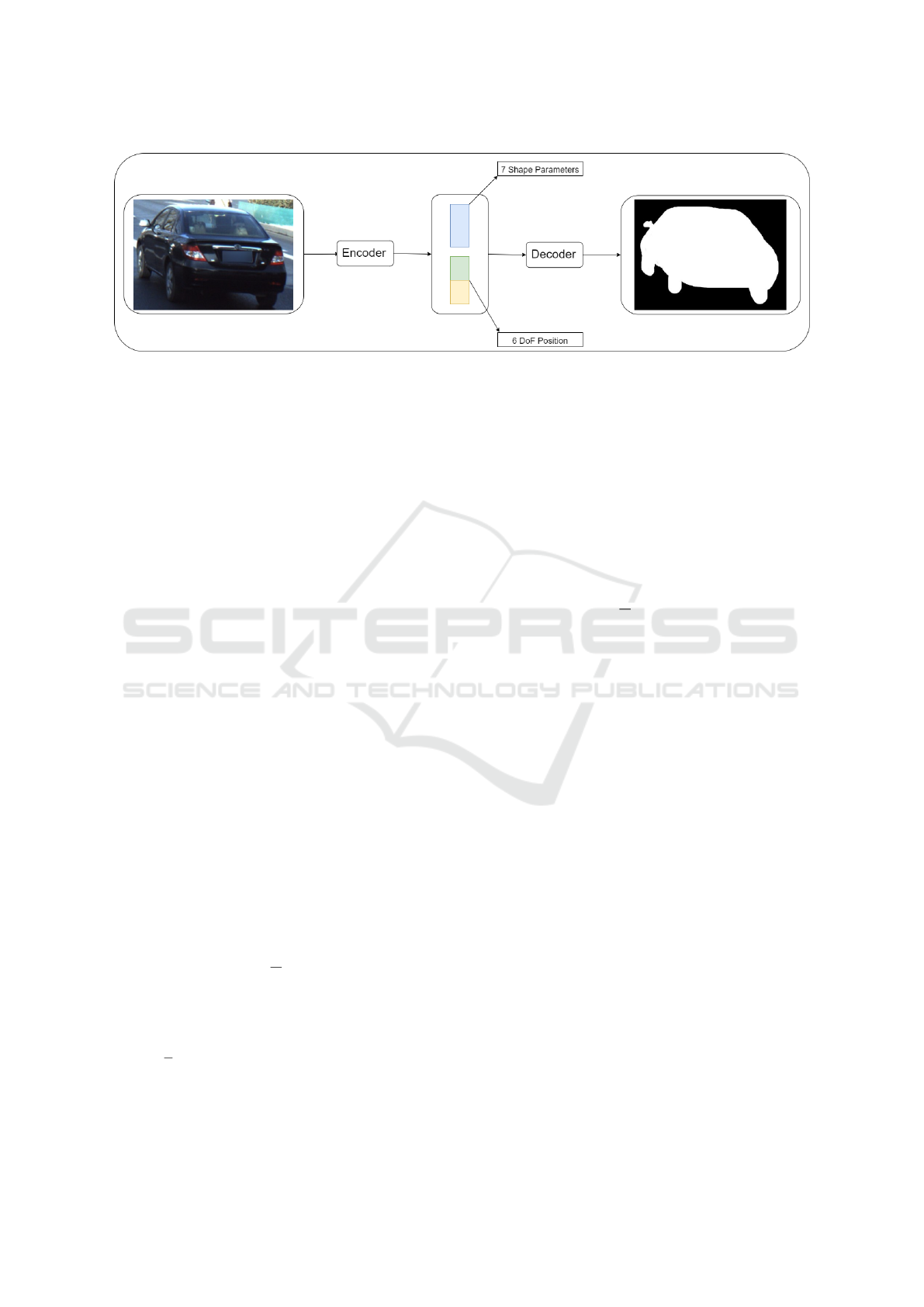
Figure 2: Overview of the workflow of the system. Cars are cropped out of the images, after detections by Detectron2 (Wu
et al., 2019). The encoder get information about the pixel-location of the crop and then reduces the crop information and the
cropped car to 14 elements. Six elements describe the translation and rotation of the car, while the remaining seven are the
shape parameters θ
i
in equation 6. The (x, y, z) distance of the car from the camera can be obtained here before the encoded
information is fed into the decoder network. The decoder then restores the position of the crop and creates a binary mask of
the car.
where C
i
is the true positions of the keypoints of car
i and C
i,p
is the estimations from Equation 1, depen-
dent on θ
i
. As mentioned in (Zuffi et al., 2017), the
SMAL model is robust enough that it can generalise
to shapes, in their context of four-footed animals, un-
seen before in training. This method should there-
fore be able to generalise to car models unseen before,
which makes this method desirable since it would be
impossible to model all car designs in the world.
3.2 Generalised Procrustes Analysis
The template shape from the description of SMAL
is calculated using Generalised Procrustes Analysis.
This method allows us to compute an average shape
that can be altered with additional low dimension in-
formation. We follow the description presented by
Stegmann and Gomez (Stegmann and Gomez, 2002).
We choose a shape as the mean shape and align all
other shapes to this, e.g. we choose x
0
, where x
i
is the
vector of car i. Normally we would need to translate,
rotate and scale all feature points, however, since all
cars, created from the data by Song et al. (Song et al.,
2019), are rotated equally and of the same size, only a
slight translation is needed. To translate we calculate
the mean
m =
1
N
N
∑
i=0
x
i
, (4)
and translate the cars x
0
i
= x
i
− m. We have N as
the number of cars. We calculate the average of all
points for all cars, thus creating a new template shape,
x
t
(k) =
1
N
∑
N
i=0
x
i
(k), where x
t
(t) is the template shape
at keypoint k. We continue to align the shapes x
i
to the template shape x
t
and calculate a new mean
m. When m converges we have found our template
shape x
t
. Typically this only takes a couple of itera-
tions (Stegmann and Gomez, 2002).
Next, we calculate a difference between all shapes
and the template dx
i
= x
i
− x
t
. By calculating the
outer product of dx
i
with it self we can calculate a
correlation matrix
D =
1
N
N
∑
i=0
dx
T
i
dx
i
. (5)
We calculate the eigenvalues and corresponding
eigenvectors to D and analyse the magnitudes of the
eigenvalues. We take the corresponding eigenvectors
to the greatest eigenvalues and form a new matrix
D
L
, where L is the number of eigenvectors used. We
can then approximate each car by x
i
= x
t
+ D
L
θ
i
, for
some θ
i
unique to each car and using all eigenvec-
tors of D
L
. By reducing the number of eigenvectors
we can simplify our model, making it more robust to
noise in the eigenvectors and also reduce the amount
of data stored. The number of eigenvectors was exper-
imentally decided on upon observing the eigenvalues
and finding that a suitable cutoff seemed to be using
seven eigenvectors (L = 7). These seven eigenvec-
tors, stacked column-wise, are denoted by the matrix
D
7
. The best approximation to each car is then given
by
θ
i
= D
7
dx
i
, (6)
where each θ
i
then can be used in Equation 1. This
method can be seen as a special case of Principal
Component Analysis (PCA).
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
392
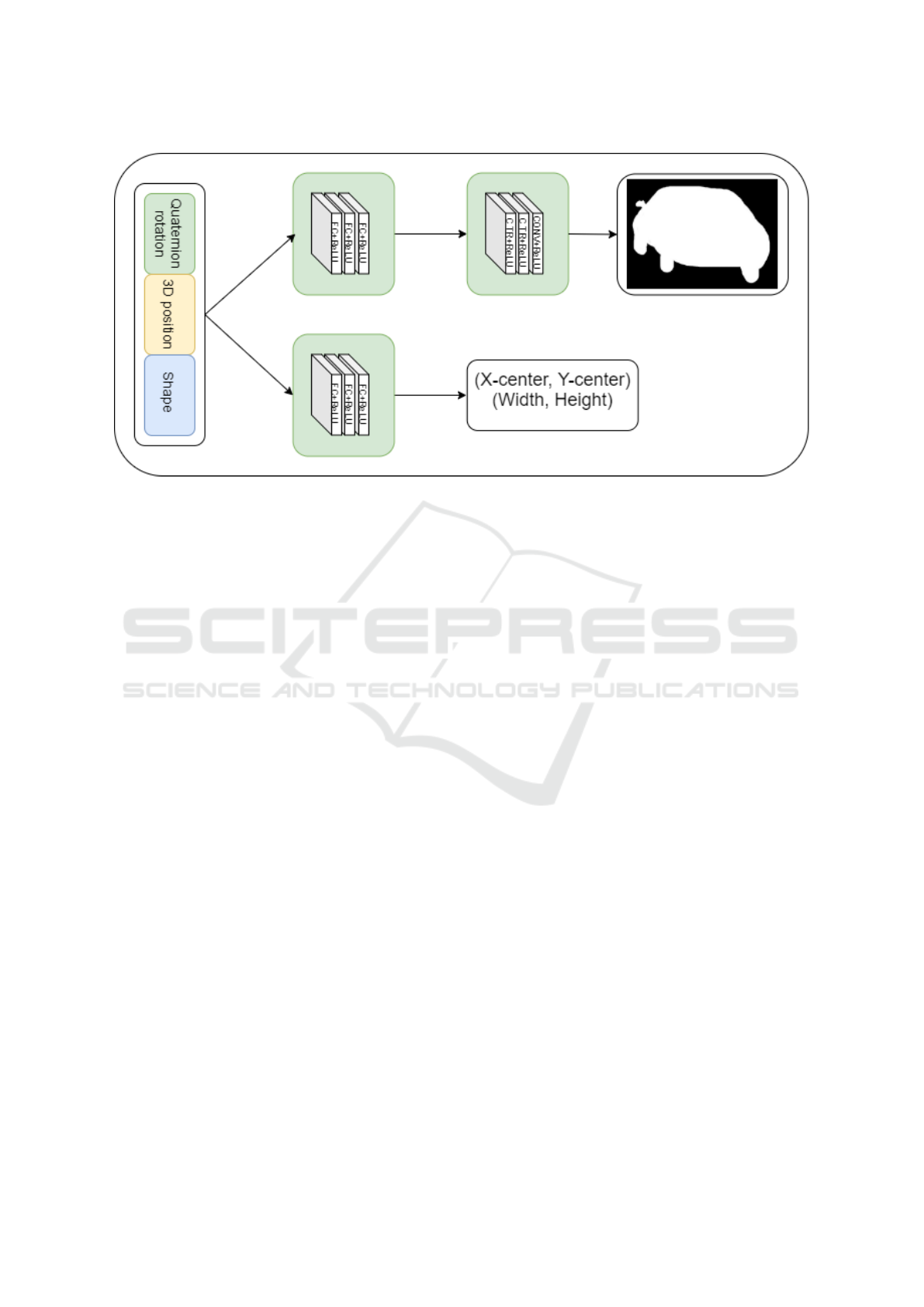
Figure 3: Workflow of the decoder network. The input is a 14 element pose-and-shape vector, consisting of seven shape
parameters and six pose parameters. The network is divided in two parts, where the mask network creates a mask, given the
pose rotation of the car, while the crop network creates pixel values (x
c
, y
c
) of the centre of the crop as well as height and
width of the crop. The exact structure of the mask and crop part of the network can be seen in Table 1). These two pixel pairs
are then used to insert the mask in the 2d-space of the image.
4 AUTOENCODER
The structure to solve this problem is by using a
encoder-decoder network and using a similar training
regime as (Tan et al., 2017) use. We use the encoder
to find pose and shape parameters, and as a second
step use a decoder network to create binary masks of
all cars present.
The seven element shape vector, θ
i
, is calculated
from equation 6 and concatenated with the pose infor-
mation, four coordinates of rotation (quartenions) and
three coordinates of translation, to form a 14 element
vector. This vector is the output from the encoder net-
work and also the input to the decoder network.
4.1 Pre-processing
All data points were normalised to a range suitable for
their purpose. The centre point of the crop informa-
tion as well as the width and height were altered to be
in the range [−1, 1], while the binary masks were al-
ready binary. The 3D-position in the encoded vector
was also normalised with the largest (absolute) value
in the dataset in order to fit the output of a tanh acti-
vation function.
4.2 Encoder
The encoder takes input in the form of cropped RGB-
images, reshaped to (256, 256, 3). These crops are
detected using Detectron2 (Wu et al., 2019), before
being used as inputs to the encoder. Along the im-
age there is also information regarding what parts in
the image the detection was made. This is fed as a
vector of six integers describing (x, y) center point,
width and height of the crop but also the area and as-
pect ratio of the crop. The output is a vector of 14
elements of which seven are the shape-parameters of
the car, four are the quaternion rotation and three are
the translation. The network structure is described
in Figure 4. The base of the network is a pre-learnt
ResNet50 feeding fully connected layers.
4.2.1 Loss Functions
The loss function is a standard mean squared error for
the shape and the 3D-position has a mean absolute
error. The quaternion rotation vector is normalised
before a scalar product and arccos is the loss for the
rotation. We get
L
rot
= acos(< Q
est
, Q
gt
>), (7)
where L
rot
is the loss in degrees and Q
est
and Q
gt
are
the estimated quaternion and the ground truth quater-
nion. Since |Q
est
| = |Q
gt
| = 1 we get the arc cosine of
Monocular Estimation of Translation, Pose and 3D Shape on Detected Objects using a Convolutional Autoencoder
393
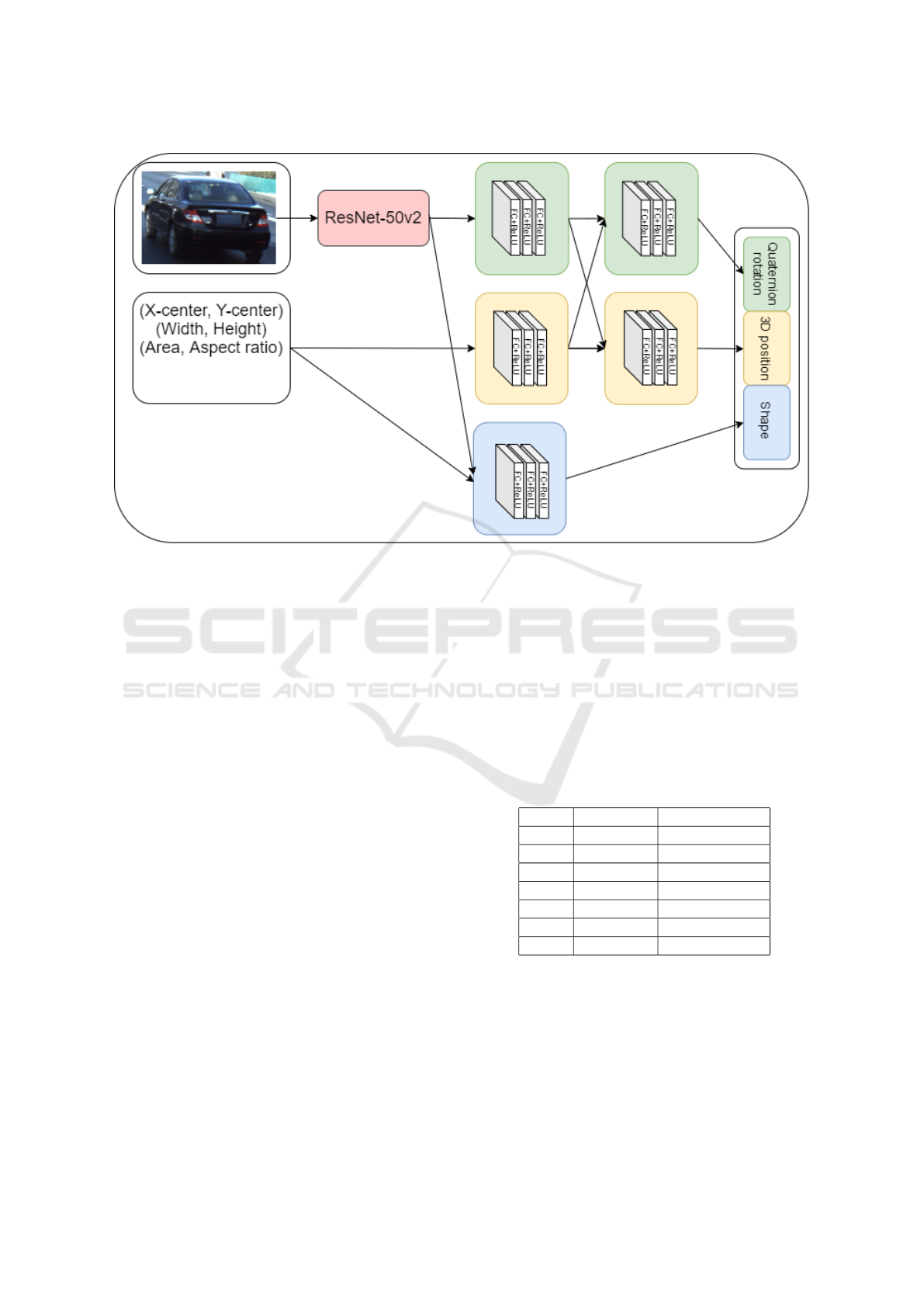
Figure 4: Workflow of the encoder network. The input is the cropped image of the car and crop information values: (x, y)
centre points, width, height and also area and aspect ratio. The image is fed through a ResNet-50 pre-trained network, where
the head is removed. The output from the ResNet-50 network as well as the crop information is fed through a series of fully
connected layers as shown in the image, the exact structure is described in 4.2.2.
the cosine of the angle between the two vectors, i.e.
the angle between the two quartenion vectors. This
is the same metric used in the original Apolloscape
challenge.
4.2.2 Structure
Each coloured square in Figure 4 is comprised of
three fully-connected layers, all with 512 units, with
Rectified Linear Unit (ReLU) activation and subse-
quent dropout of 20%. The idea is that both the
quaternion rotation and the 3D position needs the in-
formation from both the cropped image as well as the
crop information and should therefore share this in-
formation.
4.3 Decoder
The decoder network uses the output from the en-
coder, the 14 element vector, as input. Using a similar
network structure as (Tan et al., 2017), we calculate a
binary mask of the car given the encoded values, in-
cluding the shape parameters. We do, however, in par-
allel also calculate the position and size of where the
binary mask should be located in the recreated image.
This can be seen in Figure 3, where the layers of mask
calculation and the layers of the crop positioning are
done in parallel without any shared weights. These
two tasks were considered such that there would be no
benefits in combining layers such as is done in the en-
coder. The decoder network uses the calculated crop
information to reshape and place the calculated mask
in an image with the same dimensions as the original
image that was fed into Detectron2. The entire struc-
ture in detail is shown in Table 1 and 2.
Table 1: Structure of the Decoder network for the mask.
This corresponds to the top row in Figure 3.
Layer Function Size
Input 14
1 Dense 256
2 Dense 500
3 Dense 810
- Reshape 9 × 9 × 10
4 Conv2DTr 63 × 63 × 384
5 Conv2D 59 × 59 × 1
5 RESULTS
The evaluation of the results can be split up in the en-
tire Encoder-Decoder structure as well as the Encoder
and Decoder separately. For this paper we only con-
sider the Encoder and the Decoder separately. The
Encoder by itself is interesting since we can obtain
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
394

Table 2: Structure of the Decoder network for the crop in-
formation, i.e. the second row in Figure 3. The output of
four values are the (x, y) centre points and also the width
and height of the crop.
Layer Function Size
Input 14
1 Dense 512
2 Dense 256
3 Dense 4
the real-world position and rotation of the detected
cars. By analysing the Decoder by itself will yield
interesting data on how well the decoder can trans-
form real-world positions to pixel coordinates in the
images. Exploring the full Encoder-Decoder structure
on data with only segmentation and no 3D annotation,
is considered a future work direction.
The performance of the Decoder for each sample
is done by the Intersection over Union (IoU), calcu-
lated as
IoU
i
=
M
gt
i
∩ M
e
i
M
gt
i
∪ M
e
i
, (8)
where M
gt
i
is the ground truth mask of sample i and
M
e
i
is the estimated mask from sample i, giving a
score between 0 and 1 for each sample in the dataset.
A mean IoU,
mIoU =
1
N
∑
i
IoU
i
, (9)
over the entire dataset is presented as the average
score in Table 4. The entire Encoder-Decoder struc-
ture can then also be evaluated using the same met-
ric. The resulting 3D position and quaternion rota-
tion from the Encoder can be evaluated with the same
metrics used in the original Apolloscape competition
(Apolloscape, 2021). The translation error is a sim-
ple L2-norm and the rotation error is the same as the
loss function, used in the Encoder training and pre-
sented in Equation 7. The results are presented in
Table 3 where the percentage of cars with an error
smaller than a threshold are calculated. Some results
are visualised in Figure 5.
In Table 4 we present the results from the Decoder
in a manner very similar to what they did in the Apol-
loscape competition (Apolloscape, 2021), however it
can not be compared directly as we only examine the
shape conforming ability in the current view while in
the Apolloscape competition multiple views were ex-
amined.
Figure 5: Three randomly picked images from the valida-
tion set and their binary masks as overlay. Note that the im-
ages are cropped in order to display the results more clearly.
Best viewed in colour.
6 CONCLUSIONS
In this work a novel encoder-decoder framework is in-
troduced, with the focus on estimating translation, ro-
tation and shape of cars from a monocular view. The
aim is to use this network in new situations with car
models unseen in training. We have only worked with
cars in this paper, but the method could be generalised
for lorries, motorcycles, bicycles and other rigid ob-
jects directly, while some additional shape modelling
of non-rigid objects are likely warranted. Results on
the Apolloscape dataset highlight the current perfor-
mance of the system. Evaluation shows promising
performance in particular regarding the rotation and
segmentation masks.
Monocular Estimation of Translation, Pose and 3D Shape on Detected Objects using a Convolutional Autoencoder
395

Table 3: Results on the estimation of rotation and translation. Each estimation was evaluated and compared against a set of
thresholds. Results given on the validation dataset from Apolloscape.
Total: 2245 images in validation set
Rotation - 18.0
o
average error
Error (degrees) 5
o
10
o
15
o
20
o
25
o
30
o
35
o
40
o
45
o
50
o
% of cars 73.3 80.7 82.8 85.5 86.2 86.1 86.7 87.0 87.2 87.5
Translation - 4.8m average error
Error (meters) 0.1 0.4 0.7 1.0 1.3 1.6 1.9 2.2 2.5 2.8
% of cars 0.09 2.6 8.0 14.4 21.7 27.1 33.2 38.4 43.5 48.0
Table 4: Results on the quality of the binary mask, where the score of each mask was compared with a set of thresholds.
Results given on the validation dataset from Apolloscape.
Total: 2403 images in validation set
Average IoU (Decoder) - 88%
IoU 0.95 0.9 0.85 0.8 0.75 0.7 0.65 0.60 0.55 0.5
% of cars 14.9 57.8 80.8 90.4 94.3 96.4 97.8 98.7 99.3 99.5
REFERENCES
Apolloscape (2021). Apolloscape, car instance - metric for-
mula. http://apolloscape.auto/car instance.html.
Chabot, F., Chaouch, M., Rabarisoa, J., Teuli
`
ere, C., and
Chateau, T. (2017). Deep manta: A coarse-to-fine
many-task network for joint 2d and 3d vehicle analy-
sis from monocular image. In 2017 IEEE Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 1827–1836.
Chen, X., Kundu, K., Zhang, Z., Ma, H., Fidler, S., and
Urtasun, R. (2016). Monocular 3d object detection
for autonomous driving. In 2016 IEEE Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 2147–2156.
Chen, X., Kundu, K., Zhu, Y., Berneshawi, A. G., Ma, H.,
Fidler, S., and Urtasun, R. (2015). 3d object propos-
als for accurate object class detection. In Cortes, C.,
Lawrence, N., Lee, D., Sugiyama, M., and Garnett,
R., editors, Advances in Neural Information Process-
ing Systems, volume 28, pages 424–432.
Fang, H., Gupta, S., Iandola, F., Srivastava, R., Deng, L.,
Dollar, P., Gao, J., He, X., Mitchell, M., Platt, J., Zit-
nick, L., and Zweig, G. (2015). From captions to vi-
sual concepts and back. In The proceedings of CVPR.
IEEE - Institute of Electrical and Electronics Engi-
neers.
Grenzd
¨
orffer, T., G
¨
unther, M., and Hertzberg, J. (2020).
Ycb-m: A multi-camera rgb-d dataset for object
recognition and 6dof pose estimation. In 2020 IEEE
International Conference on Robotics and Automation
(ICRA), pages 3650–3656.
Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). Im-
agenet classification with deep convolutional neural
networks. In NIPS’12: Proceedings of the 25th Inter-
national Conference on Neural Information Process-
ing Systems, pages 1097–1105.
Kundu, A., Li, Y., and Rehg, J. M. (2018). 3d-rcnn:
Instance-level 3d object reconstruction via render-
and-compare. In 2018 IEEE/CVF Conference on
Computer Vision and Pattern Recognition, pages
3559–3568.
Li, Z., Yu, T., Pan, C., Zheng, Z., and Liu, Y. (2020). Robust
3d self-portraits in seconds. In 2020 IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 1344–1353.
Liu, Z., Wu, Z., and T
´
oth, R. (2020). Smoke: Single-stage
monocular 3d object detection via keypoint estima-
tion. In 2020 IEEE/CVF Conference on Computer
Vision and Pattern Recognition Workshops (CVPRW),
pages 4289–4298.
Mousavian, A., Anguelov, D., Flynn, J., and Ko
ˇ
seck
´
a, J.
(2017). 3d bounding box estimation using deep learn-
ing and geometry. In 2017 IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
5632–5640.
Song, X., Wang, P., Zhou, D., Zhu, R., Guan, C., Dai, Y.,
Su, H., Li, H., and Yang, R. (2019). Apollocar3d:
A large 3d car instance understanding benchmark for
autonomous driving. In 2019 IEEE/CVF Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 5447–5457.
Stegmann, M. B. and Gomez, D. D. (2002). A brief intro-
duction to statistical shape analysis.
Tan, V., Budvytis, I., and Cipolla, R. (2017). Indirect deep
structured learning for 3d human body shape and pose
prediction. In 2017 British Machine Vision Confer-
ence (BMVC).
Tatarchenko, M., Dosovitskiy, A., and Brox, T. (2016).
Multi-view 3d models from single images with a con-
volutional network. In European Conference on Com-
puter Vision, ECCV 2016, pages 322–337.
Wu, Y., Kirillov, A., Massa, F., Lo, W.-Y.,
and Girshick, R. (2019). Detectron2.
https://github.com/facebookresearch/detectron2.
Zou, W., Wu, D., Tian, S., Xiang, C., Li, X., and Zhang, L.
(2021). End-to-end 6dof pose estimation from monoc-
ular rgb images. IEEE Transactions on Consumer
Electronics, 67(1):87–96.
Zuffi, S., Kanazawa, A., Jacobs, D. W., and Black, M. J.
(2017). 3d menagerie: Modeling the 3d shape and
pose of animals. In 2017 IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
5524–5532.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
396
