
Iris Segmentation based on an Optimized U-Net
Sabry Abdalla M.
1 a
, Lubos Omelina
1,2 b
Jan Cornelis
1 c
and Bart Jansen
1,2 d
1
Department of Electronics and Informatics, Vrije Universiteit Brussel, Pleinlaan 2 1050 Brussels, Belgium
2
imec, Kapeldreef 75, B-3001 Leuven, Belgium
Keywords:
Iris Segmentation, Deep Learning, CNN, U-Net, Parameter Optimization.
Abstract:
Segmenting images of the human eye is a critical step in several tasks like iris recognition, eye tracking or
pupil tracking. There are a lot of well-established hand-crafted methods that have been used in commercial
practice. However, with the advances in deep learning, several deep network approaches outperform the hand-
crafted methods. Many of the approaches adapt the U-Net architecture for the segmentation task. In this paper
we propose some simple and effective new modifications of U-Net, e.g. the increase in size of convolutional
kernels, which can improve the segmentation results compared to the original U-Net design. Using these
modifications, we show that we can reach state-of-the-art performance using less model parameters. We
describe our motivation for the changes in the architecture, inspired mostly by the hand-crafted methods and
basic image processing principles and finally we show that our optimized model slightly outperforms the
original U-Net and the other state-of-the-art models.
1 INTRODUCTION
The iris is a part of the human body that does not
change substantially its appearance throughout a per-
son’s life unless it is damaged by an external force.
Iris patterns are genetically unique, identical twins
have different iris patterns, and even one person’s
eye patterns are different from each other (Daugman,
2009). These characteristics make iris recognition an
interesting topic for studies, and in fact it is largely
present in biometric and medical studies, e.g. in bio-
metric passports. Although the iris features have been
proven unique, the segmentation of the iris region
from the input image remains a challenging prob-
lem. We can split the segmentation approaches into
convolutional and non-convolutional methods. Tra-
ditionally, the segmentation has been solved using
non-convolutional techniques and considerable per-
formance has already been achieved on numerous
datasets (Shah and Ross, 2009). However, convo-
lutional endeavors using deep networks have taken
place recently since they could improve the state-
of-the-art more robustly than the non-convolutional
methods. Hence, in this paper we focus on impro-
a
https://orcid.org/0000-0001-8815-9697
b
https://orcid.org/0000-0002-2500-5217
c
https://orcid.org/0000-0002-1180-1968
d
https://orcid.org/0000-0001-8042-6834
ving the recent popular convolutional methods for ac-
curate iris segmentation. Popular non-convolutional
methods are contour-based and texture-based meth-
ods. The contour-based methods are based on integro-
differential operators, and Hough transforms. The
principle of integro-differential algorithms is based on
searching for the largest difference of intensity over a
parameter space, which normally corresponds to the
pupil and iris boundaries. Methods based on Hough
transform try to find the optimal circle (or possibly
ellipse) parameters by exploring binary edge maps.
Performance of these methods is highly dependent on
the image quality, clear contours and the boundary
contrast. However, in normal conditions, limbic or
pupillary boundaries in the images are often of low-
contrast, or may have non-circular shape. In addition,
the occlusions and specular reflections may introduce
further contrast artifacts in the images. Plenty of im-
provements were achieved, such as: occlusion detec-
tion, circle model improvement, deformation correc-
tion, noise reduction, boundary fitting and many other
methods to compensate for non-idealities in the im-
age. Nevertheless, due to their global and generic
approach to segmentation, the performance of these
methods can be undermined by the above mentioned
specific artifacts, occurring in human eye images.
Even in some cases, they may result in total failure
of the system (Tian et al., 2004).
176
M., S., Omelina, L., Cornelis, J. and Jansen, B.
Iris Segmentation based on an Optimized U-Net.
DOI: 10.5220/0010825800003123
In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 4: BIOSIGNALS, pages 176-183
ISBN: 978-989-758-552-4; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The texture-based methods exploit the individual
pixel’s visual aspects and their neighbourhood infor-
mation, such as intensity, color, and their local pat-
terns to classify the iris pixels separately from the rest
of the image. The most promising methods in this cat-
egory use some commonly known pixel-wise image
classifiers such as: support vector machines (SVMs),
Neural networks, and Gabor filters to separate iris pix-
els from the rest of the image pixels. In spite of the
efforts to improve the performance of this group of
algorithms, these methods also suffer from the same
type of problems, e.g. diffusion, reflection, and oc-
clusions (Heikkila and Pietikainen, 2006).
The convolutional methods which are nowadays
incorporated into the convolutional neural networks
(CNN), have lately been used widely to tackle the
segmentation problem. There have been many CNN-
based methods proposed, and most of them relate to
fully convolutional networks (FCN).
In this paper we will contribute to the iris seg-
mentation problem by optimizing the best performing
convolutional solution, found in our analysis of the
related work. Semantic segmentation will be used be-
cause of the nature of the considered image patches,
containing the picture of one single eye. After hav-
ing identified some baseline architectures in literature
for our work in Section 2, we address the following
problems in the remainder of the paper:
• The performance improvement of the convolu-
tional approach for iris segmentation.
• The reduction of the number of internal parame-
ters of the model without sacrificing segmentation
quality.
• Optimizing the convolutional kernel sizes based
on lessons learned from handcrafted convolutions.
• Increasing/maintaining the generalization proper-
ties for the selected data sets, based on parameter
reduction.
• Comparison with some state-of-the-art models.
The objective of this paper is to reach or to sur-
pass the state of the art in the convolutional iris seg-
mentation field in order to establish a good baseline
for other iris-based applications.
The iris segmentation is a semantic segmentation
problem, which could be defined as a pixel wise su-
pervised learning binary classification problem. In
Figure 1, an example illustrates semantic segmenta-
tion on some CASIA dataset images (CAS, 2004).
The structure of the paper is as follows. In sec-
tion 2, we describe and qualitatively compare dif-
ferent convolutional approaches for iris segmentation
and select U-Net as the baseline for our own architec-
tural design and parameter optimization. In section 3
Figure 1: Iris semantic segmentation (Lozej et al., 2018).
we define our own model and its parameters. Section
4 contains the experimental results, Section 5 contains
a discussion of the results and Section 6 summarizes
the conclusions.
2 RELATED WORK
Lately, the iris segmentation problem has been tack-
led using convolutional solutions due to the high per-
formance and accuracy of the convolutional neural
networks - CNNs. Plenty of papers and research exist.
We selected some of the most relevant ones reflecting
the state of the art in the field.
Sclera Segmentation Benchmarking Competition-
SSBC 2020 (Vitek et al., 2020) is a competition
and a group benchmarking effort held in conjunction
with the International Joint Conference on Biometrics
2020 focusing on the problem of sclera segmentation.
Results from this competition clearly highlight poten-
tial of the U-Net architecture and its derivates.
In the work of (Bazrafkan et al., 2018), the models
are fully convolutional networks (FCN) (Long et al.,
2015) with different depths, kernel sizes - each de-
signed to extract different levels of details - and lack-
ing pooling. The proposed network is evaluated on
four databases - Bath800, CASIA1000, UBIRIS, and
MobBio.The highest F1-score has been achieved on
CASIA1000 dataset with 97.5% .
Another paper tackles the problem with a similar
technique (Jalilian and Uhl, 2017). A fully convolu-
tional encoder-decoder network (FCEDN) represents
a core segmentation engine for pixel-wise semantic
segmentation. The core segmentation engine includes
a 44-layered encoder network, and the correspond-
ing decoder network. The highest F1-score has been
achieved in this paper by Bayesian-Basic FCN net-
work with 89.85%.
In (Lozej et al., 2018), the original U-Net is the
only model which has been used and the used dataset
is CASIA1000. The evaluation metric is mean av-
erage precision which is a popular evaluation met-
ric in semantic segmentation. The depth represents
the number of the corresponding concatenated layers.
The highest Average-Precision has been achieved on
Iris Segmentation based on an Optimized U-Net
177
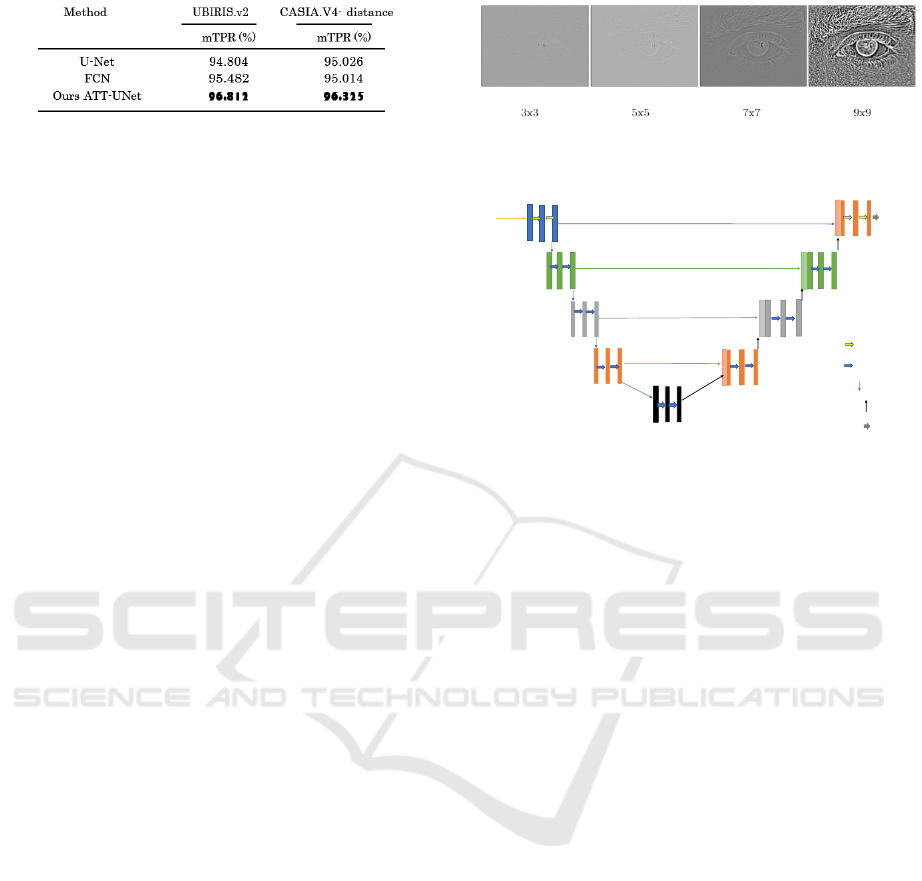
Figure 2: mAP evaluation metric (Lian et al., 2018).
the UNet model and CASIA1000 dataset with 5 layers
depth and 0.70 threshold with 94.8%.
In (Lian et al., 2018), the used models are FCN
and U-Net, but in addition they introduced some mod-
ification to the U-Net and called it Att-UNet (At-
tention Guided U-Net), and the used datasets are
UBIRISv2 and CASIAv4-distance. The main idea is
to add an attention mask generation step to estimate
the potential area where the iris is most likely to ap-
pear. They used a bounding box regression module
to estimate the coordinates. This regression step is
used to guide the final segmentation, which forces the
model to focus on a specific region. The used eval-
uation metric in this work is also Average-Precision
(mTPR) - see Figure 2. The modification they did
on the original U-Net yields better performance than
FCN and the original U-Net. The highest Average-
Precision has been achieved on the ATT-UNet model
and UBIRISv2 dataset with 96.812%.
3 METHOD
In this work, based on the papers mentioned in sec-
tion 2, we propose a modified version of U-Net in
which we adopt intuition from the image processing
domain.
3.1 Motivation
As it has been demonstrated in (Le and Kayal, 2020;
Brachmann and Redies, 2016), the early layers of
convolutional networks perform simple tasks, mainly
edge detection. However, empirically, from our expe-
rience with handcrafted image processing operators,
we can demonstrate that edge detectors with kernel
size 3x3 do not perform well on this task. Fig. 3
shows results from the Laplace operator, frequently
used for edge detection, applied on an iris image. As
we can observe, smaller kernels have weaker response
mainly on the outer boundary of the iris. Fig. 3 sug-
gests that it is useless to start with kernels that are
smaller than 7x7 in size.
Figure 3: Responses of Laplace operator with different sizes
of convolutional kernels.
Input
480X480X3
16 16
C1
P1
32
32
U8= U8 + C2
C8
32 32
input
P2
C7
64
64
U7= U7 + C3
C3
C2
64
64
128
128
128
128
U6= U6 + C4
P3
C4
C6
P4
256
256
C5
16
16
C9
1
Final
Output
Padding = Same.
Conv
7X7 filter size.
Conv 5X5 filter size.
Maxpool 2x2 with stride = 2
Upsample 2x2
Final conv 1x1
MDF-U-Net
U9= U9 + C2
Figure 4: The proposed model (MoDiFied U-Net:
MDF-U-Net) architecture.
3.2 Proposed Model
The proposed modifications are two-fold, namely to
increase the size of the convolutional kernels as ex-
plained in Figure 4, and to reduce the number of fil-
ters for each layer to 1/4 of the number of filters in the
original network.
The feature extraction part (the contracting path)
is a typical convolutional network. The first layer ap-
plies 16 convolutional kernels with size 7X7 to detect
the edges, followed by a 2X2 max-pooling layer with
stride 2 to downsample feature maps and hence sum-
marizing the presence of features in the iris images.
The same technique has been applied to the rest of
the contracting path but with 5x5 kernels as shown
in Figure 4. The expansive path combines the fea-
ture and spatial information through a sequence of up-
convolutions then concatenates it with high-resolution
features from the contracting path. The upsampling
is 2 × 2, and the ReLU activation function is used in
each convolutional layer, while at the output the sig-
moid activation function is used. The used cost func-
tion is binary cross-entropy since we have to solve a
pixel wise binary classification problem. The modi-
fied U-Net has a total of 5,079,409 trainable param-
eters, while the original U-Net has 31,032,837 train-
able parameters.
3.3 Datasets and Preprocessing
In this paper, we used 2 datasets, CSIP and UBIRIS-
v2. The CSIP database (Santos et al., 2015) contains
BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing
178

images acquired with four different mobile devices:
Sony Ericsson Xperia Arc S (rear 3,264 × 2,448 pix-
els), iPhone 4 (front 640 × 480 pixels, rear 2,592 ×
1,936 pixels), THL W200 (front 2,592 × 1,936 pix-
els, rear 3,264 × 2,448 pixels), and Huawei U8510
(front 640 × 480 pixels, rear 2,048 × 1,536 pixels).
The database contains 2,004 images from 50 sub-
jects and for each image, a binary iris segmentation
mask is provided. These masks were automatically
obtained using a state-of-the-art iris segmentation ap-
proach particularly suitable for uncontrolled acquisi-
tion conditions, which has been corroborated by the
winning contribution at the Noisy Iris Challenge Eval-
uation (Proença and Alexandre, 2007).
The UBIRIS.v2 dataset (Proenca et al., 2010) con-
tains 11,102 iris images from 261 subjects with 10 im-
ages for each subject. The images were captured un-
der unconstrained conditions (at-a-distance, on-the-
move and in the visible spectrum), with realistic noise
factors. The database does not contain the segmen-
tation masks, however segmentation masks for 2250
images are available through the work of (Hofbauer
et al., 2014a). In this paper we only used 2250 images
for which the masks were available. The dimensions
of the UBIRIS.v2 images are unified to 400x300 pix-
els, all containing 3 color channels as captured by the
camera.
The primary goal of the preprocessing of the im-
ages is to obtain iris images without downsampling.
After detailed inspection on CSIP, we observed that
all irises (even those in the highest resolution images)
have iris diameters smaller than 480 pixels. Hence,
the 2004 input image patches to our network, obtained
by cropping, have 480x480 pixels with three channels
(RGB), as shown in Figure 5
Figure 5: 480x480 eye-cropping example (an example from
the CSIP dataset).
For UBIRIS.v2 dataset, the original images and
masks are 400x300 pixels. There is a need to extend
the dimensions to 480x480 pixels. The solution as it
appears in Figure 6 is the conversion of the 400x300
image to a 480x480 image as well as the correspond-
ing mask, by padding to all sides of the image and
the mask: border-replicate padding is applied, i.e. the
row or column at the border of the original image is
replicated till the size of 480x480 pixels is reached.
Figure 6: Padding processing example for an UBIRIS.v2
image.
After the preprocessing, we have 2,004 480x480
CSIP images with their segmented masks and 2250
UBIRIS.v2 images with their corresponding seg-
mented masks with the dimensions of 480x480 pix-
els. Finally, both of the datasets have been divided
into 80% randomly selected images for the training
set and 20% for the test set.
4 EXPERIMENTAL RESULTS
4.1 Model Characteristics
To guarantee a fair comparative evaluation, we choose
the same characteristics for both the original U-
Net and our proposed modified model (MDF-U-Net).
First, the used activation function in all layers ex-
cept the output layer is ReLU. The two well-known
major benefits of ReLU compared to other activation
functions are (1) sparsity and (2) reduction of the van-
ishing gradient problem. (2) arises when the input x of
RELU is bigger than 0, where its slope has a constant
value, in contrast to the slope of a sigmoid becoming
smaller as the x value increases. The constant slope of
ReLUs results in faster learning as it prevents vanish-
ing of the gradients and thus better error back propa-
gation. (1) Sparsity arises when the input of the acti-
vation function is lower than or equal to 0. The more
such units exist in a layer, the more sparse the result-
ing representation will be (Goodfellow et al., 2016).
At the output layer sigmoid non-linearity will be used,
since we have to solve a binary classification prob-
lem. The vector of raw values at the output layer will
contain per pixel the confidence index result, which is
obtained by applying a sigmoid activation function.
The used optimisation algorithm is the Adaptive
Moment Estimation Algorithm (ADAM). Its superi-
ority compared to the other optimisation algorithms
comes from applying both RMSprop
1
(Tieleman and
1
RMSprop— is an unpublished optimization algorithm
designed for neural networks, first proposed by Geoff Hin-
ton in lecture 6 of the online course “Neural Networks for
Machine Learning” (Vit, 2018). RMSprop lies in the realm
of adaptive learning rate methods.
Iris Segmentation based on an Optimized U-Net
179
Hinton, 2012) and Momentum gradient descent op-
timization, whereby the ADAM algorithm stores
both the exponentially decaying average of the past
squared gradients and also the exponentially decay-
ing average of past gradients. Then, ADAM uses the
squared gradients to scale the learning rate like RM-
Sprop and it takes advantage of momentum by using
the moving average of the gradient instead of the gra-
dient itself (just like in Stochastic Gradient Descent
- SGD with momentum), which makes it faster than
SGD. Besides, ADAM is an adaptive learning rate
method, which means, it computes individual learn-
ing rates for different parameters. Its name is derived
from adaptive moment estimation, and the reason it
is called like that is because ADAM uses estimations
of first and second moments of gradient to adapt the
learning rate for each weight of the neural network.
We set the initial learning rate to 0.001.
The number of trainable parameters in the origi-
nal U-Net limited us to fix the batch size to 4, de-
spite that the modified proposed model (MDF-U-Net)
which has significantly less parameters could work
correctly with higher batch sizes, e.g. 8. But as men-
tioned, we need uniform training conditions to guar-
antee fair comparison and evaluation. Finally, an ini-
tial number of 25 epochs is selected to reevaluate the
loss/accuracy evolution during training of the model.
4.2 Evaluation Metrics
In this paper we use the DICE Coefficient (F1-Score),
precision-recall curve and mean average precision
(mAP) metrics to evaluate the models.
4.3 Hyperparameter Optimization
Table 1 summarises the Hyperparameter selection
section. The 5th-Approach U-Net will be selected be-
cause of its superiority over all the other models in
terms of F1-Score and the number of parameters.
The proposed model (MDF-U-Net) will be evalu-
ated using F1-Score, precision-recall curve (PR) and
AUC, and mean average precision (mAP) evalua-
tion methods for the CSIP and UBIRIS.v2 datasets.
Besides, the evaluation includes comparisons with
the original U-Net as well as another state-of-the-art
method.
4.4 Results
4.4.1 (MDF-U-Net) Evaluation on CSIP Dataset
As reported in Table 1, the F1-score of our proposed
architecture (MDF-U-Net) is actually slightly better
than the Original U-Net when evaluated on the CSIP
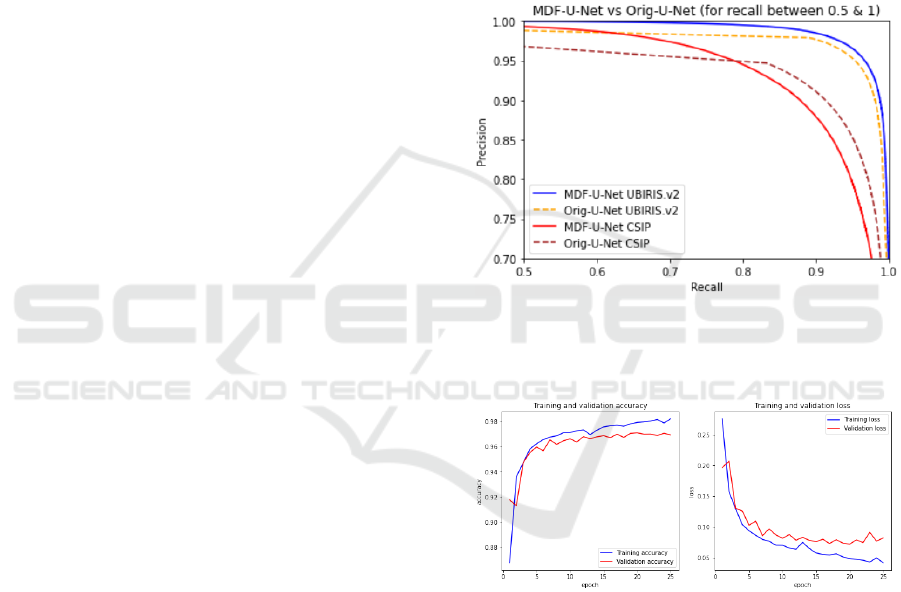
dataset. The precision-recall curve of both of the
models over the test dataset is shown in Figure 7. The
MDF-U-Net gives the best precision for all thresholds
when the recall is between 0 and 0.6 roughly speak-
ing, then it starts breaking down but not drastically
(e.g. for the recall = 0.90, the precision is still above
0.9) which indicates very good classification. For the
original U-Net for all thresholds for a recall value be-
tween 0 and 0.9, the precision is lower than for the
proposed MDF-U-Net model. Only when the recall is
between 0.85 and 1, the original U-Net is superior -
see Figure 7.
Figure 7: Precision-Recall Curve on the chosen datasets.
The total Area under the curve (AUC) as well as
mAP is higher for the proposed model (see Table-2).
Figure 8: MDF-U-Net training vs validation sets accuracy
and loss during training on CSIP.
The observation of both training and validation
accuracies during the training (Figure 8) yields good
confidence about the classification result on the CSIP
dataset.
4.4.2 (MDF-U-Net) Evaluation on UBIRIS.v2
Dataset
The MDF-U-Net works better on the UBIRIS.v2
dataset than on the CSIP dataset; this is appearing
very clearly during the training as shown in Figure 9.
The precision-recall curve clearly illustrates that
the MDF-U-Net works better than the original U-Net,
BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing
180
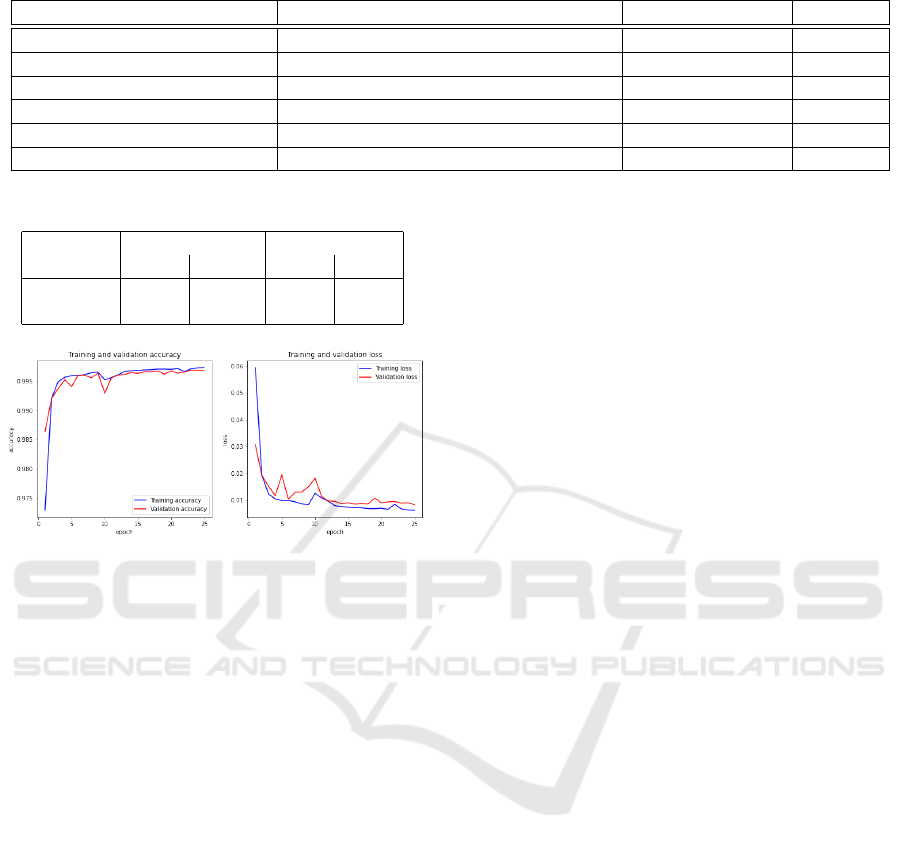
Table 1: Hyperparameters selection summary.
Model Architecture Number of param. F1-Score
Orig.U-Net Orig.U-Net with 3 Channels input layer. 31,032,837 0.9685
1st-Appr.U-Net 3x3 f-size 1,941,105 0.9272
2nd-Appr.U-Net 5x5 f-size 5,079,409 0.9571
3rd-Appr.U-Net 7x7 f-size 9,786,8657 0.9664
4th-Appr.U-Net 7x7 i&o - 3x3 for the rest. // 0.9509
5th-Appr.U-Net(MDF-U-Net) 7x7 i&o - 5x5 for the rest. 5,105,137 0.9711
Table 2: Original U-Net vs MDF-U-Net PR-AUC.
Dataset Original U-Net MDF-U-Net
mAP AUC mAP AUC
Ubiris.v2 0.973 0.983 0.993 0.993
CSIP 0.938 0.962 0.973 0.973
Figure 9: MDF-U-Net training vs validation set accuracy
and loss during training on UBIRIS.v2.
and for all the thresholds of the recall between 0 and
0.8, the MDF-U-Net has almost ideal precisions (i.e.
1), and between 0.8 and 0.95, the precision is more
than 0.95 as shown in Figure 7.
In Table 2, the total Area under the curve (AUC)
and mAP for both models illustrates again a slight su-
periority for the MDF-U-Net.
5 DISCUSSION
The number of trainable parameters in MDF-U-Net
is close to 1/7 of the number of the Original U-Net
parameters. Still it performs better in terms of mAP.
This shows that more parameters or deeper networks
do not always imply higher performance of the mod-
els. In fact, what matters is the architecture and the
design, which should ideally result in better perfor-
mance with fewer parameters. We show that edge de-
tectors (typically used by handcrafted methods) give
strong response to the outer boundary of the iris when
larger kernel sizes are used (especially, 7x7 or larger).
We took inspiration from this result and investigated
increased kernel sizes in the U-Net architecture. The
original U-Net uses the 3x3 filter size in all layers
starting with 64 filters in the first layer (i.e. 64 filters
for the first layer, multiplied with 2 for each succes-
sive next layer).
In Section 4, we compared the proposed MDF-U-
Net with the original U-Net. Here we compare MDF-
U-Net with another state-of-the-art method that was
already discussed in Section 2 (Lian et al., 2018).
We need to highlight that our version of the dataset
UBIRIS.v2 is not identical to the one used in (Lian
et al., 2018). The 1000 segmented masks they used
are not standard part of the UBIRIS.v2 dataset but
given by NICE.I competition (Proença and Alexan-
dre, 2007), which we do not have access to. We
used 2250 segmentation masks published by (Hof-
bauer et al., 2014b). Since the dataset containing 2250
masks is larger and more recent, we believe it can
better capture the performance of the segmentation
algorithm. As the evaluation dataset is not identical
and other image/masks pairs are used, the provided
comparison is not completely objective. However, we
are convinced that the comparison could still have
its scientific value. In their proposed model ATT-
U-Net , all the blocks suggest multi-channel feature
maps. The contracting path of ATT-UNet uses the
same architecture as VGG16 (Simonyan and Zisser-
man, 2014).
The ATT-UNet network (Lian et al., 2018) per-
forms two main functions, attention mask generation
and segmentation. Firstly, they added an attention
mask generation step to estimate the potential area
where the iris is most likely to appear. They used a
bounding box regression module to estimate the co-
ordinates. Besides, they added a pooling layer and
a fully connected layer at the end of the contracting
path as a regression module. (Lian et al., 2018) adopt
Mean Squared Error (MSE) as loss function in this
step. After rectangle arrays are predicted, in the at-
tention mask generation, they first create the atten-
tion mask and then use this mask to guide the final
segmentation which forces the model to focus on this
specific region instead of doing a hard attention that
only segments pixels inside the mask.
In contrast to the previously described approach,
in our model (Figure 4), the input is the preprocessed
image and not the original one. The preprocessing is
Iris Segmentation based on an Optimized U-Net
181
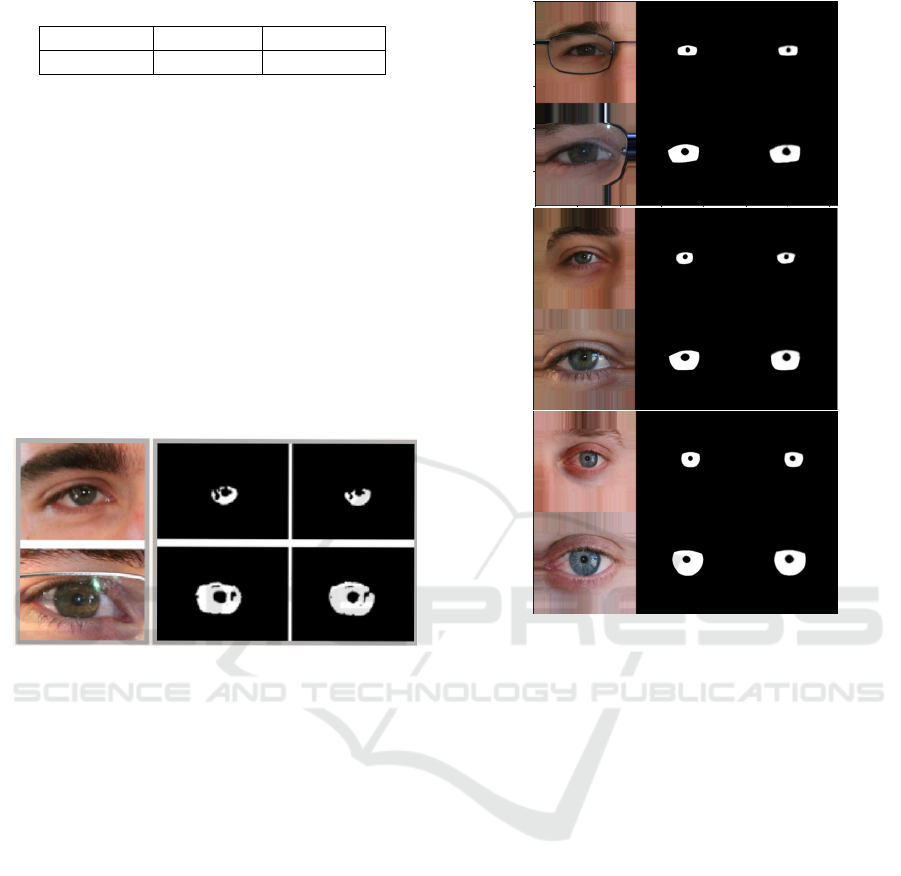
Table 3: ATT-UNet vs MDF-U-Net mAP on UBIRIS.v2.
Dataset ATT-UNet MDF-U-Net
UBIRIS.v2 96.812 0.99314
done by a simple padding to the images and the masks
from all sides to obtain one input image size. This is
done before training the model. Our approach is less
complex and we do not observe miss-segmentation
patches that are not connected to the iris region in the
results.
Since our method can reach better performance
we conclude that the larger convolution kernels can
prevent many of the errors in the segmentation.
Table 3, shows better mAP results for MDF-
U-Net than those obtained with ATT-UNet on the
UBIRIS.v2 dataset. Visual comparison can be made
from images, shown in Figure 10 (illustrating ATT-
UNet performance) and Figure 11 (illustrating perfor-
mance of MDF-U-Net).
Figure 10: UBIRIS.v2 image, groundtruth and predicted
masks using ATT-UNet (Lian et al., 2018).
In Figure 11, we observe better segmentation
results using MDF-U-Net: the iris pixels in the
groundtruth masks (middle column) and the predicted
masks (right column) are more similar.
These visualizations confirm better performance
of MDF-U-Net compared to ATT-UNet on the
UBIRIS.v2 dataset. For the CSIP dataset, MDF-U-
Net is compared with the Original U-Net only, as we
did not find recent segmentation work that uses this
dataset (see Table 2).
6 CONCLUSIONS
In this paper, the popular deep network architecture,
U-Net, is tuned to get more accurate and faster run-
ning models for the task of iris segmentation. We
adopt intuition from handcrafted methods and in-
crease the size of convolutional filters to achieve bet-
ter segmentation results. As we wanted to avoid in-
terpolating or downsampling the images in the pro-
cess, a simple preprocessing is done on two datasets,
the CSIP dataset and the UBIRIS.v2 dataset. The
Figure 11: UBIRIS.v2 image, groundtruth and predicted
masks using MDF-U-Net.
more challenging CSIP dataset, containing images
with various iris sizes, was cropped to 480X480 di-
mensions for all the 2,004 images and masks to man-
age the different image dimensions. The UBIRIS.v2,
more discussed and referenced in scientific literature,
contains smaller images. We added a padding step
that copies border pixels to be able to reuse the same
architecture for both datasets.
Along with other modifications (using 3 channel
color input, reduction of number of filters) we reached
the state-of-the-art performance that we even slightly
surpassed. The proposed model contains 5,105,137
instead of 31,032,837 trainable parameters in the orig-
inal U-Net. F1-Score, PR curve and its AUC, mAP
evaluation methods are applied on both models and
our proposed model achieves better scores than the
original U-Net on both datasets. We compared this
work with another state-of-the-art method, and our
model scored better in mAP and achieves a lower
computational complexity. We approached an ideal
mAP score. Our model scored 0.973 and 0.993 mAP
on CSIP and UBIRIS.v2 respectively. The proposed
model could be a starting point for multi-class classi-
fication and/or recognition as future work.
BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing
182

Generally, the achievements in this paper can be
summarized as follows:
• We reproduced results obtained in literature by the
simple architecture U-Net and propose a modified
model.
• The proposed network has significantly fewer pa-
rameters (approximately 6x less).
• The proposed model yields better performance re-
sults compared to other related works.
• We reach and outperform the state of the art.
REFERENCES
(2004). CASIA-IrisV3. http://www.cbsr.ia.ac.cn/english/
IrisDatabase.asp. Accessed: 2021-05-13.
(2018). Understanding RMSprop — faster neural net-
work learning. https://towardsdatascience.com/
understanding-rmsprop-faster-neural-network-
learning-62e116fcf29a. Accessed: 2021-05-3.
Bazrafkan, S., Thavalengal, S., and Corcoran, P. (2018). An
end to end deep neural network for iris segmentation
in unconstrained scenarios. Neural Networks, 106:79–
95.
Brachmann, A. and Redies, C. (2016). Using convolu-
tional neural network filters to measure left-right mir-
ror symmetry in images. Symmetry, 8(12).
Daugman, J. (2009). How iris recognition works. In The
essential guide to image processing, pages 715–739.
Elsevier.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. Adaptive computation and machine learn-
ing. MIT Press.
Heikkila, M. and Pietikainen, M. (2006). A texture-based
method for modeling the background and detecting
moving objects. IEEE transactions on pattern anal-
ysis and machine intelligence, 28(4):657–662.
Hofbauer, H., Alonso-Fernandez, F., Wild, P., Bigun, J., and
Uhl, A. (2014a). A ground truth for iris segmenta-
tion. In 2014 22nd international conference on pat-
tern recognition, pages 527–532. IEEE.
Hofbauer, H., Alonso-Fernandez, F., Wild, P., Bigun, J., and
Uhl, A. (2014b). A ground truth for iris segmenta-
tion. In 2014 22nd International Conference on Pat-
tern Recognition, pages 527–532.
Jalilian, E. and Uhl, A. (2017). Iris segmentation using fully
convolutional encoder–decoder networks. In Deep
Learning for Biometrics, pages 133–155. Springer.
Le, M. and Kayal, S. (2020). Revisiting edge detection in
convolutional neural networks.
Lian, S., Luo, Z., Zhong, Z., Lin, X., Su, S., and Li, S.
(2018). Attention guided u-net for accurate iris seg-
mentation. Journal of Visual Communication and Im-
age Representation, 56:296–304.
Long, J., Shelhamer, E., and Darrell, T. (2015). Fully con-
volutional networks for semantic segmentation. In
Proceedings of the IEEE conference on computer vi-
sion and pattern recognition, pages 3431–3440.
Lozej, J., Meden, B., Struc, V., and Peer, P. (2018). End-
to-end iris segmentation using u-net. In 2018 IEEE
International Work Conference on Bioinspired Intelli-
gence (IWOBI), pages 1–6. IEEE.
Proença, H. and Alexandre, L. A. (2007). The nice. i: noisy
iris challenge evaluation-part i. In 2007 First IEEE
International Conference on Biometrics: Theory, Ap-
plications, and Systems, pages 1–4. IEEE.
Proenca, H., Filipe, S., Santos, R., Oliveira, J., and Alexan-
dre, L. (2010). The UBIRIS.v2: A database of visi-
ble wavelength images captured on-the-move and at-
a-distance. IEEE Trans. PAMI, 32(8):1529–1535.
Santos, G., Grancho, E., Bernardo, M. V., and Fiadeiro,
P. T. (2015). Fusing iris and periocular information
for cross-sensor recognition. Pattern Recognition Let-
ters, 57:52–59. Mobile Iris CHallenge Evaluation part
I (MICHE I).
Shah, S. and Ross, A. (2009). Iris segmentation using
geodesic active contours. IEEE Transactions on In-
formation Forensics and Security, 4(4):824–836.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Tian, Q.-C., Pan, Q., Cheng, Y.-M., and Gao, Q.-X. (2004).
Fast algorithm and application of hough transform in
iris segmentation. In Proceedings of 2004 interna-
tional conference on machine learning and cybernet-
ics (IEEE Cat. No. 04EX826), volume 7, pages 3977–
3980. IEEE.
Tieleman, T. and Hinton, G. (2012). Lecture 6.5-rmsprop:
Divide the gradient by a running average of its recent
magnitude. COURSERA: Neural networks for ma-
chine learning, 4(2):26–31.
Vitek, M., Das, A., Pourcenoux, Y., Missler, A., Paumier,
C., Das, S., Ghosh, I., Lucio, D. R., Zanlorensi, L.,
Menotti, D., Boutros, F., Damer, N., Grebe, J., Kui-
jper, A., Hu, J., He, Y., Wang, C., Liu, H., Wang, Y.,
and Vyas, R. (2020). Ssbc 2020: Sclera segmenta-
tion benchmarking competition in the mobile environ-
ment.
Iris Segmentation based on an Optimized U-Net
183
