Contactless Measurement of Respiratory Volumes: A Calibration Free

Method based on Depth Information

Felix Wichum

1 a

, Jacqueline Hassel

2 b

, Christian Wiede

1 c

and Karsten Seidl

1,2 d

Fraunhofer IMS, 47057 Duisburg, Germany

Department of Electronic Components and Circuits, University of Duisburg-Essen, Duisburg, Germany

Keywords:

Depth Camera, Tidal Volume, Vital Capacity, Vital Parameter, Respiratory Parameter, Contactless

Measurement.

Abstract:

Measurements of respiratory volumes involve a great deal of effort, either by immobile equipment such as

bodyplethysmography or by consumables as with spirometers. Contactless measurement methods can remedy

this situation. In this paper, a depth camera is used to generate a contactless respiratory signal. A region of

interest is placed over the subject’s upper body and the distance-time curve of respiratory motion is recorded.

Via selected signal features and the use of an artiﬁcial neural network, we can show that this method is equal

to the use of conventional volume determination. From a comparison with a spirometer connected in parallel

as a reference, a mean error for tidal volume of −0.10 l and vital capacity of 0.09 l is obtained.

1 INTRODUCTION

Diseases of the respiratory system are responsible for

one in three deaths in the world (ERS White Book,

2012). For early diagnosis, doctors test the function-

ing of the lungs in pulmonary function tests. These

tests show changes regarding the compliance of the

lungs and constrictions in the respiratory tract. Such

constrictions become apparent as a result of diseases

such as asthma or chronic obstructive pulmonary dis-

ease (COPD). After a diagnosis, appropriate therapy

can thus be started at an early stage.

In clinical practice, spirometers and bodyplethys-

mographs are considered the gold standard for such

pulmonary function tests. In spirometry, the patient

breathes through a mouthpiece into the spirometer,

which measures the volume of air passing through

it (Moore, 2012). A nose clip prevents air volume

from escaping. Volume-time and ﬂow-volume dia-

grams are calculated by integrating the volume ﬂow

over time. In bodyplethysmography, the patient sits

in a closed glass chamber. Pressure changes in the

chamber are measured, as well as ordinary spirometry

in addition. The clear conﬁnes of the bodyplethysmo-

https://orcid.org/0000-0002-3586-2802

https://orcid.org/0000-0002-2368-9774

https://orcid.org/0000-0002-2511-4659

https://orcid.org/0000-0001-6197-5037

graph additionally allow assessment of the full lung

volume (Cri

ee et al., 2011).

Despite their advantages, both methods cannot be

used for all patients, as there are limitations due to the

nature and size of the devices on mobility. Also, a

high degree of patient cooperation is required. Non-

contact measurement techniques represent a new and

innovative approach to improving medical diagnos-

tics and therapy evaluation. In addition to easier han-

dling, optical methods are characterised by better hy-

giene and potentially reduced costs. No virus ﬁlters

need to be replaced and no consumables are required

when measuring patients.

For this reason, we propose a non-contact mea-

surement method for measuring respiratory parame-

ters based on a depth camera. While simpler res-

piratory parameters such as the respiratory rate can

already be measured with a simple RGB camera

(Wuerich et al., 2021), it requires depth information

of the chest movement to derive respiratory volumes.

In our work, we show a conceptual proof that with

suitable signal features and processing with artiﬁcial

neural networks, respiratory volumes can be deter-

mined calibration-free with a depth camera.

In this paper, we ﬁrst present the state of the art in

the determination of non-contact respiratory parame-

ters in Section 2. In Section 3, we outline the methods

used to determine the respiration parameters. There-

fore, we explain the acquisition of our dataset with

150

Wichum, F., Hassel, J., Wiede, C. and Seidl, K.

Contactless Measurement of Respiratory Volumes: A Calibration Free Method based on Depth Information.

DOI: 10.5220/0010813300003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 4: BIOSIGNALS, pages 150-158

ISBN: 978-989-758-552-4; ISSN: 2184-4305

the hardware used in Section 4. This is followed by

the results in Section 5. The discussion is presented

in Section 6. We conclude with our ﬁndings and an

outlook on future developments in Section 7.

2 STATE OF THE ART

In addition to the conventional measurement methods

for measuring respiratory parameters using spirom-

eters or bodyplethysmographs, more and more non-

contact measurement methods have been developed

in recent years.

Approaches using an RGB camera relate to the

measurement of the respiration rate. Based on fa-

cial recognition, a region of interest is selected in the

thorax region of the subjects. Prominent points are

tracked over time via the optical ﬂow. This is fol-

lowed by bandpass ﬁltering of the trajectories and

artifact reduction by principal component analysis

(PCA). Finally, the respiratory rate is determined via

frequency analysis. Thereby the strongest signal in

the power spectral density is crucial. (Wuerich et al.,

2021)

The method by (Lim et al., 2014) includes a

Kinect camera. The respiration rate is determined

from the moving average of the depth information us-

ing a spline interpolation. This is extended in (Ostad-

abbas et al., 2016) by an automatic selection of the

region of interest on the chest area.

Using projected light patterns and an RGB cam-

era, it has been possible to infer deformations of the

thorax and thus changes in volume (de Boer et al.,

2010) (Bernal et al., 2014). More promising, how-

ever, is the direct acquisition of depth information via

depth cameras.

If one measures depth information of chest move-

ments, they do not correspond to real volume-time

curves. Therefore, a calibration in the form of a scal-

ing factor is needed to reﬂect the real volume changes.

One use for determining the scaling factor is to use

keypoints, which are automatically determined from

the curve, and linear regression as described in (Sharp

et al., 2017).

(Imano et al., 2020) use a Kinect camera to infer

respiratory volumes and respiration rates from depth

data. The determined tidal volumes thereby vary by

more than 10 % from a reference value. The approach

from (Soleimani et al., 2015) and (Soleimani et al.,

2017) is based on a complex upper body reconstruc-

tion procedure. Using a point cloud, the upper body is

3D-modulated and thus volume variations are calcu-

lated. Scaling factors are determined via torso move-

ments. Even though attempts to generalize the scal-

ing factor have been made already in this case, no

patient-speciﬁc data such as age, height and weight

are included.

The use of level-set segmentation-based volume

estimation leads to errors of almost 8 %. However,

the computational effort of almost 10 min for a sin-

gle measurement of 4 s alone also hinders a practical

application in this case. (Oh et al., 2019)

In this work, a method is proposed to determine

the scaling factor automatically and without calibra-

tion, thus indicating the respiration parameters. For

this purpose, extracted features from the signal and

additionally patient data are processed by an artiﬁ-

cial neural network. This offers the possibility to

output the respiration parameters immediately after

a measurement. The possibilities of machine learn-

ing will be used in this work to speciﬁcally capture

the changes in signal quality and additionally include

patient information to thus automatically determine a

scaling factor for each measurement.

3 METHOD

The proposed method allows the separate measure-

ment of tidal volume and vital capacity based on the

data from a depth camera. The associated signal pro-

cessing is outlined below.

3.1 Overview

The measurement of normal breathing allows the de-

termination of tidal volume TV. Respectively, vi-

tal capacity VC can be measured via forced breath-

ing. For this reason, the methods presented here are

applied to both volumes. The general procedure is

shown in ﬁgure 1 and further elaborated in the fol-

lowing.

Our approach is based on using the data of a depth

camera. Subsequently, a region of interest (ROI) is

placed in the subjects’ upper body. After a back-

ground elimination, the depth values obtained are av-

eraged per frame in the ROI. A depth-time diagram

is created, which is then smoothed with a moving av-

erage. A reference measurement of a spirometer pro-

vides a volume-time diagram and the corresponding

reference volumes. To determine the respective respi-

ratory volumes V, a total of three methods are com-

pared:

• Direct Method. Via feature extraction of the pro-

cessed depth data and subsequent feature selec-

tion, an artiﬁcial neural network is trained and

then the hyperparameters are optimised. This re-

Contactless Measurement of Respiratory Volumes: A Calibration Free Method based on Depth Information

151

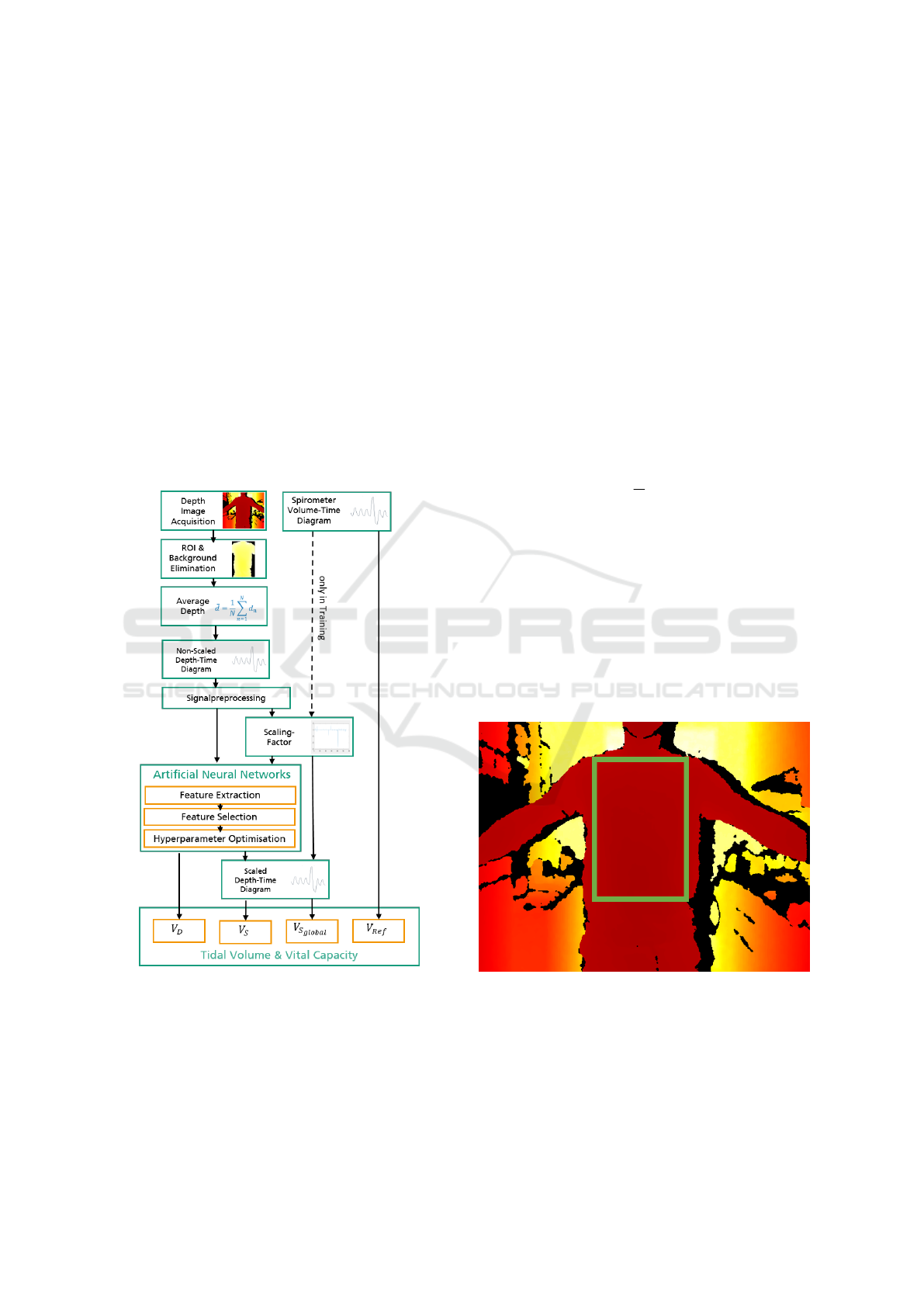
turns the corresponding volumes directly as out-

put: V

= {TV

, VC

• Individual Scaling Factor Determination. The

extracted features are used together with the fea-

ture selection and subsequent hyperparameter op-

timisation as well. However, the neural network

outputs an individual scaling factor with which

the depth data can be mapped onto the volume

data. The volumes from the scaling factor method

can be extracted from the resulting volume-time

curve: V

= {TV

, VC

• Application of the Global Scaling Factor. In

contrast, a conventional variant is tested in which

a scaling factor is derived as the mean value of all

calculated scaling factors from the training data

and then applied to the test data set. The volumes

extracted are V

global

= {TV

global

, VC

global

Figure 1: Signal processing ﬂow-chart. The volumes V re-

fer to the corresponding origins: V

Ref

as reference volume

of the spirometer, V

as direct calculation via artiﬁcial neu-

ral networks, V

as calculation via an individual scaling fac-

tor via artiﬁcial neural networks and V

Global

as result of the

application of a global scaling factor. In the training phase,

the optimal scaling factors are calculated with the spirome-

ter data.

3.2 Depth Data in Region of Interest

When recording depth information, only some image

regions contain the relevant parts of the body. A re-

gion of interest (ROI) is therefore manually selected

and considered afterwards, see ﬁgure 2. This ROI is

ﬁxed in the recording. A rectangle is manually se-

lected, always positioned to encompass the chest and

abdominal area. The region extends from the clavi-

cles to below the belly button. The arms and sides are

not included.

To ensure that no background pixels are included,

all pixels with a distance d

>2 m are excluded. From

the remaining pixels, the mean value

d is calculated

for each frame k according to equation 1. N is the

number of all pixels in the ROI within the speciﬁed

distance.

d[k] =

∑

n=1

[k] (1)

A moving average with a window size of ten sam-

ples is applied to reduce overlapping body move-

ments. The resulting signal

is then mean-

centered, see equation 2. Thereby d

LP,mean

corre-

sponds to the average depth over all frames of this

ﬁltered signal.

d[k] = d

LP,mean

−

[k] (2)

Thus, the signal pre-processing results in a single

depth information d for each frame k.

Figure 2: Selection of the Region of Interest (ROI). The

ROI is manually placed within the chest area and remains

there throughout the measurement.

3.3 Scaling of the Breathing Curve

The respiratory signal from the distance measurement

must be provided with a scaling factor in order to

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

152

determine the respiratory volumes from it. One ap-

proach of this work is to have this scaling factor es-

timated by artiﬁcial neural networks. The determina-

tion of the ground truth is described in this section.

Since the spirometer and depth camera cannot be

started synchronised, the start and end of the mea-

surement is done manually. In order to achieve

temporal synchronicity, the temporal displacement of

the signals is determined and trimmed using cross-

correlation.

The sample-wise scaling factor s is obtained by di-

viding the depth-distance and corresponding volume

V from the reference system for each sample k, see

equation 3.

s[k] =

d[k]

V [k]

(3)

The Median Absolute Deviation (MAD) is deter-

mined (see equation 4) and an outlier correction is ap-

plied. The outlier-corrected scaling factor s

MAD

is the

result of all the scaling factors within three times the

MAD.

MAD = median(|s[k] − median(s)|) (4)

The mean value from s

MAD

provides the scaling

factor S

for this measurement, see equation 5. M rep-

resents the number of all scaling factors (corresponds

to the number of frames) reduced by the number of

outliers.

∑

m=1

MAD

[m] (5)

Finally, S

global

denotes the mean of all measure-

ments C across all subject, see equation 6.

global

∑

k=1

(6)

3.4 Feature Extraction

Essentially, the respiration volumes can be deter-

mined in two ways. First, by applying the global

scaling factor S

global

to the depth signal. Second, by

machine learning methods (individual scaling factor

determination and direct volume extraction). For ma-

chine learning methods, features extracted from the

pre-processed depth signal are used.

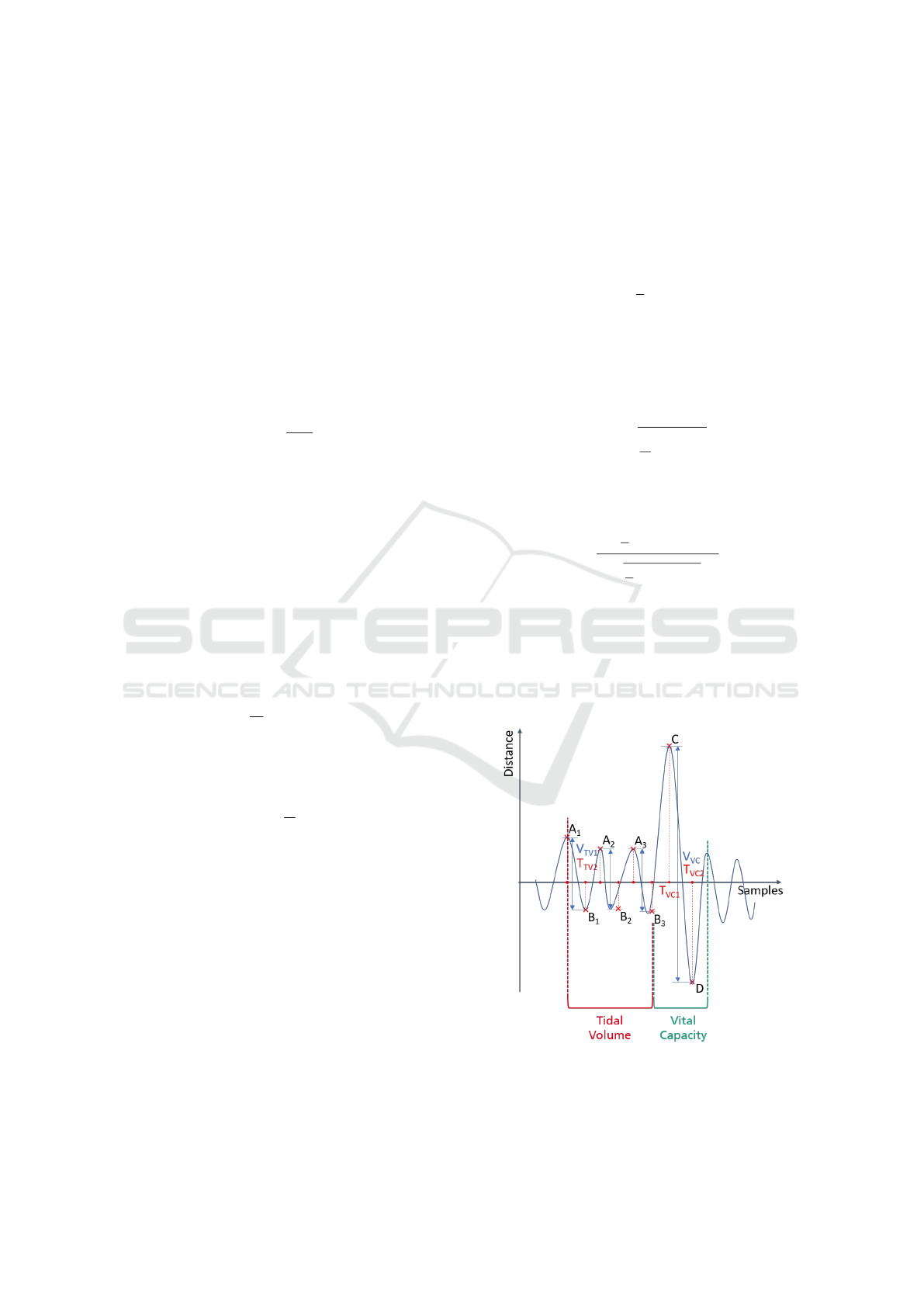
The points A

, A

, B

as well as C and

D, which represent the local extreme points of the res-

piratory signal, are referred to as keypoints and are

shown in Figure 3. The respective distance as well as

the temporal information of these keypoints are fea-

tures for the further steps. Since no scaling factor has

been applied yet, the unit of these quantities is still

in mm. Therefore, the indexing is performed with

dist for distance. In addition, the mean tidal volume

dist

and the vital capacity VC

dist

are calculated, see

equation 7 and equation 8 respectively. The enclosed

breathing curve area is another feature.

dist

∑

i=1

− B

(7)

dist

= C − D (8)

Other characteristics are mean, standard deviation

σ and skewness of the distribution. The standard de-

viation results from equation 9 as follows:

σ = +

∑

k=1

d[k]

(9)

The skewness h is deﬁned according to equation

10, where K corresponds to the number of all frames.

h =

∑

k=1

d[k]



∑

k=1

d[k]



(10)

Between the keypoints, the slope in the turning

points (Slope

) is calculated in each case. For this

purpose, the ﬁrst three derivatives of the signal are

calculated. In addition, the distances are determined

in the range of 2 samples before and after the respec-

tive maxima. This is to ensure that the environment

Figure 3: Distinctive keypoints of the signal. Global max-

ima are marked A for tidal volume and C for vital capacity.

Global minima are marked B for tidal volume and D for

vital capacity.

Contactless Measurement of Respiratory Volumes: A Calibration Free Method based on Depth Information

153

and thus noise inﬂuences around the keypoints are de-

scribed. The points obtained in this way are named

with a + (-) in the index, for example A

( A

i−

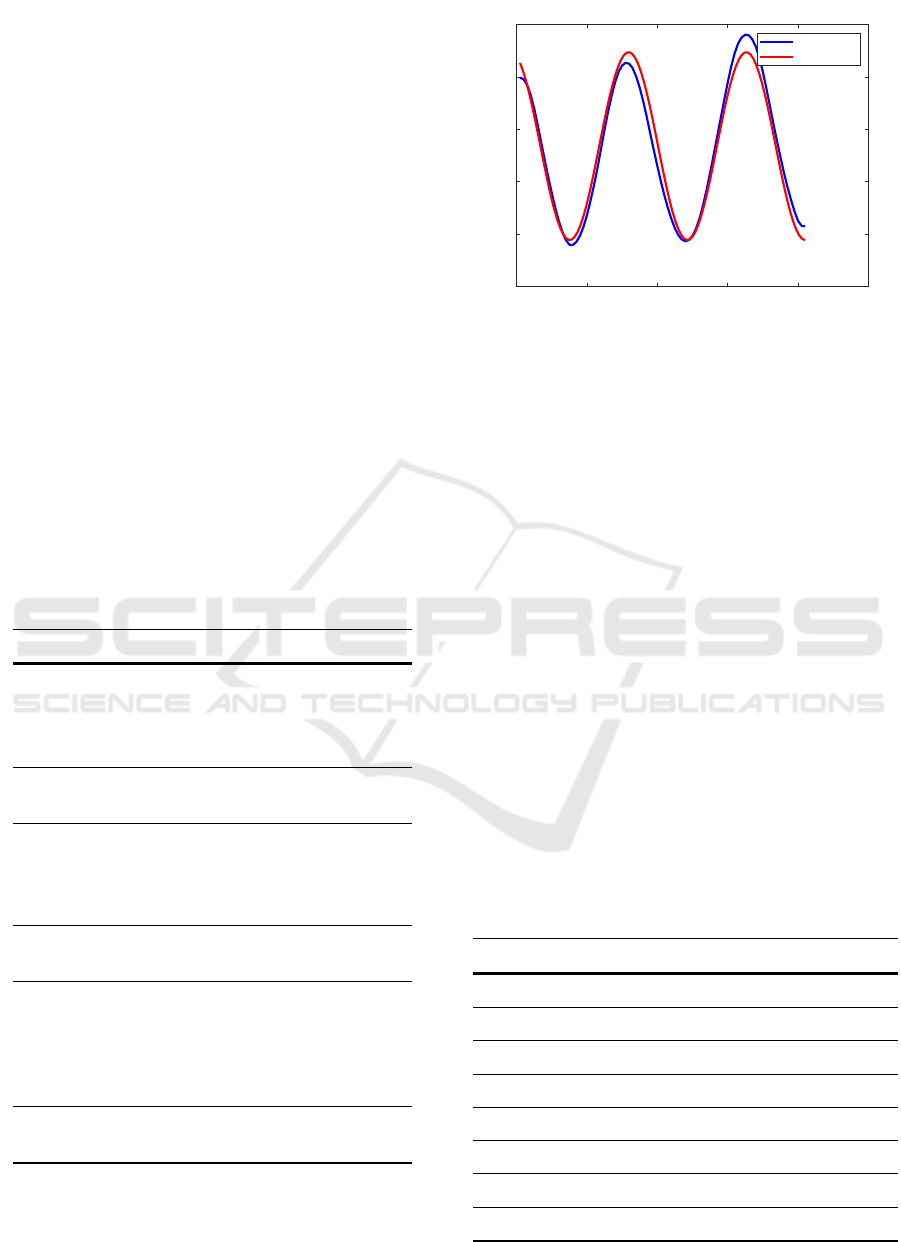
Other features result from a sinusoidal regression.

This involves ﬁtting a sine function to the breathing

curve via least squares minimisation. The resulting

features are: range of values, period w, amplitude v,

mean value u and goodness of ﬁt. The regression is

shown in ﬁgure 4. The sine function f[k] is repre-

sented in equation 11 with t representing a shift.

f [k] = u + v · sin(k · w +t) (11)

Furthermore, other characteristics of the subjects

are collected. This includes: age, gender, height and

weight of the subjects. Through these parameters, we

aim to ﬁnd a general description of the subjects and

thus a connection with the breathing characteristics.

Thus, in summary, 43 features are obtained for the

sections of tidal volume and 27 features for vital ca-

pacity. The features are shown in table 1.

Table 1: Overview of features used for vital capacity and

tidal volume. Points A (C) denote the global maxima dur-

ing natural breathing (forced breathing), and points B (D)

denote the global minima, each with ascending index. A +

(−) indicates that the value is shifted by 2 samples to the

right (left).

Tidal volume Vital capacity

, A

, B

and B

with distance

and time respectively,

dist

C and D with distance

and time respectively,

dist

mean, standard devia-

tion and skewness

mean, standard devia-

tion and skewness

slope and distance of

turning point between

and B1, A

and B2,

and B3

slope and distance of

turning point between

C and D

, A

1−

, A

2−

, A

3−

, C

−

Range of values, pe-

riod, amplitude, mean

value and goodness of

ﬁt (sinusoidal regres-

sion)

Range of values, pe-

riod, amplitude, mean

value and goodness of

ﬁt (sinusoidal regres-

sion)

age, gender, height

and weight

age, gender, height

and weight

0 20 40 60 80 100

Samples

-4

-2

Depth [mm]

Sinus Regression

Mean depth

Fitted Sinus

Figure 4: Sinusoidal Regression. A sine function is ﬁtted

into the depth signal via the least squares error. The param-

eters of the sine function serve as a feature for the further

processing steps.

3.5 Feature Selection

From this large number of features, a subset is se-

lected. This so-called feature selection has the follow-

ing advantages: faster training, reduced complexity of

the model and reduced overﬁtting.

A ﬁltering approach was used to select the fea-

tures, evaluating the relationship between feature and

target value with a score. This evaluation is based on

the calculation of statistical F-tests, which enables a

ranking of the features via a score. Based on these

rankings, the eight highest-scoring features are se-

lected for each of the four neural networks. All se-

lected features are shown as an overview in table 2.

Table 2: Selected features through the ﬁlter approach. Point

denote the second global maxima during natural breath-

ing. A + indicates that the value is shifted by 2 samples to

the right. Features created by sinusoidal regression preﬁx

the names with Sin. Range refers to the range of values,

Ampl to the amplitude of the sine and Center to the mean

value.

height gender weight weight

dist

weight gender height

weight height height gender

SinRange Slope

age age

Slope

SinRange

mean Slope

SinAmpl Slope

dist

TurnPoint

SinAmpl

Slope

SinCenter VC

dist

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

154

Weight and height of the subjects are among the

ﬁrst three features in all rankings, reﬂecting the cor-

relation of these parameters with breathing volumes.

Eight times the slope in the turning point Slope

used as well. It is noticeable that in three out of four

approaches the speciﬁc volume over distance (TV

dist

or VC

dist

) was included as a feature. For the method

, the sinus amplitude is represented as a feature

instead, which also qualitatively describes this vol-

ume. Other features of the sine regression are fre-

quently (ﬁve times) used as features as well.

3.6 Neural Network Design

After the feature selection, the structure of the neural

networks is described in this section. For this work,

a feedforward network architecture with one hidden

layer each is used. A larger number of hidden layers

did not empirically lead to better results. The sigmoid

function serves as the activation function. The output

is determined by a linear output function.

Subsequently, a hyperparameter optimisation of

the number of neurons and the learning rate

is performed. The neural networks are trained

using Levenberg-Marquardt backpropagation, ran-

domly splitting the training and test datasets. As a

cost function for the search for the global minimum

during optimisation the mean square error is utilised.

This results in four different neural networks, see ta-

ble 3.

Table 3: Optimised artiﬁcial neural network (ANN) hyper-

parameters with a total of three layers.

ANN Neurons in

Hidden Layer

Learning Rate

31 0.1

10 0.1

4 0.001

2 0.01

4 EXPERIMENTAL SETUP

A self-created data set with a total of nine healthy

subjects was collected. The Astra Pro camera from

Orbecc was used to record the depth data. The Min-

iSpir, a mobile spirometer with its own turbines for

each subject, was used as a reference.

4.1 Test Procedure

During the measurements, the subjects’ upper body

was recorded frontally with the depth camera while a

spirometer simultaneously measured volume ﬂow for

validation. For this purpose, the subjects were seated

on a chair at a distance of 1.0 m, 1.3 m or 1.6 m. This

encompasses an optimal range for comparable mea-

surements (Soleimani et al., 2017). The spirometer

is attached to a microphone stand so that the sub-

ject does not have to hold it and the arms hang down

by the upper body. Before starting the measurement,

the subject puts on a nose clip and completely sur-

rounds the spirometer with the mouth. The experi-

mental setup is shown in ﬁgure 5.

A total of 60 s of measurement is taken with a

camera frame rate of 30 fps. The probands breathed

naturally for three to four breaths until they inhaled

maximally and exhaled maximally. This breathing

manoeuvre was repeated twice in the 60 seconds. The

subjects were acoustically supported in breathing in

and out to the maximum by the study leader.

Figure 5: Setup of the experiment. The subject sits at a

deﬁned distance in front of the depth camera and breathes

through a spirometer attached to a microphone stand. The

nose is closed with a nose clip.

4.2 Structure of the Dataset

The healthy nine subjects are divided into four fe-

male and ﬁve male participants. The average age

is (25.00±1.12)yrs. The average weight is (72.20±

15.14)kg and the height is (177.33±9.59)cm.

The two breathing manoeuvres are extracted from

the recorded data. Each breathing manoeuvre is then

further divided into two sections: three breaths in rest-

ing breathing and forced maximal breathing. The sub-

division is shown in ﬁgure 3 and is obtained as fol-

lows. Starting with a local maximum, the ﬁrst three

breaths up to forced breathing are counted for tidal

Contactless Measurement of Respiratory Volumes: A Calibration Free Method based on Depth Information

155

volume. The signal section for vital capacity starts

with the global minimum and ends with and ends with

the next global maximum after complete inhalation

and exhalation.

In total, the recorded data set thus contains 43 sig-

nal segments, each for normal respiration (TV av-

erage (1.152 ± 0.617)l) and forced respiration (VC

average (4.452 ± 1.029)l). Another dataset contains

pure depth information of the subjects without refer-

ence values of a spirometer. The so-called free breath-

ing is intended to reveal potential inﬂuences of body

posture when using a spirometer as a reference mea-

surement device.

5 RESULTS

Due to the small size of the data set, 5-fold cross-

validation is used for TV and VC respectively. In

ﬁve runs, the data set is thus divided into 10 % test

data and 90 % training data. The cross-validation re-

duces the dependence of the results on the respective

data set. This is done for each of our four neural net-

works. The same split datasets for our ANN approach

are also used to test the approach of a global scaling

factor. This allows a better comparison.

5.1 Tidal Volume

The methods for determining the tidal volume are on

average all within a deviation of −0.09 l or more. The

tidal volume is thus underestimated in all tested meth-

ods, see table 4. The mean error is approximately

at the same level of −0.10 l. This does not apply to

the determination of the scaling factor and the sub-

sequent volume calculation. In this case, the devia-

tions from the reference value are larger. The larger

root mean square error (RMSE) indicates that there

are isolated larger deviations. TV

, with a value of

0.61 l, is above the errors of the other methods, which

have an RMSE of 0.45 l.

Table 4: Averaged results for determination of tidal volume

(TV) via ﬁve-fold cross-validation. Using neural networks,

a direct determination of the volumes (D) and a determina-

tion using the scaling factor (S). The results using a global

scaling factor (S

global

) are given for both data sets.

global

Mean

Error

−0.10 l −0.14 l −0.10 l −0.09 l

RMSE 0.61 l 0.46 l 0.45 l 0.45 l

Comparing the derivation of an individual scaling

factor with the application of a global scaling factor,

we ﬁnd that the mean error with the machine learn-

ing approach is 0.05 l higher and the RMSE is 0.01 l

higher. The same comparison for the direct volume

calculation via artiﬁcial neural networks shows the

same mean error and a 0.16 l higher RMSE in con-

trast to the global scaling factor.

5.2 Vital Capacity

These results are reﬂected in the vital capacity as well,

see table 5. The direct calculation of the volume per-

forms better than a prior determination of the scaling

factor. Compared to the use of a global scaling fac-

tor over all measurements, the mean error is at the

same level. In contrast to the tidal volume, the RMSE

for the direct calculation of the vital capacity is lower

compared to the use of a global scaling factor.

The only method to overestimate the vital capac-

ity on average is the direct method. The deviation is

0.01 l smaller than the method with the global scal-

ing factor. The RMSE is 0.26 l lower than with the

conventional approach. The determination of the in-

dividual scaling factor increases the mean deviation

by more than double by 0.14 l compared to the global

scaling factor.

Table 5: Averaged results for determination of vital capacity

(VC) via ﬁve-fold cross-validation. Using neural networks,

a direct determination of the volumes (D) and a determina-

tion using the scaling factor (S). The results using a global

scaling factor (S

global

) are given for both data sets.

global

Mean

Error

0.09 l −0.24 l −0.10 l −0.10 l

RMSE 0.62 l 1.23 l 0.88 l 1.07 l

5.3 Free Breathing

To test whether the setup with spirometer has an in-

ﬂuence on the body posture, another measurement of

the subjects without spirometer was performed. Since

no reference values are available, the volumes deter-

mined are compared with the previous reference vol-

umes, see ﬁgure 6. The determined volumes for free

respiration are within the previous reference values.

For the tidal volumes, there is a narrower distri-

bution of the determined measured values for free

breathing compared to the reference values. The vital

capacity also shows a slightly smaller spread in the

distribution. Thus, the measured volume values are in

the plausible range of the previous reference values.

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

156

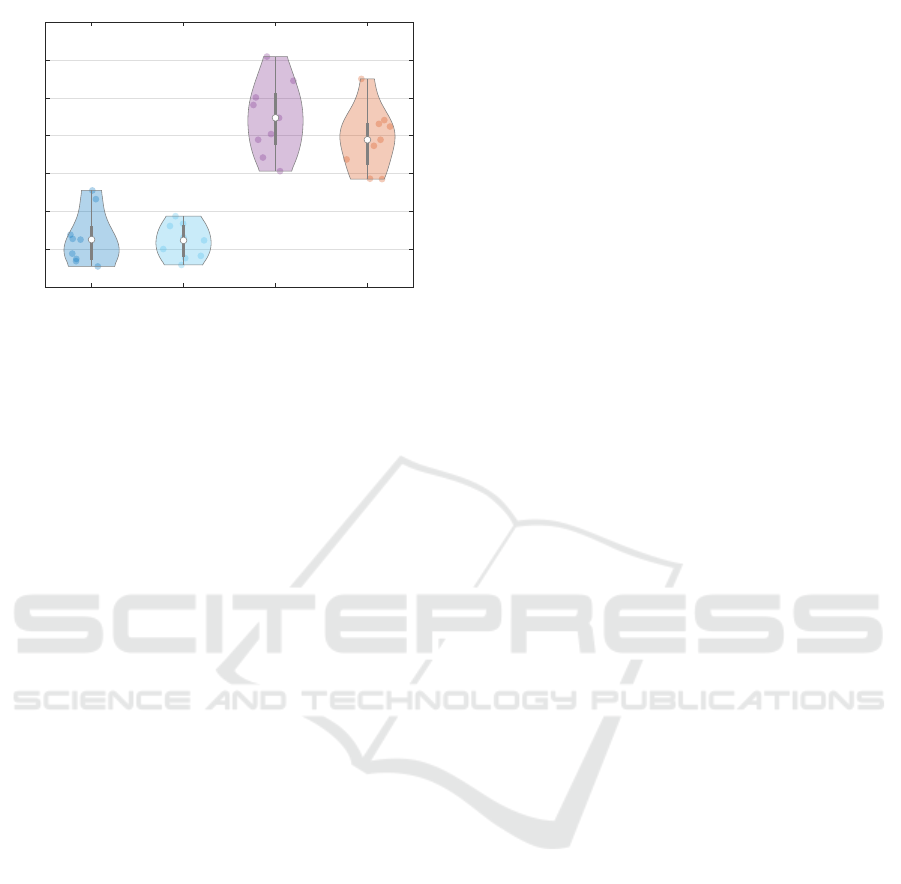
TV Ground Truth TV Free VC Ground Truth VC Free

Volume [l]

Volume Comparison

Figure 6: Violin plot of free breathing and previous

recorded spirometer data (ground truth). For tidal volume

(TV) and vital capacity (VC), measurement results of our

direct method without a spirometer are compared with ref-

erence values. These reference values are taken from previ-

ous measurements with a spirometer.

6 DISCUSSION

The results presented in the previous section show

that measurements of respiratory volumes (tidal vol-

ume and vital capacity) without contact is possible

with the developed methods. On average, the artiﬁ-

cial neural networks for direct volumes are equally

good as the use of a global scaling factor as an av-

erage over many subjects. The preceding calculation

of an individual scaling factor for each subject by an

ANN shows slightly larger deviations. Nevertheless,

this method has the advantage of being able to use the

complete distance-time diagram for the measurement

of further respiration parameters. Thus, dynamic pa-

rameters such as FEV1 can be determined in the fu-

ture.

It is noteworthy that for both tidal volume determi-

nation and vital capacity determination, the mean er-

rors are approximately at the same level. In contrast,

the RMSE for vital capacity increases. It is therefore

more difﬁcult to determine the vital capacity correctly

than the tidal volume. A possible cause can be found

in the signal sections. Three breaths are available for

tidal volume determination, whereas only one breath

was taken with forced maximal breathing. This can-

not be avoided in future measurements due to patient

stress. Repeated strong breathing manoeuvres put a

lot of stress on patients if they are performed consec-

utively without a break.

The mean deviations of 0.10 l performs better

compared to (Imano et al., 2020). Especially for vi-

tal capacity, the method proposed in this paper has

a low percentage deviation. For further comparisons

regarding (Soleimani et al., 2017), a larger data set is

needed. In this context, our estimate of the individual

scaling factor serves as a ﬁrst indication for the mea-

surement of further respiratory parameters. The trans-

ferability of the measurements to lung disease cases in

particular should be veriﬁed with additional subjects.

It should be examined whether lung diseases such as

COPD or asthma affect respiratory movements to the

extent that they inﬂuence the selected features for de-

termining the respiration rate via artiﬁcial neural net-

works.

The use of the algorithms in free breathing shows

that the measured results are plausible in comparison

to the previously determined reference values. Even if

there is a temporal offset and the effort of the test sub-

jects during breathing may have varied, it is still ev-

ident that the respiratory volumes can be determined

with this measurement setup and that there are no fur-

ther inﬂuences in, for example, the posture.

All of our subjects were normally clothed (t-shirt,

shirt, pullover) and measured at various distances. We

used an average of the depth information in the re-

gion of interest. Wrinkling or concealment of cloth-

ing could therefore also inﬂuence this value. We

aimed to reduce the inﬂuence by using artiﬁcial neu-

ral networks and features extracted for this purpose.

In the small dataset of nine subjects, the features

age, gender, height were taken very frequently. Even

though individual patient information was processed

with this, these features need to be retested in a larger

data set with more variance. Additionally, possible

inﬂuences of clothing can be addressed in the future

by splitting the ROI and collecting the previous pa-

rameters in different subregions. Texture features and

variance of the raw depth data can contribute further

information. Furthermore, it should be examined to

what extent the preprocessing of the signal has an in-

ﬂuence on the subsequent results. With our mean ﬁl-

tering, we may have neglected high frequency com-

ponents for a more comparable signal section.

7 CONCLUSIONS

In this study, we presented a non-contact, automatic,

and calibration-free approach to determine respiratory

volumes via a depth camera. This involves matching

the respiratory signal of the depth data to the respira-

tory volumes by a scaling factor. This scaling factor is

determined by processing suitable raw signal features

and patient data using an artiﬁcial neural network. We

thus achieve a mean error of −0.14 l for the tidal vol-

ume and −0.24 l for the vital capacity. Via a direct es-

timation of the respiratory volumes via artiﬁcial neu-

Contactless Measurement of Respiratory Volumes: A Calibration Free Method based on Depth Information

157

ral networks we obtain a mean error of −0.10 l and

0.09 l respectively. The method is so far equivalent to

the use of a global scaling factor.

In the future, we would like to further reduce the

error by using a larger data set and additional signal

features. The volume-time diagram can as well be

used to determine other respiration parameters. An

automatic selection and tracking of the region of in-

terest shall be implemented for a real world applica-

tion.

ACKNOWLEDGEMENTS

We would like to thank Dr. med. Sohrab for testing all

of our patients for health suitability and for advising

us from a medical perspective.

REFERENCES

Bernal, E. A., Mestha, L. K., and Shilla, E. (2014). Non

contact monitoring of respiratory function via depth

sensing. In 2014 IEEE-EMBS International Con-

ference on Biomedical and Health Informatics (BHI

2014), Piscataway, NJ. IEEE.

Cri

ee, C. P., Sorichter, S., Smith, H. J., Kardos, P., Mer-

get, R., Heise, D., Berdel, D., K

ohler, D., Magnussen,

H., Marek, W., Mitfessel, H., Rasche, K., Rolke, M.,

Worth, H., and J

orres, R. A. (2011). Body plethys-

mography – its principles and clinical use. Respira-

tory Medicine, 105(7):959–971.

de Boer, W., Lasenby, J., Cameron, J., Wareham, R., Ah-

mad, S., Roach, C., Hills, W., and Iles, R. (2010). Slp:

A zero-contact non-invasive method for pulmonary

function testing. In Labrosse, F., Zwiggelaar, R.,

Liu, Y., and Tiddeman, B., editors, Procedings of the

British Machine Vision Conference 2010, pages 85.1–

85.12. British Machine Vision Association.

ERS White Book (2012). The burden of lung disease.

Imano, W., Kameyama, K., Hollingdal, M., Refsgaard, J.,

Larsen, K., Topp, C., Kronborg, S. H., Gade, J. D., and

Dinesen, B. (2020). Non-contact respiratory measure-

ment using a depth camera for elderly people. Sensors,

20(23):6901.

Lim, S. H., Golkar, E., and Abd. Rahni, A. A. (2014).

Respiratory motion tracking using the kinect camera.

In 2014 IEEE Conference on Biomedical Engineering

and Sciences (IECBES), pages 797–800. IEEE.

Moore, V. C. (2012). Spirometry: step by step. Breathe,

8(3):232–240.

Oh, K., Shin, C. S., Kim, J., and Yoo, S. K. (2019). Level-

set segmentation-based respiratory volume estimation

using a depth camera. Ieee Journal of Biomedical and

Health Informatics, 23(4):1674–1682.

Ostadabbas, S., Sebkhi, N., Zhang, M., Rahim, S., Ander-

son, L. J., Lee, F. E.-H., and Ghovanloo, M. (2016).

A vision-based respiration monitoring system for pas-

sive airway resistance estimation. IEEE Transactions

on Biomedical Engineering, 63(9):1904–1913.

Sharp, C., Soleimani, V., Hannuna, S., Camplani, M.,

Damen, D., Viner, J., Mirmehdi, M., and Dodd, J. W.

(2017). Toward respiratory assessment using depth

measurements from a time-of-ﬂight sensor. Frontiers

in Physiology, 8:65.

Soleimani, V., Mirmehdi, M., Damen, D., Dodd, J., Han-

nuna, S., Sharp, C., Camplani, M., and Viner, J.

(2017). Remote, depth-based lung function assess-

ment. IEEE Transactions on Biomedical Engineering,

64(8):1943–1958.

Soleimani, V., Mirmehdi, M., Damen, D., Hannuna, S.,

Camplani, M., Viner, J., and Dodd, J. (2015). Remote

pulmonary function testing using a depth sensor. In

2015 IEEE Biomedical Circuits and Systems Confer-

ence (BioCAS 2015), Piscataway, NJ. IEEE.

Wuerich, C., Wichum, F., Wiede, C., and Grabmaier, A.

(2021). Contactless optical respiration rate measure-

ment for a fast triage of sars-cov-2 patients in hospi-

tals. In Proceedings of the International Conference

on Image Processing and Vision Engineering, pages

29–35. SCITEPRESS - Science and Technology Pub-

lications.

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

158