
Incremental Online Reconstruction of Locally Quadric Surfaces
Josua Bloeß
a
and Dominik Henrich
b
University of Bayreuth, Chair for Applied Computer Science III, (Robotics and Embedded Systems),
Universitaetsstrasse 30, 95447 Bayreuth, Germany
Keywords:
Reconstruction, Segmentation, Point Cloud, Surface Fitting, Quadrics, Online Computation.
Abstract:
Representing surfaces of a digital 3D model using high level geometric information is key to lots of geometric
processing and other use cases. In order to obtain these 3D models, various scanning methods have been
proposed. We contribute a method for incremental reconstruction of surfaces from a series of point clouds.
For this, we use a robust over-segmentation technique on a point cloud and build a memory efficient graph
structure upon it. Over time, we expand this graph structure as global representation. We also propose a fast
fitting algorithm for quadric surface patches to the graph structure. We validate the overall performance in our
experiments.
1 INTRODUCTION
Digital reconstruction of real world objects from point
clouds is an avid and ever evolving field of research.
Some of its various use cases are grasp planning in
robotics (Makhal et al., 2018), manifacturing (Vem-
pati et al., 2018) or creation of models for entertain-
ment (Beraldin et al., 2005). The process of digital re-
construction is a challenging task and requires special
hardware and specifically trained personal. In order
for the result to be useful in an industrial environment,
it must be compatible with established CAD con-
cepts and software. This in turn requires the geom-
etry of the digital reconstruction to be represented by
high level information like geometrical primitives or
Splines in contrast to low abstraction representations
like triangle meshes. The process of CAD reconstruc-
tion usually involves two steps: data acquisition and
a computationally expensive analysis for high level
geometric features (Buonamici et al., 2018). Due to
this separation, it is important that the data acquisi-
tion is done thoroughly and flawlessly. Otherwise,
it can take multiple iterations of data acquisition and
analysis until a sufficient result is achieved. An al-
ternative approach is an incremental reconstruction
where the analysis of point clouds is done online dur-
ing data acquisition, e.g. (Newcombe et al., 2011).
With incremental reconstruction, a user can react to
the online computed intermediate result and adapt
a
https://orcid.org/0000-0001-8636-3168
b
https://orcid.org/0000-0003-0250-2728
the data acquisition accordingly, e.g. by re-capturing
poorly scanned areas of the object. However, exist-
ing approaches for online reconstruction usually pro-
duce results with low abstraction like triangle meshes
or approximated signed distance functions. Few ap-
proaches have been proposed for incremental CAD
reconstruction. These are limited in the range of de-
tectable geometric shapes geometric primitives, e.g.
(Denker et al., 2013).
For incremental CAD reconstruction, two impor-
tant aspects have to be considered: 1. Depth images
must be accumulated in an incrementally expandable
data structure. 2. Geometric features must be ex-
tracted from this data structure online. Both aspects
must enable a responsive overall system. We consider
1 Hz a sufficient frame rate as motivated by a system
with similar premises (Sand, 2019). In this paper, we
consider incremental CAD reconstruction of quadric
surfaces and contribute to both of the aforementioned
aspects: 1. A memory-efficient expandable segment
graph of over-segmented point clouds. 2. A region-
merging algorithm that allows fast quadric fitting on
this graph.
To our best knowledge, this is the first approach
to combine reconstruction of general quadric surface
from a series of point clouds with a computational ef-
ficiency that allows an incremental online execution.
Bloeß, J. and Henrich, D.
Incremental Online Reconstruction of Locally Quadric Surfaces.
DOI: 10.5220/0010795100003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages
155-162
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
155

2 RELATED WORK
An extensive survey of techniques for reconstruction
of shapes from point clouds is given in (Kaiser et al.,
2019). According to this survey, RANSAC based ap-
proaches promise computational efficiency and ro-
bustness to outliers.
RANSAC (Random Sample Consensus) is a tech-
nique where a parameterized model of a shape is fitted
to a point cloud. A small number of points is ran-
domly drawn from the point cloud so that all model
parameters can be determined. This is repeated until
a shape is found that fits the point cloud with a high in-
lier ratio (Fischler and Bolles, 1981). The RANSAC
concept has the advantage of being robust towards
outliers and also being time efficient for the task of
finding the best fitting shape for a given point cloud.
However, if the points for each shape have to be deter-
mined first, RANSAC becomes more computationally
expensive (Gotardo et al., 2003). Hierarchical sam-
pling and lazy cost evaluation can be used to speed
up the process significantly, still the computation time
exceeds multiple seconds (Schnabel et al., 2007). For
the planar case, the algorithm was adapted to paral-
lelization on GPUs, which speeds up the computation
to a frame rate of 7 Hz (Alehdaghi et al., 2015). In
RANSAC, prior defined models limit the reconstruc-
tion to shapes of these specific models (Oesau et al.,
2016). Some works have extended RANSAC for gen-
eral quadrics (Frahm and Pollefeys, 2006). Point nor-
mals have been used as additional constraint to lower
the number of required points and thus increasing the
computational performance (Birdal et al., 2019).
Other techniques find the parameters of a shape
model using fitting methods from linear algebra. A
key requirement to this approach is that each point can
be embedded into a space where the model param-
eters have linear influence on a cost function. Then
solving an Eigenvalue problem of the scatter matrix
of the points, after said embedding, yields an alge-
braic solution (Taubin, 1991), (Luk
´
acs et al., 1998).
This embedding is possible for quadrics (Andrews
and S
´
equin, 2013). We explain this in more detail in
Section 3.3.1. These techniques can be enhanced with
knowledge about prior probabilities in order to im-
prove the fitting result when only small point clouds
are available (Beale et al., 2016). The normals of each
point can be used to increase the robustness of the fit
(Tasdizen et al., 1999). Strict type constraints can be
applied to the problem to force the result to be some
desired type of quadric (Andrews and S
´
equin, 2013).
Segmentation of point cloud is a key component
of surface reconstruction. Segmentation is the pro-
cedure of partitioning the points from a point cloud
into segments with some criterion of homogeneity.
This criterion can be based on some prior knowl-
edge about object shapes so that each segment corre-
sponds to a real-world object (Kim et al., 2012). For
general scene reconstruction, this prior information is
not available, and techniques that are based on point
feature similarity are more suitable for segmentation.
A set of point features is proposed with the point
feature histogram (Rusu et al., 2009). Point feature
based segmentation techniques produce a locally cor-
rect segmentation since point features are computed
from the local neighbourhood of a point. Smooth-
ness can be used as local homogeneity criterion to
compute an over-segmentation of a point cloud (Pa-
pon et al., 2013). In order to obtain a final segmenta-
tion from this over-segmentation, a homogeneity cri-
terion between segments is required. Principal curva-
tures and normal similarity of segments can be used to
merge them (Arbeiter et al., 2014). Another possibil-
ity is a global criterion using a priori knowledge about
shapes occurring in the scene. For many approaches
this a priori knowledge is the assumption that a scene
consists of a small set of parameterizable primitives
(Vanco and Brunnett, 2002) . We take a similar ap-
proach, but we assume general quadrics and use an ac-
cording model to impose our homogeneity criterion.
The typical process for reconstruction from point
clouds consists of a phase of data acquisition fol-
lowed by segmentation and model extraction (Buon-
amici et al., 2018). This comes with a computa-
tional load of processing all the acquired data at once,
which makes these systems unsuitable for online ap-
plications. An alternative approach is to use vol-
umetric representations where point clouds refine a
signed distance function (SDF). The SDF is defined
across the whole volume of the scene and implicitly
defines a surface at its zero-level. It can be repre-
sented by a voxel-grid of function values (Newcombe
et al., 2011). Hence, memory consumption limits the
volume of reconstruction for these techniques. Us-
ing GPU-accelerated computations, these techniques
reach high frame rates of more than 40 Hz. More so-
phisticated representations of the SDF, like octrees,
have been used to lower memory consumption (Whe-
lan et al., 2012).
For limited sets of primitives, online, incremental
reconstruction concepts have been proposed. Planar
boundary representations can be built incrementally
from the data of a hand-held device with 2 Hz (Sand,
2019). A spatial partitioning and aggregation of point
features can be used to reconstruct planes, cylinder
and spheres (Denker et al., 2013).
GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications
156

Figure 1: A schematic overview of our approach showing control flow in green arrows
and intermediate results.
Figure 2: Seg-
mentation (top)
and an over-
segmentation
(bottom).
Figure 3: Fitting
without (top)
and with (bot-
tom) normal
constraints.
3 CONCEPT
In this section, we present our approach towards in-
cremental reconstruction of quadric surfaces.
Given is a series of point clouds (P
1
, P
2
, ...). Each
P
t
is a set of points. For a point p, its position is
denoted as POS(p) ∈ R
3
. We assume that the extrinsic
parameters of the depth sensor are known, e.g. by
using a robot manipulator. Our goal is to find a set
of quadrics {q
1
, q
2
, ...} that reconstructs the surface
captured by (P
1
, P
2
, ...) with a low geometrical error.
A quadric q is a quadratic polynomial
q(x, y, z) := C
T
q
θ(x, y, z).
(1)
with
C
q
= (c
xx
, ..., c
1
)
T
∈ R
10
(2)
θ(x, y, z) := (x
2
, y
2
, z
2
, xy, xz, xy, x, y,z, 1) (3)
Each quadric q defines a surface
S
q
:= {(x, y, z) ∈ R
3
|q(x, y, z) = 0} (4)
An overview of our approach is given in Figure
1. These are the individual steps, following sections
explain them in more detail:
a) a point cloud is recorded
b) build local segment graph from over-
segmentation
c) expand a global segment graph using the local
segment graph
d) incrementally accumulate point clouds in global
segment graph
e) region-merging fits quadric surfaces
3.1 Over-segmentation
Given a point cloud P, let S
∗
= {P
∗
0
, P
∗
1
, ...}, P
∗
i
⊆ P
be the segmentation of P where each segment P
∗
i
can
be fitted by one quadric surface. The direct computa-
tion of S
∗
is a hard problem. In this work, we reduce
the complexity of this problem by first computing
an over-segmentation of S
∗
. An over-segmentation
S = {P
0
, P
1
, ...} of S
∗
is a segmentation of P where
∀P
i
∈ S∃P
∗
j
∈ S
∗
: P
i
⊆ P
∗
j
. (5)
An example of over-segmentation is visualized in Fig-
ure 2.
We use supervoxel clustering (Papon et al., 2013)
to compute S. The algorithm selects seed points in
P using a uniform grid (parameter s
size
governs the
cell size of the grid). Clusters are formed by assign-
ing each point to the respectively nearest seed using a
metric that considers spatial distance and similarity of
the estimated surface normal in a point. Afterwards,
the seed of each cluster is updated to the mean po-
sition and normal of all points in the cluster. These
steps are repeated until the clusters converge, five it-
erations are suggested (Papon et al., 2013).
3.2 Segment Graph
We define a segment graph G = (V, E). Vertices V are
segments from an over-segmentation of point clouds
and edges E indicate whether two segments are spa-
tially neighbored.
For each point cloud P
t
in a series (P
1
, P
2
, ...),
we build a local segment graph G
t
l
using an over-
segmentation of P
t
. We incrementally build a global
segment graph G
t
g
by merging G
t−1
g
and G
t
l
.
Incremental Online Reconstruction of Locally Quadric Surfaces
157

We start with G
0
g
= (
/
0,
/
0). An over-segmentation
S of P
t
is computed according to Section 3.1, G
t
l
is
computed from S. For t = 1, we set G
1
g
:= G
1
l
. For
t > 1, over-segmentation of P
t
is modified:
• the nearest point in P
t
to the center of each seg-
ment from G
t−1
g
is selected as seed. Points se-
lected by the uniform grid are only used as seeds,
if there is not already another seed withing dis-
tance s
size
• only centers of clusters not initialized by the uni-
form grid are updated. Centers of clusters initial-
ized by segments from G
t−1
g
are static.
Effects of these modifications are shown in Figure 4.
The incremental update is done by merging
G
t−1
g
= (V
t−1
g
, E
t−1
g
) and G
t
l
= (V
t
l
, E
t
l
) to G
t
g
=
(V
t
g
, E
t
g
):
We denote V
U
the set of all segments in G
t−1
g
that
initialized a cluster in the over-segmentation of P
t
.
For all P
i
∈ V
U
, we denote α(P
i
) ∈ V
t
l
the segment
whose seed center was used to select the seed of P
i
.
First, segments in V
U
are updated with the respective
points from V
t
l
:
V
∗
U
:= {P
i
∪ α(P
i
)|P
i
∈ V
U
} (6)
Segments of the next global segment graph are
formed by
V
t
g
:= V
∗
U
∪ (V
t−1
g
\V
U
) ∪ (V
t
l
\ α(V
U
)) (7)
Edges E
t
g
are the union of E
t
l
and E
t−1
g
considering
segments P
i
and α(P
i
) as equivalent.
3.3 Fitting
A region-merging algorithm is used on the global seg-
ment graph G
t
g
with a homogeneity criterion based on
the Taubin Fit (Taubin, 1991).
3.3.1 Taubin Fit
Given a set of points P, the Taubin Fit (Taubin, 1991)
can be used to compute a quadric q
P
with minimal
average approximated squared distance of the points
in P to S
q
P
. The fitting quadric q
P
minimizes
d(q, P) :=
∑
p∈P
q(POS(p))
2
∑
p∈P
k∇q(POS(p))k
2
=
C
T
q
M
P
C
q
C
T
q
N
P
C
q
(8)
for q with
M
P
:=
∑
p∈P
θ(POS(p))θ(POS(p))
T
(9)
N
P
:=
∑
p∈P
∇θ(POS(p))∇θ(POS(p))
T
(10)
Finding q
P
can then be stated as the generalized
Eigenvalue problem
q
P
= argmin
q
C
T
q
M
P
C
q
C
T
q
N
P
C
q
(11)
From Equation 8, for two point sets P
a
, P
b
, the
Taubin Fit of P
a
∪ P
b
can be stated as
d(q, P
a
∪ P
b
) =
C
T
q
M
P
a
+ M
P
b
C
q
C
T
q
N
P
a
+ N
P
b
C
q
(12)
This means that it is sufficient to store M
P
and N
P
for points P in a segment of the segment graph. No
explicit representation of P is required. In this repre-
sentation, the union of two point sets P
a
∪ P
b
is com-
puted as:
M
P
a
∪P
b
= M
P
a
+ M
P
b
N
P
a
∪P
b
= N
P
a
+ N
P
b
(13)
3.3.2 Region Merging
Since a segment graph G = (V, E) represents an over-
segmentation, segments have to be merged to use the
Taubin Fit for quadric fitting. We define a homogene-
ity criterion between sets of segments, i.e. regions,
R
a
⊆ V and R
b
⊆ V :
HOM(R
a
, R
b
)
:= max
n
d(q
˜
P
a
∪
˜
P
b
,
˜
P
a
), d(q
˜
P
a
∪
˜
P
b
,
˜
P
b
)
o
with
˜
P
a
:=
[
P
i
∈R
a
P
i
and
˜
P
b
:=
[
P
i
∈R
b
P
i
.
(14)
Region merging proceeds as follows: We initialize a
set of 1-segment regions by R ← {{P
i
}|P
i
∈V }. Then,
we iteratively unify the pair of neighboring regions
R
a
and R
b
that minimizes HOM(R
a
, R
b
) as long as this
value does not exceed a user-defined threshold t
err
.
Finally, we use the Taubin Fit to find the best
fitting general quadric for each region R
i
∈ R. We
also use constrained Taubin Fit (Andrews and S
´
equin,
2013) to find the best fitting plane for R
i
. As long as
the Taubin error for the plane is below t
err
, we prefer
the plane fit over the general fit.
Even though, quadrics in general position have a
smooth surface, an edge of e.g. a cube can be approx-
imated with arbitrary precision using a quadric. Our
algorithm often fits a common quadric to two sides of
an edge. We put an additional constraint on the edges
E. We only keep edges between vertices whose av-
erage point normals are roughly the same. We use a
threshold of 0.7 for the dot product of the normals of
two segments. The effect is depicted in Figure 3.
GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications
158

(a) G
t−1
g
and P
t
before segmentation
(b) seeds for over-segmentation (c) result of over-segmentation
Figure 4: Segments from seeds selected by vertices of G
t−1
g
are centered around these vertices. Segments initialized by
additional seeds (green) move during supervoxel clustering.
large a medium a small a
large b medium b small b
Figure 5: Images of the scenes used for our data set.
4 EXPERIMENTS
We evaluate our concept in terms of accuracy and
computational efficiency. For this, we use public and
custom-made data sets (Section 4.1) and compare our
results to existing approaches (Section 4.2). We also
analyze the influence of the parameters of our ap-
proach.
4.1 Data Sets and Evaluation Methods
Our custom-made data set compromises six scenes
(see Figure 5). For each scene, we captured 15 point
clouds from different poses using an Ensenso N10
depth sensor mounted on a robotic manipulator for
extrinsic calibration. Each point cloud consists of
752×480 = 360, 960 points. We also evaluate our ap-
proach for single view reconstruction on the ITODD
data set (Drost et al., 2017) as well as a subset of the
redwood data set (Choi et al., 2016).
We build a ground truth set of quadrics for each
data set by manually segmentation and Taubin Fit. We
refer to (Andrews and S
´
equin, 2013) for an analysis of
the accuracy of Taubin Fit itself. In order to compare
a set of ground truth quadrics Q
∗
= {q
∗
1
, q
∗
2
, ...} to a set
of reconstructed quadrics Q = {q
1
, q
2
, ...} we define a
similarity relation ∼
QUAD
: Q
∗
× Q → {TRUE, FALSE}.
For the evaluation of q
∗
∼
QUAD
q we test the type,
shape and pose of q and q
∗
for similarity. We obtain
the shape of a quadric q as the three Eigenvalues of the
upper left 3× 3 matrix of the matrix representation of
q. For evaluation we define the following sets:
true positives = {q ∈ Q|∃q
∗
∈ Q
∗
: q
∗
∼
QUAD
q}
false positives = {q ∈ Q|@q
∗
∈ Q
∗
: q
∗
∼
QUAD
q}
false negatives = {q
∗
∈ Q
∗
|@q ∈ Q : q
∗
∼
QUAD
q}
4.2 Results
We investigate the influence of following parameters:
• t
err
: error threshold for quadric fit in Section 3.3
• s
size
: grid size for seed selection in Section 3.1
• v
size
: size of a voxel grid used by (Papon et al.,
2013) to downsample a point cloud
Table 1 shows hand optimized for these parame-
ters for our data set. According to this, s
size
depends
on the size of the objects in the scene and v
size
can be
set to
s
size
v
size
= 10. Figure 6 shows the reason for false
positives with small objects: Segments like 409 mis-
takenly cross the border between 400 and 398, which
causes the two planar surfaces to be merged into one
quadric. The errors in the medium and large data sets
can mostly be attributed to partially scanned objects.
Small connected components in the segment graph
can often be fitted by a plane, even if the underlying
surface is curved, see Figure 7a. Table 1 shows the
results for primitive fitting using RANSAC (Schnabel
et al., 2007). RANSAC fails to respect surface bound-
aries or fits large spheres to planar surfaces, see Figure
7b.
We sample values for each parameter around the
optimal value for medium b, see Figure 9. False pos-
itives, false negatives and true positives show that
t
err
= 5 · 10
6
is a good value. For lower values,
the algorithm many small surfaces. For higher val-
ues, surfaces are merged mistakenly, see Figure 8a.
Incremental Online Reconstruction of Locally Quadric Surfaces
159

Table 1: Results of RANSAC (Schnabel et al., 2007) and
ours with true positives (tp), false positives (fp) and false
negatives (fn) and hand optimized parameter values.
ours RANSAC
t
err
s
size
v
size
tp fp fn tp fp fn
large a 1·10
−5
0.08 0.008 6 0 0 3 2 3
medium a 5·10
−6
0.04 0.004 6 1 1 2 1 5
small a 5·10
−6
0.02 0.002 8 3 1 3 3 6
large b 1·10
−5
0.08 0.008 5 0 2 1 0 6
medium b 1·10
−5
0.04 0.004 6 0 0 1 4 5
small b 1.5·10
−6
0.02 0.002 6 2 3 4 5 5
Figure 6: Results for small b (left and middle) with false
negative quadrics (orange), false positive quadrics (red)
and true positive quadrics (green) and the local over-
segmentation of the points causing the false positives
(right).
All metrics are optimal for s
size
= 0.04. Computa-
tion time decreases from s
size
= 0.012 to s
size
= 0.04,
because computation time of fitting depends on the
number of segments (see Section 3.3). For higher
values, the computation time increases again. This
is caused by the implementation details of (Papon
et al., 2013). Figure 8b shows that with s
size
=
0.08 over-segmentation cannot preserve the border
between cone and side of the cuboid. For s
size
= 0.02,
each segment is supported by too few points, some
segments lie on the cuboid’s edges. Figure 9 shows
that low values for v
size
cause quantization errors.
We compare computation time for a series of point
(a) Results for medium a (left) and input data (right)
(b) RANSAC (left) and ours (right) on large a
Figure 7: False negative quadrics (orange), false positive
quadrics (red) and true positive quadrics (green).
(a) Results for t
err
= 5·10
−7
, 5·10
−6
, 2·10
−5
(b) Over-segmentation with s
size
= 0.02, 0.04, 0.08
(c) Over-segmentation with v
size
= 0.004, 0.008
Figure 8: Influence of different parameters on data set
medium b, values respectively from left to right.
clouds using our approach and RANSAC (Schnabel
et al., 2007). We incrementally reconstruct the data
set medium b using our approach and measure the
time for processing of each point cloud. We compare
this to RANSAC operating on increasing numbers of
merged point clouds of this data set, see Figure 10 for
results.
Figure 11 shows the numbers of correctly detected
cylinders by RANSAC and our approach for each
of the 15 point clouds from ITODD data set. The
point clouds contain increasing numbers of cylinders.
Our approach performs well for small numbers of
shapes (≤ 4) and slightly outperforms RANSAC in
this range. For > 9 cylinders, small connected com-
ponents in the segment graph cannot be merged by
region merging, see Figure 12.
We compare our approach to 4P-RANSAC (Birdal
et al., 2019). We use the following data from red-
wood data set (Choi et al., 2016): Rugby Ball (a), Pi-
lates Ball (b), Big Globe (c), Apple (d), Orange Ball
(e). Figure 13 compares our results to those stated in
(Birdal et al., 2019). 4P-RANSAC outperforms our
system for most data sets. Our algorithm is less suited
to deal with clutter in the scene. Figure 13 shows the
false negative (orange) for the Apple data set and the
segment graph (magenta edges and black vertices).
The segment graph connects points of the hand hold-
ing an apple to the points of the apple, which causes
our algorithm to fail finding the apple as a quadric.
GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications
160
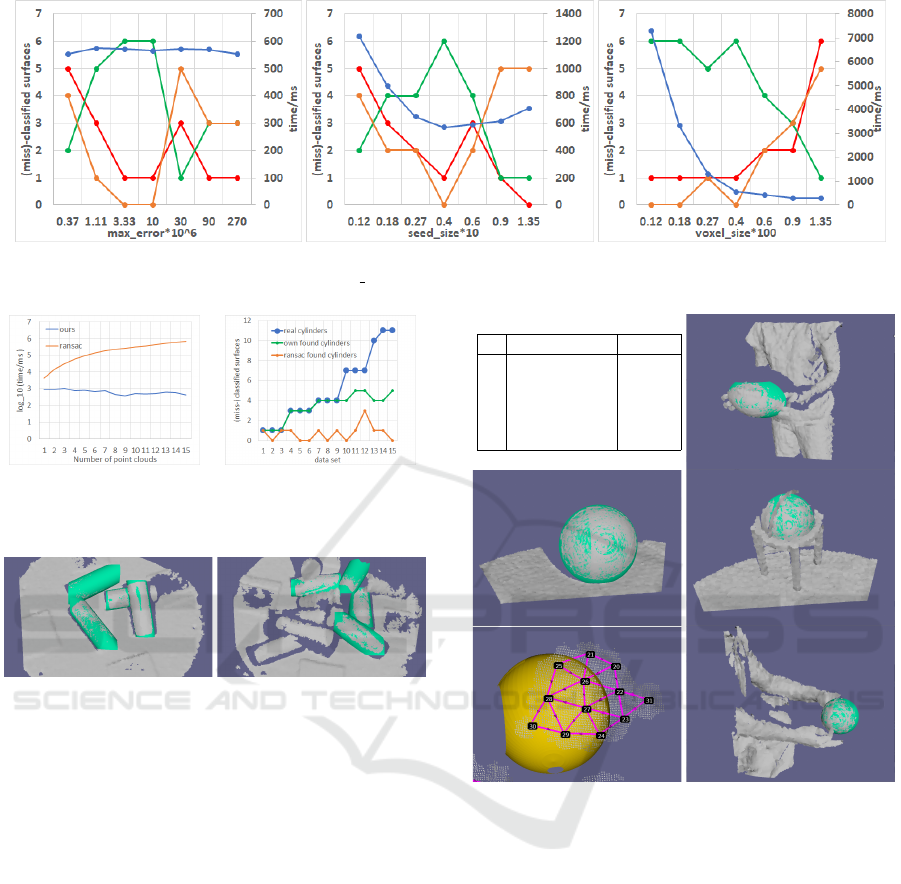
Figure 9: Average runtime per point cloud (blue), true positives (green), false positives (red) and false negatives (orange) for
different parameter values on the data set medium b.
Figure 10: Runtime of
RANSAC and ours for in-
creasing number of points.
Figure 11: Per scene metrics
for ours and (Schnabel et al.,
2007) on ITODD.
Figure 12: Cylinder detected by our approach in a scene of
4 real cylinders (left) and in a scene of 10 cylinders (right).
5 DISCUSSION AND PROSPECTS
In this paper, we present a novel technique for incre-
mental reconstruction of a piecewise quadric surface
from a series of point clouds. Our experiments show
that our memory representation of segments in a seg-
ment graph allows for fast fitting of quadric surfaces
to these segments. We show that our approach can
operate at a frame rate of 1 Hz for point clouds of
> 300, 000, which is by magnitudes faster than ex-
isting RANSAC based approaches with similar accu-
racy for scenes consisting of quadric surfaces. Fu-
ture improvements can be made on the fitting proce-
dure on our segment graph. Fitting is the only part
of our technique whose computation time depends on
the number of previously processed point clouds. We
plan to use an incremental fitting approach that only
recomputes the surface patches associated with seg-
ments that have been influenced by the current point
cloud. Furthermore, nodes from our segment graph
that belong to a quadric surface can be used to com-
4P-RANSAC Ours
a 100% 80.2%
b 100% 100%
c 90.7% 87.1%
d 99.6% 38.8%
e 93.3% 94.4%
a
b c
d e
Figure 13: Accuracy for detecting an ellipsoid within a
point cloud of the data set of (Choi et al., 2016) with ours
and 4P-RANSAC (Birdal et al., 2019).
pute an approximation of the surface’s boundary to
form a more accurate reconstruction that could also
be used for common CAD exchange formats.
ACKNOWLEDGEMENTS
This work has partly been supported by the Deutsche
Forschungsgemeinschaft (DFG) under grant agree-
ment He2696/16 HandCAD.
REFERENCES
Alehdaghi, M., Esfahani, M. A., and Harati, A. (2015).
Parallel RANSAC: Speeding up Plane Extraction in
Incremental Online Reconstruction of Locally Quadric Surfaces
161

RGBD Image Sequences using GPU. In 5th Interna-
tional Conference on Computer and Knowledge Engi-
neering, pages 295–300. IEEE.
Andrews, J. and S
´
equin, C. H. (2013). Type-Constrained
Direct Fitting of Quadric Surfaces. Computer-Aided
Design and Applications, 11(1):107–119.
Arbeiter, G., Fuchs, S., Hampp, J., and Bormann, R. (2014).
Efficient Segmentation and Surface Classification of
Range Images. In IEEE International Conference on
Robotics and Automation, pages 5502–5509. IEEE.
Beale, D., Yang, Y.-L., Campbell, N., Cosker, D., and Hall,
P. (2016). Fitting quadrics with a Bayesian prior.
Computational Visual Media, 2(2):107–117.
Beraldin, J.-A., Picard, M., El-Hakim, S. F., Godin, G.,
Valzano, V., and Bandiera, A. (2005). Combining 3D
technologies for cultural heritage interpretation and
entertainment. In Beraldin, J.-A., El-Hakim, S. F.,
Gruen, A., and Walton, J. S., editors, Videometrics
VIII, volume 5665, page 108.
Birdal, T., Busam, B., Navab, N., Ilic, S., and Sturm, P.
(2019). Generic Primitive Detection in Point Clouds
Using Novel Minimal Quadric Fits. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
pages 1–1.
Buonamici, F., Carfagni, M., Furferi, R., Governi, L., Lap-
ini, A., and Volpe, Y. (2018). Reverse engineering
modeling methods and tools: a survey. Computer-
Aided Design and Applications, 15(3):443–464.
Choi, S., Zhou, Q.-Y., Miller, S., and Koltun, V. (2016).
A Large Dataset of Object Scans. arXiv:1602.02481,
pages 1–7.
Denker, K., Hagel, D., Raible, J., Umlauf, G., and Hamann,
B. (2013). On-Line Reconstruction of CAD Geome-
try. In 2013 International Conference on 3D Vision,
pages 151–158. IEEE.
Drost, B., Ulrich, M., Bergmann, P., Hartinger, P., and Ste-
ger, C. (2017). Introducing MVTec ITODD — A
Dataset for 3D Object Recognition in Industry. In
2017 IEEE International Conference on Computer Vi-
sion Workshops (ICCVW), volume 2018-Janua, pages
2200–2208. IEEE.
Fischler, M. a. and Bolles, R. C. (1981). Random Sample
Paradigm for Model Consensus: Applications to Im-
age Analysis and Automated Cartography. Communi-
cations of the ACM, 24(6):381–395.
Frahm, J.-M. and Pollefeys, M. (2006). RANSAC for
(Quasi-)Degenerate data (QDEGSAC). In 2006 IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition - Volume 1 (CVPR’06), vol-
ume 1, pages 453–460. IEEE.
Gotardo, P., Bellon, O., and Silva, L. (2003). Range Im-
age Segmentation by Surface Extraction using an Im-
proved Robust Estimator. In IEEE Computer Society
Conference on Computer Vision and Pattern Recogni-
tion, volume 2. IEEE Comput. Soc.
Kaiser, A., Ybanez Zepeda, J. A., and Boubekeur, T. (2019).
A Survey of Simple Geometric Primitives Detection
Methods for Captured 3D Data. Computer Graphics
Forum, 38(1):167–196.
Kim, Y. M., Mitra, N. J., Yan, D.-M., and Guibas, L.
(2012). Acquiring 3D Indoor Environments with Vari-
ability and Repetition. ACM Transactions on Graph-
ics, 31(6):1.
Luk
´
acs, G., Martin, R., and Marshall, D. (1998). Faith-
ful Least-squares Fitting of Spheres, Cylinders, Cones
and Tori for Reliable Segmentation. In Computer Vi-
sion - ECCV’98, 5th European Conference on Com-
puter Vision, volume 1.
Makhal, A., Thomas, F., and Gracia, A. P. (2018). Grasping
Unknown Objects in Clutter by Superquadric Repre-
sentation. In Second IEEE International Conference
on Robotic Computing, pages 292–299. IEEE.
Newcombe, R. A., Izadi, S., Hilliges, O., Molyneaux, D.,
Kim, D., Davison, A. J., Kohli, P., Shotton, J., Hodges,
S., and Fitzgibbon, A. (2011). KinectFusion: Real-
time dense surface mapping and tracking. 2011 10th
IEEE International Symposium on Mixed and Aug-
mented Reality, ISMAR 2011, pages 127–136.
Oesau, S., Lafarge, F., and Alliez, P. (2016). Planar Shape
Detection and Regularization in Tandem. Computer
Graphics Forum, 35(1):203–215.
Papon, J., Abramov, A., Schoeler, M., and Worgotter, F.
(2013). Voxel Cloud Connectivity Segmentation -
Supervoxels for Point Clouds. Proceedings of the
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition, pages 2027–2034.
Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast Point
Feature Histograms (FPFH) for 3D registration. In
2009 IEEE International Conference on Robotics and
Automation, pages 3212–3217. IEEE.
Sand, M. (2019). Inkrementelle Rekonstruktion von
planaren Volumenmodellen mit handgehaltenen
Tiefenkameras (German). PhD thesis, University of
Bayreuth, Bayreuth.
Schnabel, R., Wahl, R., and Klein, R. (2007). Efficient
RANSAC for Point-Cloud Shape Detection. Com-
puter Graphics Forum, 26(2):214–226.
Tasdizen, T., Tarel, J. P., and Cooper, D. B. (1999). Al-
gebraic curves that work better. Proceedings of the
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition, 2(February):35–41.
Taubin, G. (1991). Estimation of Planar Curves, Sur-
faces, and Nonplanar Space Curves Defined by Im-
plicit Equations with Applications to Edge and Range
Image Segmentation. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 13(11):1115–
1138.
Vanco, M. and Brunnett, G. (2002). Direct Segmentation
for Reverse Engineering. In First International Sym-
posium on Cyber Worlds, 2002. Proceedings., pages
24–31. IEEE Comput. Soc.
Vempati, A. S., Kamel, M., Stilinovic, N., Zhang, Q.,
Reusser, D., Sa, I., Nieto, J., Siegwart, R., and Beards-
ley, P. (2018). PaintCopter: An Autonomous UAV for
Spray Painting on Three-Dimensional Surfaces. IEEE
Robotics and Automation Letters, 3(4):2862–2869.
Whelan, T., Kaess, M., and Fallon, M. (2012). Kintinuous:
Spatially extended kinectfusion. RSS Workshop on
RGB-D: Advanced Reasoning with Depth Cameras,
page 7.
GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications
162
