Salting as a Countermeasure against Attacks on Privacy Preserving

Record Linkage Techniques

Yanling Chen

, Rainer Schnell

, Frederik Armknecht

and Youzhe Heng

Methodology Research Unit, University of Duisburg-Essen, Duisburg, Germany

Practical Computer Science Unit, University of Mannheim, Mannheim, Germany

Keywords:

PPRL, Bloom Filter, Salting, Pattern Mining Attack, Graph-matching Attack.

Abstract:

Privacy-preserving record linkage (PPRL) is the research area dedicated to linking records from multiple

databases for the same patient without revealing identifying information during the linkage. A popular PPRL

approach is based on Bloom ﬁlters (BF). Recent research has shown that BF based PPRL could be vulnerable

to cryptanalysis attacks. Among several hardening techniques, salting was considered to be one of the most

suitable defences. A thorough evaluation of the amount of protection provided by salting is lacking from the

literature. In this paper, we empirically evaluate the effect of salting on privacy by demonstrating the resilience

of salted BF to the two most advanced attack methods: pattern mining and graph-matching. Experimental

results show that salting could improve resilience against both attacks, although more minor against graph-

matching attacks than pattern mining attacks.

1 INTRODUCTION

In medical research, especially in population covering

research, linking databases residing at different par-

ties such as hospitals, health insurance companies, or

population registries is often required. Records can be

easily linked if a common entity identiﬁer across the

databases is available, otherwise, record linkage could

be already a challenge task since common attributes

must be used. In medical research, these common

attributes (often referred to as quasi-identiﬁers) are

typically names, dates of birth, addresses etc. They

are usually neither stable over time nor available for

all cases, and could be recorded with errors in many

cases. Finally, quasi-identiﬁers such as names are

widely considered as sensitive information, the leak-

age of which would violate data privacy regulations.

Over the last decade, many different PPRL meth-

ods have been suggested that are usually divided into

two categories: perturbation and secure multiparty

computation (SMC) based techniques (Vatsalan et al.,

2013). Perturbation-based techniques are generally

efﬁcient; they provide adequate linkage quality and

are scalable to link large databases but lack privacy

protection proofs. SMC based techniques, although

provably secure and accurate, generally have high

computation and communication costs. Therefore,

the former is better suited for real-world applications.

One popular perturbation based technique is based

on Bloom ﬁlter (BF) encoding. In the context of

PPRL, (Schnell et al., 2009) initially suggested gen-

erating one BF per attribute, allowing multiple simi-

larities to be calculated if several attributes are used

to compare records. This approach is now usually

denoted as Attribute Bloom Filters (ABFs). Since

ABFs are susceptible to frequency-based privacy at-

tacks (Niedermeyer et al., 2014), encoding multiple

attribute values from a record into one single BF us-

ing an OR operation on separate BFs for each at-

tribute has been suggested under the label Crypto-

graphic Long term Key (CLK) (Schnell et al., 2011)

encoding. Record level Bloom ﬁlter (RBF) encoding

(Durham et al., 2014), as an alternative to CLK, also

encodes values from several attributes into one BF per

record. Different from CLK, RBF uses a weighted bit

sampling process to generate record level BFs.

1.1 Related Work

BF based PPRL is now being used in a variety of

real-world applications (Boyd et al., 2015; Antoni and

Schnell, 2019). However, research (Kuzu et al., 2011;

Niedermeyer et al., 2014; Christen et al., 2019; Chris-

ten et al., 2018; Vidanage et al., 2020) has shown that

BF based PPRL can be vulnerable to cryptanalysis at-

tacks aiming to re-identify some sensitive values in

Chen, Y., Schnell, R., Armknecht, F. and Heng, Y.

Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques.

DOI: 10.5220/0010787200003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 5: HEALTHINF, pages 353-360

ISBN: 978-989-758-552-4; ISSN: 2184-4305

353

plaintext. Among the existing attacks, recently pro-

posed pattern mining attack (Christen et al., 2018)

and graph-matching attack (Vidanage et al., 2020) are

considered to be the most powerful since they could

provide more accurate re-identiﬁcations and they are

computationally efﬁcient.

In response to earlier attacks, various BF harden-

ing techniques have been proposed, including balanc-

ing, salting, XOR-folding and so on (Christen et al.,

2020). In general, there is a trade-off between the

level of privacy and the linkage quality obtained when

using these techniques because hardened BFs likely

result in distorted similarities compared to plaintext

similarities (Christen et al., 2020; Franke et al., 2021).

As is remarked by (Christen et al., 2020), so far, for no

hardening technique, a proper proof of security exists.

Nevertheless, given the state of cryptanalysis attack

methods, salting seems to be one of the most promis-

ing. (Christen et al., 2020) recommended using salted

BF for PPRL if a stable salt could be extracted from

the available quasi-identiﬁers.

1.2 Our Contribution

In this paper, we evaluate the resilience of salted BF

against the two most advanced attack methods: pat-

tern mining and graph-matching. These attacks are

so far considered to be the most powerful attacks on

PPRL techniques. Therefore, investigating the limi-

tations of the attacks and their potential countermea-

sures are important for PPRL applications in practice.

To the best of our knowledge, this paper is the ﬁrst

study on how different salt choices modify the fre-

quency distribution of the q-grams in the records and

the neighbourhood of the records in a dataset. Our re-

sults on investigating why salting is effective against

the pattern mining attack and how salting impacts the

performance of the graph matching attack is new. Fi-

nally, we provide additional evidence that the success

of both attacks depends critically on the data available

to the attacker.

2 PRELIMINARIES

2.1 Bloom Filter Encoding

BFs were developed to test whether an element is a

member of a certain set (Bloom, 1970). Formally, a

BF can be deﬁned as follows.

Deﬁnition 1 (BF encoding). A Bloom ﬁlter bf con-

sists of an array of n bits, bf[0] to bf[n − 1], ini-

tially all set to 0. It uses k independent random hash

functions h

,··· , h

with range [0,··· ,n − 1]. Denote

H = {h

,··· , h

}. To store a set X = {x

,...,x

|X |

} in

the Bloom ﬁlter, for x ∈ X , the bits at positions h

(x)

in bf are set to 1, for 1 ≤ j ≤ k. Formally, we have

bf : X → {0, 1}

, where

bf[i] =



1, if ∃ x ∈ X ,h ∈ H s.t. h(x) = i;

0, else.

A Bloom ﬁlter based PPRL uses a BF to repre-

sent the set of q-grams generated from one or more

attribute values from each record that needs to be en-

coded. A q-gram is a sub-string of length q charac-

ters extracted from a string using a sliding window

approach. For instance, when using q = 2 (known as

bigrams), the string “bloom” is converted into the set

of bigrams: {bl,lo, oo, om}. Using BF encoding, each

bigram in the set {bl, lo,oo,om} is mapped to a set of

bit positions which are set to 1 in the resulting BF.

2.2 BF Encoding with Salting

In the PPRL literature, salting has been proposed as a

hardening technique in (Niedermeyer et al., 2014) to

incapacitate re-identiﬁcation attacks on Bloom ﬁlters

by adding an extra string value to each q-gram be-

fore it is hashed. That is, instead of hashing q-grams,

salted q-grams are hashed.

As suggested in (Niedermeyer et al., 2014), for

PPRL, the salt values should be record-speciﬁc and

do not contain any errors (so preferably do not change

over time). In our application here we choose the fol-

lowing salts:

• the year of birth, or the full date of birth,

• the 2nd, 3rd letters of the ﬁrst name, and if a ﬁrst

name has less than 3 letters, pad it with ’2’,

• the 2nd, 3rd, 5th letters of the last name, and if the

last name has less than 5 letters, pad it with ’2’.

These salt choices are inspired by the Statistical

Linkage Key (often denoted as ’581’) used by the

Australian Institute of Health and Welfare (for de-

tails, see (Christen et al., 2020)). For simplicity,

we use ’salt-FN’, ’salt-LN’, ’salt-YOB’ to denote

the record-speciﬁc salt extracted from the ﬁrst name

(FN), last name (LN) and year of birth (YOB) as de-

scribed above, respectively; and ’salt-FN+LN+YOB’

(or ”salt-All” for simplicity) be their concatenation.

2.3 Information and Statistical

Measures for a Distribution

As pointed out in (Christen et al., 2020), exploiting

frequency information is the main approach for many

HEALTHINF 2022 - 15th International Conference on Health Informatics

354

cryptanalysis attacks on PPRL based on BF encoding.

So a good hardening technique aims to reduce the fre-

quency information to the minimum. Ideally, the fre-

quency distribution of interest should be as close as

possible to be uniform, since this distribution gives

no speciﬁc information to an attacker. Here we re-

call some suitable measures of the deviation from the

uniform distribution.

2.3.1 Information Measures for a Distribution

Given a random variable W, we denote its probability

at W = w to be Pr{W = w}. Then the entropy H(W )

is deﬁned by

H(W ) = −

∑

Pr{W = w}log

Pr{W = w}. (1)

The predictability of W is deﬁned by max

Pr{W =

w} (i.e., the probability of the most likely case). Cor-

respondingly, the min-entropy H

∞

(W ) is

∞

(W ) = − log

(max

Pr{W = w}), (2)

that can be interpreted as the ”worst-case” entropy.

2.3.2 Distance Measures of Distributions

A method of measuring the distance between two

probability distributions is the Jensen-Shannon (JS)

divergence. In general, for two distributions P and Q,

their JS divergence D

(P||Q) is deﬁned by

(P||Q) =

(P||M) +

(Q||M), (3)

where M = (P + Q)/2; and D

(P||M) is the

Kullback-Leibler (KL) divergence:

(P||M) =

∑

P(x)log

P(x)

M(x)

. (4)

2.3.3 Measures of Distributional Discrepancy

The inequality among values of a frequency distribu-

tion can be measured by its Gini coefﬁcient. Let x

the frequency of label i, and there are n labels, then

the Gini coefﬁcient G is given by:

G =

¯x

∑

i=1

∑

j=1

− x

|, (5)

where ¯x is the mean of the frequency distribution. A

Gini coefﬁcient of 0 expresses perfect equality, while

a Gini coefﬁcient of 1 expresses maximal inequality.

3 IMPACT OF SALTING ON THE

FREQUENCY DISTRIBUTION

Recall that in PPRL based on BF encoding, each

record string is ﬁrst converted into a set of q-grams,

which is then mapped to a BF. If salting is applied, an

additional step prior to the BF encoding is to attach

the salt value to each q-gram before it is hashed. Let

X be the random variable (r.v.) of the q-gram; S be the

r.v. of the salt; X k S be the r.v. of the salted q-gram.

We have the following theorems, those proofs can

be obtained by applying basic inequalities in informa-

tion theory (Cover and Thomas, 2006).

Theorem 2. Sating increases the min-entropy, i.e.,

∞

(X) ≤ H

∞

(X kS).

Theorem 3. Sating increases the entropy, i.e.,

H(X) ≤ H(X k S) ≤ H(X) + H(S).

Theorem 2 and Theorem 3 show that salting in-

creases the min-entropy and the entropy of the ran-

dom variable applied; and the increase on the entropy

is upper bounded by the entropy of the salt. By def-

inition, min-entropy reﬂects the difﬁculty for a suc-

cessful guess of the random variable’s most probable

value, whilst entropy reﬂects the average difﬁculty for

a successful guess.

As an example, we consider X to be the random

variable of the q-gram in the attributes: FN, LN and

YOB, S be the random variable of ’salt-YOB’. As one

can see from Table 1, we have H(S) = 6.519. Ap-

plying ’salt-YOB’, we see from Table 2 that without

salting H

∞

(X) = 3.853 and H(X ) = 7.654; while with

salting H

∞

(X k S) = 9.366 and H(X k S) = 13.273.

Salting with ’salt-YOB’ leads to a min-entropy in-

crease by 5.513 and an entropy increase by 5.619 (up-

per bounded by the entropy of the salt, 6.519).

4 EXPERIMENTAL SETUP

4.1 Datasets

To evaluate the effectiveness of the salting technique

in enhancing the privacy against known attacks on

PPRL, we use for the experiments two public avail-

able synthetic training dataset (’census’, ’prd’) pro-

duced by the European Statistical Agency (Eurostat).

The datasets include about 25000 records containing

names, addresses, dates of birth, and gender etc.

Available at https://ec.europa.eu/eurostat/cros/content/

job-training en.

Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques

355

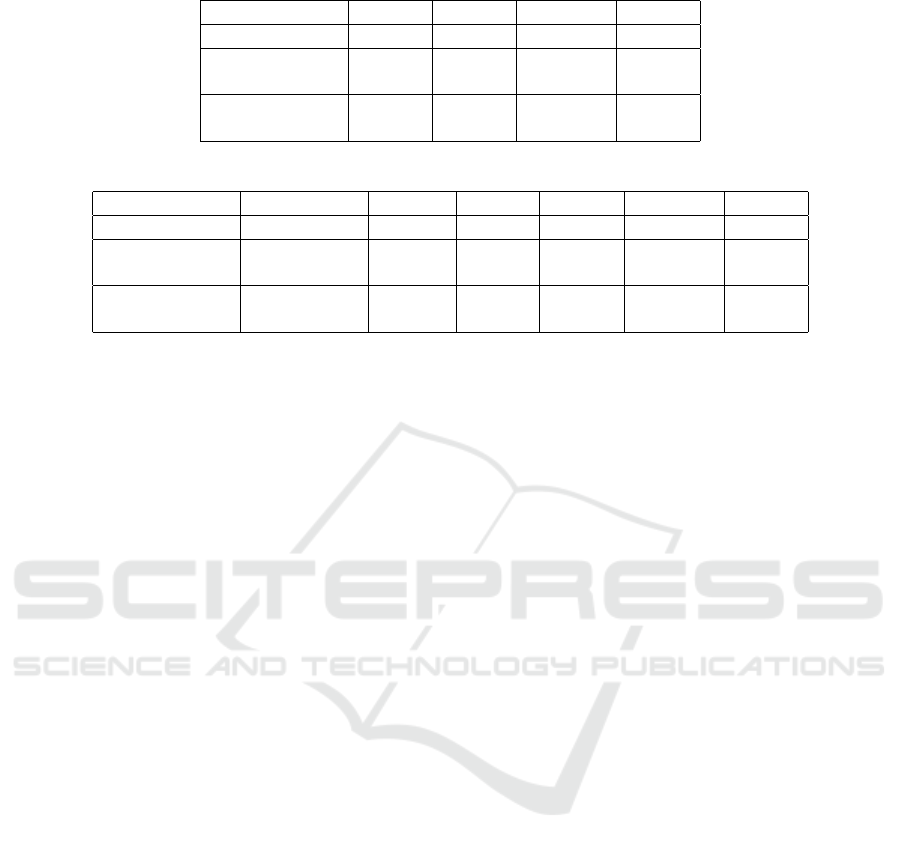
Table 1: Eurostat ’census’: Statistical summaries of salt-FN, salt-LN, salt-YOB and salt-ALL.

salt-FN salt-LN salt-YOB salt-All

Total number 261 427 104 24706

Entropy 6.626 6.862 6.519 14.578

Min-entropy 4.593 4.426 5.774 12.629

JS divergence 0.339 0.447 0.050 0.003

Gini coefﬁcient 0.718 0.773 0.264 0.025

Table 2: Eurostat ’census’: (concatenated) FN, LN and YOB, their bigrams, and the four variants of salted bigrams.

FN,LN,YOB bigrams salt-FN salt-LN salt-YOB salt-All

Total number 25225 585 36333 38682 27999 299595

Entropy 14.620 7.654 13.137 12.990 13.273 18.182

Min-entropy 13.629 3.853 8.185 8.018 9.366 16.221

JS divergence 0.00057 0.339 0.349 0.366 0.278 0.0024

Gini coefﬁcient 0.0046 0.720 0.733 0.741 0.666 0.019

4.2 Parameter Setup

The attributes under consideration for the generation

of salts include FN, LN and YOB. The resulting salts

are denoted as ’salt-FN’, ’salt-LN’, ’salt-YOB’ and

’salt-All’.

For BF encoding, we use the parameter settings:

q = 2,l = 1000, and k = 15, where q = 2 indicates that

bigrams are used in the BF encoding, l is the length of

the Bloom ﬁlter, and k is the number of hashing func-

tions. Note that BFs were encoded using the CLK

approach (Schnell et al., 2011) with random hashing

(Niedermeyer et al., 2014). These are parameters cur-

rently recommended or widely used in the literature

(Christen et al., 2020).

5 SALTING DIVERSIFIES THE

FREQUENCY DISTRIBUTION

The statistical summaries of different salt choices are

shown in Table 1. Among the single salt choices ’salt-

LN’ has the largest entropy; while ’salt-YOB’ has

the lowest JS divergence to the uniform distribution

and the smallest Gini coefﬁcien, However, overall the

combination ’salt-ALL’ yields the smallest JS diver-

gence to the uniform distribution, the smallest Gini

coefﬁcient and has the largest entropy. It is almost

unique for each record (24706 values of ’salt-All’ for

25343 entities).

Since a potential non-uniformity of the frequency

distribution of (salted) q-grams could be exploited by

an attacker (Christen et al., 2018), a comparison of

the frequency distributions of salted and unsalted q-

grams is of special interest here.

Using the three concatenated attributes FN, LN

and YOB as an example, the descriptive statistics of

the salted and unsalted bigram distributions are shown

in Table 2. Among the possible salt choices using a

single salt, the frequency distribution of the salted q-

grams using ’salt-YOB’ as salt is closest to the uni-

form distribution since its JS divergence and Gini co-

efﬁcient are smallest, and its min-entropy is largest.

Nevertheless, the frequency distribution of the

salted q-grams with ’salt-ALL’ yields the best unifor-

mity among the considered salt variants, in terms of

both the JS divergence and Gini coefﬁcient. In ad-

dition, its entropy and min-entropy increase are also

the largest. Consequently it would serve as the best

choice if it is stable for entities across datasets. How-

ever, in general, ’salt-ALL’ could be much less stable

since any error in ’salt-FN’, ’salt-LN’ or ’salt-YOB’

would remain in ’salt-ALL’, that might cause degra-

dation on the linkage quality.

6 SALTING AFFECTS LINKAGE

QUALITY

For the evaluation of linkage quality, we use samples

of n = 10000 records each of the Eurostat datasets

’census’ and ’prd’ with at least 90% of the records be-

ing true matches. In this section, ’salt-YOB’ is used

in the experiments. To assess linkage quality, we use

precision, recall, and the F-measure. To account for

the recent critique of the F-measure by (Hand and

Christen, 2017), we also use the mean of precision

and recall (MPR) as an alternative univariate measure

for the linkage quality.

The linkage quality (measured by MPR) as a func-

tion of a similarity threshold is shown in Fig. 1 (left).

Four different choices of the number of attributes and

the kind of salting are shown. We observe:

HEALTHINF 2022 - 15th International Conference on Health Informatics

356

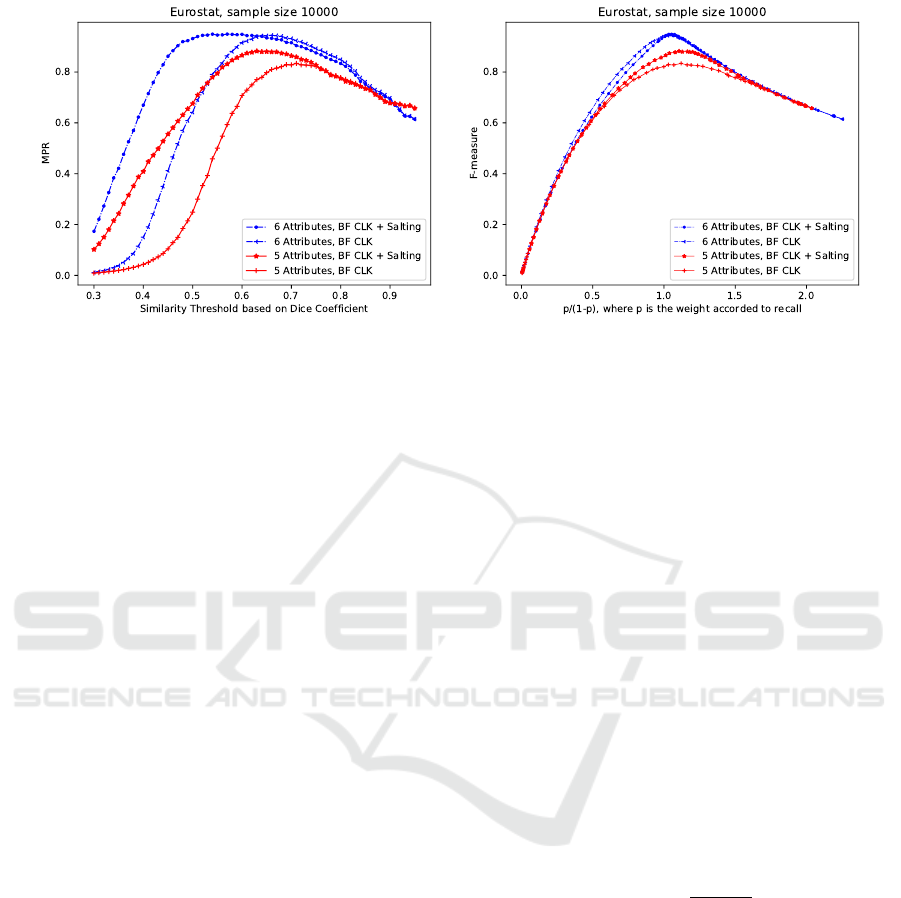
Figure 1: Linkage quality after different saltings (MPR left, F-measure right).

• For lower levels of similarity, salted BF might

yield higher MPR, indicating better linkage qual-

ity. This fact is caused by the propagation of dif-

ferences of salt values to other attribute values,

which could eliminate some false positives.

• Salting yields higher maximum MPR. Errors in

salt values may cause a slight decrease in linkage

quality at high thresholds, since some unwanted

false negatives may occur. However, this degra-

dation diminishes as the threshold increases until

the high threshold becomes the main cause of the

most false negatives.

The stability of the salt could be evaluated by

Pr{salt

= salt

|(record

,record

) is a match}. (6)

To obtain high linkage quality, a salt should be chosen

with high stability. For the sampled Eurostat datasets

in our experiments, the mean stability for salt-YOB

is 94.69% on average (with a standard derivation of

0.24%). The other salts show lower stabilities (salt-

FN: 84.68%, salt-LN: 84.86%, salt-ALL: 69.90%).

The plot in Fig. 1 (right) shows the effect of

salting on the F-measure of linkage quality. The x-

axis in the plot is the range of p/(1 − p), where p

and (1 − p) are the weights given to recall and pre-

cision, respectively, when interpreting F-measure as a

weighted arithmetic mean (Hand and Christen, 2017).

Salting results in higher F-values when a high weight

p is given to recall. Furthermore, the gain by salting

seems to be larger if fewer attributes are used.

7 SALTING IMPROVES PRIVACY

In this section, we assess the salting technique

with regard to the privacy protection it provides,

by demonstrating its resilience to the two most ad-

vanced attack methods: pattern mining (PM) and

graph matching (GM).

Before we proceed, we note that both attacks have

the following assumptions:

• The attacker has access to an encoded database E,

which contains sensitive data of people encoded

using a PPRL method such as BF encoding.

• The attacker has access to a plaintext database

P, which can be a publicly available population

database such as a telephone directory.

• The attacker does know or can guess the quasi-

identifying attributes that were encoded in E.

The goal of the attacker is to correctly re-identify as

many as possible the encoded records in plaintext.

Suppose that the encoded dataset E has n

en-

coded records, and the plaintext dataset P has n

records, where n

records are true matches between

them. Then the overlap rate between the plain and

encoded dataset can be deﬁned by

overlap

+ n

. (7)

Further, we assume that the attacker is aware of

whether salting is employed, and if yes, what kind of

salt value is applied.

7.1 Pattern Mining Attack

The pattern mining attack was proposed in (Chris-

ten et al., 2018). The codes using Python 2.7 in

Ubuntu 16.04 are made available by the authors at

https://dmm.anu.edu.au/pprlattack/.

The attack is based on the assumption that the dis-

tribution of the q-grams in the plaintext database P

provides a good approximation of the distribution of

Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques

357

Table 3: Results of PM Attack (Overlap 100%).

Attributes hardening

identiﬁed correct correctly identiﬁed # identical

q-grams bit-positions 1-to-1 record matches attributes values

None 33/438 470/485 1822/1967

2169

salt-FN 5/4272 74/74 0

FN, LN

None 76/485 1093/1132 4609/4993

19026salt-FN 5/26189 72/73 0

salt-LN 3/27532 43/48 0

FN, LN, YOB

None 43/585 604/623 2906/3089

salt-FN 6/36333 87/87 0

salt-LN 5/38682 57/80 0 25225

salt-YOB 0/27999 0 0

salt-ALL 0/299595 0 0

Table 4: Results of PM Attack (Overlap 96%).

Attributes hardening

identiﬁed correct correctly identiﬁed # unique # identical

q-grams bit-positions 1-to-1 record matches attributes values attributes values

None 8/432 102/103 294/294 2127(E)

1535

salt-FN 5/4212 74/74 0 2169(P)

FN, LN

None 73/483 985/1083 2089/2634 18629(E)

10701salt-FN 5/25900 72/72 0

salt-LN 3/27246 43/48 0 19026(P)

FN, LN, YOB

None 42/583 565/610 983/1625

12395

salt-FN 6/36021 86/88 0 24647(E)

salt-LN 5/38171 57/80 0

salt-YOB 0/27859 0 0 25225(P)

salt-ALL 0/293281 0 0

the q-grams in the corresponding plaintext of E. Espe-

cially, those frequent q-grams should have sufﬁciently

different frequencies so that they could be perfectly

aligned. Basically, the pattern mining technique ex-

ploits the non-uniformity and the inequality of the fre-

quencies in the frequency distribution of the q-grams.

For the evaluation of the attack performance, we

assess both the quality of re-identiﬁed q-grams and

the quality of re-identiﬁed records. In particular, we

consider the number of identiﬁed q-grams (over all

possible q-grams) and the accuracy of identiﬁed q-

grams for the former; and the number of identiﬁed 1-

to-1 record matches and how many were indeed true

matches for the latter.

As ﬁrst example, we consider a case where an at-

tacker has access to a BF encoded database E and the

same dataset in plaintext P. Therefore, their overlap

rate is 100%. For the example, we use the ’census’

dataset. Table 3 shows the results for the pattern min-

ing attack, where different choices of attributes for a

record are considered. Using attribute FN as an ex-

ample, we observe:

• Without salting, the attacker could re-identify 33

out of 438 q-grams, which could lead to 1822 cor-

rect record matches out of 1967 identiﬁed 1-to-1

record matches. Since there are in total 2169 1-

to-1 true record matches, the accuracy of the re-

identiﬁcation of the correspondence of the record

in plaintext and the encoded record is high.

• With salting (using ’salt-FN’), the total number of

q-grams is increased to 4272, out of which the

attacker could re-identify the bit positions for 5

salted q-grams. However, these are not sufﬁcient

to identify any 1-to-1 record matches.

Moreover, as the number of attributes used for link-

age increases, the number of the salted q-grams be-

comes larger (salting increases the entropy). At the

same time, fewer (salted) q-grams will be identi-

ﬁed than without salting (salting increases the min-

entropy). Therefore, salting is an effective counter-

measure against the pattern mining attack.

As a second example, we consider a high overlap

between the encoded dataset E and plaintext P. With

the example datasets ’prd’ as E and ’census’ as P we

observe an overlap of ≈ 96.2%. Table 4 shows the

results of the pattern mining attack. In this case, with-

out salting, the performance of the attack drops sub-

stantially compared to the previous case with com-

plete overlap between P and E. Furthermore, salt-

ing proves to be an effective countermeasure against

a pattern mining attack since it reduces the number of

identiﬁed q-grams considerably.

HEALTHINF 2022 - 15th International Conference on Health Informatics

358

Table 5: Eurostat: Results of GM Attack (Overlap 100%).

Sample size hardening

(# correct re-id, # wrong re-id)

max F-measure

max # correct re-id min # wrong re-id

1000

None (967, 6) (897, 0) 98.02%

Salt-FN (527, 147) (227, 33) 62.96%

Salt-LN (718, 78) (1, 0) 79.95%

Salt-YOB (299, 219) (22, 0) 39.39%

5000

None (4878, 0) (4878, 0) 98.76%

Salt-FN (4126, 235) (1036, 0) 88.18%

Salt-LN (4464, 123) (1, 0) 93.13%

Salt-YOB (3823, 502) (454, 0) 82.18%

Salt-ALL (5, 39) (2, 9) 0.20%

10000

None [9499, 2] [9494, 0] 97.42%

Salt-FN (8601, 290) (1, 0) 91.06%

Salt-LN (8874, 237) (1, 0) 93.17%

Salt-YOB (8737, 348) (639, 0) 91.56%

Salt-ALL (21, 130) (5, 2) 0.41%

Table 6: Eurostat: Results of GM Attack (Overlap > 80%).

Sample size hardening

(# correct re-id, # wrong re-id)

max F-measure

max # correct re-id min # wrong re-id

None (28, 729) (4, 35) 4.02%

1000 salt-FN (22, 406) (3, 31) 3.50%

overlap

= 83% salt-LN (14, 507) (4, 82) 2.07%

salt-YOB (14, 398) (3, 25) 2.25%

None (32, 1150) (6, 422) 2.44%

5000 salt-FN (88, 2656) (1, 0) 2.49%

overlap

= 86.66% salt-LN (97, 3159) (8, 378) 2.95%

salt-YOB (61, 3867) (1, 0) 1.55%

salt-ALL (2, 36) (2, 36) 0.09%

None (122, 7210) (15, 1846) 1.77%

10000 salt-FN (171, 5980) (10, 677) 2.34%

overlap

= 93.17% salt-LN (133, 5162) (63, 1856) 1.85%

salt-YOB (99, 6935) (12, 156) 1.21%

salt-ALL (7, 119) (1, 0) 0.15%

7.2 Graph Matching Attack

A very different type of attack from pattern mining is

graph-based, which was ﬁrst discussed by Culnane et

al. (Culnane et al., 2017) on a PPRL method based on

a keyed-hash message authentication code (HMAC)

and similarity tables, and further extended by (Vidan-

age et al., 2020), who considered several PPRL en-

coding methods including BF encoding.

The basic idea behind the graph matching attack

is that given the two databases that are from the same

domain, their graph representations will contain sim-

ilar neighborhoods for nodes that represent the same

value (plaintext or encoded corresponding to one or

more entities) across the two databases. To evaluate

the performance of the attack, we consider the num-

ber of correct record re-identiﬁcations, the number of

wrong record re-identiﬁcations, and the F-measure of

the record re-identiﬁcation. In the Tables 5 and 6 we

report the following statistics: 1) the maximum num-

ber of correct re-identiﬁcations followed by the least

number of wrong re-identiﬁcations, 2) the least num-

ber of wrong re-identiﬁcations followed by the maxi-

mum number of correct re-identiﬁcations, and 3) the

maximum F-measure of the record re-identiﬁcation.

The graph similarity attack was initially imple-

mented on a large server (Xeon 2.1 GHz 16-Core

CPUs, 512 GBytes of memory) by (Vidanage et al.,

2020) using Python 2.7. Their code is available at

https://dmm.anu.edu.au/pprlattack/. For our simula-

tions, we randomly sampled records from the ’census’

dataset, resulting in samples of n = 1000,5000,10000

(to circumvent memory problems on a PC). As at-

tributes, we considered FN, LN and YOB.

Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques

359

First we consider the case where the attacker has

access to a BF encoded database E and the same

dataset in plaintext P. Clearly their overlap rate is

100%. Table 5 shows results for the graph matching

attack in this scenario. It is apparent that

• without salting, the attacker could re-identify

records with a maximum F-measure approaching

or exceeding 98%;

• With salting, the performance of the attacks drops,

regardless which measure is used for comparison.

Interestingly, this drop decreases with increasing

sample size.

However, a stable salt value, almost unique for each

record, could effectively thwart the graph-matching

attack. Salt-ALL reduced the maximum F-measure

of the re-identiﬁcation from over 97% to below 0.5%.

Among the other salt variants, salt-YOB performs

best, especially for smaller samples.

As second example, we consider a case where

overlap

6= 100% but r

overlap

> 80%. Table 6 shows the

importance of the overlap rate for the success of the

graph matching attack. Given an overlap rate above

80%, both the maximum number of correct record

re-identiﬁcations and the maximum F-measure drops

strongly compared to the previous example given per-

fect overlap. For example, the maximum F-measure

drops from above 98% to about 1% ∼ 4%.

8 CONCLUSION

We studied the effect of salting on the resilience

against pattern mining and graph matching attacks in

PPRL. Salting was shown to be an effective counter-

measure against pattern mining attacks while less ef-

fective against graph matching attacks (unless a sta-

ble salt that is almost unique to each record value is

available). As an additional safeguard, salting is rec-

ommended for perturbation-based PPRL whenever a

stable salt is available.

REFERENCES

Antoni, M. and Schnell, R. (2019). The past, present

and future of the German Record Linkage Cen-

ter (GRLC). Jahrb

ucher f

ur National

okonomie und

Statistik, 239(2):319 – 331.

Bloom, B. H. (1970). Space/time trade-offs in hash coding

with allowable errors. Communications of the ACM,

13:422–426.

Boyd, J., Randall, S., and Ferrante, A. (2015). Application

of privacy preserving techniques in operational record

linkage centres. In Medical Data Privacy Handbook,

pages 267–287. Springer, Netherlands.

Christen, P., Ranbaduge, T., and Schnell, R. (2020). Linking

Sensitive Data. Methods and Techniques for Practical

Privacy-Preserving Information Sharing. Springer,

Cham, Switzerland.

Christen, P., Ranbaduge, T., Vatsalan, D., and Schnell, R.

(2019). Precise and fast cryptanalysis for Bloom ﬁl-

ter based privacy-preserving record linkage. IEEE

Transactions on Knowledge and Data Engineering,

31(11):2164–2177.

Christen, P., Vidanage, A., Ranbaduge, T., and Schnell, R.

(2018). Pattern-mining based cryptanalysis of Bloom

ﬁlters for privacy-preserving record linkage. In Ad-

vances in Knowledge Discovery and Data Mining,

pages 530–542, Cham. Springer Int. Publishing.

Cover, T. M. and Thomas, J. A. (2006). Elements of Infor-

mation Theory. Wiley-Interscience, USA.

Culnane, C., Rubinstein, B. I. P., and Teague, V. (2017).

Vulnerabilities in the use of similarity tables in com-

bination with pseudonymisation to preserve data pri-

vacy in the UK Ofﬁce for National Statistics’ privacy-

preserving record linkage. CoRR, abs/1712.00871.

Durham, E. A., Kantarcioglu, M., Xue, Y., Toth, C., Kuzu,

M., and Malin, B. (2014). Composite Bloom ﬁlters for

secure record linkage. IEEE Transactions on Knowl-

edge and Data Engineering, 26(12):2956–2968.

Franke, M., Sehili, Z., Rohde, F., and Rahm, E. (2021).

Evaluation of hardening techniques for privacy-

preserving record linkage. In Proceedings of the

24th International Conference on Extending Database

Technology, EDBT 2021, Nicosia, Cyprus, March 23 -

26, 2021, pages 289–300. OpenProceedings.org.

Hand, D. and Christen, P. (2017). A note on using the

F-measure for evaluating record linkage algorithms.

Statistics and Computing, 28:539–547.

Kuzu, M., Kantarcioglu, M., Durham, E., and Malin, B.

(2011). A constraint satisfaction cryptanalysis of

Bloom ﬁlters in private record linkage. In Privacy En-

hancing Technologies 11th International Symposium,

PETS 2011 Waterloo, ON, Canada, July 27-29, 2011,

volume 6794, pages 226–245, Heidelberg. Springer.

Niedermeyer, F., Steinmetzer, S., Kroll, M., and Schnell, R.

(2014). Cryptanalysis of basic Bloom ﬁlters used for

privacy preserving record linkage. Journal of Privacy

and Conﬁdentiality, 6(2):59–69.

Schnell, R., Bachteler, T., and Reiher, J. (2009). Privacy-

preserving Record Linkage Using Bloom ﬁlters. BMC

Medical Informatics & Decision Making, 9:41.

Schnell, R., Bachteler, T., and Reiher, J. (2011). A

novel error-tolerant anonymous linking code. Work-

ing Paper WP-GRLC-2011-02, German Record Link-

age Center, Duisburg.

Vatsalan, D., Christen, P., and Verykios, V. S. (2013). A

taxonomy of privacy-preserving record linkage tech-

niques. Information Systems, 38(6):946–969.

Vidanage, A., Christen, P., Ranbaduge, T., and Schnell,

R. (2020). A graph matching attack on privacy-

preserving record linkage. In CIKM ’20: The 29th

ACM International Conference on Information and

Knowledge Management, Virtual Event, Ireland, Oc-

tober 19-23, 2020, pages 1485–1494. ACM.

HEALTHINF 2022 - 15th International Conference on Health Informatics

360