
AAEGAN Loss Optimizations Supporting Data Augmentation on
Cerebral Organoid Bright-field Images
Clara Br
´
emond Martin
12 a
, Camille Simon Chane
1 b
, C
´
edric Clouchoux
2 c
and Aymeric Histace
1 d
1
ETIS Laboratory UMR 8051 (CY Cergy Paris Universit
´
e, ENSEA, CNRS), 6 Avenue du Ponceau, 95000 Cergy, France
2
Witsee, 33 Av. des Champs-
´
Elys
´
ees, 75008 Paris, France
Keywords:
Cerebral Organoid, Loss, Adversarial Autoencoder (AAE), Generation, Segmentation, t-SNE.
Abstract:
Cerebral Organoids (CO) are brain-like structures that are paving the way to promising alternatives to in vivo
models for brain structure analysis. Available microscopic image databases of CO cultures contain only a
few tens of images and are not widespread due to their recency. However, developing and comparing reliable
analysis methods, be they semi-automatic or learning-based, requires larger datasets with a trusted ground
truth. We extend a small database of bright-field CO using an Adversarial Autoencoder(AAEGAN) after
comparing various Generative Adversarial Network (GAN) architectures. We test several loss variations,
by metric calculations, to overcome the generation of blurry images and to increase the similitude between
original and generated images. To observe how the optimization could enrich the input dataset in variability,
we perform a dimensional reduction by t-distributed Stochastic Neighbor Embedding (t-SNE). To highlight a
potential benefit effect of one of these optimizations we implement a U-Net segmentation task with the newly
generated images compared to classical data augmentation strategies. The Perceptual wasserstein loss prove
to be an efficient baseline for future investigations of bright-field CO database augmentation in term of quality
and similitude. The segmentation is the best perform when training step include images from this generative
process. According to the t-SNE representation we have generated high quality images which enrich the
input dataset regardless of loss optimization. We are convinced each loss optimization could bring a different
information during the generative process that are still yet to be discovered.
1 INTRODUCTION
Cerebral organoids (CO) are brain-like structures that
are paving the way to promising alternatives to in
vivo models for brain structure analysis. Method im-
plementations such as automatic extraction of shape
parameters or size of organoid cultures, requires a
large amount of images (Kassis et al., 2019). The
scarcity of available data (worsened by the pandemic)
is currently a strong limitation to the development
of tools to support a more systematic use of CO
(Br
´
emond Martin et al., 2021). Data augmentation, a
prevalent method in the biomedical domain (Yi et al.,
2019), is a possible solution to overcome this issue.
Classical data augmentation strategies transform
the input images with a combination of rotations,
a
https://orcid.org/0000-0001-5472-9866
b
https://orcid.org/0000-0002-4833-6190
c
https://orcid.org/0000-0003-3343-6524
d
https://orcid.org/0000-0002-3029-4412
rescalings, etc, but the content variability that can be
observed when acquiring real bright-field images is
not reproduced. Deep learning generative methods,
called Generative Adversarial Networks (GAN), can
solve this problem. Originally introduced by Good-
fellow et al, (Goodfellow et al., 2014), GANs are
constituted by a generator and a discriminator net-
work trained in an adversarial strategy. Since their
introduction GANs have evolved and variations such
as CGAN, DCGAN, InfoGAN, Adversarial Auto En-
coder (AAE) etc. have been proposed to increase the
size of biomedical datasets (Yi et al., 2019).
In this paper, we select and improve the best GAN
architecture (AAE) to generate cerebral organoid
bright-field images. If the loss effect has already been
explored for others biological models in MRI (Lv
et al., 2021), to our knowledge, there is no systematic
comparative study proposed in the specific context of
CO bright-field image generation that gives a quan-
titative appreciation of this effect. In particular, we
Brémond Martin, C., Simon Chane, C., Clouchoux, C. and Histace, A.
AAEGAN Loss Optimizations Supporting Data Augmentation on Cerebral Organoid Bright-field Images.
DOI: 10.5220/0010780000003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
307-314
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
307
are interested in choosing a loss while guaranteeing
good quality of the generated data, as well as a good
variability of images obtained compared with the in-
puts in order to improve characterization tasks. The
contribution of this paper is to quantitatively investi-
gate the influence of various GAN-based approaches
and particularly AAEGAN losses in the specific case
of bright-field CO image generation using quantita-
tive metrics from the literature and a dimensional re-
duction of parameters. The second contribution is to
compare data augmentation optimizations using a U-
Net-based segmentation task.
2 METHOD
2.1 Resources
Our dataset is composed of 40 images from an open
access database (Gomez-Giro et al., 2019). 20 patho-
logical and 20 healthy CO were numerized with a
bright-field microscope over 3 days. The grayscale
images are 1088 × 1388 pixels. However, to compare
several networks within a reasonable time, the input
images are cropped and resized to 250 × 250 pixels,
maintaining the original proportions.
All algorithms are implemented in Python 3.6 (us-
ing an Anaconda framework containing Keras 2.3.1
and Tensorflow 2.1) and run on an Intel Core i7-
9850H CPU with 2.60 GHz and a NVIDIA Quadro
RTX 3000s GPU device.
2.2 Generative Adversarial Networks
Generative Adversarial Networks (GAN) are made
of two competing networks (Goodfellow et al.,
2014): the discriminative model (D) computes the
probability that a point in the space is an origi-
nal sample (o) from the dataset distribution(data).
However the generative model (G) maps the sam-
ples to the data space (z) by an objective func-
tion (F). D is trained to maximize the probability
of identifying the correct label (true/false) to both
generated (g) and original (o) samples. Simulta-
neously, G is trained to leverage the discrimina-
tor function expressed by: min
𝐺
max
𝐷
𝐹 (𝐷, 𝐺) =
𝐸
𝑜
𝑝
𝑑𝑎𝑡𝑎
[𝑙𝑜𝑔𝐷
𝑜
] + 𝐸
𝑔
𝑝
𝑔
[𝑙𝑜𝑔(1 − 𝐷(𝐺
𝑧
))].
Various GAN variations have been created since
its first implementation. To find the best suited net-
work, we consider five of the most known GAN-
architectures to increase the dataset: GAN (Good-
fellow et al., 2014) is the original implementation;
CGAN (Yi et al., 2019) gives to the generator in-
put the correct label (physiological or pathological);
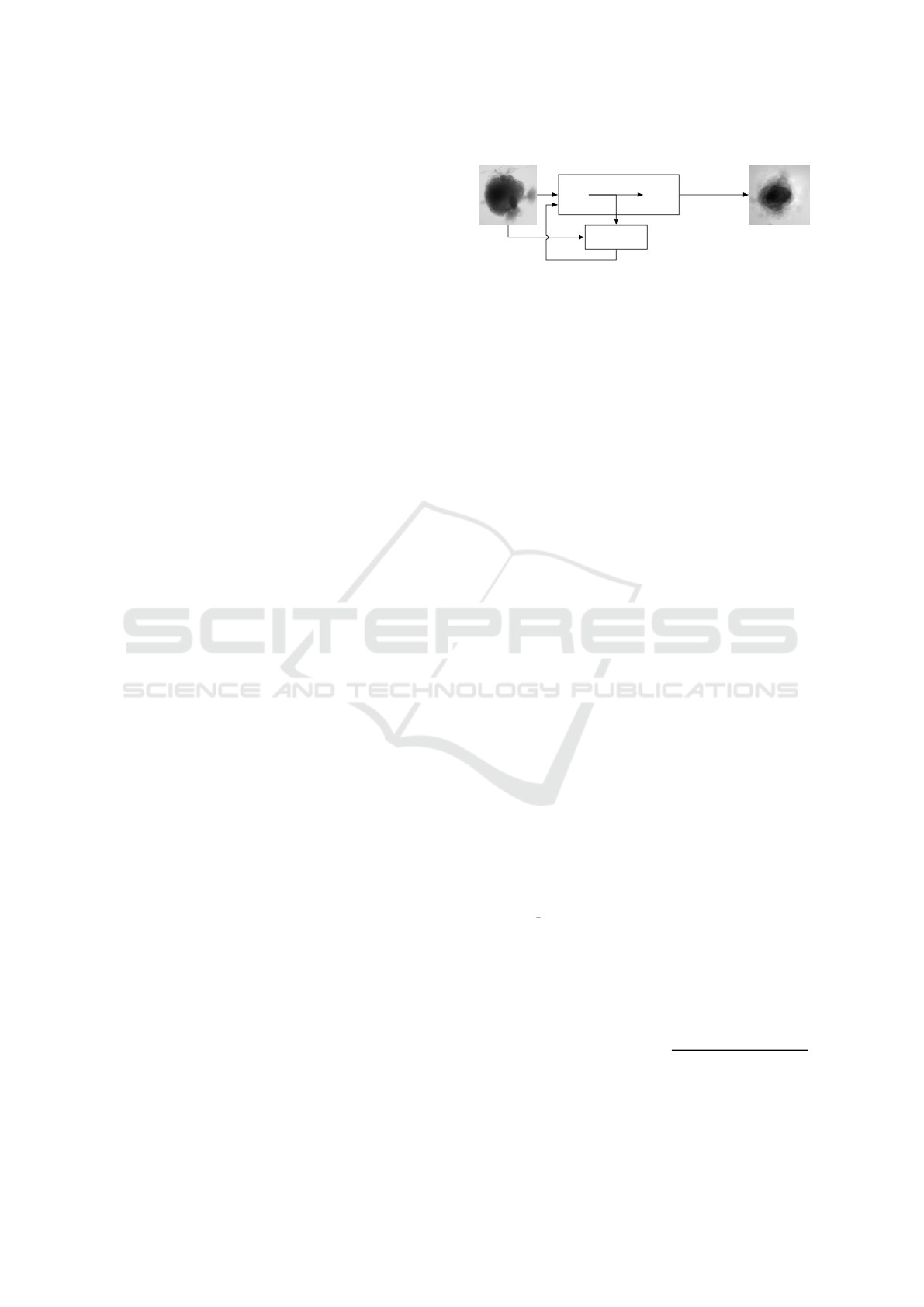
Input
Generator
Encoder Decoder
Output
Discriminator
every 100 epochs
∆loss
Figure 1: Experimental scheme of AAE supporting data
augmentation of cerebral organoids bright-field images.
The generator tries to persuade the discriminator that it has
generated a true and slightly variable image of input dataset.
The discriminator tries to find the true ones. They improve
each other by backpropagation, formulated by an objective
function based on a loss. Losses variations implemented
in this article are symbolized by Δ. Input image is from
(Gomez-Giro et al., 2019).
DCGAN (Yi et al., 2019) is constituted by a con-
volutional neural networks instead of the generator;
INFOGAN (Yi et al., 2019) uses the generated im-
ages at an epoch to train the subsequent; AAEGAN
(Makhzani et al., 2016) uses an autoencoder as a gen-
erator.
During a 1000 epoch duration training step, input
images of size 250 × 250 pixels are used to generate
synthetic images. In this work, the original 40 images
of the dataset are used to generate 40 synthetic im-
ages for a better follow-up by each architecture. The
number of images generated are chosen to guarantee
no mode collapse, as explained section 3.1.
2.3 Comparative Metrics
We calculate six metrics to compare the quality and
similitude of originals and generated images from the
various GAN architectures.
FID:Frechet Inception Distance satisfies most of the
requirements such as discriminability, or comparisons
of efficiency. This metric is used to determine the
image quality: a lower FID means smaller distance
between generated (g) and input data distribution (o
for original). In this equation, 𝜇 and Σ are respec-
tively the mean and co-variance of original and gen-
erated images: 𝐹𝐼𝐷(𝑜, 𝑔) = ∥𝜇
𝑜
− 𝜇
𝑔
∥
2
+
𝑇
(Σ
𝑜
+ Σ
𝑔
−
2(Σ
𝑜
Σ
𝑔
)
1
2
).
SSIM: The Structural Similarity Index compares pix-
els and their neighborhoods between two images us-
ing luminance, contrast and their structure. SSIM
has become a standard similarity measure to com-
pare synthetic and natural images even in the bi-
ological/medical domain. A high score stands for
high similitude: 𝑆𝑆𝐼 𝑀 (𝑜, 𝑔) =
(2𝜇
𝑜
𝜇
𝑔
+𝐶1) (2𝜎
𝑜
𝑔+𝐶2)
(𝜇
2
𝑜
+𝜇
2
𝑔
+𝐶1) ( 𝜎
2
𝑜
+𝜎
2
𝑔
+𝐶2)
Constants are added to stabilize the equations.
UQM:We have also implemented the universal qual-
ity metric which use the same contrast luminescence
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
308

and structures as the 𝑆𝑆𝐼 𝑀. A score of 1 indicate
an identical image. This metric is exposed below:
𝑈𝑄𝑀 (𝑜, 𝑔) =
4𝜇
𝑜
𝜇
𝑔
𝜇
𝑜
𝑔
(𝜇
2
𝑜
+𝜇
2
𝑔
) ( 𝜎
2
𝑜
+𝜎
2
𝑔
)
.
MI:In addition to these well established metrics, we
have also calculated the entropy-based Mutual Infor-
mation between input and generated images in order
to measure their correlation (highest score is equal to
1): 𝑀 𝐼 (𝑂, 𝐺) =
Í
𝑜∈𝑂
Í
𝑔∈𝐺
𝑃(𝑜,𝑔)𝑙𝑜𝑔
𝑃 (𝑜,𝑔)
𝑃 (𝑜) 𝑃 (𝑔)
.
Blur:To quantify the loss impact on the blurring
effect mentioned before, we use the blur met-
ric based on a sharpness quantification of ob-
tained images and local variance value: 𝜎
2
𝑏 =
1
𝑚(𝑛−1)
Í
𝑚
𝑖=1
Í
𝑛−1
𝑗=1
[𝑝 (𝑖, 𝑗) − 𝑝
′
]
2
In this equation, 𝑚
and 𝑛 are subblocks of images, 𝑝(𝑜,𝑔) the predictive
residues of images vector and 𝑝
′
its mediane. The
lowest score of the global variance corresponds to the
sharpest images.
PSNR and MSE:To investigate the quality of gen-
erated images, we calculate the peak signal to noise
ratio and the mean square error: 𝑃𝑆𝑁 𝑅(𝑜, 𝑔) =
20log 10(𝑚𝑎𝑥(𝑜)) − 20 log 10(𝑀𝑆𝐸𝑜, 𝑔) and
𝑀𝑆𝐸 (𝑜,𝑔) =
1
𝑚𝑛
Í
𝑚−1
𝑖=0
Í
𝑛−1
𝑗=0
(𝑜(𝑚
𝑖
, 𝑛
𝑗
) − 𝑔(𝑚
𝑖
, 𝑛
𝑗
))
2
.
Here 𝑚𝑎𝑥(𝑜) corresponds to the maximum pixel
value of an original image (255).
We calculate 𝐹𝐼 𝐷 between each group of gener-
ated and the dataset of input images, whereas we com-
pute 𝐵𝑙𝑢𝑟 on each image and rendered as a mean. We
process 𝑆𝑆𝐼 𝑀, 𝑀 𝐼, 𝑃𝑆𝑁 𝑅, 𝑀𝑆𝐸, 𝑈𝑄𝑀 between
each input and generated images and their mean is
rendered for each group.
2.4 Loss Optimizations
To generate the most qualitative and similar images,
we choose to optimize the best architecture based
upon the previously described metrics. Whatever the
architecture considered, all the generated images are
somewhat blurry. We choose to overcome this phe-
nomenon by studying how the discriminator loss can
influence the quality of the image generation. We in-
troduce six loss with some of them known in litera-
ture to resolve similar issues (Kupyn et al., 2018; Lan
et al., 2020; Mao et al., 2017).
BCE: The most commonly used loss in GANs is the
binary cross entropy (BCE) calculated by (Makhzani
et al., 2016) with 𝑦 the real image tensor and 𝑦
′
the predicted ones: 𝐵𝐶𝐸 = −
1
𝑛
Í
𝑛
𝑖=1
(𝑦
𝑖
∗ (log(𝑦
′
𝑖
))) −
((1− 𝑦
𝑖
) ∗ (log(1− 𝑦
′
𝑖
))). The BCE loss is the baseline
of this work. Additionally, we have implemented five
discriminator losses which are chosen for their aim to
improve the generated images quality with respect to
contrast, sharpness, and blur effect.
BCE + L1: First, the original BCE is replaced with
BCE and a L1 normalisation (Wargnier-Dauchelle
et al., 2019). We hypothesize that such update could
improve the quality of the generation as reported in
image restoration tasks for instance: 𝐿1 =
1
𝑛
Í
𝑛
𝑖=1
|𝑜
𝑖
−
𝑔
𝑖
|
1
and 𝐵𝐶𝐸 𝐿1 = 𝐵𝐶𝐸 + 𝛼 ∗ 𝐿1 (10) 𝛼 is equal to
10
−
4, as in the original paper.
LS:In (Mao et al., 2017) the least square loss al-
lowed to avoid gradient vanishing in the learning pro-
cess step, contributing to create high quality images:
𝐿𝑆 =
1
𝑛
Í
𝑛
𝑖=1
(𝑜
𝑖
− 𝑔
𝑖
)
2
.
Poisson:In (Wargnier-Dauchelle et al., 2019), a Pois-
son loss is used to obtain more sensitive results
for segmentation tasks: 𝐿
𝑃𝑜𝑖𝑠𝑠𝑜𝑛
=
1
𝑛
Í
𝑛
𝑖=1
𝑔
𝑖
− 𝑜
𝑖
∗
log(𝑔
𝑖
+ 𝜖).
Wasserstein and Perceptual Wasserstein:The De-
blurGAN was developed to deblur images (Kupyn
et al., 2018), using a combination of the Wasserstein
and Perceptual loss. Since we are also interested in
deblurring the output images, we have tested both
losses with the proposed AAEGAN.
We launch loss optimizations on the best architec-
ture during 5000 epochs first to train the model. Dur-
ing the training step, 250 × 250 pixel input images are
used to generate 40 synthetic images every 100 epoch.
The global representation explaining this training step
on the best architecture is shown Figure 1. We then
create a loss value per epoch representation, to high-
light when the training has to stop. We have stopped
the training at 2000 epochs which corresponds to the
plateau before the over-fitting for each loss optimiza-
tion.
During the testing step based upon the model pre-
viously created, 40 images are created by each opti-
mization as explained in section 3.1. We then com-
pare the 40 images generated from each loss opti-
mization based upon the quality and similitude met-
rics described in section 2.3.
2.5 Dimensional Reduction
The dimensional reduction goal is to observe in the
same statistical space if, for each optimization, gener-
ated image representations are close or far from the
original image representations. We choose to per-
form a t-distributed Stochastic Neighboor Enbending
(t-SNE) dimensional reduction. Contrary to others
dimensional reduction methods, t-SNE preserves the
local dataset structure by minimizing the divergence
between the two distributions with respect to the loca-
tions of the points in the map. To avoid subjective or
calculated indexes, we perform t-SNE directly on fea-
tures of images extracted from the GAN networks. t-
SNE is constituted with Stochastic Neighbor Embed-
ding where first an asymmetric probability (𝑝) based
AAEGAN Loss Optimizations Supporting Data Augmentation on Cerebral Organoid Bright-field Images
309

on dissimilarities (symmetric) is calculated between
each object (𝑥
𝑖
), and its probably neighborhood (𝑥
𝑗
)
(Hinton and Roweis, 2003). The effective number of
local neighbors called perplexity (𝑘) is chosen man-
ually: 𝑝
𝑖, 𝑗
= exp
−
∥ 𝑥
𝑖
−𝑥
𝑗
∥
2
2𝜎
2
𝑖
/
Í
𝑘≠𝑖
exp
−
∥ 𝑥
𝑖
−𝑥
𝑘
∥
2
2𝜎
2
𝑖
.
The larger the perplexity, the larger the variance
of a Gaussian kernel used to have an uniform in-
duced distribution. Thus we choose the maximal
value possible which is 80, the number of individ-
uals in our dataset. To match the original (𝑝
𝑖, 𝑗
)
and induced distributions (𝑝
′
𝑖, 𝑗
) in a low dimensional
space (the enbending aim), the objective is to mini-
mize the Kullback–Leibler (KL) cost function: 𝐶 =
Í
𝑖
Í
𝑗
𝑝
𝑖, 𝑗
log
𝑝
𝑖, 𝑗
𝑝
′
𝑖, 𝑗
. This minimization allows t-SNE
to preserve the dataset structure contrary to others di-
mensional reduction methods (as Principal Compo-
nent Analysis). Then a Student t-distribution with one
degree of freedom is used to avoid the crowding prob-
lem (van der Maaten and Hinton, 2008).
We use a momentum term to reduce the number of
iterations required (set at 1000 iterations at the begin-
ning) (van der Maaten and Hinton, 2008). The map
points have become organized at 450 iterations in a
scatterplot. Each point in the map corresponds to the
feature vector while the axes are the embedding fol-
lowing the similarity properties i.e. the neighborhood
of points. Each run of the t-SNE algorithm generates a
different setting of the scatterplot. The points location
might be different, but the grouping remains similar.
We have launched the t-SNE between original and all
the generated features 10 times to validate the similar
grouping. We have retrieved the best KL divergence
values between original and each generated distribu-
tions which could indicate a degree of similitude. A
low KL divergence means the two distributions are
close.
2.6 Segmentation
To determine the effect of data augmentation with the
AAE loss optimizations on a segmentation task, we
suggest to consider several training scenarios using a
U-Net architecture (Ronneberger et al., 2015). Seg-
mentation allows the extraction of an image content
from its background. Various segmentation proce-
dures exist but we have chosen U-Net for its advan-
tages to work well for small training sets with data
augmentation strategies, and to have already been
used for images of cleared CO (Albanese et al., 2020).
For comparison we perform 40 classical augmen-
tations involving flip-flops, rotations, whitenings, or
crops. Second, 40 images generated using an AAE
loss optimization are considered. The specific amount
of 40 is chosen in order to keep the balance between
original images and generated ones in the training
dataset, as explained further in section 3.1. To make
the performance evaluation more robust, a ”leave-
one-out” strategy is used, resulting in 40 training ses-
sions (numbers of images in our original dataset).
Thus each training is perform on 79 images. We
stopped the training at 1000 epochs with an average
time of training of more than 1 hour for each leave
one out loop (7 cases of augmentations × 40 images =
280 hours almost for the total training step). To com-
pare ground truth cerebral organoid content segmen-
tation (gt) and U-Net (u) ones in various conditions,
mean DICE scores are calculated as : DICE(𝑔𝑡,𝑢) =
2|𝑔𝑡∩𝑢|
|𝑔𝑡 |+|𝑢|
.
To highlight real/false positive/negative segmenta-
tion we created a superimposed image composed by
the ground truth and a sample of each segmentation
resulting from the various trainings. We updated the
pixels values in magenta (255, 0, 255) the false posi-
tive cerebral organoid segmentations and, in cyan (0,
255, 255) the false negatives.
3 RESULTS
We aim at generating qualitative images of cerebral
organoid by GAN strategies to increase the open-
source dataset (Gomez-Giro et al., 2019).
To determine the maximum number of images
generated without collapse, we calculate the SSIM
between original and generated images. We set that
the maximal similitude without creating a twin con-
tent is 0.90 (the maximum of similitude between two
original images is only of 0.87). Generated images
are at the minimum 45 % similar to original images.
When we double the generative process, some identi-
cal images appear. Thus we choose to generate only
40 images for each case in the testing phase to avoid
these duplicates.
3.1 GAN Architecture Choice
To verify the best suited GAN architecture for cere-
bral organoid bright field images, we first compare the
original images and the ones generated using the five
architectures.
In Table 1, sample images produced with GAN,
CGAN and AAEGAN are the most resembling im-
ages compared to the originals. Mode collapse is the
most seen in GAN and CGAN architectures as re-
ported in the literature. We can observe also a strong
noise for these two architectures results with a white
imprint around the shape of the organoid in the GAN
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
310

Table 1: Image quality and similitude of cerebral organoids generated by various GAN architectures. Scores within the
original range are underlined, best values are displayed in bold.
Original GAN CGAN DCGAN INFOGAN AAE
metric best
FID low 0.47 ≤ 𝑥 ≤ 0.80 2.02 2.13 ≥ 4 2.89 1.20
SSIM high 0.65 ≤ 𝑥 ≤ 0.71 0.12 0.12 0.27 0.10 0.63
UQM high 0.63 ≤ 𝑥 ≤ 0.87 0.79 0.80 0.69 0.66 0.81
MI high 0.21 ≤ 𝑥 ≤ 0.47 0.17 0.24 0.25 0.19 0.37
BLUR low 0.10 ≤ 𝑥 ≤ 86.28 2504.24 7561.47 704.48 724.38 135.93
PSNR low 11.90 ≤ 𝑥 ≤ 16.60 12.16 12.64 28.35 28.35 12.89
MSE low 93.25 ≤ 𝑥 ≤ 106.23 105.41 103.07 107.12 107.14 102.72
case. While AAEGAN generated images are char-
acterized with blurry contours, DCGAN and INFO-
GAN generate a divergent background making the
images difficult to exploit. To verify these observa-
tions, we calculate qualitative and similitude metrics,
introduced in the section 2.3, by pairing first original
images and then original and generated images.
Table 1, presents these results. For the output im-
ages, we underline the metric values within range of
the original images. We observe only a low propor-
tion of architecture metric within the original range.
Indeed, only the AAEGAN and the CGAN answer
to only four metrics (UQM, MI, PSNR, MSE) on
the seven calculated and only the UQM is within the
range of original ones for all the architectures. Re-
garding FID, SSIM, UQM, and MI scores, AAEGAN
generate the most comparable images to the original
ones.
In term of quality, this architecture generate the
sharpest images, even if the blur index is higher than
original images indexes. All the architectures express
MSE of between the minimal and maximal values of
this metric calculated for the original images. How-
ever, regarding the PSNR only the GAN, CGAN and
AAEGAN produce images with a score of between
the original images limits. To summarize, according
to the metric values, AAEGAN is the most suited ar-
chitecture to generate cerebral organoid images.
3.2 AAEGAN Loss Optimization
Once we have confirmed AAEGAN is the most suited
generation architecture for our study, we update the
discriminative loss of AAEGAN in order to evaluate
the corresponding influence on the generated images
quality. Results are shown in Table 2, using the same
metrics for quality (PSNR, MSE and Blur) and simil-
itude (FID, UQM, SSIM and MI) of images.
Table 2 shows one of the 40 images generated for
each of the six AAE variations. While some of the
generated samples are blurry and present a white im-
print (BCE, BCE+L1, LS), others show sharper edges
and less visible imprints (Poisson, Wasserstein and
Perceptual Wasserstein). For this group of losses,
only a few of the generated data seem to be identi-
cal to the input images: these networks do not suffer
from mode collapse.
To quantitatively confirm the visual analysis of the
generated images, we calculate comparative metrics
between original and generated datasets. Results are
shown Table 2. The AAEGAN loss optimizations al-
low generated images to be within the range on five
metrics with the Wasserstein and Perceptual Wasser-
stein loss (against four for the other loss). Indeed, the
Blur index is with these two optimizations within the
range of original images. Of the 7 metrics calculated,
only FID and SSIM are not in the range for all the
optimizations. However, the FID for the Perceptual
Wasserstein loss is quite close to the upper bound of
the input range (0.82 vs. 0.80).
Quantitatively, Wasserstein and Perceptual
Wasserstein networks generate better image quality
than other networks, based on lower PSNR, MSE
score and Blur index. However they are still higher
than the original scores shown in Table 1.
Otherwise, the similarity seems to depend on the
architecture. Based upon the FID, the Perceptual
Wasserstein loss generates the most similar images.
MI is higher for the images generated using Wasser-
stein networks. However, compared to images pro-
duced with BCE and Poisson, images produced with
Perceptual Wasserstein loss are not similar to the orig-
inal dataset regarding the SSIM. Images generated
with a Poisson or LS loss have the best UQM index.
The Perceptual Wasserstein loss is the most ap-
propriate loss optimization for generating cerebral
organoid images with the AAEGAN. It performs best
AAEGAN Loss Optimizations Supporting Data Augmentation on Cerebral Organoid Bright-field Images
311

Table 2: Sample of images generated for each AAE loss variation. We have calculated metrics on generated images from
each AAE loss variations, with the BCE loss as the baseline. Scores within the original range are underlined, best values are
displayed in bold.
Original BCE BCE + L1 LS Poisson Wass. Per. + Wass.
metric best
FID low 0.47 ≤ 𝑥 ≤ 0.80 1.20 1.41 1.33 1.41 1.10 0.82
SSIM high 0.65 ≤ 𝑥 ≤ 0.71 0.63 0.62 0.60 0.63 0.62 0.50
UQM high 0.63 ≤ 𝑥 ≤ 0.87 0.83 0.83 0,84 0,84 0.83 0.82
MI high 0.21 ≤ 𝑥 ≤ 0.47 0.37 0.39 0.36 0.41 0.46 0.42
BLUR low 0.10 ≤ 𝑥 ≤ 86.28 135.93 116.30 135.01 106.71 59.84 59.00
PSNR low 11.90 ≤ 𝑥 ≤ 16.60 13.47 13.74 13.53 13.74 13.17 12.86
MSE low 93.25 ≤ 𝑥 ≤ 106.23 103.13 103.35 104.01 103.33 103.11 102.93
for four metrics and is within the original range for
five metrics.
3.3 Dimensional Reduction
To analyze all at once the similitude and the vari-
ability of the generated images with AAEGAN loss
optimization, we study images in the same statistical
space. We implement a dimensional reduction on the
features extracted on images in the generative process
with t-SNE, see Figure 2. The first observation that
can be made is the maintenance of similar positions in
the map between original and generated images and
that whatever the loss optimization. Some original
images constitute a cluster and are almost foreigner
to the generated ones. This could be explained by the
incapacity of generated images to replicate a back-
ground similar to the bright-field acquisition with a
light gradient. While at the exterior of the map im-
ages generated with a Poisson a Wasserstein or a Per-
ceptual Wasserstein loss are represented, inside the
map BCE, BCE+L1, and LS losses are. This observa-
tion suggests that each loss optimization could bring
different information during the generative process.
We compare the KL divergences between original and
generated images which remains similar (all results
are approximating the null : inferior at 0.3). To sum-
marize, loss optimizations generate similar contents
to original images keeping its variability and creating
intermediate shapes not seen in original population.
3.4 Segmentation
To illustrate the influence of generated images by an
optimised AAEGAN against classical data augmen-
tation, we suggest to tackle a segmentation task in a
leave-one-out strategy (n=79 for training and n=1 for
testing). We choose the classic U-Net architecture and
Figure 2: t-SNE representation of original and generated
images with optimized AAEGAN.
we consider the different losses to compare the seg-
mentation performance for each data augmentation.
Psychovisually, samples in Table 3 are the best
segmented with a training involving images result-
ing from the AAEGAN Perceptual Wasserstein opti-
mization. They show the less false positive and nega-
tive segmentations compared to others AAEGAN op-
timizations and to classical data augmentation. Quan-
titatively the mean DICE index highlight the segmen-
tation performance. Results are summarized in Table
3. Mean DICE index is higher for segmented images
with Perceptual Wasserstein augmentation, in accor-
dance with the selected visual illustration.
In conclusion, images generated from Perceptual
Wasserstein AAEGAN allow a more accurate seg-
mentation than other AAEGAN loss, in accordance
with previous results on quality. The influence of the
Perceptual loss combined with Wasserstein distance,
such as a data attachment term based on the difference
of generated and images features maps, improve their
sharpness and textural information, making it a viable
strategy for data augmentation in this context.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
312

Table 3: Sample Cerebral Organoid image (left) with ground truth (GT) segmentation (our baseline), compared to Classical
and AAEGAN-based data augmentation, and the corresponding Mean DICE index and Standard Deviation (SD). Pixels are
colored according to the following legend: Black and white represent respectively true negatives and true positives while
magenta highligths false positives and cyan a false negatives. The best Dice index is displayed in bold.
GT Classic BCE BCE + L1 LS Poisson Wass. Per. + Wass.
Mean DICE 0.87 0.85 0.87 0.86 0.87 0.88 0.90
SD 0.03 0.05 0.05 0.14 0.09 0.05 0.04
4 DISCUSSION
This paper presents for the first time to our knowledge
data augmentation of cerebral organoids bright-field
images, using an Adversarial Autoencoder with var-
ious loss optimizations. The Perceptual Wasserstein
discriminator loss optimization outperforms the state-
of-the-art original article to generate these images, ac-
cording to the metrics used. Nevertheless, our dimen-
sional reduction experiments suggest all the loss op-
timizations could bring some variability to the gen-
erative process while remaining similar to the origi-
nal dataset. Approaching a segmentation experiment,
images generated with a Perceptual Wasserstein loss
could bring a better precision to a segmentation task.
Other losses may be interesting for different tasks.
Synthetic images generated with AAEGAN are
coherent with original dataset quality contrary to
other architectures, with almost no collapse mode but
also adding a sought diversity similar to the acquisi-
tion of the original dataset. An update of this archi-
tecture (for example replacing the autoencoder part by
a U-Net) may improve these results. Results remains
exploratory with the mentioned small dataset we used.
Improvements could be augmenting the number of in-
put images for all of the architectures, increasing the
training time for DCGAN and, giving to the INFO-
GAN generator only high-quality images to avoid the
divergence behavior. We only optimize the best archi-
tecture for time consideration, but the effect of loss
variations on others architectures may be interesting
to quantify.
The Perceptual Wasserstein loss optimization of
AAEGAN performs best according to metrics. Other
loss optimizations show also high similitude, though
with a lower quality. However, the dimensional re-
duction experiment suggests that several loss could
be used to generate more images and a good diver-
sity enriching the original training set. In this context,
we plan to explore what type of information each loss
brings during the image generation. We aim at trying
others embedded losses (already used for segmenta-
tion tasks) during the generative process based upon
high level prior like object shape, size topology or
inter-regions constraints (El Jurdi et al., 2021). These
losses could be used on condition that the morpholog-
ical development of CO is better characterized.
Attempting to distinguish the contribution of each
loss optimization, this strategy can potentially bring
better pixel-wise precision for segmentation tasks.
Shown here as a proof of concept, using a U-Net
architecture, we demonstrate the Perceptual Wasser-
stein loss can fruitfully enrich the original dataset.
This may also show a kind of regularization achieved
by the Perceptual loss leading to a good variability of
generated data without being too generic. The contri-
bution of others loss could not been highlighted in this
task. Nevertheless, segmentation could be even more
appropriate with algorithms suited for small datasets
or increasing the training step.
We plan also to train the segmentation task with
all the generated images (whatever the optimization)
in order to observe the modulation of its accuracy. In-
deed, we plan to extract morphological parameters,
such as areas, perimeters or higher-order statistics
needed for the growth follow-up of cerebral organoid
cultures on segmented images. In this work, we only
segmented organoid vs. non organoid regions. We
aim at reproducing the same work differentiating the
peripheral and the core zones of the cerebral organoid
in these images.
There is still room for improvement in the pro-
posed AAEGAN network strategy. First, to propose
a quantitative evaluation of the generalization of the
results obtained on cerebral organoid bright-field im-
ages : we would like to use this methodology on oth-
ers bright-field biomedical images. Biological experts
aim at psychovisually evaluating the generated im-
ages, and strengthen the quantitative evaluation pro-
posed. In particular, we project to validate the suit-
ability of the metrics we use and observe the training
effect on the segmentation task with only validated
images by biological experts.
AAEGAN Loss Optimizations Supporting Data Augmentation on Cerebral Organoid Bright-field Images
313

Second, we chose to focus only on the use of an
AAEGAN architecture to generate our images, we
aim at comparing these results with other types of
GANs such as CycleGAN or PixtoPix using U-Net
in its generator (Yi et al., 2019). Then, we have to
mention the resembling of original images in the t-
SNE right corner. It appears generated images could
not really generate a similar background such as the
lightning gradient of some bright-field acquisition in
white light. To resolve this issue, we aim at studying
the effect of a similar bright-field background injec-
tion during the generative process.
Finally, given the input dataset containing phys-
iological and pathological models of CO, it would
be interesting to investigate the generation of specific
pathological content in future studies.
5 CONCLUSION
This study answer to the first emerging issue in the
cerebral organoid field highlighted in (Br
´
emond Mar-
tin et al., 2021) i.e the lack of datasets. These
first results show that small databases augmentation
of cerebral organoids bright-field images is possi-
ble using GANs. Particularly the AAEGAN Per-
ceptual Wasserstein loss optimisation generates the
most qualitative content, remains similar to the orig-
inal dataset and images it generates are useful to im-
prove a segmentation task. However it remains to
discover what kind of information other loss opti-
mizations with coherent diversity to the initial dataset
could bring during the generative process. This data
generation strategy will be valuable to develop char-
acterization methods on CO by enabling large statisti-
cal study, but also to develop deep-based approaches
for classification and characterization of the various
morphologies. Such characterization could help to
better understand the growing process once in ade-
quate cultures and help to use cerebral organoids as
models for neuropathological disease or for testing
therapeutics.
REFERENCES
Albanese, A., Swaney, J. M., Yun, D. H., Evans, N. B.,
Antonucci, J. M., Velasco, S., Sohn, C. H., Arlotta,
P., Gehrke, L., and Chung, K. (2020). Multiscale 3D
phenotyping of human cerebral organoids. Scientific
Reports, 10(1):21487.
Br
´
emond Martin, C., Simon Chane, C., Clouchoux, C., and
Histace, A. (2021). Recent Trends and Perspectives in
Cerebral Organoids Imaging and Analysis. Frontiers
in Neuroscience, 15:629067.
El Jurdi, R., Petitjean, C., Honeine, P., Cheplygina, V.,
and Abdallah, F. (2021). High-level prior-based loss
functions for medical image segmentation: A sur-
vey. Computer Vision and Image Understanding,
210:103248.
Gomez-Giro, G., Arias-Fuenzalida, J., Jarazo, J.,
Zeuschner, D., Ali, M., Possemis, N., Bolognin,
S., Halder, R., J
¨
ager, C., Kuper, W. F. E., van Hasselt,
P. M., Zaehres, H., del Sol, A., van der Putten,
H., Sch
¨
oler, H. R., and Schwamborn, J. C. (2019).
Synapse alterations precede neuronal damage and
storage pathology in a human cerebral organoid
model of CLN3-juvenile neuronal ceroid lipofus-
cinosis. Acta Neuropathologica Communications,
7(1).
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative Adversarial Networks. In
Proceedings of NIPS, page 2672–2680.
Hinton, G. and Roweis, S. (2003). Stochastic neighbor em-
bedding. Advances in neural information processing
systems, 0(no):857–864.
Kassis, T., Hernandez-Gordillo, V., Langer, R., and Griffith,
L. G. (2019). OrgaQuant: Human Intestinal Organoid
Localization and Quantification Using Deep Convolu-
tional Neural Networks. Scientific Reports, 9(1).
Kupyn, O., Budzan, V., Mykhailych, M., Mishkin, D., and
Matas, J. (2018). DeblurGAN: Blind Motion Deblur-
ring Using Conditional Adversarial Networks. Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 8183–8192.
Lan, L., You, L., Zhang, Z., Fan, Z., Zhao, W., Zeng, N.,
Chen, Y., and Zhou, X. (2020). Generative Adversar-
ial Networks and Its Applications in Biomedical In-
formatics. Frontiers in Public Health, 8.
Lv, J., Zhu, J., and Yang, G. (2021). Which GAN? A
comparative study of generative adversarial network-
based fast MRI reconstruction. Philosophical Trans-
actions of the Royal Society A: Mathematical, Physi-
cal and Engineering Sciences, 379(2200):20200203.
Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., and
Frey, B. (2016). Adversarial Autoencoders. Interna-
tional Conference on Learning Representations.
Mao, X., Li, Q., Xie, H., Lau, R. Y. K., Wang, Z., and Smol-
ley, S. P. (2017). Least Squares Generative Adver-
sarial Networks. IEEE International Conference on
Computer Vision (ICCV), pages 2813–2821.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-
Net: Convolutional Networks for Biomedical Im-
age Segmentation. arXiv:1505.04597 [cs]. arXiv:
1505.04597.
van der Maaten, L. and Hinton, G. (2008). Visualizing data
using tsne. Journal of Machine Learning Research,
9(1):2579–2605.
Wargnier-Dauchelle, V., Simon-Chane, C., and Histace, A.
(2019). Retinal Blood Vessels Segmentation: Im-
proving State-of-the-Art Deep Methods. In Computer
Analysis of Images and Patterns, volume 1089, pages
5–16. -, Cham.
Yi, X., Walia, E., and Babyn, P. (2019). Generative Adver-
sarial Network in Medical Imaging: A Review. Medi-
cal Image Analysis, 58:101552.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
314
