
Category-level Part-based 3D Object Non-rigid Registration
Diego Rodriguez
a
, Florian Huber and Sven Behnke
b
Autonomous Intelligent Systems, University of Bonn, Bonn, Germany
Keywords:
Non-rigid Registration, Robot Vision, Shape Spaces.
Abstract:
In this paper, we propose a novel approach for registering objects in a non-rigid manner based on decomposed
parts of an object category. By performing part-based registration, the deforming points match better local
geometric structures of the observed instance. Moreover, the knowledge acquired of an object part can be
transferred to different object categories that share the same decomposed part. This is possible because the
registration is based on a learned latent space that encodes typical geometrical variations of each part inde-
pendently. We evaluate our approach extensively on different object categories and demonstrate its robustness
against outliers, noise and misalignments of the object pose.
1 INTRODUCTION
The non-rigid registration problem aims to model the
deformation between two different feature sets such
as meshes or point clouds. The underlying transfor-
mation between the sets is unknown, which makes
the non-rigid registration problem challenging. These
kind of registrations are used in several applications
such as medical imaging, object reconstruction and
robot vision tasks (Krebs et al., 2017; Zollh
¨
ofer et al.,
2014; Stouraitis et al., 2015). Particularly, non-rigid
registration methods are employed in robot grasping
applications in order to transfer knowledge between
object instances (Stouraitis et al., 2015; Stueckler
et al., 2011; Rodriguez et al., 2018). In this manner,
associated grasping knowledge of an object instance
is adapted to a novel one based on its geometry. The
approach presented in this paper is intended to be used
for grasping transfer knowledge.
Online robot grasping tasks pose several chal-
lenges in terms of perception and planning. One
of these difficulties lies in the inference of the non-
observable (from the robot camera perspective) por-
tions of the novel instance, especially because multi-
ple plausible geometries can explain the current ob-
served geometry. Data-driven approaches, as the one
presented in this paper, often learn latent spaces of the
object category for generating plausible shapes based
on the data presented during training (Allen et al.,
2003; Burghard et al., 2013; Rodriguez and Behnke,
a
https://orcid.org/0000-0002-1416-7392
b
https://orcid.org/0000-0002-5040-7525
2018). Thanks to the embedded knowledge in these
latent spaces, the reconstruction can be performed on-
line.
In this paper, we propose a novel approach for reg-
istering instances belonging to the same object cate-
gory that registers decomposed parts independently.
Our approach is inspired by the observation that some
object parts are common across different categories.
For example, a chair and a table both contain legs
with similar geometries and handles often have sim-
ilar shape and function. In this manner, knowledge
acquired from an object category can be transferred
to another. In addition, the registration by parts can
increase the registration accuracy of local structures
by reducing the number of constraints and degrees of
freedom a holistic registration of complex geometries
requires.
The main contribution of this paper is the formula-
tion of a novel approach for part-based non-rigid reg-
istration that can be employed for transferring grasp-
ing knowledge for online robot applications. We eval-
uate our approach on different categories and demon-
strate that our part-based algorithms achieve better re-
sults compared to a holistic-only registration. In ad-
dition, we create a new dataset that contains meshes
and corresponding point clouds together with the re-
spective part decomposition. The part segmentation
is done manually to express semantic concepts and to
ensure the quality of the dataset. The dataset and the
source code of our implementation will be released
upon acceptance.
Rodriguez, D., Huber, F. and Behnke, S.
Category-level Part-based 3D Object Non-rigid Registration.
DOI: 10.5220/0010761800003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
795-802
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
795

Our approach is especially robust against occlu-
sions because of the embedded knowledge in the
learned shape spaces. Thus, this it is very relevant for
online robot applications where objects are not fully
observable.
2 RELATED WORK
Different approaches have been proposed to address
the non-rigid registration problem according to the
restrictions of the deforming point set to match the
observed one. The most widely used constraints in-
clude: conformal maps (Kim et al., 2011; Zeng et al.,
2010), isometry (Tevs et al., 2009; Ovsjanikov et al.,
2010), thin-plate splines (Chui and Rangarajan, 2003;
Zou et al., 2007), Gaussian fields (Haehnel et al.,
2003), and motion coherence theory (Myronenko and
Song, 2010). The non-rigid registration has been also
formulated as a probability density estimation prob-
lem (Myronenko and Song, 2010; Horaud et al., 2010;
Ma et al., 2016), where parameters of Gaussian Mix-
ture Models (GMMs) are optimized by means of the
Expectation Maximization (EM) algorithm. The Co-
herent Point Drift (CPD) algorithm (Myronenko and
Song, 2010) makes use of such methods.
These traditional algorithms, however, have dif-
ficulties with partially observed data, because they
do not incorporate any information on the observed
point sets. Shape priors and latent spaces are fre-
quently used to address this issue with different fea-
ture sets such as body shapes (Allen et al., 2003;
Hasler et al., 2009), brain images (Marsland et al.,
2003), faces (Blanz and Vetter, 1999), and collections
of shapes (Nguyen et al., 2011; Huang et al., 2012).
Dense correspondences can be also inferred based on
a compact shape space of similar shapes (Burghard
et al., 2013; Engelmann et al., 2016).
The decomposition of complex object geometries
into parts holds the promise to reduce the registration
error. In (Adeshina and Cootes, 2010), an image-
based approach was developed to find correspon-
dences between segment parts of bones and their lo-
cation. Dense correspondences between 3D shapes
have been also estimated by considering independent
parts (Burghard et al., 2013). A hierarchical approach
for registering 2D point sets was proposed in (Xiong
et al., 2018). The method iteratively segments a 2D
point cloud in different parts and finds the deforma-
tions of each individual part in an ICP (Iterative Clos-
est Point) manner. Similarly, several grasping plan-
ning approaches aim to reduce complexity by trans-
ferring grasp skills between simpler parts or geometri-
cal primitives (cylinders, boxes, spheres) (Aleotti and
Caselli, 2011; Aleotti et al., 2014; Vahrenkamp et al.,
2016).
3 PART-BASED NON-RIGID
REGISTRATION
We propose a learning-based approach for registering
instances belonging to an object category in a non-
rigid manner which considers both the complete ge-
ometry of the objects and their decomposed parts.
We define a category as a set objects with similar
extrinsic geometry and usage, e.g., drill, spray bot-
tle, etc. Our method defines a training phase in
which multiple shape spaces are learned based on the
point sets of the training instances. A shape space
is a low-dimensional manifold that describes typi-
cal intra-class geometrical variations. The construc-
tion of these spaces is explained in Section 3.1. The
learned shape spaces are used during inference for
finding geometries that match best the observed ones.
This search is formulated as an optimization problem
as described in Section 3.2. For a category with p
number of parts, p + 1 shape spaces are learned: one
for each part and an additional one for the entire not
decomposed instances. This additional shape space
is referred as the holistic shape space. Our approach
has two variants: partwise and hol+part. The former
formulates the non-rigid registration as the result of
independent parallel registrations for each object part
(Figure 1). The latter performs first a holistic reg-
istration to capture the global features and to initial-
ize the search inside the shape spaces of the decom-
posed parts. Comparisons between both variants are
presented in the evaluation (Section 4).
3.1 Shape Space
The shape spaces presented here are constructed
based on a collection of training 3D point sets. From
the collection, a 3D point set is selected as the canon-
ical model C ∈ R
M×3
= (c
1
, ··· , c
M
)
T
which repre-
sents a nominal instance of the collection, where M
represents the number of 3D points in C. The canoni-
cal model is then registered non-rigidly towards each
of the remaining training point sets T
i
by means of the
Coherent Point Drift (CPD) algorithm (Myronenko
and Song, 2010). Note that all object frames are
aligned before performing the registration. In the mug
category, for example, all axes of the cylinders are
aligned and all handles are placed in the same posi-
tion. The resulting registered point set T
i
is formu-
lated as:
T
i
(C, W
i
) = C + GW
i
, (1)
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
796

Holistic shape space
Shape space drill tops
Figure 1: Category-level part-based registration. Multiple
shape (latent) spaces are learned. Initially, a holistic shape
space of the entire geometries is learned. Then, for each of
the parts, an individual shape space is constructed following
the same algorithm, i.e., by computing deformation fields
using CPD and by finding a lower-dimensional space using
PCA-EM. For example, the drill category will establish four
shape spaces, one holistic (green), and one for each of the
parts: shank, base and top (magenta).
where G is a Gaussian kernel matrix defined element-
wise as:
g
i j
:
= G(c
i
, c
j
) = exp
−
1
2β
2
k
c
i
−c
j
k
2
, (2)
and W
i
∈ R
M×3
is a matrix of kernel weights which
can be interpreted as unnormalized deformation field
matrix. The deduction of these matrices is out of the
scope of this paper, please refer to (Myronenko and
Song, 2010) for an in-depth analysis.
Interestingly, the registration is uniquely captured
by the matrix W
i
since C is the same across all train-
ing instances, i.e., G depends only on the canonical
model C. Moreover, the dimensionality of W
i
also
remains constant for all registrations and more impor-
tantly it is ordered, such that a k-row corresponds to
a 3D deformation vector of the k-point in C. This
allows us to find a lower-dimensional latent space by
finding the principal components of all these deforma-
tion field matrices W
i
. This latent space is calculated
by the Principal Component Analysis - Expectation
Maximization (PCA-EM) algorithm.
The top of Figure 1 shows a holistic learned shape
space of a drill category. Note that the presented
principal components correlate qualitatively with the
width and the height of the instances.
3.2 Part-based Registration
The input of our approach is a point set belonging to
an object category, for instance, a point cloud com-
ing from real sensory data (e.g., a RGB-D camera).
As result of the registration, the canonical point set is
deformed to match the geometry of a novel observed
instance. In this manner, the observed object is recon-
structed. In addition, a deformation field is inferred
which can be used to transform points and 3D frames
associated to the canonical model.
Novel category-like shapes can be generated by
interpolating and extrapolating in the shape spaces. In
this manner, the non-rigid registration of shapes, ei-
ther of the entire object or of an object part, is formu-
lated as an optimization problem that minimizes the
closest distance between the observed point set O and
the deformed one T (C, Wm(x)). The energy function
to minimize is formulated as:
E(x, θ) =
M
∑
m=1
min
n
k
O
n
− Θ(T (C
m
, W
m
(x)), θ)
k
2
.
(3)
where θ defines the parameters of a rigid transforma-
tion incorporated to account for misalignments of the
observed object pose and Θ is a function that applies
this rigid transformation. A good initialization of the
object pose is however required because of many lo-
cal minima of the optimization problem. In Equation
(3), the notation A
n
refers to the point n of matrix A.
Note that by the incorporation of the rigid term, the
optimization becomes non-linear. This optimization
problem is solved by using the ceres optimizer
1
.
In order to improve the registration accuracy of
complex local structures, our approach includes the
registration of each object part independently. There-
fore, initially, the objects are decomposed into sim-
pler parts. The decomposition is done manually by
experts to express semantic concepts and to ensure the
quality of the segmentation. Automatic approaches
such as (Araslanov et al., 2016; Palafox et al., 2021)
are alternatives to perform the part decomposition.
The partwise variant registers each part indepen-
dently. In this manner, for an object with three parts,
three different shape spaces will be learned and three
different optimization problems will be solved, one
for each part. Note that the rigid transformation with
parameters θ added in the energy function (Eq. 3)
helps to align the point sets. For instance, for the drill
category shown in Figure 1, three shape spaces are
required: base, top part, and shank.
The hol+part variant of our method is composed
of two steps. In the first step, an initial registration
takes place that registers the full geometry of the ob-
ject in a holistic manner, i.e., the registration of the
canonical model towards the observed one without
any part decomposition. In the second step, a partwise
1
http://ceres-solver.org
Category-level Part-based 3D Object Non-rigid Registration
797
Holistic-only registration
Part-based registration
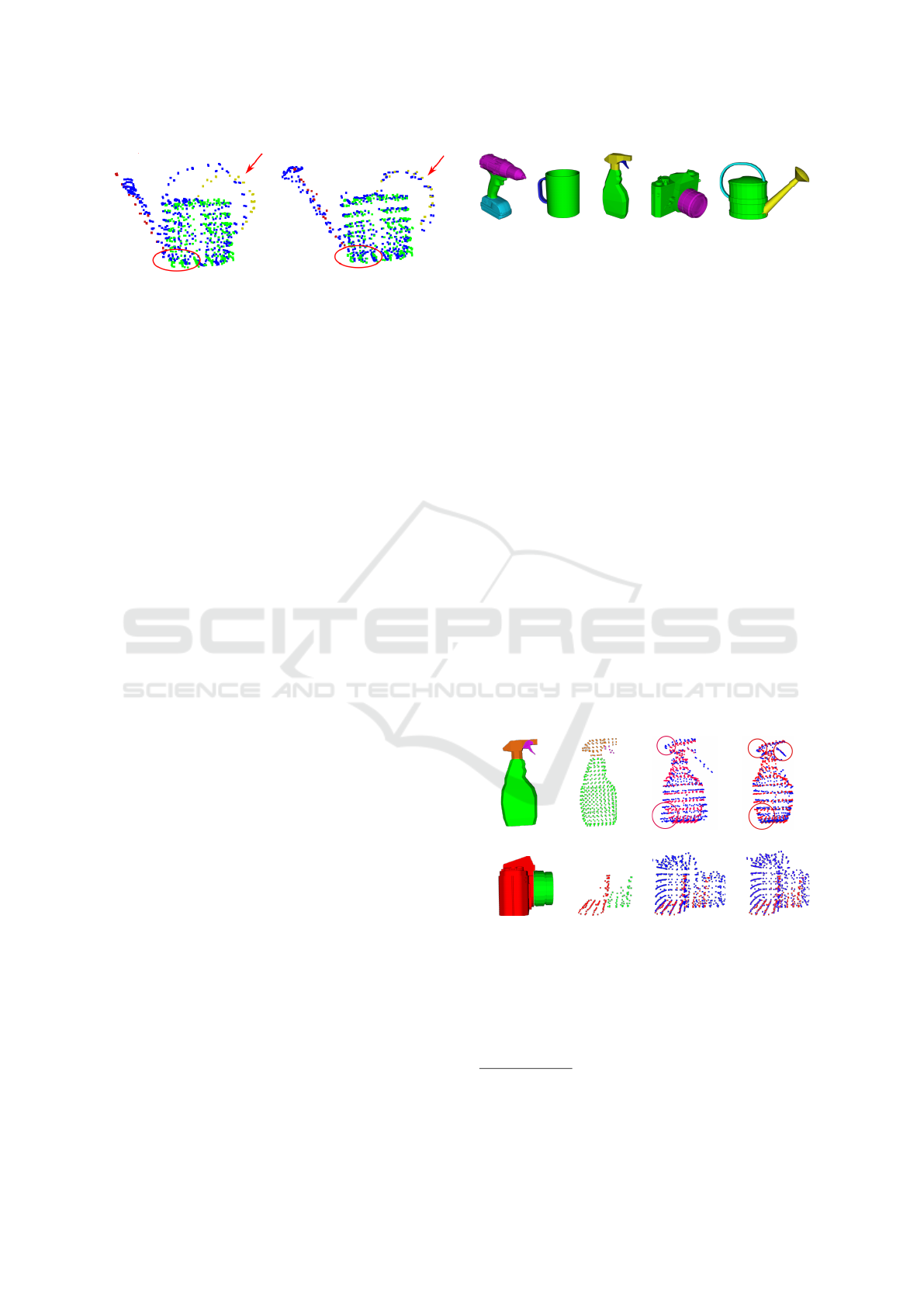
Figure 2: Holistic and partwise registration of a watering
can with three parts: sprout (red), tank (green) and han-
dle(gold). Note how the registration accuracy of the local
structures (e.g., the handle) is improved by the part-based
registration. The blue points represent the deforming point
set.
registration is carried out, i.e., each individual part is
registered. The holistic registration aims to capture
global structures such as the dimensions of the object,
while the objective of partwise registration is to im-
prove registration accuracy of local structures.
The holistic registration serves as an initialization
of the optimization for each of the parts. In this man-
ner, Eq.(3) finds an optimum latent vector x
h
and the
parameters of a local registration θ
h
. The values of θ
h
are passed directly to the optimization of each of the
parts. However, the latent vector x
h
cannot be passed
directly, since each shape space represents the defor-
mation fields of different shapes. The latent vector
x
h
maps to a deformation field W
h
. This matrix is
separated in multiple matrices according to the part
each deformation vector belongs to. By doing this,
we avoid to perform an additional optimization that
finds the latent vector of each part that matches the
results of the holistic registration. On the other hand,
this matrix separation assumes the contribution of de-
formation vectors of different parts as negligible. Be-
cause the holistic registration serves as initialization,
the final result is given by the deformation vectors de-
fined by each of the individual parts.
Both variants, i.e., the partwise and the hol+part,
are evaluated in Section 4. Figure 2 shows the results
of the non-rigid registration performed in a holistic-
only and in a part-based manner. Note especially for
the handle how the registration by parts improve the
registration accuracy.
Our approach works directly on point sets but it
can also be used to register meshes. An additional
affinity matrix G(T
m
, T) is introduced for this pur-
pose. This matrix maps the deformations from a point
set T to the corresponding mesh vertices T
m
. The
point set T of a mesh T
m
is defined by ray-casting
operations and a voxel filter. This results in a point
cloud of uniform density. The deformed mesh ver-
tices C
m
0
of the canonical mesh will be then defined
Figure 3: Canonical models of the evaluated categories:
drill, mug, spray bottle, camera and watering can with the
corresponding part decomposition.
as:
C
m
0
= C
m
+ G(C
m
, C) ∗ W
i
. (4)
4 EVALUATION
We tested the category-level part-based registration
approach on five different categories: drill (17), cam-
era (13), spray bottle (19), watering can (9), and mug
(24). The number of instances for training the shape
spaces are given inside parenthesis. Figure 3 presents
the canonical model of each category with their part
decomposition. The meshes were collected from
online databases: Sketchfab
2
, GrabCad
3
, 3DWare-
house
4
, and from the object meshes recently released
in (Wang et al., 2019). For constructing the shape
spaces, CPD is parametrized with λ = 2, β = 2 and 5
latent dimensions.
Our approach is evaluated with fully and partially
observed shapes. All the testing instances are pre-
sented for the first time to our registration method.
The partial views are generated by ray-casting a sin-
gle view of the object from 42 different observation
poses on a tessellated sphere, emulating what a robot
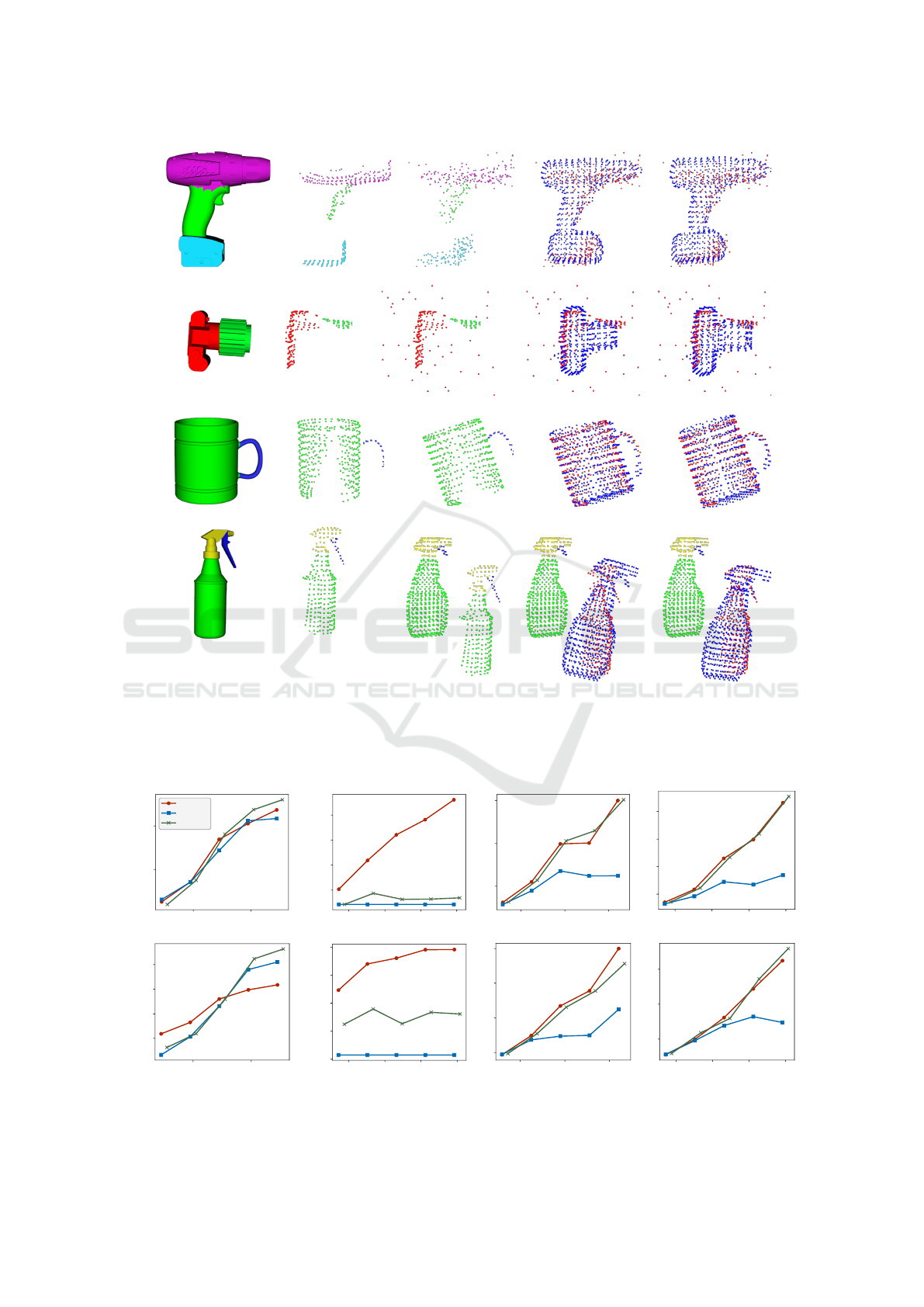
Fully observed
Partially observed
Observed mesh
Segmented cloud
Holistic-only
Hol+part
Figure 4: Results of the non-rigid registration performed on
the spraybottle and camera categories by the hol+part vari-
ant of our approach, compared with a holistic registration.
Observe how the quality of the local structures is improved
by the part-based registration. The canonical deforming
model is shown in blue. For clarity of the registered im-
ages, the observed instances are colored red.
2
https://sketchfab.com/
3
https://grabcad.com/library
4
https://3dwarehouse.sketchup.com/
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
798
0.01 0.02
8.0
8.2
8.4
8.6
8.8
Reg. Error - Drills
Hol
Part
Hol+Part
0.05 0.10 0.15 0.20
8.0
8.5
9.0
9.5
10.0
0.2 0.4 0.6
25
50
75
100
0.025 0.050 0.075 0.100
50
100
150
0.01 0.02
Noise [m]
6.5
7.0
7.5
8.0
Reg. Error - Spraybottles
0.05 0.10 0.15 0.20
Outlier
6
7
8
9
0.2 0.4 0.6
Rotation [rad]
10
20
30
40
50
0.025 0.050 0.075 0.100
Translation [m]
20
40
60
80
100
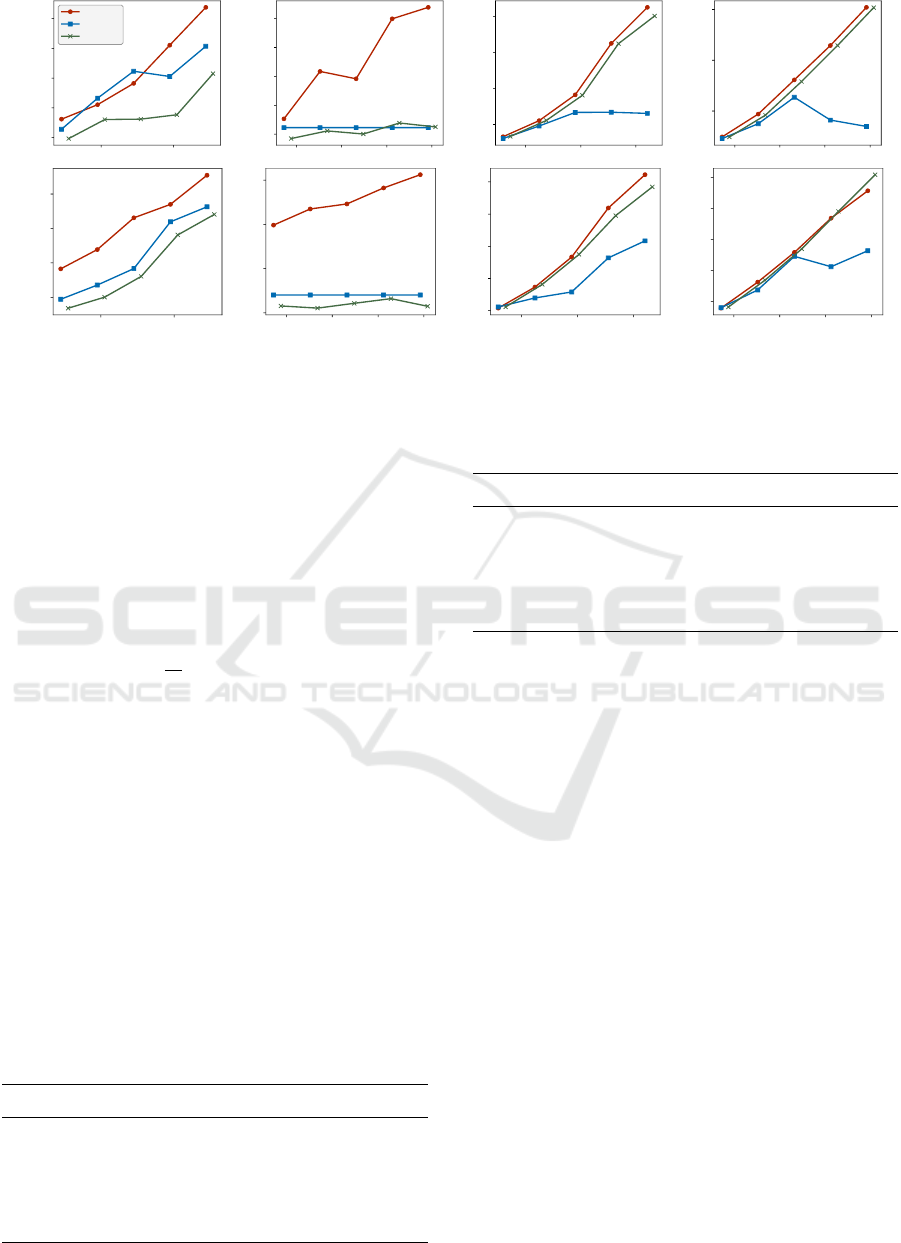
Figure 5: Average registration errors on full views of the drill and spray bottle categories with respect to different levels of
noise, outliers, rotation and translation.
perceives in a real application. We compare the part-
wise and the hol+part variants of our method against
the holistic registration that do not consider decom-
posed parts. Qualitative results of fully and partially
observed instances are presented in Figure 4. Note
how local structures are better captured by the regis-
tration on the part level.
In order to perform a quantitative evaluation, we
define the following registration error:
E(T, C) =
1
M
M−1
∑
m=0
min
n
k
T
n
− C
m
k
2
, (5)
which aggregates a normalized distance to the closest
point from the ground truth points T. The numerical
comparison between partwise, hol+part and holistic
on complete ground truth observed instances is pre-
sented in Table 1. Observe that the hol+part variant
outperforms the holistic-only and the partwise regis-
tration variant for fully observed models for all cate-
gories. This means that the registration by parts im-
proves the overall accuracy and that an initial global
registration is beneficial for initializing the subse-
quent partwise one with fully observed instances.
A similar evaluation is performed on partially ob-
served instances whose results are presented in Ta-
Table 1: Average registration error on the evaluated cate-
gories with fully observed instances.
Holistic Partwise Hol+Part
Camera 3.96 3.96 3.67
Drill 7.19 7.06 7.04
Mug 5.21 5.41 5.20
Spray bottle 7.60 7.22 7.05
Watering can 18.72 15.61 15.55
Table 2: Average registration error on the evaluated cate-
gories with 42 partial views.
Holistic Partwise Hol+Part
Camera 0.241 0.20 0.24
Drill 0.67 0.64 0.68
Mug 0.21 0.22 0.22
Spray bottle 0.64 0.65 0.68
Watering can 1.99 1.84 1.90
ble 2. Note that when objects are not complete, the
hol+part variant does not perform well compared to
the other two methods. With partial views, some parts
might have very few points and their contribution to
the holistic registration is low, for this reason, using
the result of an initial holistic registration might lead
to a bad initialization for the subsequent partwise reg-
istration.
We also evaluate the robustness of our approach
against different degrees of noise, outliers, rotation
and translation. We initially add noise to the position
of the observed point set. This noise is sampled from
a Gaussian distribution with zero mean. The value
of the standard deviation is increased gradually from
0.005 to 0.025. Secondly, outliers are incorporated
to the observed instances, i.e., the position of the ob-
served points is not altered but random points sam-
pled from a Uniform distribution inside the bounding
box of the object are added. The ratio of number of
outliers goes from 0.04 to 0.2. We also analyze the
effect of having errors on the observed object pose.
We consider rotation and translation separately. We
rotate the observed instance in each of the global x-,
y- and z-axis consecutively with the same angle. The
direction of rotation of each axis is randomized. The
angle values goes from 0.13 to 0.65 rad with a step of
Category-level Part-based 3D Object Non-rigid Registration
799
Noise
Outliers
Rotation
Translation
Figure 6: Registration results of the holistic-only and part-based registration on partial views on four different categories with
noise, outliers, rotation and translation. The aim is to deform the canonical model (blue) onto the observed instances (red).
The first three columns show the observed models with the segmented parts. For clarity in the registered images, the observed
instances are completely colored red. Observe how the registration accuracy of the lens of the camera, the handle of the mug
and the trigger of the spray bottle is improved by the part-based registration. For the translation, the canonical model is also
presented to indicate the observed object pose.
0.01 0.02
0.8
1.0
Reg. Error - Drills
Hol
Part
Hol+Part
0.05 0.10 0.15 0.20
0.65
0.70
0.75
0.80
0.2 0.4 0.6
2
4
6
0.025 0.050 0.075 0.100
2.5
5.0
7.5
10.0
0.01 0.02
Noise [m]
0.6
0.7
0.8
0.9
Reg. Error - Spraybottles
0.05 0.10 0.15 0.20
Outlier
0.50
0.55
0.60
0.65
0.70
0.2 0.4 0.6
Rotation [rad]
1
2
3
4
0.025 0.050 0.075 0.100
Translation [m]
2
4
6
Figure 7: Average registration errors on partial views of the drill and spray bottle categories with respect to different levels of
noise, outliers, rotation and translation. Each point represents the mean error over 42 partial views.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
800

0.13 rad. Finally, the observed instance is translated
in all three axes from 0.02 to 0.1 m. Examples of the
altered observed instances with the noise, outliers, ro-
tation and translation together with their correspond-
ing holistic and hol+part registrations are presented
in Figure 6. Note how local geometries such as the
lens of the camera, the handle of the mug and the trig-
ger of the spray bottles are better captured with the
hol+part registration.
Numerical results of the drill and spray bottle cat-
egories with fully observed instances are presented in
Figure 5. Figure 7 reports the average registration er-
rors of partial views. Only two categories are pre-
sented but the remaining three behave similarly. The
hol+part variant continues outperforming the other
two methods with noise and outliers on fully observed
instances. However, for rotation and translation, the
partwise variant is more robust, which implies that
misalignments on a global level of the object are more
difficult to refine. Moreover, on partial views the part-
wise variant continues outperforming the other two
methods and is more robust against noise, outliers ro-
tation and translation.
5 CONCLUSION
In this paper, we have presented a novel part-based
non-rigid registration method that improves the accu-
racy of local structures by registering individually de-
composed parts of the object. The method is based
on learned shape spaces of each of the decomposed
parts. We have shown in the experimental section that
a holistic registration followed by a partwise registra-
tion (hol+part) is very effective for registering fully
observed objects, while a partwise registration per-
forms better with partial views. We demonstrated the
robustness of our approach against noise, outliers and
misalignments in rotation and translation. In the fu-
ture, we plan to investigate hierarchies and dependen-
cies between parts of more complex objects. More-
over, we will evaluate the strengths and limitations of
the part-based registration when applied to grasping
skill transfer methods.
REFERENCES
Adeshina, S. A. and Cootes, T. F. (2010). Evaluation of
performance of part-based models for groupwise reg-
istration. Medical Image Understanding and Analysis
Conf. (MIUA), pages 221–251.
Aleotti, J. and Caselli, S. (2011). Part-based robot grasp
planning from human demonstration. In IEEE Int.
Conf. on Robotics and Automation (ICRA), pages
4554–4560.
Aleotti, J., Rizzini, D. L., and Caselli, S. (2014). Percep-
tion and grasping of object parts from active robot ex-
ploration. Journal of Intelligent & Robotic Systems
(JINT), 76(3):401–425.
Allen, B., Curless, B., and Popovi
´
c, Z. (2003). The space
of human body shapes: Reconstruction and parame-
terization from range scans. ACM Transactions on
Graphics (TOG).
Araslanov, N., Koo, S., Gall, J., and Behnke, S. (2016).
Efficient single-view 3D co-segmentation using shape
similarity and spatial part relations. In German Conf.
on Pattern Recognition (GCPR), pages 297–308.
Blanz, V. and Vetter, T. (1999). A morphable model for the
synthesis of 3D faces. In Proc. of the 26th Conf. on
Computer Graphics and Interactive Techniques (SIG-
GRAPH), pages 187–194.
Burghard, O., Berner, A., Wand, M., Mitra, N., Seidel, H.-
P., and Klein, R. (2013). Compact part-based shape
spaces for dense correspondences. arXiv preprint
arXiv:1311.7535.
Chui, H. and Rangarajan, A. (2003). A new point matching
algorithm for non-rigid registration. Computer Vision
and Image Understanding (CVIU), pages 114–141.
Engelmann, F., St
¨
uckler, J., and Leibe, B. (2016). Joint ob-
ject pose estimation and shape reconstruction in urban
street scenes using 3D shape priors. In German Conf.
on Pattern Recognition (GCPR).
Haehnel, D., Thrun, S., and Burgard, W. (2003). An ex-
tension of the ICP algorithm for modeling nonrigid
objects with mobile robots. In Int. Joint Conf. on Ar-
tificial Intelligence (IJCAI).
Hasler, N., Stoll, C., Sunkel, M., Rosenhahn, B., and Sei-
del, H.-P. (2009). A statistical model of human pose
and body shape. In Computer Graphics Forum (Euro-
graphics).
Horaud, R., Forbes, F., Yguel, M., Dewaele, G., and Zhang,
J. (2010). Rigid and articulated point registration with
expectation conditional maximization. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence
(TPAMI), pages 587–602.
Huang, Q.-X., Zhang, G.-X., Gao, L., Hu, S.-M., Butscher,
A., and Guibas, L. (2012). An optimization approach
for extracting and encoding consistent maps in a shape
collection. ACM Transactions on Graphics (TOG),
page 167.
Kim, V. G., Lipman, Y., and Funkhouser, T. (2011).
Blended intrinsic maps. In ACM Transactions on
Graphics (TOG).
Krebs, J., Mansi, T., Delingette, H., Zhang, L., Ghesu, F. C.,
Miao, S., Maier, A. K., Ayache, N., Liao, R., and Ka-
men, A. (2017). Robust non-rigid registration through
agent-based action learning. In Int. Conf. on Medi-
cal Image Computing and Computer-Assisted Inter-
vention (MICCAI), pages 344–352.
Ma, J., Zhao, J., and Yuille, A. L. (2016). Non-rigid point
set registration by preserving global and structures.
IEEE Transactions on Image Processing, pages 53–
64.
Category-level Part-based 3D Object Non-rigid Registration
801

Marsland, S., Twining, C. J., and Taylor, C. J. (2003).
Groupwise non-rigid registration using polyharmonic
clamped-plate splines. In Int. Conf. on Medical Im-
age Computing and Computer-Assisted Intervention
(MICCAI), pages 771–779.
Myronenko, A. and Song, X. (2010). Point set registration:
Coherent point drift. IEEE Transactions on Pattern
Analysis and Machine Intelligence (TPAMI).
Nguyen, A., Ben-Chen, M., Welnicka, K., Ye, Y., and
Guibas, L. (2011). An optimization approach to im-
proving collections of shape maps. In Computer
Graphics Forum, pages 1481–1491.
Ovsjanikov, M., M
´
erigot, Q., M
´
emoli, F., and Guibas, L.
(2010). One point isometric matching with the heat
kernel. In Computer Graphics Forum.
Palafox, P., Bo
ˇ
zi
ˇ
c, A., Thies, J., Nießner, M., and Dai, A.
(2021). NPMs: Neural parametric models for 3D de-
formable shapes. arXiv:2104.00702.
Rodriguez, D. and Behnke, S. (2018). Transferring
category-based functional grasping skills by latent
space non-rigid registration. In IEEE Robotics and
Automation Letters (RA-L), volume 3, pages 2662–
2669.
Rodriguez, D., Cogswell, C., Koo, S., and Behnke, S.
(2018). Transferring grasping skills to novel instances
by latent space non-rigid registration. In IEEE In-
ternational Conference on Robotics and Automation
(ICRA).
Stouraitis, T., Hillenbrand, U., and Roa, M. A. (2015).
Functional power grasps transferred through warping
and replanning. In IEEE Int. Conf. on Robotics and
Automation (ICRA).
Stueckler, J., Steffens, R., Holz, D., and Behnke, S. (2011).
Real-time 3D perception and efficient grasp planning
for everyday manipulation tasks. In European Conf.
on Mobile Robots (ECMR), pages 177–182.
Tevs, A., Bokeloh, M., Wand, M., Schilling, A., and Seidel,
H.-P. (2009). Isometric registration of ambiguous and
partial data. In IEEE Conf. on Computer Vision and
Pattern Recognition (CVPR).
Vahrenkamp, N., Westkamp, L., Yamanobe, N., Aksoy,
E. E., and Asfour, T. (2016). Part-based grasp plan-
ning for familiar objects. In IEEE-RAS 16th Int. Conf.
on Humanoid Robots (Humanoids), pages 919–925.
Wang, H., Sridhar, S., Huang, J., Valentin, J., Song, S., and
Guibas, L. J. (2019). Normalized object coordinate
space for category-level 6D object pose and size esti-
mation. In The IEEE Conf. on Computer Vision and
Pattern Recognition (CVPR).
Xiong, L., Wu, L., Cui, W., Zhang, S., Xu, G., and Hu, H.
(2018). Robust non-rigid registration based on affine
ICP algorithm and part-based method. Neural Pro-
cessing Letters, 48(3):1305–1321.
Zeng, Y., Wang, C., Wang, Y., Gu, X., Samaras, D., and
Paragios, N. (2010). Dense non-rigid surface registra-
tion using high-order graph matching. In IEEE Conf.
on Computer Vision and Pattern Recognition (CVPR).
Zollh
¨
ofer, M., Nießner, M., Izadi, S., Rehmann, C., Zach,
C., Fisher, M., Wu, C., Fitzgibbon, A., Loop, C.,
Theobalt, C., et al. (2014). Real-time non-rigid recon-
struction using an RGB-D camera. ACM Transactions
on Graphics (TOG), page 156.
Zou, G., Hua, J., and Muzik, O. (2007). Non-rigid surface
registration using spherical thin-plate splines. In Int.
Conf. on Medical Image Computing and Computer-
Assisted Intervention (MICCAI), pages 367–374.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
802
