A Unity-norm Preserving Quaternion Extended Kalman Filter
Iyad Hashlamon
Mechanical Engineering Department, Palestine Polytechnic University, Hebron, West Bank, Palestine
Keywords: Extended Kalman Filter, Quaternion, Robots.
Abstract: Preserving the quaternion unity norm has significant importance when combined with the extended Kalman
filter (EKF) for state estimation of nonlinear systems perturbed by noise using noisy measurements. Although
this unity challenge is solved numerically on the estimated quaternion, it is normalized out of the EKF
algorithm. Projecting this constraint on the derivation of the EKF algorithm to preserve the quaternion unity
norm is the purpose of this paper. The quaternion unity norm constraint is derived in two forms and projected
on the EKF gain derivation. Then this gain is used to update the quaternion vector keeping its unity norm.
The results show that the unity norm is preserved using the proposed constrained quaternion EKF (CQEKF)
even though sudden changes occur.
1 INTRODUCTION
The state of art of estimation based on the extended
Kalman filter EKF integrates the Bayesian approach
with the observer theory. The system nonlinear model
along with stochastic models form the EKF structure
(Simon, 2006); (Grewal, 2001); (Maybeck, 1982).
The time behavior of the system is described by the
former while the later describe the noise properties.
This filter is used extensively in many applications
(Ulrich, 2011); (Jassemi-Zargani, 2002); (Hedberg,
2017); (Bussi, 2017); (Xu, 2018). The EKF works in
two steps, the first one predicts the states of the
nonlinear system based on the previous known
states and input. The next step updates the
predicted states based on the measurement residual.
In robotic applications, the quaternion
representation combines the advantages of both Euler
based orientation and direct cosine matrix
representations (Phuong, 2009). Therefore it is used
for orientation representation. However, it is used
with the constraint of unity norm (Murray, 1994).
Quaternion based Kalman filters are reported in
the literature (Choukroun, 2006); (Kim, 2004); (Suh,
2010). The quaternion EKF is implemented for rigid
body orientation estimation based on the
measurements of the angular velocity (Hashlamon,
2010). The quaternion vector forms the EKF states.
However, the quaternion is constrained to unity norm
which is not preserved by the EKF (Leffert, 1982). To
overcome this problem, numerical techniques are
applied on the post estimated quaternion to maintain
its unity norm after the estimation is finished .
However, this is an approximation and the constraint
is not included into the filter derivation. Kalman
filtering with state constraints is reported in (Simon,
2009).
This paper proposes a systematic method of
including the unity norm constraint into the filter
derivation to form the constrained quaternion
extended Kalman filter (CQEKF). The constraint is
derived in two forms. Then the EKF gain is derived
based on minimizing the state covariance subjected to
the given constraint.
The rest of the paper is organized as follows: The
conventional EKF is introduced in section II. The unit
quaternion is in section III. The model derivation is in
section IV. The problem is defined in section V. The
CQEKF derivation is in section VI The results are
presented in section VII and the paper is concluded in
section VIII.
2 CONVENTIONAL EKF AND
DESIGN ASSUMPTIONS
Consider the discrete-time nonlinear state space
model
()
11 11
,
kkkkk
xfxu υ
−− −−
=+Φ
, (1)
Hashlamon, I.
A Unity-norm Preserving Quaternion Extended Kalman Filter.
DOI: 10.5220/0010966900003260
In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), pages 1435-1439
ISBN: 978-989-758-615-6; ISSN: 2975-8246
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
1435

kkk
Hxyv=+, (2)
where 𝑥∈ℝ

is the vector of states, u is the
input, 𝑦∈ℝ

represents the measurement vector,
and
k
is the time index.𝜐∈ℝ

and 𝑣∈ℝ

are the
Gaussian process and measurement noises with
covariances
Q
and
R
respectively. It is assumed
that they are independent and uncorrelated. 𝛷∈
ℝ
×
maps the noise to the states space.
H
is the
output matrix and given as
[
]
443
HI
×
≡ 0
.
4
I
is
identity matrix of size four and
43×
0 is 43× zero
matrix.
Then for the given system in (1), the conventional
EKF algorithm is composed of two steps:
The prediction step
()
11
ˆˆ
,
kkk
xfxu
−
−−
=
, (3)
11 1 11 1
T
kkkk
T
kk k
PAP Q A
−
−− −
−− −
=+ ΦΦ
, (4)
where
11
1
ˆ
,
kk
u
k
x
x
A
f
−−
−
∂
=
∂
, (5)
ˆ
x
and
P
are the posterior estimated state and the
estimation error covariance matrix respectively.
ˆ
x
−
and
P
−
are the prior estimates.
The measurement update step updates the
estimates using the measurement residual e and
Kalman gain
K
as
ˆˆ
kk kk
xxKe
−
=+
, (6)
where
K
1T
kk k
KPHS
−−
=
, (7)
and
ˆ
kk k
eYHx
−
=−
, (8)
Y
is the measurement vector with the same
dimension as
y and S is
T
kk k
SHPHR
−
=+
, (9)
The time update of
P
is given by
()
kkk
P
IKHP
−
=−
, (10)
where
I
is the identity matrix, and The Kalman
gain in (7) can be expressed as
1T
kk k
KPHR
−
=
(11)
3 UNIT QUATERNION
The quaternion is a four elements vector, one element
is scalar represented by
0
qR∈ and the remaining
three elements form a vector represented by
3
nR∈

.
The quaternion is written mathematically as
0
qn=+q

(12)
or can be extended using the three imaginary axes
ˆˆ
,,ij
and
ˆ
k
as
[]
01 2 3
012 3
ˆ
ˆˆ
k
T
qqiqjq
qqqq
=+ + +
≡
q
(13)
The quaternion norm is
3
2
2
2
1
i
i
qq
=
=

(14)
For rigid bodies, representing the rotations and
orientation is of significant importance. The
quaternion
q subjected to the constraint of unit
2
2

norm (
2
2
1=q
) is employed to represent the
orientation of a rigid body with respect to a reference
frame (Murray, 1994). This necessitates deriving the
quaternion model.
4 MODEL DERIVATION
There is a direct relation between the measured
angular velocity 𝜴∈ℝ

and the quaternion time
derivative
q

. This relation utilizes the quaternion
multiplication
⊗ as
⊗q=q Ω

. (15)
However, the measured angular velocity has bias
𝒃∈ℝ

and contaminated white zero mean noise 𝒗∈
ℝ

(Roetenberg, 2006)
Ω = ω +b+v, (16)
where
ω
is the true angular velocity and b is
given by
1,1kk bk−−
=+bb v
. (17)
where 𝒗

∈ ℝ

is white zero mean noise.
Equation (15) is nonlinear and perturbed by noise.
Therefore the EKF is employed to estimate the
quaternion and bias.
iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science
1436

Define the state vector as
T
TT
kkk
x

≡

qb
, then
after mathematical manipulation and discretization,
the model (1) is obtained with
4111
11
1
1
()
(,)
2
kk k
kk
k
IT
fx u
−−−
−−
−


+−


≡




F Ω bq
b
,
(18)
1
1
,1
k
k
bk
υ
−
−
−

≡


v
v
, (19)
where
0- - -
0-
()
-0
-0
x
yz
x
zy
yz x
zy x
λλλ
λλλ
λ
λλ λ
λλ λ



=




F
, (20)
and
123
032
43
30 1
1
21 0
1
33 3
1
2
k
k
qqq
qqq
T
qq q
qq q
I
×
−
−
×
 −−− 



−


−


−
Φ=


−




0
0
.
(21)
This model is used in the EKF algorithm and the
quaternion
q is considered to be the output.
5 PROBLEM DEFINITION
Maintaining the quaternion unity norm during the
estimation is a challenge. The conventional EKF does
not preserve this constraint. In the previous studies,
this challenge is solved numerically by normalizing
the posterior estimates
ˆ
q
out of the EKF algorithm as
in
2
2
ˆ
ˆ
ˆ
N
=
q
q
q
, (22)
or as reported in (Hashlamon, 2010)
()
2
2
ˆˆ ˆˆ
1
N
=+−qq qq
, (23)
where
ˆ
N
q is the normalized estimated quaternion
vector. It is a low cost method of unity preserving
done out of the EKF algorithm. Here the unity norm
constraint is projected on the Kalman gain derivation
and included into the EKF algorithm.
6 CQEKF DERIVATION
The unity norm of the estimated quaternion
ˆ
q
is given
as
()
3
2
2
2
0
ˆˆ
ˆ
1
i
i
fq
=
== =

qq
, (24)
however,
ˆ
q
is unknown before the updating step
in the EKF. The best known quaternion vector is the
predicted quaternion vector
ˆ
k
−
q
obtained from (3).
Then (24) can be written in terms of
ˆ
k
−
q
as
()
2
2
ˆˆ
1f
−−
==qq
and linearized about
ˆ
k
−
q
using
Taylor series in two forms.
The first form is
() () ()( )
ˆˆˆˆˆ
1
k k kkk
fff
− − −−−
=+ −=qqqqq

. (25)
then (25) can be simplified as
() () ()
ˆˆ ˆ ˆˆ
1
kk k kk
fff
−− − −−
=− +qq q qq

, (26)
which has only
ˆ
−
q
as unknown, (26) is written as
ˆ
k
Gd
−
=q
, (27)
where
()
()
()
01,23
ˆ
ˆ
ˆˆˆˆ
2
ˆ
k
k
k
k
f
Gf qqqq
−
− −−−−
−
∂

== =

∂
q
q
q

, (28)
and
()
3
2
0
ˆ
1
i
k
i
dq
−
=
=+

. (29)
The second form used the previous known value of
the estimated quaternion as
() () ()( )
1
ˆˆˆˆˆ
1
kkkkk
fff
−−−−
−
=+ −=qqqqq

. (30)
then (30) can be simplified as
() () ()
1
ˆˆ ˆ ˆˆ
1
kk k kk
fff
−− − −
−
=− +qq q qq

, (31)
A Unity-norm Preserving Quaternion Extended Kalman Filter
1437

For this case, G and
d
in (27) are as expressed as in
(28) and
()
3
2
1
0
ˆ
ˆ
1
ik
k
i
dqG
−
−
=
=− +

q
. (32)
respectively.
The gain in (7) is the solution of (33)
()()
arg min
k
T
kk k kk
k
T
K
kk k
IKHPIKH
KTr
KRK
−

−−

=

+

,
(33)
In the same way, minimizing (33) subjected to the
constraint
ˆ
k
Gd
−
=q
yields to the constraint system
Kalman gain
k
K

34
k
kk
KK
δ
×

=−


0

, (34)
where
k
K
is given in (7) and δ is
()
()()
1
1
11
ˆ
TT TT
kkkkkkk
GGG G deSe eS δ
−
−
−−−
=−q
. (35)
where
d
is as in (29) or (32).
As a final estimation, the CQEKF has the
equations(3)-(9) and
1T
kkkk
KPHS
−−
=
, (36)
34
k
kk
KK
δ
×

=−


0

, (37)
00
31
00
1
ˆˆ
ˆˆ ˆ
T
k
qq n n
e
qn qn n n
−−
−− −
×

+

=−


−−×


0
, (38)
ˆˆ
kk kk
xx Ke
−
=+

, (39)
()
kkkk
PIKHP
−
=−

, (40)
where
[]
0
T
qn≡q

is considered as the
measured quaternion. The zero error in quaternion
means that both of the quaternions, the measured and
the estimated, are coinciding on each other and in the
same direction i.e.
00
ˆˆ
1
T
qq nn+=
and
00 31
ˆˆ ˆ
qn qn n n
×
−−×=0
. Accordingly,
k
e in
quaternion representation is as in (38).
The derived CQEKF can be projected directly on
the adaptive EKF proposed in (Hashlamon,2020).
7 RESULT
In this part, the CQEKF is tested. MATLAB Simulink
is used as an experimental platform. The noise with
the specified covariance matrices are generated using
the Simulink Gaussian noise generator. The input
u
in (1) is the measured angular velocity
Ω
. To form
Ω
, the bias and process noise with covariance
Q
are
added to
ω
. The measured vector
Y
in (8) has
contaminated noise with covariance .
.
. The model
equations (18) -(21) are used to form the CQEKF
algorithm. The true bias values are generated based
on time
t
as in (41) .
[]
[]
[]
0.5 0.1 0 20
121 20 50
002
T
T
T
t
t
else

≤


=<≤




b
. (41)
The initialization, simulation parameters, and the
corresponding constants values are listed in Table 1.
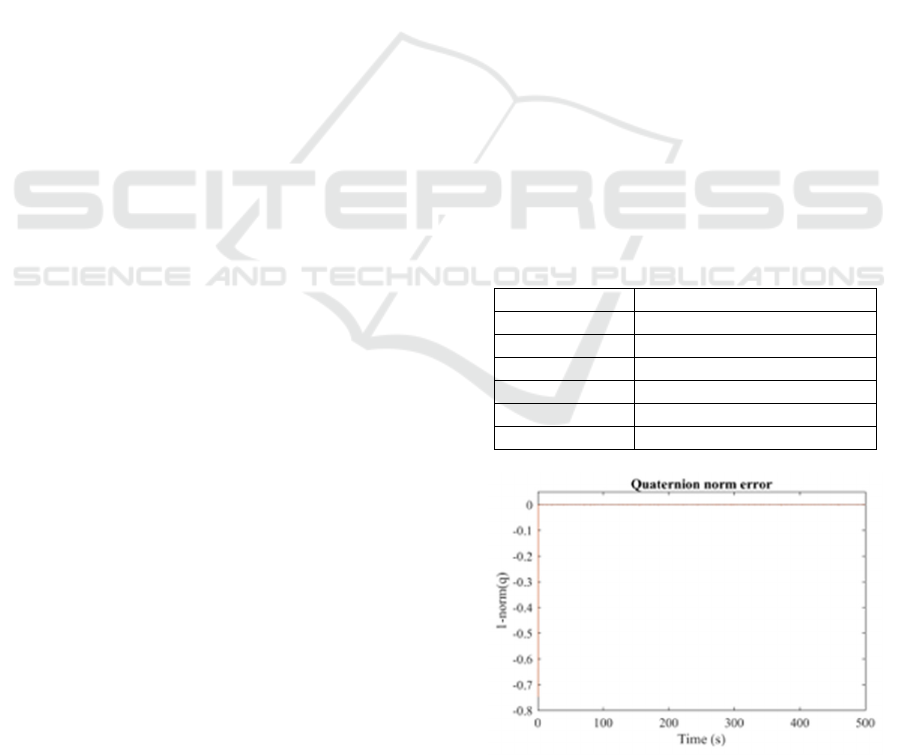
The experiment duration is 500 sec. The performance
of the CQEKF displays its ability to preserve the
quaternion constraint as depicted in Fig. 1. This also
shows that though sudden changes in the bias take
place, the norm still unity. Both forms in (28), (29) or
(32) show the same steady state behavior.
Table 1: Initialization and simulation parameters.
Parameter Value
T
0.01 sec
R
6
4
10
I
−
Q
2
6
10
I
−
0
P
7
10
I
0
q
[
]
0.50.50.50.5
T
0
b
[
]
000
T
Figure 1: The estimated quaternion norm error.
iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science
1438

8 CONCLUSIONS
A constrained quaternion extended Kalman filter
CQEKF is proposed. The norm constraint is projected
on the derivation of the EKF gain. Two forms of the
constraint are obtained, both have the same effect.
The obtained CQEKF preserves the unity norm
constraint for the quaternion during the running of the
algorithm. The results show that unity norm is
preserved even sudden changes to the states may
occur.
REFERENCES
Simon, D. (2006). Optimal state estimation: Kalman, H
infinity, and nonlinear approaches. John Wiley & Sons.
Grewal, M. S., & AP, A. K. (2001). Filtering: Theory and
Practice Using MATLAB 2nded.
Maybeck, P. S. (1982). Stochastic models, estimation, and
control. Academic press.
Ulrich, S., & Sasiadek, J. Z. (2011, June). Extended Kalman
filtering for flexible joint space robot control. In
Proceedings of the 2011 American control conference
(pp. 1021-1026). IEEE.
Jassemi-Zargani, R., & Necsulescu, D. (2002). Extended
Kalman filter-based sensor fusion for operational space
control of a robot arm. IEEE Transactions on
Instrumentation and Measurement, 51(6), 1279-1282.
Hedberg, E., Norén, J., Norrlöf, M., & Gunnarsson, S.
(2017). Industrial robot tool position estimation using
inertial measurements in a complementary filter and an
EKF. IFAC-PapersOnLine, 50(1), 12748-12752.
Bussi, U., Mazzone, V., & Oliva, D. (2017, September).
Control strategies analysis using EKF applied to a
mobile robot. In 2017 XVII Workshop on Information
Processing and Control (RPIC) (pp. 1-6). IEEE.
Xu, Y., Shmaliy, Y. S., Ahn, C. K., Tian, G., & Chen, X.
(2018). Robust and accurate UWB‐based indoor robot
localisation using integrated EKF/EFIR filtering. IET
radar, sonar & navigation, 12(7), 750-756.
Phuong, N. H. Q., Kang, H. J., Suh, Y. S., & Ro, Y. S.
(2009). A DCM based orientation estimation algorithm
with an inertial measurement unit and a magnetic
compass. Journal of Universal Computer Science,
15(4), 859-876.
Murray, R. M., Li, Z., & Sastry, S. S. (1994). A
mathematical introduction to robotic manipulation
CRC Press. Boca Raton, FL.
Choukroun, D., Bar-Itzhack, I. Y., & Oshman, Y. (2006).
Novel quaternion Kalman filter. IEEE Transactions on
Aerospace and Electronic Systems, 42(1), 174-190.
Kim, A., & Golnaraghi, M. F. (2004, April). A quaternion-
based orientation estimation algorithm using an inertial
measurement unit. In PLANS 2004. Position Location
and Navigation Symposium (IEEE Cat. No.
04CH37556) (pp. 268-272). IEEE.
Suh, Y. S. (2010). Orientation estimation using a
quaternion-based indirect Kalman filter with adaptive
estimation of external acceleration. IEEE Transactions
on Instrumentation and Measurement, 59(12), 3296-
3305.
Hashlamon, I. (2010). Experimental verification of an
orientation estimation technique for autonomous
robotic platforms (Doctoral dissertation).
Lefferts, E. J., Markley, F. L., & Shuster, M. D. (1982).
Kalman filtering for spacecraft attitude estimation.
Journal of Guidance, Control, and Dynamics, 5(5),
417-429.
Simon, D. (2010). Kalman filtering with state constraints: a
survey of linear and nonlinear algorithms. IET Control
Theory & Applications, 4(8), 1303-1318.
Roetenberg, D. (2006). Inertial and magnetic sensing of
human motion (p. 126). These de doctorat.
Hashlamon, I. (2020). A new adaptive extended Kalman
filter for a class of nonlinear systems. Journal of
Applied and Computational Mechanics, 6(1), 1-12.
A Unity-norm Preserving Quaternion Extended Kalman Filter
1439