Effect of the Size and Position of Two Heat-generating Blocks on
Natural Convection inside a Closed Cavity
R. Hidki
a
, L. El Moutaouakil, Z. Charqui
b
, M. Boukendil
c
and Z. Zrikem
d
LMFE, Department of Physics, Cadi Ayyad University, Faculty of Sciences Semlalia, Marrakesh, Morocco
Keywords: Natural convection, Heat-generating, Square blocks, Closed cavity, Finite volume method.
Abstract: This work aims to numerically study natural convection in a square cavity with two heat-generating blocks.
The cavity is cooled uniformly via its right vertical wall, while the remaining walls are thermally insulated.
The Finite Volume Method (FVM) with the SIMPLE algorithm is employed for discretization and solving
the differential equations. The results are presented to clarify the effect of the size and position of the two
blocks for Ra
m
= 10
6
, Pr = 0.71, and K = 0.1. These results are reported in terms of streamlines and isotherms.
According to our findings, the size and position of two generating blocks significantly influence the cavity's
fluid flow and heat transfer.
1 INTRODUCTION
Because of its practical importance, natural
convection in a closed cavity contains heating blocks
(active or inactive) has attracted the attention of
several scientific researchers (Pandey et al., 2019).
This cavity model can be applied in many engineering
fields, namely cooling of electronic devices, solar
collectors, cooling, and heating of buildings. Many
researchers have focused on this problem (Nardini et
al., 2016, Paroncini and Corvaro, 2019, and Hidki et
al., 2021), either from the numerical accuracy point
of view of the calculation or the point of view to
improve the thermal behavior.
In the literature, the authors considered the case of
one or several isothermal blocks (Dash and Lee,
2014, Pordanjani et al., 2018, and Sheikholeslami and
Vajravelu, 2018), the case of a conductive block
(House et al., 1990 and Lima and Ganzarolli, 2016),
and the case of a heat-generating block (Sivaraj et al.,
2020). In the last case, which is the most practical,
few studies were found. Among them, the
contributions of (Oh et al., 1997 and Ha et al., 1999),
who numerically studied the effect of a heat-
generating square block on natural convection in a
differentially heated cavity. The authors analyzed the
a
https://orcid.org/0000-0002-6727-3092
b
https://orcid.org/0000-0002-2987-3046
c
https://orcid.org/0000-0001-7058-2120
d
https://orcid.org/0000-0002-1786-4310
impact of the internal temperature difference (ΔT)
and the Rayleigh number on the flow and heat transfer
in the cavity. Later on, the same problem was studied
by (Lee and Ha, 2006) in a cavity heated from below
and cooled from above. The authors analyzed the
effect of the internal and external Rayleigh numbers,
the thermal conductivity ratio on the dynamic and
thermal characteristics in the cavity. Their results
show that if ΔT = 25, the isotherms are insensitive to
the variation of the thermal conductivity ratio.
This literature review shows that natural
convection in closed cavities with heat-generating
blocks is up-to-date research due to its practical
application in engineering, such as cooling of
electronic components, heat exchangers, buildings,
etc. Therefore, according to these findings and our
knowledge, the case of two square heat-generating
blocks of different sizes and positions in a closed
cavity cooled by one of its sides has not been treated.
However, the main objective of the present work is to
study the effect of the size and position of two heat-
generating blocks on the dynamic and thermal
characteristics of the flow in a square closed cavity.
376
Hidki, R., El Moutaouakil, L., Charqui, Z., Boukendil, M. and Zrikem, Z.
Effect of the Size and Position of Two Heat-generating Blocks on Natural Convection inside a Closed Cavity.
DOI: 10.5220/0010734800003101
In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 376-380
ISBN: 978-989-758-559-3
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 MATHEMATICAL
FORMULATION
The physical problem considered is schematized in
Figure 1. It is an air-filled square-shaped cavity, with
the right vertical wall cooled with a constant
temperature T
c
. The remaining walls are thermally
insulated. Two square heat-generating blocks with
different sizes S
1,2
= w
1
,
2
/L are placed inside the
cavity. The blocks generate the same amount of
energy (Q
1
(W/m
3
) = Q
1
(W/m
3
) = Q
m
(W/m
3
)). The
latter are placed at three different heights (Y
1
= 0.25,
Y
2
= 0.5, and Y
3
= 0.75) and fixed in the X-direction
(block 1 at X
1
= 0.25 and block 2 at X
2
= 0.75). All
thermophysical properties of air are independent of
temperature, except for the density in the buoyancy
term for which the Boussinesq approximation is
adopted. The thermal radiation is negligible.
By introducing these approximations in the
continuity, Navies-Stokes, and energy equations, we
obtain the following system of non-dimensional
equations:
Figure 1: Studied configuration.
UV
0
XY



(1)
22
22
UUUP UU
UV Pr
XYX
XY

 
 


   


(2)
22
22
m
VVVP VV
UV Pr
XYY
XY
Pr Ra

 
 


   



(3)
22
22
UV
XY
XY

      
 


  


(4)
22
i
22
m
Ra
K
Ra
XY

    






(5)
The non-dimensional parameters, i.e., Rayleigh
number, Prandtl number, and thermal conductivity
ratio involved in these equations, are given by:
5
m
m
ff
gLQ
Ra
k



;
f
Pr



;
s
f
k
K
k

The non-dimensional boundaries conditions are
specified as follows:
 On all solid walls:
UV0
 On the right vertical wall:
(1, Y ) 0
 On the bottom, left, and top walls:
 
0, Y X, 0 or 1 0
XY
 


 On the solid-fluid interfaces of the blocks:
s
f
K
nn




where n is the normal direction to
the block surfaces.
3 NUMERICAL APPROACH AND
VA L I D AT I O N
The above governing equations (1)-(5) and different
boundary conditions are solved by using the SIMPLE
(Semi Implicit Method for Pressure Linked
Equations) algorithm based on the finite volume
method. The uniform grid was used in the x and y
directions.
The numerical code has been validated with the
experimental and numerical data of (Paroncini and
Corvaro, 2009). They studied natural convection in
the presence of a hot rectangular block inside a square
cavity cooled by its vertical walls. Comparative
results in terms of the mean Nusselt number, at the
upper surface of the hot block, are shown in Table 1.
The obtained results show good agreement with the
numerical simulation and also with experimental
results.
Effect of the Size and Position of Two Heat-generating Blocks on Natural Convection inside a Closed Cavity
377

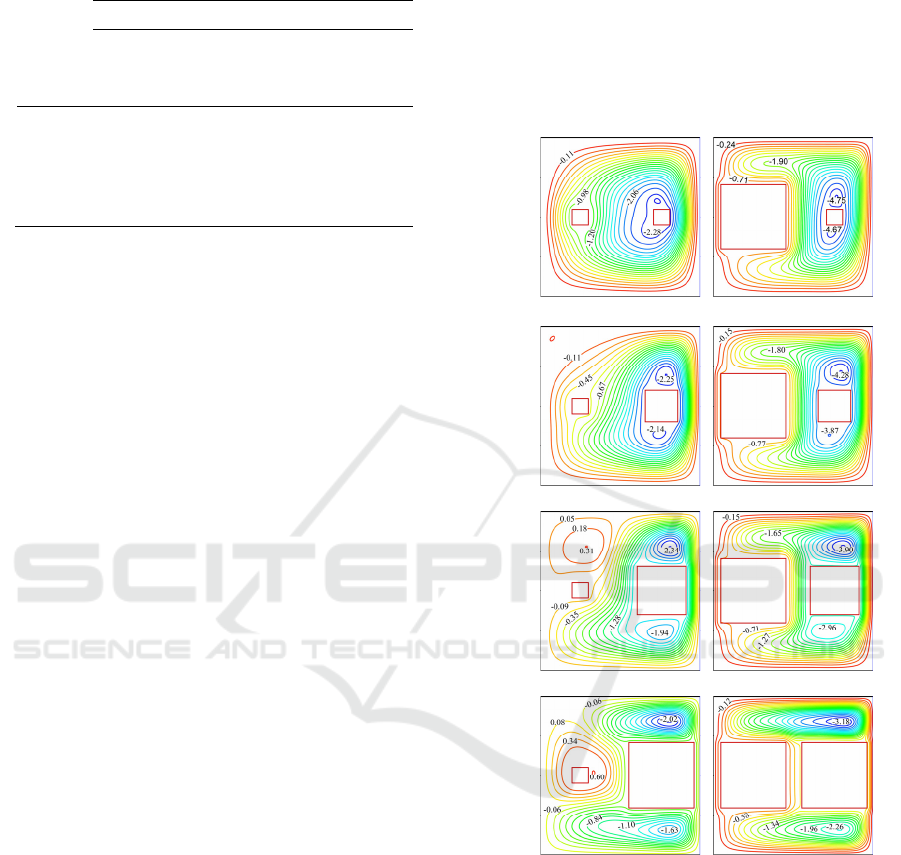
Table 1: Mean Nusselt number for different values of
Rayleigh number.
Ra×10
5
Mean Nusselt numbe
r
Paroncini and Corvaro,
2009
Present work Num Exp
1.24
1.46
1.76
2.05
2.25
3.67
3.74
3.82
3.89
3.93
3.58
3.62
3.78
3.85
3.93
3.71
3.79
3.89
3.98
4.03
4 RESULTS AND DISCUSSION
4.1 Effect of Block Size
To investigate the effect of the block size, Figures 2
and 3 give, respectively, the streamlines and
isotherms for different values of S
1
and S
2
with Ra
m
=
10
6
, Pr = 0.71, and K = 0.1.
For S
1
= S
2
= 0.1 (Figure 2a), the streamlines
show that the flow structure is almost symmetrical
concerning the horizontal median of the cavity even
though the Rayleigh number is important (Ra
m
= 10
6
).
This can be explained by the fact that the blocks have
a small size and therefore do not produce enough
energy to circulate the air quickly in the cavity. This
structure consists of a large clockwise cell encircling
block 1 and descending into the space limited by the
cold wall and block 2. Two low-intensity cells appear
just below and above block 2 (closest to the cold
wall), contributing to its cooling. For S
2
= 0.4 (Figure
2a), the flow comprises two primary cells in opposite
directions. One clockwise cell encircles block 2, and
another counterclockwise cell surrounds block 1. The
first cell is three times more intense than the second
and occupies a large part of the cavity. The secondary
cells appearing around block 2 in the previous case
are still present, but this time with large sizes. It
should be noted that the flow symmetry observed in
the case S
1
= S
2
= 0.1 is broken after increasing S
2
.
On the other hand, Figure 2a also shows that the
maximum streamline function (Ψ
max
) is not very
sensitive to the variation of S
2
. Indeed, when S
2
varies
from 0.1 to 0.4, Ψ
max
goes from 2.28 to 2.03, i.e., a
relative difference that does not exceed 11%. In the
case where S
1
= 0.4 and S
2
= 0.1 (Figure 2b), the flow
is more intense around block 2, and it is almost
stagnant between block 1 and the vertical passive
wall. It should also be noted that the flow intensity is
very sensitive to the variation of S
2
. Indeed, Ψ
max
changes from 4.75 to 3.19 when S
2
passes from 0.1 to
0.4, i.e., a relative difference of 33%. Since when the
size of the blocks is large, the fluid does not have
enough space to flow freely in the cavity. In addition,
the viscous friction forces are high because they are
proportional to the size of the blocks.
Ψ
max
= 2.28 Ψ
max
= 4.75
S
2
= 0.1
Ψ
max
= 2.25 Ψ
max
= 4.28
S
2
= 0.2
Ψ
max
= 2.34 Ψ
max
= 3.91
S
2
= 0.3
Ψ
max
= 2.03 Ψ
max
= 3.19
S
2
= 0.4
(a). S
1
= 0.1 (b). S
1
= 0.4
Figure 2: Streamlines obtained for different combinations
(S
1
, S
2
).
The isotherms, Figure 3 shows that, in general,
these lines are concentrated in the largest block and
tight in the fluid medium. The isotherms are almost
parallel to the cold wall for S
1
= S
2
= 0.1 (Figure 3a).
This means that the local heat transfer is uniform on
it. It can be noted that when we increase S
2
while
keeping S
1
fixed at a given value, the maximum
temperature rises rapidly. This is because of the
domination of conductive heat exchange over
convective one. Consequently, the fluid is unable to
evacuate the heat generated by two blocks. For S
1
=
0.4, the maximum temperature is insensitive to the
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
378

variation of S
2
(0.1 ≤ S
2
≤ 0.3). It should be noted that
the temperature of block 2 is the lowest for all values
of S
2
≤ S
1
.
θ
max
= 0.02 θ
max
= 0.17
S
2
= 0.1
θ
max
= 0.04 θ
max
= 0.18
S
2
= 0.2
θ
max
= 0.09 θ
max
= 0.19
S
2
= 0.3
θ
max
= 0.16 θ
max
= 0.24
S
2
= 0.4
(
a
)
. S
1
= 0.1
(
b
)
. S
1
= 0.4
Figure 3: Isotherms obtained for different combinations (S
1
,
S
2
).
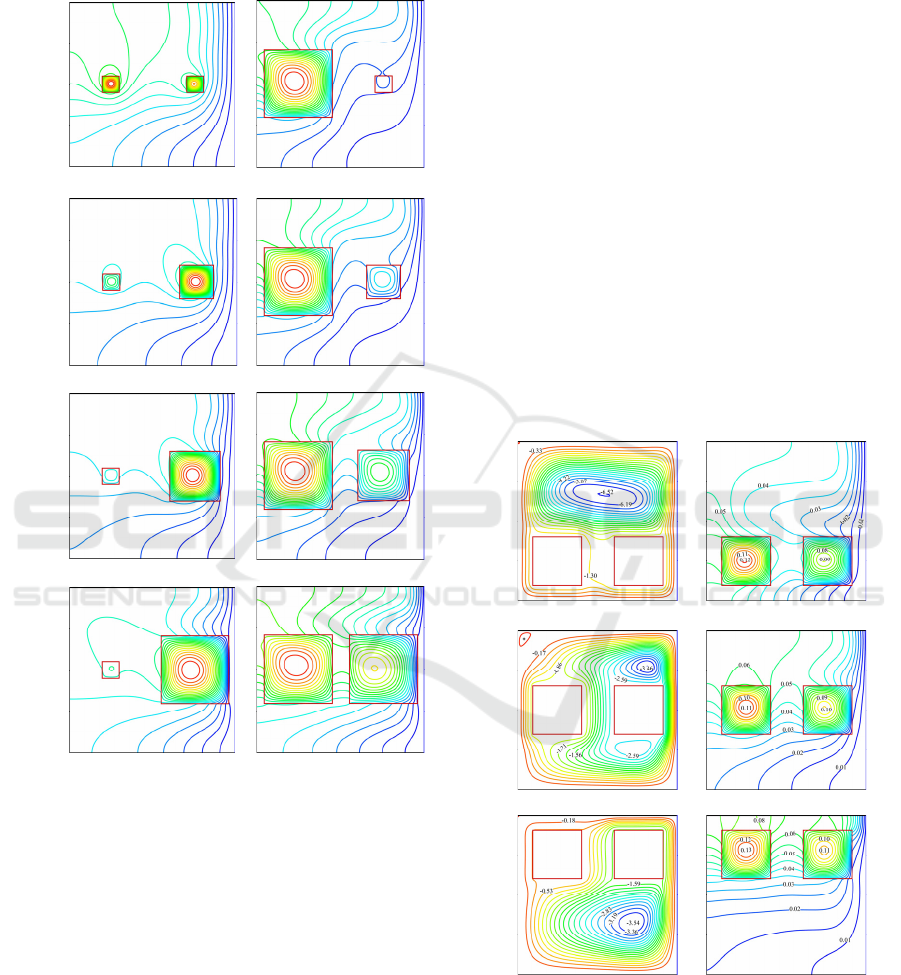
4.2 Effect of the Position of the Blocks
In this section, the effect of the blocks' position on
streamlines and isotherms is studied for S
1
= S
2
= 0.3
and Ra
m
= 10
6
.
In Figure 4, the streamlines and isotherms are
plotted for three different positions of the blocks (P
1
:
bottom position, P
2
: center position, P
3
: top position).
The streamlines (Figure 4a) show that the position of
the blocks significantly affects the structure and
intensity of the flow in the cavity. Indeed, when the
blocks are placed at position P
1
, the flow structure
consists of two primary cells; the first one encircles
the two blocks, and the second one develops above
the two blocks. The latter has a vital role in the
simultaneous cooling of the blocks. When moving
from P
1
to P
2
, the flow changes from bicellular to
multicellular, and the flow intensity reduces by 47%
(Ѱ
max
goes from 6.53 to 3.46). On the other hand,
switching from position P
2
to P
3
, Ѱ
max
remains
practically unchanged (2.3% difference). The
structure of the flow changes from multicellular to the
initial state (i.e., bicellular).
The isotherms in Figure 4b show that these lines
are always concentrated in the heat-generating blocks
for the three positions analyzed. It can be noted, when
comparing the three positions, that the lowest
maximum temperature of the blocks is indicated in
the two positions P
1
and P
2
, and the highest
temperature is noted in position P
3
. From these
findings (Figure 4), it can be concluded that positions
P
1
and P
2
are the best for the excellent cooling of both
heat-generating blocks.
Ѱ
max
= 6.53 θ
max
(1,2) = (0.118,0.091)
P
1
Ѱ
max
= 3.46 θ
max
(1,2) = (0.114,0.097)
P
2
Ѱ
max
= 3.54 θ
max
(1,2) = (0.130,0.114)
P
3
(a) (
b
)
Figure 4: Streamlines (a) and isotherms (b) for S
1
=
S
2
= 0.3 and different positions of the blocks.
Effect of the Size and Position of Two Heat-generating Blocks on Natural Convection inside a Closed Cavity
379

5 CONCLUSION
In this work, the effect of the size and position of two
heat-generating blocks inside a closed air-filled
cavity on the streamlines and isotherms is
numerically analyzed for Ra
m
= 10
6
using FVM. The
main results that can be drawn from this study are as
follows:
 The size and position of the two blocks
significantly affect the flow and temperature
field inside the cavity.
 The isotherms are more concentrated in the
largest block.
 The maximum temperature increases rapidly
with S
1
and S
2
.
 The position P
1
or P
2
should be chosen for
the excellent cooling of the two studied
blocks.
REFERENCES
Pandey, S., Park, Y. G., Ha, M. Y. 2019. An exhaustive
review of studies on natural convection in enclosures
with and without internal bodies of various shapes. Int.
J. Heat Mass Transf., 138:762–795.
Nardini, G., Paroncini, M., Vitali, R. 2016. Experimental
and numerical analysis of the effect of the position of a
bottom wall hot source on natural convection. Appl.
Therm. Eng., 92:236–245.
Paroncini, M., Corvaro, F. 2009. Natural convection in a
square enclosure with a hot source. Int. J. Therm. Sci.,
48(9):1683–1695.
Hidki, R., El Moutaouakil, L., Charqui, Z., Boukendil, M.,
Zrikem, Z. 2021. Natural convection in a square cavity
containing two heat-generating cylinders with different
geometries. Mater. Today Proc., 45:7415-7423.
Dash, S. M., Lee T. S. 2015. Natural convection in a square
enclosure with a square heat source at different
horizontal and diagonal eccentricities. Numer. Heat
Transf. Part A, 68(6):686-710.
Pordanjani, A. H., Jahanbakhshi A., Nadooshan, A. A.,
Afrand, M. 2018. Effect of two isothermal obstacles on
the natural convection of nanofluid in the presence of
magnetic field inside an enclosure with sinusoidal wall
temperature distribution, Int. J. Heat Mass Transf.,
121:565–578.
Sheikholeslami, M., Vajravelu, K. 2018. Lattice Boltzmann
method for nanofluid flow in a porous cavity with heat
sources and magnetic field. Chinese J. Phys.,
56(4):1578-1587.
House, J. M., Beckermann, C., Smith, T. F. 1990. Effect of
a centered conducting body on natural convection heat
transfer in an enclosure. Numer. Heat Transf. Part A,
18(2):213-225.
Lima, T. P., Ganzarolli, M. M. 2016. A heatline approach
on the analysis of the heat transfer enhancement in a
square enclosure with an internal conducting solid
body. Int. J. Therm. Sci., 105:45–56.
Oh, Y. Y., Ha, M. Y., Kim, K. C. 1997. Numerical study of
heat transfer and flow of natural convection in an
enclosure with a heat-generating conducting body.
Numer. Heat Transf. Part A Appl., 31(3):289–303.
Ha, M. Y., Jung, M. J., Kim, Y. S. 1999. Numerical study
on transient heat transfer and fluid flow of natural
convection in an enclosure with a heat-generating
conducting body. Numer. Heat Transf. Part A Appl. An
Int. J. Comput. Methodol., 35(4):415–433.
Sivaraj, C., Miroshnichenko, I. V., Sheremet, M. A. 2020.
Influence of thermal radiation on thermogravitational
convection in a tilted chamber having heat-producing
solid body. Int. Commun. Heat Mass Transf.,
115:104611.
Lee, J. R., Ha, M. Y. 2006. Numerical simulation of natural
convection in a horizontal enclosure with a heat-
generating conducting body. Int. J. Heat Mass Transf.,
49(15-16):2684–2702.
BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)
380