The Role of Gas to Power in Supporting Large-scale Renewable

Energy Integration in Morocco: Insights from Optimization through

Long-term Bottom-up Modelling

Jabrane Slimani

, Abdeslam Kadrani

, Imad El Harraki

and El Hadj Ezzahid

Research Laboratory in Information Systems, Intelligent Systems and Mathematical Modelling, National Institute of

Statistics and Applied Economics, Rabat, Morocco

Laboratory of Applied Mathematics and Business Intelligence, National School of Mines of Rabat, Rabat, Morocco

Mohammed V University in Rabat, Morocco

Keywords: Energy modelling, Power system, Natural gas, OSeMOSYS, Optimisation model, Morocco.

Abstract: To strengthen its energy sector, Morocco adopted at the end of 2009 an energy strategy based mainly on the

increased penetration of renewable sources, the improvement of energy efficiency, and the reinforcement of

regional integration. Morocco's energy strategy called for increasing the share of renewable electricity to 42%

of installed capacity by 2020 and over 52% of installed renewable capacity by 2030. However, as renewable

energy becomes more widespread, the national power system will face new challenges due to its intermittent

nature. It is, therefore, necessary to deploy flexible resources to cope with this intermittency and improve the

stability of the power system. In this work, we used a bottom-up linear optimization model to identify the best

options for developing gas to power technology in Morocco. We find out that the new gas to power facilities

development, and the import of liquefied natural gas (LNG), is not the optimal solution. Instead, it would be

interesting for Morocco to negotiate its natural gas supply via the GME with one of its neighbours, Spain or

Algeria.

1 INTRODUCTION

Today, the world's energy sector's main challenge is

to ensure, while preserving the environment,

sustainable energy security for emerging countries,

maintaining growth and living standards for

developed countries, and providing access to energy

at affordable costs for less developed countries

(Sarkis

and Tamarkin, 2008)

. In this perspective, renewable

energies (RES) have emerged as an appropriate

solution to the challenges of security of supply, access

to energy and preservation of the environment

(Gasparatos, 2017)

In Morocco, the power generation sector faces the

same challenges, including increasing demand for

electricity at an average rate of 7% per year since

2002, a commitment to reduce greenhouse gas

emissions by 32% by 2030, and heavy dependence on

imported fossil fuels (98% in 2009)

(Nfaoui, 2020)

https://orcid.org/0000-0002-3001-103X

https://orcid.org/0000-0002-7116-4702

Thus, Morroco adopted, in 2009, a new energy

strategy. This strategy was based primarily on

increasing clean energy, improving energy

efficiency, and strengthening regional integration.

However, a power system with a high share of

renewable resources faces the problem of power

quality and reliability

(McPherson,2018)

. Although

many flexible generation options exist to facilitate

RES system integration, one of the main challenges is

to select the most optimal alternative to meet the

power system requirements. Historically, one of the

most appropriate ways to address the intermittency

generated by renewable energy was to develop

natural gas-fired power plants (GFPPs) such as

combined cycle power plants (CCGTs)

(Ibrahim,

2018)

. However, Morocco's gas resources are not

sufficient for the large-scale development of gas to

power technologies. Indeed, the Tahaddart CCGT

plant, developed in 2005, and the Aïn Beni Mathar

integrated combined cycle solar power plant

Slimani, J., Kadrani, A., El Harraki, I. and Ezzahid, E.

The Role of Gas to Power in Supporting Large-scale Renewable Energy Integration in Morocco: Insights from Optimization through Long-term Bottom-up Modelling.

DOI: 10.5220/0010733600003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 327-332

ISBN: 978-989-758-559-3

327

("ISCC"), set in 2010, take advantage of the

Maghreb-Europe (GME) gas pipeline arrangement

between Morocco and Algeria.

This agreement will expire towards the end of

2021. At the time of submitting this paper, there has

been no announcement regarding the renewal of this

agreement. Given this situation, Morocco may

continue the development of the Gas to Power field

through several options. These include mainly:

1) Renewal of the GME contract or negotiation of a

new contract but this time with Spain to import gas

from Spain through the same pipeline; 2) Making use

of recently discovered deposits in the Tendrara region

and seeking new deposits; or, 3) Importing Liquefied

Natural Gas (LNG).

This paper intends to evaluate the optimal choice

for natural gas development in Morocco under the

guidelines of the National Energy Strategy The focus

will be on assessing whether the choice of importing

LNG or purchasing natural gas directly from Algeria

or Spain through the GME is optimal. To do so, we

will describe, in section 2, the optimization tool used

as well as the approach followed to integrate the

renewed installed capacity objectives in its equation

system. In the 3

section, we introduce our case

study: the Moroccan electrical system and its

characteristics. We also present the scope of our

research. Finally, in the 4

section, we will discuss

the results of our study and explain the upcoming

research work.

2 MATERIALS AND METHODS

2.1 Tool: Open-Source Energy

Modelling System

Optimizing power systems in developing countries to

meet demand with available supply technologies and

resources can be solved by bottom-up modelling

techniques. The Open-Source Energy Modelling

System (OSeMOSYS) is one of the bottom-up,

dynamic, and linear optimization models applied to

integrated assessment and energy planning

(Dhakouani, 2019). It aims to satisfy demand by

accounting for technical, economic, and

environmental parameters while optimizing the total

discounted cost (Howells, 2011). The developers of

this model designed it around a series of "blocks" of

functionality. These functionalities are related to the

following aspects: costs, capacity adequacy, energy

balance, renewable energies, emissions, and

provisions. The parameters introduced by the analyst,

the intermediate variables, and the equations and the

constraints are what characterize each block (Howells

et al., 2011).

Initially, the code for OSeMOSYS was written in

GNU MathProg, and recently, it has been translated

into GAMS (General algebraic modelling system)

and Python. Our study uses the GAMS version of

OSeMOSYS. OSeMOSYS allows the modeller to

introduce a constraint of integration of RES in the

energy system through equation (1).

"r" and "y" represent the data sets for the region

and the modelling year, respectively. The

REMinProductionTarget(r,y) parameter is the

minimum renewable production target desired by the

analyst. Also, the variable

RETotalProductionOfTargetFuelAnnual(r,y)

stands for

the Annual Production of the fuels marked as

renewable in the model, and the variable

TotalREProductionAnnual(r,y)

denotes the annual

production of all technologies marked as renewable

in the model. However, using this equation for the

case of the Moroccan energy strategy is not viable.

The objectives of the Moroccan energy strategy are

expressed as renewable installed capacity and not as

annual renewable energy production. A modification

of the code is necessary before proceeding with the

modelling.

2.2 Implementation of the Renewable

Installed Capacity Constraint in

OSeMOSYS

In this section, we explain the formulas for modelling

the installed capacity constraints of renewable energy

sources. To impose a constraint on renewable

generation, we used the same method as that used by

(Howells et al., 2011). Thus, we initially converted

equation (1) to equation (2).

Equation (2) is composed of 3 terms. The first one

is the variable TotalRECapacityAnnual, which is a

new variable introduced to the system. It allows

identifying the total annual renewable capacity.

Equation (3) determines the computing method of this

variable.

(2)

(1)

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

328

The variable TotalCapacityAnnual is the existing

total capacity of technology "t" for year "y". The

RETagTechnology parameter represents a binary

parameter flagging renewable technologies. It has the

value 1 for renewable technologies and 0 otherwise.

The 2

term is the variable

TotalPowerCapacityAnnual(r,y). This variable

accounts for the total annual capacity of the

technologies generating electricity. It is derived from

the TotalCapacityAnnual variable and the

PowerTagTechnology parameter as shown in

equation (4). The new parameter was added to allow

the model to identify electricity-generating

technologies and separate them from other

technologies defined in the model.

The 3

term is the REMinCapacityTarget(r,y)

parameter. It has been introduced to be able to define

a minimum target of renewable capacity.

3 CASE DESCRIPTION

The research framework of our study covers the

period from 2010 to 2050. The periodic modelling

cycle follows a five-year capacity investment

decision cycle. Our analysis will be based on two

distinct scenarios.

In the first scenario, we will assume that Morocco

has decided to develop flexible power plants running

on natural gas through the development of a gas

infrastructure based on the import of LNG,

development of an LNG regasification terminal and a

network for the transport of the gas towards the power

plants. The second scenario would be based on the

hypothesis that Morocco successfully negotiated a

natural gas supply contract via the GME with Algeria

or Spain. The other assumptions commonly used in

the two scenarios included in Table 1 are:

Table 1: Assumptions and Scenarios characteristics

Assumption

categories

Scenarios

Scenario 1

(LNG development)

Scenario 2

(GME contracts)

Objectives

in terms of

RES

The national energy strategy targets regarding

renewable installed capacity have been adopted for

the years 2020 and 2030. They are 42% and 52%

respectively. For the other years, a linear

extrapolation has been established. This gives a

37% for 2015; 47% in 2025; 57% in 2035; 62% in

2040; 67% in 2047 and 72% in 2050.

Candidate

renewable

technologies

- Onshore wind

(WIND)

- Photovoltaic utility

(PV_UTIL)

- Concentrated Solar

Power (CSP)

- Hydropower plants

(HYDRO_PP)

Flexible

backup

echnologies

- Gas power plants

developed before

2010 supplied through

GME or Tendrara gas.

- New natural gas

plants to be supplied

through regasification

terminal.

- Pumped Hydro

storages (PHS)

- Old and new gas

power plants fed by

Gazuduc.

- Pumped Hydro

storages (PHS)

Discount

rate

Minimum

reserve

margin

15% after 2015 and 20% starting from 2020.

Emission

Limits

Nan

3.1 Energy System of Reference of Our

Study

In the framework of energy modelling, a graphical

network representation of all the technical activities

needed to supply various forms of energy to the end-

use activities is often used, known as the Reference

Energy System (RES) (Hermelee, 1979). The RES

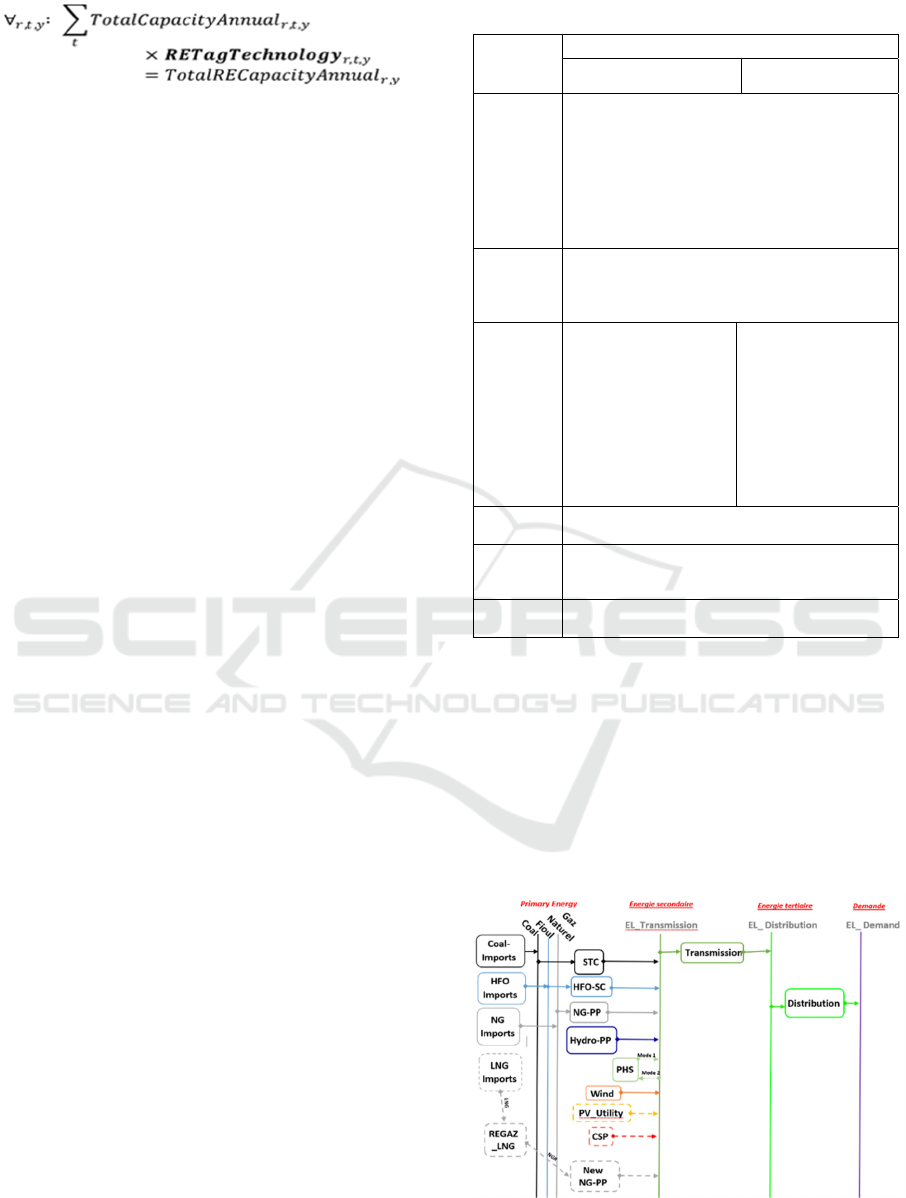
adopted for our case is shown in (Figure 1).

Figure 1: Electricity supply model of Morocco's or the

reference energy system.

∀

,,

∶ 𝑇𝑜𝑡𝑎𝑙𝐶𝑎𝑝𝑎𝑐𝑖𝑡𝑦𝐴𝑛𝑛𝑢𝑎𝑙

,,



 𝑷𝒐𝒘𝒆𝒓𝑻𝒂𝒈𝑻𝒆𝒄𝒉𝒏𝒐𝒍𝒐𝒈𝒚

,,

 𝑇𝑜𝑡𝑎𝑙𝑃𝑜𝑤𝑒𝑟𝐶𝑎𝑝𝑎𝑐𝑖𝑡𝑦𝐴𝑛𝑛𝑢𝑎𝑙

,

(4)

(3)

The Role of Gas to Power in Supporting Large-scale Renewable Energy Integration in Morocco: Insights from Optimization through

Long-term Bottom-up Modelling

329

The model takes into account the Moroccan

power generation fleet at the end of 2009

(http://www.one.org.ma). Table 2 presents additional

information on the installed capacity of the Moroccan

electricity system during this period. In the RES

shown in Figure 1, the technologies and energy

carriers represented in a continuous line represent the

technologies in the system at the beginning of the

modeling process. Technologies and energy carriers

represented in split line represent proposed

technologies and energy carriers to meet the demand

throughout the modelling period.

For the first scenario, all the GFPPs will use only

regasified LNG. Under the second scenario, all

GFPPs will be supplied directly by pipeline, and there

will be no LNG imports

Table 2: Installed capacity at the end of 2009 in Morocco.

Power plants Capacity in MW

Hydraulic Power Plants

1 284

Pumped Hydro Storages

464

Steam Heat Plants (Coal Fired)

465

Steam Heat Plants (Oil Fired)

600

Coal-Fired Power Plant

1 320

CCGT/ ISCC

680

WIND

222

TOTAL

5035

3.2 Inputs and Data

Several inputs and data were adopted for the

modelling of the Moroccan power system by

OSeMOSYS. Firstly, and in order to simulate the

seasonal and daily variability of the electricity

demand, together with the intermittent availability of

renewable energy sources, we divided the model

years into 6-time steps (3 seasons: Winter,

Intermediate and Summer, and two sub-periods:

Night and Day). For demand, we are referring to the

data provided by the ONEE in its various activity

reports between 2010 and 2018

(http://www.one.org.ma)

. Concerning the electricity

demand between 2020 and 2050, we relied on the

analysis of the 2050 energy demand made by the

Moroccan Ministry of Energy and Mines

(https://www.mem.gov.ma).

This type of analysis is

highly dependent on the capital costs of the

technologies under consideration. Similar

considerations apply to fuel costs, operations and

maintenance (O&M) costs and non-operating costs.

These costs have been identified from several sources

(https://taqamorocco.ma)(https://atb.nrel.gov)(https:/

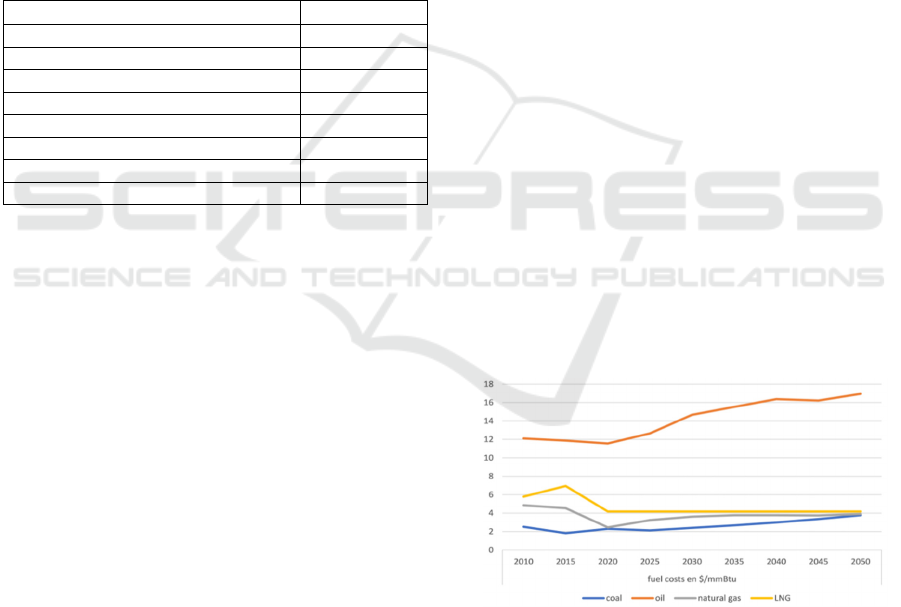
/energydata.info). Figures (2, 3 and 4) show the fuel

costs, capital costs and fixed operating and

maintenance costs of the main technologies used in

the analysis.

4 RESULTS

The modelling study we conducted showed that the

most economically advantageous scenario for

Morocco is the 2

one. Morocco will save more than

17 billion dollars by adopting scenario 2 (

Figure

5).

The 2

scenario is also the best one regarding

greenhouse gas emissions. It prevents more than 12

million tons of CO2 equivalent emissions. (Figure.6)

The comparison between the 1

and 2

scenarios

highlights the dominant role of Pumped Hydro

Storage (PHS)

(Figure.7).

In fact, in the 1

scenario,

the model considered that it was more optimal to

invest in PHS to deal with the intermittent nature of

RES than to invest in the construction and

commissioning of new power plants fuelled by LNG.

In addition, this scenario shows that it is only after

the year 2040 when the share of renewables will have

exceeded 62%, that new GFPP could become

interesting.

One explanation for this is that the development

of GFPPs and their supply of regasified LNG requires

significant investment in terms of infrastructure. Wile

the implementation of PHS does not require as much

capital investment.

For the second scenario (Figure 8), natural gas is

used the most to cope with the intermittency of

renewables in the first years of their installed capacity

development. Then, as their share increases, there is

a balance between PHS and CCGT/ISGC.

Figure 2: Energy Prices by Source (2010-2050)

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

330

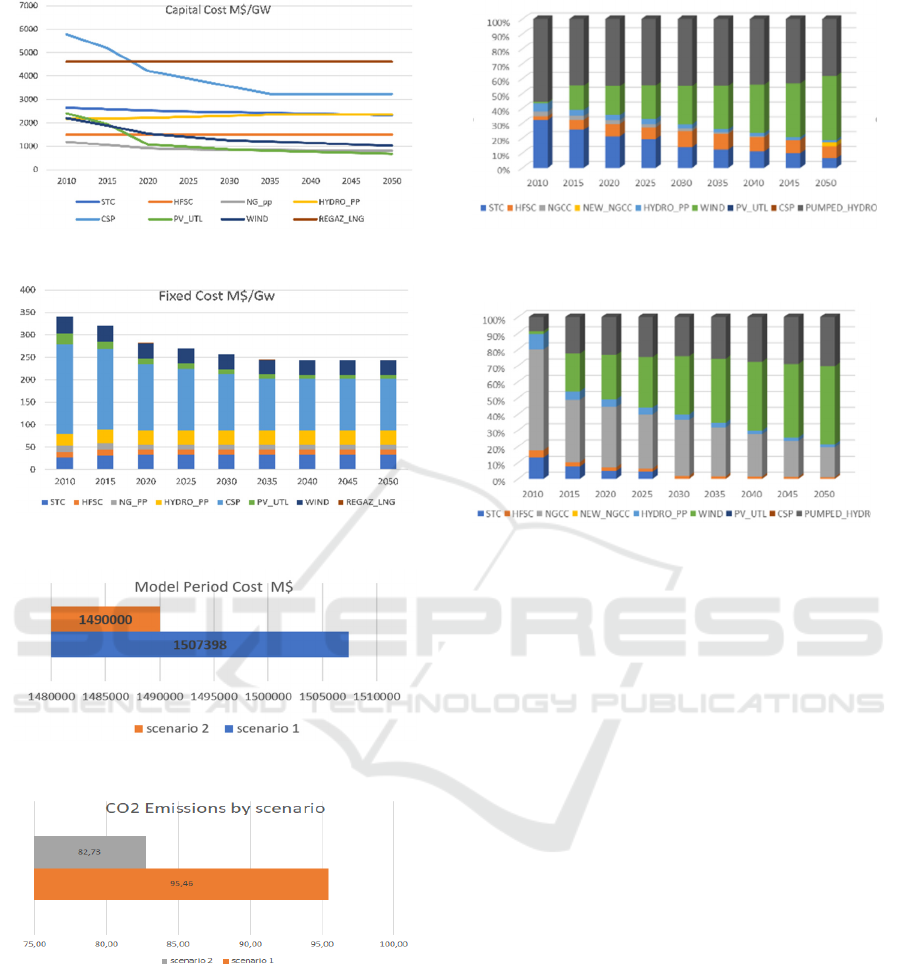
Figure 3: Capital cost of the technologies (2010-2050).

Figure 4: Fixed cost of the technologies (2010-2050).

Figure 5: Total discounted cost of the scenarios.

Figure 6: CO2 Emissions by scenario

Figure 7: Share of Total Annual Capacity by Technology

(Scenario 1).

Figure 8: Share of Total Annual Capacity by Technology

(Scenario 2)

5 CONCLUSION

This study has shown that the choice of importing

LNG and regasifying it to supply new GFPPs for

power generation is not necessarily the optimal

solution to provide flexibility to renewable

generation. We observe that the option of developing

PHS is more interesting for Morocco, especially with

its geological capacities allowing the country to have

sufficient conditions for the development of PHS on

a large scale. On the other hand, it would be

interesting for Morocco to negotiate its natural gas

supply through the GME with one of its neighbours,

Spain or Algeria. It would also be interesting for

Morocco to develop gas infrastructure around this

pipeline, which would allow it to benefit from the

Morocco-Nigeria gas pipeline project. Future

research may consider evaluating the concept of

floating storage and regasification units (FSRUs).

FSRUs are becoming increasingly relevant as they

can reduce the costs associated with gas terminal

development.

The Role of Gas to Power in Supporting Large-scale Renewable Energy Integration in Morocco: Insights from Optimization through

Long-term Bottom-up Modelling

331

6 FURTHER RESEARCH

Our future research will address other issues related

to the Moroccan energy system. For that, we will

proceed to a new configuration of the model. We will

consider new parameters such as the exchange of

electricity with neighbouring countries and the

possibility of exporting electricity. We will try to

build a machine learning that estimates most of the

parameters needs by the model. We will also look at

the storage capacities needed to support the

development of renewable energies.

REFERENCES

Dhakouani, A., Znouda, E., & Bouden, C. (2019). Impacts

of energy efficiency policies on the integration of

renewable energy. Energy Policy, 133, 110922.

Gasparatos, A., Doll, C. N., Esteban, M., Ahmed, A., &

Olang, T. A. (2017). Renewable energy and

biodiversity: Implications for transitioning to a Green

Economy. Renewable and Sustainable Energy

Reviews, 70, 161-184.

Hermelee, A. L. A. N. (1979). Regional reference energy

systems: electric utility applications (No. BNL-50962).

Brookhaven National Lab., Upton, NY (USA).

National Center for Analysis of Energy Systems.

Howells, M., Rogner, H., Strachan, N., Heaps, C.,

Huntington, H., Kypreos, S., & Roehrl, A. (2011).

OSeMOSYS: the open-source energy modeling system:

an introduction to its ethos, structure and development.

Energy Policy, 39(10), 5850-5870.

Ibrahim, T. K., Mohammed, M. K., Awad, O. I., Abdalla,

A. N., Basrawi, F., Mohammed, M. N., ... & Mamat, R.

(2018). A comprehensive review on the exergy analysis

of combined cycle power plants. Renewable and

Sustainable Energy Reviews, 90, 835-850.

McPherson, M., & Tahseen, S. (2018). Deploying storage

assets to facilitate variable renewable energy

integration: The impacts of grid flexibility, renewable

penetration, and market structure. Energy, 145, 856-

870.

Nfaoui, H., & Sayigh, A. (2020). New horizons for

renewable energies in Morocco and Africa. In

Renewable Energy and Sustainable Buildings (pp. 551-

565). Springer, Cham.

Sarkis, J., & Tamarkin, M. (2008). Real options analysis for

renewable energy technologies in a GHG emissions

trading environment. In Emissions trading (pp. 103-

119). Springer, New York, NY.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

332