Decomposition of Classification Context as a Tool for Big Data

Management

Xenia Naidenova

Military medical academy, Lebedev Street, Saint Petersburg, Russia

Keywords: Big data, formal concept, classification context, context decomposition, good classification tests.

Abstract: The paper considers a problem of generating all classification Good Maximally Redundant Tests (GMRTs)

as the set of all maximal elements of the formal concept lattice generated over a classification context. The

number of concepts is exponential in the size of input context and decomposing contexts is one of the methods

to decrease the computational complexity of inferring GMRTs. Three kinds of sub-contexts are defined:

attributive, object and object-attributive ones. The rules of reducing sub-contexts are given. The properties of

the sub-contexts are analysed related to the fact that the set of all GMRTs in a classification context is a

completely separating system. Some strategies are considered for choosing sub-contexts based on the

definition of essential objects and attribute values. The rules of the decomposition proposed imply

constructing some incremental procedures to construct GMRTs. Two methods of pre-processing the formal

contexts greatly decreasing the computational complexity of inferring GMRTs are proposed: finding the

number of subtasks to be solved (the number of essential values) and the initial content of the set of GMRTs.

Some unsolved problems difficult for analytical investigations have been formulated. The decomposition

proposed can be fruitful in processing big data based on machine learning algorithm.

1 INTRODUCTION

The paper considers a symbolic machine learning

problem of generating all classification Good

Maximally Redundant Tests (GMRTs) as the set of

all maximal elements of the formal concept lattice

generated over a classification context. GMRTs

provides a basis for mining logical rules from data.

The number of concepts is exponential in the size of

input context and decomposing contexts is one of the

methods to decrease the computational complexity of

inferring GMRTs.

Unfortunately, not enough attention has been paid

to the methods of formal context decomposition due

to its analytical difficulty and, at least in part, by the

consideration that having good algorithm for lattice

construction is more important than decomposing

formal contexts in sub-contexts.

Our attention has been attracted to the following

methods of decomposing formal contexts described

in literature. The first one has been developed by Ch.

Mongush and V. Bykova, 2019. In this method, some

fragments of the initial context are partitioned into the

https://orcid.org/0000-0003-2377-7093

so-called boxes. The division of context into boxes is

“safety”, i. e. the formal concepts are not lost and new

formal concepts do not arise during the

decomposition. It is proved that the number of boxes

arising at each iteration of the decomposition is equal

to the number of unit elements of the 0,1-matrix

representing the initial formal context. The number of

boxes at each iteration can be reduced by constructing

mutually disjoint chains of boxes.

The second method of decomposition has been

proposed by T. Qian, L. Wei, J.-J. Qi, 2017. This

method is based on sub-contexts, closed relation and

pairwise non-inclusion covering on the attribute set.

The authors provide the method and algorithm of

constructing the concept lattice based on a

decomposition theory proposed. They also consider

the similar decomposition theory based on the object

set. Combining the above two decompositions is

used.

In our paper, three kinds of sub-contexts are

defined: attributive, object and object-attributive

ones. The rules of forming and reducing sub-contexts

are given. The properties of the determined sub-

Naidenova, X.

Decomposition of Classiﬁcation Context as a Tool for Big Data Management.

DOI: 10.5220/0010732800003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 295-300

ISBN: 978-989-758-559-3

295

contexts are analyzed related to considering all the

GMRTs for a given formal context as a completely

separating system of the subsets of a finite set

(Dickson, 1969). The definition of GMRTs is given

via two interrelated Sperner systems (Sperner, 1928):

the family of test’s intents and the family of test’s

extents. Some strategies are considered for choosing

sub-contexts in inferring GMRTs based on the

definition of essential object and value of attribute.

We formulate, in conclusion, some very important but

not yet investigated problems connected with the

formal context decomposition considered in this

paper.

The paper is organized as follows: Section 2

describes GMRT as a formal concept, Section 3 gives

the rules of decomposing classification contexts,

Section 4 gives the rules for reducing classification

contexts, Section 5 represents some strategies for

decomposing contexts. We complete with a short

conclusion.

2 DEFINITION OF GMRT

A classification context is a set (G, M, I, AClass),

where G is a set of objects, M is a set of attribute

values (values, for short), I = GM is a binary relation

between G and M, and AClass is a set of additional

attributes by values of which the given set of objects

is partitioned into disjoint classes.

Denote a description of object g ∈ G by δ(g), and

descriptions of positive and negative objects by D+ =

{δ(g)| g ∈ G+} and D− = {δ(g)| g ∈ G−}, respectively.

The Galois connection (Ore, 1944) between the

ordered sets (2

, ⊆) and (2

, ⊆), is defined by the

following mappings called derivation operators

(Ganter & Wille, 1999): for A ⊆ G and B ⊆ M, val(A)

= ⋂δ(g), g∈A, and obj(B) = {g|B ⊆ δ(g), g ∈ G}.

In our approach, there are two closure operators:

generalization_of(B) = val(obj(B)) and

generalization_of(A) = obj(val(A)). A is closed if A

= obj(val(A)) and B is closed if B = val(obj(B)). If

(val(A) = B) & (obj(B) = A), then a pair (A, B) is

called a formal concept (Ganter & Wille, 1999),

subsets A and B of which are called concept extent

and intent, respectively. According to the values of a

goal attribute K from AClass, we get some possible

forms of the formal contexts: Kϵ := (Gϵ, M, Iϵ ) and

Iϵ := I ∩ (Gϵ × M), where ϵ ∈ rng(K), rng(K) = {+,

−}. A classification context K± (G±, K, G± × K) is

formed after adding the classification attribute. A

context K± is illustrated by Table 1.

Definition 1. A diagnostic test (DT) for K+ is a

pair (A, B) such that B ⊆ M, A = obj(B) ̸= ∅, A ⊆ G+,

and obj(B)∩G− = ∅.

Table 1: An example of classification context

No Height Color of

hai

Color of

K1 K2

1 Small Blon

Blue + +

2 Small Brown Blue

−

3 Tall Brown Hazel

−

4 Tall Blond Hazel

− −

5 Tall Brown Blue

− −

6 Small Blond Hazel

− −

7 Tall Red Blue +

−

8 Tall Blond Blue +

−

Definition 2. A diagnostic test (A, B) for K+ is

said to be maximally redundant if obj(B ∪ m) ⊂ A for

all m ∈ M \ B.

Definition 3. A diagnostic test (A, B) for K+ is

said to be good iff any extension A1 = A ∪ i, i ∈ G+

\ A, implies that (A1, val(A1)) is not a DT for K+.

A maximally redundant DT which is

simultaneously good is called a good maximally

redundant DT. Any object description (g) is a

maximally redundant collection of values because for

any value m  (g), m  M, obj((g)  m) = .

Definitions of tests (as well as other definitions),

associated with K+, are applicable to K−. In general,

a set B is not closed for DT (A, B), consequently, DT

is not necessarily a formal concept. A GMRT can be

regarded as a special type of formal concept

[Naidenova, 2012].

An example in Table 1: ({1, 8},{Blond, Blue}) is

a GMRT for K1 = + (K1+), ({4, 6},{Blond, Hazel})

is a DT for K1 = − (K1−) but not a good one, and ({3,

4, 6}, {Hazel}) is a GMRT for K1−.

2.1 GMRT as a Sperner System

It is clear that the set of intents of all diagnostic tests

for K+ (call it ‘DT(+)) is the set of all the collections

t of values for which the condition obj(t)  G+ is true.

The set DT(+) is the ordered set w. r. t. inclusion

relation. This consideration leads to the next

definition of good diagnostic test.

Definition 4. A diagnostic test (A, B) for K+ is

said to be good iff obj(B)  G+ and, simultaneously,

the condition obj(B)  obj(B*)  G+ is not satisfied

for any B*, B* M, such that B*  B.

This definition means that the family of the

extents of all good tests for K+ is a family of maximal

elements of DT(+) and it is therefore a Sperner system

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

296

(Sperner, 1928). On this basis, we can give the

following definition for the GMRTs.

Definition 5. To find all the GMRTs for a given

K+ means to construct a family PS of subsets s1, s2,

…, sj, …, snp of G+ such that:

1) PS is a Sperner system;

2) each sj is a maximal set in the sense that adding

to it any object g such that g  sj, g  G+ implies that

obj(val(sj  g)) ̸⊆ δ(g), ∀g ∈ G+.

3) The set of all GMRTs is determined as follows:

{(sj, val(sj)), sj  PS, j = 1, …, np}, where {val(sj)}

is also a Sperner System.

Some algorithms NIAGaRa and DIAGaRa to find

all the GMRTs in a classification context are

described in (Naidenova, 2006). The Diagnostic Test

Machine (DTM) is given in (Naidenova & Shagalov,

2009). The experiment conducted with the publicly

available database (Schlimmer, 1987) of 8124

mushrooms showed that the result of the DTM turned

out to be 97,5% w.r.t. classification accuracy.

3 RULES OF DECOMPOSING

CLASSIFICATION CONTEXT

To transform inferring GMRTs into an incremental

process, we introduce three kinds of subtasks for K+

(K−), called subtasks of the first, second and third

kind, respectively:

1. Given a positive object g, find all GMRTs

(obj(B), B) for K+ such that B is contained in δ(g). In

the general case, instead of δ(g) we can consider any

subset of values B1, such that B1 ⊆ M, obj(B1) ̸= ∅,

B1 ̸⊆ δ(g), ∀g ∈ G−.

2. Given a non-empty set of values B ⊆ M such

that (obj(B), B) is not a DT for positive objects, find

all GMRTs (obj(B1), B1) such that B ⊂ B1.

3. Given a value m  M and object g  G+, find

all the GMRTs (X, val(X)) such that X  obj(m),

val(X)  (g).

One can easily see that each subtask of the first,

second or third kind is simpler than the initial one,

because each object description contains only some

subset of values from M and each subset B ⊆ M

appears only in a part of the set of objects

descriptions.

Accordingly, we define three kinds of sub-

contexts of a given classification context called the

object, attribute value and attribute value-object (or

object-attribute value) projections, respectively. If

(G, M, I) is a context and if N ⊆ G, and H ⊆ M, then

(N, H, I ∩ N × H) is called a sub-context of (G, M, I).

Definition 6 (Naidenova & Parkhomenko, 2020).

The object projection ψ(K+, g) returns the sub-

context (N, δ(g), J), where N = {n ∈ G+ | n satisfies

(δ(n) ∩ δ(g) is the intent of a test for K+)}, J = I+ ∩

(N × δ(g)).

Definition 7 (Naidenova & Parkhomenko, 2020).

The attribute value projection ψ(K+, B) returns the

sub-context (N, B, J), where N = {n ∈ G+ | n satisfies

(B ⊆ δ(n))}, J = I+ ∩ (N × B).

Definition 8. The attribute value-object

projection ψ(K+, m, g) is the intersection of two

projections: attribute value projection ψ(K+, m) and

object projection ψ(K+, g).

In the case of negative objects, symbol + is

replaced by symbol − and vice versa.

The decomposition of inferring GMRTs into the

subtasks requires the following actions:

1. Select an object, attribute value or a pair of

attribute value - object to form a subtask.

2. Form the subtask (projection).

3. Reduce the subtask (projection).

4. Solve the subtask.

5. Reduce the parent classification context when

the subtask is over.

4 RULES OF REDUCING

CLASSIFICATION CONTEXT

It is essentially that the projection is simply a subset

A* of objects defined on a certain restricted subset B*

of values.

Let objϵ(m) be a set of positive or negative objects

{obj(m) ∩ Gϵ}, where ϵ ∈ rng(K). Then for any B ⊆

M objϵ(B) = ⋂m∈B objϵ(m), where ϵ ∈ rng(K).

Let Sgood+ be the partially ordered set of

obj+(m), m ∈ M satisfying the condition that

(obj+(m), val(obj+(m))) is a current GMRT (in any

algorithm of inferring GMRTs) for K+. Sgood− for

K− is defined based on obj− (m).

Essentially, the process of forming Sgood is an

incremental procedure of finding all maximal

elements of a partially ordered (by the inclusion

relation) set. It is based on topological sorting of

partially ordered sets. Thus, when the algorithm is

over, Sgood contains the extents of all the GMRTs for

K+ (for K−) and only them (Naidenova &

Parkhomenko, 2020). The operation of inserting an

element A∗ into Sgood (in the algorithm formSgood

(Naidenova & Parkhomenko, 2020) under the

lexicographical ordering of these sets is reduced to

lexicographically sorting a sequence of k-element

collections of integers. A sequence of n-collections

Decomposition of Classiﬁcation Context as a Tool for Big Data Management

297

whose components are represented by integers from

1 to |M|, is sorted in time of O(|M| + L), where L is

the sum of lengths of all the collections of this

sequence (Hopcroft et al., 1975). Consequently, if

Lgood is the sum of lengths of all the collections A of

Sgood, then the time complexity of inserting an

element A∗ into Sgood is of order O(|M| + Lgood).

The set Tgood of all the GMRTs is obtained as

follows: Tgood = {t | t = (A, val(A)), A ∈ Sgood}

It is useful to introduce the characteristic W(m),

m  B* named by the weight of m in the projection:

W(m) = obj+(m) or W(m) = obj− (m) is the

number of positive (negative) examples of the

projection containing m. Let WMIN be the minimal

permissible value of the weight.

The following reduction rules are determined:

Rule 1. For each value m in the projection, the

weight W(m) is determined and if the weight is less

than WMIN, then the value m is deleted from the

projection.

Rule 2. We can delete the value m if W(m) is

equal to WMIN and (obj+(m), val(obj+(m)) is not a

test; in this case m will not appear in a GMRT with

the weight of its intent equal to or greater than

WMIN.

Rule 3. The value m can be deleted from the

projection if obj+(m)  s’ for some s’  Sgood+.

Rule 4. If obj(val(obj+(A)) = obj+(A), then the

value A is deleted from the projection and obj+(A) is

stored in SGOOD+ if obj+(A) corresponds to a

GMRT at the current step.

Rule 5. If at least one value has been deleted from

the projection, then the following its reduction is

necessary. The reduction consists of deleting the

elements of projection that do not correspond to tests

(as a result of previous eliminating values). If, under

reduction, at least one element has been deleted from

the projection, then applying Rule 1 – Rule 5 are

repeated.

Algorithms for GMRTs inferring based on these

rules have been described in (Naidenova, 2006;

Naidenova & Parkhomenko, 2020].

Rule 1 is based on the following Theorem 1

(Naidenova, 2006):

THEOREM 1.

Let m  M, (Y, X) be a maximally redundant test

for G+ and obj(m)  obj(X) =Y. Then m does not

belong to the intent of any maximally redundant good

test for G+ different from X.

Consider an example of reducing a sub-context

for K−, where − is the value of K2 in Table 1. The

result of the attribute value projection ψ(K−, Tall) is

in Table 2. In Table 2, obj−(Blue) = {5, 7, 8}, but

obj(Tall, Blue) = {5, 7, 8}, and, consequently,

(obj(Tall, Blue),{Tall, Blue}) is a DT for K2 = −. We

have also obj−(Brown) = {5} and obj−(Red) = {7},

but both {5} ⊂ {5, 7, 8} and {7} ⊂ {5, 7, 8}, and,

consequently, there does not exist any good test

which contains simultaneously the values ‘‘Tall’’ and

‘‘Brown’’. ‘‘Red’’ is not a good test for K−. Then one

can delete ‘‘Blue’’, ‘‘Red’’ and ‘‘Brown’’ from the

sub-context. The result is shown in Table 3. Note, that

the descriptions of objects 5 and 7 are included in the

description of object 3 for K+ (see Table 1) and these

objects are deleted. Objects 4 and 8 form the extent of

a test for K− equal to (obj(Tall, Blond),{Tall,

Blond}).

Table 2: Attribute-value projection for K2 = − in Table 1.

No Height Color of

hai

Color of

4TallBlon

Hazel

5TallBrown Blue

7TallRe

Blue

8TallBlon

Blue

Table 3: The projection of Table 2 after reducing.

No Height Color of

hai

Color of

eyes

4TallBlon

Hazel

5Tall

7Tall

8TallBlon

5 STRATEGIES OF

DECOMPOSING

The advantage of a projection-forming operation is to

increase the likelihood of finding all the GMRTs

(contained in the projection) by only one passing of

it. By limiting the number of tests contained in the

projection, we increase the probability of their

separation, that is, the probability of finding exactly

those attributes (values) or objects that will enter only

one test in the projection considered. Let's explain this

idea.

Any subset t1,…, ti, tj,.. , tk of GMRTs and

corresponding to it subset val(t1), val(t2), …, val(ti),

val(tj),...., val(tk), where t1,…, ti, tj,.. , tk are intents

of GMRTs are two systems of completely separating

subsets. It means that for any pair (ti, tj) there is such

a pair of values (mq, mf) that mq occurs in ti and does

not occur in tj, and mf occurs in tj and is not found in

ti. Analogously, for any pair of val(ti), val (tj), there

is such a pair of objects (gq, gf), that gq is found in

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

298

val(ti) and is not found in val(tj), and gf is found in

val(tj) and is not found in val(ti).

The phenomenon of a completely separating

system of GMRTS can be illustrated in a projection

in Table 4 (this example is extracted from a real task).

In this example, the projections t9, t12 of objects

9 and 12 do not contain any intents of tests, we can

delete the corresponding lines. The result is in Table

5, where:

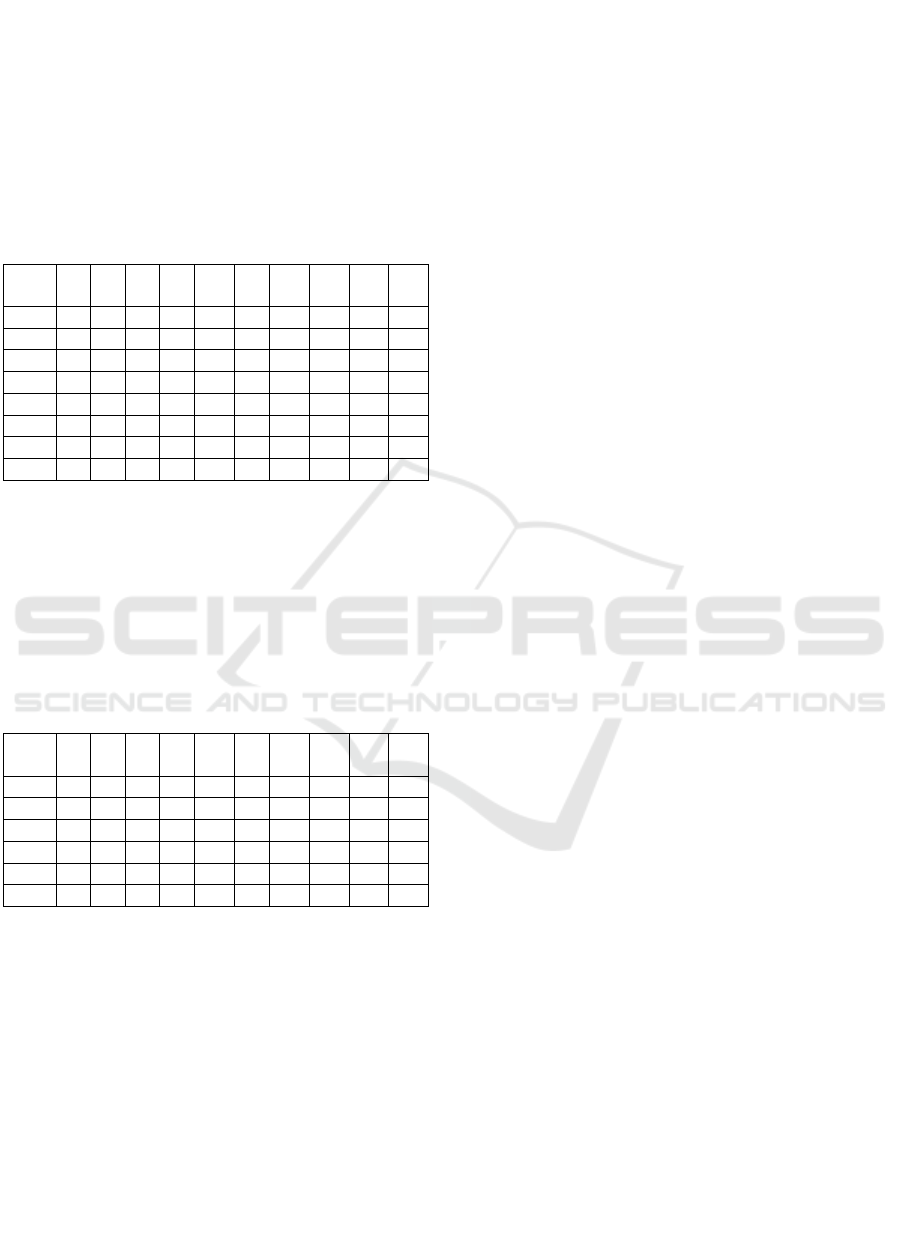
Table 4: Example of a projection.

t\A A

8 1 1 1 1 1 1 1 1 1 1

6 0 0 1 0 0 0 0 1 1 0

4 0 1 1 0 0 1 0 1 1 0

7 1 1 0 0 0 1 0 1 0 1

9 0 0 0 0 0 0 1 1 1 1

11 1 0 1 0 0 0 1 1 1 1

10 1 1 0 1 1 0 0 1 1 0

12 1 0 0 0 0 0 0 1 1 0

Obj+(m7) = {4,6,8,11}, val({4,6,8,11}) = {m7

m20 m21 } corresponds to a test,

Obj+(m22) = {7,8,11}, val({7,8,11}) = {m3 m20

m22} corresponds to a test,

obj(m13) = obj(A*) = {8,10}, valt({8,10}) = {m3

m6 m* m13 m20 m21 } corresponds to a test.

Delete m22, m7, m13, and m* and reducing the

projection. After reducing, this subtask is over.

Table 5: The projection after reducing.

t\A A

8 1 1 1 1 1 1 1 1 1 1

6 0 0 1 0 0 0 0 1 1 0

4 0 1 1 0 0 1 0 1 1 0

7 1 1 0 0 0 1 0 1 0 1

11 1 0 1 0 0 0 1 1 1 1

10 1 1 0 1 1 0 0 1 1 0

All the GMRTs in this projection have been

revealed by only one passing.

Before entering into the details of choosing

projections when decomposing the classification

contexts, we need the following definitions of

essential value and essential object.

Definition 9. Let B be a set of values such that

(obj(B), B) is a DT for K+ (K−). The value m ∈ B, B

⊆ M is essential in B if (obj(B \ m), (B \ m)) is not a

DT for a given set of objects.

Generally, we are interested in finding one of the

maximal subsets sbmax(B) ⊂ B such that (obj(B), B)

is a DT but (obj(sbmax(B)), sbmax(B)) is not a DT

for a given set of positive (negative) objects. Then

sbmin(B) = B \ sbmax(B) is one of minimal subsets

of essential values in B.

The number of subtasks of the second kind is

determined by the number of essential values in M or

its subsets. Let the set Lev be equal to sbmin(M).

Proposition 1. Each essential value is included in

at least one positive object description.

Proof of Proposition 1. Assume that for an object

description δ(g), g ∈ G+, we have δ(g) ∩ Lev = ∅.

Then δ(g) ⊆ M \ Lev. But M \ Lev is included in at

least one of the negative object descriptions and,

consequently, δ(g) also possesses this property. But

this contradicts the fact that δ(g) is the description of

a positive object.

Corollary 1 (of Proposition 1). If B ⊆ M and B ∩

Lev = ∅, then (obj(B), B) is not a test for K+.

Corollary 2 (of Proposition 1). For finding all the

GMRTs contained in K+, it is sufficient to find all the

GMRTs only for sub-contexts associated with

essential values in Lev for M.

Definition 10. Let A ⊆ G+, assume that (A,

val(A)) is not a DT for K+ (K−). The object g, g ∈ A

is said to be an essential in A, if (A\g, val(A\g))

proves to be a DT for a given set of positive objects.

Generally, we are interested in finding one of the

maximal subsets sbmax(A) ⊂ A such that (A, val(A))

is not a DT but (sbmax(A), val(sbmax(A))) is a DT

for K+.

It is clear that if m enters into the intent of a test

for K+, then its extent is in obj+(m). It is theoretically

possible to find one of the maximal A* subsets of

obj+(m), such that (A*, val(A*)) is a DT for K+ (K−).

This operation allows to find the initial content of

Sgood (Naidenova & Parkhomenko, 2020).

The quasi-minimal subset of essential values in M

and quasi-minimal subset of essential objects in

obj+(m), for all mM can be found by a simple

procedure described in (Naidenova & Parkhomenko,

2020). This procedure is of linear computational

complexity w.r.t. the cardinality of M.

The process of using the decomposition of formal

context based on choosing essential object or value to

form the projections consists in the following steps:

Choose an essential value (object) in a projection;

forming the corresponding sub-projection;

Find all the GMRTs in the sub-projection (sub-

context);

Delete value (object) from the parental context;

Reducing the parental context;

Determine whether the procedure of finding all

the GMRTs is over.

Using the third decomposition based on selecting

an essential object and an essential value

simultaneously is effective when this value enters the

Decomposition of Classiﬁcation Context as a Tool for Big Data Management

299

quasi-minimal set of essential values in the

description of this selected object and this essential

object enters the quasi-minimal set of essential

objects for this selected value.

If the essential value is the only one w.r.t. the

selected object, then one can remove this object from

consideration after the subtask is resolved. Similarly,

if the essential object is the only one related to

selected value, then one can remove this value from

consideration after the subtask is over. These

deletions result in a very effective reduction in the

formal context considered.

Another advantage of selecting essential values

and objects simultaneously is the fact that this way

greatly supports the property of the complete

separating the families of extents and intents of

GMRTs.

It is important to formulate some unsolved and

nontrivial problems related to the decomposition

considered in this paper. These problems are:

How to recognize a situation that current formal

classification context contains only the GMRTs

already obtained (current context does not contain

any new GMRTs)?

How to evaluate the number of recurrences

necessary to resolve a subtask in inferring GMRTs?

(if we use a recursive algorithm like DIAGARA)?

How to evaluate the perspective of a selected sub-

context with respect to finding any new GMRT?

These problems are interconnected and the

subject of our further research. The effectiveness of

the decomposition depends on the properties of the

initial classification context (initial data). Now we

can propose some characteristics of data (contexts

and sub-contexts) useful for choosing a projection:

the number of objects, the number of attribute values,

the number of the GMRTs already obtained and

covered by this projection. It may be expedient to

select essential object with the smallest number of

entering elements of Sgood and, simultaneously, with

the largest number of entering obj+(m), mM.

Our experiments show that the number of

subtasks to be solved always proved to be smaller

than the number of essential values.

6 CONCLUSION

In this paper, we considered one of the possible

methods for decomposing classification contexts to

find all GMRTs in them. We gave the definitions of

three type of decomposing and, accordingly, three

type of context projections and subtasks of inferring

GMRTs. We revealed the role of finding essential

attribute values and objects for choosing and

resolving subtasks. Some ways to select the

projections were given in this paper. Two methods of

preprocessing the formal contexts (sub-contexts)

greatly decreasing the computational complexity of

inferring GMRTS are proposed: finding the number

of subtasks to be solved (the number of essential

values) and the initial content of the set Sgood. Some

unsolved problems difficult for analytical

investigations have been formulated. Currently,

experimental studies of the decompositions’

computational effectiveness on various data sets are

conducted.

REFERENCES

Bykova, V., Mongush, Ch., 2019. Decompositional

approach to research of formal contexts. Applied

Discrete Mathematics, 44, 113–126 DOI:

https://doi.org/10.17223/20710410/44/9

Dickson, T.J., 1969. On a problem concerning separating

systems of a finite set. J. Combin. Theory 7(3), 191-

196.

Ganter, B. and Wille, R., 1999. Formal Concept Analysis:

Mathematical Foundations, Springer, Berlin.

Hopcroft, J., Ullman, J., and Aho, A., 1975. The Design and

Analysis of Computer Algorithms, Addison-Wesley.

Naidenova, X. and Parkhomenko, V., 2020. Contribution to

attribute and object sub-contexts in inferring good

maximally redundant tests. Discrete Applied

Mathematics 273, 217–231.

Naidenova, X. and Shagalov, V., 2009. Diagnostic test

machine. In Proceedings of the ICL 2009, Kassel

University Press, pp. 79–84.

Naidenova, X., 2012. Good classification tests as formal

concepts. In F. Domenach, D. Ignatov, J. Poelmans

(Eds.), LNAI 7278, pp. 211–226.

Naidenova, X., 2006. An incremental learning algorithm

for inferring logical rules from examples in the

framework of the common reasoning process. In E.

Triantaphyllou, G. Felici (Eds.), Data Mining and

Knowledge Discovery Approaches Based on Rule

Induction Techniques, in Massive Comp., vol. 6,

Springer, pp. 89–147.

Ore, O., 1944. Galois connections. Trans. Amer. Math. Soc.

55,494–513.

Qian, T., Wei, L., and Qi, J.-J., 2017. Decomposition

methods of formal contexts to construct concept

lattices. International Journal of Machine Learning and

Cybernetics 8, 95-108.

Schlimmer, J.C., 1987. Concept acquisition through

representational adjustment (Ph.D. thesis), University

of California, Irvine.

Sperner, E., 1928. Ein Satz über Untermengen einer

endlichen Menge. Mathematische Zeitschrift, 27(1):

544–548.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

300